Условие - Reshaem.Net
реклама
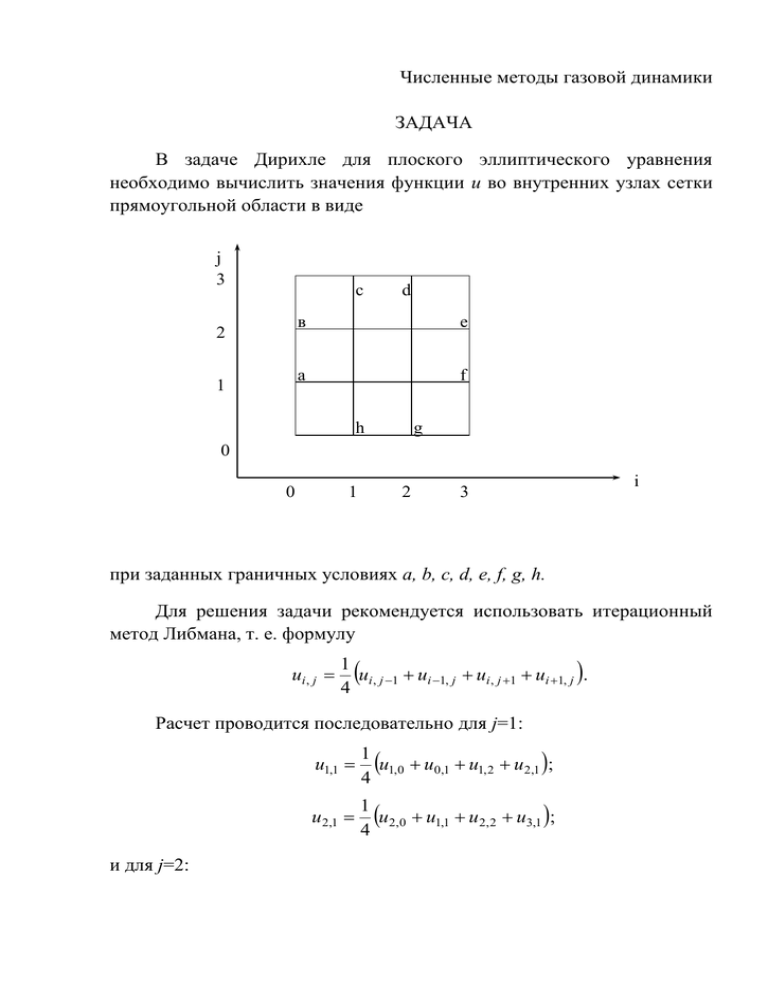
Численные методы газовой динамики ЗАДАЧА В задаче Дирихле для плоского эллиптического уравнения необходимо вычислить значения функции u во внутренних узлах сетки прямоугольной области в виде j 3 с 2 1 d в e а f h g 0 0 1 2 3 i при заданных граничных условиях a, b, c, d, e, f, g, h. Для решения задачи рекомендуется использовать итерационный метод Либмана, т. е. формулу ui , j 1 ui, j 1 ui 1, j ui, j 1 ui 1, j . 4 Расчет проводится последовательно для j=1: и для j=2: u1,1 1 u1,0 u0,1 u1,2 u2,1 ; 4 u 2,1 1 u2,0 u1,1 u2,2 u3,1 ; 4 u1, 2 1 u1,1 u0,2 u1,3 u2,2 ; 4 u 2, 2 1 u2,1 u1,2 u12 ,3 u3,2 . 4 Очевидно, функции, содержащие в индексе число 0 или 3 равны соответствующим граничным условиям – их и следует подставлять в формулу. Значения функций с иными индексами следует принимать равными их значениям в предыдущем приближении. В нулевом приближении обычно принимают ui,0j 0 . Для этих условий в 1-ом приближении будем иметь u11,1 1 u1,0 u0,1 0 0; 4 u 21,1 1 u2,0 u1,1 0 u3,1 ; 4 u1(,12) 1 u1,1 u0,2 u1,3 0; 4 u 21,2 1 u2,1 u1,2 u2,3 u3,2 . 4 Здесь следует обратить внимание на то, что поскольку в первой строчке функция u11,1 уже выведена, то в последующих строках значение u11, 0 следует принимать равным, найденным в 1-ой строчке. Аналогично в последней строчке используется значение u1,3 , u 2 ,1 , u1, 2 из предыдущих строчек, т. е. найденные функции немедленно используются в дальнейших вычислениях. После определения функций в первом приближении переходим к выполнению второго приближения. Достаточность выполненных итераций определим сравнением результатов итераций max ui,nj ui,nj1 ui,nj 0,0001. ТАБЛИЦА ВАРИАНТОВ ГРАНИЧНЫХ УСЛОВИЙ Номер варианта 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 a 2 2 2 10 10 5 4 12 14 15 16 0 0 4 2 12 12 1 4 8 11 3 18 6 1 16 12 6 14 b 1 2 1 5 5 10 2 8 5 4 14 0 0 14 12 4 16 1 12 2 3 11 12 4 2 8 6 8 4 Значения граничных функций c d e f 1 2 2 1 0 0 0 0 1 2 4 5 0 0 0 0 0 0 1 2 2 1 0 0 1 0 0 1 1 2 0 0 2 1 1 2 1 2 1 4 6 0 0 0 0 1 0 1 15 2 2 15 2 1 1 2 0 0 0 0 1 2 2 1 1 1 1 1 0 0 1 1 12 4 2 1 1 2 2 2 2 1 3 13 1 2 13 2 6 1 1 0 1 2 2 1 4 6 6 4 4 2 1 1 2 1 1 2 3 1 1 3 1 2 2 1 g 1 0 5 0 0 1 0 0 0 1 2 0 0 1 2 1 0 10 1 0 1 0 0 5 1 2 1 1 0 h 2 0 4 0 0 2 2 0 0 1 1 0 0 1 1 1 0 5 2 0 0 1 0 4 1 4 1 1 0











