3.01 Изучение интерференции света с помощью

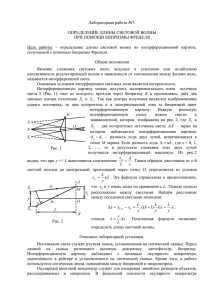
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ «МАМИ»
Кафедра
физики
ЛАБОРАТОРНАЯ РАБОТА 3.01
Изучение интерференции света с
помощью бипризмы Френеля
Москва
2005 г.
1
ЛАБОРАТОРНАЯ
РАБОТА 3.01
Изучение интерференции света с помощью бипризмы Френеля
Цель работы:
Определение расстояния между мнимыми источниками
в интерференционном опыте с бипризмой Френеля,
определение преломляющего угла призмы, длины
световой волны.
Теоретическое введение
В данной лабораторной работе для получения интерференционной картины
используют бипризму Френеля. Бипризма Френеля представляет собой две призмы с
очень малым преломляющим углом , сложенные основаниями. Схема установки для
получения интерференционной картины с помощью бипризмы Френеля показана на
рис. 1.1. Исходным источником света служит узкая щель S, расположенная
параллельно ребру тупого угла бипризмы и освещаемая монохроматическим светом
от осветителя S0 . От источника света S (щели) лучи падают на обе половинки
бипризмы и преломляются в ней. В результате преломления лучей образуются два
когерентных световых пучка, ограниченных лучами 1 и 1 и лучами 2 и 2, как бы
исходящих из мнимых источников S1 и S2. За бипризмой имеется область
пространства, в которой световые пучки, преломленные ее верхней и нижней
половинами, накладываются, образуя зону интерференции (на рис. 1.1 эта область
заштрихована).
2
Если в поле интерференции внести экран, то на нем будет видна интерференционная картина, которая будет иметь вид чередующихся светлых и темных
прямолинейных полос, параллельных ребру бипризмы. Результат сложения
колебаний, возбуждаемых в точке Р на экране волнами, приходящими от когерентных
источников S1 и S2, зависит от оптической разности хода   n2l2  n1l1, где n1 и n2
 показатели преломления сред; l1 и l2  расстояния (геометрические пути),
пройденные соответственно волнами 1 и 2 от источников света S1 и S2 до точки
наблюдения Р. Светлые полосы лежат в тех местах экрана, куда волны от источников
света S1 и S2 приходят с разностью хода, равной целому числу длин волн
  mλ m  1,2,3...,
(условие максимума),
(1.1)
темные - в тех местах, куда приходят волны с разностью хода, равной нечетному
числу длин полуволн:
  (2m  1)  λ/2
m  1,2,3...,
(условие минимума).
(1.2)
Расстояние между двумя соседними максимумами интенсивности называется
расстоянием между интерференционными полосами. Вычислим координаты светлых
полос, предполагая, что экран параллелен плоскости, в которой лежат источники
света S1 и S2 (рис. 1.2). Выберем на экране координатную ось х. Начало координат
поместим в точке О, относительно которой источники света S1 и S2
расположены симметрично.
рис. 1.2 видно, что
Из
l22  l 2  ( x  d / 2) 2 ,
l12  l 2  ( x  d / 2) 2 ,
Отсюда следует, что
l22  l12  2 xd или
(l2  l1 )(l2  l1 )  2 xd .
Для получения различимой
интерференционной
картины
расстояние между источниками d
должно
быть
значительно
меньше расстояния до экрана l.
Расстояние
x, в пределах
которого образуются интерференционные полосы, также бывает значительно меньше
l.
При этих условиях можно положить
l2  l1  2l. Тогда l2  l1 
xd
. В среде с
l
показателем преломления n  1 разность l2  l1 дает оптическую разность хода ..
Следовательно, можно написать:

xd
.
l
3
Подстановка этого значения  в условие максимума (1.1) приводит к тому, что
максимумы интенсивности будут наблюдаться при значениях х, равных
xmax 
ml

d
(m  0,1,2,3...).
Отсюда следует, что расстояние между соседними максимумами будет иметь
значение, равное
Δx 
l
 , или, учитывая, что l  (a  b) , будем иметь
d
Δx 
Следовательно

(a  b)
λ,
d
d
 x
(a  b)
(1.3)
где a и b, соответственно, расстояния от щели до бипризмы и от бипризмы до
экрана. Эта формула является расчетной в данной работе.
Если преломляющий угол  призмы очень мал и углы падения лучей на грань
призмы не очень велики, то можно показать, что все лучи будут отклоняться призмой
на практически одинаковый угол, равный
  (n  1)θ ,
где
(1.4)
n - показатель преломления призмы, поэтому для расстояния d, как видно
из рис. 1.1, получаем
Откуда следует
d
 a  tg  a (n - 1).
2
d
θ
.
2a(n  1)
(1.5)
С учетом этого соотношения вместо выражения (1.3) имеем
Δx 
(a  b)λ
.
2a (n - 1)
(1.6)
Отсюда
λ  2a (n  1)x/(a  b).
(1.7)
Расстояние d между источниками S1 и S2 можно не только рассчитать по
формуле (1.5), но и непосредственно измерить. С помощью линзы, которая
расположена между бипризмой и экраном (рис.1.3), на экране можно получить
изображения источников света S1 и S2. В данной лабораторной работе экраном
служит фокальная плоскость окуляра оптического микрометра.
С помощью
окулярного оптического микрометра измеряют расстояние d между изображениями
мнимых источников света S1 и S2, а затем, используя формулу тонкой линзы,
определяют расстояние
4
d
D1
 d ,
D2
(1.8)
где d  искомое расстояние
между источниками света
S1 и S2,
D1 и D 2 
соответственно расстояния
от источников света и их
изображений до линзы L.
Четкость интерференционной картины зависит от
размеров источника света.
Экспериментальная установка
Экспериментальная установка включает в себя лампу накаливания,
коллиматор, светофильтр, щель с регулируемым просветом, бипризму Френеля,
окулярный оптический микрометр, линзу и оптическую скамью с мерной линейкой.
Схема установки изображена условно на рис. 1.1. Щель S, освещаемая через
светофильтр и коллиматор лампой, бипризма и оптический микрометр смонтированы
на оптической скамье, снабженной миллиметровой линейкой. Ширину щели можно
регулировать при помощи винта. Экраном, где наблюдается интерференционная
картина, служит фокальная плоскость окуляра оптического микрометра. Окуляр
снабжен шкалой для измерения расстояния х между интерференционными
полосами. Для наблюдения четкой интерференционной картины необходимо, чтобы
щель была параллельна ребру бипризмы. Для наблюдения мнимого изображения
щелей между бипризмой и окуляром размещают вспомогательную линзу.
Проведение эксперимента
А. Определение расстояния между двумя когерентными источниками
1.
Ознакомиться с устройством и принципом действия оптического
микрометра, по описанию, прилагаемому к данной работе.
2.
Включить осветитель. Установить между бипризмой и оптическим
микрометром вспомогательный объектив. Осторожно перемещая объектив вместе с
рейтером вдоль оптической скамьи получить в поле зрения оптического микрометра
резкое двойное изображение щели.
3. Измерить расстояние d между S1 и S2. Для этого визирную линию
оптического микрометра навести на середину источника света S1 и сделать отсчет
N1 , затем вращением барабана оптического микрометра визирную линию навести на
середину источника света S2 и сделать отсчет N2. Измерения проводить не менее
пяти раз.
5
4. Измерить расстояние D1 от щели до линзы и расстояние D2 от линзы до фокальной плоскости окуляра микрометра, положение которой отмечено.
5. Данные всех измерений занести в таблицу 1.
Таблица 1.
№
N1  10 -3
N2  10 –3
d 10 –3
м
м
м
D1
м
D2
м
d  10 –3
dср.  10 –3
м
м
1.
2.
3.
4.
5.
В. Определение длины волны света
1. С оптической скамьи снять линзу. При этом положение щели, бипризмы и
окулярного микрометра остается неизменным.
2. Изменяя ширину щели, добиться того, чтобы интерференционные полосы
были достаточно яркими.
3. Навести визирную линию на середину какой-либо светлой полосы, и сделать отсчет N3 . Затем вращением барабана микрометра перевести визирную линию
на середину другой светлой полосы, достаточно удаленной от первой, и сделать
отсчет N4. Одновременно с перемещением визирной линии сосчитать число темных
полос k, расположенных между отмеченными светлыми полосами.
4. Измерить расстояние а от щели до бипризмы и расстояние b от бипризмы
до фокальной плоскости оптического микрометра, положение которой отмечено.
5. Данные всех измерений занести в таблицу 2.
Таблица 2.
№
1.
2.
3.
4.
5.
N3  10-3
N4  10 –3
м
м
k
a
b
м
м
х

ср.

м
м
м
град.
3
4
5
6
7
Обработка результатов
1. По данным таблицы 1 определить величину d  N 2  N1 .
2. Определить расстояние d между мнимыми источниками света, используя
для этого соотношение (1.8). Найти dср.
3. Принимая показатель преломления стекла бипризмы n = 1.51, рассчитать
по формуле (1.5) преломляющий угол  бипризмы в радианах.
6
4. Полученный результат выразить в градусах и занести в таблицу 2.
5. Вычислить расстояние х между светлыми полосами в интерференционной
картине Δx  (N4  N3 )/k .
6. Рассчитать по формуле (1.3) длину волны  света. Вычислить среднее
значение длины волны света ср..
7. Результаты всех вычислений занести в таблицу 2.
Контрольные вопросы
1. Дайте определение явления интерференции света.
2. Какие волны называются когерентными?
3. Почему для получения интерференционной картины необходимы
когерентные волны?
4. Почему два независимых источника света не являются когерентными?
5. Назовите способы получения когерентных световых волн. Что общего
6. между всеми этими способами?
7. Что такое оптическая разность хода волн?
8. Какая существует зависимость между разностью фаз  колебаний,
создаваемых в какой-либо точке пространства плоскими
монохроматическими волнами, и оптической разностью хода волн?
9. Покажите ход лучей в бипризме Френеля? Объясните появление мнимых
источников света при помощи бипризмы Френеля.
10. Сформулируйте условие максимума и минимума при наблюдении
интерференции света.
11. Какой вид будет иметь интерференционная картина, если убрать
светофильтр?
Литература
1. Трофимова Т.И.
2. Савельев И.В.
Курс физики.  М.: Высшая школа, 2003.
Глава 22, с. 252…264.
Курс общей физики. Книга 4. Волны. Оптика. 
М.: Наука, 2003. Глава 4, с. 93…125.
3. Детлаф А.А.
Яворский Б.М.
Курс физики.  М.: Высшая школа, 1999.
Глава 31, с. 347…360.
4. Сивухин Д.В.
Общий курс физики. Т. IV. Оптика.  М.: Наука, 2002.
Глава III, с. 188…261.
5.
Оптика.  СПб: Невский Диалект, 2003. Глава 5,
с.189…251.
Бутиков Е.И.