ОСНОВНЫЕ ПОДХОДЫ К ЧИСЛЕННОМУ МОДЕЛИРОВАНИЮ

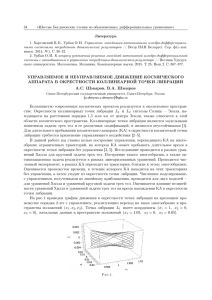
Вестник СГТУ. 2013. № 1 (69)
УДК 517.9:521+523.3:629.7
Ю.А. Окишев, Ю.В. Клинаев
ОСНОВНЫЕ ПОДХОДЫ К ЧИСЛЕННОМУ МОДЕЛИРОВАНИЮ ЧАСТНОЙ ЗАДАЧИ
ТРЕХ ТЕЛ ДЛЯ БАЛЛИСТИЧЕСКОГО АНАЛИЗА ПЕРЕЛЕТА КОСМИЧЕСКОГО АППАРАТА
С НИЗКОЙ ОКОЛОЗЕМНОЙ ОРБИТЫ В ТОЧКУ L1 СИСТЕМЫ «ЗЕМЛЯ-ЛУНА»
Рассмотрены ключевые подходы решения частного случая ограниченной
задачи трех тел. Указаны условия и ограничения, при которых решение поставленной задачи будет иметь наибольшее практическое значение и максимально
приближенное к реальности.
Математическое моделирование, баллистический анализ, точка либрации,
система «Земля-Луна», ограниченная задача трех тел
Yu.A. Okishev, Yu.V. Klinaev
BASIC APPROACHES TO SOLVING THE THREE BODIES PROBLEM
FOR THE BALLISTIC ANALYSIS OF THE LOW-EARTH ORBIT TO THE L1 POINT FLIGHT
OF THE «EARTH-MOON» SPACECRAFT
The article reviews the key approaches to the solution of the particular case of
the three bodies problem. Conditions and limits are indicated under which the solution to
the problem could be maximally close to the real life and have a great practical value.
Mathematical modeling, ballistic analysis, libration point, the «Earth-Moon» system, restricted three-body
Несмотря на то, что в двадцатом веке вопросы исследования Луны были рассмотрены достаточно широко, вплоть до забора грунта, доставки его на Землю и высадки астронавтов, по-прежнему,
задачи, связанные с изучением Луны в иных аспектах, остаются актуальными. Забор и доставка на
Землю вещества поверхности Луны из разных ее районов могут оказаться весьма полезными для геохимиков, изучающих строение верхней мантии Земли [1]. Реализация этих и других исследовательских экспериментов предусматривает обеспечение доставки космических аппаратов в заданные точки
окололунного пространства с высокой степенью точности и надёжности.
Таким образом, мы приходим к задаче баллистического анализа перелета с низкой околоземной орбиты в точку либрации L1 системы Земля-Луна. Эта задача является частным случаем ограниченной задачи трех тел, т.к. на космический аппарат (КА) оказывают существенное влияние Земля и
Луна. Необходимость решения задачи трех тел вызвана реализацией в 60-е гг. ХХ века Лунной программы и полетов Земля-Луна-Земля. В качестве рассматриваемых трех тел принимаются КА, Луна и
Земля.
Основной задачей небесной механики со времен Ньютона является осуществление возможности определять положение и скорость интересующего нас небесного тела для всякого момента времени. Для решения этой задачи Кеплер создал теорию невозмущенного (кеплерова) движения, а
Ньютон разработал основные методы теории возмущений. Знаменитый Леонард Эйлер, – создатель
одной из первых теорий движения Луны, ввел в обиход небесной механики так называемую ограниченную задачу трех тел.
Подробно решению задачи трех тел посвящена фундаментальная работа В. Себехея «Теория
орбит: ограниченная задача трех тел» [2], в которой рассмотрены основные принципы и методики
аналитического и численного решения задач. Разумеется, уровень научных достижений, затрагиваемых в этой книге, соответствует эпохе ее создания, т.е. 60-м годам двадцатого столетия. С тех пор
небесная механика и ее приложения получили широкое развитие, и эти новые результаты, естественно, не нашли отражения в книге Себехея. Однако автор подробно рассмотрел все стороны этой задачи, искусно связывая их друг с другом, получая, таким образом, единую стройную теорию.
Задача двух неподвижных центров хорошо известна со времен Эйлера, Лагранжа и Якоби.
Впервые эту задачу для случая плоского движения исследовал и свел к квадратурам Эйлер. Поэтому
44
Физика, радиотехника и электроника
ее также называют задачей Эйлера. Лагранж и Якоби показали интегрируемость задачи в пространственном случае и сделали ряд обобщений.
Но несмотря на интегрируемость, практическое приложение этой задачи на данный момент
незначительно [3].
Рис. 1. Общая задача трех тел
Общую задачу трех тел можно сформулировать следующим образом: три частицы произвольной массы притягиваются друг к другу согласно ньютоновскому закону гравитации. Начальное движение их задано, и они могут занимать любое положение в пространстве (рис. 1). Требуется найти их
движение.
Различие между общей задачей трех тел и ограниченной задачей заключается, прежде всего, в
том, что в ограниченной задаче массы только двух частиц являются произвольными, третья масса
намного меньше двух первых. В общей задаче допускаются любые начальные условия для трех частиц, тогда как в ограниченной задаче требуется, чтобы точки конечной массы двигались по круговым орбитам.
На рис. 1 приводятся обычные обозначения. Массы трех тел: m1, m2, m3, а радиус-векторы через r1(q1, q2,q3), r2(q4, q5,q6), r3(q7, q8,q9). Векторы, идущие от одной массы к другой, равны
r12 = r1 − r2 , r23 = r2 − r3 , r31 = r3 − r1 ,
(1)
а расстояния между массами m1, m2 и m3 равны
1
2
[
]
[
]
[
]
r12 = (q1 − q 4 ) 2 + (q 2 − q5 ) 2 + (q3 − q 6 ) 2
1
2
r23 = (q 4 − q 7 ) 2 + (q5 − q8 ) 2 + (q 6 − q9 ) 2
r31 = (q 7 − q1 ) 2 + (q8 − q 2 ) 2 + (q 9 − q3 ) 2
.
(2)
1
2
Силовая функция имеет вид


 m1 ⋅ m 2 m 2 ⋅ m3 m3 ⋅ m1 
F = f
+
+
2
2
2 ,
 r12
r23
r31 


(3)
где f – гравитационная постоянная.
Уравнение движения запишем в виде
mi ⋅ r&&i =
∂F
, i = 1,2,3.
∂ri
(4)
Таким образом, имеем систему трех дифференциальных векторных уравнений второго порядка относительно векторов ri или систему девяти скалярных уравнений второго порядка относительно
координат qi . Получающаяся результирующая система восемнадцатого порядка указывает на довольно сложный характер общей задачи трех тел. В подробном виде уравнения (4) записываются следующим образом:
45
Вестник СГТУ. 2013. № 1 (69)
&r&1 = − f ⋅ m2 ⋅
r&&2 = − f ⋅ m3 ⋅
r&&3 = − f ⋅ m1 ⋅
r1 − r2
r1 − r2
3
r2 − r3
r2 − r3
3
r3 − r1
r3 − r1
3
+ f ⋅ m3 ⋅
+ f ⋅ m1 ⋅
+ f ⋅ m2 ⋅
r3 − r1
r3 − r1
3
r1 − r2
r1 − r2
(5)
3
r2 − r3
r2 − r3
3
Система восемнадцатого порядка может быть сведена к системе шестого порядка, и это совсем не тривиальное приведение является одной из важных процедур, рассматриваемых в классической литературе по общей задаче трех тел, что было наилучшим образом выполнено Лагранжем в
1772 г. [4].
Предполагая, что m3 → 0 и не оказывает влияния на движения масс m1 и m2 , переходим к
ограниченной задаче трех тел и уравнение движения примет вид:
r&&3 = − f ⋅ m1 ⋅
r3 − r1
r3 − r1
3
+ f ⋅ m2 ⋅
r2 − r3
r2 − r3
3
.
(6)
Точки либрации – особые точки в ограниченной задаче трех тел, в которых третье тело с пренебрежимо малой массой, на которое не действуют никакие другие силы, кроме гравитационных сил
со стороны этих двух массивных тел, может оставаться неподвижным относительно этих тел. Таких
точек в окрестности двух массивных тел пять (рис. 2). Точки Лагранжа обозначают заглавной латинской буквой L с числовым индексом от 1 до 5.
Рис. 2. Положение точек либрации в окрестности двух массивных тел
Все точки Лагранжа лежат в плоскости орбит массивных тел. Первые три точки расположены
на линии, проходящей через оба массивных тела. Эти точки Лагранжа называются коллинеарными и
обозначаются L1, L2 и L3.
L1 находится между двумя телами системы, ближе к менее массивному телу, L2 – снаружи, за
менее массивным телом и L3 – за более массивным.
Ещё две точки (L4 и L5) расположены в вершинах равносторонних треугольников с основанием, совпадающим с отрезком, соединяющим два массивных тела. Если масса одного из этих тел
много меньше массы другого, точки L4 и L5 расположены на орбите менее массивного тела, на 60°
впереди и позади него. Эти точки называют треугольными или троянскими.
В настоящее время несколько космических аппаратов, в первую очередь, астрофизических
обсерваторий, размещены в различных точках либрации Солнечной системы:
1. SOHO (англ. Solar and Heliospheric Observatory, «Солнечная и гелиосферная обсерватория») находится на орбите в точке L1 системы «Солнце-Земля».
2. WMAP (англ. Wilkinson Microwave Anisotropy Probe), изучающий реликтовое излучение в
точке L2 системы «Солнце-Земля».
3. Advanced Composition Explorer расположен в точке L1 системы «Солнце-Земля».
46
Физика, радиотехника и электроника
4. Телескоп «Гершель» и телескоп «Планк», запущенные 14 мая 2009 года, находятся в точке
L2 системы «Солнце-Земля».
5. Космический аппарат WIND, предназначенный для исследования солнечного ветра. Аппарат запущен в 1994 году и функционирует в настоящее время, находится в точке L1 системы «Солнце-Земля».
Точка L1 системы Земля-Луна удобна для размещения ретрансляционной станции или орбитальной базы обслуживания и заправки в период освоения Луны. Она будет находиться в зоне прямой видимости для большей части обращенного к Земле полушария Луны, а для связи с ней понадобятся передатчики в десятки раз менее мощные, чем для связи с Землей.
Так как КА в точке либрации неподвижен относительно двух тел, очевидно, что правая часть
уравнения (6) равна нулю. Задача баллистического анализа перелета с низкой околоземной орбиты в
точку либрации сводится к поиску суммарного импульса скорости КА. Оптимальным перелетом будем считать решение с минимальным суммарным импульсом скорости.
Основные математические методы, используемые при решении задач небесной механики –
методы Адамса, Рунге, Штурмера, Коуэлла, Нумерова и др. Для нахождения промежуточных и периодических орбит ограниченной или общей задачи трех тел используются разнообразные методы,
например Пуанкаре, Ляпунова, Шварцшильда и др. [5]
О сокращении времени интегрирования движения с помощью принципа Рунге рассмотрено в [6].
Коллинеарные точки либрации являются неустойчивыми, поэтому при решении задачи стоит
обратиться к методу общей теории устойчивости движения, разработанному А.М. Ляпуновым. Этот
метод позволяет установить, будет ли исследуемое движение устойчивым или оно, наоборот, окажется неустойчивым, а также позволяет установить связь между начальными и последующими отклонениями (возмущениями), не производя самого интегрирования уравнения движения ни в аналитической форме, ни численными методами. Проблема устойчивости коллинеарных точек либрации является интересной и актуальной на данный момент, ей уделено серьезное внимание научным сообществом [7].
(Проблему устойчивости точек либрации подробно рассматривает Крейсман Б.Б.:
http://elibrary.ru/item.asp?id=15108447,
http://elibrary.ru/item.asp?id=16525565,
http://elibrary.ru/
item.asp?id=17313008).
Данный вопрос в рамках исследуемой задачи не обсуждается.
В рассматриваемой проблеме стоит обратить внимание на функциональный метод Ньютона
применительно к решению краевых задач для обыкновенных дифференциальных уравнений, который
заключается в замене на каждом шаге итерационного процесса исходной нелинейной системы на линейную и решении краевой задачи для последней [8].
В решении задачи интегрирования уравнений движений стоит обратить внимание на два метода [9]:
1. Метод численного интегрирования, использующего опорную траекторию и линеаризацию
уравнений движения относительно фазовых переменных этой траектории.
2. Метод дополнительных переменных, приводящий исходную систему уравнений к некоторой эквивалентной системе с правыми частями, имеющими вид полиномов от фазовых переменных.
Сущность первого метода состоит в замене переменных исходной системы уравнений на другие переменные, причем формулы перехода от старых к новым используют знание параметров некоторой опорной траектории и построении на ней сопряженной системы уравнений в вариациях. Переход к новым переменным дает выигрыш в скорости численного интегрирования системы уравнений
движения каким-либо стандартным методом (например, Эйлера, Рунге-Кутта) по сравнению с интегрированием системы в старых переменных.
Второй метод не является численным. Суть его – введение дополнительных переменных, в
результате чего, правые части уравнений движения становятся многочленами от фазовых переменных, однако порядок системы в общем случае увеличивается.
Для снижения количества топлива КА для стабилизации в точке либрации необходимо обратить внимание, что точка L1 коллинеарная и неустойчивая, отсюда рождаются требования к точности
расчета суммарного импульса скорости, а также крайне необходимо учесть все возмущающие факторы и особенности системы «Земля-Луна». Таким образом, математическое моделирование баллистического анализа перелета космического аппарата с низкой околоземной орбиты в точку L1 системы
«Земля-Луна» можно свести к поиску оптимального решения ограниченной задачи трех тел (6) с
определенными особенностями:
47
Вестник СГТУ. 2013. № 1 (69)
1. Прецессия орбиты Луны и, как следствие, изменения наклонения с периодичностью в 18,6
лет.
(Первым
про
прецессию
орбиты
Луны
сообщил
Дж.
Брадлей
(http://www.eduhmao.ru/var/db/files/3257.su9.pdf). Впервые свои исследования он представил Лондонскому Королевскому Обществу в 1748 году.)
2. Нецентральность поля тяготения Земли. При этом учитывать в качестве основного возмущения вторую зональную гармонику [10]. Для этой гармоники, характеризующей полярное сжатие
Земли, потенциал сил притяжения имеет вид
U сж = −
ε
3r
3
(3 ⋅ sin 2 i ⋅ sin 2 u − 1) ,
(7)
где ε = 2,634·1013 м5/с – константа, определяющая сжатие Земли, r – текущий радиус КА, i – наклонение орбиты, u – аргумент перицентра.
Составляющие возмущающего ускорения, обусловленного (7), определяют соотношениями:
∂U сж
ε
= 4 ⋅ (3 ⋅ sin 2 i ⋅ sin 2 u − 1)
∂r
r
ε
1 ∂U сж
T=
= 4 sin 2 i ⋅ sin 2u )
,
r ∂u
r
1 ∂U сж
ε
W=
= − 4 ⋅ (sin 2i ⋅ sin u )
r ⋅ sin u ∂r
r
S=
(8)
где S – радиальная составляющая, T и W – трансверсальная и бинормальная составляющие возмущающего ускорения. Стоит учитывать интегрируемые случаи в задаче об эволюции орбиты спутника
при совместном влиянии внешнего тела и нецентральности поля планеты [11].
3. Нецентральность гравитационного поля Луны [12]. Но стоит учесть, что Луна обращена к
Земле всегда одной стороной.
4. Гравитационное влияние Солнца. Т.к. орбита Земли имеет эллиптическую форму, выбор
даты старта может повлиять на суммарный импульс скорости. А также при определенных условиях
влияние Солнца может как «помогать» перелету, снижая импульс скорости, так и, наоборот, увеличивая в зависимости от выбора узловой точки старта. В качестве приближения следует считать, что в
выбранном для анализа промежутка времени влияние Солнца постоянно.
По итогам решения необходимо оценить устойчивость КА точке либрации L1 системы «Земля-Луна»
Решая ограниченную задачу трех тел с учетом вышеуказанных особенностей, получим максимально приближенное к действительности решение для перелета КА с низкой околоземной орбиты
в точку либрации L1 системы «Земля-Луна».
ЛИТЕРАТУРА
1. Энеев Т.М.. Актуальные задачи исследования дальнего Космоса / Т.М. Энеев // Космические исследования. 2005. Т. 43. №6. С. 403-407.
2. Себехей В. Теория орбит: ограниченная задача трех тел. / В. Себехей; пер. с англ. под
ред. Г.Н. Дубошина. М.: Наука. Гл. ред. физ.-мат. лит., 1982. 656 с.
3. Лукьянов Л.Г. Об обобщенной задаче двух неподвижных центров / Л.Г. Лукьянов // Космические исследования. 2006. Т. 44. № 2. С. 162-169.
4. Lagrange J. Mecanique Analytique. Paris: 1788. / Русский перевод: Лагранж Ж. Аналитическая механика. М.: Гостехиздат, 1950. Т. 1. 594 с. Т. 2. 440 с.
5. Дубошин Г.Н. Некоторые проблемы астродинамики и небесной механики / Г.Н. Дубошин, Д.Е. Охоцимский // Космические исследования. 1963. Т. 1. № 2. С. 195-208.
6. Чарный В.И. О сокращении времени интегрирования движения с помощью принципа
Рунге / В.И. Чарный // Космические исследования. 1969. Т. 7. № 1. С. 87-95.
7. Крейсман Б.Б. Устойчивые пространственные орбиты «вокруг» коллинеарных точек либрации / Б.Б. Крейсман // Космические исследования. 2010 Т. 48. № 3. С. 271-278.
8. Винокуров В.А. Обобщенный метод Ньютона для решения краевых задач / В.А. Винокуров, Ю.Н. Иванов // Космические исследования. 1965 Т. 3. № 4. С. 234-248.
9. Чарный В.И. О двух методах интегрирования уравнений движения / В.И. Чарный // Космические исследования. 1970. Т. 8 № 5. С. 341-354.
48
Физика, радиотехника и электроника
10. Иванов Н.М. Баллистика и навигация космических аппаратов / Н.М. Иванов, Л.Н. Лысенко. М.: Дрофа, 2004. 544 с.
11. Лидов М.Л. Интегрируемые случаи в задаче об эволюции орбиты спутника при совместном влиянии внешнего тела и нецентрального поля планеты / М.Л. Лидов, М.В. Ярская // Космические исследования. 1974. Т. 12. № 2 С. 155-170.
12. Аким Э.Л. Определение поля тяготения Луны по движению искусственного спутника
Луны «Луна-10» / Э.Л. Аким // ДАН СССР. 1966. Т. 170. № 4. С. 799-802.
Окишев Юрий Александрович –
аспирант кафедры «Техническая физика
и информационные технологии»
Энгельсского технологического института
(филиала) Саратовского государственного
технического университета имени Гагарина Ю.А.
Yuri A. Okishev –
Postgraduate
Department of Technical Physics
and Information Technology,
Engels Institute of Technology:
Part of Gagarin Saratov State Technical University
Клинаев Юрий Васильевич –
доктор физико-математических наук,
профессор кафедры «Техническая физика
и информационные технологии»
Энгельсского технологического института
(филиала) Саратовского государственного
технического университета имени Гагарина Ю.А.
Yuri V. Klinaev –
Dr. Sc., Professor
Department Technical Physics
and Information Technology,
Engels Institute of Technology:
Part of Gagarin Saratov State Technical University
Статья поступила в редакцию 02.12.12, принята к опубликованию 20.02.13
49