8 Расчет выборочных характеристик
реклама

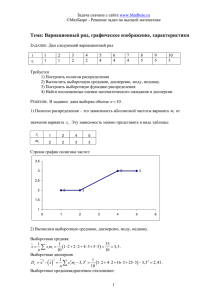
8. Расчет выборочных характеристик В результате наблюдений над случайной величиной выборка X объема n 30 : x1 1,37 x2 0,11 получена x3 x4 x5 x6 x7 x8 x9 x10 1,56 –0,11 0,23 –0,76 –0,13 –0,64 –0,46 –0,88 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 –0,56 1,28 1,16 –0,3 –0,31 1,13 –0,17 0,6 –1,16 2,65 x21 x22 x23 x24 x25 x26 x27 x28 x29 x30 1,55 0,29 –2,16 –0,77 0,93 0,01 –1,56 1,59 –1,13 –1,74 Для заданной выборки X построить вариационный ряд, вычислить следующие выборочные характеристики: 1) среднее; 2) дисперсию (смещенную и несмещенную); 3) среднее квадратическое отклонение; 4) медиану. Построить гистограмму частот. Решение Вариационный ряд выборки X имеет следующий вид: x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) –2,16 –1,74 –1,56 –1,16 –1,13 –0,88 –0,77 –0,76 –0,64 –0,56 x(11) x(12) x(13) x(14) x(15) x(16) x(17) –0,46 –0,31 –0,3 –0,17 –0,13 –0,11 0,01 x(21) 0,6 x(22) 0,93 x(23) 1,13 x(24) 1,16 x(25) 1,28 x(26) 1,37 x(27) 1,55 x(18) 0,11 x(19) 0,23 x(20) 0,29 x(28) 1,56 x(29) 1,59 x(30) 2,65 Вычислим выборочные характеристики. 1) выборочное среднее x x 1 30 xi 30 i 1 1 n n xi , i 1 1 1,37 0,11 1,56 ... ( 1,74) 30 2) выборочная смещенная дисперсия ~ S2 1 n ( xi ni1 x)2 1 n n xi2 i 1 (x)2 , 0,05 ; 1 30 2 xi 30 i 1 ~ S2 1 1,37 2 30 (x)2 0,112 1,56 2 ... ( 1,74) 2 0,052 1,26 . Выборочная несмещенная дисперсия 30 ~ 2 S 30 1 S2 30 1,26 1,3 ; 29 3) выборочное среднее квадратическое отклонение ~ S ~ S2 1,26 1,12 ; 4) выборочная медиана x(l 1) , n 2l 1; ˆ Me x(l ) x(l 2 1) , n 2l. Объем выборки n 30 – четное число, поэтому выборочная медиана x(15) ˆ Me x(15 1) 0,13 ( 0,11) 2 2 0,12 . Построим интервальный вариационный ряд выборки. Разобьем отрезок x(1) , x(30) 2,16; 2,65 на 6 равных промежутков. Длина интервала h x( 30) x(1) k 2,65 ( 2,16) 6 0,8 . Найдем концы интервалов по формуле z1 x(1) 2,16 , z2 z5 x(1) x(1) (i 1)h , i 1,7 . zi x(1) h 1,36 , z3 4h 1,04 , z6 x(1) x(1) 2h 5h 1,84 , z7 0,56 , z4 x(1) x(1) 3h 0,24 , 6h 2,65 . Найдем i – количество элементов выборки, попавших в i -й интервал [ zi ; zi 1 ) : 3 , 2 6 , 3 10 , 4 3 , 5 7 , 6 1 . 1 Таким образом, интервальный вариационный ряд выборки Интерв [ 2,16; 1,36) [ 1,36; 0,56)[ 0,56; 0,24)[0, 24;1,04)[1,04;1,84) [1,84; 2,65] ал Частота 3 6 10 3 7 1 Гистограмма частот изображена на рисунке 1. 12 10 8 6 4 2 0 -3 -2 -1 0 Рисунок 1 1 2 3