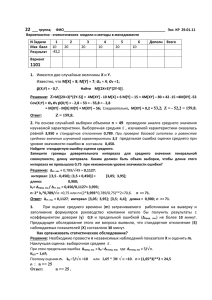
Руководство к выполнению заданий по математической
реклама

МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ ФЕДЕРАЛЬНОГО АГЕНТСТВА ПО ЗДРАВООХРАНЕНИЮ И СОЦИАЛЬНОМУ РАЗВИТИЮ имени Н.И.Пирогова» РУКОВОДСТВО К ВЫПОЛНЕНИЮ ЗАДАНИЙ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ Учебно-методическое пособие для студентов медико-биологических специальностей Москва, 2012 1 Доцент Е.Н. Занина, старший преподаватель А.А. Парпара. Руководство к выполнению заданий по математической статистике. – 2012. Под редакцией профессора В.Н.Акимова Задания по математической статистике составлены для статистической обработки экспериментальных данных с целью выяснения закона распределения, числовых характеристик и статических связей исследуемых признаков. Они включают методологические разработки по четырем темам: вариационный ряд и его числовые характеристики, точечные и интервальные оценки, проверка статистических гипотез и корреляционный анализ. Задания рассчитаны на медиков и биологов, имеющих подготовку по курсу математической статистики. Они с успехом могут быть использованы практическими врачами при статистической обработке экспериментального материала. © Е.Н. Занина, А.А. Парпара, под редакцией В.Н.Акимова .2012. © Государственное образовательное учреждение высшего профессионального образования «Российский государственный университет Федерального агентства по здравоохранению и социальному развитию», 2012. 2 Задание №1 Построение интервального ряда и вычисление основных статистических характеристик 1.1. Предварительные сведения 1.1.1. Понятие таблицы данных Наиболее распространѐнная форма, в которой представляются исходные данные для статистических вычислений — это таблица данных. При постановке эксперимента форма регистрации значений выбранного признака должна быть наиболее простой и удобной для обработки экспериментальных данных. Выбор формы, в свою очередь, зависит от вида признака (количественного или качественного), числа регистрируемых признаков (переменных) и метода обработки полученных данных. В этом случае выбирается несколько величин признаков (переменных), каждая из которых измеряется одинаковое число раз, причѐм измерения разных переменных, как правило, являются связанными, то есть относятся к одному и тому же объекту или моменту времени. В статистике набор измеренных значений переменной часто называют выборкой, а их количество — объѐмом выборки по числу измеренных объектов. Например, пусть в исследовании участвуют 50 пациентов. Для каждого из них фиксируются 4 переменные: схема терапии, самочувствие (плохое, удовлетворительное, хорошее, отличное), число сеансов терапии и температура тела. В таблице данных переменные откладываются в столбцах, а измеренные значения — в строках. Так, в результате вышеописанного исследования получится таблица из 4 столбцов и 50 строк, причѐм значения в каждой строке будут связаны, потому что относятся к одному и тому же пациенту. Нужно заметить, что в нашем примере все переменные имеют различные типы. Это важно понимать, поскольку от типа данных зависит способ статистической обработки. Типы статистических данных различаются в зависимости от того, как они могут быть пронумерованы. Так, схемы терапии не имеют никакого естественного способа подсчета: их можно нумеровать в любом порядке любыми числами. Такой тип переменной называют неупорядоченным фактором. Уровень самочувствия отличается тем, что имеет естественный порядок: от «плохого» к «отличному». Однако какая-либо определѐнная мера у него отсутствует: нельзя сказать, во сколько раз «хорошее» самочувствие лучше «плохого». Поэтому его уровни можно пронумеровать любыми четырьмя различными числами, нужно только чтобы «плохому» соответствовало 3 наименьшее, «удовлетворительному» - следующее по величине, а «отличному» — наибольшее. Такой тип называют упорядоченным фактором. Число же сеансов терапии имеет свою меру: один сеанс, поэтому никакого произвола в подсчѐте не допускает. Но эта величина может принимать лишь ряд отдельных значений, между которыми промежуточные величины невозможны, например, может быть проведено 5 или 6 сеансов, а 5,5 — уже нет. Такого типа переменную называют дискретной. о Наконец, температура тела имеет меру (1 С) и может непрерывно изменяться. Такую переменную называют непрерывной. Впрочем, нужно заметить, что в статистике различие между дискретными и непрерывными величинами не столь принципиально, как в теории вероятностей. Дело в том, что статистика работает с данными измерений, а любой измерительный прибор позволяет получать результат лишь с точностью до цены деления шкалы. Таким образом, при измерении непрерывная величина неизбежно становится дискретной. 1.1.2. Правила приближѐнных вычислений Итак, если целочисленная переменная, как правило, известна абсолютно точно, то вещественная — всегда с какой-то степенью точности. Вещественную переменную характеризуют числом десятичных знаков или числом значащих цифр. Десятичные знаки (д.з.) — точно известные цифры после запятой. Если последние цифры являются нулями, их записывают для обозначения точности, например, 2,3 имеет 1 д.з., а 2,300 — 3 д.з. Значащие цифры (з.ц.) — это все цифры числа от первой ненулевой до последней точно известной. Например, 210,20 содержит 5 з.ц., а 0,00193 — 3 з.ц. Если возникает необходимость округлить число до п з.ц., поступают следующим образом. Если (п + 1)-я цифра меньше 5, лишние цифры просто отбрасывают, если больше или равна 5 — п-ю цифру при этом увеличивают на 1, кроме случая, когда п-я цифра чѐтная, (п + 1)-я равна 5, а (п + 2)-я — 0. Так, при округлении до 3 з.ц. числа 21,335, получаем 21,3, для 1,34708 - 1,35, для 344,512 - 345, для 7,45501 - 7,46, но для 33,450 - 33,4. При вычислениях часто получаются неверные д.з., которые нужно округлять. При сложении и вычитании нужно оставлять столько д.з., сколько содержится в наименее точном слагаемом. Например, 2,78 + 3,9313 ≈ 6,71. При умножении и делении оставляют столько з.ц., сколько содержится в наименее точном множителе. Например, 0,0321 • 8,7678 ≈ 0,281. Обратите внимание, что при сложении и вычитании имеет значение число д.з., которое характеризует абсолютную погрешность числа, а при умножении и делении — число з.ц., характеризующее относительную погрешность. При возведении в степень и извлечении корня следует оставлять столько з.ц., сколько имеет основание. 4 1.1.3. Данные для задания. Для выполнения задания требуется таблица данных, содержащая две вещественные выборки объѐмом п = 50, полученные на пятидесяти объектах. Будем называть их А и Б. Каждая выборка содержит значения признаков (переменных), измеренных у объектов определенного типа, например, площадь (area) и оптическая плотность ядра лимфоцитов (ODR). Соответствующие значения выборок А и В измерены у одного и того же объекта, поэтому их можно рассматривать как связанные переменные. При выполнении заданий с первого по четвертый используются оба признака (к примеру area, ODR), представленные выборками А и В. Каждому из студентов в группе выдаются две выборки А и В, представляющие измерения двух признаков (например area, ODR) для одного из 2-х разных типов объектов (например лимфоцитов или сегментоядерных нейтрофилов). При выполнении первых двух заданий для построения вариационного ряда и вычисления его основных числовых характеристик, а также для нахождения точечных и интервальных оценок рассматриваемых признаков одного из типов объектов, кроме исходных данных, дополнительных сведений не требуется. Однако в третьем задании, посвященном проверке статистических гипотез, требуется сравнить одинаковые признаки (например, area, ODR), относящиеся к разным типам объектов (например, лимфоцитам и нейтрофилам). При этом требуется знать оценки математического ожидания (МО) и дисперсии (σ2) распределения вариационного ряда исследуемых признаков, а также значения ошибок репрезентативности (представительности выборки) представленных выборками А и В для разных типов объектов (например, лимфоцитов и нейтрофилов). , Поэтому студенты, работающие в парах, изучают одни и те же признаки для разных типов. В 3-ем задании они обмениваются полученными точечными оценками для МО для одинаковых признаков разных типов объектов. Кроме того, для проверки статистических гипотез в задании 3 требуются эталонные значения математического ожидания и дисперсии по одному для каждого признака, а в задании 4 — эталонное значение коэффициента корреляции r0 между этими признаками (переменными), которые содержатся в задании или выдаются преподавателем. 1.2. Построение интервального ряда, заполнение статистической таблицы Первый шаг при статистической обработке выборки — группировка данных. Она нужна для следующих целей. 5 Для построения гистограммы, полигона и кумуляты, нахождения медианы (Ме) и моды (Мо). 2. Для проверки гипотезы о законе распределения с помощью критерия Пирсона . (см. 3.2.1.) 3. Для составления корреляционной решетки при вычислении коэффициента корреляции. 4. Для облегчения работы с большими выборками, если вычисления производятся без помощи ЭВМ. 1. = Рисунок 1. Построение интервального ряда. Кружки – выборочные данные, - границы интервалов, - шаг разбиения, и минимальное и максимальное выборочные значения, - начальная точка отсчета, – середины интервалов, где k= . Итак, разделим числовой промежуток, в пределах которого изменяются данные, на равные интервалы-классы (рис. 1) и подсчитаем количество выборочных точек, попавших в каждый интервал. Таким образом, получим возрастающий вариационный интервальный ряд — таблицу из двух столбцов, в первом из которых записываются границы интервалов, а во втором — выборочная частота, то есть число выборочных данных, которые попали в интервал. 1.2.1. Работаем с исходной выборкой объѐма п. 1.2.2. Среди всех выборочных значений найдите минимальное . 1.2.3. Среди всех выборочных значений найдите максимальное значение . 1.2.4. Вычислите размах . 1.2.5. Определите число интервалов . 1.2.6. Определите длину интервала (шаг разбиения) . Значение округлите до числа десятичных знаков после запятой, содержащихся в выборочных значениях изучаемого признака (см. 1.1.2) так, чтобы на конце была четная цифра. 1.2.7. Выбор точки отсчѐта . 1.2.7.1. Всем значениям выборок A и B приписываем номера от 00÷n-1: для выборки А – значения ; для выборки В – значения , где к = 00 1.2.7.2. С помощью таблицы I случайных чисел приложений выберите 10 двузначных чисел (номеров) (можно с помощью генератора случайных чисел). Например, для выборки А появились номера 01; 18; 34; …49. Всего 10 номеров. 1.2.7.3. Из исходной выборки выпишите 10 выборочных значений с этими номерами, то есть ; ; ;… (продолжение примера). Всего 10 значений . 1.2.7.4. Вычислите 6 и округлите до стольких знаков после запятой, сколько имеется в . 1.2.8. Нахождение границ интервалов . 1.2.8.1. От отложите вправо и влево по значению (см. рис. 1). 1.2.8.2. От полученных граничных значений отложите по целому значению . 1.2.8.3. От новых граничных значений ещѐ раз отложите не будут покрыты и и так далее, пока . 1.2.8.4. Полученные таблица). внесите в таблицу № 1 (статистическая 1.2.8.5. Рассчитайте середины интервалов: или ; где k: 2, 3, 4, …, s и внесите в таблицу №1. 1.2.8.6. При составлении статистической таблицы №1 к левой границе каждого следующего интервала прибавляется единица последнего знака правой границы предыдущего интервала. Например, интервала, - единица его последнего знака, интервала, а граница – правая граница - левая граница - правая его граница. Если интервала , откуда левая . Таким образом, каждый интервал имеет открытую левую "( и закрытую правую (при этом , то меняется от 0 до ] границы интервала, то есть , где – число интервалов). 1.2.9. Подсчет частот. 1.2.9.1. Просмотрите по порядку все выборочные значения от до Для каждого из них найдите интервал, в который оно попадает, и в соответствующей строке столбца «Кодировка» таблицы 1 поставьте вертикальную черту. Когда накапливаются 4 вертикальные черты, перечеркивайте их горизонтальной, чтобы считать пятерками. Кодировка «пятками»: 1- 2-ІІ; 3-ІІІ; 4-ІІІІ; 5-ІІІІ; 6-ІІІІ І; 7-ІІІІ І 12- ІІІІ ІІІІ ІІ … 1.2.9.2. В каждом интервале сосчитайте черты в столбце «Кодировка» и запишите их количество в столбец « Частота» . 1.2.9.3. Сосчитайте накопленные частоты: 3, …, s.? , , где k: 2, 7 Таблица №1. Статистическая таблица. № Границы интервала Кодировка Частота Накопленная 1 2 3 4 5 6 7 ... частота , Середина интервала 1 2 , 3 , … … … … … … , , 1.3. Графическое представление статистической таблицы. С помощью статистической таблицы постройте гистограмму, полигон и кумуляту. Гистограмма – это график зависимости выборочных частот от значения переменной. Внутри интервала частота считается постоянной (рис. 2.), Полигон отличается от гистограммы тем, что выборочные частоты откладываются в серединах интервалов и соединяются отрезками прямых (рис. 2). Кумулята отличается от гистограммы тем, что на графике откладываются накопленные частоты, то есть сумма выборочных частот во всех интервалах левее данного включительно (рис. 3). Гистограмма и полигон дают оценку плотности распределения генеральной совокупности (ГС), а кумулята – еѐ функции распределения. Гистограмму обязательно нужно строить перед началом анализа данных, чтобы 8 получить наглядное представление о характере их распределения. На графике гистограммы можно приблизительно оценить основные характеристики выборки (среднее, медиану, моду, стандартное отклонение), оценить симметричность распределения и наличие выбросов. Выбросами в статистике называют нетипичные наблюдения, которые расположены далеко от основной массы данных. Они возникают обычно в качестве ошибки при проведении эксперимента. Наличие выбросов может сильно исказить результаты статистического анализа, особенно корреляционного. На гистограмме они выглядят как столбики с одной – двумя точками, отделенные от остального графика несколькими пустыми интервалами (рис. 4). Часто выбросы появляются из-за несоблюдения условий эксперимента или случайного включения в выборку объектов, нетипичных для исследуемой ГС (например, в выборку жителей Архангельска попал один уроженец Анголы). В этом случае, возможно, следует исключить такое измерение из статистического анализа. 5 10 15 k 0 0 5 10 15 k Рисунок 2. Гистограмма (слева) и полигон (справа). Пунктирная линия – плотность нормального распределения с параметрами равными выборочным значениям среднего и дисперсии. По оси – значение переменной, по оси – частота . – границы интервалов, - середины интервалов. 9 Mk 0 10 20 30 40 50 k Рисунок 3. Кумулята. По оси - значение переменной, по оси частоты . - границы интервалов. - накопленные Примечание: При построении гистограммы, полигона и кумуляты вместо буквенных значений и , записываются и отмечаются на графиках расчетные значения из табл.№1. 10 5 выброс Рисунок 4. Выброс - наблюдение, далекое от основной массы данных. 1.3.1 Нахождение медианы 0 Медиана – это значение переменной, которое делит распределение пополам, то есть вероятность того, что половина значений случайной величины окажется медианы, равна вероятности того, что половина окажется нее и равна ½. 10 Для оценки значения медианы по гистограмме в таблице №1 выберете первую строку, в которой накопленная частота . 1.3.2. Рассчитайте оценку медианы по формуле 1.3.3. Нахождение моды (Мо). Модой называется наиболее вероятное значение случайной величины, то есть то значение, при котором достигается максимальная вероятность или плотность вероятности. Для оценки значения моды по гистограмме в таблице №1 выберите строку с максимальной частотой . 1.3.4. Вычислите оценку моды по формуле 1.3.5. Если соседних интервалов от –го до – го имеют одинаковую максимальную частоту, возьмите среднее арифметическое середин этих интервалов 1.3.6. Если одинаковую максимальную частоту имеют 2 не соседних интервала, нужно вычислить соответствующее количество мод. Возможно, имеется бимодальное распределение. 11 40 50 15 20 30 10 10 5 0 0 M0 Mе Рисунок 5. Мода и медиана. Слева. Нахождение моды: K –номер модального интервала; γk-1 и γk – его левая и правая границы; , , – соответствующие частоты предмодального (k-1) , модального (k) и постмодального (k+1) интервалов , – мода . Справа. Нахождение медианы: K –номер интервала, содержащий медиану; γk-1 и γk – его левая и правая границы; Мk – его накопленная частота, Мe – медиана. Показано, что Мk>n/2, а Мk-1< n/2. Таблица № 2. Метод произведений yk+1 (yk+1)4 x1 m1 y1 m1y1 m1 m1 m1 y1+1 m1(y1+1)4 x2 m2 y2 m2y2 m2 m2 m2 y2+1 m2(y2+1)4 … … … … … … … … … 0 0 0 0 0 1 mi a= xi max 12 … … … Σ0 … … … … Σ1 Σ2 Σ3 Σ4 … … Σконтр. 1.4. Метод произведений для вычисления характеристик вариационного ряда. Характеристиками распределения вариационного ряда изучаемого признака являются оценки неизвестных параметров генеральной совокупности, из которой была сделана выборка. Точечными оценками МО, Мо, Ме являются соответственно среднее значение выборочные значения моды и медианы е; оценками дисперсии оценка ; оценками начальных и центральных моментов соответственно характеристики являются смещенная и и , где и несмещенная являются Выборочные являются точечными оценками соответственно коэффициентов асимметрии и эксцесса в генеральной совокупности. 2 Для расчета оценок МО, дисперсии (σ ), асимметрии (AS) и эксцесса (EX) понадобятся выборочные начальные и центральные моменты с первого по четвертый порядок, то есть Если объем выборки велик, их вычисление без помощи ЭВМ становится слишком трудоемким. Поэтому можно применить приближенный метод произведения. Уменьшение объема вычислений достигается путем группировки данных и перехода к целым числам с помощью изменения масштаба и переноса начала отсчета (метод «ложного нуля»). 1.4.1. Работаем со статистической таблицей №1. Статистическая таблица №1 используется для составления таблицы №2 (метод произведения) и таблицы №3 (метод сумм), которые позволяют с помощью замены переменной простейшим способом рассчитать выборочные начальные моменты , где 1.4.2. Выберите в качестве «ложного нуля» a=xi середину интервала с максимальной частотой mi ,где i=1 Если таких несколько, возьмите тот, который ближе к середине интервального ряда. 13 1.4.3. Вычислите масштабированные значения =( интервальный ряд построен правильно, значения и соседние -a)/h , где k=1 . Если должны получиться целыми, должны отличатся на 1. 1.4.4. Вычислите столбцы yk÷ слева направо, каждый раз числа, стоящие в предыдущем столбце, умножая на , где k=1 1.4.5. Сформируйте столбцы контрольных значений +1 и ( +1)4 1.4.6. Найдите суммы по столбцам Σ0÷ Σ4 и Σконтр. 1.4.7. Проверьте правильность вычислений. Они произведены правильно, если выполняется равенство Σконтр= Σ0+4 Σ1+6 Σ2+ 4Σ3+ Σ4. 1.4.8. Рассчитайте начальные моменты для масштабированной переменной y: 1.4.9. Рассчитайте центральные моменты для y по формулам. ; = 1.4.10. Вычислите числовые характеристики исходной выборки по формулам. 1.5. Метод сумм Метод сумм является контрольным для метода произведений при вычислении начальных моментов (l=1,2,3,4) для нахождения числовых характеристик распределения частот вариационного ряда без применения сложной вычислительной техники. Может применяться самостоятельно без метода произведений. 14 1.5.1. Работаем с таблицей №2. 1.5.2. Перепишем три первых столбца в таблицу№ 3. 1.5.3. Столбцы (1); (2); (3); (4); (5) – столбцы накопленных частот 1.5.4. Строка, в которой называется нулевой . ―0‖ – й строкой, относительно которой происходит накопление частот сверху - вниз выше ―0‖ – й строки снизу вверх ниже ―0‖ – й строки. 1.5.6. В столбце (1) накопление частот из 3-го столбца таблицы №3 происходит вплоть до ―0‖ – й строки по правилу: m1=m1 mk=mk-1+mk, k: 2, 3, … до ―0‖ – ой строки и ms=ms ms-1=ms+ms-1, s: 8, 7, … снизу вверх до ―0‖ – ой строки (см. табл. № 3) 1.5.7. В каждом следующем столбце (2)÷(5) накопление происходит на строчку меньше выше и ниже ―0‖ – й строки пока в строчках не останется частот. 1.5.8. В каждом из накопленных столбцов подсчитываем сумму частот под и над нулевой строкой. 1.5.9. Рассчитываем , где 1.5.9.1. Значения моментов , где и . подставляем в формулы для нахождения начальных . 15 1.5.9.2. Сравниваем полученные значения с соответствующими значениями, полученными методом произведений (совпадение абсолютное!). Таблица № 3. (1) (2) (3) (4) (5) -3 - - - - - - - - - строка - - - - - - - - - - - - -2 -1 0 нулевая 1 2 3 4 … … … … … … … … 0 1.6. Результаты выполненного задания представить в следующем виде: 1) Рисунки 1,2,3 (отметить характеристики распределения , на рис. 1, 3) , , , , x 16 2) На основе полученных результатов выдвинуть гипотезу о законе распределения изучаемого признака. 3) Таблицы с №1, 2, 3, 4. Таблица № 4 № зад 17 Задание №2 Оценки параметров распределения 2.1. Общие сведения В данном задании мы научимся вычислять точечные и интервальные оценки МО и дисперсии генеральной совокупности. Эти оценки имеют большое значение в статистике. Первая дает представление о характерной величине изучаемого признака, а вторая – о его разбросе. Для того чтобы научиться вычислять значения оценок по точным формулам и увидеть влияние объема выборки на точность оценивания, будем проводить вычисления для выборки двух объемов: исходной и сокращенной (малой выборки). В качестве второй возьмем первые 10 чисел с номерами k=00 исходной выборки объемом =50 (Не путать с 10 числами, которые использовались в задании №1 для выбора точки отсчета интервального ряда !). Интервальные оценки вычислим двумя способами: 1) с помощью точных распределений Стьюдента и , а также 2) с помощью асимптотической нормальной аппроксимации. Это нужно, чтобы иметь представление о точности асимптотической нормальной аппроксимации при разных объемах выборки. Для асимптотической интервальной оценки дисперсии необходима также оценка четвертого центрального момента. Обратите внимание на правила приближенных вычислений: оценка МО должна иметь столько цифр после запятой, сколько имеют выборочные данные. Оценки дисперсии и 4-го момента должны иметь столько значащих цифр, сколько имеет размах выборки . 2.2 Точечные оценки параметров. Таблица №5. Ошибки репрезентативности. 50 10 18 2.2.1. Построим таблицу №5. Заполняем первые три столбца верхней строчки для значениями, найденными в разделе 1.4 с помощью метода произведений. 2.2.2. Точечную оценку МО вносим в таблицу №5 без изменений. 2.2.3. В качестве оценки дисперсии принимаем несмещенную оценку ; 2.2.4. Оценка четвертого центрального момента 2.2.5. Заполняем первые три столбца нижней строчки для точных формул. Для удобства вычислений строим таблицу № 6. с помощью Таблица №6. Вычисление моментов для выборки объемом n = 10. 00 … … … … … 09 2.2.6. Во второй столбец заносим первые 10 чисел выборки с номерами k: 00÷09, складываем их, делим на 10 и получаем . 2.2.7. Вычитаем столбец. из каждого числа второго столбца и вносим в третий 2.2.8. Возводим каждое число третьего столбца в квадрат и вносим в четвертый столбец. Складываем числа в четвертом столбце, делим на 9, получаем (Примечание: при малых значениях выделяем мантиссу и порядок) 2.2.9. Возводим каждое число четвертого столбца в квадрат и вносим в пятый столбец. Складываем числа в пятом столбце, делим на 10, получаем . 2.3. Асимптотические нормальные интервальные оценки. 19 2.3.0. Вычисляем ошибки репрезентативности: - ошибка среднего значения; – ошибка несмещенной оценки дисперсии по формулам из таблицы №5 соответственно для n=50 и n=10, используя данные второго и третьего столбцов. 2.3.1. Заполняем оставшиеся 2 столбца таблицы №5 следующим образом: 2.3.1.1. Ошибка среднего значения : = 2.3.1.2. Ошибка несмещенной оценки дисперсии : 2.3.2. Строим две таблицы №7 для выборок и . Заполняем каждую из них для трех уровней значимости : 0,1, 0,05 и 0,01 следующим образом: 2.3.2.1.Используя таблицы II значений функции приложений, найдем значения статистик для трех уровней значимости α: 0,1;0,05 и 0,01. 2.3.2.2. Вычисляем границы интервалов для МО: , 2.3.2.3. Вычисляем границы интервалов для дисперсии , (значения : и берем из таблицы №5 для соответствующего объема n и исследуемого признака) Таблица №7 (n=50) Интервальные оценки. Пара- Оценка метр 0,1 0,05 0,01 Асимптоти ческая m 50 Точная Асимптоти 20 ческая Точная Таблица №7 (n=10). Асимптоти ческая m Точная 10 Асимптоти ческая Точная При заполнении таблицы № 7 обратите внимание, что первой записывается левая граница интервала (меньшее число), второй – правая (большее число). 2.4. Точные интервальные оценки параметров нормального закона. 2.4.1. Продолжаем заполнять таблицу №7. 2.4.2. Точные интервальные оценки для МО: 2.4.2.1. Найдем число степеней свободы 2.4.2.2. Используя таблицы III приложений (Критерий Стьюдента , 2Q),находим табличные значения статистики для трех уровней значимости α:0,1;0,05 и 0,01 . 21 2.4.2.3. Вычисляем границы интервалов для МО: , 2.4.3. Точные интервальные оценки для дисперсии: 2.4.3.1. Находим табличные значения и для трех уровней значимости α: 0,1;0,05;0,01; (Таблица XI приложений для графическая линейная интерполяция для неизвестных значений 2.4.3.2. Значения и + ).(Рис.6) для объема выборки n=50 находятся по формуле: Рисунок 6. Графическая линейная интерполяция. 2.4.3.3. Вычислите границы интервалов для дисперсии: 22 2.4.4. Таблица №7 заполняется для объемов выборки исследуемых признаков. и 23 Задание №3 Проверка статистических гипотез 3.1. Общие сведения В данном задании мы научимся проверять гипотезы о МО (математическом ожидании) и дисперсии ГС (генеральной совокупности), из которой была извлечена выборка. Во-первых, проверим гипотезы о равенстве МО и дисперсии ГС заданным значениям (одно выборочные гипотезы). Проверка этих гипотез может решить следующие практические задачи: 1. Извлечена ли данная выборка случайным образом из ГС с некоторым эталонным значением МО ( ) или дисперсией ( )? Эта задача требует проверки двусторонней гипотезы. 2. Превышает ли МО или дисперсия ГС, из которой извлечена данная выборка, некоторое критическое значение? Здесь требуется проверить одностороннюю гипотезу. 3. Укладывается ли МО или дисперсия ГС, из которой извлечена данная выборка, в заданный интервал? Эта задача сводится к проверке двух односторонних гипотез. Во-вторых, будем проверять двух выборочные гипотезы о МО и дисперсии. Для этого потребуется вторая выборка с тем же признаком, но относящаяся к другому типу объектов (см. 1.1.3). Сравнение выборок позволяет установить: 1. Отличаются ли ГС, из которых они были извлечены, по уровню величины МО? 2. Отличаются ли эти ГС по разбросу величин? Утверждение, которое требуется проверить, закладывается в нулевую гипотезу и обозначается . В противовес содержанию нулевой гипотезы выдвигается альтернативная гипотеза и обозначается через . Для проверки каждой гипотезы в зависимости от ее содержания существует свое правило. Это правило называется статистическим критерием значимости. Каждому критерию значимости соответствует статистика, закон распределения которой известен из теории вероятностей. Для принятия решения в пользу той или иной гипотезы строится решающее правило, согласно которому если значение критерия превышает критическое значение, то справедливо утверждение, что найдены статистически значимые различия ( ). Если значение критерия меньше критического, то статистически значимые различия отсутствуют ( ). Статистические критерии делятся на две большие группы: параметрические и непараметрические. При использовании параметрических критериев вид распределения ГС предполагается известным. Чаще всего предполагается, что это нормальное распределение. И если это действительно 24 так, то параметрические критерии имеют наибольшую мощность. Но если в действительности распределение ГС существенно отличается от нормального распределения, то используя параметрические критерии, созданные для нормального распределения, можно сделать совершенно необоснованные выводы. Поэтому перед применением параметрических критериев требуется производить проверку гипотезы о законе распределения. Если гипотеза о нормальности распределения отклоняется или данных для ее проверки недостаточно (объем выборки ), необходимо пользоваться непараметрическими критериями. За счет некоторой потери мощности эти критерии позволяют не делать предположений о форме распределения ГС. Часто свойства критериев значимости описывают в несколько иных терминах: не вероятностью правильного результата, а вероятностью ошибки. Каждую гипотезу будем проверять при трех уровнях значимости и . Максимально приемлемая вероятность ошибки I рода называется уровнем значимости и обозначается α, то есть вероятность принятия при справедливости (α=Р(Н1/Н0)). Соответственно, если H0 отклоняется при уровне значимости α, она отклоняется и при всех больших уровнях значимости (то есть меньших α). Ошибка первого рода оказывается меньше минимального уровня значимости, при котором отклоняется , поэтому, когда хотят охарактеризовать эту ошибку, пишут « », например . На практике при проверке гипотез для заданных трех уровней значимости α могут встретиться результаты принятия гипотез, которые описываются следующим образом: 1. принимается при всех : нет оснований предполагать справедливость . 2. отклоняется при и принимается при и : можно предполагать с низкой степенью достоверности. 3. отклоняется при α=0,1 и 0,05 и принимается при α=0,01, 0,05: принимается со средней степенью достоверности. 4. отклоняется при всех фиксированных α, p 0,01: гипотеза H1 принимается с высокой степенью достоверности. При формулировке вывода следует переписать соответствующий пункт приведенного выше списка, заменяя и их словесными формулировками и указав значение p. Например, если МО двух ГС равны», а МО первой ГС больше, чем второй», возможны следующие выводы. 1. Нет оснований предполагать, что МО первой ГС больше, чем МО второй . 2. Можно предполагать с низкой степенью достоверности, что МО первой ГС больше, чем второй , то есть при 10% уровне значимости. 25 3. МО первой ГС больше, чем МО второй со средней степенью достоверности , то есть при 5% уровне значимости. 4. МО первой ГС больше, чем МО второй с высокой степенью достоверности (p , то есть при 1% уровне значимости. Как правило, рассматриваются два вида альтернатив: двусторонние и односторонние. В первом случае критическими являются как очень большие, так и очень маленькие значения статистики, поэтому с обеих сторон ее распределения отсекаются интервалы с вероятностью . То есть H1 принимается, если или , где значение статистики, а квантиль ее распределения порядка p. Если альтернатива односторонняя, то критическими являются только очень большие (правая односторонняя альтернатива) или только очень маленькие (левая) значения статистики. В случае правой альтернативы критическим будет интервал , а в случае левой . Таблица №8. Критерий Пирсона. γk … … … … … … … 1 = 3.2. Проверка гипотез о законе распределения В этом разделе мы рассмотрим два критерия проверки сложной гипотезы о нормальности. H0: f(x) = - Распределение ГС является нормальным с неизвестными заранее параметрами ГС математическим ожиданием m и дисперсией . H1: f (m, ) ( ) - Распределение ГС отлично от нормального. 3.2.1. Критерий согласия Пирсона (χ2) Критерий χ2 это универсальный критерий для проверки гипотез о законе распределения, которым можно пользоваться для распределения любого вида. Кроме того, критерий Пирсона можно применять для проверки сложных 26 гипотез, когда параметры теоретического распределения оцениваются по выборке. Недостатком этого критерия является необходимость группировки данных. В каждом интервале должно быть не меньше 5 значений. Это конечно снижает мощность критерия, особенно при небольшом объеме выборки. Однако если вычисления производятся вручную, это свойство имеет положительную сторону: группировка данных снижает объем вычислений. 3.2.1.1. Заполняем табл.№8. Из статистической табл. 1 перепишите правые границы интервалов и соответственно их частоты . 3.2.1.2. Вычисляем нормированные границы интервалов (используя значения и из табл. №4 первого задания). 3.2.1.3. По табл.II Значений функции F(x) стандартного нормального распределения приложений найдем значения Фk соответствующие так что = ). Учтите, что в таблице приведены значения только для . Величины для можно получить по формуле . 3.2.1.4. Вычисляем теоретические вероятности : , для к 3.2.1.5. Умножаем теоретические вероятности на объем выборки . 3.2.1.6. Полученные значения называются ожидаемыми частотами. Часто оказывается, что в крайних интервалах вариационного ряда ожидаемых частот очень мало, поэтому интервалы объединяются так, чтобы минимальная частота (соответственно и ) была по возможности , но при этом получилось не меньше 4 интервалов. Количество интервалов после объединения обозначается 3.2.1.7. Вносим в последний столбец слагаемые статистики , равные 3.2.1.8. Вычисляем статистику , сложив числа в последнем столбце таблицы №8. 3.2.1.9. Сосчитаем число степеней свободы , где - число параметров, оцениваемых по выборке, равное в данном случае 2 ( и ); число новых интервалов после объединения. 3.2.1.10. В таблице XI квантилей распределения приложений найдем квантили для 0,1, 0,05 и 0,01 для данного числа степеней свободы. Гипотеза принимается, если . 3.2.1.11. Сформулируйте вывод о законе распределения и представьте в виде таблицы №9: 27 : 3.2.2. Критерий согласия Колмогорова-Смирнова-Лильефорса Классический - критерий Колмогорова-Смирнова рассчитан на проверку простой гипотезы о виде распределения, когда все его параметры известны априори. В этом случае распределение статистики не зависит от распределения ГС. Когда параметры оцениваются по выборке, теоретическое распределение фактически подгоняется к данным, поэтому невязка, естественно, будет меньше при всех прочих равных условиях. Статистика при этом не меняет вид распределения, только уменьшается число степеней свободы. А вот распределение – статистики становится другим. Более того, оно начинает зависеть от вида распределения ГС. Критерий Колмогорова-Смирнова для проверки сложной гипотезы о нормальности называется критерием Лильефорса. Статистика вычисляется так же, как в классическом случае, но критические значения будут другими. Статистика Лильефорса считается по не группированным данным следующим образом: 1. Расположите выборочные значения в порядке возрастания. 2. Вычислите нормированные значения выборочных значений (вычесть среднее и поделить на оценку , как выше описано в критерии Пирсона). 3. Вычислите для каждого значения функции стандартного нормального распределения ( по табл.II (см. приложения), умноженное на объем выборки . 4. Запишите значения эмпирической функции распределения, умноженные на n. Поскольку эта функция ступенчатая, каждому значению будут соответствовать два значения , справа и слева: k и k-1. 5. Найти максимальный модуль разности между теоретической и эмпирической функциями распределения . Поскольку для удобства вычислений мы использовали значения функций, умноженные на , теперь мы должны поделить на . Таблица №10. Критерий Колмогорова-Смирнова-Лильефорса. 28 … … … … … Но поскольку без помощи ЭВМ довольно сложно отсортировать 50 чисел, в учебных целях будем считать критерий по группированным данным. Надо подчеркнуть, что при группировке значение статистики уменьшается, и мощность критерия заметно падает. Поэтому на практике следует проводить вычисления по не группированным данным. 3.2.2.1. Заполните таблицу 10. Из статистической таблицы №1 перепишите правые границы интервалов . Объединять интервалы не нужно, поскольку, чем больше интервалов, тем больше мощность критерия. 3.2.2.2. Вычислите нормированные границы интервалов . 3.2.2.3. По таблице ΙΙ приложений функции стандартного нормального распределения найдите значения , умножьте их на . 3.2.2.4. Запишите накопленные частоты для каждого интервала из таблицы 1. 3.2.2.5. Вычислите модули разностей между и Mk (т. е. см. табл.10 ) и, найдите максимальный из них . 3.2.2.6. В Таблице YIII Критерий Колмогорова приложений найдите критические значения статистики Лильефорса для и 0,1, 0,05 и 0,01, где ν=s-r-1. Гипотеза принимается, если . 3.2.2.7. Сформулируйте вывод о законе распределения и представьте в виде таблицы: Таблица № 11 L : 3.3. Непараметрические критерии для проверки гипотез о совпадении двух распределений. 29 Проверяется гипотеза о совпадении двух распределений: При проверке данной гипотезы применяется непараметрические методы, которые используют знаки, ранги, инверсии и не требуют знаний о законах распределения в генеральной совокупности исследуемых признаков и . Непараметрические критерии работают на малых выборках ( ), на связанных (зависимых) и несвязанных (независимых) совокупностях. Зависимые совокупности и признаков и связываются, как правило, через объект, причем объемы совокупностей должны быть равными, то есть = . Например, исследуется число сердечных сокращений (ЧСС) до нагрузки и после нагрузки – на одних и тех же объектах. Для независимых совокупностей признак и (ЧСС) исследуется на разных объектах (например, контрольная совокупность, экспериментальная), при этом объемы выборок и не обязательно одинаковые, то есть может быть больше или . Итак, для связанных (зависимых) совокупностей используется критерий знаков и парный критерий Уилкоксона. При проверке гипотезы о совпадении двух распределений требуются данные партнера, исследующего тот же признак только другого типа. Таблица № 12. … … … 3.3.1. Критерий знаков. 3.3.1.1. Формируем две связанные совокупности X: и с номерами k = из исходных выборок одного и того же признака разных типов (например, площадь лимфоцитов и нейтрофилов, или ЧСС до эксперимента и ЧСС после эксперимента) одинакового объема 3.3.1.2. Вычитаем , (см. табл.12) 3.3.1.3. Статистика, соответствующая критерию знаков, равна , где сумма при положительных разностях; сумма при отрицательных разностях. 3.3.1.4. Проверочная формула 3.3.1.5.По табл. XIII приложений находим критическое значение критерия знаков. 3.3.1.6. Условие принятия гипотез: отклоняется (принимается ) 3.3.1.7. Полученный результат принятия гипотез представляем в виде таблицы: 30 Таблица № 13. : 3.3.2. Парный критерий Уилкоксона (Вилкоксона). 3.3.2.1.В таблице 12 отбрасываем знаки у разностей и расставляем порядковые номера (ранги) по возрастанию модуля разностей от меньшего модуля к большему. 3.3.2.2. Статистика парного критерия Уилкоксона , где сумма рангов при положитеьных разностях и отрицательных разностях. 3.3.2.3. Проверочная формула сумма рангов при 3.3.2.4. По табл.XIY приложений находим критическое значение парного Tкритерия Уилкоксона. 3.3.2.5. Условие принятия гипотез: T , то есть отклоняется гипотеза , принимается . 3.3.2.6. Полученные результаты принятия гипотез представляем в виде таблицы: Таблица № 14. : Для несвязанных (независимых) совокупностей мы проверяем гипотезы о совпадении двух распределений, используя критерий Уилкоксона и критерий инверсий. 3.3.3. Критерий Уилкоксона. 3.3.3.1. Составляем общий вариационный ряд признака своего задания и такого же признака У из задания партнера, относящегося к другому типу объектов по возрастанию признака, оставляя значения признака в своей строке. Таблица № 15. … … 1 2 3 4 5 6 7 … 19 20 31 3.3.3.2. Присваиваем ранги по возрастанию признака (табл.№15). 3.3.3.3. По критерию Уилкоксона подсчитываем статистику , где сумма рангов при значениях , сумма рангов при значениях . 3.3.3.4. По таблицам приложений №XX находим теоретические значения для независимых (несовместных) совокупностей критерия Уилкоксона. 3.3.3.5.Гипотеза принимается, если 3.3.3.6. Проверочная формула: + = . 3.3.3.7. Результаты принятия гипотез собираем в таблицу: Таблица № 16. : 3.3.4. Критерий инверсий 3.3.4.1.Выбираем статистику , где число инверсий по (изменение порядка по отношению ), и число инверсий по (изменение порядка следования по отношению ). 3.3.4.2. Для этого выписывается общий ряд следования x x y y y y x x x … x x y 3.3.4.3.Подсчитываем количество x-в перед каждым у-ом от начала ряда слева направо. Полученные значения суммируем и обозначаем . И, наоборот, подсчитываем количество у-в перед каждым x-ом от начала ряда слева направо. Полученные значения суммируем и обозначают 3.3.4.4. Проверочная формула: + = 3.3.4.5. По табл.XII приложений U –критерия Манна-Уитни находят критическое значение . 3.3.4.6. Гипотеза принимается, если Иначе, если U ) 3.3.4.7. Результаты принятия собираем в таблицу: Таблица № 17. 32 3.4 Проверка гипотез о параметрах распределения 3.4.1. Критерий Стьюдента для одной выборки. Критерий Стьюдента применяется для проверки гипотез о математическом ожидании (МО). Этот критерий позволяет сравнивать МО с некоторым фиксированным значением . К критерию Стьюдента для одной выборки сводится так же критерий для двух выборок, если ГС связанные. Альтернатива может быть как двусторонней (2Q) , так и односторонней (Q). 3.4.1.1. Поверяем гипотезу о совпадении со значением против правой односторонней альтернативы . Впредь, гипотезы будем записывать в следующем виде: (Q) указано в задании, расчеты выполняются и для 3.4.1.2. Вычислите статистику , и для , где значения n, . и берутся из табл.№5, ν=n-1 – число степеней свободы. 3.4.1.3. Найдите в таблице III приложений критерий Стьюдента для Q критические значения для и трех 0,1, 0,05 и 0,01. 3.4.1.4. Сравните и : гипотеза принимается, если 3.4.1.5. Результаты оформите в виде 2-х таблиц №18: для n=50 и n=10 3.4.1.6. Запишите выводы. 3.4.1.7. Сравните выводы для и . Таблица № 18 (n=50) : Таблица №18 (n=10) 33 3.4.1.8. Теперь проверим эту же гипотезу альтернативы: против двусторонней :m= :m (2Q) 3.4.1.9 . Найдите в таблице III приложений критерий Стьюдента для 2Q критические значения для ν = n-1 и трех α = 0,1;0,05 и 0.01. 3.4.1.10. Сравните и : гипотеза принимается, если 3.4.1.11. Результаты оформите в виде 2-х таблиц №19 для n=50 и n=10 Таблица №19 (n=50). Таблица №19 (n=10). 3.4.1.12. Запишите выводы. 3.4.1.13. Сравните выводы для n = 50 и n = 10. 34 3.4.2. Критерий Этот критерий позволяет проверить аналогичную гипотезу для дисперсии , сравнивать ее с некоторым фиксированным значением . Правая односторонняя альтернатива используется при контроле качества: если дисперсия показаний прибора достоверно превышает паспортное значение, возможна его неисправность. 3.4.2.1. Проверяем гипотезу о совпадении с фиксированным значением дисперсии против двусторонней альтернативы : (2Q) указано в задании. Расчеты выполняются и для 3.4.2.2. Вычисляем статистику , где , и для ;nи табл.№5. 3.4.2.3. Найдите в таблице XI приложений распределения значения и . берутся из критические для и трех 0,1, 0,05 и 0,01. 3.4.2.4. Сравните с критическими значениями: гипотеза принимается, если или Либо принимается гипотеза , если 3.4.2.5. Результаты оформите в виде 2-х таблиц №20 для n=50 и n=10. 3.4.2.6. Запишите выводы. 3.4.2.7. Сравните выводы для и . Таблица № 20 (n=50). Таблица №20 (n=10) 35 3.4.3. Критерий Фишера Этот критерий позволяет сравнивать дисперсии двух генеральных совокупностей между собой для одноименной переменной, используя полученные несмещенные оценки для разных типов объектов. берется из табл.№5 своего задания, а – из табл.№5 партнера для одноименной переменной, но другого типа объектов. 3.4.3.1. Проверяем гипотезу о совпадении двух дисперсий против двусторонней альтернативы (2Q) Расчеты выполняются и для 3.4.3.2. Вычислите статистику , и для . , если , иначе , если То есть в числитель дроби ставите большую дисперсию из двух дисперсий и , где . 3.4.3.3. Найдите в таблицах IY, Y и YII критерия Фишера F критические значения для и трех , 3.4.3.4. Сравните и если . : гипотеза 0,1, 0,05 и 0,01. принимается, 3.4.3.5. Результаты оформите в виде 2-х таблиц № 21 для n=50 и n=10 . 3.4.3.6. Запишите выводы. 3.4.3.7. Сравните выводы для и . Таблица № 21(n=50). Таблица № 21 (n=10) 3.4.4. Критерий Стьюдента для двух выборок. 36 Этот критерий позволяет сравнивать математические ожидания между собой и доказывает достоверность различий двух ГС по уровню данного признака. Критерий Стьюдента для двух выборок можно применять только при отсутствии достоверных различий по дисперсии. 3.4.4.1. Используем критерий Стьюдента для проверки гипотезы о совпадении математических ожиданий для одного и того же признака, относящихся к разным типам объектов против двусторонней альтернативы о неравенстве МО. Значения берутся из таблицы №5 своего задания, а значения того же признака, но относящегося к другому типу объектов, из таблицы №5 партнера. (2Q) Расчеты выполняются и для 3.4.4.2. Вычислите статистику , и для . . 3.4.4.3. Найдите в таблице III приложений критерия Стьюдента критические значения для 2Q и для и трех 0,1; 0,05 и 0,01. 3.4.4.4. Сравните и : гипотеза принимается, если 3.4.4.5. Результаты оформите в виде 2-х таблиц № 22 для n=50 и n=10. 3.4.4.6. Запишите выводы. 3.4.4.7. Сравните выводы для и . . Таблица № 22 (n=50). Таблица № 22 (n=10) 37 Задание №4 Элементы корреляционного анализа 4.1. Общие сведения В данном задании мы будем анализировать зависимость между двумя признаками (переменными) X и Y. Во-первых, исследуем линейную зависимость между признаками Χ и Υ в генеральной совокупности. Для этого вычислим точечные и интервальные оценки ( неизвестного параметрического коэффициента корреляции Пирсона в генеральной совокупности. Проверим гипотезы о значимости вычисленных КК и о равенстве КК Пирсона заданному значению . Во-вторых, исследуем нелинейную зависимость между признаками Χ и Υ в генеральной совокупности с помощью непараметрических коэффициентов корреляции ρ Спирмена и τ Кенделла. Если КК оказывается, достоверно отличен от 0, это говорит о наличии линейной зависимости между переменными. Условия применения параметрического и непараметрических КК аналогичны условиям применения параметрических и непараметрических критериев при проверке статистических гипотез о законах распределения и параметрах распределения: непараметрические КК применяются при отличии распределения от нормального, при или если данные не являются числовыми. 4.2. Построение корреляционной решетки Корреляционная решетка – это двумерная статистическая таблица, с помощью которой можно оценить вид совместного распределения, наличие и вид зависимости между переменными. Для выполнения задания используем исходную двумерную выборку, где первый столбец принимаем за X, второй за Y. Таким образом, получаем n пар (в данной работе ) значений (хk,уk), где и рассматриваем, как точку с двумя координатами. 4.2.1. Работаем с исходной выборкой nx=ny=50 . 4.2.2. Для выборок X и Y границы интервалов берем из первого задания. 38 4.2.3. Строим корреляционную решетку, как на рис. 6, располагая границы интервалов для X по оси абсцисс, а – по оси ординат для Y. Обратите внимание, что возрастает слева направо, а – снизу вверх! 4.2.4. Просмотрите последовательно пары выборочных значений. Определяйте, в какую клетку попадает пара, используя кодировку пятерками, как в задании 1. 4.2.5. Оцените наличие зависимости между переменными и ее характер (прямая или обратная). … … Рисунок №6. Корреляционная решетка. 4.3. Метод произведений для вычисления коэффициента корреляции 4.3.1. Заполняем табл. №23. Занесите в первую строчку слева направо середины интервалов xk, а в первый столбец снизу верх - yk (из статистической таблицы первого задания). 4.3.2. В середину каждой клетки запишите частоту совместного появления mxy=muv, перенося значения из корреляционной решетки. 39 4.3.3. Выберите любую клетку поближе к середине таблицы с большой частотой muv. В качестве ax, ложного нуля по x, возьмите xk, стоящее в столбце, в котором находится выбранная клетка, а в качестве в соответствующей строке. 4.3.4. Заполните строку mu.= . То есть mu. равно сумме всех в данном столбце. Найденные mu. должны в точности совпадать с частотами mk в табл. 1. Аналогично заполните столбец m.v= , складывая все в данной строке. 4.3.5. Запишите значения , аналогично - 4.3.6. Сформируйте строчки значений и . Аналогично столбцы и . 4.3.7. Найдите значения muvuv: 4.3.7.1. В нижнем левом углу ячейки запишите значение произведения uv. 4.3.7.2. В верхнем правом углу запишите произведение muv на uv. 4.3.7.3. Заполните столбец muvuv, суммируя значения, полученные в каждой строке. Таблица № 23. x1 x2 … xk=ax … m.v v mvv mvv2 muvuv … yk=ay muvuv muv uv … y2 40 y1 mu . n Σv Σuv u Σu u2 4.3.8. Найдите суммы Σv, , Σuv, Σu и . 4.3.9. Вычислите оценку КК 4.3.10. Найдите значения , по формулам: , , и ; и должны точно совпадать с соответствующими значениями, найденными в задании 1. 4.4. Вычисление доверительного интервала для . Для вычисления доверительных интервалов и проверки гипотезы о значении КК используют преобразование Фишера Таблица №24. Интервальные оценки коэффициента корреляции. n 50 10 α 0,1 ( , ( , ,) ,) 0,05 ( , ,) ( , ,) 0,01 ( , ,) ( , ,) Обратное преобразование Фишера 41 z Если выборка была сделана из двумерного нормального распределения, то имеет распределение, близкое к нормальному распределению с математическим ожиданием и дисперсией . Поэтому, используя данное преобразование, можно вычислять интервальные оценки для r с помощью квантилей нормального распределения. 4.4.1. Найдите преобразование Фишера от вычисленной оценки КК: (таблица X приложения). 4.4.2. Вычислите ошибку z: 4.4.3. Для трех уровней значимости α найдите границы интервалов для z: 4.4.4. C помощью обратного преобразования Фишера перейдите к интервалам для r: , . (таблица IX приложения) 4.4.5. Занесите найденные значения в табл. № 24 4.5. Проверка гипотезы о значении коэффициента корреляции Проверка этой гипотезы позволяет сравнить КК с заданным значением, например, измеренным на очень большой выборке. Если же требуется сравнить два КК 1 и 2, измеренные на выборках сравнимого объема, нужно действовать аналогично, только статистика будет равна где . 42 Проверяем гипотезу против двусторонней альтернативы (2Q) указано в задании. 4.5.1. Вычислите статистику , где . 4.5.2. Найдите в таблице критические значения 4.5.3. Сравните t и для трех α. : H1 принимается, если . Запишите вывод. Таблица № 25 (n=50). 4.6. Проверка гипотезы о равенстве коэффициента корреляции нулю Сравнивая КК с нулем мы можем доказать наличие зависимости между двумя характеристиками объекта: если КК достоверно отличен от 0, то зависимость есть. Однако обратное несправедливо: КК может быть равен нулю при наличии зависимости, если она не является монотонной (линейной). Проверяем гипотезу против двусторонней альтернативы :r=0 (2Q) 4.6.1. Вычислите статистику . 4.6.2. Найдите в таблице критические значения 4.6.3. Сравните и : принимается если для и трех α. . Запишите вывод. 43 Таблица № 26 (n=50). : 4.7. Прямой способ вычисления коэффициента корреляции 4.7.1. Работаем с первыми 10 парами выборочных значений исходной таблицы , где k: ( ) 4.7.2. Вычислите 4.7.3. Возьмите , и , для nx=ny=10 из второго задания (таблица №5). 4.7.4. Вычислите 4.7.5. Постройте интервальные оценки, используя ошибку для преобразование Фишера и для трех уровней значимости α: 0,1; 0,05; 0,01. Полученные результаты впишите в таблицу № 24. 4.7.6. Проверьте для гипотезы о значении КК и о равенстве его нулю. 4.7.7. Запишите выводы, сравните с результатами для . Таблица № 27 (n=10) 44 Таблица № 28 (n=10) 4.8. Коэффициент ранговой корреляции Спирмена Коэффициент ранговой корреляции Спирмена ρ вычисляется так же, как КК Пирсона r, но вместо самих выборочных значений берутся их ранги – порядковые номера вариант, расположенных в виде возрастающего вариационного ряда. Это позволяет сделать КК при отсутствии статистической связи между случайными величинами (гипотеза H0) независимым от их распределения. Кроме того, КК Спирмена близок по модулю к 1 не только в случае линейной, но и в случае любой монотонной нелинейной зависимости. Таблица № 29. Пример вычисления ранговых коэффициентов корреляции. 1 2 3 4 5 6 7 8 9 10 x 523 466 438 436 409 408 379 351 294 264 y 519 877 806 802 235 231 661 590 448 373 6 1 2 3 9 10 4 5 7 8 Σ 25 1 1 1 16 16 9 9 4 4 86 5 8 7 6 1 0 3 2 1 0 33 5 0 0 0 4 4 0 0 0 0 13 4.8.1. Составьте и заполните таблицу, аналогичную табл.29. 4.8.2. Выберите первые 10 i=00 порядке убывания пар выборочных значений из исходной выборки. Расположите их в Обратите внимание, что сортируется только x, а y 45 следует за своей парой, так как у них одинаковые индексы. Ни в коем случае нельзя разрывать пары ! 4.8.3. Каждому присвойте ранг , а каждому большему значению варианты – ранг по правилу: присваивается меньший ранг (у минимального значения будет ранг - n, у максимального ). Если среди чисел есть одинаковые, им присваиваются одинаковые ранги, равные среднему арифметическому суммы их рангов. 4.8.4. Если все ранги различны, можно вычислить по упрощенной формуле. Для этого запишите квадраты разностей рангов и воспользуйтесь формулой 4.8.5. Если в обоих сопоставляемых ранговых рядах и группы одинаковых рангов, то перед подсчетом коэффициента ранговой корреляции необходимо внести поправки на одинаковые ранги и ; , где u – объем каждой группы = одинаковых рангов в ранговом ряду одинаковых рангов в ранговом ряду , . v - объем каждой группы Тогда для подсчета рангового коэффициента корреляции Спирмена используем формулу: =1 6 . Для вычисления рангового коэффициента корреляции можно использовать также общую формулу, аналогичную формуле линейного коэффициента корреляции 4.8.1.6. Проверьте гипотезу о равенстве нулю: 46 : : Найдите в таблице критические значения для n =10 и трех уровней значимости : 0,1;0,05;0,01. Таблицы ХХ приложений. Гипотеза принимается, если превышает критическое значение. Запишите вывод. Сравните с аналогичным выводом для КК Пирсона. a) б) в) г) Рисунок. 7. Интерпретация коэффициента корреляции Кенделла. а) конкордантная пара точек; б) дискордантная пара точек; в), г) такие пары не считаются ни конкордантными, ни дискордантными. 4.9. Коэффициент ранговой корреляции Кенделла Коэффициент ранговой корреляции Кенделла τ обладает теми же преимуществами, что и КК Спирмена, но также имеет простую интерпретацию. Каждую пару выборочных значений можно изобразить точкой на плоскости. В свою очередь, точки тоже можно брать парами. Всего можно составить пар точек. 47 Если все числа разные, то пары точек могут быть двух типов. Если при переходе от первой точки ко второй обе переменные меняются в одну сторону, такую пару называют конкордантной, если в разные дискордантной (рис.7). Так вот τ равен разности между количеством конкордантных пар P и дискордантных Q, деленной на их общее Соответственно, если все пары конкордантные, τ , если тех и других поровну, количество: , если дискордантные, . Если же среди чисел есть одинаковые, то появляются пары такие как на рис. 7 в) и г). Они не учитываются при подсчете τ. А это значит, что общее количество пар уменьшается и знаменатель формулы для τ должен быть уже другим 4.9.1. Заполните оставшиеся 2 столбца табл. 10. 4.9.2. Столбец сформируйте по правилу: последовательно просматривая строки табл. 10 сверху вниз, подсчитайте число строк, лежащих ниже первой, в которых строго больше ,а строго больше . Затем число строк, лежащих ниже второй, в которых строго больше 4.9.3. Столбец строго больше ,а и т. д. вплоть до последней строки. сформируйте по аналогичному правилу, только теперь считайте строки, в которых строго больше ,а строго меньше . 4.9.4. Вычислите суммы значений P и Q по обоим столбцам. 4.9.5 Если все ранги разные, вычислите τ по формуле . Если все сосчитано правильно, то P+Q должно быть равно n(n-1)/2. 4.8.6. Если же среди рангов есть повторяющиеся, где это количество одинаковых чисел для i-го повторяющегося значения x, а то же самое для y. 48 Допустим, например, что в выборке X ранг 3,5 повторяется 2 раза и 2 раза повторяется ранг 7,5, а в выборке Y - 3 раза повторяется ранг 6. Это значит, что . Тогда знаменатель формулы для будет равен 4.9.7. Проверьте гипотезу о равенстве τ нулю. Найдите в таблице критические значения для и трех α. Гипотеза принимается, если τ превышает критическое значение. Запишите вывод, сравните с аналогичным выводом для КК Пирсона и непараметрического КК ρ Спирмена. 4.10. Построение линий регрессий Итак, мы вычислили для двумерной случайной выборки коэффициенты корреляции и для малого , где для большого объема выборки объема . Полученные коэффициенты корреляции являются точечными оценками неизвестного параметра генерального совокупности . Для него построили интервальные оценки и проверили гипотезы о значении коэффициента корреляции, которые указывают на наличие и силу линейной зависимости между переменными и . Известно, что линейный характер зависимости между уравнением прямой абсцисс, , где и определяется угловой коэффициент прямой к оси отрезок, отсекаемый на оси ординат. Так как переменные можно менять местами, то есть , где аргумент, а , где аргумент, а и функция, или функция, то существуют две прямые линии, которые определяют линейный характер зависимости между переменными и и называются линиями регрессии. Таким образом, для каждого коэффициента корреляции , можно построить две линии регрессии. Уравнение линии регрессии находится по методу наименьших квадратов и имеет вид: для и для , где ; –коэффициенты регрессии Y по X и X по Y соответственно. Из этих уравнений видно, что линии регрессии проходят через одну и ту же точку , если уравнение представить в виде: 49 (уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом). Приведем уравнения к виду: где ; и регрессии в виде , то есть получим две линии и . Поведение линий регрессии легко увидеть, если на корреляционной решетке найти усредненную точку с координатами на оси ординат отложить отрезок , а на оси абсцисс . Через точки полученные таким образом, проведем две линии регрессии: первую через точку на оси ординат и усредненную точку , вторую через точку и на оси абсцисс и точку На корреляционной решетке одна и та же точка. Усредненная точка является центром эллипса рассеивания, около которой группируются остальные точки с координатами При стремлении ), k: 00÷49. к единице эллипс рассеивания вытягивается вдоль диагонали корреляционной решетки, в зависимости от знака коэффициента корреляции, а угол между линиями регрессии стремится к нулю. При стремлении к нулю, эллипс рассеивания стремится к окружности, внутри которой находится основная масса случайных точек ), угол между линиями регрессии стремится к , а сами линии регрессии стремятся занять положение параллельное осям координат. Расположение линий регрессий полностью отражает распределение частот внутри корреляционной решетки, в которой проходят линии регрессии. Примечание: Каждый студент получает индивидуальное задание в виде двумерной выборки объема n=50, представленное выборочными значениями, как показано в Приложении. 50 51 Приложение. Пример двумерной выборки для разных типов объектов LYMPH, 7 m0 = 83.2; 18.1 = 908.1; 0.9007 rо = 0.353 FFACT 18.720 17.884 17.718 17.634 18.045 17.318 17.383 18.297 18.665 17.366 18.568 18.092 17.989 17.453 17.453 17.157 18.399 17.120 18.808 17.664 17.327 18.119 19.030 18.855 17.800 17.750 17.625 18.682 17.043 18.521 19.411 18.154 16.971 19.191 17.911 17.738 19.156 17.163 17.638 17.957 16.978 17.716 17.184 18.129 17.593 17.641 18.430 18.525 AREA 155.18 135.94 149.80 100.98 129.39 130.47 117.29 137.11 139.45 159.77 112.89 114.55 111.13 126.37 154.30 102.93 107.52 144.14 110.94 153.42 112.50 93.36 131.45 119.73 120.70 149.61 142.29 111.23 104.88 129.59 113.57 139.55 166.02 109.08 116.21 114.55 110.64 153.91 144.73 130.86 129.10 59.18 157.42 115.92 103.12 137.99 120.80 124.80 SEGM, 7 m0 = 130; 18.5 = 882.5; 1.221 rо = 0.295 FFACT 18.851 17.687 17.970 17.750 17.683 18.346 17.934 18.747 19.312 18.988 18.104 18.312 17.910 18.025 18.705 18.129 17.094 18.751 18.384 17.731 18.159 18.364 18.642 18.908 17.062 18.529 18.563 17.455 18.382 18.457 18.008 18.074 18.344 18.206 18.080 17.872 17.980 18.451 18.683 18.840 18.087 18.025 18.851 18.322 18.121 17.852 17.895 18.225 FFACT 18.851 17.687 17.970 17.750 17.683 18.346 17.934 18.747 19.312 18.988 18.104 18.312 17.910 18.025 18.705 18.129 17.094 18.751 18.384 17.731 18.159 18.364 18.642 18.908 17.062 18.529 18.563 17.455 18.382 18.457 18.008 18.074 18.344 18.206 18.080 17.872 17.980 18.451 18.683 18.840 18.087 18.025 18.851 18.322 18.121 17.852 17.895 18.225 52 18.228 18.259 118.85 103.42 18.156 17.237 18.156 17.237 Таблица I. Таблица случайных чисел (1) 1534 6128 6047 0806 9915 2882 9213 8410 9974 3402 8188 3825 9801 5603 0714 4617 6789 6705 3840 7662 7639 3237 3917 9138 8358 1030 6606 4533 4258 5224 6872 8638 9958 0265 8987 5552 9383 9903 6530 8679 5765 7198 2385 0732 1642 4514 8744 3729 (2) 7106 8993 8566 5201 8274 7158 1223 9836 2362 8162 6596 7020 8788 1251 3757 5652 6279 4978 1086 3939 2868 7203 6271 9395 5896 5094 6305 8841 2012 5128 7492 8407 7172 3086 5441 3529 6640 4059 5070 8953 4987 2447 0605 8732 6094 1956 5580 6225 (3) 2836 4102 8644 5705 4525 4341 4388 3899 2103 8226 1492 1124 6338 6352 0378 7627 7306 8621 0774 2965 4391 4246 1721 6005 6286 1745 1564 4922 0992 8949 7962 7198 5822 2996 7878 9627 7394 0332 7589 8310 1639 6716 2678 8660 3795 7212 8038 5397 (4) 7873 2551 9343 7355 5695 3463 9760 3683 4326 0782 2139 7483 5899 6467 8266 0372 1856 1790 9241 3273 2950 7329 5469 6423 9242 2975 6668 9365 0106 7928 1867 0956 4224 0699 9404 9362 9592 9109 6928 2060 3512 0291 1399 5836 2600 0687 9087 6790 (5) 5574 0330 9297 1448 5752 1178 6691 1253 3825 3364 8823 9155 3309 0231 8864 8151 7028 4433 9297 0551 7122 7936 1914 7977 5040 2018 7822 1361 1542 7267 7437 0950 6701 3584 0487 6298 9903 0182 6014 6277 9843 5585 2371 9065 4532 7632 7222 2157 (6) 7545 2358 6751 9562 9630 5786 6861 1683 9079 7871 6878 4919 0807 3556 1374 3668 9043 6298 4239 1645 7325 0065 8653 1873 8509 7340 7142 6692 4760 0116 1526 7753 7559 9702 2939 6021 7699 6721 1832 1773 5286 1106 7968 4603 9740 2106 0424 3414 (7) 7590 6427 3500 7514 7172 1173 8214 6988 6187 4500 0613 3209 0968 2569 6687 1994 7161 0854 1739 8477 9727 4146 0387 7103 2941 6547 6564 1633 0392 1476 3516 5144 4985 1665 3805 0024 8939 9163 9307 7979 3786 5330 1212 0029 0376 0846 0028 6509 (8) 5574 7067 8754 9205 6988 0670 8813 9978 2721 5598 7161 5959 0539 9446 1221 4402 7526 9127 7734 1877 0080 0866 2756 4267 3913 0207 1659 6764 4057 2009 9129 3914 4856 0446 9172 9520 9972 9008 5107 6741 2384 0504 9569 8042 4384 7055 4511 5204 (9) 1202 9325 2913 0402 0227 0820 0611 8026 1489 9421 0241 2364 4205 4174 0678 2124 6913 3445 0119 5327 7464 4916 6073 9316 3028 5587 5369 0747 0092 1772 4153 5596 4461 9107 7887 9154 1257 2542 1354 6033 4919 6346 8650 0159 9203 4106 3191 4779 (10) 7712 2454 1258 2427 4264 5067 3131 6751 4216 3816 3834 2555 8257 9219 3714 0016 6396 1111 2436 8629 7947 8648 8984 7206 1563 0300 1659 3881 5203 3860 8084 6104 6147 6437 5197 0643 0994 4461 9257 3588 5611 3679 5841 0345 5387 9157 9846 5641 53 8858 3522 3147 5601 8410 6197 2783 6051 1290 3470 9796 8283 8873 5702 7585 0103 7185 8726 4726 5282 (14) 0835 5665 2487 9074 3196 2623 5119 8447 0368 8638 1013 5245 9083 0275 6565 5694 5402 3425 7497 5348 4707 3301 8851 9080 1704 4439 4998 1090 0424 0703 9629 4903 4220 5276 5761 3365 5773 0670 5735 8649 7085 8718 1217 2251 9484 0579 3197 4993 3623 6738 (15) 1988 7020 9477 7001 7231 7803 6350 0503 7890 6137 2867 5700 2254 0144 6981 0377 7937 7267 5969 1641 1880 4279 6432 5925 0345 7276 4298 8989 8924 1678 4819 5916 2533 2233 2575 1117 5412 3013 1469 8327 1129 7418 4732 0607 2577 8171 4919 0345 1973 7323 (16) 3912 9255 0864 6249 2918 8374 0120 5654 2473 8070 9938 5564 2435 8034 9842 5336 1993 7285 8682 3652 9660 4168 4635 8519 3275 6353 5204 7273 0005 0841 7219 6576 6345 3956 6837 2417 8114 1351 9545 0110 0460 8004 0150 4301 7859 8224 2792 8958 4112 5643 (17) 0938 7379 2349 3224 7380 2191 5026 3254 4240 5345 3930 7352 2965 8122 0171 6460 4332 1130 4191 0852 8446 4305 5757 0127 4738 6912 3965 3213 1969 7543 7241 8368 8227 4118 3336 3176 0930 3886 9331 4549 6821 3425 1637 8730 1976 8641 5991 1289 1795 4767 (18) 7460 7124 1012 6368 0438 0464 3684 7336 8652 4865 3203 0891 5154 3213 2284 9585 2327 7722 2976 5296 1883 9937 6656 9233 4862 0731 4028 1935 1636 0308 5128 3270 1904 8199 9322 2434 4697 3268 5303 7955 8373 3706 1097 7690 0623 7034 4058 8825 8465 0106 (19) 0869 7878 8250 9102 7547 0696 5657 9536 9435 2456 5696 6249 1209 7666 2707 3415 6875 0164 0361 4538 9768 3120 1660 2452 2556 9033 8936 9321 7237 9732 3853 6641 5138 6380 7403 5240 6919 9469 9914 5275 2572 8822 1040 6235 1418 3595 9769 6941 2110 2372 (20) 4420 5544 2633 2672 2644 9529 0304 1944 1422 5708 1769 6568 7069 0230 3008 2358 5230 8573 9334 4456 0881 5547 5389 7341 8333 5294 5148 4820 1227 1289 1921 0033 2537 6340 8345 5455 4569 2584 6394 2890 8962 1494 7372 3477 6685 3875 1918 7685 8045 9862 Продолжение таблицы I (11) 5489 3522 7555 5759 6303 7351 7068 3613 5143 9815 5780 1187 4184 2916 5524 0146 4920 7978 7453 1473 8162 5642 2042 5470 4045 5880 9083 1762 2023 7965 7690 9292 0867 0505 6295 6323 8672 1422 2653 0438 2851 7962 3837 8542 0139 6687 6242 6859 6590 3482 (12) 5583 0935 7579 3554 6895 5634 7803 1428 4534 5141 1277 0951 2179 2972 1341 5291 2826 1947 0653 6938 8797 4219 1192 7702 1730 1257 4260 8713 2589 3855 0480 0426 1656 2127 9795 2615 8536 5507 1472 4376 2157 2753 4098 4126 0765 1943 5582 9606 1932 0478 (13) 3156 7877 2550 5080 3371 5323 8832 1796 2105 7649 6316 5991 4554 9885 9860 2354 5238 6380 3645 4899 8000 0807 1175 6958 6005 6163 5277 1189 1740 4765 8098 9573 7016 8255 1112 3410 2966 7596 5113 3328 0047 3077 0220 9274 8039 4307 5872 0522 6043 0221 54 Таблица II. Значения функции F ( х ) . х 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0 0 50000 53983 57926 61791 65542 69146 72575 75804 78814 81594 84134 86433 88493 90320 91924 93319 94520 95543 96407 97128 97725 98214 98610 98928 99180 99379 99534 99653 99744 99813 99865 99903 99931 99952 99966 99977 99984 99989 99993 99995 99997 1 50399 54380 58317 62172 65910 69497 72907 76115 79103 81859 84375 86650 88686 90490 92073 93448 94630 95637 96485 97193 97778 98257 98645 98956 99202 99396 99547 99664 99752 99819 99869 99906 99934 99953 99968 99978 99985 99990 99993 99995 99998 2 50798 54776 58706 62552 66276 69847 73237 76424 79389 82121 84614 86864 88877 90658 92220 93574 94738 95728 96562 97257 97831 98300 98679 98983 99224 99413 99560 99674 99760 99825 99874 99910 99936 99955 99969 99978 99985 99990 99993 99996 99999 3 51197 55172 59095 62930 66640 70194 73565 76730 79673 82381 84850 87076 89065 90824 92364 93699 94845 95818 96638 97320 97882 98341 98713 99010 99245 99430 99573 99683 99767 99831 99878 99913 99938 99957 99970 99979 99986 99990 99994 99996 99999 4 51595 55567 59483 63307 67003 70540 73891 77035 79955 82639 85083 87286 89251 90988 92507 93822 94950 95907 96712 97381 97932 98382 98745 99036 99266 99446 99585 99693 99774 99836 99882 99916 99940 99958 99971 99980 99986 99991 99994 99996 99999 5 51994 55962 59871 63683 67364 70884 74215 77337 80234 82894 85314 87493 89435 91149 92647 93943 95053 95994 96784 97441 97982 98422 98778 99061 99286 99461 99598 99702 99781 99841 99886 99918 99942 99960 99972 99981 99987 99991 99994 99996 — 6 52392 56356 60257 64058 67724 71226 74537 77637 80511 83147 85543 87698 89617 91308 92786 94062 95154 96080 96856 97500 98030 98461 98809 99086 99305 99477 99609 99711 99788 99846 99889 99921 99944 99961 99973 99981 99987 99992 99994 99996 — 7 52790 56749 60642 64431 68082 71566 74857 77935 80785 83398 85769 87900 89796 91466 92922 94179 95254 96164 96926 97558 98077 98500 98840 99111 99324 99492 99621 99720 99795 99851 99893 99924 99946 99962 99974 99982 99988 99992 99995 99996 — 8 53188 57142 61026 64803 68439 71904 75175 78230 81057 83646 85993 88100 89973 91621 93056 94295 95352 96246 96995 97615 98124 98537 98870 99134 99343 99506 99632 99728 99801 99856 99896 99926 99948 99964 99975 99983 99988 99992 99995 99997 — 9 53586 57535 61409 65173 68793 72240 75490 78524 81327 83891 86214 88298 90147 91774 93189 94408 95449 96327 97062 97670 98169 98574 98899 99158 99361 99520 99643 99736 99807 99861 99900 99929 99950 99965 99976 99983 99989 99992 99995 99997 — 55 Таблица III. Значение t при разных уровнях значимости и данном числе степеней свободы . 1 2 3 4 5 б 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 60 120 0,1 0,05 0,2 3,08 1,89 1,64 1,53 1,48 1,44 1,41 1,40 1,38 1,37 1,36 1,36 1,35 1,34 1,34 1,34 1,33 1,33 1,33 1,33 1,32 1,32 1,32 1,32 1,32 1,32 1,31 1,31 1,31 1,31 1,30 1,30 1,29 1,28 0,1 6,31 2,92 2,35 2,13 2,02 1,94 1,89 1,86 1,83 1,81 1,80 1,78 1,77 1,76 1,75 1,75 1,74 1,73 1,73 1,72 1,72 1,72 1,71 1,71 1,71 1,71 1,70 1,70 1,70 1,70 1,68 1,67 1,66 1,64 Уровни значимости для одностороннего критерия (Q) 0,025 0,01 0,005 0,0025 0,001 Уровни значимости для двустороннего критерия (2Q) 0,05 0,02 0,01 0,005 0,002 12,71 31,82 63,66 127,32 318,30 4,30 6,96 9,92 14,09 22,33 3,18 4,54 5,84 7,45 10,21 2,78 3,75 4,60 5,60 7,17 2,57 3,36 4,03 4,77 5,89 2,45 3,14 3,71 4,32 5,21 2,36 3,00 3,50 4,03 4,79 2,31 2,90 3,36 3,83 4,50 2,26 2,82 3,25 3,69 4,30 2,23 2,76 3,17 3,58 4,14 2,20 2,72 3,11 3,50 4,02 2,18 2,68 3,05 3,43 3,93 2,16 2,65 3,01 3,37 3,85 2,14 2,62 2,98 3,33 3,79 2,13 2,60 2,95 3,29 3,73 2,12 2,58 2,92 3,25 3,69 2,11 2,57 2,90 3,22 3,65 2,10 2,55 2,88 3,20 3,61 2,09 2,54 2,86 3,17 3,58 2,09 2,53 2,85 3,15 3,55 2,08 2,52 2,83 3,14 3,53 2,07 2,51 2,82 3,12 3,51 2,07 2,50 2,81 3,10 3,48 2,06 2,49 2,80 3,09 3,47 2,06 2,49 2,79 3,08 3,45 2,06 2,48 2,78 3,07 3,44 2,05 2,47 2,77 3,06 3,42 2,05 2,47 2,76 3,05 3,41 2,05 2,46 2,76 3,04 3,40 2,04 2,46 2,75 3,03 3,39 2,02 2,42 2,70 2,97 3,31 2,00 2,39 2,66 2,91 3,23 1,98 2,36 2,62 2,86 3,16 1,96 2,33 2,58 2,81 3,09 0,0005 0,001 636,61 31,60 12,92 8,61 6,87 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 3,88 3,85 3,82 3,79 3,77 3,75 3,73 3,71 3,69 3,67 3,66 3,65 3,55 3,46 3,37 3,29 56 Таблица IV. Значение F при = 0,05 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 60 120 1 1 161,4 18,51 10,13 7,71 6,61 5,99 5,59 5,32 5,12 4,96 4,84 4,75 4,67 4,60 4,54 4,49 4,45 4,41 4,38 4,35 4,32 4,30 4,28 4,26 4,24 4,22 4,21 4,20 4,18 4,17 4,08 4,00 3,92 3,84 2 199,5 19,00 9,55 6,94 5,79 5,14 4,74 4,46 4,26 4,10 3,98 3,88 3,80 3,74 3,68 3,63 3,59 3,55 3,52 3,49 3,47 3,44 3,42 3,40 3,38 3,37 3,35 3,34 3,33 3,32 3,23 3,15 3,07 2,90 3 215,7 19,16 9,28 6,59 5,41 4,76 4,35 4,07 3,86 3,71 3,59 3,49 3,41 3,34 3,29 3,24 3,20 3,16 3,13 3,10 3,07 3,05 3,03 3,01 2,99 2,98 2,96 2,95 2,93 2,92 2,84 2,76 2,68 2,60 4 224,6 19,25 9,12 6,39 5,19 4,53 4,12 3,84 3,63 3,48 3,36 3,26 3,18 3,11 3,06 3,01 2,96 2,93 2,90 2,87 2,84 2,82 2,80 2,78 2,76 2,74 2,73 2,71 2,70 2,69 2,61 2,52 2,45 2,37 5 230,2 19,30 9,01 6,26 5,05 4,39 3,97 3,69 3,48 3,33 3,20 3,11 3,02 2,96 2,90 2,85 2,81 2,77 2,74 2,71 2,68 2,66 2,64 2,62 2,60 2,59 2,57 2,56 2,54 2,53 2,45 2,37 2,29 2,21 6 234,0 19,33 8,94 6,16 4,95 4,28 3,87 3,58 3,37 3,22 3,09 3,00 2,92 2,85 2,79 2,74 2,70 2,66 2,63 2,60 2,57 2,55 2,53 2,51 2,49 2,47 2,46 2,44 2,43 2,42 2,34 2,25 2,17 2,09 8 238,9 19,37 8,84 6,04 4,82 4,15 3,73 3,44 3,23 3,07 2,95 2,85 2,77 2,70 2,64 2,59 2,55 2,51 2,48 2,45 2,42 2,40 2,38 2 36 2,34 2,32 2,30 2,29 2,28 2,27 2,18 2,10 2,02 1,94 12 243,9 19,41 8,74 5,91 4,68 4,00 3,57 3,28 3,07 2,91 2,79 2,69 2,60 2,53 2,48 2,42 2,38 2,34 2,31 2,28 2,25 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,10 2,09 2,00 1,92 1,83 1,75 24 249,0 19,45 8,64 5,77 4,53 3,84 3,41 3,12 2,90 2,74 2,61 2,50 2,42 2,35 2,29 2,24 2,19 2,15 2,11 2,08 2,05 2,03 2,00 1,98 1,96 1,95 1,93 1,91 1,90 1,89 1,79 1,70 1,61 1,52 254,3 19,50 8,53 5,63 4,36 3,67 3,23 2,93 2,71 2,54 2,40 2,30 2,21 2,13 2,07 2,01 1,96 1,92 1,88 1,84 1,81 1,78 1,76 1,73 1,71 1,69 1,67 1,65 1,64 1,62 1,52 1,39 1,25 1,00 57 Таблица V. Значения F при = 0,025 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 60 120 1 1 647,79 38,51 17,43 12,22 10,01 8,81 8,07 7,57 7,21 6,94 6,72 6,55 6,41 6,30 6,20 6,12 6,04 5,98 5,92 5,87 5,83 5,79 5,75 5,72 5,69 5,66 5,63 5,61 5,59 5,57 5,42 5,29 5,15 5,02 2 799,50 39,00 16,04 10,65 8,43 7,26 6,54 6,06 5,72 5,46 5,26 5,10 4,96 4,86 4,76 4,69 4,62 4,56 4,51 4,46 4,42 4,38 4,35 4,32 4,29 4,27 4,24 4,22 4,20 4,18 4,05 3,92 3,80 3,69 3 864,16 39,16 15,44 9,98 7,76 6,60 5,89 5,42 5,08 4,83 4,64 4,47 4,35 4,24 4,15 4,08 4,01 3,95 3,90 3,86 3,82 3,78 3,75 3,72 3,69 3,67 3,65 3,63 3,61 3,59 3,46 3,34 3,23 3,12 4 899,58 39,25 15,10 9,60 7,39 6,23 5,52 5,05 4,72 4,47 4,28 4,12 4,00 3,89 3,80 3,73 3,66 3,61 3,56 3,52 3,48 3,44 3,41 3,38 3,35 3,33 3,31 3,29 3,27 3,25 3,13 3,01 2,89 2,79 5 921,85 39,30 14,88 9,36 7,15 5,99 5,28 4,82 4,48 4,24 4,04 3,89 3,77 3,68 3,58 3,50 3,44 3,38 3,33 3,29 3,25 3,22 3,18 3,16 3,13 3,10 3,08 3,06 3,04 3,03 2,90 2,79 2,67 2,57 6 937,11 39,33 14,74 9,20 6,98 5,82 5,12 4,65 4,32 4,07 3,88 3,73 3,60 3,50 3,42 3,34 3,28 3,22 3,17 3,13 3,09 3,06 3,02 3,00 2,97 2,94 2,92 2,90 2,88 2,87 2,74 2,63 2,52 2,41 8 956,66 39,37 14,54 8,98 6,76 5,60 4,90 4,43 4,10 3,86 3,66 3,51 3,39 3,28 3,20 3,12 3,06 3,00 2,96 2,91 2,87 2,84 2,81 2,78 2,75 2,73 2,71 2,69 2,67 2,65 2,53 2,41 2,30 2,19 12 976,71 39,42 14,34 8,75 6,52 5,37 4,67 4,20 3,87 3,62 3,43 3,28 3,15 3,05 2,96 2,89 2,82 2,77 2,72 2,68 2,64 2,60 2,57 2,54 2,52 2,49 2,47 2,45 2,43 2,41 2,29 2,17 2,06 1,94 24 997,25 39,46 14,12 8,51 6,28 5,12 4,42 3,95 3,61 3,36 3,17 3,02 2,89 2,79 2,70 2,62 2,56 2,50 2,45 2,41 2,37 2,33 2,30 2,27 2,24 2,22 2,20 2,17 2,15 2,14 2,01 1,88 1,76 1,64 1018,3 39,50 13,90 8,26 6,02 4,85 4,14 3,67 3,33 3,08 2,88 2,72 2,60 2,49 2,40 2,32 2,25 2,19 2,13 2,08 2,04 2,00 1,97 1,94 1,91 1,88 1,85 1,83 1,81 1,79 1,64 1,48 1,31 1,00 58 Таблица VI. Значения F при = 0,01 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 60 120 1 1 4052 98,49 34,12 21,20 16,26 13,74 12,25 11,26 10,56 10,04 9,65 9,33 9,07 8,86 8,68 8,53 8,40 8,28 8,18 8,10 8,02 7,94 7,88 7,82 7,77 7,72 7,68 7,64 7,60 7,56 7,31 7,08 6,85 6,64 2 4999 99,00 30,81 18,00 13,27 10,92 9,55 8,65 8,02 7,56 7,20 6,93 6,70 6,51 6,36 6,23 6,11 6,01 5,93 5,85 5,78 5,72 5,66 5,61 5,57 5,53 5,49 5,45 5,42 5,39 5,18 4,98 4,79 4,60 3 5403 99,17 29,46 16,69 12,05 9,78 8,45 7,59 6,99 6,55 6,22 5,95 5,74 5,56 5,42 5,29 5,18 5,09 5,01 4,94 4,87 4,82 4,76 4,72 4,68 4,64 4,60 4,57 4,54 4,51 4,31 4,13 3,95 3,78 4 5625 99,25 28,71 15,98 11,39 9,15 7,85 7,01 6,42 5,99 5,67 5,41 5,20 5,03 4,89 4,77 4,67 4,58 4,50 4,43 4,37 4,31 4,26 4,22 4,18 4,14 4,11 4,07 4,04 4,02 3,83 3,65 3,48 3,32 5 5764 99,30 28,24 15,52 10,97 8,75 7,46 6,63 6,05 5,64 5,32 5,06 4,86 4,69 4,56 4,44 4,34 4,25 4,17 4,10 4,04 3,99 3,94 3,90 3,86 3,82 3,78 3,75 3,73 3,70 3,51 3,34 3,17 3,02 6 5859 99,33 27,91 15,21 10,67 8,47 7,19 6,37 5,80 5,39 5,07 4,82 4,62 4,46 4,32 4,20 4,10 4,01 3,94 3,87 3,81 3,76 3,71 3,67 3,63 3,59 3,56 3,53 3,50 3,47 3,29 3,12 2,96 2,80 8 5981 99,36 27,49 14,80 10,29 8,10 6,84 6,03 5,47 5,06 4,74 4,50 4,30 4,14 4,00 3,89 3,79 3,71 3,63 3,56 3,51 3,45 3,41 3,36 3,32 3,29 3,26 3,23 3,20 3,17 2,99 2,82 2,66 2,51 12 6106 99,42 27,05 14,37 9,89 7,72 6,47 5,67 5,11 4,71 4,40 4,16 3,96 3,80 3,67 3,55 3,45 3,37 3,30 3,23 3,17 3,12 3,07 3,03 2,99 2,96 2,93 2,90 2,87 2,84 2,66 2,50 2,34 2,18 24 6234 99,46 26,60 13,93 9,47 7,31 6,07 5,28 4,73 4,33 4,02 3,78 3,59 3,43 3,29 3,18 3,08 3,00 2,92 2,85 2,80 2,75 2,70 2,66 2,62 2,58 2,55 2,52 2,49 2,47 2,29 2,12 1,95 1,79 6366 99,50 26,12 13,46 9,02 6,88 5,65 4,86 4,31 3,91 3,60 3,36 3,16 3,00 2,87 2,75 2,65 2,57 2,49 2,42 2,36 2,31 2,26 2,21 2,17 2,13 2,10 2,06 2,03 2,01 1,80 1,60 1,38 1,00 59 Таблица VII. Значения F при = 0,005 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 60 120 1 1 16211 198,50 55,55 31,33 22,78 18,64 16,24 14,69 13,61 12,83 12,23 11,75 11,37 11,06 10,80 10,58 10,38 10,22 10,07 9,94 9,83 9,73 9,64 9,55 9,48 9,41 9,34 9,28 9,23 9,18 8,83 8,50 8,18 7,88 2 20 000 199,00 49,80 26,28 18,31 14,54 12,40 11,04 10,11 9,43 8,91 8,51 8,19 7,92 7,70 7,51 7,35 7,22 7,09 6,99 6,89 6,81 6,73 6,66 6,60 6,54 6,49 6,44 6,40 6,36 6,07 5,80 5,54 5,30 3 21 615 199,17 47,47 24,26 16,53 12,92 10,88 9,60 8,72 8,08 7,60 7,23 6,93 6,68 6,48 6,30 6,16 6,03 5,92 5,82 5,73 5,65 5,58 5,52 5,46 5,41 5,36 5,32 5,28 5,24 4,98 4,73 4,50 4,28 4 22 500 199,25 46,20 23,16 15,56 12,03 10,05 8,80 7,96 7,34 6,88 6,52 6,23 6,00 5,80 5,64 5,50 5,38 5,27 5,17 5,09 5,02 4,95 4,89 4,84 4,78 4,74 4,70 4,66 4,62 4,37 4,14 3,92 3,72 5 23 056 199,30 45,39 22,46 14,94 11,46 9,52 8,30 7,47 6,87 6,42 6,07 5,79 5,56 5,37 5,21 5,08 4,96 4,85 4,76 4,68 4,61 4,54 4,49 4,43 4,38 4,34 4,30 4,26 4,23 3,99 3,76 3,55 3,35 6 23 437 199,33 44,84 21,98 14,51 11,07 9,16 7,95 7,13 6,54 6,10 5,76 5,48 5,26 5,07 4,91 4,78 4,66 4,56 4,47 4,39 4,32 4,26 4,20 4,15 4,10 4,06 4,02 3,98 3,95 3,71 3,49 3,28 3,09 8 23 925 199,37 44,13 21,35 13,96 10,57 8,68 7,50 6,69 6,12 5,68 5,34 5,08 4,86 4,67 4,52 4,39 4,28 4,18 4,09 4,01 3,94 3,88 3,83 3,78 3,73 3,69 3,65 3,61 3,58 3,35 3,13 2,93 2,74 12 24 426 199,42 43,39 20,70 13,38 10,03 8,18 7,02 6,23 5,66 5,24 4,91 4,64 4,43 4,25 4,10 3,97 3,86 3,76 3,68 3,60 3,54 3,48 3,42 3,37 3,32 3,28 3,25 3,21 3,18 2,95 2,74 2,54 2,36 24 24 940 199,46 42,62 20,03 12,78 9,47 7,64 6,50 5,73 5,17 4,76 4,43 4,17 3,96 3,79 3,64 3,51 3,40 3,31 3,22 3,15 3,08 3,02 2,97 2,92 2,87 2,83 2,79 2,76 2,73 2,50 2,29 2,09 1,90 25 465 199,51 41,83 19,32 12,14 8,88 7,08 5,95 5,19 4,64 4,23 3,90 3,65 3,44 3,26 3,11 2,98 2,87 2,78 2,69 2,61 2,55 2,48 2,43 2,38 2,33 2,29 2,24 2,21 2,18 1,93 1,69 1,43 1,00 60 Таблица VIII. Критерий согласия Колмогорова. Значения 1-К() 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 0 99999 99719 96394 86428 71124 54414 39273 27000 17772 11225 06809 03968 02222 01195 00618 00307 00146 00067 00030 00013 00005 00002 1 99998 99603 95719 85077 69453 52796 37907 25943 17005 10697 06463 03751 02092 01121 00577 00285 00136 00062 00027 00011 00005 00002 2 99995 99452 94969 83678 67774 51197 36571 24917 16264 10190 06132 03545 01969 01051 00539 00265 00126 00057 00025 00010 00004 00002 3 99991 99262 94147 82225 66089 49619 35266 23922 15550 09703 05815 03348 01852 00985 00503 00247 00116 00053 00023 00010 00004 00001 4 99983 99027 93250 80732 64402 48063 33992 22957 14861 09235 05513 03162 01742 00922 00469 00229 00108 00048 00021 00009 00004 00001 5 99970 98741 92282 79201 62717 46532 32748 22021 14196 08787 05224 02984 01638 00864 00438 00213 00100 00045 00019 00008 00003 00001 б 99949 98400 91242 77636 61036 45026 31536 21114 13556 08357 04949 02815 01539 00808 00408 00198 00092 00041 00018 00007 00003 00001 7 99917 97998 90134 76042 59363 43545 30356 20236 12939 07944 04686 02655 01446 00756 00380 00186 00085 00038 00016 00007 00003 00001 8 99872 97532 88960 74422 57700 42093 29206 19387 12345 07550 04435 02503 01357 00707 00354 00170 00079 00035 00015 00006 00002 00001 9 99807 96998 87724 72781 56050 40668 28087 18566 11774 07171 04196 02359 01274 00661 00330 00158 00073 00032 00014 00006 00002 00001 61 Таблица IX. Значения величины r для значений z от 0,00 до 2,99 z 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 0 0000 0997 1974 2913 3800 4621 5370 6044 6640 7163 7616 8005 8337 8617 8854 9051 9217 9354 9468 9562 9640 9704 9757 9801 9837 9866 9890 9910 9926 9940 1 0100 1096 2070 3004 3885 4699 5441 6107 6696 7211 7658 8041 8367 8643 8875 9069 9232 9366 9478 9571 9647 9710 9762 9805 9840 9869 9892 9912 9928 9941 2 0200 1194 2165 3095 3969 4777 5511 6169 6751 7259 7699 8076 8397 8668 8896 9087 9246 9379 9488 9579 9654 9716 9767 9809 9843 9871 9894 9914 9929 9942 3 0300 1293 2260 3185 4053 4854 5580 6231 6805 7306 7739 8110 8426 8692 8917 9104 9261 9391 9498 9587 9661 9722 9771 9812 9846 9874 9897 9915 9931 9943 4 0400 1391 2355 3275 4136 4930 5649 6291 6858 7352 7779 8144 8455 8717 8937 9121 9275 9402 9508 9595 9668 9727 9776 9816 9849 9876 9899 9917 9932 9944 5 0500 1489 2449 3364 4219 5005 5717 6351 6911 7398 7818 8178 8483 8741 8957 9138 9289 9414 9518 9603 9674 9732 9780 9820 9852 9879 9901 9919 9933 9945 6 0599 1586 2543 3452 4301 5080 5784 6411 6963 7443 7857 8210 8511 8764 8977 9154 9302 9425 9527 9611 9680 9738 9785 9823 9855 9881 9903 9920 9935 9946 7 0699 1684 2636 3540 4382 5154 5850 6469 7014 7487 7895 8243 8538 8787 8996 9170 9316 9436 9536 9618 9686 9743 9789 9827 9858 9884 9904 9922 9936 9947 8 0798 1781 2729 3627 4462 5227 5915 6527 7064 7531 7932 8275 8565 8810 9015 9186 9329 9447 9545 9626 9693 9748 9793 9830 9861 9886 9906 9923 9937 9948 9 0898 1877 2821 3714 4542 5299 5980 6584 7114 7574 7969 8306 8591 8832 9033 9201 9341 9458 9554 9633 9699 9753 9797 9834 9864 9888 9908 9925 9938 9949 8 0,0802 0,1820 0,2877 0,4001 0,5230 0,6625 0,8291 1,0454 1,3758 2,2976 9 0,0902 0,1923 0,2986 0,4118 0,5361 0,6777 0,8480 1,0714 1,4219 2,6467 Таблица X. Значения величины z для значений r от 0,00 до 0,99 r 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 0 0,0000 0,1003 0,2027 0,3095 0,4236 0,5493 0,6931 0,8673 1,0986 1,4722 1 0,0100 0,1105 0,2132 0,3206 0,4356 0,5627 0,7089 0,8872 1,1270 1,5275 2 0,0200 0,1206 0,2237 0,3317 0,4477 0,5763 0,7250 0,9076 1,1568 1,5890 3 0,0300 0,1308 0,2342 0,3428 0,4599 0,5901 0,7414 0,9287 1,1881 1,6584 4 0,0400 0,1409 0,2448 0,3541 0,4722 0,6042 0,7582 0,9505 1,2212 1,7380 5 0,0501 0,1511 0,2554 0,3654 0,4847 0,6184 0,7753 1,9730 1,2562 1,8318 6 0,0601 0,1614 0,2661 0,3769 0,4973 0,6328 0,7928 0,9962 1,2933 1,9459 7 0,0701 0,1717 0,2769 0,3884 0,5101 0,6475 0,8107 1,0203 1,3331 2,0923 62 Таблица XI. 2-Распределение. Критические (процентные) точки для разных значений вероятности α и чисел степеней свободы ν ν 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 5,0 3,84 5,99 7,82 9,49 11,07 12,59 14,07 15,51 16,92 18,31 19,68 21,03 22,36 23,68 25,00 26,30 27,59 28,87 30,14 31,41 32,67 33,92 35,17 36,42 37,65 38,88 40,11 41,34 42,56 43,77 44,93 46,19 47,40 48,60 49,80 51,00 52,19 53,38 54,57 55,76 56,94 58,12 59,30 60,48 61,66 62,83 64,00 65,17 66,34 2,5 5,02 7,38 9,35 11,14 12,83 14,15 16,01 17,54 19,02 20,48 21,92 23,34 24,74 26,12 27,49 28,84 30,19 31,53 32,85 34,17 35,48 36,78 38,08 39,36 40,65 41,92 43,19 44,46 45,72 46,98 48,23 49,48 50,72 51,97 53,20 54,44 55,67 56,90 58,12 59,34 60,56 61,78 62,99 64,20 65,41 66,62 67,82 69,02 70,22 , % 1,0 6,64 9,21 11,34 13,28 15,09 16,81 18,48 20,09 21,67 23,21 24,72 26,22 27,69 29,14 30,58 32,00 33,41 34,80 36,19 37,57 38,93 40,29 41,64 42,98 44,31 45,64 46,95 48,28 49,59 50,89 52,19 53,49 54,78 56,06 57,34 58,62 59,89 61,18 62,43 63,69 64,95 66,21 67,46 68,71 69,96 71,20 72,44 73,68 74,92 0,5 7;88 10,60 12,84 14,86 16,75 18,55 20,28 21,96 23,59 25,19 26,76 28,30 29,82 31,32 32,80 34,27 35,72 37,16 38,18 40,00 41,40 42,80 44,18 45,56 46,93 48,29 49,64 50,99 52,34 53,67 55,00 56,33 57,65 58,96 60,28 61,58 62,88 64,18 65,48 66,77 68,05 69,34 70,62 71,89 73,17 74,44 75,70 76,97 78,23 0,1 10,83 13,82 16,27 18,47 20,52 22,46 24,32 26,12 27,88 29,59 31,26 32,91 34,53 36,12 37,70 39,25 40,79 42,31 43,82 45,32 46,80 48,27 49,73 51,18 52,62 54,05 55,48 56,89 58,30 59,70 61,10 62,49 63,87 65,25 66,62 67,98 69,35 70,70 72,06 73,40 74,74 76,08 77,42 78,75 80,08 81,40 82,72 84,04 85,35 99,9 — — 0,02 0,09 0,21 0,38 0,60 0,86 1,15 1,48 1,83 2,21 2,62 3,04 3,48 3,94 4,42 4,91 5,41 5,92 6,45 6,98 7,53 8,09 8,65 9,22 9,80 10,39 10,99 11,59 12,20 12,81 13,43 14,06 14,69 15,32 15,94 16,61 17,26 17,92 18,58 19,24 19,91 20,58 21,25 21,93 22,61 23,30 23,98 99,5 — 0,01 0,07 0,21 0,41 0,68 0,99 1,44 1,54 2,65 2,31 3,47 3,56 4,57 4,11 5,24 5,80 6,56 6,45 7,43 8,43 8,35 9,06 9,69 10,02 11,06 11,81 12,46 13,12 13,79 14,46 15,13 15,82 16,50 17,19 17,89 18,59 19,29 20,00 20,71 21,42 22,14 22,86 23,58 24,31 25,04 25,78 26,51 27,25 α, % 99,0 — 0,02 0,12 0,30 0,55 0,87 1,24 1,65 2,09 2,56 3,05 3,57 4,11 4,66 5,23 5,81 6,41 7,02 7,63 8,27 8,90 9,54 10,20 10,86 11,52 12,20 12,88 13,56 14,25 14,95 15,66 16,36 17,07 17,79 18,51 19,23 19,96 20,69 21,43 22,16 22,91 23,65 24,40 25,15 25,90 26,66 27,42 28,18 28,94 97,5 — 0,05 0,22 0,48 0,83 1,24 1,69 2,18 2,70 3,25 3,82 4,40 5,01 5,63 6,26 6,91 7,56 8,23 8,91 9,59 10,28 10,98 11,69 12,40 13,12 13,84 14,57 15,31 16,05 16,79 17,54 18,29 19,05 19,81 20,57 21,34 22,11 22,88 23,65 24,43 25,22 26,00 26,78 27,58 28,37 29,16 29,96 30,76 31,56 95,0 — 0,10 0,35 0,71 1,14 1,64 2,17 2,73 3,32 3,94 4,58 5,23 5,89 6,57 7,26 7,96 8,67 9,39 10,12 10,85 11,59 12,34 13,09 13,85 14,61 15,38 16,15 16,93 17,71 18,49 19,28 20,07 20,88 21,66 22,46 23,27 24,08 24,88 25,70 26,51 27,33 28,14 28,97 29,79 30,61 31,44 32,27 33,10 33,93 63 50 51 67,51 68,67 71,42 72,62 76,15 77,39 79,49 80,75 86,66 87,97 24,67 25,37 27,99 28,74 29,71 30,48 32,36 53,16 34,76 35,60 97,5 33,97 34,78 35,59 36,40 37,21 38,03 38,84 39,66 40,48 41,30 42,13 42,95 43,78 44,60 45,43 46,26 47,09 47,92 48,76 49,59 50,43 51,26 52,10 52,94 53,78 54,62 55,47 56,31 57,15 58,00 58,84 59,69 60,54 61,39 62,24 63,09 63,94 64,79 65,65 66,50 67,36 68,21 69,07 69,92 70,78 71,64 72,50 73,36 74,22 0,975 95,0 36,44 37,28 38,12 38,96 39,80 40,65 41,49 42,34 43,19 44,04 44,89 45,74 46,60 47,45 48,30 49,16 50,02 50,88 51,74 52,60 53,46 54,32 55,19 56,05 56,92 57,79 58,65 59,52 60,39 61,26 62,13 63,00 63,88 64,75 65,62 66,50 67,37 68,25 69,13 70,00 70,88 71,76 72,64 73,52 74,40 75,28 76,16 77,05 77,93 0,950 Продолжение таблицы XI ν 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 , % , % 5,0 69,83 70,99 72,15 73,31 74,47 75,62 76,78 77,93 79,08 80,23 81,38 82,53 83,68 84,82 85,97 87,11 88,25 89,39 90,53 91,67 92,81 93,94 95,08 96,22 97,35 98,48 99,62 100,75 101,88 103,01 104,14 105,27 106,40 107,52 108,65 109,77 110,90 112,02 113,14 114,27 115,39 116,51 117,63 118,75 119,87 120,99 122,11 123,22 124,34 0,05 2,5 73,81 75,00 76,19 77,38 78,57 79,75 80,94 82,12 83,30 84,48 85,65 86,83 88,00 89,18 90,35 91,52 92,69 93,86 95,02 96,19 97,35 98,52 99,68 100,8 102,00 103,16 104,32 105,47 106,63 107,78 108,94 110,09 111,24 112,39 113,54 114,69 115,84 117,00 118,14 119,28 120,43 121,57 122,72 123,86 125,00 126,14 127,29 128,42 129,56 0,025 1,0 78,62 79,84 81,07 82,29 83,51 84,73 85,95 87,17 88,38 89,59 90,80 92,01 93,22 94,42 95,63 96,83 98,03 99,23 100,4 101,6 102,8 104,0 105,2 106,4 107,58 108,77 109,96 111,14 112,33 113,51 114,70 115,88 117,06 118,24 119,41 120,59 121,77 122,94 124,12 125,29 126,46 127,63 128,80 129,97 131,14 132,31 133,48 134,64 135,81 0,01 0,5 82,00 83,25 84,50 85,75 86,99 88,24 89,48 90,72 91,95 93,19 94,42 95,65 96,88 98,11 99,33 100,6 101,8 103,0 104,2 105,4 106,6 107,8 109,1 110,3 111,50 112,70 113,91 115,12 116,32 117,52 118,73 119,93 121,13 122,32 123,52 124,72 125,91 127,11 128,30 129,49 130,68 131,87 133,06 134,25 135,43 136,62 137,80 138,99 140,17 0,005 0,1 89,27 90,57 91,87 93,17 94,46 95,75 97,04 98,32 99,61 100,89 102,17 103,44 104,72 105,99 107,26 108,53 109,79 111,06 112,32 113,58 114,84 116,09 117,35 118,60 119,85 121,10 122,35 123,59 124,84 126,08 127,32 128,56 129,80 131,04 132,28 133,51 134,74 135,98 137,21 138,44 139,67 140,89 142,12 143,34 144,57 145,79 147,01 148,23 149,45 0,001 99,9 26,06 26,76 27,47 28,17 28,88 29,59 30,30 31,02 31,74 32,46 33,18 33,91 34,63 35,36 36,09 36,83 37,56 38,30 39,04 39,78 40,52 41,26 42,01 42,76 43,51 44,26 45,01 45,76 46,52 47,28 48,04 48,80 49,56 50,32 51,08 51,85 52,62 53,39 54,16 54,93 55,70 56,47 57,25 58,02 58,80 59,58 60,36 61,14 61,92 0,999 99,5 29,48 30,23 30,98 31,74 32,49 33,25 34,01 34,77 35,54 36,30 37,07 37,84 38,61 39,38 40,16 40,94 41,71 42,49 43,28 44,06 44,84 45,63 46,42 47,21 48,00 48,79 49,58 50,38 51,17 51,97 52,77 53,57 54,37 55,17 55,97 56,78 57,58 58,39 59,20 60,00 60,82 61,62 62,44 63,25 64,06 64,88 65,69 66,51 67,33 0,995 99,0 31,25 32,02 32,79 33,57 34,35 35,13 35,91 36,70 37,48 38,27 39,06 39,86 40,65 41,44 42,24 43,04 43,84 44,64 45,44 46,25 47,05 47,86 48,67 49,48 50,29 51,10 51,91 52,72 53,54 54,36 55,17 55,99 56,81 57,63 58,46 59,28 60,10 60,93 61,75 62,58 63,41 64,24 65,07 65,90 66,73 67,56 68,40 69,23 70,06 0,990 64 Таблица XII. Критические значения U-критерия Уилкоксона (Манна-Уитни) (односторонний критерий, =0,01) n1 n2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 0 1 0 1 2 3 0 1 3 4 6 0 2 4 6 7 9 1 3 5 7 9 11 14 1 3 6 8 11 13 16 19 1 4 7 9 12 15 19 22 25 2 5 8 11 14 17 21 24 28 31 2 5 9 12 16 20 23 27 31 35 39 2 6 10 14 18 22 26 30 34 38 43 47 3 7 11 15 19 24 28 33 37 42 47 51 56 3 7 12 16 21 26 31 36 41 46 51 56 61 66 4 8 13 18 23 28 33 38 44 49 55 60 66 71 77 4 9 14 19 24 30 36 41 47 53 59 65 70 76 82 88 4 9 15 20 26 32 38 44 50 56 63 69 75 82 88 94 101 5 10 16 22 28 34 40 47 53 60 67 73 80 87 94 100 107 114 Продолжение таблицы XII (двусторонний критерий, = 0,01) n2 n1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0 0 0 0 0 0 0 1 1 1 2 2 2 2 3 3 3 4 4 4 5 0 0 0 1 1 2 2 3 4 4 5 5 6 6 7 8 8 9 9 10 10 0 1 1 2 3 4 5 6 7 7 8 9 10 11 12 13 14 14 15 16 17 2 3 4 5 6 7 9 10 11 12 13 15 16 17 18 19 21 22 23 24 4 6 7 9 10 12 13 15 16 18 19 21 22 24 25 27 29 30 32 7 9 11 13 15 17 18 20 22 24 26 28 30 32 34 36 37 39 11 13 16 18 20 22 25 27 29 31 34 36 38 40 43 45 47 16 19 21 24 26 29 31 34 37 39 42 44 47 50 52 55 16 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 28 31 34 37 41 44 47 51 54 58 61 64 68 71 34 38 42 46 49 53 57 60 64 68 72 76 79 42 46 50 54 59 63 67 71 75 79 83 88 51 55 60 64 69 73 78 82 87 91 96 60 65 70 70 75 77 81 75 81 87 93 79 86 92 99 84 91 98 105 89 97 104 111 94 102 109 117 99 107 115 123 104 113 121 129 105 112 118 125 131 138 65 Таблица XIII. Критические значения z-критерия знаков при разных уровнях значимости и объеме выборки n , % п 5 6 7 8 8 9 10 10 11 12 12 13 13 14 15 15 16 17 17 18 18 19 20 20 21 0,05 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 1 — — 8 9 10 11 11 12 13 13 14 15 15 16 17 17 18 19 19 20 20 21 22 22 0,01 п 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 — , % 5 21 22 23 23 24 24 25 25 26 27 27 28 28 29 29 30 31 31 32 32 33 33 34 35 0,05 1 23 24 24 25 25 26 27 27 28 28 29 30 30 31 31 32 33 33 34 34 35 36 36 37 0,01 п 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 — , % 5 35 36 36 37 37 38 39 39 40 40 41 41 42 42 43 44 44 45 45 46 46 47 48 48 0,05 1 37 38 39 39 40 40 41 41 42 43 43 44 44 45 46 46 47 47 48 48 49 50 50 51 0,01 п 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 — — , % 5 49 49 50 50 51 51 52 53 53 54 54 55 55 56 56 57 57 58 59 59 60 60 61 — 0,05 1 51 52 52 53 54 54 55 55 56 56 57 58 58 59 59 60 60 61 62 62 63 63 64 — 0,01 Таблица XIV. Критические значения парного Т-критерия Уилкоксона (односторонний критерий) Число парных наблюдений п 5 6 7 8 9 10 11 12 13 α Уровни значимости , % 5 1 — 0 2 0 3 0 5 1 8 3 10 5 13 7 17 10 21 12 0,05 0,01 Число парных наблюдений п 14 15 16 17 18 19 20 21 22 — Уровни значимости , % 5 1 25 16 30 19 35 23 41 28 47 33 53 38 60 42 67 50 74 56 0,05 0,01 66 Продолжение таблицы XIV, (двусторонний критерий) Число парных наблюдений п 6 7 8 9 10 11 12 13 14 15 Уровни значимости , % 5 1 — 1 — 3 5 1 7 3 9 4 12 6 15 8 18 11 22 14 26 17 0,05 0,01 Число парных наблюдений п 16 17 18 19 20 21 22 23 24 25 — Уровни значимости , % 5 1 31 21 36 24 41 29 47 33 53 39 60 44 67 50 74 56 82 62 90 69 0,05 0,01 Примечание. Для n>25 критические значения Т-критерия можно определить по формуле nn 1 nn 12n 1 , 4 24 где n- число парных наблюдений; t зависит от принятого уровня значимости, т. е. t0,05=1,96 и t0,01=2,58. Tst Таблица XV. Критические значения коэффициента асимметрии As Объем выборки n Уровни значимости , % 25 30 35 40 45 50 60 70 80 90 100 125 150 175 200 5 0,711 0,661 0,621 0,587 0,558 0,533 0,492 0,459 0,432 0,409 0,389 0,350 0,321 0,298 0,280 1 1,061 0,982 0,921 0,869 0,825 0,787 0,723 0,673 0,631 0,596 0,567 0,508 0,464 0,430 0,403 0,05 0,01 Объем выборки n 250 300 350 400 450 500 550 600 650 700 750 800 850 900 950 1000 — Уровни значимости , % 5 0,251 0,230 0,213 0,200 0,188 0,179 0,171 0,163 0,157 0,151 0,146 0,142 0,138 0,134 0,130 0,127 0,05 1 0,360 0,329 0,305 0,285 0,269 0,255 0,243 0,233 0,224 0,215 0,208 0,202 0,196 0,190 0,185 0,180 0,01 67 Таблица XVI. Критические значения коэффициента эксцесса Ех Объем выборки п 10 0,890 0,873 0,863 0,857 0,851 0,847 0,844 0,841 0,839 0,835 0,832 0,830 0,828 0,826 0,818 0,814 0,812 0,810 0,10 11 16 21 26 31 36 41 46 51 61 71 81 91 101 201 01 401 501 Уровни значимости , % 5 0,907 0,888 0,877 0,869 0,863 0,858 0,854 0,851 0,848 0,843 0,840 0,838 0,835 0,834 0,823 0,818 0,816 0,814 0,05 1 0,936 0,914 0,900 0,890 0,883 0,877 0,872 0,868 0,865 0,859 0,855 0,852 0,848 0,846 0,832 0,826 0,822 0,820 0,01 Таблица XVII. Критические значения величины нормированного отклонения при оценке сомнительных вариант с учетом объема выборки n и уровней значимости п 4 5 6 7 8 9 10 11 12 , % 5 1,71 1,92 2,07 2,18 2,27 2,35 2,41 2,47 2,52 0,05 1 1,73 1,97 2,16 2,31 2,43 2,53 2,62 2,69 2,75 0,01 п 13 14 15 16 17 18 19 20 21 — , % 5 2,56 2,60 2,64 2,67 2,70 2,73 2,75 2,78 2,80 0,05 1 2,81 2,86 2,90 2,95 2,98 3,02 3,05 3,08 3,11 0,01 п , % 23 24 25 26 27 28 29 30 5 2,84 2,86 2,88 2,90 2,91 2,93 2,94 2,96 1 3,16 3,18 3,20 3,22 3,24 3,26 3,28 3,29 — 0,05 0,01 68 Таблица XVIII. Критические значения критерия п 4 5 6 7 8 9 10 11 12 α Уровни значимости , % 5 0,76 0,64 0,56 0,31 0,47 0,44 0,41 0,39 0,38 0,05 1 0,89 0,78 0,70 0,64 0,59 0,54 0,53 0,50 0,48 0,01 п 13 14 15 16 17 18 19 20 21 — t1 x 2 x1 x n 1 x1 Уровни значимости , % 5 0,36 0,35 0,34 0,33 0,32 0,31 0,31 0,30 0,30 0,05 1 0,46 0,45 0,44 0,43 0,42 0,41 0,40 0,39 0,38 0,01 . п 22 23 24 25 26 27 28 29 30 — Уровни значимости , % 5 0,29 0,28 0,28 0,28 0,27 0,27 0,27 0,26 0,26 0,05 1 0,38 0,37 0,37 0,36 0,36 0,35 0,35 0,34 0,34 0,01 69 Таблица XIX. Критические значения коэффициента корреляции rх,y Степени свободы ν=n-2 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Уровни значимости , % 5 1 0,75 0,71 0,67 0,63 0,60 0,58 0,55 0,53 0,51 0,50 0,48 0,47 0,46 0,44 0,43 0,42 0,41 0,40 0,40 0,39 0,38 0,37 0,05 0,87 0,83 0,80 0,77 0,74 0,71 0,68 0,66 0,64 0,62 0,61 0,59 0,58 0,56 0,55 0,54 0,53 0,52 0,51 0,50 0,49 0,48 0,01 Степени свободы ν=n-2 27 28 29 30 35 40 45 50 60 70 80 90 100 125 150 200 300 400 500 700 900 1000 — Уровни значимости , % 5 1 0,37 0,36 0,36 0,35 0,33 0,30 0,29 0,27 0,25 0,23 0,22 0,21 0,20 0,17 0,16 0,14 0,11 0,10 0,09 0,07 0,06 0,06 0,05 0,47 0,46 0,46 0,45 0,42 0,39 0,37 0,35 0,33 0,30 0,28 0,27 0,25 0,23 0,21 0,18 0,15 0,13 0,12 0,10 0,09 0,09 0,01 Таблица XX. Критические значения коэффициента корреляции рангов при различных уровнях значимости и объемах выборки n n 5 6 7 8 9 10 11 12 13 14 15 16 , % 5 0,94 0,85 0,78 0,72 0,68 0,64 0,61 0,58 0,56 0,54 0,52 0,50 0,05 1 — — 0,94 0,88 0,83 0,79 0,76 0,73 0,70 0,68 0,66 0,64 0,01 п 17 18 19 20 21 22 23 24 25 26 27 28 — , % 5 0,48 0,47 0,46 0,45 0,44 0,43 0,42 0,41 0,40 0,39 0,38 0,38 0,05 1 0,62 0,60 0,58 0,57 0,56 0,54 0,53 0,52 0,51 0,50 0,49 0,48 0,01 п 29 30 31 32 33 34 35 36 37 38 39 40 — , % 5 0,37 0,36 0,36 0,36 0,34 0,34 0,33 0,33 0,33 0,32 0,32 0,31 0,05 1 0,48 0,47 0,46 0,45 0,45 0,44 0,43 0,43 0,42 0,41 0,41 0,40 0,01 70 Таблица XXI. Критические значения критерия Уилкоксона (двусторонний критерий) Нижняя граница n1 4 5 6 7 8 9 10 11 12 n2 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 7 8 9 10 11 12 8 9 10 11 12 9 10 11 12 10 11 12 11 12 12 Уровни значимости 0.005 0.01 0.025 0.05 0.10 10 11 13 10 11 12 14 10 11 12 13 15 10 11 13 14 16 11 12 14 15 17 11 13 14 16 19 12 13 15 17 20 12 14 16 18 21 13 15 17 19 22 15 16 17 19 20 16 17 18 20 22 16 18 20 21 23 17 19 21 23 25 18 20 22 24 27 19 21 23 26 28 20 22 24 27 30 21 23 26 28 32 23 24 26 28 30 24 25 27 29 32 25 27 29 31 34 26 28 31 33 36 27 29 32 35 38 28 30 34 37 40 30 32 35 38 42 32 34 36 39 41 34 35 38 41 44 35 37 40 43 46 37 39 42 45 49 38 40 44 47 51 40 42 46 49 54 43 45 49 51 55 45 47 51 54 58 47 49 53 56 60 49 51 55 59 63 51 53 58 62 66 56 59 62 66 70 58 61 65 69 73 61 63 68 72 76 63 66 71 75 80 71 74 78 82 87 73 77 81 86 91 76 79 84 89 94 87 91 96 100 106 90 94 99 104 110 105 109 115 120 127 Верхняя граница 0.20 14 15 17 18 20 21 23 24 26 22 24 26 28 30 32 34 36 33 35 37 40 42 44 47 45 48 50 53 56 59 59 62 65 69 72 75 78 82 86 93 97 101 112 117 134 0.20 22 25 27 30 32 35 37 40 42 33 36 39 42 45 48 51 54 45 49 53 56 60 64 67 60 64 69 73 77 81 77 82 87 91 96 96 102 107 112 117 123 129 141 147 166 Уровни значимости 0.10 0.05 0.025 0.01 23 25 26 26 28 29 30 29 31 32 33 32 34 35 37 35 37 38 40 37 40 42 43 40 43 45 47 43 46 48 50 46 49 51 53 35 36 38 39 38 40 42 43 42 44 45 47 45 47 49 51 48 51 53 55 52 54 57 59 55 58 61 63 58 62 64 67 48 50 52 54 52 55 57 59 56 59 61 63 60 63 65 68 64 67 70 73 68 71 74 78 72 76 79 82 64 66 69 71 68 71 74 77 73 76 79 82 77 81 84 87 82 86 89 93 86 91 94 98 81 85 87 91 86 90 93 97 92 96 99 103 97 101 105 109 102 106 110 115 101 105 109 112 107 111 115 119 113 117 121 126 118 123 127 132 123 128 132 136 129 134 139 143 136 141 146 151 147 153 157 162 154 160 165 170 173 180 185 191 0.005 34 38 41 45 48 52 55 40 44 49 53 57 61 65 69 55 60 65 70 75 80 84 73 78 84 89 95 100 93 99 105 111 117 115 122 128 135 139 147 154 166 174 195 71 ЛИТЕРАТУРА 1. Плохинский Н.А. Биометрия. 2-е изд.-М: МГУ, 1970, 368 стр. 2. Митропольский А.К. Техника статистических вычислений. 2-е изд.- М: Наука, Главная редакция физико-математической литературы, 1971. 3. Гублер Е.В., Генкин А.А. Применение непараметрических критериев в медико-биологических исследованиях. – Ленинград: Медицина, Ленинградское отд., 1971. 4. СидоренкоЕ.В. Методы математической обработки в психологии.- Речь, Санкт-Петербург,2002 ,346 с. 5. Сборник задач по математике для ВТУЗОВ. Теория вероятностей и математическая статистика под ред. А.В. Ефимова. М: Наука, Главная редакция физико-математической литературы, 1990. 6. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. Под ред. В.В. Фигурнова. М: Финансы и статистика, 1995, 384 с. 7. Урбах В.Ю. Статистический анализ в биологических и медицинских исследованиях. М: Медицина, 1975, 295 с. 8. Кендел М. Ранговые корреляции. М: Статистика, 1975, 214 с. 9. Холлендер М. Вулф Д.А. Непараметрические методы статистики. Перевод с анг. Под ред. Ю.П.Адлера и Ю.П. Тюрина. М: Финансы и статистика, 1983, 518 с. 10.Гланц С. Медико-биологическая статистика. Пер. с англ. Доктора ф-м наук Ю.А. Данилова под ред. Н.Е.Бузикашвили и Д.В. Самойлова. Практика, Москва, 1999, 459 с 11.Реброва О.Ю. Статистический анализ медицинских данных. Применение прикладных программ СТАТИСТИКА. М: Издательство Медиа Сфера, 2002, 305 с 72 СОДЕРЖАНИЕ 1. 2. 3. 4. 5. 6. Задание 1. Построение интервального ряда и вычисление основных статистических характеристик. Задание 2. Оценка параметров распределения…………………………. Задание 3. Проверка статистических гипотез…………………………... Задание 4. Элементы корреляционного анализа ………………………. Приложение……………….......................................................................... Литература………………………………………………………………….. 73