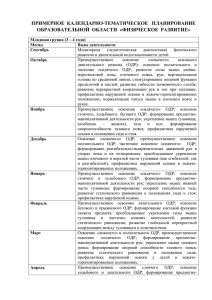
1, m x c x d i n + = = НЕЛИНЕЙНАЯ ЗАДАЧА МАКСИМИЗАЦИИ

Экономические науки
Вестник
Нижегородского
университетаприбыли
им. Н.И. Лобачевского,
2011, №
4 (1), с. 241–242
Нелинейная
задача максимизации
в условиях колебания
рыночных
цен
241
УДК 519.86
НЕЛИНЕЙНАЯ ЗАДАЧА МАКСИМИЗАЦИИ ПРИБЫЛИ
В УСЛОВИЯХ КОЛЕБАНИЯ РЫНОЧНЫХ ЦЕН
 2011 г.
О.В. Подчищаева, М.С. Бурова
Нижегородский госуниверситет им. Н.И. Лобачевского
schocolate@yandex.ru
Поступила в редакцию 25.06.2010
Решается задача максимизации прибыли предприятия, выпускающего два вида продукции, причем
цены на продукцию берутся не постоянными, а линейно зависящими от количества продукции на рынке. В этом случае задача получается уже нелинейной, хотя ограничения остаются по-прежнему линейными. Задача рассматривается на примере товаров, выпускаемых фирмой NOKIA.
Ключевые слова: максимизация, товар, прибыль, цена, линейность, нелинейность, программирование, экстремум, стационарность, точка.
Как известно, в классической задаче максимизации прибыли цены на производимый товар
берутся фиксированными, что позволяет решить эту задачу линейного программирования
стандартными методами [1]. Реальная рыночная
ситуация диктует изменение цен в зависимости
от объема товара на рынке, в простейшем приближении линейное [2].
Таким образом, функция прибыли будет
иметь уже нелинейный вид, например для двух
видов выпускаемого товара:
L ( x)  p1 ( x1 ) x1  p2 ( x2 ) x2 .
Здесь p1 ( x1 ) , p 2 ( x 2 ) – цены на товар как
функции его количества на рынке, в простейшем случае линейные:
p1 ( x1 )  a1  b1 x1 ,
p 2 ( x 2 )  a 2  b2 x 2 [2].
В итоге получается уже задача нелинейного
программирования с квадратичной функцией
прибыли и линейными ограничениями [1]:
L( x )  b1 x12  b2 x22  a1 x1  a2 x2 ,
(1)
ai , bi  0, i  1, 2.
Линейные ограничения:
mi x1  ci x2  d1 , i  1, n ,
где n – количество ограничений.
Квадратичная функция (1) может иметь максимум как внутри или вне области допустимых
решений (ОДР), так и на ее границе. Рассмотрим вначале возможность максимизации функции (1) внутри или вне области допустимых решений. Найдем стационарную точку функции (1):
a
a
(2)
x0  1 , x0  2 ,
1
2b1
2
2b2
причем характеристические величины [1]
  L''x1 x1  L''x2 x2  L''x1 x2  0
(3)
и L''x1x1  0 в точке x10 и x20 говорят о том, что
данный экстремум является максимумом.
Также наибольшее значение функция (1)
может принимать на границах области допустимых решений или на ее сторонах или в вершинах.
Сначала рассмотрим процесс поиска максимума на сторонах ОДР. Из системы ограничений выражаем:
d  mi x1
(4)
x2  i
, i  1, n .
ci
Получаем на границах ОДР функцию L:
2
 d  mi x1 
 d i  mi x1  (5)
L( x1 )  b1 x12  b2  i
  a1 x1  a2 

ci
ci




Исследуя функцию (5) на экстремумы обычным способом, получаем, что на границах ОДР
она всегда имеет максимумы в точках:
a c 2  2b2 d i mi  a2 mi ci
x1G  1 i
,
2b1ci2  2b2 mi2
(6)
d i  mi x1G
G
x2 
, i  1, n.
ci
Теперь рассмотрим вопрос о возможности
максимума функции (1) в вершинах ОДР
Ai , i  1, n .
1
1
1
Координаты вершин x1Ai , x2Ai , i  1, n находятся путем попарного решения уравнений системы ограничений.
Координаты A1 из системы:
m1 x1  c1 x 2  d 1

mn x1  c n x 2  d n
Координаты Ai , i  2, n :
(7)
242
О.В. Подчищаева, М.С. Бурова
X 1A1
X 1Ai 
mi 1 x1  c i 1 x 2  d i 1

mi x1  c i x 2  d i
d c  d 2 c1
m d  mn d1
 1 n
, X 2A1  1 2
,
m1c n  mn c1
m1 c n  m n c1
(8)
(9)
d i 1c i  d i ci 1
m d  mi d i 1
, X 2Ai  i 1 i
.(10)
mi 1c i  m i ci 1
mi 1ci  mi c i 1
Затем вычисляется значение функции L( X )
в вершинах Ai .
В итоге при поиске максимума функции
прибыли выбирается наибольшее значение из:
L ( X 10 , X 20 ), L( X 1G , X 2G ), L( X 1A , X 2A ) , где i=1, n.
i
1
i
i
Таким образом, решается задача максимизации прибыли уже не с фиксированными ценами, а с учетом их реального колебания, что может существенно влиять на значение прибыли.
Для примера рассмотрим выпуск фирмой
NOKIA 45% от общего рыночного объема двух
видов продукции:
1) смартфоны и коммуникаторы,
2) 3-G телефоны.
По исследованиям рынка за 2004–2009 годы
можно составить следующие зависимости цен
от количества товара на рынке:
p1 ( x1 )  605.8  6 x1 ,
p2 ( x2 )  545  40.05 x2 .
Здесь p1 и p 2 – цены на продукцию 1-го и
2-го типа в долларах, x1 и x2 – количество продукции 1-го и 2-го типа соответственно в миллионах штук. Получим нелинейную задачу максимизации прибыли:
L ( X )  (605.8  6 x1 ) x1  (545  40.05 x2 ) x2  max . (11)
При линейных ограничениях, полученных из
маркетинговых исследований:
0.1305  x1  1.98,
(12)
0.1575  x2  3.231.
Сначала найдем критические точки функции
прибыли, не учитывая ОДР.
Из формулы (2) получим x10  50 млн шт. и
x20  7 млн шт.
Эта точка не попадает в область допустимых
решений, значит, оптимальное количество продукции, обеспечивающее максимальную прибыль, нужно искать в вершинах данной прямоугольной ОДР (12) и на ее границах.
Рассмотрим 4 вершины ОДР – A1 , A2 , A3 , A4
и вычислим в них значения функции прибыли:
A1 : x1  0.1305; x2  1.575; L( x1A , x2A )  837.98
млн долл.
A2 : x1  0.1305; x2  3.231; L( x1A , x2A )  1421.752
млн долл.
A3 : x1  1.98; x2  3.231; L( x1A , x2A )  2518.759
млн долл.
A4 : x1  1.98; x2  1.575; L ( x1A , x2A )  1934.988
млн долл.
По прямоугольной форме ОДР можно определить, что на ее границах значения функции L
будут меньше, чем в вершине A3 [2].
Таким образом, мы получим максимальное
значение
прибыли
в
вершине A3 ,
1
1
2
2
3
3
4
4
Lmax ( x1A , x2A )  2518.759 млн долл.; x1opt  1.98
3
3
млн штук смартфонов; x2 opt  3.231 млн штук
3-G телефонов.
Если бы мы не учитывали рыночного колебания цен, то оптимальное решение задачи могло быть совсем другим:
Lmax ( x1A , x2A )  605.8 1.98  545  3.231  2960.375
млн долл.
3
3
Список литературы
1. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании.
М.: Дело, 2008.
2. Малыхин В.И. Математика в экономике. М.:
ИНФРА, 2007.
3. Цены и ценообразование: Учебник для вузов.
5-е изд. / Под ред. В. Есипова. СПб.: Питер Пресс,
2009.
NONLINEAR PROBLEM OF PROFIT MAXIMIZATION UNDER CONDITIONS
OF FLUCTUATION OF MARKET PRICES
O.V. Podchishchaeva, M.S. Burova
We consider and solve the problem of maximizing the profits of a company producing two types of products, when
prices for products are not constant, but linearly dependent on the quantity of products on the market. In this case, the
problem is non-linear, although the constraints still remain linear. As an example of such a problem, we refer to the
case of the Nokia company.
Keywords: maximization, product, profit, price, linearity, nonlinearity, programming, extremum, stationarity, point.