Фрагментация релятивистских ядер 16O, 22Ne, 32S и

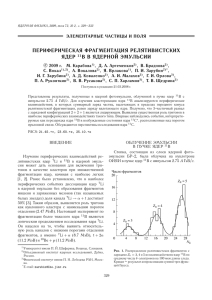
РОССИЙСКАЯ АКАДЕМИЯ НАУК
ПЕТЕРБУРГСКИЙ ИНСТИТУТ ЯДЕРНОЙ ФИЗИКИ
им. Б.П. КОНСТАНТИНОВА
На правах рукописи
УДК 539.171.017
ЛЕВИЦКАЯ Ольга Васильевна
ФРАГМЕНТАЦИЯ РЕЛЯТИВИСТСКИХ ЯДЕР 16O, 22Ne, 32S
И 208Pb В ДИАПАЗОНЕ ЭНЕРГИЙ 3,7–200 А ГэВ
В ЯДЕРНЫХ ФОТОЭМУЛЬСИЯХ
01.04.16 – физика атомного ядра и элементарных частиц
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Гатчина
2007
Работа выполнена в Отделении физики высоких энергий
Петербургского института ядерной физики
им. Б.П. Константинова РАН
Официальные оппоненты:
доктор физико-математических наук,
профессор
–
кандидат физико-математических наук,
старший научный сотрудник
–
Ведущая организация
–
А.Б. Курепин,
В.П. Кондратьев.
Физический институт
им. П.Н. Лебедева РАН.
Защита состоится ”……” ………… 2007 года в .................часов
на заседании диссертационного совета Д 002.115.01 при
Петербургском
институте
ядерной
физики
им. Б.П. Константинова РАН по адресу:
188300, г. Гатчина Ленинградской области, Орлова роща.
С диссертацией можно ознакомиться в библиотеке ПИЯФ РАН.
Автореферат разослан ”……” ………. … 2007 г.
Ученый секретарь
диссертационного совета
И.А. Митропольский
2
Общая характеристика работы
Актуальность работы
Диссертация посвящена изучению механизма фрагментации
релятивистских ядер различной массы (16O, 22Ne, 32S и 208Pb) в широком
диапазоне энергий (от ≈ 3,7 до 200 ГэВ/нуклон) при их неупругих
взаимодействиях с ядрами в фотоэмульсии. Исследование механизма
фрагментации релятивистских ядер наряду с поисками кварк-глюонной
плазмы – одна из центральных проблем физики ядро-ядерных
взаимодействий при высоких энергиях. Целью работы является
установление общих закономерностей процесса фрагментации легких и
тяжелых ядер, которые необходимы для понимания механизма ядроядерных взаимодействий (определения доминирующего механизма и
вклада других возможных каналов фрагментации, таких как
электромагнитная диссоциация, образование префрагментов, распад
нестабильных промежуточных ядер, взаимодействие в конечном
состоянии), его связи с процессами деления ядер и множественного
рождения частиц. В первую очередь это относится к распределению
поперечных импульсов фрагментов, которое является источником
информации о структуре релятивистских ядер в условиях малых
передаваемых импульсов.
Хотя спектр моделей, описывающих этот процесс, достаточно широк, в
их основе лежат два альтернативных подхода. В первом, до сих пор
встречающемся, фрагментация трактуется как распад возбужденных
остаточных ядер и происходит после процесса множественного рождения
частиц во второй медленной фазе ядро-ядерного взаимодействия. Во
втором представление о механизме предельной фрагментации адронов при
высоких энергиях распространено на релятивистские ядра. Т. е.
фрагментация рассматривается как быстрый, холодный процесс
освобождения виртуальных кластеров, существующих в релятивистском
ядре еще до его взаимодействия с ядром-мишенью. После взаимодействия
виртуальные кластеры, т. е. фрагменты, становятся реально наблюдаемыми
с импульсами, близкими к тем, которые они имели в собственной системе
фрагментирующего ядра. Распределение поперечных импульсов
фрагментов описывается статистической моделью Гольдгабер–Фешбаха–
Хуанга и определяется граничным импульсом Ферми исходного
фрагментирующего ядра.
Виртуальные фрагменты можно рассматривать как квазичастицы,
возникающие в результате самосогласованного движения нуклонов в ядре
3
при нулевой температуре. Эта способность образовывать квазичастицы
является общим свойством системы многих тел. Поэтому фрагментация как
физический процесс представляет интерес и в связи с проблемой
многочастичных систем.
Среди виртуальных кластеров в ядрах могут существовать и
нестабильные изотопы, такие как 5He, 5Li, 8Be. Вследствие этого часть
двухзарядных фрагментов может образовываться, в частности, через распад
8
Be → 2α. Экспериментальное определение доли этого канала при
фрагментации релятивистских ядер различной массы может оказаться
полезным для уточнения существующих представлений о процессе
нуклеосинтеза в гелиевых звездах. Знание фрагментационных
характеристик релятивистских ядер при различных начальных энергиях
необходимо и для решения ряда задач ядерной астрофизики.
В свете вышеизложенного результаты исследования фрагментации
релятивистских ядер, проведенные в диссертации, существенны для
понимания механизма ядро-ядерных взаимодействий при высоких
энергиях, процессов кластеризации нуклонов в ядрах, квантовых эффектов
в системе тождественных частиц, процесса нуклеосинтеза (как процесса,
обратного фрагментации).
Научная новизна и практическая ценность работы
1. Разработан новый метод экспериментального определения зарядов
легких фрагментов, основанный на измерении суммарной длины спектра
сгустков.
2. Разработана методика измерения малых углов, позволяющая
измерять парные углы в плоскости фотоэмульсии между легкими
фрагментами свинца с энергией 160 А ГэВ порядка 0,1 – 0,5 мрад с
точностью ≈ 0,01 мрад.
3. Исследована фрагментации группы легких ядер: 22Ne, 16O и 32S в
диапазоне энергиий 3,7 – 200 А ГэВ. Показано, что для всех фрагментов
исследуемой группы ядер экспериментальные распределения величины
P⊥*Y = P⊥Y ⋅
A −1
(где P⊥ Y – проекция поперечного импульса фрагмента
F(A − F)
с массой F на плоскость эмульсии, А – массовое число первичного ядра)
описываются нормальным распределением. Экспериментальные оценки
стадартных отклонений σ0exp(y) с хорошей точностью совпадают со
значениями σ0, определяемой его граничным импульсом Ферми, ранее
измеренными в эксперименте по квазиупругому рассеянию электронов на
ядрах и со значениями, вычисленными через радиусы ядер кислорода,
неона
и серы. Для ядра 16O (4,5 A ГэВ/c) оценка константы этого
4
распределения
σ0exp(y) = 102,3 ± 1,2 МэВ/с, для ядра 22Ne (4,1 A ГэВ/c)
σ0exp(y) = 102,5 ±2,5 МэВ/с, для ядра 32S (4,5 A ГэВ/c) σ0exp(y) = 105,0 ± 1,3 МэВ/с,
а для ядра 32S (200 А ГэВ/c) σ0exp(y) = 102,9 ± 1,5 МэВ/с.
Экспериментальные оценки дисперсий распределений величин P⊥Y
22
для фрагментов ядра
Ne с различными зарядами описываются
параболической зависимостью от F в соответствии со статистической
моделью фрагментации Гольдгабер.
4. Экспериментальные распределения коэффициентов азимутальной
асимметрии (α) и коллинеарности (β) для фрагментов вышеуказанных ядер
согласуются с полученными в модели независимого испускания (МНИ).
5. Исследовано распределение поперечных импульсов вторичных
фрагментов ядер 22Ne. Показано, что совокупность величин
Z ⋅ (2Z1 − 1) 1/ 2
Py = P0 ⋅ [ 2
] ⋅ tgϕ 2 для вторичных фрагментов распределена по
( Z1 − Z 2 )
Гауссу со средним значением, близким к нулю, и стандартным
отклонением σexp = (105 ± 7) МэВ/с, равным ≈ PF/√5 исходного ядра 22Ne
(Z1, Z2 – заряды первичного и вторичного фрагментов, φ2 – “плоский” угол
вторичного фрагмента относительно направления вектора импульса
первичного фрагмента, P0 – импульс на нуклон ядра 22Ne).
6. Исследована фрагментация тяжелого релятивистского ядра 208Pb в
глубоко неупругих Pb+Em взаимодействиях при энергии 160 А ГэВ. По
измеренным углам ϕij между парами следов легких фрагментов ядер
свинца (с зарядами Z = 2, 3, 4) в плоскости эмульсии получена оценка
константы нормального распределения “плоских” углов ϕ фрагментов
относительно вектора импульса первичного ядра P0, σϕ = (0,38 ± 0,02) мрад.
Полученная оценка также совпадает с величиной, определяемой из
импульса Ферми для ядра свинца.
7. В распределениях плоских парных углов ϕij между следами
двухзарядных фрагментов ядер 16O, 22Ne и 32S имеется избыток в области
малых углов ≤2,5 мрад, обусловленный дополнительным каскадным
8
механизмом их образования через канал
Be → 2α. Из анализа
распределений парных “плоских” углов и парных азимутальных углов
между двухзарядными фрагментами в реакциях 16O → ≥ 2α + X,
22
Ne → ≥ 2α + X, 32S → ≥ 2α + X сделан вывод о существовании двух
механизмов их образования. Основная их часть есть результат холодной
фрагментации ядер. Доля α-частиц от распада промежуточного состояния
8
Ве→2α в вышеуказанных реакциях для ядер 16O составляет ≈ 9,7 %, 22Ne ≈
8,7 % и 32S ≈ 4, 6%.
5
8. В глубоко неупругих Pb+Em взаимодействиях (160 А ГэВ) в
распределении парных углов в плоскости эмульсии между следами
двухзарядных фрагментов ядер свинца в области ϕij ≤ 0,03 мрад также
имеется избыток, обусловленный распадом 8Be → 2α, оценка доли этого
канала составляет (13 ± 2) %.
Апробация диссертации
Полученные результаты докладывались на XV Международной
конференции LEND-95, на рабочих совещаниях EMU01-коллаборации
(Кошице, 1996; Дубна, 1999), на Всероссийском совещании "Применение
метода
ядерных
фотоэмульсий
для
исследования
структуры
релятивистских ядер" (Дубна, 1998), на Международном совещании
"Использование фотоэмульсионного метода для исследования структуры
релятивистских ядер" (Дубна, 2000) на “International Symposium on Nuclear
Physics” (BARC Mumbai, India, 2000), на XIII International Baldin Seminar
on High Energy Physics Problems (Dubna, 2006).
Структура и объем работы
Диссертация состоит из введения, четырех глав, заключения и списка
литературы. Общий объем диссертации (включая 34 рисунка, 8 таблиц и
список литературы из 144 наименований) составляет 112 страниц
машинописного текста.
Краткое содержание диссертации
Во введении обосновывается актуальность исследования, даются
краткие комментарии экспериментов по проблематике, затронутой в
работе, кратко излагается содержание четырех глав диссертации.
В первой главе изложены результаты эксперимента по изучению
фрагментации ядер 22Ne с импульсом 4,1 А ГэВ/с в фотоэмульсии. Для
фрагментов с различными зарядами ZF получены экспериментальные
оценки дисперсий нормальных распределений проекций поперечных
импульсов на плоскость эмульсии. Показано, что величины этих дисперсий
описываются параболической зависимостью от ZF в соответствии со
статистической моделью фрагментации Гольдгабер–Фешбаха–Хуанга
(рис. 1). Показано, что распределение величины
A −1
(1)
P* = P ⋅
Y
Y
F(A − F)
описывается распределением Гаусса (А – массовое число 22Ne, F – массовое
число фрагмента) (рис. 2). Стандартное отклонение распределения (1) σexp
6
= (102,5 ± 2,5) МэВ/с совпадает с ожидаемой величиной σ 0 = PF / 5 ,
определяемой через граничный импульс Ферми (PF) для ядра 22Ne из
эксперимента по квазиупругому рассеянию электронов на ядрах и равной
105,1 МэВ/с.
Рис. 1. Экспериментальная зависимость константы σF от массы фрагмента АF. Кривая –
ожидаемая параболическая зависимость с константой σ0 = 105,1 МэВ/c
Полученные экспериментальные распределения
азимутальной асимметрии
1
α=
⋅ ∑ Cosε i , j
k ⋅ (k − 1)
и коэффициента коллинеарности
β=
коэффициента
(2)
1
⋅ ∑ Cos(2ε i , j )
k ⋅ (k − 1)
(3)
также подтверждают гипотезу независимого разлета фрагментов. При
исследовании явления мультифрагментации в событиях, содержащих
k = 2, 3, 4 фрагментов, распределение модулей векторных сумм
поперечных импульсов фрагментов согласуется с ожидаемым по модели
независимого испускания (МНИ).
7
Распределение PY* -проекций поперечных импульсов фрагментов ядра 22Ne на
плоскость эмульсии. Гистограмма – эксперимент, плавная кривая – нормальное
распределение с константой σexp = (102,5 ± 2,5) МэВ/с
Рис. 2.
Продукты фрагментации первичного релятивистского ядра также
представляют собой релятивистские ядра меньшей массы, т. н.
’’первичные’’ фрагменты. Последующая фрагментация таких первичных
фрагментов может служить инструментом для исследования их структуры.
В частности, величина σ 02 , дисперсия распределения проекций поперечных
импульсов, но уже вторичных фрагментов, характеризует граничный
импульс Ферми нуклонов в первичном фрагменте или ’’температуру’’
вырожденного газа нуклонов в нем. В § 3 представлены результаты
исследования свойств 163 первичных фрагментов релятивистского ядра
22
Ne на основании полученных экспериментальных угловых распределений
255 их вторичных фрагментов. Показано, что совокупность величин
Z ⋅ (2Z1 − 1) 1/ 2
(4)
Py = P0 ⋅ [ 2
] ⋅ tgϕ 2
( Z1 − Z 2 )
описывается распределением Гаусса со средним значением, равным нулю,
и стандартным отклонением σexp = (105 ± 7) МэВ/с.
8
Рис. 3. Экспериментальное распределение величины Py (ГэВ/с) для вторичных фрагментов
ядра 22Ne (гистограмма). Плавная кривая соответствует нормальному распределению с
константой σexp = 105 МэВ/с. Распределение поперечных импульсов вторичных фрагментов
ядра 22Ne (гистограмма). Плавная кривая – распределение Рэлея с константой
σexp = 113 МэВ/с
Распределение величины
P⊥ = P0 ⋅ [
Z 2 ⋅ (2Z1 − 1) 1 / 2
] ⋅ (tgα 22 + tgϕ 22 )1 / 2
( Z1 − Z 2 )
(5)
для вторичных фрагментов
описывается распределением Рэлея с
константой σexp = (113 ± 7) МэВ/с, близкой к величине стандартного
отклонения нормального распределения величины Py (рис. 3). В формулах
(4) и (5) Z1 – заряды первичных фрагментов, Z2 – заряды вторичных
углы первичных
фрагментов, ϕ1 – “плоские”, α1 – ”глубинные”
22
фрагментов относительно направления импульса ядра Ne, ϕ2 – “плоские”,
α2 – “глубинные” углы вторичных фрагментов относительно направления
импульса первичного фрагмента, P0 – импульс на нуклон в ядре 22Ne.
Распределение азимутальных углов вторичных фрагментов ψQ
с
плоскостью реакции Q не отличается от равномерного распределения.
Cделан вывод о том, что на имеющейся статистике свойства первичных
фрагментов, продуктов фрагментации ядра 22Ne (в основном это ядра с
9
зарядами 5, 6, 7, 8 и 9), не отличаются от свойств стабильных изотопов. Их
последующая фрагментация также описывается в рамках статистической
модели Г-Ф-Х.
Во второй главе изложены экспериментальные результаты по
изучению фрагментации релятивистских ядер 16O с импульсом 4,5 А ГэВ/с
и 32S (4,5 и 200 А ГэВ/с). Показано, что при фрагментации вышеуказанных
ядер распределения величин PY* (1) описываются распределениями Гаусса.
Для ядра 16O оценка константы этого распределения σ0exp(y) = 102,3 ± 1,2 МэВ/с,
для ядра 32S (4,5 A ГэВ/c) σ0exp(y) = 105,0 ± 1,3 МэВ/с, а для 32S (200 А ГэВ/c)
σ0exp(y) = 102,9 ± 1,5 МэВ/с (рис. 4 – 6). Это хорошо согласуется со
значениями σ0 = 100,9 МэВ/с и 108,7 МэВ/с, вычисленными из граничных
импульсов Ферми из эксперимента по квазиупругому рассеянию
электронов на ядрах, и со значениями 99,6 МэВ/с и 104,2 МэВ/с,
вычисленными через радиусы ядер кислорода и серы по формуле
(9π )1 / 3 h .
(6)
5 2ro
Переход к безразмерной переменной, равной величине поперечного
импульса фрагмента на деленной на соответствующее стандартное
отклонение (т. н. “универсальный поперечный импульс”), исключает уже
зависимость и от величины σ0 (или, что то же самое, от PF).
Экспериментальное распределение ее проекций на плоскость эмульсии
(Pyun = Py(F)/σF) описывается стандартным нормальным распределением.
При таком представлении данных достигается унификация в описании
экспериментальных инклюзивных распределений поперечных импульсов
для фрагментов любых ядер. На рис. 7 представлено суммарное
стандартное нормальное распределение Pyun со стандартным отклонением
σun(y) ≈ 1 и средним < Pyun > ≈ 0 для всех фрагментов ядер 16O (4,5 А ГэВ/c), 32S
σ 0 (ro ) =
(4,5 А ГэВ/c) и
32
S (200 А ГэВ/c).
10
N
400
a)
32
S (4.5 A GeV/c)
300
200
100
0
-200
200 Py*, MeV/c
0
N проекций поперечных импульсов Py* для фрагментов ядра 32S (4,5 А
Рис. 4. Распределение
ГэВ/c). Гистограмма – эксперимент, плавная32Sкривая
– нормальное распределение со
(4.5 A GeV/c)
стандартным отклонениемb)
σ0(y) = 105,0 ± 1,3 МэВ/с
300
N
200
200
32
a)
S (200 A GeV/c)
100
150
100
0
-200
200 Pz*, MeV/c
0
50
0
-200
0
200 Py*, MeV/c
N
Рис. 5. Распределение проекций поперечных импульсов Py* для фрагментов ядра 32S (200 А
ГэВ/c). Гистограмма – эксперимент, плавная 32
кривая – нормальное распределение со
стандартным отклонением σ0b)
(y) = 102,9 ± 1,5 МэВ/с S (200 A GeV/c)
200
150
11
100
50
0
-200
0
200 Pz*, MeV/c
N
a)
400
16
N
)
16
300
O (4.5 A GeV/c)
b)
32
O (4.5 A GeV/c)
S (4.5 A GeV/c)
400
200
100
200
0
-200
-2
0
200 Py*, MeV/c
0
*
16
Рис. 6. Распределение
N 0 проекций поперечных импульсов Py для фрагментов ядра O с
импульсом 4,5 А ГэВ/c.
Гистограмма – эксперимент, плавная кривая – нормальное
un
2 P
-2
2 Pyun
распредел
стандартным
σ0(y0) = 102,3
енyие со400
± 1,2 МэВ/с
b) отклонением
16
O (4.5 A GeV/c)
N
)
32
300
S (200 A GeV/c)
d) =
a) + b) + c)
1000
200
100
500
0
-200
-2
0
2
0
Pyun
-2
0
0
200 Pz*, MeV/c
2
Pyun
Рис. 7. Суммарное распределение проекций “универсальных поперечных импульсов” Pyun
для всех фрагментов вышеуказанных ядер: 16O (4,5 А ГэВ/c), 32S (4,5 А ГэВ/c) и 32S
(200 А ГэВ/c). Гистограмма – эксперимент, плавная кривая – нормальное распределение со
стандартным отклонением σ yun = 1,01 ± 0,01
12
Экспериментальные распределения событий, содержащих 2 и более
фрагментов,
по
коэффициентам
азимутальной
асимметрии
и
коллинеарности не отличаются от распределений, полученных в модели
независимого испускания (рис. 8) (за исключением коэффициента
32
азимутальной
асимметрии
для
ядра
S
с
импульсом
200 А ГэВ/c).
dN/dα
32
S (4.5 A GeV/c)
200
100
0
-1
0
1
2
α
2
β
dN/dβ
300
32
S (4.5 A GeV/c)
200
100
0
-1
0
1
Рис. 8. Распределение по коэффициентам азимутальной асимметрии α и коллинеарности β
для ядра 32S с импульсом 4,5 А ГэВ/c. Точки – эксперимент, гистограмма – Монте-Карло
(МНИ)
В третьей главе приведены результаты по изучению механизма
фрагментации релятивистского ядра свинца с энергией 160 А ГэВ в
глубоко неупругих 208Pb+Em взаимодействиях. Изучение распределений
13
поперечных импульсов легких фрагментов ядра свинца должно было дать
ответ на вопрос: происходит ли в момент взаимодействия передача
энергии, приводящая к его заметному "нагреванию", по сравнению c
исходной температурой ядра как вырожденной системы нуклонов.
В 20 слоях фотоэмульсионной камеры (NIKFI BR-2, сотрудничество
EMU01), облученной параллельно плоскости эмульсии пучком
релятивистских ионов 208Pb (160 А ГэВ) на ускорителе SPS, Церн, методом
просмотра по площади было найдено 122 глубоко неупругих
взаимодействия ядер свинца с тяжелыми ядрами фотоэмульсии (Ag, Br).
Вместо обычно используемого трудоемкого метода оценки заряда счетом
δ-электронов был внедрен метод, основанный на измерении суммарной
длины спектра сгустков на участке следа фрагмента с неизвестным Z.
Данным методом были определены заряды 672 легких фрагментов с
зарядами от 1 до 9. Проблема измерения малых пространственных углов
вылета
фрагментов θ связана с трудностями, которые стали
значительными именно с появлением тяжелых (Au, Pb) релятивистских
ядер с энергией 100–200 ГэВ на нуклон. Увеличение толщины следов
первичных ионов в фотоэмульсии до нескольких микрон при
одновременном уменьшении самих величин углов θ фрагментов делает
невозможным прямое измерение углов θ и плоских углов ϕ фрагментов
порядка 0,1–0,5 мрад относительно направления импульса релятивистского
ядра ро (т. к. дисперсия нулевого угла первичного следа становится
соизмеримой с самой величиной измеряемого угла).
Это привело к необходимости измерений углов φij между парами всех
фрагментов в событии. Для разработки оптимальной процедуры
относительных угловых измерений в таком малом угловом диапазоне были
получены экспериментальные оценки статистических шумов при
измерении углов между парами следов с Z = 82 и Z = 2 в ядерной
фотоэмульсии при параллельном ее облучении на ячейках t от 1 до 25 мм.
Для пары двухзарядных фрагментов при условии, что углы эти
оцениваются по 10–20 точкам, статистический шум составляет около
0,01–0,02 мрад. Увеличение точности при измерении углов φij данным
методом достигнуто за счет использования большого числа (около 100–200)
усредненных Y-координат оптических центров проявленных зерен, что
привело к уменьшению эффективной величины шума зерен.
Используя эмпирическую функцию распределения плоских углов φi,j
между парами всех фрагментов в событии методом минимизации
эмпирического риска
получена оценка σφ, константы нормального
распределения “плоских” углов φ фрагментов с Z = 2, 3, 4 относительно
вектора ро, хотя сами углы φ фрагментов с этим вектором неизвестны.
Полученная оценка равна σφ = 0,37 ± 0,02 мрад. Этому соответствует
14
константа σо = 121 ± 6 МэВ/с, что практически совпадает с ожидаемой ее
оценкой из PF для ядра свинца. При этом непосредственно измеренная
величина равна σехр = 0,43 ± 0,02 мрад. Экспериментальное и ожидаемое
(с учетом ошибок измерения углов) распределения приведены на рис. 9.
Рис. 7. Экспериментальное распределение модуля угла ϕ для фрагментов ядра свинца
с зарядами Z = 2, 3, 4 (гистограмма). Точки (•) – ожидаемое распределение при нормальном
распределении истинных углов фрагментов с σ φ = 0,37 мрад
Таким образом, фрагментация ядер свинца с энергией 160 А ГэВ в глубоко
неупругих взаимодействиях с ядрами фотоэмульсии является “холодной” и
полностью описывается статистической моделью Г-Ф-Х. Нет никаких
следов “разогревания” фрагментирующего ядра.
Четвертая глава посвящена поискам отклонений от общего
статистического механизма фрагментации Ф-Г-Х. В частности,
экспериментальному обнаружению канала 8Be → 2α, который может
вызывать динамические корреляции поперечных импульсов двухзарядных
фрагментов. Для анализа были использованы экспериментальные выборки
из 484 (16O+Em), 857 (22Ne+Em) и 406 (32S+Em) неупругих событий,
содержащих среди прочих релятивистских фрагментов по две и более αчастицы. Из анализа распределений парных плоских углов и парных
15
азимутальных углов εij = |ψi −ψj| между двухзарядными фрагментами в
реакциях 16O → ≥ 2α+X, 22Ne → ≥ 2α+X, 32S → ≥ 2α+X сделан вывод о
существовании двух механизмов их образования. Основная их часть есть
результат холодной фрагментации ядер. Доля α-частиц от распада
промежуточного состояния 8Ве→2α в вышеуказанных реакциях для ядер
16
O составляет ≈ 9,7 %, 22Ne ≈ 8,7 % и 32S ≈ 4, 6%.
Достигнутая точность измерения относительных углов в плоскости
эмульсии ≈ 0,01 мрад позволила обнаружить этот канал и среди α-частиц,
фрагментов ядра свинца с энергией 160 А ГэВ. Рассчет показывает, что в
этом случае средний угол между парами следов должен быть ≈ 0,02 мрад. В
угловом распределении 476 парных плоских углов для α-частиц
действительно имеется максимум при ϕ ij ≈ 0.02 мрад в области малых
углов (< 0.1 мрад). Верхняя оценка доли этого канала для α-частиц,
фрагментов ядра свинца с энергией 158 А ГэВ, составляет порядка 13 %.
Рис. 9. Распределение плоских парных углов между всеми α-частицами в событии в области
углов < 0,1 мрад (гистограмма). Избыток событий в эксперименте над точками в области ϕi,j ≤
3·10-5рад указывает на возможное существование канала 8Ве → 2α
16
Заключение
1) Опираясь на всю совокупность полученных данных (8740 событий,
содержащих 20733 заряженных релятивистских фрагмента), проведен
эмпирический анализ, позволивший выявить основные закономерности
процесса фрагментации релятивистских ядер при их неупругих
взаимодействиях с ядрами в фотоэмульсии в достаточно широком
диапазоне масс (16O, 22Ne, 32S и 208Pb) и энергий (от ≈ 3,7 до 200 ГэВ на
нуклон). Анализ полученного экспериментального материала, наряду с
другими экспериментами в этой области, обнаруживает его глубокую
аналогию с процессом фрагментации адронов, первые представления о
котором сформулированы Фейнманом, Грибовым и Янгом. Суть этого
процесса
состоит
в
освобождении
виртуальных
фрагментов,
существующих в ядре, и в превращении их в реальные наблюдаемые
фрагменты после взаимодействия с ядром-мишенью. При этом они
сохраняют направление и величины импульсов предшествующих им
виртуальных фрагментов. Т. е. имеет место явление предельной
фрагментации, начиная с энергии около 1 ГэВ на нуклон и вплоть до
200 ГэВ на нуклон.
Показано, что простая статистическая модель прямой фрагментации
Гольдгабер–Фешбаха–Хуанга позволяет с единых позиций и с помощью
одной константы r0, определяющей радиус ядра, как качественно, так и
количественно описать и предсказать целый ряд импульсных и
корреляционных характеристик фрагментов.
2) Наблюдаются и отклонения от этих общих закономерностей. Так,
среди двухзарядных фрагментов исходных релятивистских ядер
существует примесь за счет дополнительного каскадного механизма их
образования через распад основного состояния 8Be → 2α. Из анализа
распределений парных плоских углов и парных азимутальных углов между
двухзарядными фрагментами в реакциях 16O → ≥ 2α + X, 22Ne → ≥ 2α + X,
32
S → ≥ 2α + X сделан вывод о существовании двух механизмов их
образования. Основная их часть есть результат холодной фрагментации
ядер. Доля α-частиц от распада промежуточного состояния 8Ве→2α в
вышеуказанных реакциях для ядер 16O составляет ≈ 9,7 %, 22Ne ≈ 8,7 % и
32
S ≈ 4, 6%. При мультифрагментации ядра свинца с энергией 160 А ГэВ
оценка доли этого канала для α-частиц составляет порядка 13 %.
Возможно, что обнаруженные довольно значительные вероятности
фрагментации релятивистских ядер 16O, 22Ne, 32S и 208Pb через
промежуточное состояние 8Be→2α можно рассматривать как указание на
его определенную роль в нуклеосинтезе и более тяжелых ядер, чем 12С.
17
СПИСОК ОСНОВНЫХ РАБОТ ПО ТЕМЕ ДИССЕРТАЦИИ
1. О.В. Левицкая, Ф.Г. Лепехин, Б.Б. Симонов, "Распределение
поперечных импульсов фрагментов релятивистского ядра неон-22 в
ядерной фотоэмульсии", Препринт ЛИЯФ–1310, Ленинград , 1987, 20 с.
2. О.В. Левицкая, Ф.Г. Лепехин, Б.Б. Симонов, "Основные
закономерности в распределениях поперечных импульсов фрагментов
релятивистских ядер в ядерной фотоэмульсии", Препринт ЛИЯФ–1550,
Ленинград , 1989, 20 с.
3.
О.В.
Левицкая,
Ф.Г.
Лепехин,
"Модельные
описания
экспериментальных данных и коллективные эффекты при взаимодействии
релятивистских ядер неона-22 с ядрами в фотоэмульсии", Препринт
ЛИЯФ–1564, Ленинград, 1989, 29 с.
4. F.G. Lepekhin, O.V. Levitskaya, "Determination of Relativistic Nuclei
Light Fragment Charges in Photoemulsion", Preprint PNPI EP-29-1997 № 2172,
Gatchina, 1997, 13 p.
5. О.В. Левицкая, Ф.Г. Лепехин, Д.М. Селиверстов, Б.Б. Симонов,
"Легкие фрагменты ядер свинца с энергией 160 А ГэВ в центральных
взаимодействиях с ядрами в фотоэмульсии", Препринт ПИЯФ NP-14-1996
№ 2106, Гатчина, 1996, 22 с.
6. L. Just, …, O.V. Levitskaya et al., “Fragmentation of relativistic sulphur
nuclei in nuclear emulsion”, Proc. of the 15th EMU01 Collaboration Meeting,
Constantsa, 1996.
7. M.I. Adamovich, …, O.V. Levitskaya et al., “Nuclear Effect in HigherDimensional Factorial Moment Analysis of the O-16, S-32 and Au-197
Emulsion Interaction Data at 200, 60 and 11 A GeV/c”, Z. Phys. C76 (1997)
659–663.
8. M.I. Adamovich,…, O.V. Levitskaya et al., “Charged particles
multiplicities, densities and fluctuations in Pb+Pb interactions at 158 A GeV”,
Phys. Lett. B407 (1997) 92–96.
9. F.G. Lepekhin, O.V. Levitskaya, D.M. Seliverstov, B.B. Simonov, “The
Angular Distribution of Light Projectile Fragments in Deep Inelastic Pb+Em
Interactions at 160 A GeV”, Preprint PNPI NP-38-1998 № 2252, Gatchina,
1998, 11 p.
10. О.В. Левицкая, Ф.Г. Лепехин, Д.М. Селиверстов, Б.Б. Симонов,
"Угловые распределения легких фрагментов в глубоко неупругих Pb+Em
взаимодействиях при энергии 160 А ГэВ", Известия Российской академии
наук, серия физическая, № 63 (1999) 501–503; Бюллетень Российской
академии наук, № 63 (1999) 405–407.
11. F.G. Lepekhin, O.V. Levitskaya, B.B. Simonov, “About the Correlations
of Fragment Transverse Momenta at Multifragmentation of Relativistic Nuclei”,
Preprint PNPI NP-28-1999 № 2313, Gatchina, 1999, 19 p.
18
12. F.G. Lepekhin, O.V. Levitskaya, B.B. Simonov, “Main Results of
Estimation of Statistic Noise at Measurement of Angles Between Tracks of
Fragments of Relativistic Lead Nuclei at 160 A GeV”, Proc. of 17-th Meeting of
the EMU01 Coll., Dubna, Russia, May 18–20, 1999, p.140.
13. M.I. Adamovich, …, O.V. Levitskaya et al. (EMU01-collaboration),
“The Angular Distribution of Light Projectile Fragments in Deep Inelastic
Pb+Em Interactions at 160 A GeV”, Eur. Phys. J. A6 (1999) 421–425.
14. M.I. Adamovich,…, O.V. Levitskaya et al., “Azimuthal correlations of
secondary particles in S induced interactions with Ag (Br) nuclei at
4.5 GeV/c/nucleon”, Particles and Nuclei, Letters № 4[101] (2000) 75–82.
15. F.G. Lepekhin, O.V. Levitskaya, B.B. Simonov, “Statistical
multifragmentation of nuclei and Azimuthal Correlations”, PNPI Research
Report 1998–1999, Part 1, Gatchina, 2000, pp. 165–166.
16. F.G. Lepekhin, O.V. Levitskaya, B.B. Simonov, “The Projectile
Fragments in Nuclear Emulsion”, PNPI High Energy Physics Divisions Main
Scientific Activities 1997–2001, Gatchina, 2002, pp. 210–217.
17. F.G. Lepekhin, O.V. Levitskaya, “Methods of Small Angles
Measurement in Emulsion Plane”, Preprint PNPI № 2448, Gatchina, 2001, 18 р.
18. O.V. Levitskaya, F.G. Lepekhin, “Secondary fragments of relativistic
Ne-22 at 4.1 A GeV/c nuclei in nuclear emulsion”, Particles and Nuclei, Letters
№ 2 [117] (2003) 34–38.
19. Ф.Г. Лепехин, О.В. Левицкая, Б.Б. Симонов “Оценка импульсов
однозарядных фрагментов релятивистских ядер свинца с энергией
160 А ГэВ”, Препринт ПИЯФ–2492, Гатчина, 2002, 16 с.
20. Н.П. Андреева, ..., О.В. Левицкая и др., “Топология “белых звезд”
в релятивистской фрагментации легких ядер”, ЯФ 68, № 3 (2006) 484–491.
21. О.В. Левицкая, “Фрагментации релятивистских ядер 16O, 32S в
диапазоне энергий 4,5–200 ГэВ/нуклон”, Препринт ПИЯФ-2660, Гатчина,
2006, 18 с.
19