Кристаллофизика. Лекция 2

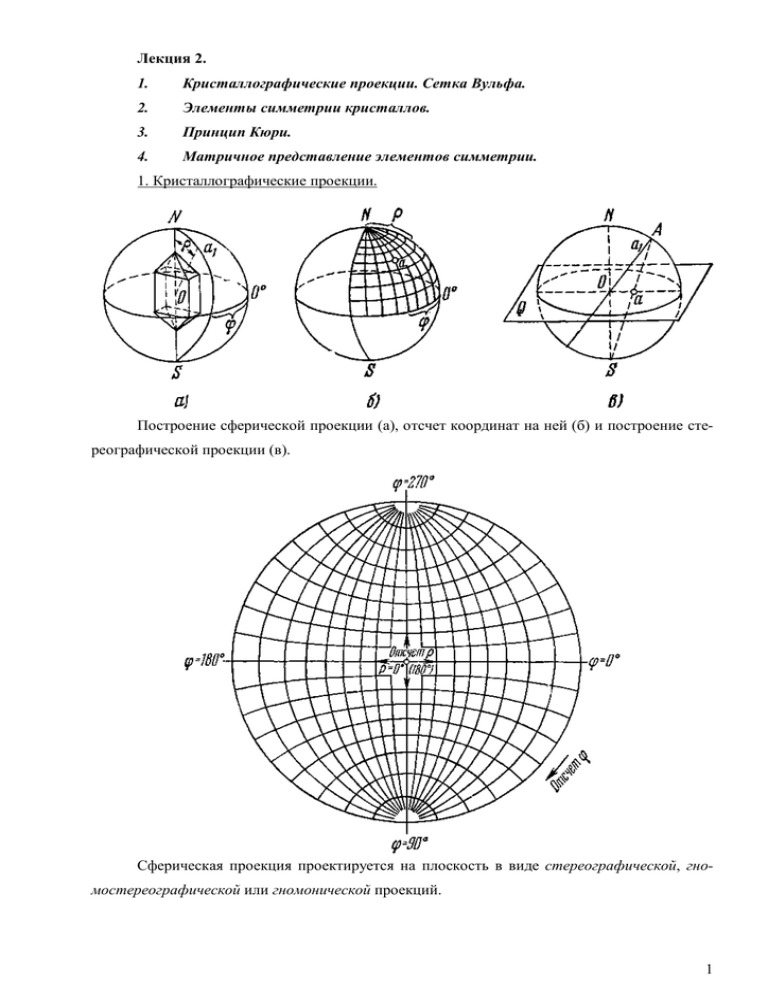
Лекция 2.
1.
Кристаллографические проекции. Сетка Вульфа.
2.
Элементы симметрии кристаллов.
3.
Принцип Кюри.
4.
Матричное представление элементов симметрии.
1. Кристаллографические проекции.
Построение сферической проекции (а), отсчет координат на ней (б) и построение стереографической проекции (в).
Сферическая проекция проектируется на плоскость в виде стереографической, гномостереографической или гномонической проекций.
1
Стереографическая проекция применяется главным образом для изображения элементов симметрии кристалла. Ее плоскостью служит экваториальная плоскость Q сферы проекций. Гномостереографическая проекция применяется главным образом для изображения
форм кристалла, его граней и ребер.
Проекция направления ОА дает на сферической проекции радиуса r точку а, определенную координатами φ, ρ, на гномонической проекции (плоскость ММ) – точку а2,
на стереографической проекции (плоскость
РР) – точку а1. На гномостереографической
проекции (плоскость РР) точка а1 – это проекция плоскости перпендикулярной к направлению Оа.
Тип проекции
Изображение
плоскости
прямой
Стереографическая
Дуга большого круга
Точка
Гномостереографическая
Точка
Дуга большого круга
Гномоническая
Точка
Прямая
2. Элементы симметрии кристаллов.
Геометрической симметрией кристаллического пространства (или фигуры) называется свойство совмещаться с самим собой путем некоторых симметричных преобразований.
Операции (преобразования симметрии) – это отражения, вращения, переносы, приводящие
пространство (фигуру) в совмещение с самим собой.
Элементы симметрии – вспомогательные образы (точки, прямые линии, плоскости), с
помощью которых обнаруживается симметрия фигуры
2
К вопросу о порядке оси симметрии:
  N  2  2

, где N=3, 4, 5… – число сторон
N
k
многоугольника; k – порядок оси симметрии.
3
Симметрия треугольника: ось 3 нейтральная и три плоскости симметрии (а) ось 3 правая, плоскостей нет (б) и ось 3 левая, плоскостей нет (в).
Три координатных и шесть диагональных плоскостей симметрии куба.
3. Принцип Кюри
Когда накладываются друг на друга два явления или явление и окружающая его среда,
сохраняются лишь те элементы симметрии, которые являются общими для обоих.
Например: наложив на восьмиугольник равносторонний треугольник, увидим, что
«выживает» лишь одна плоскость симметрии, общая для обеих фигур, да и го лишь при
симметричном расположении треугольника.
4
К иллюстрации принципа Кюри: а) исчезла ось  круга, осталась ось 8 и восемь плоскостей
симметрии; б) исчезла ось  и ось 8, осталась только общая плоскость симметрии; в) нет
общих элементов симметрии.
4. Матричное представление элементов симметрии.
  
При переходе от некоторой системы координат (СК) с базисными векторами a , b , c к
  
новой СК с базисными векторами A, B, C точка, имевшая в старом базисе координаты
x, y , z , в новом будет иметь координаты X , Y , Z . Связь этих
  
  
хода – разложение векторов базиса A, B, C по базису a , b , c :




A  11a  12b  13c
 11




B   21a   22b   23c
или
 X1 X 2 X 3     21





C  31a  32b   33c
 31
координат дает матрица пере-
12
 22
32
13  x1 
 
 23  x2 

33 
 x3 
или
3
X i   ij x j . (сокращенная запись Эйнштейна для суммирования по j: X i    ij x j )
j 1

Здесь индекс i относится к новой СК, а j – к старой:  ij  cos  X i , x j  .
  
  
Аналогично, каждый вектор базиса a , b , c можно разложить по базису A, B, C :




a  11 A  12 B  13C




b  21 A   22 B  23C
или
xi  ij X j .




c  31 A  32 B  33C
Матрицы αij и βij являются взаимно обратными: αij = βij-1 = βijТ.
Каждой операции симметрии соответствуют матрицы. В соответствии со значением
детерминанта матрицы преобразования все операции симметрии подразделяются на операции первого рода (det aij = +1) и второго рода (det aij = –1). Операции первого рода (повороты) не изменяют системы координат, операции второго рода (отражения, инверсия) преобразуют правую систему координат в левую и наоборот. Матрица преобразования системы координат, эквивалентная двум последовательно выполненным преобразованиям, равна произведению матриц этих преобразований.
Матрица тождественного преобразования
1 0 0


e  0 1 0
0 0 1


Поворот на угол φ вокруг оси, задаваемой вектором [k1 k2 k3]
5
 cos   k12 (1  cos )
k3 sin   k1k2 (1  cos )  k2 sin   k1 k3 (1  cos ) 


ij   k3 sin   k1 k2 (1  cos )
cos   k 22 (1  cos )
k1 sin   k 2k3 (1  cos )  . (1)
 k2 sin   k1 k3 (1  cos ) k1 sin   k2 k3 (1  cos )
cos   k32 (1  cos ) 

Например, для правого поворота на угол  
2
(n – порядок оси симметрии) вокруг
n
оси Z – [001], из геометрических соображений матрица абсолютных величин углов между
осями новой и старой СК




 
2
2





ij 


,
2
2



 
0 
2
 2

а матрица направляющих косинусов
 cos  sin  0 


ij    sin  cos  0  . Аналогично, получаем из (1) для вектора оси [001].
 0
0
1 

6
Примеры решения
Ось симметрии 3xyz [111] – углы с каждой из осей       arccos
1
 54.7
3
X3
O
X2
X1
X'2 X3
X'1
X2
O
X1 X'3
C3 xyz
 cos


  cos

 cos

X , X 

X , X 

X , X 

1
1
2
1
3
1
cos 
X1, X 2
 
cos  
X , X 
cos  
X , X 
2
2
3
2
cos 
X 1, X 3 
 0 1 0
 



cos X
0 1
2, X3   0
  1 0 0 

3 , X 3  
cos X







7
Ось симметрии 4x [100] – параллельная оси X1
X3
O
X2
X1
X3
X'2
X'3
O
X2
X1
X'1
 cos


C4 x   cos

 cos

X , X 

X , X 

X , X 

1
1
2
1
3
1
cos 
X 1, X 2
 

, X 
cos  X

, X 
cos  X
2
2
3
2



cos X
1, X 3
 1 0 0
 

cos 
X 2 , X 3    0 0 1 
  0 1 0 
cos 
X 3 , X 3  







8
Плоскость (111)
X3
X2
X1
X3 X'3
X'2
X'1
X2
X1
Плоскость симметрии mxy (110)
Cmxy
 cos


  cos

 cos

X , X 

X , X 

X , X 

1
1
2
1
3
1
cos 
X 1, X 2
 

, X 
cos  X

, X 
cos  X
2
2
3
2



cos X
1, X 3
  0 1 0 
 

cos 
X 2 , X 3    1 0 0 
  0 0 1 
cos 
X 3 , X 3  







9
Задача 1. Записать в матричной форме результаты последовательного действия операций: а) 2 x  1 ; б) 6 z  mx ; в) 2 x  3111  mz ; г) 2 x  mz  3111 ; д) 3z  mx ; е) mx  3z и определите полученную операцию.
Задача 2. Записать матрицы – генераторы групп: а) 222; б) 4mm ; в) 4 mmm ; г) 23; д)
432.
10