8 9 КУЛОНОВСКИЕ СУММЫ ЯДРА 4HE ПРИ ПЕРЕДАННЫХ 3

89
«Â³ñíèê Õàðê³âñüêîãî óí³âåðñèòåòó», ¹ 642, 2004
ñåð³ÿ ô³çè÷íà «ßäðà, ÷àñòèíêè, ïîëÿ», âèï. 3 /25/
À.Þ. Áóêè, È.À. Íåíüêî, Í.Ã. Øåâ÷åíêî ...
Êóëîíîâñêèå ñóììû ÿäðà 4He ïðè ïåðåäàííûõ ...
УДК 539.171
КУЛОНОВСКИЕ СУММЫ ЯДРА 4HE
ПРИ ПЕРЕДАННЫХ 3-ИМПУЛЬСАХ ВБЛИЗИ 1 Фм−1
А.Ю. Буки*, И.А. Ненько*, Н.Г. Шевченко*, И.С. Тимченко**
* ННЦ “Харьковский физико-технический институт”, 61108, Украина, г. Харьков, ул. Академическая 1
** Харьковский национальный университет, 61077, Украина, г. Харьков, пл. Свободы 4
E-mail:abuki@ukr.net
Поступила в редакцию 27 октября 2004 г.
На линейном ускорителе электронов ЛУЭ-300 измерены 8 спектров рассеянных ядрами 4Не электронов. Спектры
измерялись в широком диапазоне переданных энергий при начальных энергиях электронов E0 от 91 МэВ до 262 МэВ и
углах рассеяния θ = 160° и θ = 55° ÷ 65°. Из полученных данных выделены поперечные и продольные функции отклика ядра
4
Не при эффективных переданных 3-импульсах q = 0,9; 1,0; 1,2 Фм−1. Экспериментальные продольные функции отклика
использованы для определения значений их нулевого момента (кулоновской суммы). Найденные значения этого момента
сравниваются с теоретическими расчётами.
КЛЮЧЕВЫЕ СЛОВА: рассеяние электронов, легчайшие ядра, функции отклика, кулоновская сумма, ядерные силы.
Ядро 4He относится к малонуклонным системам, но имеет энергию связи на нуклон, характерную для
более тяжёлых ядер. Эти качества делают его уникальным тестом для проверки наших представлений о нуклоннуклонном взаимодействии в ядре.
Одним из наиболее информативных экспериментальных методов исследования ядра является получение
из анализа рассеяния электронов на ядрах продольной (RL(q,ω)) и поперечной (RT(q,ω)) функций отклика. Эти
функции описывают взаимодействие ядра с соответственно продольным и поперечным компонентом
электромагнитного поля налетающего на него электрона и их расчёт чувствителен к выбору нуклон-нуклонного
(NN) потенциала и проявлению внутриядерных токов. В настоящее время, базирующиеся на реалистических
NN-потенциалах, расчёты продольных функций отклика ядра 4He довольно близки к экспериментальным
данным при q = 2,0; 2,5 фм−1 [1]. При q = 1,5 фм−1 согласие теории с экспериментом значительно хуже. Надо
сказать, что результаты расчёта функций отклика зависят не только от вида выбранного NN-потенциала, но и от
некоторых других предположений, использованных в расчёте. Более корректными, в этом плане, являются
расчёты моментов функций отклика методом правил сумм, так как в этом случае не требуется знание волновой
функции конечного состояния системы (в отличие от расчёта собственно функций отклика). Обычно
рассматривается кулоновская сумма SL(q) − нулевой момент продольной функции отклика [1]. Расчёт этой
суммы зависит от вида NN-потенциала, но не содержит вклада от внутриядерных токов.
Для ядра 4He экспериментальные значения кулоновской суммы получены в лабораториях Bates [2] при q =
1,5 ÷ 2,5 фм−1, Saclay [1] в диапазоне q = 1,5 ÷ 3,2 фм−1 и Stanford [3] при q = 5,3 фм−1. Данные работ [1] и [2] неплохо согласуются между собой, а при q = 1,5 ÷ 2,2 фм−1 с расчётом работы [4], выполненным на основе
Аргонского потенциала с трёхчастичным взаимодействием Урбана VII. Согласно работе [5], чувствительность
расчёта SL(q) к выбору вида NN-потенциала возрастает с уменьшением переданного импульса. Поэтому
представляет интерес измерение величины SL(q) при q < 1,5 фм−1.
ЭКСПЕРИМЕНТ И ОБРАБОТКА ДАННЫХ
Функции отклика связаны с дважды-дифференциальным сечением рассеяния электронов на ядре
dσ2 / dΩdω уравнением (см. [6])
2
⎡ q2
⎤
q μ4
d σ
θ
1 μ
R (q, ω) =
(θ, E , ω) σ (θ, E ) =
R L (q, ω) + ⎢
+ tg 2 ⎥ RT (q, ω) ,
0
M
0
θ
⎢2 q2
dΩ dω
2⎥
q4
⎢⎣
⎥⎦
(1)
где E0 − начальная энергия электрона рассеявшегося на угол θ с передачей ядру энергии ω, 3-импульса
q = {4 E0 [E0 − ω] sin2(θ/2) + ω2}1/2
(1а)
и 4-импульса qμ = (q2 − ω2)1/2; σM(E0,θ) = е4сos2 (θ/2) / [4 E02 sin4(θ/2)] − сечение Мотта, е − заряд электрона.
Заметим, что величина E0 является эффективной энергией, учитывающей влияние на налетающий электрон
электростатического поля ядра [7].
90
À.Þ. Áóêè, È.À. Íåíüêî, Í.Ã. Øåâ÷åíêî ...
«Â³ñíèê Õàðê³âñüêîãî óí³âåðñèòåòó», ¹ 642, 2004
Кулоновская сумма имеет вид
∞
S L (q) =
R L (q, ω)
∫ ηG
+
ωel
2
(q μ2 )
dω ,
(2)
q, фм–1
RT/L ×103, MэВ−1
где G(qμ2) = (1 + qμ2/18,24)−2 − электрический форм-фактор протона (qμ в единицах фм−1); η = [1+qμ2/(4M 2)] ×
[1+qμ2/(2M 2)]−1 − поправка на релятивистский эффект движения нуклона в ядре, M − масса протона; символ ωel+
означает, что нижней границей области интегрирования является переданная энергия упругого рассеяния
электрона на ядре, но форм-фактор этого процесса в интеграл не входит.
Для получения функций отклика использованы спектры рассеянных электронов, измеренные на
ускорителе ЛУЭ-300 ННЦ ХФТИ. Ниже приведено краткое описание измерений и обработки данных (более
детально эти вопросы освещены в работе [8]).
Пучок электронов из ускорителя (ток до 0,2 μA) падал на газовую мишень. В эксперименте использовались две газовые мишени: ГМ-1 − для измерений под углом рассеяния θ = 160° и ГМ-2 − для измерений под
другими углами [9]. Рабочее давление газа в этих мишенях 100 атм. при комнатной температуре. Толщина
мишеней по траектории электронов, рассеянных на ядрах 4He, в радиационных длинах равна 0,013 ÷ 0,018.
Рассеянные электроны попадают в спектрометр СП-95, имеющий угловой захват 2,89×10−3 стрд и дисперсию
13,7 мм / % [10]. В фокальной плоскости спектрометра электроны детектируются 8-мю сцинтилляторами с
энергетическим захватом 1,4 % каждый и попадают в черенковские радиаторы из оргстекла. Импульсы от фотоэлектронных умножителей сцинтилляционных и черенковских детекторов регистрируются схемой совпадений
с временным разрешением 25 нсек [11].
Измерения проводились в следующих условиях: E0 = 91, 114, 133, 141 МэВ и θ = 160°; E0 = 200 МэВ и θ =
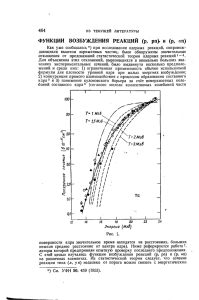
55°, θ = 65°; E0 = 262 МэВ и θ = 55°, θ = 62°. На рис.1 показаны соответствующие этим условиям переданные
импульсы и энергии (расчёт по уравнению 1а). Перед измерением каждого из спектров электронов, рассеянных
на ядрах 4Не, а также после него, измерялся фон от пустой газовой мишени. Величина этого фона относительно
счётов в максимуме квазиупругого пика составляла 0,5÷2 % при θ = 55°÷65° и 2÷7 % при θ = 160°. После
вычитания фона проводилась корректировка спектров на радиационно-ионизационные эффекты по уравнениям
работы [12] и абсолютизация сечений посредством нормировки упругого рассеяния электронов на ядрах 4Не по
данным работы [13]. Деление полученных сечений на соответствующие им моттовские сечения преобразовывает спектры в функции Rθ(q,ω).
Из уравнения (1) видно, что, располагая значениями Rθ1(q1,ω1) и Rθ2(q2,ω2), которые соответствуют q1 = q2,
ω1 = ω2 и θ1 ≠ θ2, можно определить величины RT(q1,ω1) и RL(q1,ω1). В качестве Rθ1-функции мы использовали
значения Rθ<160°(qi,ωi), измеренные при θ = 55° ÷ 65°. Соответствующие аргументам функции Rθ<160°(qi,ωi)
значения Rθ2-функции находились из интерполяции к этим qi и ωi всех измеренных при θ=160° данных, то есть
Rθ=160°(q,ω). Таким образом, с помощью уравнения (1), были определены RT- и RL-функции для qi и ωi
соответствующих Rθ-функциям углов 55°, 62°, 65°. Как видно из рис.1 в этих функциях отклика значения q
ω, MэВ
Рис.1. Переданные импульсы и энергии спектров. Сплошные линии – θ = 160°, штриховые линии – θ = 55°÷65°,
пунктирные – линии постоянных переданных импульсов, к
которым интерполируются данные.
ω, MэВ
Рис.2. Экспериментальные значения продольной (открытые кружки) и поперечной (закрытые кружки) функций отклика при qc= 1,0 фм−1. Сплошная и штриховая линии – соответствующие этим функциям экстраполяции, рассчитанные по выр.(4).
ñåð³ÿ ô³çè÷íà «ßäðà, ÷àñòèíêè, ïîëÿ», âèï. 3 /25/
91
Êóëîíîâñêèå ñóììû ÿäðà 4He ïðè ïåðåäàííûõ ...
изменяются с ростом ω. Однако для вычисления интегралов (2) необходимы функции отклика RT/L(qc,ω), которые в широком интервале переданных энергий соответствуют постоянным значениям переданного импульса qc.
Такие функции были найдены путём интерполяции функций отклика с непостоянными q к значениям qc = 0,9;
1,0; 1,2 фм−1. Рис.2 показывает функции RT/L(qc,ω) при qc= 1,0 фм−1.
Из этого рисунка видно, что найденные значения RT/L(qc,ω) очерчивают большую часть интегралов (2). Для
определения недостающих частей интегралов используется экстраполяция функций отклика в область ω→∞
t
(R T/L(qc,ω)). В качестве экстраполирующей функции обычно применяется выражение вида
или
t ,б
RT/L
(q, щ) = C q ,бω − б
(3)
t ,в
RT/L
(q, щ) = C q ,в e −вщ
(4)
где Cq,α и Cq,β − параметры, зависящие от переданного импульса и атомного номера ядра, и их значения
находятся из подгонки этих выражений к каждой экспериментальной функции отклика; α и возможно β − более
универсальные параметры. Выражение (3) предложено в работе [14]. Расчётное значение параметра α = 2,5 [14]
или α = 3 ÷ 4 [15]. Согласно работе [15] параметр α не зависит от переданного импульса и мало зависит от типа
ядра. Экспериментальное значение α ≅ 2,9 получено для ядра 2H при qc = 1,05 фм−1 в работе [16]. Выражение (4)
является эмпирической функцией. В экспериментах по определению SL(q) ядра 4He функция RT/Lt,α(qc,ω)
использовалась в работе [3], а функция RT/Lt,β(qc,ω) − в работе [2].
С учётом изложенного выше, мы приняли для расчёта сумм: α = 2,9 и, из подгонки выражения (4) к нашим
данным, β = 0,04 МэВ−1. Из полученных с использованием экстраполяций (3) и (4) сумм как результат бралось
среднее. Найденные таким образом значения SL(q) приведены на рис.3. Экспериментальные погрешности
включают статистические и систематические ошибки и равны 7%. Неопределённость значений SL(q),
обусловленная применением различных экстраполяционных функций, составляет в среднем половину
величины погрешности.
SL/Z
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ И ВЫВОДЫ
Из рис.3 видно, что при q = 0,9 ÷ 1,2 фм−1 расчёт с Аргонским потенциалом работы [4] согласуется с экспериментальными значениями SL(q) так же хорошо, как и в диапазоне q = 1,5 ÷ 2,2 фм−1. Таким образом, полученные данные вдвое расширили область переданных импульсов, где этот расчёт не противоречит эксперименту.
q, фм-1
Рис.3 Кулоновские суммы 4Не SL , нормированные на заряд ядра Z. Экспериментальные значения: закрытые кружки −
настоящей работы; открытые кружки − работы [1]. Расчётные кривые: сплошная − из работы [4]; штриховая − тот же расчёт
с поправкой из работы [17].
92
«Â³ñíèê Õàðê³âñüêîãî óí³âåðñèòåòó», ¹ 642, 2004
À.Þ. Áóêè, È.À. Íåíüêî, Í.Ã. Øåâ÷åíêî ...
Если не ограничиваться сравнением теории с результатами только наших измерений, то, как видно на
рис.3, данные [1] показывают недоисчерпание кулоновских сумм при q > 2 фм−1. Подобное явление в области
q > 2 фм−1 наблюдается как в случае 4He, так и на всех ядрах с А > 3, для которых получены экспериментальные
значения SL (см., например, работы [1] и [15]). Возможным объяснением этого эффекта является модификация
нуклона в среде ядерной материи. Учёт поправки, полученной на основании этой гипотезы в работе [17],
согласует рассматриваемый расчёт с экспериментальными данными во всём диапазоне измерений.
СПИСОК ЛИТЕРАТУРЫ
1. Zghiche A., Danelet J.F., Bernhheim M. et al. Longitudinal and transverse responses in quasi-elastic electron scattering from
208
Pb and 4He // Nucl. Phys. − 1994. − V.A572. − P.513-559.
2. von Reden K.F., Alcorn C., Dytman S.A. et. al. Quasielastic electron scattering and Coulomb sum rule in 4He // Phys. Rev. −
1990. − V.С41. − №3. − P.1084-1094.
3. Meziani Z.-E., Chen J.P., Besk D. et. al. High Momentum Transfer RT,L Inclusive Response Functions for 3,4He // Phys. Rev.
Lett. − 1992. − V.69.− №1. − P.41-44.
4. Shiavilla R., Pandharipande V.R., Fabrocini A. Coulomb sum rule of A = 2, 3, and 4 nuclei // Phys. Rev. − 1989. − V.C40. − №3.
− P.1484-1490.
5. Эфрос В.Д. Электроядерные правила сумм для легчайших ядер // Ядерная физика. − 1992. − Т.55. − №9. − С.2348-2359.
6. de Forest T. Jr. and Walecka J.D. Electron Scattering and Nuclear Structure // Ann. Phys. N.Y. − 1966. −V.15. −№57. −P.1-109.
7. Yennie D.R., Boos F.L., Ravenhall D.C. Analytic Distorted-Wave Approximation for High-Energy Electron Scattering
Calculations // Phys. Rev. − 1965. − V.B137. − №3. − P.882-993.
8. Буки А.Ю., Шевченко Н.Г., Ненько И.А. и др. Моменты функций отклика ядра 2Н при q = 1,05 Фм-1 // Ядерная физика. −
2002 . − Т.65. − №5. − С.787-796.
9. Буки А.Ю. Газовые мишени ГM-1 и ГM-2 для экспериментов по рассеянию электронов // Воп. атом. науки и тех. Сер.
общ. и яд. физ. Харьков. − 1999. − Т.1(33). − С.45-47.
10. Афанасьев Н.Г., Гольдштейн В.А., Савицкий Г.А. и др. Регистрация спектра частиц с импульсом до 400 Мэв/c
магнитным спектрометром // ЖТФ. – 1967. – Т.37. – С.1671-1676.
11. Полищук В.Н., Шевченко Н.Г., Афанасьев Н.Г. и др. Многоканальный счётчик для регистрации электронов высоких
энергий. – Харьков, 1972. – 20 с. – (Препринт / АН Украины. ХФТИ: 72-40).
12. Mo L.W., Tsai Y.S. Radiative Corrections to Elastic and Inelastic ep and up Scattering // Rev. Mod. Phys. − 1969. − V.41. − №1.
− P.205-235.
13. McCarthy J.S., Sick I., Whitney R.R. Electromagnetic structure of the helium isotopes // Phys. Rev. − 1977. − V.C15. − №4. −
P.1396-1414.
14. Tornow V., Orlandini G., Traini M. et. al. A study of electronuclear sum rules in light and medium-weight nuclei // Nucl. Phys. −
1980. − V.A348. − №2. − P.157-178.
15. Orlandini G. and Traini M. Sum rules for electron-nucleus scattering // Rep. Prog. Phys. − 1991. − V.54. − P.257-338.
16. Buki A.Yu., Nenko I.A. Response Functions Extrapolation of 2H Nucleus in the Region of High Transfer Energy // Воп. атом.
науки и тех. Сер.: яд.-физ. исслед. Харьков. − 2000. − Т.2(36). − С.13-15.
17. Buki A.Yu. Coulomb Sums and Modification of Nucleons in The Atomic Nucleus // Proceedings of the 9th Seminar
Electromagnetic Interactions of Nuclei at Low and Medium Energies. Moscow, Sept. 20-22. − 2000. − ISBN 5-94274-002-X. −
P.206-213.
COULOMB SUMS OF 4HE FOR THE 3-MOMENTUM TRANSFERS NEAR 1 Fm-1
A.Yu. Buki*, I.A. Nenko*, N.G. Shevchenko*, I.S. Timchenko**
* NSC “Kharkov Institute of Physics and Technology”, 1, Akademicheskaya st., Kharkov, Ukraine , 61108
** Kharkov national university, 4, Svobody sq., Kharkov, Ukraine, 61077
E-mail:abuki@ukr.net
The 8 spectra of electrons scattered by 4Не have been measured with the use of the electron linear accelerator LEA-300. The spectra
have been measured in the wide energy transfers region at different incident energies (91 ≤ E0 ≤ 262 MeV) and different scattering
angles (55°≤ θ ≤ 65°; θ = 160°). The longitudinal and transverse response functions of 4He have been separated for effective 3momentum transfers q = 0.9, 1.0, 1.2 Fm-1 from the received data. The experimental longitudinal response functions have been used
to determine their zero moment values (the Coulomb sum). The received moment values have been compared with theoretical
calculations.
KEY WORDS: electron scattering, lightest nuclei, response functions, Coulomb sum, nuclear forces.