взаимодействие ионов гелия и быстрых нейтронов с веществом

(Computer Simulation) № CS-01-001
В.В. Дьячков, А.В. Юшков
ВИРТУАЛЬНЫЕ ЛАБОРАТОРИИ
ПРОЕКТ
КОМПЬЮТЕРНЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ «МОДЕЛИРОВАНИЕ
ФИЗИЧЕСКИХ ПРОЦЕССОВ МЕТОДОМ МОНТЕ-КАРЛО» НА БАЗЕ НЯЦ РК
I
ВЗАИМОДЕЙСТВИЕ ИОНОВ ГЕЛИЯ И БЫСТРЫХ
НЕЙТРОНОВ С ВЕЩЕСТВОМ
Алматы 2005
1.1. Цель работы
Изучение взаимодействий заряженных частиц и нейтронов с веществом. Измерения
параметров ядерных реакций. Исследование дифференциальных сечений упруго рассеянных
нейтральных и заряженных частиц на атомных ядрах.
1.2. Краткое теоретическое введение
1.2.1. Ядерные взаимодействия заряженных частиц с веществом
При прохождении через вещество заряженные частицы взаимодействуют с атомами
этого вещества (электронами и атомными ядрами). И, соответственно, эти частицы
участвуют в трех видах взаимодействия – это сильное (ядерное), электромагнитное и слабое.
В рамках лабораторной работы рассматривается ядерное и электромагнитное
взаимодействия заряженных частиц с веществом.
Электромагнитное взаимодействие относится к числу интенсивных взаимодействий в
природе, но оно слабее ядерного (примерно в 100-1000 раз). При прохождении заряженной
частицы через вещество потери энергии происходят, главным образом, за счет
ионизационного торможения.
Ядерное взаимодействие (наиболее сильное взаимодействие в природе) проявляется в
одной из интересных форм, в форме процессов прямого взаимодействия (рассеяние частиц
на ядрах, ядерные реакции) и эти процессы характеризуются большими сечениями (10-27 –
10-24 см2). Из-за больших сечений процессов сильного взаимодействия, быстрые частицы,
при прохождении через вещество, теряют энергию уже за счет процессов ядерного
поглощения и рассеяния.
Рисунок 1 – Взаимодействие налетающей частицы с ядром-мишенью
Одним из часто рассматриваемых в ядерной физике процессов взаимодействия двух
частиц является процесс упругого рассеяния, при котором суммарная кинетическая энергия
и импульсы сталкивающихся обеих частиц сохраняются и только перераспределяются между
ними. В результате частицы изменяют энергию и свое направление движения. В качестве
сил, благодаря действию которых может происходить упругое рассеяние, здесь взяты
кулоновские и ядерные силы. Характер рассеяния на кулоновских или ядерных силах
определяется параметром прицеливания b. Очевидно, что заряженная частица (рис. 1),
пролетающая с данной скоростью близко от другой заряженной частицы с b1, рассеивается
на больший угол, чем частица, пролетающая далеко – b2 где b2>>b1 .
2
Заряженные частицы малых энергий рассеиваются на кулоновских силах, заряженные
частицы больших энергий и нейтроны – на кулоновских и ядерных, а также присутствует
интерференция кулон-ядерных взаимодействий.
1.2.2. Взаимодействие нейтронов с веществом
Основным видом взаимодействия нейтронов с веществом являются ядерные реакции
разных типов и упругое рассеяние на ядрах-мишенях. В зависимости от того, попадет
нейтрон в ядро или нет, его взаимодействие с ядрами можно разделить на два класса: а)
упругое потенциальное рассеяние на ядерных силах без попадания нейтрона в ядро (n, n); б)
ядерные реакции разных типов ((n, γ), (n, p), (n, α)), реакция деления и др., неупругое
рассеяние (n, n`), упругое рассеяние с заходом нейтрона в ядро (упругое резонансное
рассеяние).
Относительная роль каждого процесса определяется величиной соответствующих
сечений. В некоторых веществах, для которых роль упругого рассеяния относительно
высока, быстрый нейтрон теряет свою энергию в серии последовательных актов упругого
соударения с ядрами вещества (замедление нейтронов). Процесс замедления продолжается
до тех пор, пока кинетическая энергия нейтрона не сравняется с энергией теплового
движения атомов замедляющего вещества (замедлителя). Такие нейтроны называются
тепловыми. Дальнейшие столкновения тепловых нейтронов с атомами замедлителя
практически не изменяют энергии нейтронов и приводят только к перемещению их в
веществе (диффузия тепловых нейтронов), которое продолжается до тех пор, пока нейтрон
не поглотится ядром.
1.3. Математическое описание теории
Основными характеристиками ядерной реакции
a+ A→b+B
dσ
являются: дифференциальное
(θ , E ) , интегральное σ int (E ) и полное σ tot сечения
dΩ
Рисунок 2 – Результат взаимодействия различных встречных частиц и вылет вторичных частиц в данный
телесный угол при условии аксиальной симметрии (симметрии относительно оси пучка)
3
(1)
dσ
(θ , E ) характеризует вылет продуктов ядерной реакции
dΩ
под определенным углом θ к пучку падающих частиц (при фиксированной энергии пучка E).
Интегральное сечение σ int
Дифференциальное сечение
π
σ int = 2π ∫
dσ
sin θdθ
(2)
dΩ
характеризует полное количество частиц, вылетающих из мишени в данной реакции при
фиксированной энергии налетающих частиц. Полное сечение σ tot
0
σ tot = ∑ (σ int )i
i
(3)
есть сумма всех интегральных сечений по всем открытым выходным каналам. Для
получения абсолютного дифференциального сечения необходимо измерить следующие
основные величины:
Nа – количество частиц, упавших на мишень за время эксперимента;
NА – количество ядер в мишени, приходящихся на 1 кв.см.;
Nb – число частиц, вылетевших из мишени при данной реакции;
Ω – телесный угол детектора, регистрирующего вылетающие частицы (в радианах)
(элемент телесного угла это величина, численно равная площади, вырезаемой на единичной
сфере конусами, как показано на рис. 2);
ε – эффективность этого детектора при регистрации частиц b (в %) или в долях
единицы.
Кроме этих компонент, которые определяют абсолютную величину сечения,
необходимо измерить дополнительные параметры, характеризующие качество падающего
пучка и мишени. Эти дополнительные характеристики следующие:
•
разброс по энергии пучка падающих частиц (∆Е пучка);
•
толщина мишени, выраженная в потере энергии падающими частицами ∆Е мишени;
•
полное интегральное сечение вещества мишени для падающих частиц
(необходимо только в случаях, если падающие частицы – нейтроны или гамма
кванты и мишень толстая).
В случае если потеря энергии падающих частиц в мишени ∆Е мишени больше, чем
неоднородность пучка по энергии падающих частиц ∆Е пучка (это всегда почти имеет место
для работы с ускорителями Ван-де-Граафа), т.е. если
(4)
∆Е пучка << ∆Е мишени ,
то неоднородность энергии пучка можно не учитывать. Тонкая мишень будет в том случае,
если потеря энергии падающего пучка в ней имеет порядок величины 5-10 кэВ (иногда и
более до 100-200 кэВ); полутолстая – от 100 кэВ до 1-2 МэВ и толстая – когда пучок
падающих частиц полностью тормозится в мишени. Конечно, определение тонкая или
толстая мишень зависит от характеристик изучаемой реакции. Хотя грубо сечение можно
определить, зная только первые пять величин, указанных выше, измерение дополнительных
величин необходимо для уточнения сечения, введения в его значение некоторых поправок.
Разберем сначала, как определяется сечение для случая падающих заряженных частиц.
В случае тонкой мишени выражение, связывающее дифференциальное сечение реакции с
другими величинами, определяется формулой
Nb = N a N A
1
sin ϕ
4
⎛ ∂σ ⎞
⎜
⎟ Ω ⋅ε ,
⎝ ∂Ω ⎠b
(5)
где Nb – число частиц сорта b, вылетевших в результате реакции (1) и зарегистрированных
детектором за время эксперимента; Nа – число частиц, упавших на мишень за время
эксперимента; ϕ – угол между плоскостью мишени и направлением падающего пучка.
Обычно число Nа определяется путем измерения заряда пучка ускоренных частиц с
помощью цилиндра Фарадея и интегратора тока. Если за время эксперимента интегратор
тока зарегистрировал q мкКл, то
N а = 6,25 ⋅1012 q ,
(6)
2
/
где NA – число ядер в мишени на 1см поверхности. Если известна толщина мишени d в µ
(микрометрах), то толщина ее d в мг/см2 будет определена как
d / ⋅ µ ⋅ d 0 мг
(7)
d=
,
10
см 2
где d0 – удельный вес вещества мишени в г/см2 . Число ядер в мишени будет тогда
определяться выражением
6.02 ⋅10 20 d
⎡ ядер ⎤
K% ⎢ 2 ⎥ ,
(8)
A
⎣ см ⎦
где К% – процентное содержание ядер А в изотопически обогащенном веществе мишени, А –
массовое число ядра мишени (если вещество мишени есть химическое соединение, тогда
берется М – молекулярный вес этого вещества и добавить коэффициент К1% – содержание
⎛ ∂σ ⎞
данного химического элемента в веществе мишени; ⎜
⎟ – абсолютное дифференциальное
⎝ ∂Ω ⎠ b
поперечное сечение реакции (1), когда, вылетает частица сорта b под углом θ по отношению
к пучку падающих частиц; Ω – телесный угол детектора в стерадианах; ε – эффективность
детектора при регистрации частиц b.
В случае полутолстой мишени, т.е. для мишени, в которой налетающие частицы могут
потерять значительную часть своей энергии (∆Еа), вместо формулы (5), следует использовать
аналогичную формулу
NA =
1 ⎛ ∂σ ⎞
(9)
⎜
⎟ Ω ⋅ε ,
sin ϕ ⎝ ∂Ω ⎠ b
где все величины, входящие в нее, те же, что и в предыдущем случае, за исключением
⎛ ∂σ ⎞
⎛ ∂σ ⎞
⎟ . Величина ⎜
⎟ – есть среднее абсолютное дифференциальное поперечное
⎜
⎝ ∂Ω ⎠ b
⎝ ∂Ω ⎠ b
сечение в интервале энергий падающих частиц от Еа до Еа – ∆Еа ; ∆Еа – потери энергии
заряженными частицами (для данного случая альфа-частицами) при прохождении сквозь
вещество (приложение А).
Выражения (5) и (9) для связи между количеством вылетающих частиц и
дифференциальным сечением реакций обычно используются, если налетающая или
вылетающая частица заряжена.
Для расчетов дифференциальных сечений реакций с заряженными частицами
применялась модель резерфордовского рассеяния
Nb = N a N A
∂σ R (θ ) ⎛ zZe 2 ⎞
⎟⎟
= ⎜⎜
∂Ω
⎝ 4E ⎠
2
2
⎡ мбарн ⎤
1
⎛m+M ⎞
, ⎢
⋅⎜
⎟ ⋅
⎥,
(10)
⎝ M ⎠ sin 4 ⎛ θ ⎞ ⎣ стер ⎦
⎜ ⎟
⎝2⎠
где z и Z – заряд налетающей частицы и ядра-мишени соответственно; E – энергия
налетающей частицы; m и M – масса налетающей частицы и ядра-мишени, соответственно.
5
В случае же, если изучаются реакции с участием только нейтронов, используются
другие соотношения. Это связано с различием между механизмами взаимодействия
заряженных частиц с веществом и взаимодействия нейтронов с веществом.
Расчет дифференциальных сечений реакций с нейтронами выполняется в рамках
модели сильно поглощающего ядра – одном из вариантов точной теории S-матрицы –
дифракционного метода комплексных угловых моментов (МКУМ). Согласно этому варианту
модели угловые распределения дифференциальных сечений упругого рассеяния нейтронов
для тонкой мишени имеют вид
⎡ мбарн ⎤
∂σ (θ ) 8π
1
2
= 2 ⋅ a ⋅ l0 ⋅
⋅ b 2 + cos 2 [(l0 + 0,5)θ + γ ] , ⎢
(11)
⎥,
∂Ω
sin θ ⋅ exp(2 βθ )
k
⎣ стер ⎦
где a, l0, β, b, γ – свободные параметры теории, извлекаемые из экспериментальных
зависимостей сечений от угла рассеяния (приложение Б); k – волновое число, которое
определяется как
{
}
⎡ 1 ⎤
AA
Aa ⋅ E , ⎢
(12)
⎥,
AA + Aa
⎣ фм ⎦
где АА, Аа – массовое число ядра-мишени и налетающей частицы, соответственно; E –
энергия налетающей частицы [МэВ].
В
случае
же
полутолстой
мишени
соотношение
между
количеством
зарегистрированных частиц сорта b, вылетевших из реакции (1) и абсолютным
дифференциальным поперечным сечением этой реакции будет иметь вид
k = 0,21875
⎛ ∂σ ⎞ ω ⋅ ε
N b = N a 1 − e − N A ⋅σ tot ⋅ ⎜
,
⎟ ⋅
⎝ ∂Ω ⎠ b σ tot
где ω – телесный угол детектора.
(
)
(13)
Для расчета интегрального сечения реакции (1) используются следующие понятия и
выражения. Интегральное сечение σв характеризует суммарное количество частиц сорта b,
вылетевших из мишени под всеми углами в результате данного канала реакции (1). Если в
этой реакции вылетает несколько групп частиц b0, b1, b2,…, bi, соответствующих различным
уровням конечного ядра В, то каждой из этих групп будут соответствовать свои собственные
⎛ ∂σ ⎞
как дифференциальное сечение ⎜
⎟ , так и интегральное сечение σbi. Интегральное
⎝ ∂Ω ⎠ b i
сечение может быть получено несколькими различными путями:
а) путем прямого измерения его, в тех случаях, когда детектор регистрирует частицы b,
вылетевшие под всеми углами Для соотношения между количеством вылетевших частиц
может быль использовано выражение
N b = N a N A ⋅σ b ⋅ ε ;
(14)
б) интегральное сечение можно получить, измерив дифференциальные сечения под
несколькими углами и затем проинтегрировав его (на практике интегрирование заменяется
суммированием)
⎤⎫
2π 2 ⎧ n ⎡⎛ ∂σ ⎞
⎟ sin θ i ⎥ ⎬ ;
(15)
⎨∑ ⎢⎜
n ⎩ i =1 ⎣⎝ ∂Ω ⎠ i
⎦⎭
где n – число углов, под которыми проведены измерения. Интервалы между углами должны
быть взяты одинаковыми.
σb =
6
1.4. Алгоритм и описание программы
Используя математическое описание теории, построена математическая модель для
расчетов. На рис.3 показано взаимодействие пучка с мишенью и ее слои, на которых
производились вычисления.
Рисунок 3 – Расчетная модель
Принцип построения и всех необходимых вычислений программы следующий. На рис.4
и рис.5 представлена функциональная блок-схема программы. Рассмотрим каждый блок
подробно.
Рисунок 4 – Функциональная блок-схема программы «Ввод основных параметров»
7
Рисунок 5 – Функциональная блок-схема программы «Основной расчетный блок»
При запуске, программа предлагает выбор одной из двух виртуальных лабораторий по
ядерной физике. Для старта виртуальной лаборатории №1 необходимо щелкнуть по
соответствующей кнопке.
Рисунок 6 – «Основной интерфейс виртуальной лаборатории №1»
8
После открытия основного интерфейса, по умолчанию загружаются все необходимые
входные данные.
Следующий этап – установка собственных входных данных.
1.4.1. Ввод параметров эксперимента
•
Параметры пучка
При выборе из основного меню окна «параметры пучка» выполняется их ввод:
Рисунок 7 – «Параметры пучка»
Aa
Za
Ia
– атомный номер налетающих частиц;
– заряд налетающих частиц;
– начальный ток пучка налетающих частиц, [нА] (для ионов гелия);
⎡ 1 ⎤
– плотность потока пучка налетающих частиц, ⎢
(для нейтронов);
2
⎣ с ⋅ см ⎥⎦
E0 – энергия налетающих частиц (предполагается моноэнергетический пучок) ,
[МэВ];
После ввода всех данных вычисляется количество частиц, упавших на поверхность
вещества мишени
(N a )0 = I a ,
(16)
Za ⋅ e
Na
где e = 1,6 ⋅10 −19 Кл – элементарный заряд. Вычислить число ядер в мишени можно по (8).
•
Параметры мишени
Аналогично выполняется установка входных параметров для мишени:
Рисунок 8 – «Параметры мишени»
AA – атомный номер вещества (мишени);
Z A – заряд вещества (мишени);
d sub – толщина вещества (мишени), [мкм];
9
AM ∈ [1,2]
– модель мишени (1 – тонкая мишень d sub << R ; 2 – полутолстая мишень
d sub ≈ 0,3 ⋅ R , где R – длина свободного пробега частиц в веществе).
Значение числа атомов в 1 см3 ρ A – берется из справочных данных. Вычисление массы
Плотность
как
осуществляется
как
M t arg et = AA ⋅1,660531⋅10 -24 .
ρ t arg et = AA ⋅ ρ A ⋅1,660531⋅10 -24 . Соответственно толщина мишени пересчитывается в
мг/см2 как d t arg et =
•
d sub ⋅ AA ⋅ ρ A ⋅1,660531 ⋅10 -24
.
10
Основные параметры эксперимента
Ввод параметров эксперимента устанавливается аналогично предыдущему разделу:
Рисунок 9 – «Параметры эксперимента».
Θ1 = 1o , Θ 2 = 179 o
– начальный и конечный углы, соответственно, (определяют
диапазон «углового анализатора частиц»);
∆Θ – шаг углового распределения (определяет число каналов «углового анализатора
частиц»);
n
– количество элементарных слоев мишени;
ω – телесный угол детектора [стер].
Геометрия экспериментальной установки представлена на рис. 10.
Рисунок 10 – «Геометрия экспериментальной установки».
10
1.4.2. Основной расчет
Взаимодействие заряженных частиц с веществом
После установки всех необходимых параметров регистрация вторичных частиц
детектором осуществляется после нажатия кнопки «Пуск». Детектор начинает регистрацию,
что можно наблюдать в виде «вспышек» на развернутом по углу условном детекторе и в этот
же момент на «угловом анализаторе частиц», который фиксирует вероятность отклонения
вторичных частиц в заданном диапазоне углов согласно статистическому весу
резерфордовского дифференциального сечения (10). Погрешности виртуального измерения
дифференциальных сечений для каждого угла вычисляются как статистические
1
∆( N b )i =
⋅100% . Автоматически рассчитывается и интегральное сечение согласно
(N b )i
формуле (15) с погрешностью ∆σ b =
100%
σb
Θ2
∑ ∆(N ) . Расчет потерь энергии заряженными
i = Θ1
b i
частицами, проходящими i-ый слой вещества выполняется следующим образом: а) из базы
данных (приложение А) извлекается значение величины поглощения энергии на
dE
элементарный пробег частицы
; б) согласно толщине мишени и количеству расчетных
dx
dE
слоев вычисляется ∆Ei = Ei −1 −
⋅ d i , где d i – толщина расчетного слоя. В случае
dx
применения модели «полутолстая мишень» дополнительно рассчитывается и интенсивность
пучка на каждом слое по формуле (9).
Взаимодействие нейтронов с веществом
Аналогично алгоритму расчета взаимодействия заряженных частиц с веществом
выполняется расчет и для взаимодействия нейтронов с веществом. Только вычисления
дифференциальных сечений осуществляются по формуле (11) в рамках модели МКУМ,
свободные параметры для которой берутся из базы данных (приложение Б).
В случае модели «полутолстая мишень» расчет дифференциальных сечений можно
выполнить по формуле (13), где полное сечение σ tot (3) для данной модели вычисляется в
следующем приближении σ tot = 2 ⋅ σ int , где σ int = σ b (15). Для расчета числа частиц
прошедших толщину x используется следующая формула
N a = ( N a )0 ⋅ e − n A ⋅x⋅σ tot ,
(17)
где (N a )0 – число частиц, падающих на поверхность мишени; nA – число атомов в одном
кубическом см. вещества мишени.
1.4.3. Вывод результатов
В процессе расчета дифференциальных сечений и набора статистики можно
просмотреть зависимость углового распределения дифференциального сечения, как
теоретического так «экспериментального», в декартовых и полярных координатах. При этом,
нажав на пиктограмму «параметры моделей», в зависимости от типа пучка появится
соответствующее диалоговое окно (см. рис.11).
11
(а)
(б)
Рисунок 11 – «Параметры моделей» (тип пучка: альфа-частицы (а); нейтроны (б)).
И
выбрав
«Дифференциальное
сечение
(декартовы
координаты)»
или
«Дифференциальное сечение (полярные координаты)», появятся соответствующие
зависимости (на рис.12-13 представлены примеры дифференциальных сечений).
(а)
12
(б)
Рисунок 12 – «Графические зависимости для альфа-частиц в различных системах координат».
Рисунок 13 – 3D-график угловых распределений дифференциальных сечений в зависимости от энергий пучка
альфа-частиц».
На рисунке 13, в качестве примера, изображен 3D-график угловых распределений
дифференциальных сечений как функция энергии пучка альфа-частиц, данные которых при
необходимости можно сохранить в текстовом файле.
13
(а)
(б)
Рисунок 14 – «Графические зависимости для нейтронов в различных системах координат».
После выполнения лабораторной работы программа формирует полный отчет (рис. 15),
в котором отражаются все входные параметры эксперимента и все величины, которые были
измерены в ходе виртуальных экспериментов. При необходимости отчет можно сохранить на
жесткий диск виде текстового файла и открыть, например, в электронной таблице Microsoft
Excel для дальнейших дополнительных вычислений или построения графиков
дифференциальных сечений.
14
Рисунок 15 – «Отчет лабораторной работы».
1.5. Методика выполнения работы
1.5.1. Задание 1. Исследование дифференциальных сечений взаимодействия заряженных
частиц с веществом.
•
•
•
•
Задайте 7Li в качестве мишени с толщиной в 10 мкм и модель «Тонкая мишень»;
В качестве пучка налетающих частиц выберите альфа-частицы (4He) с энергией 10 МэВ
и током пучка 10 нА;
Угловой диапазон детектора задайте в интервале от 10 до 179 градусов с телесным
углом в 10-4 стер и установите 10 расчетных слоев;
С помощью программы рассчитайте интегральное и дифференциальное сечения с
•
•
•
•
π
< Θ < π ) не более ∆ = ±40% ;
2
Засеките начало и окончание виртуального эксперимента ∆tэксп. Исследуйте
зависимость ∆tэксп от начальных условий: начального угла, конечного угла, шага по
углу. Объесните физический смысл полученных результатов;
Измените мишень на 64Cu , не меняя всех остальных параметров эксперимента и
выполните все выше указанные шаги;
Сравните и проанализируйте полученные результаты и сделайте соответствующие
выводы;
Для самостоятельной работы выполните данное задание, используя мишень из
различных элементов и их изотопов меняя остальные параметры эксперимента.
погрешностью для углов задней полусферы (
15
1.5.2. Задание 2. Определение толщины мишени для полного поглощения заряженных частиц
веществом.
•
•
•
•
•
•
Задайте 7Li в качестве мишени с толщиной в 265 мкм и модель «Тонкая мишень»;
В качестве пучка налетающих частиц выберите альфа-частицы (4He) с энергией 10 МэВ
и током пучка 10 нА;
Изменяя количество слоев с помощью виртуального эксперимента с использованием
таблицы ПРИЛОЖЕНИЯ А определите полный пробег альфа-частиц с заданной
энергией;
Измените мишень на 64Cu с толщиной в 28 мкм, не меняя всех остальных параметров
эксперимента;
Сравните и проанализируйте полученные результаты и сделайте соответствующие
выводы;
Для самостоятельной работы выполните данное задание, используя мишень из
различных элементов и их изотопов, меняя остальные параметры эксперимента.
1.5.3. Задание 3. Исследование дифференциальных сечений и потери энергии заряженными
частицами в веществе по модели «полутолстая мишень».
•
•
•
•
•
•
Задайте 7Li в качестве мишени с толщиной в 20 мкм и модель «Полутолстая мишень»;
В качестве пучка налетающих частиц выберите альфа-частицы (4He) с энергией 10 МэВ
и током пучка 10 нА;
Установите 30 расчетных слоев. Экспериментально определите потери энергии;
Измените мишень на 190Os, не меняя всех остальных параметров эксперимента;
Сравните и проанализируйте полученные результаты и сделайте соответствующие
выводы;
Для самостоятельной работы выполните данное задание, используя мишень из
различных элементов и их изотопов, меняя остальные параметры эксперимента.
Комбинируя 1-3 задания, выявите закономерности изменения энергии пучка, толщины
мишени, вещества мишени от различных параметров эксперимента и проанализируйте их.
1.5.4. Задание 4. Определение страглинга и полной немоноэнергетичности прямого пучка.
•
•
•
Задайте параметры эксперимента по аналогии с предыдущими задачами. При данной
плотности мишени ρ1 и входной энергии E0 определите энергию прямого пучка на
выходе из мишени E1. Вычислите ∆E1=E0–E1;
Задайте разное ∆ρ плотности вещества мишени. Экспериментальным путем найдите
∆E2, ∆E3, … и вычислите средний разброс-страглинг;
Исследуйте немоноэнергетичность прямого пучка путем задания его углового разброса
за счет входного коллиматора.
1.5.5. Задание 5. Определение среднеквадратичного угла.
•
Пусть налетающая альфа-частица, взаимодействующая с ядром с заданным зарядом Z,
пролетает мимо него с прицельным параметром b. После этого она испытывает n
θ Z ⋅ z ⋅ e2 1
аналогичных упругих столкновений. Оценить по формулам tg =
⋅
и
m ⋅ v2 b
2
16
α = Nθ 2 ~
Z ⋅z⋅ x ⋅ n
p⋅v
[1] среднеквадратичный угол расходимости первичного
пучка.
1.5.6. Задание 6. ПВА (первично выбитые атомы).
•
•
•
Пользуясь законами сохранения энергии и импульса, вычислите энергию ядер отдачи
EВ из реакции (1) для случая упругого рассеяния;
Исследуйте зависимость энергии ядер отдачи (ПВА) от угла рассеяния, типа
налетающих частиц, ядер-мишеней и энергии первичного пучка;
Задав один и тот же угол рассеяния для ПВА вычислите их число для данного угла.
1.5.7. Задание 7. Эквивалентные флюенсы.
•
•
•
С учетом того, что при имитационных экспериментах, когда повреждаемость от 14,1
МэВ нейтронов заменяется радиационной повреждаемостью от альфа-частиц или
протонов, эквивалентная энергия альфа-частиц Eα-экв≈4En найти эквивалентные
флюенсы;
Для этого с данными энергиями Eα-экв и En выполните виртуальные эксперименты и
найдите отношения интегральных сечений;
Объясните полученный результат.
1.5.8. Задание 8. Исследование дифференциальных сечений взаимодействия нейтральных с
энергией 14,1 МэВ частиц с веществом.
•
•
•
•
В качестве пучка налетающих частиц выберите нейтроны с произвольным потоком
частиц;
Задайте 7Li в качестве мишени с толщиной в 20 мкм и модель «тонкая мишень»;
Угловой диапазон детектора задайте в интервале от 5 до 179 градусов с телесным углом
в 10-4 стер и установите 10 расчетных слоев;
С помощью программы рассчитайте интегральное и дифференциальное сечения с
•
•
•
π
< Θ < π ) не более ∆ = ±40% ;
2
Измените мишень на 64Cu , не меняя всех остальных параметров эксперимента и
выполните все выше указанные шаги;
Сравните и проанализируйте полученные результаты и сделайте соответствующие
выводы;
Для самостоятельной работы выполните данное задание, используя мишень из
различных элементов и их изотопов меняя остальные параметры эксперимента.
погрешностью для углов задней полусферы (
1.5.9. Задание 9. Поглощение 14,1 МэВ нейтронов в веществе.
•
•
•
•
Задайте мишень на 64Cu модель «Полутолстая мишень»;
В качестве пучка налетающих частиц выберите нейтроны с произвольным потоком
частиц;
Меняя толщину мишени, сравните и проанализируйте полученные результаты и
сделайте соответствующие выводы;
Для самостоятельной работы выполните данное задание, используя мишень из
различных элементов и их изотопов, меняя остальные параметры эксперимента.
17
1.5.10. Задание 10. Оценка радиуса взаимодействия упругого рассеяния нейтронов.
•
•
Из дифракционной картины угловых распределений дифференциальных сечений
упругого рассеяния нейтронов определите средний радиус взаимодействия по формуле
⎡ 1 ⎤
1
π
Rвз = ⋅ l0 ⋅ (l0 − 1) , где k , ⎢
− 0,5 –
– волновое число нейтрона (12); l0 =
⎥
∆θ
k
⎣ фм ⎦
угловой момент нейтрона на касательных к поверхности ядра траектории (см. рис.1); ∆θ
– период осцилляций угловых распределений дифференциальных сечений;
Постройте зависимость среднего радиуса взаимодействия нейтронов от массового
числа ядер-мишени.
1.6. Вопросы для самопроверки
•
•
•
•
•
Какие существуют основные механизмы и типы взаимодействия заряженных частиц с
веществом;
Какие существуют основные механизмы и типы взаимодействия нейтральных частиц с
веществом;
Для чего исследуются дифференциальные сечения и какую информацию о структуре
ядра можно из них извлечь;
Основные свойства упругого рассеяния частиц;
В чем разница между интегральным и полным сечениями.
1.7. Рекомендуемая литература
1.
2.
3.
4.
К.Н. Мухин. Введение в ядерную физику. М.: Атомиздат, 1963, 588 с.
О.Ф. Немец, Ю.В. Гофман. Справочник по ядерной физике. Киев "Наукова думка",
1975, 415 с.
Ю.М. Широков, Н.П. Юдин. Ядерная физика. М.: Наука, 1972, 671 с.
А.В. Юшков, В.И. Канашевич, М.А. Жусупов. Ядерная физика. Понятийный аппарат.
Алматы: Казахский университет, 2002, 151 с.
18
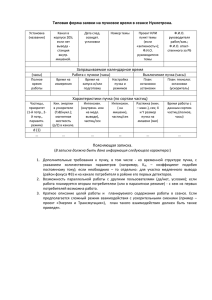
ПРИЛОЖЕНИЕ А
Энергии налетающих частиц Е, МэВ
Потери энергии альфа-частицами при прохождении через вещество с массовым числом А
⎡ кэВ ⎤
⎢⎣ мг / см 2 ⎥⎦
имя файла с данными – LP_alpha.bin
Таблица А.1
0,2
0,4
0,6
0,8
1
1,2
1,6
2
2,5
3
3,5
4
5
6
8
10
12
15
20
25
30
40
60
6
1500
2000
2080
2000
1850
1750
1560
1350
1220
1080
990
900
785
675
540
465
400
330
260
220
190
150
115
18
1500
2000
2080
2000
1850
1750
1560
1350
1220
1080
990
900
785
675
540
465
400
330
260
220
190
150
115
Массовые числа мишеней А
19
32
55
68
840
840
420
420
1100
1100
650
650
1220
1220
720
720
1300
1300
750
750
1300
1300
760
760
1250
1250
750
750
1170
1170
730
730
1030
1030
690
690
880
880
634
634
805
805
560
560
750
750
525
525
700
700
480
480
610
610
440
440
530
530
400
400
440
440
330
330
385
385
295
295
340
340
260
260
286
286
220
220
233
233
175
175
200
200
153
153
167
167
135
135
136
136
112
112
108
108
80
80
69
300
470
540
600
640
635
620
555
485
430
405
380
355
320
260
230
210
185
156
137
122
100
76
130
300
470
540
600
640
635
620
555
485
430
405
380
355
320
260
230
210
185
156
137
122
100
76
170
210
290
340
370
380
406
395
365
330
305
280
255
235
215
187
164
148
135
108
96
88
72
56
210
210
290
340
370
380
406
395
365
330
305
280
255
235
215
187
164
148
135
108
96
88
72
56
Потери энергий альфа-частицами при прохождении через в еществ о с массов ых числом А,
МэВ/(мг/см^2)
1
0,1
0,1
1
10
100
Энергия альфа-частиц, МэВ
А=(6-18)
А=(19-32)
А=(55-68)
19
А=(69-130)
А=(170-210)
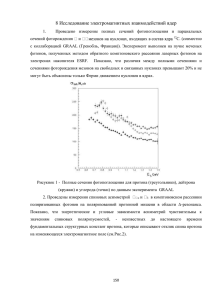
ПРИЛОЖЕНИЕ Б
Оптимальные параметры метода комплексных угловых моментов (МКУМ) для упруго
рассеянных нейтронов с энергией 14,1 МэВ
имя файла с данными – МКУМ_n_14.bin
A
Z
6
13
35
40
48
54
56
58
63
65
89
92
Символ
хим.
элемента
Li
C
Cl
Ca
Ti
Fe
Fe
Fe
Cu
Cu
Y
Zr
3
6
17
20
22
26
26
26
29
29
39
40
Таблица Б.1
β
L0
1,95
1,93
4,05
4,08
4,72
3,04
2,71
2,71
3,46
3,76
4,3
4,3
b
1,05
0,61
0,45
0,61
0,79
0,3
0,05
0,12
0,22
0,28
0,23
0,05
γ
a
0,81
0,75
0,46
0,81
0,73
0,59
0,59
0,59
0,5
0,52
0,94
0,77
2,27
1,39
0,92
0,81
1,034
0,62
0,54
0,54
0,5
0,71
0,52
0,36
0,95
1,82
1,25
1,23
1,22
0,65
1,05
1,05
0,13
0,28
0,41
0,63
Параметры метода комплексных углов ых моментов
4,5
4
3,5
3
2,5
2
1,5
1
0,5
10
15
20
25
30
35
40
45
50
55
60
65
70
Массовое число, А
L0
бета
20
b
a
гамма
75
80
85
90