ДЗ№6

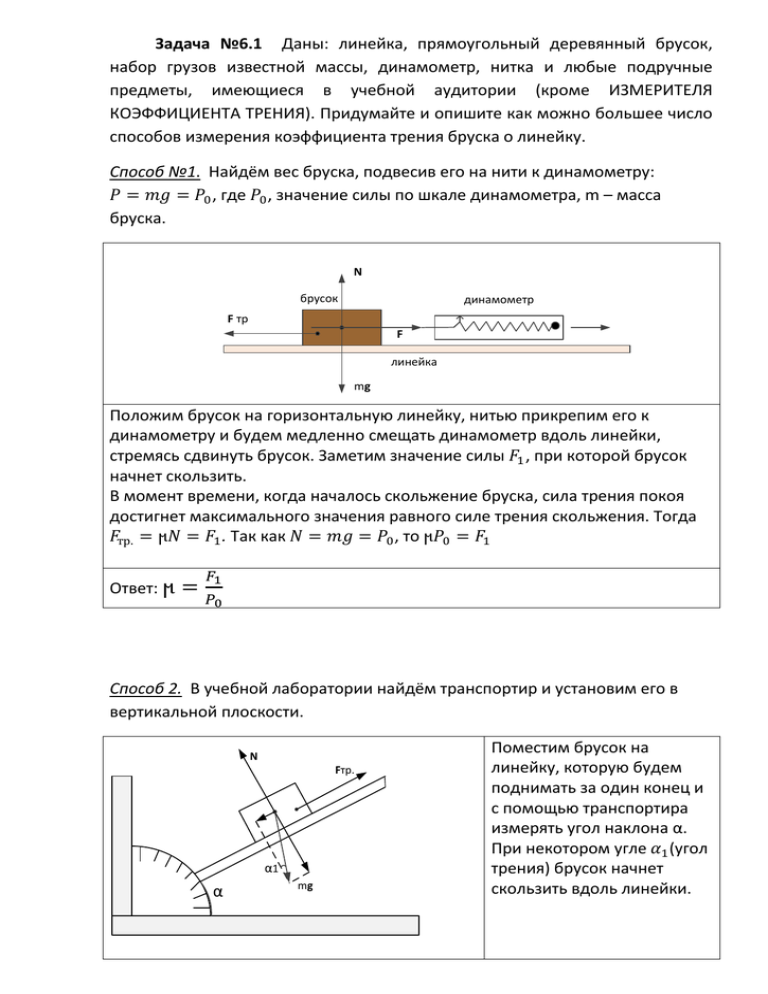
Задача №6.1 Даны: линейка, прямоугольный деревянный брусок,
набор грузов известной массы, динамометр, нитка и любые подручные
предметы, имеющиеся в учебной аудитории (кроме ИЗМЕРИТЕЛЯ
КОЭФФИЦИЕНТА ТРЕНИЯ). Придумайте и опишите как можно большее число
способов измерения коэффициента трения бруска о линейку.
Способ №1. Найдём вес бруска, подвесив его на нити к динамометру:
, где , значение силы по шкале динамометра, m – масса
бруска.
N
брусок
динамометр
F тр
F
линейка
mg
Положим брусок на горизонтальную линейку, нитью прикрепим его к
динамометру и будем медленно смещать динамометр вдоль линейки,
стремясь сдвинуть брусок. Заметим значение силы , при которой брусок
начнет скользить.
В момент времени, когда началось скольжение бруска, сила трения покоя
достигнет максимального значения равного силе трения скольжения. Тогда
. Так как
, то
Ответ:
Способ 2. В учебной лаборатории найдём транспортир и установим его в
вертикальной плоскости.
N
Fтр.
α1
α
mg
Поместим брусок на
линейку, которую будем
поднимать за один конец и
с помощью транспортира
измерять угол наклона α.
При некотором угле (угол
трения) брусок начнет
скользить вдоль линейки.
Из рисунка находим
Из системы уравнений получаем
Ответ:
Кроме рассмотренных способов можно предложить еще очень много иных
вариантов измерения коэффициента трения:
3. По величине направленной вдоль наклонно расположенной линиейке
силы, которую следует приложить для того, чтобы брусок начал скользить
вверх или вниз.
4. По минимальной величине направленной перпендикулярно наклонной
линейке отрывающей брусок от поверхности линейки силы, приводящей к
началу проскальзывания бруска.
5. По величине угла приложения воздействия силы на брусок, лежащий на
горизонтальной линейке, при которой возникает явление заклинивания.
6. По максимальной величине силы, с которой следует тянуть линейку по
скользкому полу для того, чтобы брусок не соскальзывал с поверхности
линейки.
7. По пути, пройденному грузиком по горизонтальной поверхности стола
после его разгона по наклонной линейке.
Для следующего блока измерений нужны часы. Их можно найти в
лаборатории, воспользоваться мобильным телефоном или изготовить из
нитки известной длины с подвешенным грузиком. Можно выполнять
измерения
8. По времени соскальзывания грузика по наклонно расположенной
линейке.
9. По времени движения грузика по горизонтальной линейке до момента
его остановки и по пройденному им пути.
Задача 6.2 Однажды Лебедь, Рак и Щука решили сдвинуть с места воз
массой M, первоначально покоившейся на горизонтальной поверхности.
Лебедь и Щука сочли разумным тащить воз в северном направлении с
силами FЛ и FЩ, направленными под углами α и β к горизонту «слегка
вверх» и «слегка вниз» соответственно. Рак же потащил воз точно на юг,
прикладывая к нему силу FР точно в горизонтальном направлении. В каком
направлении и с каким ускорением будет двигаться воз? Воз имеет хорошо
смазанные колеса, действующая на него сила трения пренебрежимо мала.
Идея решения: Изобразить все силы, действующие на воз и воспользоваться
вторым законом Ньютона. Учесть, что сила реакции опоры
может быть направлена только вверх (если получается, что Ny
< 0, это означает, что тело оторвалось от горизонтальной
поверхности).
Y
Рисунок,
поясняющий
решение.
Нужно добавить 2
силы
F1
1
F3
α
M
β
F2
2
+
3
4
OY:
5.
X
Второй закон
Ньютона
Проекция (2) на
ось
Важное свойство
силы реакции
опоры.
Проекция (2) на
ось Y и условие
«взлета» груза
, то воз
Ответ: если
и
останется на месте;
если
воз будет двигаться
горизонтально с ускорением
6
если
, воз будет взлетать вверх с ускорением
.
;
Задача 6.3 Брусок массой m покоится на горизонтальной шероховатой
поверхности. Коэффициент трения бруска о поверхность равен μ. С какой
силой F , направленной «вверх» под углом α к горизонту, нужно тянуть
брусок, для того, чтобы он сдвинулся с места?
Идея решения: Рассмотрим силы, действующие на брусок, и воспользуемся
вторым законом Ньютона. Полезно учесть, что брусок может не только
скользить, но и при некоторых условиях может оторваться от горизонтальной
поверхности.
Y
1
N
Q
F
α
X
Рисунок, поясняющий
решение.
Fтр.
Второй закон Ньютона
Результат проектирования (2)
на выбранную систему
координат c учетом того, что
при движении возможно
вдоль оси Х возможно
скольжение, а вдоль оси Y –
можно двигаться только
вверх
Условие того, что груз не
оторвался от пола.
Условие скольжения по полу
2
3
4
5
Условие взлета
6
Из (5) и (6) следует, что
проскальзывание бруска
ВСЕГДА начнется раньше,
чем его взлет
3
Ответ : для того, чтобы брусок сдвинулся с места, его надо тянуть с
силой
Задача 6.4 Автомобиль массой М, движущийся с включенным
мотором подъезжает со скоростью V к началу подъема шоссе,
составляющего угол α с горизонтом. На какую максимальную высоту может
подняться автомобиль, если коэффициент трения его колес о поверхность
дороге равен μ.
Идея решения:
Если колеса не проскальзывают относительно дороги,
автомобиль с достаточно мощным мотором сможет
подняться по горке на любую высоту. Если возникает
проскальзывание, автомобиль может начать скатываться
вниз….
V
N
1
Y
V=0
Fтр.
Fтр.
V
S
X
Рисунок, поясняющий
решение.
h
α
mg
Второй закон Ньютона
Проекция (2) на оси
координат.
2
3
4
5
-
3
4
Ответ: если
Величина силы трения в
случае проскальзывания
колес.
Условие того, что при
проскальзывании колес
автомобиль покатится
вниз
Ускорение автомобиля в
случае выполнения (5)
Путь, пройденный
автомобилем вверх при
проскальзывании
Максимальная высота
подъема автомобиля в
случае проскальзывания
, максимальная высота, на которую может въехать
, в противном случае –
автомобиль, равна
автомобиль может подняться на любую высоту.
Задача 6.5. Прикрепленный к потолку невесомый нерастяжимый канат
пропущен через подвижный и неподвижный блоки (невесомые, без трения в
осях). К подвижному блоку подвешен груз массой m. На свободном конце
каната висит обезьяна массой М, которая перебирает лапами так, что все
время остается на месте. Найти ускорение груза, висящего на подвижном
блоке.
Идея решения: По третьему закону Ньютона с какой силой F обезьяна
действует на канат, с той же силой и канат действует на обезьяну.
0
F
F
1
F
T
Mg
Рисунок, поясняющий
решение.
m
mg
X
F
Ускорение обезьяны равно
нулю.
Уравнение движения груза.
2
3
,
4
5
Е ли m>2M, о г уз опу ка
ли m<2M – под има я
я,