Идентификация и прогнозирование обобщающих показателей
реклама
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹3(15) 2009
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
Èäåíòèôèêàöèÿ è ïðîãíîçèðîâàíèå
îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíîé
ýêîíîìè÷åñêîé ñèñòåìû
 ðàáîòå ïðåäëîæåíà ýêîíîìèêî-ìàòåìàòè÷åñêàÿ ìîäåëü ðåãèîíàëüíîé ýêîíîìè÷åñêîé ñèñòåìû, êîòîðàÿ íàðÿäó ñ âåùåñòâåííûì êàïèòàëîì ó÷èòûâàåò ÷åëîâå÷åñêèé êàïèòàë. Ïîñòðîåí àëãîðèòì èäåíòèôèêàöèè íåèçâåñòíûõ ïàðàìåòðîâ ìîäåëè
íà îñíîâå ãåíåòè÷åñêîãî àëãîðèòìà ñ âåùåñòâåííûì êîäèðîâàíèåì è ìåòîäà Õóêà—
Äæèâñà. Ðàñ÷åòû ïî èäåíòèôèêàöèè è ïðîãíîçèðîâàíèþ ïðîâåäåíû íà ïðèìåðå Óäìóðòñêîé Ðåñïóáëèêè.
1. Ââåäåíèå. Ìàòåìàòè÷åñêàÿ ìîäåëü ýêîíîìè÷åñêîé ñèñòåìû ðåãèîíà
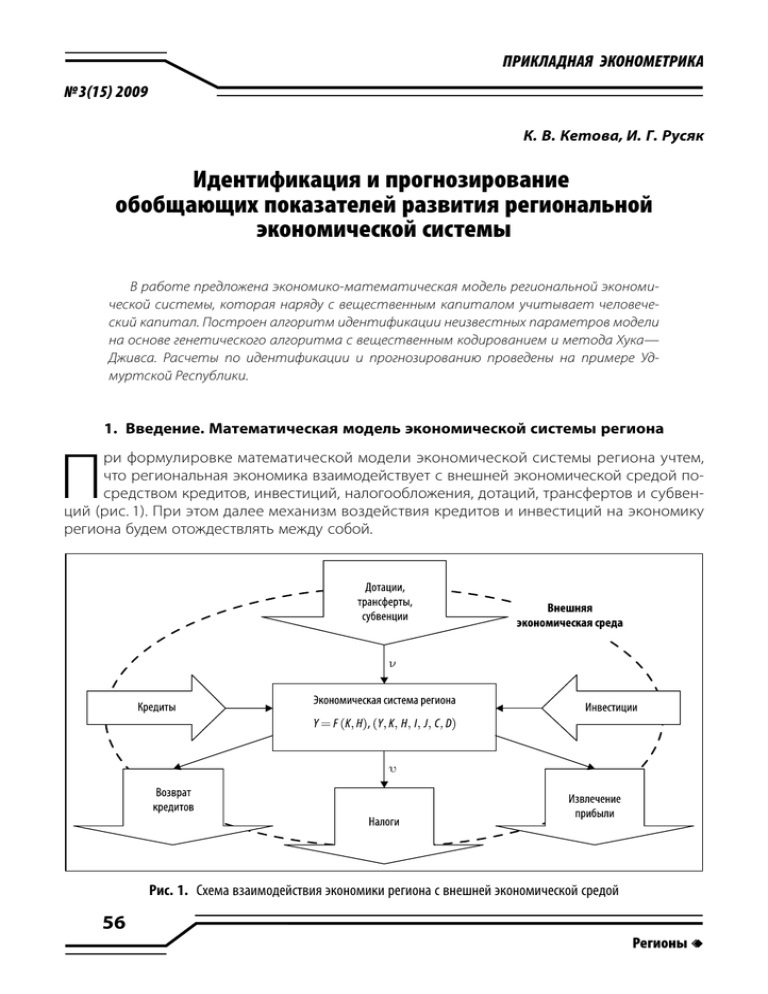
ðè ôîðìóëèðîâêå ìàòåìàòè÷åñêîé ìîäåëè ýêîíîìè÷åñêîé ñèñòåìû ðåãèîíà ó÷òåì,
÷òî ðåãèîíàëüíàÿ ýêîíîìèêà âçàèìîäåéñòâóåò ñ âíåøíåé ýêîíîìè÷åñêîé ñðåäîé ïîñðåäñòâîì êðåäèòîâ, èíâåñòèöèé, íàëîãîîáëîæåíèÿ, äîòàöèé, òðàíñôåðòîâ è ñóáâåíöèé (ðèñ. 1). Ïðè ýòîì äàëåå ìåõàíèçì âîçäåéñòâèÿ êðåäèòîâ è èíâåñòèöèé íà ýêîíîìèêó
ðåãèîíà áóäåì îòîæäåñòâëÿòü ìåæäó ñîáîé.
Ï
Ðèñ. 1. Ñõåìà âçàèìîäåéñòâèÿ ýêîíîìèêè ðåãèîíà ñ âíåøíåé ýêîíîìè÷åñêîé ñðåäîé
56
Ðåãèîíû R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
 êà÷åñòâå ïîêàçàòåëåé ìàêðîýêîíîìè÷åñêîé ñèñòåìû ðåãèîíà ïðèìåì:
1) îáúåì ïðîèçâåäåííîé ïðîäóêöèè Y;
2) ñòîèìîñòü îñíîâíûõ ïðîèçâîäñòâåííûõ ôîíäîâ (ÎÏÔ) èëè ïðîèçâîäñòâåííîãî êàïèòàëà K;
3) ñòîèìîñòü ÷åëîâå÷åñêîãî êàïèòàëà H;
4) îáúåìû èíâåñòèöèé â ïðîèçâîäñòâåííûé êàïèòàë I;
5) îáúåìû èíâåñòèöèé â ÷åëîâå÷åñêèé êàïèòàë J;
6) îáúåì ïîòðåáëåíèÿ C;
7) äîõîäû ðåãèîíàëüíîãî áþäæåòà D.
Òàêèì îáðàçîì, ñîîòâåòñòâóþùèé ïàñïîðò íåèçâåñòíûõ çàäà÷è èìååò âèä:
(Y , K , H , I , J , C , D ) t ,
ãäå t — âðåìÿ.
Êîýôôèöèåíòû n è u áóäóò îïðåäåëåíû íèæå.
Ïðîèçâîäñòâåííóþ ôóíêöèþ ïðèìåì â âèäå
Y = F(K , H) = AK a H b ,
ãäå ïàðàìåòðû A, a , b îïðåäåëÿþòñÿ ïî ñòàòèñòè÷åñêèì äàííûì ýêîíîìè÷åñêîé ñèñòåìû
[Ðóñÿê, Êåòîâà (2008)].
Çàïèøåì îñíîâíîå áàëàíñîâîå óðàâíåíèå ìàêðîýêîíîìè÷åñêîé ìîäåëè ðåãèîíà, èñïîëüçóÿ ñõåìó âîñïðîèçâîäñòâà ýêîíîìèêè, ïðèâåäåííóþ íà ðèñ. 2:
Yt + B t + T t - N tF - R t = I t +1 + J t +1 + C t +1 ,
(1)
ãäå B t — âíåøíèå èíâåñòèöèè â ýêîíîìèêó ðåãèîíà;
R t — âíåøíèé äîëã;
N tF — íàëîãîâûå îò÷èñëåíèÿ â ôåäåðàëüíûé áþäæåò;
T t — äîòàöèè, òðàíñôåðòû, ñóáâåíöèè. Íèæíèé èíäåêñ â äàííîì ñëó÷àå õàðàêòåðèçóåò
çàâèñèìîñòü ïåðåìåííûõ îò âðåìåíè.
Ðèñ. 2. Ñõåìà öèêëà âîñïðîèçâîäñòâà ðåãèîíàëüíîé ýêîíîìèêè
 îòíîñèòåëüíûõ ïåðåìåííûõ áàëàíñîâîå óðàâíåíèå èìååò âèä:
s0 + sk + sh - sb = 1,
57
R Ðåãèîíû
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
¹3(15) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹3(15) 2009
Ñ
E
I
sk =
E
J
sh =
E
B
sb =
E
Èäåíòèôèêàöèÿ è ïðîãíîçèðîâàíèå îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíîé ýêîíîìè÷åñêîé ñèñòåìû
ãäå s0 =
— óðîâåíü ïîòðåáëåíèÿ;
— íîðìà èíâåñòèöèé â îñíîâíûå ïðîèçâîäñòâåííûå ôîíäû (êàïèòàëîâëîæåíèÿ);
— íîðìà èíâåñòèöèé â ÷åëîâå÷åñêèé êàïèòàë;
— óðîâåíü âíåøíèõ èíâåñòèöèé; E = Y + T - N F - R.
Áàëàíñîâîå óðàâíåíèå (1) ñîäåðæèò ýíäîãåííûå è ýêçîãåííûå ïàðàìåòðû. Ê ïîñëåäíèì
îòíîñÿòñÿ ïàðàìåòðû (B , R , N F , T ) t . Ïðè ýòîì âíåøíèé äîëã R t îïðåäåëÿåòñÿ äèíàìèêîé ïîñòóïëåíèÿ êðåäèòîâ B t , ïîëèòèêîé âîçâðàòà êðåäèòà, èëè òåìïîì åãî ïîãàøåíèÿ s, è ïðîöåíòíîé ñòàâêîé ïî êðåäèòàì p.
Äëÿ îïèñàíèÿ ôîðìèðîâàíèÿ äîõîäà ðåãèîíàëüíîãî áþäæåòà èñïîëüçóåì ñõåìó, ïðèâåäåííóþ íà ðèñ. 3.
Ðèñ. 3. Ñõåìà áþäæåòíîãî âçàèìîäåéñòâèÿ ðåãèîíà ñ âíåøíåé ñðåäîé
Ïóñòü
N = N F + NR ,
ãäå N F , N R — íàëîãè, ñîáèðàåìûå íà òåððèòîðèè ðåãèîíà, ïîñòóïàþùèå â ôåäåðàëüíûé
è ðåãèîíàëüíûé áþäæåòû ñîîòâåòñòâåííî.
Îáîçíà÷èì
rF =
N F R NR
, r = ,
N
N
ãäå r F è r R — ñîîòâåòñòâóþùèå äîëè îò÷èñëåíèé,
òîãäà r F + r R = 1.
58
Ðåãèîíû R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Îáúåì íàëîãîâ îïðåäåëÿåòñÿ ÷åðåç äîëþ u îáúåìà ðåàëèçîâàííîé ïðîäóêöèè Y (ðèñ. 1):
N = uY . Ôåäåðàëüíîå áþäæåòíîå ðåãóëèðîâàíèå âûðàçèì ÷åðåç ïðîïîðöèþ n (ðèñ. 1) âîçâðàòà ñðåäñòâ â âèäå äîòàöèé, òðàíñôåðòîâ, ñóáâåíöèé êàê äîëþ îò óðîâíÿ ðåãèîíàëüíûõ
íàëîãîâ [Áóëãàêîâ Â. Ê., Áóëãàêîâ Î. Â. (2006)]:
T = nN R ,
ãäå N R = r R uY .
Êîíñîëèäèðîâàííûé äîõîä ðåãèîíà ìîæíî çàïèñàòü â âèäå:
D = N R + T = (1+ n)r R uY .
Äëÿ îïèñàíèÿ äèíàìèêè ÎÏÔ, èëè K, ÷åëîâå÷åñêîãî êàïèòàëà H è âíåøíåãî äîëãà Z èñïîëüçóåì ýâîëþöèîííûå óðàâíåíèÿ, ðàññìîòðåííûå â ðàáîòàõ [Êåòîâà (2007)]; [Ðóñÿê, Êåòîâà (2007)].
Òàêèì îáðàçîì, îáùàÿ ïîñòàíîâêà çàäà÷è ìàêðîýêîíîìè÷åñêîé äèíàìèêè âêëþ÷àåò ñëåäóþùèå ñîîòíîøåíèÿ:
E = Y + T - N F - R = I + J + C - B,
(2)
s0 + sk + sh - sb = 1,
(3)
Y = F (K , H) = AK a H b ,
(4)
C = s0E , I = sk E , J = shE , B = sb E , T = nr R uY , N F = r F uY ,
(5)
é ærR ö ù
E = wF (K , H), w = 1+ ur F ênçç F ÷÷÷- 1ú, D = (1+ n)r R uY ,
êë è r ø úû
&
K (t ) = sk E (t ) - hK (t ), K 0 = K (t 0 ), K T = K (t T ),
(7)
H&(t ) = sh eE (t ) - cH(t ), H 0 = H(t 0 ), HT = H(t T ),
(8)
Z&(t ) = sb E (t ) -sZ (t ), Z 0 = Z (t 0 ), Z T = Z (t T ); R(t ) = (p + s)Z (t ),
(9)
(6)
ãäå h è c —êîýôôèöèåíòû âûáûòèÿ ïðîèçâîäñòâåííîãî è ÷åëîâå÷åñêîãî êàïèòàëà ñîîòâåòñòâåííî;
s — êàê áûëî óêàçàíî âûøå, òåìï ïîãàøåíèÿ êðåäèòà;
e — óñðåäíåííàÿ ïî âñåì âîçðàñòàì äîëÿ íàñåëåíèÿ, ó÷àñòâóþùåãî â îáùåñòâåííîì
ïðîèçâîäñòâå.
2. Àëãîðèòì èäåíòèôèêàöèè ìîäåëè
Ñèñòåìó óðàâíåíèé (2)—(9) ìîæíî ïðåäñòàâèòü â âèäå:
x& = f ( x , z , a , t ),
(10)
F1( x , z , a) = 0,
(11)
F2 ( x , z , a) £ 0,
(12)
59
R Ðåãèîíû
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
¹3(15) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹3(15) 2009
ãäå x = (K , H , Z ) — âåêòîð ôàçîâûõ ïåðåìåííûõ;
F1 , F2 —âåêòîð-ôóíêöèè îãðàíè÷åíèé;
z = (Y , P , L , Lo , I , J , C , D , B , T , R , N F , N R ) — âåêòîð äîïîëíèòåëüíûõ ïåðåìåííûõ
(çäåñü P — îáùàÿ ÷èñëåííîñòü íàñåëåíèÿ (population); L — ÷èñëåííîñòü òðóäîâûõ ðåñóðñîâ (labor); Lo — ÷èñëåííîñòü íàñåëåíèÿ òðóäîñïîñîáíîãî âîçðàñòà);
a = (a i ) = ( A, a , b , h , e , c , u , n , r F , r R , s, p , s0 , sk , sh , sb ) âåêòîð ïàðàìåòðîâ ñèñòåìû, ïðè÷åì
,
0 £ a min
£ a i £ a max
i
i
Èäåíòèôèêàöèÿ è ïðîãíîçèðîâàíèå îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíîé ýêîíîìè÷åñêîé ñèñòåìû
ãäå a min
—ìèíèìàëüíûå è ìàêñèìàëüíûå çíà÷åíèÿ ñîîòâåòñòâóþùèõ ïàðàìåòðîâ.
, a max
i
i
Çàäà÷à èäåíòèôèêàöèè ñîñòîèò â ñëåäóþùåì. Èçâåñòíî (íàïðèìåð, èç îïûòà) ïîâåäåíèå
ñèñòåìû x(t ). Íåîáõîäèìî ïîäîáðàòü êîýôôèöèåíòû a i òàêèì îáðàçîì, ÷òîáû îòêëîíåíèå
ïîâåäåíèÿ ñèñòåìû, êîòîðîå îïðåäåëÿåòñÿ ðåøåíèåì óðàâíåíèé (10) ïðè íàëè÷èè îãðàíè÷åíèé (11) è (12), îò çàäàííîãî ïîâåäåíèÿ áûëî áû ìèíèìàëüíûì.
Òî÷íîå ðåøåíèå çàäà÷è èäåíòèôèêàöèè âî ìíîãèõ ñëó÷àÿõ íå ïðåäñòàâëÿåòñÿ âîçìîæíûì. Àëãîðèòìû åå ïðèáëèæåííîãî ðåøåíèÿ ôîðìàëüíî ìàëî îòëè÷àþòñÿ îò àëãîðèòìîâ
ðåøåíèÿ çàäà÷ ìàòåìàòè÷åñêîãî ïðîãðàììèðîâàíèÿ [Ôåäîðåíêî (1994)]. Ïðè ïðàêòè÷åñêîé
ðåàëèçàöèè àëãîðèòìîâ ñóùåñòâóþò ïðîáëåìû, ñâÿçàííûå ñ äèôôåðåíöèðóåìîñòüþ ôóíêöèîíàëîâ è íàëè÷èåì ìíîãèõ ýêñòðåìóìîâ öåëåâîé ôóíêöèè.
Ðåàëèçàöèÿ âû÷èñëèòåëüíîé ñõåìû òðåáóåò êîíå÷íî-ðàçíîñòíîé àïïðîêñèìàöèè çàäà÷è
(10). Íà îòðåçêå [ t 0 , t T ] ââîäèòñÿ ñåòêà t 0 < t 1 < K < t N = t T ; ïðè ýòîì äèôôåðåíöèàëüíûå
óðàâíåíèÿ (10) çàìåíÿþòñÿ äèñêðåòíûì àíàëîãîì
y n+1 = L( y n+1 , y n , z n+1 , z n , a , t n ), n = 0, N - 1,
(13)
ãäå L — îïåðàòîð, îïðåäåëÿþùèé ìåòîä ÷èñëåííîãî èíòåãðèðîâàíèÿ;
y — ñåòî÷íàÿ ôóíêöèÿ, àïïðîêñèìèðóþùàÿ x.
Óñëîâèå ìèíèìèçàöèè îòêëîíåíèÿ ïîâåäåíèÿ ñèñòåìû (13) îò çàäàííîãî ïîâåäåíèÿ x d
â çàäàííûõ òî÷êàõ îñè âðåìåíè t Î [T 0 , T1 ] ïðèíèìàåòñÿ â âèäå
( y t - x dt )
, a max
J(a) = å
® min; a i Î [ a min
].
i
i
2
ai
t Î[ T 0 , T1 ]
( x dt )
2
(14)
Åñëè J(a) ® 0, òî y t ® x dt , a ® a 0 , ãäå a 0 ðåøåíèå çàäà÷è èäåíòèôèêàöèè (10)—(14).
Òàêèì îáðàçîì, çàäà÷à èäåíòèôèêàöèè ñâîäèòñÿ ê çàäà÷å ìàòåìàòè÷åñêîãî ïðîãðàììèðîâàíèÿ:
J(a) Þ ext; G1 (a) = 0, G 2 (a) £ 0.
(15)
Âûáîð ìåòîäà îïòèìèçàöèè îïðåäåëÿåòñÿ îñîáåííîñòÿìè ðåøàåìîé çàäà÷è. Õîðîøî
ðàçðàáîòàííûé àïïàðàò ìàòåìàòè÷åñêîãî ïðîãðàììèðîâàíèÿ ïðåäëàãàåò ìíîæåñòâî ðàçëè÷íûõ àëãîðèòìîâ, íî ïðè èõ ïðàêòè÷åñêîé ðåàëèçàöèè ñóùåñòâóþò òàêèå ïðîáëåìû, êàê
ìíîãîýêñòðåìàëüíîñòü è âûáîð íà÷àëüíîãî ïðèáëèæåíèÿ. Äëÿ ðåøåíèÿ îïòèìèçàöèîííûõ
çàäà÷, èìåþùèõ ñëîæíîñòè òàêîãî ðîäà, ïðåäëàãàåòñÿ ïðèìåíÿòü ãèáðèäíûå àëãîðèòìû
60
Ðåãèîíû R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
(ÃÁÀ): ãåíåòè÷åñêèå àëãîðèòìû (ÃÀ) â êîìáèíàöèè ñ ãðàäèåíòíûìè ìåòîäàìè îïòèìèçàöèè
[Êóðåé÷èê (2000)]; [Òåíåíåâ, Ïàêëèí (2003)].
Ïðè èñïîëüçîâàíèè ÃÀ äëÿ ðåøåíèÿ îïòèìèçàöèîííûõ çàäà÷ ïàðàìåòðû îïòèìèçàöèè
ïðåäñòàâëÿþòñÿ â âèäå êîäèðîâàííûõ çíà÷åíèé (ãåíîâ) [Ðóòêîâñêàÿ (2004)]. Ñîâîêóïíîñòü ãåíîâ îáðàçóåò õðîìîñîìó. Èç õðîìîñîì ñîñòàâëÿåòñÿ ïîïóëÿöèÿ. Êàæäîé õðîìîñîìå ñòàâèòñÿ
â ñîîòâåòñòâèå ôóíêöèÿ ïðèñïîñîáëåííîñòè, êîòîðàÿ âûñòóïàåò ìåðîé êà÷åñòâà ðåøåíèÿ,
îïèñûâàåìîãî äàííîé îñîáüþ.  êà÷åñòâå ôóíêöèè ïðèñïîñîáëåííîñòè âûñòóïàåò öåëåâàÿ
ôóíêöèÿ çàäà÷è (14).
Íà êàæäîé èòåðàöèè ÃÀ ïóòåì ïðèìåíåíèÿ ãåíåòè÷åñêèõ îïåðàòîðîâ ïðîèñõîäèò ýâîëþöèÿ èñõîäíîé ïîïóëÿöèè, ò. å. ïðîèñõîäèò èçìåíåíèå èíôîðìàöèè, ñîäåðæàùåéñÿ â õðîìîñîìàõ. Áëîê-ñõåìà ÃÀ ïðåäñòàâëåíà íà ðèñ. 4.
Ðèñ. 4. Áëîê-ñõåìà ãåíåòè÷åñêîãî àëãîðèòìà
Äëÿ ïðåäñòàâëåíèÿ ïàðàìåòðà îïòèìèçàöèè â âèäå ãåíà õðîìîñîìû ïðèìåíÿþòñÿ ðàçëè÷íûå ñïîñîáû êîäèðîâàíèÿ [Ðóòêîâñêàÿ (2004)], [Òåíåíåâ (2006)].  ñëó÷àå âåùåñòâåííîãî
êîäèðîâàíèÿ ïàðàìåòð ïðèâîäèòñÿ ê áåçðàçìåðíîìó âèäó ñ ïîìîùüþ ïðåîáðàçîâàíèÿ:
bi =
a i - a min
i
, i = 1, N.
max
a i - a min
i
(16)
Ñîîòâåòñòâåííî îáðàòíîå ïðåîáðàçîâàíèå áóäåò èìåòü âèä:
a i = a min
+ b i (a max
- a min
i
i
i ), i = 1, N.
(17)
Ïðèìåð õðîìîñîìû â ñëó÷àå âåùåñòâåííîãî êîäèðîâàíèÿ ïðåäñòàâëåí íà ðèñ. 5.
Ïîñëå òîãî êàê êàæäîé îñîáè ïîñòàâëåíî â ñîîòâåòñòâèå çíà÷åíèå ôóíêöèè ïðèñïîñîáëåííîñòè (14), îñóùåñòâëÿåòñÿ îòáîð îñîáåé ñ öåëüþ âûáîðà òåõ ïðåäñòàâèòåëåé, êîòîðûå
áóäóò ó÷àñòâîâàòü â ñîçäàíèè íîâîé ïîïóëÿöèè.
61
R Ðåãèîíû
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
¹3(15) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹3(15) 2009
Èäåíòèôèêàöèÿ è ïðîãíîçèðîâàíèå îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíîé ýêîíîìè÷åñêîé ñèñòåìû
Ðèñ. 5. Ïðèìåð õðîìîñîìû â ñëó÷àå âåùåñòâåííîãî êîäèðîâàíèÿ
Ñóùåñòâóåò ìíîæåñòâî òèïîâ îïåðàòîðîâ îòáîðà: íàïðèìåð, ìåòîä ðóëåòêè, òóðíèðíûé
îòáîð, ðàíãîâûé îòáîð. Áóäåì ïðèìåíÿòü òóðíèðíûé îòáîð, ñóòü êîòîðîãî çàêëþ÷àåòñÿ
â òîì, ÷òî èç ïîïóëÿöèè âûáèðàþòñÿ ms îñîáåé è ñðåäè íèõ îïðåäåëÿåòñÿ îñîáü, èìåþùàÿ
íàèëó÷øåå çíà÷åíèå ôóíêöèè ïðèñïîñîáëåííîñòè. Ýòà îïåðàöèÿ ïðîäîëæàåòñÿ äî òåõ ïîð,
ïîêà íå áóäåò ïîëó÷åíî íóæíîå ÷èñëî ðîäèòåëüñêèõ îñîáåé äëÿ ôîðìèðîâàíèÿ ñëåäóþùåãî ïîêîëåíèÿ. Çíà÷åíèå ms íàçûâàåòñÿ ðàçìåðîì òóðíèðà.
Ïîñëå ñîçäàíèÿ ðîäèòåëüñêîé ïîïóëÿöèè ê íåé ïðèìåíÿþòñÿ òàê íàçûâàåìûå ãåíåòè÷åñêèå îïåðàòîðû. Ñðåäè ãåíåòè÷åñêèõ îïåðàòîðîâ, êàê ïðàâèëî, èñïîëüçóþòñÿ îïåðàòîðû
ñêðåùèâàíèÿ, ìóòàöèè è èíâåðñèè.
Ðåçóëüòàòîì ðåàëèçàöèè îïåðàòîðà ñêðåùèâàíèÿ ÿâëÿåòñÿ ôîðìèðîâàíèå ïîòîìêîâ
íà îñíîâå ðîäèòåëüñêèõ îñîáåé. Ñóòü äåéñòâèÿ îïåðàòîðà ñêðåùèâàíèÿ ñîñòîèò â âûáîðå
òî÷êè ðàçðûâà âíóòðè õðîìîñîìû ñ ïîñëåäóþùèì îáìåíîì èíôîðìàöèè, ðàñïîëàãàþùåéñÿ
çà òî÷êîé ðàçðûâà, ìåæäó äâóìÿ ðîäèòåëüñêèìè îñîáÿìè. Ïðèìåð ìåõàíèçìà äåéñòâèÿ îäíîòî÷å÷íîãî îïåðàòîðà ñêðåùèâàíèÿ äëÿ âåùåñòâåííîãî êîäèðîâàíèÿ ïðèâåäåí íà ðèñ. 6.
Îòìåòèì, ÷òî îïåðàòîðîâ ñêðåùèâàíèÿ, èëè ìåõàíèçìîâ ôîðìèðîâàíèÿ îñîáåé ïîòîì-
Ðèñ. 6. Ìåõàíèçì äåéñòâèÿ îäíîòî÷å÷íîãî îïåðàòîðà ñêðåùèâàíèÿ
êîâ, ñóùåñòâóåò äîñòàòî÷íî ìíîãî. Âîñïîëüçóåìñÿ îïåðàòîðîì ñêðåùèâàíèÿ Bin2, êîòîðûé
ïðèâåäåí â ðàáîòå [Òåíåíåâ (2006)]:
c i = ab i1 + bb i2 , i = 1, N,
(18)
ãäå c i — çíà÷åíèå i-ãî ýëåìåíòà ïîòîìêà;
b i — çíà÷åíèå i-ãî ãåíà ðîäèòåëüñêîé îñîáè;
R -1
b = 2-1( 2-u ) ; a = 1- b; u Î [ 0; 1] — ñëó÷àéíàÿ âåëè÷èíà, èìåþùàÿ ðàâíîìåðíûé çàêîí
ðàñïðåäåëåíèÿ;
R — ïàðàìåòð, îòðàæàþùèé êîëè÷åñòâî ðàçðÿäîâ äëÿ êîäèðîâàíèÿ âåùåñòâåííîãî ÷èñëà.
Ñëåäóþùèì ãåíåòè÷åñêèì îïåðàòîðîì ÿâëÿåòñÿ îïåðàòîð ìóòàöèè. Îí ïðåäíàçíà÷åí
äëÿ âíåñåíèÿ ñëó÷àéíûõ èçìåíåíèé â èíôîðìàöèþ, ñîäåðæàùóþñÿ â õðîìîñîìå, è, êàê îïåðàòîð ñêðåùèâàíèÿ, èìååò äîñòàòî÷íî ðàçíîîáðàçíûå âàðèàíòû ðåàëèçàöèè. Êðèòåðèåì êà-
62
Ðåãèîíû R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
÷åñòâà îïåðàòîðà ìóòàöèè ñëóæèò åãî ñïîñîáíîñòü ïðîèçâîäèòü íåáîëüøèå èçìåíåíèÿ
ñ âûñîêîé äîëåé âåðîÿòíîñòè è ñ íèçêîé âåðîÿòíîñòüþ — áîëüøèå.
Áóäåì èñïîëüçîâàòü îïåðàòîð ìóòàöèè, îïðåäåëÿåìûé ïî ôîðìóëå [Muhlenbein, SchlierkampVoosen (1993)]:
c mi = c i + si ri b i ,
(19)
ãäå b i = 2 ; k Î [ 4; 20];
ri Î [ 4; 5] — äèàïàçîí øàãà ðåêîìáèíàöèè;
si Î {-1, +1} — íàïðàâëåíèå ðåêîìáèíàöèè.
-ku
 ãåíåòè÷åñêèõ àëãîðèòìàõ òàêæå ïðèìåíÿåòñÿ îïåðàòîð èíâåðñèè. Ñóòü åãî ðàáîòû çàêëþ÷àåòñÿ â ðàçáèåíèè õðîìîñîìû ñëó÷àéíûì îáðàçîì íà äâå ÷àñòè ñ ïîñëåäóþùåé èõ ïåðåñòàíîâêîé (ðèñ. 7).
Ðèñ. 7. Äåéñòâèå îïåðàòîðà èíâåðñèè
Ðåàëèçàöèÿ îïåðàòîðîâ ñêðåùèâàíèÿ, ìóòàöèè è èíâåðñèè íîñèò âåðîÿòíîñòíûé õàðàêòåð. Ïðè ïðàêòè÷åñêîé ðåàëèçàöèè ãåíåòè÷åñêèõ îïåðàòîðîâ çàäàþò íåêîòîðîå ôèêñèðîâàííîå ÷èñëî p f , çàòåì ïðîèçâîäèòñÿ ãåíåðàöèÿ ñëó÷àéíîãî ÷èñëà p èç îòðåçêà [ 0; 1]. Åñëè p £ p f ,
òî îïåðàòîð âûïîëíÿåòñÿ. Äëÿ îïåðàòîðà ñêðåùèâàíèÿ p f Î [ 0, 5; 1], â òî âðåìÿ êàê äëÿ îïåðàòîðîâ ìóòàöèè è èíâåðñèè p f Î [ 0; 0,1] [Ðóòêîâñêàÿ (2004)].
Åùå îäíèì âàæíûì àñïåêòîì ÃÀ ÿâëÿåòñÿ ñïîñîá ôîðìèðîâàíèÿ ñëåäóþùåãî ïîêîëåíèÿ
îñîáåé, êîòîðûé ìîæåò ïðîèñõîäèòü íà îñíîâå ðàçëè÷íûõ ñòðàòåãèé.  íàøåì ñëó÷àå áûëà
èñïîëüçîâàíà ýëèòàðíàÿ ñòðàòåãèÿ. Ïðè âûáîðå äàííîé ñòðàòåãèè îäíà èëè íåñêîëüêî
ëó÷øèõ îñîáåé ïåðåõîäÿò â ñëåäóþùóþ ïîïóëÿöèþ â ñëó÷àå, åñëè â ðåçóëüòàòå ïðèìåíåíèÿ
ãåíåòè÷åñêèõ îïåðàòîðîâ áûëè ïîëó÷åíû îñîáè, ñðåäè êîòîðûõ ëó÷øåå çíà÷åíèå ôóíêöèè
ïðèñïîñîáëåííîñòè õóæå, ÷åì ó ëó÷øåé îñîáè (îäíîé èëè íåñêîëüêèõ) ïðåäûäóùåãî ïîêîëåíèÿ. Ýòî ñäåëàíî äëÿ òîãî, ÷òîáû ïðåäîòâðàòèòü ïîòåðþ ëó÷øåãî ðåøåíèÿ ïðè ïåðåõîäå
îò ñòàðîãî ïîêîëåíèÿ ê íîâîìó.
Äëÿ ðåøåíèÿ çàäà÷è èäåíòèôèêàöèè ïàðàìåòðîâ ìîäåëè (15) áûë èñïîëüçîâàí ãåíåòè÷åñêèé àëãîðèòì ñ âåùåñòâåííûì êîäèðîâàíèåì ñ ïðèìåíåíèåì ñëåäóþùèõ ãåíåòè÷åñêèõ
îïåðàòîðîâ è ñòðàòåãèé:
1) ñòðàòåãèÿ îòáîðà — òóðíèðíûé îòáîð (ðàçìåð òóðíèðà — 4);
2) îïåðàòîð ñêðåùèâàíèÿ, êîòîðûé îñíîâàí íà âåðîÿòíîñòíîì ïðèìåíåíèè äâóõ òèïîâ
îïåðàòîðîâ — ïðèìåíÿåòñÿ äâóõòî÷å÷íûé îïåðàòîð, è â äàííîì ñëó÷àå ìåæäó äâóìÿ òî÷êàìè
ðàçðûâà õðîìîñîìû ïðîèñõîäèò ïîëó÷åíèå íîâûõ ãåíîâ ñ èñïîëüçîâàíèåì îïåðàòîðà Bin2 âèäà (18) (ðèñ. 8);
1
3) îïåðàòîð ìóòàöèè. Êàæäûé ãåí ïîäâåðãàåòñÿ ìóòàöèè ñ âåðîÿòíîñòüþ, ðàâíîé
,
mg
ãäå m g — êîëè÷åñòâî ãåíîâ. Íîâîå çíà÷åíèå ãåíà âû÷èñëÿåòñÿ ïî ôîðìóëå (19);
63
R Ðåãèîíû
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
¹3(15) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹3(15) 2009
Èäåíòèôèêàöèÿ è ïðîãíîçèðîâàíèå îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíîé ýêîíîìè÷åñêîé ñèñòåìû
Ðèñ. 8. Äåéñòâèå äâóõòî÷å÷íîãî îïåðàòîðà ñêðåùèâàíèÿ ñîâìåñòíî ñ îïåðàòîðîì Bin2
4) îïåðàòîð èíâåðñèè, êîòîðûé ñîñòîèò â ïåðåñòàíîâêå ÷àñòåé õðîìîñîì, ðàçäåëåííûõ
ñëó÷àéíûì îáðàçîì;
5) ñòðàòåãèÿ ôîðìèðîâàíèÿ ñëåäóþùåãî ïîêîëåíèÿ — ýëèòàðíàÿ ñòðàòåãèÿ (îäíà ýëèòíàÿ îñîáü).
 èñïîëüçóåìîé ãèáðèäíîé ñõåìå ãåíåòè÷åñêèé àëãîðèòì ñ âåùåñòâåííûì êîäèðîâàíèåì ÿâëÿåòñÿ îñíîâíûì ìåòîäîì îïòèìèçàöèè. Äîïîëíèòåëüíûì ìåòîäîì ÿâëÿåòñÿ ìåòîä Õóêà—Äæèâñà.
Ìåòîä Õóêà—Äæèâñà èìååò ðÿä ïðåèìóùåñòâ [Ëåñèí, Ëèñîâåö (1995)], à èìåííî:
1) â îòëè÷èå îò ìåòîäîâ îïòèìèçàöèè, èñïîëüçóþùèõ ïðîèçâîäíûå, îí íå òðåáóåò äèôôåðåíöèðóåìîñòè öåëåâîé ôóíêöèè;
2) â ïðîöåññå îðãàíèçàöèè âû÷èñëèòåëüíîãî ïîèñêà íå òðåáóåòñÿ ðåøåíèÿ çàäà÷ îäíîìåðíîé ìèíèìèçàöèè (êàê, íàïðèìåð, ïðè ìåòîäå ñîïðÿæåííûõ íàïðàâëåíèé);
3) â îòëè÷èå îò ãåíåòè÷åñêîãî àëãîðèòìà îáëàäàåò áîëåå âûñîêîé ñêîðîñòüþ ñõîäèìîñòè âáëèçè òî÷êè ýêñòðåìóìà.
Àëãîðèòì ìåòîäà Õóêà—Äæèâñà ñîñòîèò èç ïðîöåäóðû, îïðåäåëÿþùåé íàïðàâëåíèå
óáûâàíèÿ ìèíèìèçèðóåìîé ôóíêöèè (èññëåäóþùèé ïîêîîðäèíàòíûé ïîèñê), è ïðîöåäóðû
ïåðåìåùåíèÿ â íàïðàâëåíèè óáûâàíèÿ.
Ïðèìåíÿåìûé ãèáðèäíûé àëãîðèòì îñíîâàí íà ïîñëåäîâàòåëüíîé ðàáîòå ãåíåòè÷åñêîãî
àëãîðèòìà è ìåòîäà Õóêà—Äæèâñà. Ñóòü ðàáîòû ãèáðèäíîãî àëãîðèòìà çàêëþ÷àåòñÿ â òîì,
÷òî íà êàæäîé (î÷åðåäíîé) èòåðàöèè îñíîâíîãî ìåòîäà ïðåäïðèíèìàåòñÿ ïîïûòêà óëó÷øåíèÿ ðåøåíèÿ ñ ïîìîùüþ äîïîëíèòåëüíîãî ìåòîäà îïòèìèçàöèè. Áëàãîäàðÿ ýòîìó ãèáðèäíûé àëãîðèòì ïîâûøàåò àäàïòàöèîííûå ñâîéñòâà êàæäîãî èç ìåòîäîâ, ïðèìåíÿåìûõ â äàííîé ñõåìå, è äàåò â áîëüøèíñòâå ñëó÷àåâ ëó÷øèå ðåçóëüòàòû, ÷åì îòäåëüíûå ìåòîäû.
Òåñòèðîâàíèå àëãîðèòìîâ ïðîèçâîäèëîñü íà íàáîðå ñòàíäàðòíûõ ôóíêöèé, òàêèõ êàê
ôóíêöèè Ðîçåíáðîêà, Ðàñòðèãèíà, Ýêëè [Åâòóøåíêî (1982)] è äð. Âî âñåõ ñëó÷àÿõ äîñòèãíóòà
ïðèåìëåìàÿ òî÷íîñòü îïðåäåëåíèÿ ãëîáàëüíîãî ýêñòðåìóìà, ïðè ýòîì ïîäòâåðæäåíà âûñîêàÿ ðàáîòîñïîñîáíîñòü äàííîãî ãèáðèäíîãî àëãîðèòìà.
3. Ðåçóëüòàòû ïðîãðàììíîé ðåàëèçàöèè ìîäåëè
Ðàññìîòðèì ïðåäñòàâëåííóþ ìîäåëü íà ïðèìåðå ñòàòèñòè÷åñêèõ äàííûõ ïî Óäìóðòñêîé
Ðåñïóáëèêå (ÓÐ).
Èñïîëüçîâàòü ñòàòèñòè÷åñêèå äàííûå ïåðåõîäíîãî ïåðèîäà ýêîíîìèêè â èõ ïåðâîíà÷àëüíîì âèäå ïðàêòè÷åñêè íåâîçìîæíî, ïîñêîëüêó îíè èñïûòûâàþò çíà÷èòåëüíûå è òðóäíî-
64
Ðåãèîíû R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
îáúÿñíèìûå êîëåáàíèÿ, âûçâàííûå ïåðåñòðîéêîé ýêîíîìè÷åñêîé ñèñòåìû. Ïîýòîìó äëÿ ïîâûøåíèÿ òî÷íîñòè ìîäåëèðîâàíèÿ âíà÷àëå ïðîèçâîäèëîñü ñãëàæèâàíèå êîëåáàíèé âðåìåííû´õ ðÿäîâ ìåòîäîì ñêîëüçÿùåé ñðåäíåé.
Ïîëó÷åííûå òàêèì îáðàçîì èñõîäíûå âðåìåííû´å ðÿäû îñíîâíûõ ýêîíîìè÷åñêèõ ïàðàìåòðîâ ÓÐ çà 1996–2006 ãã., ïîñòðîåííûå ïî ñòàòèñòè÷åñêèì äàííûì [Óäìóðòèÿ â öèôðàõ
(1996–2006)]; [Çàêîí î áþäæåòå ÓÐ (1996–2006)]; [Îñíîâíûå ôîíäû ÓÐ (1996–2006)]; [Äîõîäû,
ðàñõîäû è ïîòðåáëåíèå äîìàøíèõ õîçÿéñòâ (2006)]; [Îò÷åòíîñòü Ôåäåðàëüíîé íàëîãîâîé
ñëóæáû (2007)]; [Îñíîâíûå èòîãè äåÿòåëüíîñòè Ãîñóäàðñòâåííîãî ñîâåòà ÓÐ (2007)], ïðåäñòàâëåíû â òàáë. 1.
Ïðè ðåøåíèè çàäà÷è èäåíòèôèêàöèè, ñëåäóÿ «Îò÷åòíîñòè Ôåäåðàëüíîé íàëîãîâîé ñëóæáû» (2007), ïîëàãàëè, ÷òî äîëè îò÷èñëåíèé â ôåäåðàëüíûé è ðåãèîíàëüíûé áþäæåòû äî
2002 ã. âêëþ÷èòåëüíî îäèíàêîâû: r F = r R = 0, 5. Íà÷èíàÿ æå ñ 2006 ã. ýòè äîëè ñîñòàâëÿþò:
r F = 0,7 è r R = 0, 3, ïðè ýòîì â äàííîì âðåìåííî´ì ïðîìåæóòêå îíè èçìåíÿþòñÿ ëèíåéíûì
îáðàçîì. Íàïîìíèì, ÷òî r F + r R = 1.
 êà÷åñòâå ìèíèìèçèðóåìîãî ôóíêöèîíàëà âûáðàí ôóíêöèîíàë (14), ãäå âåêòîð ìîäåëèðóåìûõ ìàêðîýêîíîìè÷åñêèõ õàðàêòåðèñòèê, îïðåäåëÿåìûé èç ñèñòåìû óðàâíåíèé (2)—(8),
çàäàí â âèäå y = (Y , K , H , I , J , N F , N R , T ); t Î [ 1996 , 2006 ]. Èçâåñòíîå ïîâåäåíèå ñèñòåìû
x d = (Y , K , H , I , J , N F , N R , T ) d , â çàäàííûõ òî÷êàõ îñè âðåìåíè t Î [ 1996 , 2006 ] îïðåäåëÿåòñÿ
èç òàáë. 1. Âåêòîð âàðüèðóåìûõ ïàðàìåòðîâ èìåë âèä a = (a i ) = ( h , e , c , u , n , s0 , sk , sh ).
Ðåøåíèå çàäà÷è èäåíòèôèêàöèè ïðåäñòàâëåíî â òàáë. 2 è 3.
 òàáë. 4 ïðèâåäåíû ñðåäíèå îòíîñèòåëüíûå îòêëîíåíèÿ ðàñ÷åòíûõ ýêîíîìè÷åñêèõ ïîêàçàòåëåé îò èõ ñòàòèñòè÷åñêèõ çíà÷åíèé çà ïåðèîä ðåòðîïðîãíîçà, îïðåäåëÿåìûå ïî ôîðìóëå:
1
zy =
Mxd
å
t Î[T 0 ,T1 ]
| y t - x dt |
x
t
d
, y = {Y , K , H , I , J , N F , N R , T , D},
(20)
ãäå M x d — êîëè÷åñòâî çàäàííûõ òî÷åê ïîêàçàòåëÿ x íà îñè âðåìåíè â ïåðèîäå ðåòðîïðîãíîçà.
Èç àíàëèçà âåëè÷èíû z y ñëåäóåò, ÷òî äëÿ ãîäîâîãî ïðîèçâîäñòâà ïðîäóêöèè ñðåäíåå
çà 1996–2006 ãã. îòêëîíåíèå ñîñòàâëÿåò 4,09%, âåëè÷èíà îñíîâíîãî ðåãèîíàëüíîãî êàïèòàëà — 8,05%, ÷åëîâå÷åñêîãî êàïèòàëà — 8,11%. Ðàñõîæäåíèå ìåæäó ðàñ÷åòíûìè è ñòàòèñòè÷åñêèìè äàííûìè ïî óðîâíþ ñóììàðíîãî ïîòðåáëåíèÿ è ðåãèîíàëüíûì áþäæåòîì çà èññëåäóåìûé ïåðèîä ñîñòàâëÿåò 11,20 è 7,07% ñîîòâåòñòâåííî.
Ïîëó÷åííûå òàêèì îáðàçîì çíà÷åíèÿ ïàðàìåòðîâ ñèñòåìû (ñì. òàáë. 3) áûëè ïðèíÿòû áàçîâûìè â ïðîãíîçíûõ ðàñ÷åòàõ íà 2007–2016 ãã. Ðåçóëüòàòû ïðîãíîçèðîâàíèÿ àáñîëþòíûõ è îòíîñèòåëüíûõ (íà äåìîãðàôè÷åñêóþ åäèíèöó èëè åäèíèöó òðóäîâûõ ðåñóðñîâ) ïàðàìåòðîâ ýêîíîìèêè ÓÐ íà îñíîâå ïðåäëîæåííîé ìîäåëè ïðèâåäåíû
â òàáë. 5 è 6.
Íà ðèñ. 9–11 ïðåäñòàâëåíû èçìåíåíèÿ ðàñ÷åòíûõ ìàêðîýêîíîìè÷åñêèõ ïàðàìåòðîâ
ñ 1996 ïî 2016 ã. Çäåñü æå îòðàæåíû ðåçóëüòàòû ñðàâíåíèÿ ðàñ÷åòíûõ è ñòàòèñòè÷åñêèõ äàííûõ çà ïåðèîä ðåòðîïðîãíîçà. Íà ðèñ. 12 è 13 ïðèâåäåíû êðèâûå èçìåíåíèÿ ñîîòâåòñòâóþùèõ óäåëüíûõ ïîêàçàòåëåé çà ýòîò æå ïåðèîä.
65
R Ðåãèîíû
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
¹3(15) 2009
775 903,5
67 539,8
—
24 222,7
7265,2
—
—
—
—
—
K, ìëí ðóá.
H, ìëí ðóá.
B, ìëí ðóá.
I, ìëí ðóá.
J, ìëí ðóá.
C, ìëí ðóá.
N F , ìëí ðóá.
N R , ìëí ðóá.
T , ìëí ðóá.
D, ìëí ðóá.
639 600
1 612 600
L, ÷åë.
P, ÷åë.
933 400
113 971,6
Y, ìëí ðóá.
Lo , ÷åë.
1996 ã.
Îáîçíà÷åíèå
1 607 700
669 700
948 100
—
—
—
—
—
7977,9
20 423,8
—
70 974,9
721 594,0
103 819,9
1997 ã.
1 604 000
700 800
959 300
—
—
—
—
—
8700,5
22 193,3
5161,8
77 373,4
675 827,1
119 805,9
1998 ã.
1 601 400
744 700
973 000
—
—
—
—
—
9579,9
22 516,9
5144,3
86 067,0
599 839,1
130 629,8
1999 ã.
1 595 600
767 800
986 800
—
—
—
—
—
10 973,1
25 522,2
5016,2
93 306,4
500 876,7
140 412,9
2000 ã.
1 588 100
792 900
968 437
—
—
—
—
—
11 663,2
21 949,4
2913,5
94 036,6
409 730,0
128 794,0
2001 ã.
1 578 200
782 000
972 298
25 760,9
4485,8
21 275,1
22 233,8
—
9781,8
19 584,6
2944,3
88 870,5
381 166,2
125 684,2
2002 ã.
1 568 200
781 200
979 074
23 396,5
3007,8
20 388,6
23 573,5
—
7867,2
17 465,3
2898,6
83 584,7
371 453,7
125 957,8
2003 ã.
1 560 200
772 900
988 658
21 846,7
2648,9
19 197,8
29 459,1
-
8011,8
21 255,0
1165,9
82 175,0
373 078,2
128 024,2
2004 ã.
1 552 800
792 900
993 052
21 159,9
2268,4
18 891,5
36 924,2
-
9638,5
26 117,9
1266,7
86 617,0
386 568,4
131 817,0
2005 ã.
Èñõîäíûå äàííûå ìàêðîýêîíîìè÷åñêèõ ïîêàçàòåëåé ýêîíîìèêè ÓÐ â öåíàõ 2006 ã.
Èäåíòèôèêàöèÿ è ïðîãíîçèðîâàíèå îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíîé ýêîíîìè÷åñêîé ñèñòåìû
1 544 400
766 000
989 600
20 946,7
2405,3
18 541,3
46 288,3
-
11 668,3
32 656,5
1707,4
92 848,9
399 996,8
136 655,1
2006 ã.
Òàáëèöà 1
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹3(15) 2009
66
Ðåãèîíû R
R Ðåãèîíû
68 106,1
0,0
20 433,3
8531,3
68 461,2
21 242,6
2974,0
24 216,6
64 821,9
0,0
19 994,7
8348,1
66 991,5
20 786,6
20 786,6
2910,1
23 696,7
H
B
J
C
NF
R
I
T
D
0,180
1,120
0,820
0,131
h
24 712,8
3034,9
21 677,9
21 677,9
69 863,9
8706,1
20 852,0
0,0
71 374,7
623 095,7
118 071,3
1998 ã.
0,750
e
25 646,0
3149,5
22 496,5
22 496,5
72 502,6
9034,9
21 639,6
0,0
77 845,9
515 581,8
122 530,7
2000 ã.
26 089,8
3204,0
22 885,8
22 885,8
73 756,8
9191,2
22 013,9
0,0
81 041,2
472 164,8
124 650,5
2001 ã.
0,046
c
0,367
u
Ïàðàìåòðû ìîäåëè
25 188,2
3093,3
22 094,9
22 094,9
71 208,1
8873,6
21 253,2
0,0
74 622,7
565 575,9
120 343,0
1999 ã.
0,140
n
26 521,2
3253,1
23 268,1
23 268,1
74 980,4
9343,7
22 379,1
0,0
84 206,6
434 497
126 718,4
2002 ã.
0,704
s0
24 251,9
2974,7
21 277,1
26 005,4
74 289,4
9257,6
22 172,9
0,0
87 340,9
401 856,1
128 750,6
2003 ã.
0,208
sk
21 852,6
2680,4
19 172,1
28 758,1
73 387,6
9145,2
21 903,7
0,0
90 263,8
373 055,8
130 514,4
2004 ã.
0,088
sh
19 341,1
2372,4
16 968,7
31 513,3
72 290,8
9008,5
21 576,4
0,0
92 965,9
347 560,5
132 016,7
2005 ã.
0,760
w
Òàáëèöà 3
16 734,7
2052,7
14 681,9
34 257,9
71 013,8
8849,4
21 195,2
0,0
95 439,7
324 905,2
133 263,8
2006 ã.
Y
4,09
Ïàðàìåòð
Ïîãðåøíîñòü, z y , %
67
8,05
K
8,11
H
12,86
I
12,28
J
11,60
NF
8,97
NR
7,07
D
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
9,80
T
Òàáëèöà 4
Ñðåäíÿÿ ïîãðåøíîñòü îïðåäåëåíèÿ ìàêðîýêîíîìè÷åñêèõ ïîêàçàòåëåé ýêîíîìèêè ÓÐ çà ïåðèîä ðåòðîïðîãíîçà
a
A
b
689 227,6
765 214,6
K
N
115 700,7
113 216,9
Y
21 242,6
1997 ã.
1996 ã.
Îáîçíà÷åíèå
Ðàñ÷åòíûå äàííûå ìàêðîýêîíîìè÷åñêèõ ïîêàçàòåëåé ýêîíîìèêè ÓÐ â öåíàõ 2006 ã., ìëí ðóá.
Òàáëèöà 2
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹3(15) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Èäåíòèôèêàöèÿ è ïðîãíîçèðîâàíèå îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíîé ýêîíîìè÷åñêîé ñèñòåìû
¹3(15) 2009
Ðèñ. 9. Äèíàìèêà èçìåíåíèÿ âàëîâîãî ðåãèîíàëüíîãî ïðîäóêòà
Ðèñ. 10. Äèíàìèêà èçìåíåíèÿ ïðîèçâîäñòâåííîãî êàïèòàëà
Ðèñ. 11. Äèíàìèêà èçìåíåíèÿ ÷åëîâå÷åñêîãî êàïèòàëà
68
Ðåãèîíû R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
¹3(15) 2009
Ðèñ. 12. Äèíàìèêà èçìåíåíèÿ óäåëüíûõ çíà÷åíèé âàëîâîãî ðåãèîíàëüíîãî ïðîäóêòà (1)
è îáùåñòâåííîãî ïîòðåáëåíèÿ (2)
Ðèñ. 13. Äèíàìèêà èçìåíåíèÿ ôîíäîâîîðóæåííîñòè (1) è êàïèòàëîâîîðóæåííîñòè (2) òðóäà
Àíàëèçèðóÿ ïîëó÷åííûå äàííûå, ìîæíî ñäåëàòü ñëåäóþùèå âûâîäû:
· ýêîíîìèêà Óäìóðòñêîé Ðåñïóáëèêè íàõîäèòñÿ íà ýòàïå ñòàáèëüíîãî ðîñòà âñåõ ìàêðîýêîíîìè÷åñêèõ ïîêàçàòåëåé;
· òåìï ðîñòà ýêîíîìèêè íåâåëèê; ïî óäåëüíîìó ÂÐÏ ñîñòàâëÿåò îêîëî 2%, ïî óðîâíþ
óäåëüíîãî îáùåãî ïîòðåáëåíèÿ — îêîëî 1% â ãîä.
 òàáë. 6 ïðèâåäåíû óäåëüíûå ïîêàçàòåëè (ñì. ôîðìóëó (20)); âåðõíèé èíäåêñ p óêàçûâàåò
íà òî, ÷òî ïîêàçàòåëü ðàññ÷èòàí íà åäèíèöó îáùåé ÷èñëåííîñòè íàñåëåíèÿ ðåãèîíà, âåðõíèé èíäåêñ L — ÷òî ïîêàçàòåëü ïðèâåäåí â ðàñ÷åòå íà åäèíèöó òðóäîâûõ ðåñóðñîâ.
69
R Ðåãèîíû
Òàáëèöà 5
14 727,9
2061,9
16 789,8
2058,0
16 758,1
T
D
16 821,6
2065,8
14 755,8
34 430,3
71 363,8
8945,8
21 348,1
0,0
96 802,7
314 337,7
134 022,4
2009 ã.
16 853,5
2069,7
14 783,8
34 495,5
71 499,0
8962,8
21 388,5
0,0
97 254,0
311 000,3
134 276,3
2010 ã.
16 885,4
2073,6
14 811,8
34 560,9
71 634,4
8979,8
21 429,1
0,0
97 703,7
307 751,8
134 530,7
2011 ã.
16 917,4
2077,5
14 839,9
34 626,4
71 770,2
8996,8
21 469,7
0,0
98 151,8
304 590,1
134 785,6
2012 ã.
16 949,5
2081,5
14 868,0
34 692,0
71 906,3
9013,8
21 510,4
0,0
98 598,3
301 512,9
135 041,2
2013 ã.
16 981,7
2085,4
14 896,2
34 757,9
72 042,7
9030,9
21 551,2
0,0
99 043,3
298 518,4
135 297,4
2014 ã.
17 013,9
2089,4
14 924,5
34 823,9
72 179,5
9048,1
21 592,1
0,0
99 486,7
295 604,5
135 554,4
2015 ã.
Òàáëèöà 6
16 984,5
2085,8
14 898,7
34 763,6
72 267,8
9032,4
21 554,8
0,0
99 907,2
287 203,4
135 319,8
2016 ã.
405,20
120,94
26,82
kL
L
L
11,24
46,31
10,92
L
p
p
j
c
d
i
h
y
86,97
2007 ã.
p
Îáîçíà÷åíèå
10,98
46,59
11,06
26,38
119,30
393,46
87,49
2008 ã.
11,05
46,87
11,07
26,41
119,77
388,90
88,03
2009 ã.
11,12
47,18
11,12
26,53
120,64
385,78
88,60
2010 ã.
11,20
47,50
11,21
26,75
121,97
384,20
89,21
2011 ã.
11,28
47,85
11,34
27,05
123,67
383,78
89,87
2012 ã.
11,37
48,23
11,49
27,41
125,65
384,23
90,57
2013 ã.
11,46
48,63
11,67
27,84
127,97
385,70
91,33
2014 ã.
11,57
49,06
11,87
28,32
130,50
387,76
92,14
2015 ã.
11,63
49,49
12,05
28,75
133,26
383,10
92,67
2016 ã.
Ïðîãíîçíûå çíà÷åíèÿ îòíîñèòåëüíûõ ìàêðîýêîíîìè÷åñêèõ ïîêàçàòåëåé ýêîíîìèêè ÓÐ â öåíàõ 2006 ã., òûñ. ðóá./÷åë.
34 365,2
14 700,0
71 228,8
N
8928,9
8912,0
J
34 300,2
21 307,7
21 267,4
I
R
0,0
0,0
B
N
96 349,8
95 895,2
H
71 094,0
317 766,1
321 287,7
K
F
133 768,9
133 515,8
Y
C
2008 ã.
2007 ã.
Îáîçíà÷åíèå
Ïðîãíîçíûå çíà÷åíèÿ àáñîëþòíûõ ìàêðîýêîíîìè÷åñêèõ ïîêàçàòåëåé ýêîíîìèêè ÓÐ â öåíàõ 2006 ã., ìëí ðóá.
Èäåíòèôèêàöèÿ è ïðîãíîçèðîâàíèå îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíîé ýêîíîìè÷åñêîé ñèñòåìû
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹3(15) 2009
70
Ðåãèîíû R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Ñïèñîê ëèòåðàòóðû
Áóëãàêîâ Â. Ê., Áóëãàêîâ Î. Â. Ìîäåëèðîâàíèå äèíàìèêè îáîáùàþùèõ ïîêàçàòåëåé ðàçâèòèÿ ðåãèîíàëüíûõ ýêîíîìè÷åñêèõ ñèñòåì Ðîññèè // Ýêîíîìèêà è ìàòåìàòè÷åñêèå ìåòîäû. 2006. Ò. 42. ¹ 1.
Ñ. 32.
Äîõîäû, ðàñõîäû è ïîòðåáëåíèå äîìàøíèõ õîçÿéñòâ â 2002–2006 ãîäàõ (ïî èòîãàì âûáîðî÷íîãî
îáñëåäîâàíèÿ áþäæåòîâ äîìàøíèõ õîçÿéñòâ): Ñòàò. ñá. Ãîñóäàðñòâåííîãî êîìèòåòà ÐÔ ïî ñòàòèñòèêå,
2006.
Åâòóøåíêî Þ. Ã. Ìåòîäû ðåøåíèÿ ýêñòðåìàëüíûõ çàäà÷ è èõ ïðèìåíåíèå â ñèñòåìàõ îïòèìèçàöèè.
Ì.: Íàóêà, 1982.
Çàêîí î áþäæåòå Óäìóðòñêîé Ðåñïóáëèêè íà 1996, ..., 2006 ãã.
Êåòîâà Ê. Â. Îá îäíîé çàäà÷å ìàêðîýêîíîìè÷åñêîé äèíàìèêè ðåãèîíà ñ ó÷åòîì ôàêòîðîâ ýêîíîìè÷åñêîãî ðàçâèòèÿ // Ïåðèîäè÷åñêèé íàó÷íî-òåîðåòè÷åñêèé æóðíàë «Âåñòíèê ÈæÃÒÓ». Èæåâñê:
Èçä-âî ÈæÃÒÓ. 2007. ¹ 3(35). Ñ. 33.
Êóðåé÷èê Â. Ì. Ãåíåòè÷åñêèå àëãîðèòìû // Ïåðñïåêòèâíûå èíôîðìàöèîííûå òåõíîëîãèè è èíòåëëåêòóàëüíûå ñèñòåìû. 2000. ¹ 1. Ñ. 18.
Ëåñèí Â. Â., Ëèñîâåö Þ. Ï. Îñíîâû ìåòîäîâ îïòèìèçàöèè. Ì.: Èçä-âî ÌÀÈ, 1995.
Îñíîâíûå èòîãè äåÿòåëüíîñòè Ãîñóäàðñòâåííîãî ñîâåòà ÓÐ òðåòüåãî ñîçûâà ïî ïðàâîâîìó îáåñïå÷åíèþ ñîöèàëüíî-ýêîíîìè÷åñêîãî ðàçâèòèÿ ÓÐ. Óïðàâëåíèå àíàëèòè÷åñêîãî îáåñïå÷åíèÿ è èíôîðìàöèîííûõ ðåñóðñîâ ïðè àïïàðàòå Ãîñóäàðñòâåííîãî ñîâåòà ÓÐ. Èæåâñê. 2007.
Îñíîâíûå ôîíäû Óäìóðòñêîé Ðåñïóáëèêè: Ñòàò. ñá. Ãîñêîìñòàòà ÓÐ. 1996–2006. Èæåâñê, 2007
Îò÷åòíîñòü Ôåäåðàëüíîé íàëîãîâîé ñëóæáû «Îò÷åò î íà÷èñëåíèè è ïîñòóïëåíèÿì íàëîãîâ, ñáîðîâ è èíûõ îáÿçàòåëüíûõ ïëàòåæåé â áþäæåòíóþ ñèñòåìó Ðîññèéñêîé Ôåäåðàöèè», ïî ñîñòîÿíèþ
íà 1 ÿíâàðÿ 2007 ã.
Ðóñÿê È. Ã., Êåòîâà Ê. Â. Ïîñòðîåíèå ïðîèçâîäñòâåííîé ôóíêöèè ýêîíîìè÷åñêîé ñèñòåìû ðåãèîíà
ñ ó÷åòîì ÷åëîâå÷åñêîãî êàïèòàëà // Âåñòíèê ÌÃÓ. 2008. ¹ 3. (Ýêîíîìèêà).
Ðóñÿê È. Ã., Êåòîâà Ê. Â. Ýêîíîìèêî-ìàòåìàòè÷åñêàÿ ìîäåëü àíàëèçà è ïðîãíîçà ôàêòîðà ÷åëîâå÷åñêîãî êàïèòàëà // Íàó÷íî-ïðàêòè÷åñêèé æóðíàë «Ýêîíîìèêà, ñòàòèñòèêà, èíôîðìàòèêà. Âåñòíèê
ÓÌλ, [ðàçäåë «Ñòàòèñòèêà è ìàòåìàòè÷åñêèå ìåòîäû â ýêîíîìèêå»]. Ì.: Èçä-âî ÃÎÓ ÂÏÎ ÌÝÑÈ. ¹ 2.
2007. C. 56–60.
Ðóòêîâñêàÿ Ä. Íåéðîííûå ñåòè, ãåíåòè÷åñêèå àëãîðèòìû è íå÷åòêèå ñèñòåìû. Ì.: Ãîðÿ÷àÿ ëèíèÿ
Òåëåêîì, 2004.
Òåíåíåâ Â. À. Ïðèìåíåíèå ãåíåòè÷åñêèõ àëãîðèòìîâ ñ âåùåñòâåííûì êðîññîâåðîì äëÿ ìèíèìèçàöèè ôóíêöèé áîëüøîé ðàçìåðíîñòè // Èíòåëëåêòóàëüíûå ñèñòåìû â ïðîèçâîäñòâå. Èæåâñê: Èçä-âî
ÈæÃÒÓ. 2006. ¹ 1. C. 93–107.
Òåíåíåâ Â. À., Ïàêëèí Í. Á. Ãèáðèäíûé ãåíåòè÷åñêèé àëãîðèòì ñ äîïîëíèòåëüíûì îáó÷åíèåì ëèäåðà // Èíòåëëåêòóàëüíûå ñèñòåìû â ïðîèçâîäñòâå. 2003. ¹ 2. Ñ. 181.
Óäìóðòèÿ â öèôðàõ: ñòàò. ñá. Ãîñêîìñòàòà ÓÐ. 1996–2006. Èæåâñê, 2007.
Ôåäîðåíêî Ð. Ï. Ââåäåíèå â âû÷èñëèòåëüíóþ ôèçèêó. Ì.: Èçä-âî ÌÔÒÈ, 1994.
Muhlenbein H., Schlierkamp-Voosen D. Predictive Models for the Breeder Genetic Algorithm: I. Continuous Parameter Optimization // Evolutionary Computation. 1993. Vol. 1. ¹ 1. P. 25–49.
71
R Ðåãèîíû
Ê. Â. Êåòîâà, È. Ã. Ðóñÿê
¹3(15) 2009











