Сколько весит вода в перевернутом стакане ? (Решение

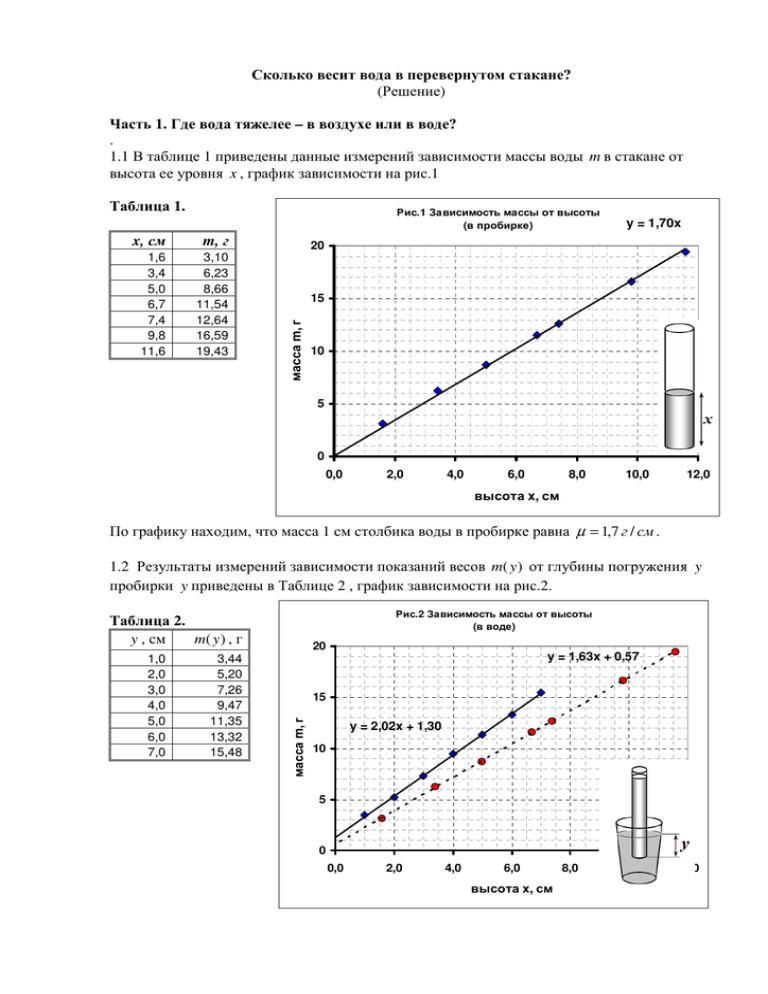
Сколько весит вода в перевернутом стакане?
(Решение)
Часть 1. Где вода тяжелее – в воздухе или в воде?
.
1.1 В таблице 1 приведены данные измерений зависимости массы воды m в стакане от
высота ее уровня x , график зависимости на рис.1
Таблица 1.
Рис.1 Зависимость массы от высоты
(в пробирке)
m, г
1,6
3,4
5,0
6,7
7,4
9,8
11,6
3,10
6,23
8,66
11,54
12,64
16,59
19,43
20
15
масса m, г
x, см
y = 1,70x
10
5
0
0,0
2,0
4,0
6,0
8,0
10,0
12,0
высота x, см
По графику находим, что масса 1 см столбика воды в пробирке равна µ = 1,7 г / см .
1.2 Результаты измерений зависимости показаний весов m( y ) от глубины погружения y
пробирки y приведены в Таблице 2 , график зависимости на рис.2.
Рис.2 Зависимость массы от высоты
(в воде)
Таблица 2.
y , см
m( y ) , г
3,44
5,20
7,26
9,47
11,35
13,32
15,48
20
y = 1,63x + 0,57
15
масса m, г
1,0
2,0
3,0
4,0
5,0
6,0
7,0
y = 2,02x + 1,30
10
5
0
0,0
2,0
4,0
6,0
высота x, см
8,0
10,0
12,0
1.3 Сравнение показывает, что наклон графика больше, чем в предыдущем случае – вода в
воде тяжелее? Но в данном случае взвешивали массу вытесненной воды, а она больше изза конечной толщины стенок.
Часть 2. Что тяжелее вода или воздух?
2.1 На рис. 3 показан график зависимости показаний весов от глубины погружения
пробирки при «заталкивании воздуха (данные в Таблице 3).
Таблица 3.
y , см
m( y ) , г
1,87
3,84
5,93
7,81
9,77
11,69
13,50
15,91
20
15
масса m, г
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
Рис.3 Зависимость массы от высоты
(воздух в воде)
y = 2,02x + 1,30
y = 1,97x - 0,09
10
5
0
0,0
2,0
4,0
6,0
8,0
10,0
высота x, см
2.2 На том же рисунке показан аналогичный график для погружения воды. Наклоны
графиков одинаковы, но это не значит, что воздух тяжелее (воздух здесь не причем!) – в
этом случае тоже измеряли массу вытесненной воды. Сдвиг графика за счет эффекта «дна
пробирки».
Часть 3. Весит ли вода в перевернутом стакане?
3.1 Можно провести непосредственные измерения силы: обнулить весы, когда на них
стоит
стакан
с пробиркой
Рис.4 Вес воды в перевернутом стакане
стоящей на дне, после чего
y = 2,09x + 15,73
считывать
показания
весов,
35
поднимая пробирку. Результаты
измерений в Таблице и на рис. 4.
2,0
3,2
4,5
5,5
6,5
8,2
9,1
20,09
22,27
25,01
27,19
29,49
32,91
34,74
масса m, г
30
Таблица 4.
m( z ) , г
z , см
25
20
15
0
2
4
6
высота x, см
В этом случае измеряется масса
пробирки и воды в пробирке, поднятой над уровнем воды в стакане.
8
10
Обработка результатов оценивается, если результаты измерений отличаются от
результатов жюри не более чем на 13%.
Пункт
задачи
1.1
1.2
1.3
2.1
2.2
3.1
3.2
Оценивание
Проведение измерений:
- 0,2б за точку (до 6 точек);
- диапазон не менее 10 см;
- найдено значение массы 1 см воды
0,5 если в диапазоне 1,6 – 1,8
0,3 если в диапазоне 1,5 – 1,9
Построение графика:
- нанесены все точки;
- оси подписаны и оцифрованы;
- проведена сглаживающая прямая;
Проведение измерений:
- 0,2б за точку (до 5 точек);
- диапазон не менее 7 см;
- коэффициент наклона в диапазоне 1,9 – 2,1
Построение графика:
- нанесены все точки;
- проведена сглаживающая прямая;
Сравнение
-наклон больше, чем в п. 1.1
-Это обусловлено влиянием стенок
Измеряли массу вытесненной воды
Проведение измерений:
- 0,2б за точку (до 5 точек);
- диапазон не менее 7 см;
- коэффициент наклона в диапазоне 1,9 – 2,1
Построение графика:
- нанесены все точки;
- оси подписаны и оцифрованы;
- проведена сглаживающая прямая;
Наклон совпадает с наклоном в п. 1.2
Измеряли массу вытесненной воды
Проведение измерений:
- 0,2б за точку (до 5 точек);
- диапазон не менее 7 см;
- коэффициент наклона в диапазоне 1,9 – 2,1
Построение графика:
- нанесены все точки;
- оси подписаны и оцифрованы;
- проведена сглаживающая прямая;
Сила равна весу пробирки и поднятой воды
ВСЕГО
Всего
1,2
0,3
0,5
0,3
0,1
0,1
1,0
0,2
0,3
0,3
0,1
0,2
0,2
0,2
1,0
0,2
0,3
0,3
0,1
0,1
0,25
0,25
1,0
0,2
0,3
0,3
0,1
0,1
0,5
10,0
оценка
АП!