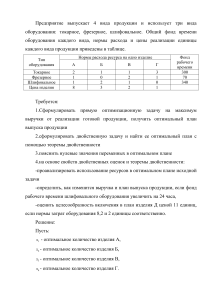
Задание на контрольную работу

Методические указания к выполнению контрольных работ по
исследованию операций
Выбор метода решения.
Список методов.
1.
Симплекс-метод.
2.
Улучшенный симплекс-метод.
3.
Двойственный симплекс-метод.
6. Выбор методов решения.
Первый метод – порядковый номер студента в журнале по модулю 3.
Второй метод – номер первого метода +2 по модулю 3.
Содержание.
Титульный лист.
Оглавление.
Задание.
Введение.
Математическая модель задачи
Алгоритм решения задачи.
Программа решения задачи.
Анализ результатов вычислений.
Выводы по работе.
Литература.
Задание.
Составить диету, содержащую по крайней мере 20 + N единиц белков, 30
+N единиц углеводов, 10 +N единиц жиров и 40 +N единиц витаминов, где N –
№ варианта. Как дешевле всего достичь этого при указанных в таблицах ценах
на 1 кг (или на 1 л) пяти имеющихся продуктов?
Хлеб
Соя
Сушеная рыба
Фрукты
Молоко
Белки
2
12
10
1
2
Углеводы
12
0
0
4
3
Жиры
1
8
3
0
4
витамины
2
2
4
6
2
Цена
12
36
32
18
10
Методические указания
Алгоритмы симплекс-методов.
А. Симплекс-метод.
1.
Ввести размерность задачи. Ввести коэффициенты в канонической
форме, базисные переменные и задать небазисные переменные.
Найти наименьший из коэффициентов C 'm 1 ,...,C 's ,...,C 'n .
Пусть это коэффициент C's . Если C 's  0 , то конец, оптимум найден. Иначе:
C 's  0 , и переменная Xs и прейти к 3.
2.
Если все a'is  0 , то конец.
Решение лежит вне заданных границ. Иначе вычислить B 'i / a 'is для всех ais  0
и найти минимум B 'i / a 'is .
Пусть этот минимум равен br / a' rs . Тогда Xs – базисная переменная, а Xr –
свободная переменная.
3.
Построить новую каноническую форму, изменить базис и перейти к 2.
Б. Двойственный симплекс-метод.
Пусть все коэффициенты целевой функции положительны .
Найти отрицательную базисную переменную. Если ее нет, то оптимальное
решение найдено; если их более чем одна, надо взять из них наименьшую. Путь
эта базисная переменная в r-м ограничении, она является переменной для
исключения из базиса.
В r-й строке найти отрицательный коэффициент a rj .
Если такого коэффициента нет, то не существует допустимого решения задачи.
Для отрицательных коэффициентов в этой строке найти MIN C ' j / a'rj .
j
Если этот минимум найден в S-м столбце, переменная Xs должна быть
включена в базис.
Провести
обычные
симплекс-преобразования,
выбрав
в
качестве
ведущего элемента a rj .
В. Улучшенный симплекс-алгоритм.
Пусть задача представлена в канонической форме.
Базисные переменные X n 1 ,..., X n  m равны соответственно в1 ,...,вm . Обращение
базиса
есть
просто
Im
–
единичная
матрица
размерностью
m m .
Соответствующие симплекс-множители – это  1  0,...., m  0 , поскольку в
целевую функцию Z не входят базисные переменные.
На k-й итерации базисные переменные – это X 1 ,..., X m , некоторые принимают
значения b'1 ,...b'm .
Обращение базиса – матрица
B 1
размерностью m  m ,
а симплекс-множители равны  1 ,..., m .
Вычислить коэффициенты небазисных переменных в канонической форме
целевой функции в текущем базисе
 aij 
 
C ' j  C j   aij   j  C j  ( 1 ,..., m )    
i 1
a 
 mj 
m
где  i - текущие симплекс-множители , aij - исходные коэффициенты из
уравнения.
Величины C' j вычисляются для каждой небазисной переменной.
Найти наименьший из коэффициентов C 'm 1 ,...,C 'n .
Если C 's  0 , то минимум функции Z найден, конец. Иначе: C 's  0 , и
переменная Xs войдет в базис.
Определить переменную, которая будет заменена переменной Xs. С этой целью
вычислить a's  B 1  as ;
Определить строку базисной переменной, предназначенной для исключения из
базиса MIN
b'i
b'
 r  MAX X s ; a'is  0 .
a'is a'rs
Заменить старый базис
X 1 ,..., X r ,..., X m на новый
X 1 ,..., X s ,..., X m ; новые
значения базисных переменных равны
X s  bi 
b 'r
; X 1  bi  b'i ais  br ; (i  r ) .
a'rs
Cформировать матрицу
 a'is


0 0
1 0
a'rs


 a '2 s


0 0
0 1
a'rs



   r  я
 
1
0 0
0 0


a'rs


 a 'm s
 0 0
0 1  
a'rs


5 - я строка
строка
Вычислить (новое обращение) =Е  (исходное обращение).
Найти
новые
симплекс-множители;
исходные
m
симплекс-множителей
 i    ki  Ck .
k 1
Новые значения симплекс множителей
 i   i 
 ki 
m

  a'ks Ck  Cs    i  C 's  ri .
a'rs  k 1

(Вернутся к 2.)
2. Контрольные вопросы.
значения
Как
определяется
направление
возрастания
целевой
функции
в
графическом методе решения задачи линейного программирования (ЛП).
Дайте
характеристику
стандартной
формы
задач
линейного
программирования.
Приведите
основные
правила
для
преобразования
задачи
ЛП
к
стандартному виду.
Каким соотношением задается отрезок в n-мерном пространстве.
Дайте определение экстремальной точки
Какое множество называется выпуклым?
Докажите, что если ограничения имеют допустимое решение, то они
имеют и базисное решение.
Докажите, что допустимая область является выпуклым множеством.
Докажите, что базисные допустимые решения соответствуют вершинам
выпуклого множества.
Докажите, что если целевая функция имеет конечный минимум, то, по
крайней мере, одно оптимальное решение является базисным.
Дайте характеристику канонической формы задачи ЛП.
Выведете основные соотношения для симплекс-метода.
Назовите основные шаги симплекс-метода.
Какой базис называется вырожденным?
Рассмотрите изменения значений правых частей.
Рассмотрите изменения коэффициентов целевой функции.
Как решается задача ЛП при появлении дополнительных переменных?
Опишите
решение
задачи
ЛП
при
включении
дополнительных
ограничений.
Приведите основные шаги двойственного симплекс-метода.
Приведите основные шаги улучшенного симплекс-метода.
Основные правила перехода к двойственной задаче.
Докажите, что двойственной задачей к двойственной есть прямая задача.
Докажите, что Z  W , где W – целевая функция двойственной задачи.
Докажите, что если прямая задача имеет конечное решение, то
двойственная задача имеет конечное решение Wmax  Z min .
Докажите, что значения симплекс-множителей оптимального решения
двойственной задачи являются значениями переменных в оптимальном
решении прямой задачи.
Рекомендуемая литература.
1. Карманов В.Г. Математическое программирование. М .:Наука, 1980.
2. Банди Б. Метод оптимизации: Вводный курс. Пер. с англ. М.: Радио и связь,
1988.