Метод нахождения координат источника сигнала в подводной
реклама

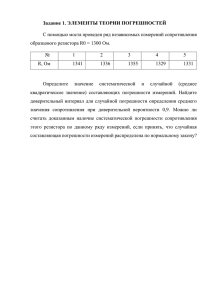
Метод нахождения координат источника сигнала в подводной среде Шарабанова А. В. Шарабанова А. В. Метод нахождения координат источника сигнала в подводной среде Шарабанова Анастасия Вадимовна / Sharabanova Anastasia Vadimovna – студент, кафедра систем автоматического управления и контроля, Национальный исследовательский университет, Московский институт электронной техники, г. Зеленоград Аннотация: в статье рассматривается метод поиска координат с помощью двух комбинированных приемников. Рассмотрен алгоритм расчета координат при помощи метода триангуляции. Местоположение источника определяется как точка пересечения плоскостей, образованных углами направления на источник. Представлены результаты расчета для отношения сигнал/шум больше единицы. Оценена погрешность результатов. Ключевые слова: векторно-фазовые методы, комбинированный приемник, триангуляция, поиск координат. В настоящее время гидроакустическое поле, создаваемое малошумными источниками, имеет в водной среде сложную нестационарную структуру, в результате чего уровень звукового давления в двух точках, разнесенных всего на десяток метров, может различаться в одно и то же время на 30-40 дБ. В таких условиях большое значение приобретают алгоритмы обработки сигналов, позволяющие по измерениям в ограниченной области пространства определять свойства источника, его координаты и элементы движения с последующей их идентификацией. Сохраняя габариты приемных систем, Векторно-фазовые методы позволяют увеличить объем акустической информации за счет одновременной регистрации звукового давления и вектора колебательной скорости [1]. Исследуемая приемная система состоит из источника сигнала, аналого-цифрового преобразователя и двух комбинированных гидроакустических приемников (КГП). КГП является измерительным устройством, состоящим из гидрофона и приемника колебательной скорости. Он измеряет одновременно в одной точке акустического поля четыре физические величины: акустическое давление и три ортогональные компоненты вектора колебательной скорости [2]. Для расчета координат используется метод триангуляции. Для его реализации будем использовать азимут и два угла места. Положение источника сигнала определится как точка пересечения плоскостей, задаваемых этими углами. Имеется два КГП с известными координатами, и известна частота тонального источника. Требуется найти координаты источника. Вертикальные оси z КГП направим параллельно. Источник тонального сигнала на заданной частоте единственный. Расстояния до приемника и углы направления на него обозначим, согласно рисунку 1. Рис. 1. Обозначение сторон и углов Проекция потока акустической мощности на направление определяется через вектор Умова: Где – эффективные значения звукового давления и проекции скорости на направление r, - разность фаз между давлением и колебательной скоростью. Восстановим частотный спектр сигнала. Для каждого канала дискретное преобразование Фурье (ДПФ) на заданной частоте . проводим Где –частота дискретизации, – оконная функция Хемминга. После того формируем значения, пропорциональные реактивным составляющим проекций потока акустической мощности. Эти значения характеризуют часть энергии, передаваемую в пространстве, собственно поток акустической мощности. Пеленг на объект горизонтальной области определяется соотношением Где i=1, 2 – Номер КГП Далее находим углы и для первого и второго КГП соответственно. Где i=1, 2 – Номер КГП Расстояние между гидроакустическими приемниками найдем, используя их координаты размещения в пространстве. Расстояния a и b (от проекции источника на плоскость XY до КГП1 и КГП2 соответственно) найдем по формулам: Высоту h от плоскости XY до источника найдем по формуле: Расстояния и находим, используя высоту h и найденные ранее углы и Для расчета координат источника сигнала введем декартову систему координат, оси которой будут пересекаться в точке размещения КГП1. В таком случае, координата источника будет равна расстоянию h от плоскости XY до источника. Для вычисления координаты источника сигнала , воспользуемся формулой: Координату источника , найдем по формуле: С помощью программной реализации метода для сигнала с добавлением нормально распределенного шума амплитудой 100 дБ, была оценена погрешность расчета алгоритма (таблица 1). Таблица 1. Оценка погрешности результатов расчета Амплитуда сигнала, дБ Угол , ° Угол , ° Угол , ° Угол , ° Сторона a, м Сторона b, м x3 y3 z3 Смоделирован ное значение Рассчитан ное значение Абсолютная погрешность расчета Относительная погрешность расчета, % 109,542 109,127 0,415 0,379 68,199 32,005 41,909 57,544 5,385 9,434 2 5 68 31 42 56 5,215 9,387 1,953 4,835 0,199 1,005 0,091 1,544 0,17 0,047 0,047 0,165 0,292 3,14 0,217 2,683 3,157 0,498 2,35 3,3 6 5,8 0,2 3,3 При отношении сигнал/шум больше единицы, результаты поиска координат источника тонального сигнала в подводной среде с помощью представленного алгоритма имеют максимальную погрешность расчета 3,3 %. Литература 1. Гордиенко В. А. Векторно-фазовые измерения в гидроакустике. – М.: ВНИИФТРИ, 2007. – 451 с.: ил. 2. Щуров В. А. Векторная акустика океана [Текст]. / В. А. Щуров. – Владивосток: Дальнаука, 2003. – 307 с.