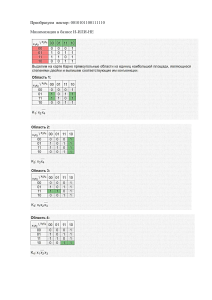
В другом базисе
реклама

1) Доказать, что векторы a 3 ; 0 ; 1 , b 2 ; 7 ; 3 , c 4 ; 3 ; 5 образуют базис, и найти координаты вектора d 16 ; 33 ; 13 в этом базисе. Векторы образуют базис пространства, если выполнены два условия: ● их количество равно размерности пространства (матрица, составленная из координат векторов, квадратная); ● они линейно независимы. Линейную независимость можно установить: ● через анализ определителя матрицы (матрица квадратная): - если 0 , то векторы линейно независимы; - если 0 , то векторы имеют линейную зависимость. ● через анализ ранга матрицы (матрица произвольная): - если ранг матрицы меньше её размерности, т.е. r A n , то векторы линейно зависимы; - если ранг матрицы равен её размерности, т.е. r A n , то векторы линейно независимы. ► Количество данных векторов равно размерности пространства n dim R 3 3. Вычислим определитель 3 0 1 4 3 4 3 2 3 7 3 7 15 4 3 9 2 77 21 98 0 1 5 1 3 3 5 2 7 - следовательно, данная система векторов линейно независима (определитель раскрыт по 2-й строке). 3 Вывод: векторы a , b , c образуют базис в пространстве R . ► Найдём координаты вектора d в базисе a ; b ; c . 1-й способ решения x1 a x2 b x 3 c d , Выразим вектор d через линейную комбинацию векторов a , b , c : т.е. d x 1 ; x 2 ; x 3 - координаты вектора d в базисе a ; b ; c . Решаем неоднородную систему линейных уравнений методом Гаусса 3 2 0 7 1 3 21 0 0 7 0 0 4 16 3 2 4 16 21 0 34 178 21 0 34 178 3 33 0 7 3 33 0 7 3 33 0 7 3 33 5 13 0 7 11 23 0 0 14 56 0 0 1 4 0 42 1 0 0 2 0 21 0 1 0 3 1 4 0 0 1 4 Итак, в базисе a ; b ; c вектор d имеет координаты: d 2 ; 3 ; 4 . 1 2-й способ решения Если обозначить представление некого вектора в базисе а его представление в базисе a ; b ; c как d *, e ; e ; e как d , 1 2 3 d * T 1 d , где T a b c - матрица перехода от старого базиса e 1 ; e 2 ; e 3 к новому базису a ; b ; c ; при этом векторы a , b , c даны в представлении в базисе e 1 ; e 2 ; e 3 . то d 1* 1 3 2 4 d 1 44 2 34 16 2 * 1 * 3 11 9 33 3 d d2 0 7 3 d 2 98 7 21 13 4 d * 1 3 5 d 3 7 3 2) Линейное превращение в базисе e : e 1 8 ; 6 ; 7 , e 2 16 ;7 ; 13 , e 3 9 ; 3 ; 7 имеет матрицу 1 18 15 A 1 22 20 1 25 22 Найти его матрицу в базисе e : e 1 1 ; 2 ; 1 , e 2 3 ; 1 ; 2 , e 3 2 ; 1 ; 2 . Матрица T перехода от базиса e к базису e : e eT T e 1e 8 16 9 3 T 6 7 7 13 7 1 1 3 2 1 1 3 2 1 1 1 2 5 1 2 2 1 3 6 Матрица линейного преобразования в новом базисе e : 1 1 3 1 A T AT 1 2 5 1 3 6 1 1 18 15 1 1 3 1 2 2 1 22 20 1 2 5 3 1 2 1 25 22 1 3 6 2 3 1 2