development, evolvement развитие, involute – развертка

Воображение
Описания
1. Отсечь лишнее
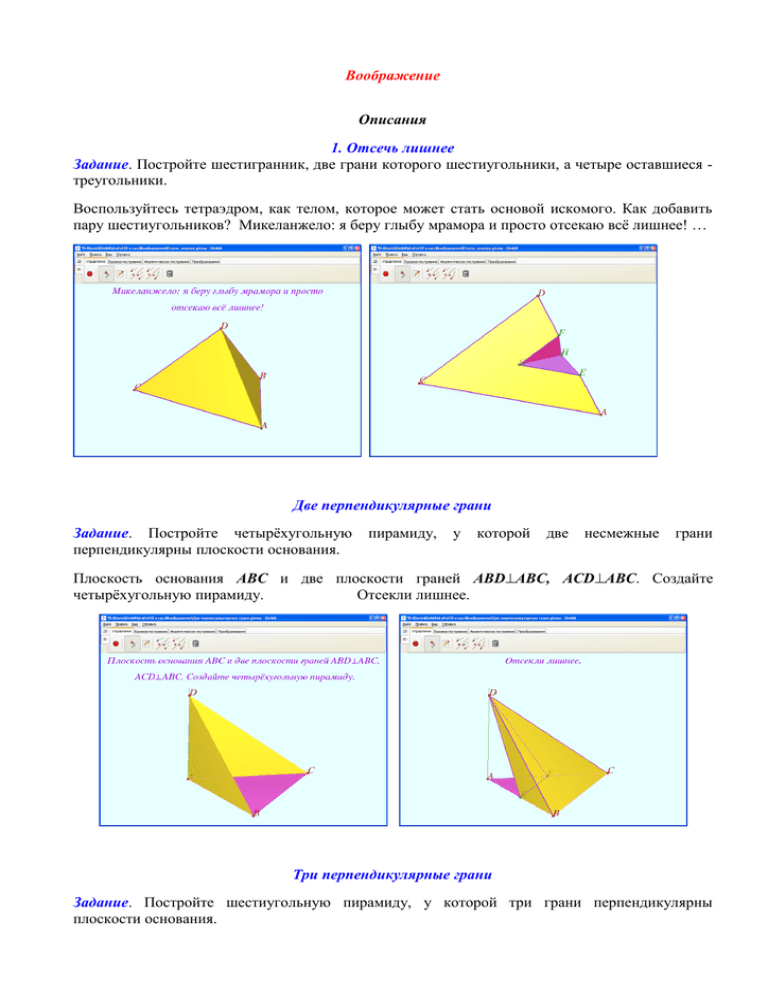
Задание. Постройте шестигранник, две грани которого шестиугольники, а четыре оставшиеся треугольники.
Воспользуйтесь тетраэдром, как телом, которое может стать основой искомого. Как добавить
пару шестиугольников? Микеланжело: я беру глыбу мрамора и просто отсекаю всё лишнее! …
Две перпендикулярные грани
Задание. Постройте четырёхугольную
перпендикулярны плоскости основания.
пирамиду,
у
которой
две
несмежные
грани
Плоскость основания ABC и две плоскости граней ABD⊥ABC, ACD⊥ABC. Создайте
четырёхугольную пирамиду.
Отсекли лишнее.
Три перпендикулярные грани
Задание. Постройте шестиугольную пирамиду, у которой три грани перпендикулярны
плоскости основания.
Плоскость основания ABC. Три плоскости граней ABD⊥ABC, ACD⊥ABC, AЕD⊥ABC. Создайте
шестиугольную пирамиду.
Добавили нужное.
Четыре касающихся треугольника
Задание. Расположите на плоскости 4 непересекающихся треугольника так, чтобы любые два
соприкасались частью своей границы, имеющей ненулевую длину.
Пусть один из треугольников правильный. Остальные равны между собой. Что тогда? …
Восемь касающихся тетраэдров
Задание. Расположите в пространстве 8 непересекающихся тетраэдров так, чтобы любые два
соприкасались частью своей поверхности, имеющей ненулевую площадь.
Пользуемся симметрией: строим четыре касающихся друг друга тетраэдра, стоящие на
плоскости симметрии. Постройте в плоскости основания АВС четыре треугольника,
касающихся друг друга по отрезку. Создайте четыре пирамиды с основаниями - найденными
треугольниками. ABCD окажется внутри. Проверьте, что каждый из построенных верхних
тетраэдров может касаться каждого из симметричных им нижних.
Совпадающая часть кубов
Задание. Центры двух единичных кубов совпадают. Докажите, что объём их общей части не
меньше, чем π/6.
Синяя сфера с центром О и диаметром чуть больше АВ слегка выступает из кубов. Если D =
AB, то V = π/6.
Куб, проходящий сквозь равный ему куб
Как в кубе проделать такое отверстие, через которое можно протащить куб, равный данному?
Квадрат EFGH имеет сторону, равную стороне куба, он перпендикулярен диагонали AC'. Его
можно перемещать за точку Q и вращать за точку E. Проверьте, как может куб пройти сквозь
равный ему куб.
Тетраэдры в кубе
Задание.Разместите внутри куба три правильных тетраэдра, не имеющих общих внутренних
точек, рёбра которых равны ребру куба.
Найдите расстояние между скрещивающимися рёбрами тетраэдров. Расстояние между
скрещивающимися рёбрами тетраэдров равно расстоянию от центра куба до его рёбер.
Разместите тетраэдры между ребром и центром куба. Как могут размещаться ребра тетраэдров,
проходящих через О? Исследуйте взаимное расположение тетраэдров.
Пересечение двух цилиндров
Задание. Оси двух равных цилиндров перпендикулярны и проходят через одну точку. Как
выглядит общая часть этих цилиндров?
Найдите линию пересечения цилиндров. Что о ней можно сказать? Как выглядит сечение тела
пересечения плоскостью, параллельной осям?
Пары касательных
Задание. В плоскости расположены три окружности, не имеющие общих точек. Пусть D,E и F
– точки пересечения пар внешних касательных. Докажите, что DEF – прямая.
Что получится, если окружности вложить в сферы? DEF – линия пересечения двух
плоскостей, касающихся сфер. Между ними лежат конусы, содержащие пары сфер.
Сферы, касающиеся всех граней тетраэдра
Задание. Сколько существует сфер, лежащих в трёхгранных углах вершин тетраэдра
касающихся плоскостей всех его граней.
Показана вписанная сфера. Какие ещё могут быть сферы? Сфера касается грани BCD извне.
Сколько подобных сфер существует? Как проверить, что показанные сферы касаются всех
граней? Показаны прямые, содержащие рёбра. Разворачивайте конфигурацию так, чтобы одно
из рёбер вырождалось в точку.
Как доказать, что подобных сфер больше нет? Каждая сфера лежит внутри одного из четырёх
трёхгранных углов. Число сфер ровно пять.
Сферы, касающиеся всех граней тетраэдра 2
Задание. Сколько существует сфер, не лежащих в трёхгранных углах вершин тетраэдра
касающихся плоскостей всех его граней.
Как может располагаться сфера, касающаяся плоскостей всех граней, не лежащая в
трёхгранном угле тетраэдра? Может ли сфера разместиться в области типа «крыши», для
которой «коньком» является рёбро тетраэдра.
Построена «крыша» с «коньком» CD и одна из сфер. Вращая рисунок, проверьте, что
построенная сфера касается плоскостей ABD и ABC. Где могут быть другие сферы? Исследуйте
построенные сферы, их возможное число. Оказывается, что число сфер этого типа не более, чем
три.
Окружность в квадранте 1
Задание. Окружность радиуса R касается трёх граней квадранта OXYZ, причем её плоскость
параллельна одному из рёбер. Найдите геометрическое место точек касания окружности с
гранями и центров окружности.
Исследуйте поведение окружности при перемещении точки А (плоскость параллельна OZ). Где
расположен центр окружности? AI⊥OXY ⇒ AI || OZ, |AI| = R. Исследуйте положение В и С (BC
|| OXY). Диаметр BC||OXY, |BC| = 2R. Точка В движется по отрезку длиной 2R параллельному
OX. Как движутся точки A и I? Середины отрезков длины 2R удалены на R от оси OZ и
движутся по дугам радиуса R c центром на OZ. Где ещё возможно касание?
Плоскость окружности может быть параллельна любой оси. Постройте гмт касания и гмт
центров окружности. Зелёным показано гмт центров окружностей, синим - точек касания.
Окружность в квадранте
Задание. Окружность радиуса R с центром А касается граней квадранта. Найдите
геометрическое место точек А. Сколько окружностей можно построить при заданной точке А?
Изображены окружность и геометрическое место точек центров окружности, если её плоскость
параллельна одному из рёбер квадранта. Пусть угол наклона плоскости окружности к
плоскости OXY равен α, к OYZ – β, к OXZ – γ (cos²α +cos²β +cos²γ = 1). Найдите длину отрезка
OA. Пусть В – точка касания, АВ = R, AH⊥OXY ⇒ ∠ABH = α, AH = Rsin α, OA = R{sin β, sin
γ, sin α}. AO2 = R2(sin2α + sin2β + sin2γ) = R2 (3 – cos2α – cos2β – cos2γ) = 2R2.
Точки A расположены на сфере с центром O и радиусом R 2 , причём, не далее, чем на
расстоянии R от граней. Сколько возможно окружностей с центром в заданной точке А?
Сфера и ломаная
Задание. AD = 2 - диаметр сферы, АВ = √2, ВС = 1 - хорды. Найдите CD, если угол между AD и
ВС равен 60°.
Пусть АЕ = ВС, AE||BC. Где находится E?. Пусть АЕ = ВС, AE||BC. Точка E на сфере радиуса 1
(AO = AE,∠OAE = 60°⇒ OE = 1). Чему равно АС? ABCE - вписанный параллелограмм,
∠AВС = 90°⇒ АС = √3. Найдите CD. CD = 1 (AC2 + CD2 = AD2).
Литература
Шарыгин И.Ф. Геометрия 10 – 11 классы. 4. Задачи и методы стереометрии. 4.4.
Развёртка.
Шарыгин И.Ф. Стереометрия Задачник 10 – 11 классы. Разные задачи. №467.
Терёшин Д.А. Стереометрия 10. 6. Элементы теории многогранников.
Key words: imagination, intersection, crossing, tangent, perpendicularity.
Ключевые слова: воображение, пересечение тел, касание, перпендикулярность.
Содержание
1. Отсечь лишнее
Постройте шестигранник, две грани которого шестиугольники, а четыре оставшиеся треугольники.
2. Две перпендикулярные грани
Постройте четырёхугольную пирамиду, у которой две несмежные грани перпендикулярны
плоскости основания.
3. Три перпендикулярные грани
Постройте шестиугольную пирамиду, у которой три грани перпендикулярны плоскости
основания.
4. Четыре касающихся треугольника
Расположите на плоскости 4 непересекающихся треугольника так, чтобы любые два
соприкасались частью своей границы, имеющей ненулевую длину.
5. Восемь касающихся тетраэдров
Расположите в пространстве 8 непересекающихся тетраэдров так, чтобы любые два
соприкасались частью своей поверхности, имеющей ненулевую площадь.
6. Совпадающая часть кубов
Центры двух единичных кубов совпадают. Докажите, что объём их общей части не меньше, чем
π/6.
7. Куб, проходящий сквозь равный ему куб
Как в кубе проделать такое отверстие, через которое можно протащить куб, равный данному?
8. Тетраэдры в кубе
Разместите внутри куба три правильных тетраэдра, не имеющих общих внутренних точек,
рёбра которых равны ребру куба.
9. Пересечение двух цилиндров
Оси двух равных цилиндров перпендикулярны и проходят через одну точку. Как выглядит
общая часть этих цилиндров?
10. Пары касательных
В плоскости расположены три окружности, не имеющие общих точек. Пусть D,E и F – точки
пересечения пар внешних касательных. Докажите, что DEF – прямая.
9. Сферы, касающиеся всех граней тетраэдра
Сколько существует сфер, лежащих в трёхгранных углах вершин тетраэдра касающихся
плоскостей всех его граней.
10. Сферы, касающиеся всех граней тетраэдра 2
Сколько существует сфер, не лежащих в трёхгранных углах вершин тетраэдра касающихся
плоскостей всех его граней.
11. Окружность в квадранте 1
Окружность радиуса R с центром А касается граней квадранта. Найдите гмт, если плоскость
окружности параллельна одному из рёбер квадранта.
12. Окружность в квадранте
Окружность радиуса R с центром А касается граней квадранта. Найдите гмт А. Сколько
окружностей можно построить при заданной точке А?
13. Сфера и ломаная
AD = 2 - диаметр сферы, АВ = √2, ВС = 1 - хорды. Найдите CD, если угол между AD и ВС равен
60°.