Закон сохранения момента импульса

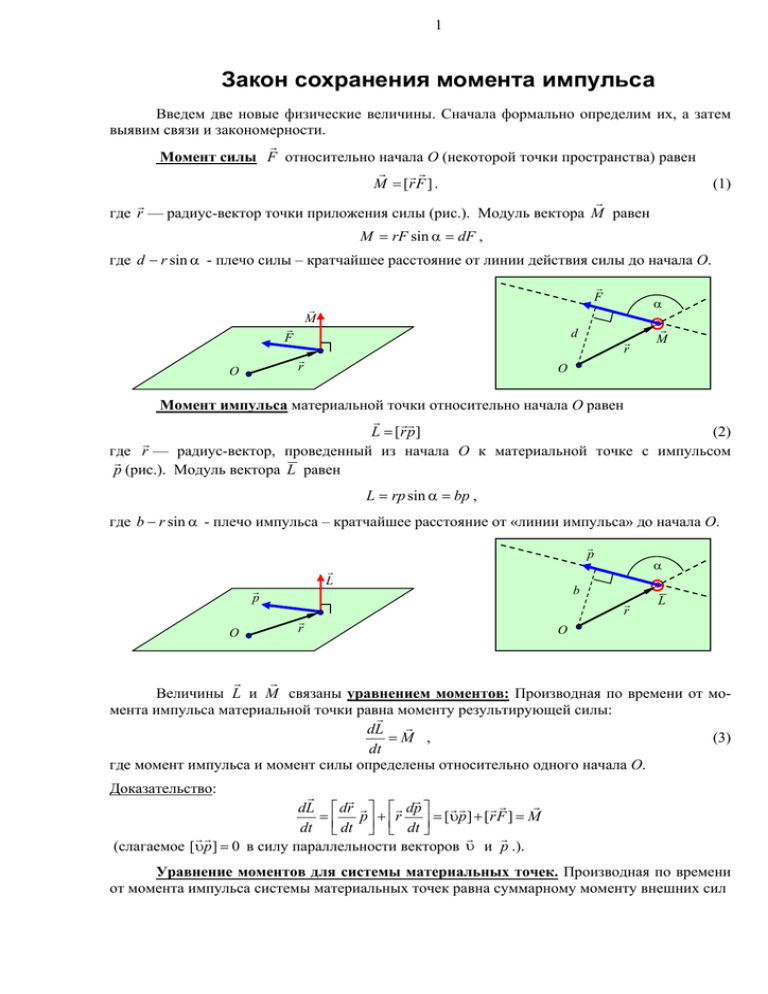
1
Закон сохранения момента импульса
Введем две новые физические величины. Сначала формально определим их, а затем
выявим связи и закономерности.

Момент силы F относительно начала O (некоторой точки пространства) равен


M  [r F ] .
(1)


где r — радиус-вектор точки приложения силы (рис.). Модуль вектора M равен
M  rF sin   dF ,
где d  r sin  - плечо силы – кратчайшее расстояние от линии действия силы до начала O.

F

M

F
d

r
O


r

M
O
Момент импульса материальной точки относительно начала O равен
 
L  [r p]
(2)

где r — радиус-вектор, проведенный из начала O к материальной точке с импульсом

p (рис.). Модуль вектора L равен
L  rp sin   bp ,
где b  r sin  - плечо импульса – кратчайшее расстояние от «линии импульса» до начала O.

p

L

p
O

r

b

r
L
O


Величины L и M связаны уравнением моментов: Производная по времени от момента импульса материальной точки равна
 моменту результирующей силы:
dL 
M ,
(3)
dt
где момент импульса и момент силы определены относительно одного начала O.
Доказательство:





dL  dr     dp   
  p    r   [ p ]  [ r F ]  M
dt  dt   dt 



(слагаемое [p]  0 в силу параллельности векторов  и p .).
Уравнение моментов для системы материальных точек. Производная по времени
от момента импульса системы материальных точек равна суммарному моменту внешних сил
2

dL 
 M внеш ,
dt
(4)
Доказательство. Суммируя уравнение (3) по всем точкам системы получим:





dLi
dL

  M внутр i   M внеш i  M внеш .
dt
dt
Здесь учтено, что суммарный момент внутренних сил равен нулю. Это следует из третьего
закона Ньютона. Существенно, что силы взаимодействия материальных точек не только равны по величине и противоположны по направлению, но и направлены вдоль прямой, соединяющей эти точки.
Закон сохранения момента импульса. Из уравнения (4) следует, что момент импульса замкнутой системы сохраняется.
Закон сохранения момента импульса является фундаментальным законом, отражающим изотропность пространства, т. е. равноправие всех его направлений. Как и в случае законов сохранения импульса и энергии, действие закона сохранения момента импульса выходит за пределы ньютоновской механики, в рамках которой он был выведен.
Момент импульса незамкнутой системы сохраняется, если суммарный момент

внешних сил M внеш равен нулю.
Примеры
Пример 1. Частица движется в центральном поле, например, гравитационном или
электростатическом. На частицу действует сила, направленная в сторону центра O поля (или
от центра). Поэтому момент этой силы относительно центра тождественно равен нулю:

| M | Fr sin   0 , т.к sin   0 .

Следовательно, вектор момента импульса L относительно центра O сохраняется. Из форму 


лы L  [r p] следует, что векторы r и p лежат в плоскости, перпендикулярной постоянному

вектору L , следовательно, движение происходит в одной плоскости (рис.) и при движении
сохраняется величина L  mr sin  .

L
O

F

r


p
Эта величина пропорциональна скорости «заметания» площади ра
диусом-вектором r :
ds 1 r (dt ) sin 
L


dt 2
dt
2m
(рис.), так что утверждение о сохранении момента импульса при
движении в центральном поле эквивалентно знаменитому второму
закону Кеплера:
За равные промежутки времени радиус-вектор, соединяющий
Солнце и планету, заметает равные площади.
Этот закон относится к любому центральному полю и является
3
прямым следствием закона сохранения момента импульса.
Пример 2. Прицельный параметр. Пусть частица массы m издалека приближается
к силовому центру со скоростью  0 . Расстояние от центра поля до линии движения удаленной частицы называется прицельным параметром b (рис). Момент импульса частицы в центральном поле сохраняется и может быть легко вычислен, когда частица находится на большом расстоянии от центра и на минимальном расстоянии:
L  m 0 r sin   m 0 b ,
L  m m rmin ,
где  m - скорость частицы на минимальном
расстоянии rmin от силового центра. Отсюда
получаем простое и важное соотношение:
m

0
 0 b   m rmin .
b
Если записать еще закон сохранения энергии
rmin

m
O
1
1
m 02  m m2  E p (rmin ) ,
2
2
то по известным  0 и b можно вычислить
rmin и  m .Комп. демонстрация
Пример 3. Несколько взаимодействующих частиц движутся в центральном поле.
Траектории движения могут быть очень сложными, но суммарный момент импульса остается постоянным. Эта важная закономерность существенно упрощает решение задачи: наряду с
механической энергией и импульсом сохраняется еще одна величина – момент импульса.
Компьютерное моделирование: два заряда в центральном поле третьего неподвижного заряда.
Момент силы и момент импульса относительно оси


 
  
Векторные величины L и M не очень наглядны: векторы r , p , F , M , L по
разному ориентированы в пространстве. Заметно проще ведут себя проекции векторов M и

L на некоторую ось z . При этом вместо (4) имеем скалярное уравнение
dL z
 Mz.
dt
Проекции M z и Lz называются моментом силы и моментом импульса относительно оси z . Эти величины зависят только от составляющих силы и импульса, которые
перпендикулярны оси z . Так
M z   F d ,
(5)

где d - плечо силы F - кратчайшее расстояние от линии действия силы до оси z (рис). Знак

«  » берем в формуле, когда сила F и направление оси z связаны правилом винта.
4

F

F|| r

F
z
O

F||
d
z
z

F
d
Аналогично момент импульса относительно оси равен произведению импульса p  на плечо
l (рис.):
Lz  p  l .
(6)

p||

p

p
z

p|| 
O
r
l
z
z

p
l
Докажем две важные теоремы:
1) Если сумма сил равна нулю, то суммарный момент этих сил не зависит от выбора начала O.
Доказательство: Рассмотрим два начала O1 и O2 (см.
рис). Тогда

  
 
M 1   [r1i Fi ]   [( R  r2i ) Fi ] 



 
 
 [ R  Fi ]   [r2i Fi ]   [r2i Fi ]  M 2

Fi

r1i

R
O1
2). Если импульс системы равен нулю, то момент

импульса L не зависит от выбора начала O.
Доказательство. Рассмотрим два начала O1 и O2 .
 


Пусть вектор R проведен от O1 к O2 . Тогда r1i  R  r2i и

  
 
 O1
 
 
L1   [( R  r2i ) pi ]  [ R  pi ]   [r2i pi ]   [r2i pi ]  L2

r2i
O2

pi
mi

r1i

r2i

R
O2
5
Введем понятие равнодействующей силы – это сила, равная векторной сумме нескольких сил и приложенная таким образом, что ее момент относительно любого начала равен суммарному моменту этих сил.
Пример. Суммарный момент сил тяжести, действующих на точки системы равен:

 
 
 
М   ri mi g    ri mi g  rc mg  ,

где m - масса системы, rc -радиус вектор центра масс. Видно, что равнодействующая сил тяжести проходит через центр масс системы.


Поле тяготения
Закон всемирного тяготения. Две точечные массы m1 и m2 , находящиеся на расстоянии r друг от друга, притягиваются с силой тяготения (гравитационной силой), равной
F G
m1m2
,
r2
(1)
где G  6,67 • 10-11 H • м2/кг2 — гравитационная постоянная. Сила тяготения — центральная
сила, т.е. она действует вдоль линии, соединяющей частицы.
Силу, действующую на материальную точку массой m в центральном поле тяготения
(гравитационном поле), создаваемым неподвижной точечной массой М, можно записать в
виде:


mM r
mM
F  G 2
или Fr (r )  G 2 .
(2)
r r
r
Потенциальную энергию точки в центральном поле тяготения можно найти, используя соотношение между силой и потенциальной энергией:
Fx  
Направив ось X по радиусу, получим Fr  
dE p
dr
G
E p
x
.
или
dE p
mM


.
dr
r2
Отсюда находим
E p  G
mM
 const .
r
Константу обычно полагают равной нулю, т. е. принимают за нуль потенциальную энергию
на бесконечности:
Eп  G
mM
.
r
(3)
Космические скорости. Первой космической скоростью называют скорость движения по круговой орбите вблизи поверхности планеты. Она определяется из уравнения движения спутника
6
mg 
m12
R
и равна 1  gR  GM / R , где M - масса планеты (для Земли 1  7,9 км/с.).
Вторая космическая скорость — минимальная скорость, которую надо сообщить телу на поверхности планеты, чтобы оно преодолело силу тяготения и ушло на бесконечность.
Из закона сохранения энергии
m 22
mM m 2
G

 0,
2
2
R
где   - скорость на бесконечности, получим для второй космической скорости
 2  2GM / R  2 gR  1 2 (для Земли  2  11,2 км/с).
Движение в центральном поле тяготения. Законы Кеплера. Применение законов сохранения энергии и момента импульса позволяет установить, как зависит от времени расстояние до центра r , точнее, свести эту задачу к одномерному движению. Для этого
надо разложить скорость частицы на две компоненты
(рис. ): радиальную  r  dr / dt и перпендикулярную к
ней азимутальную   . Момент импульса выражается
через азимутальную скорость: L  mr . Следовательно, механическую энергию точки можно представить в виде:
E
m( r2   2 )
2
2

m  dr   L2
 E p (r ) .
 E p (r )     
2
2  dt   2mr

Видно, что зависимость r (t ) такая же, как при одномерном движении с эффективной потенциальной энергией, определяемой равенством
U эфф
E  U эфф 
L2
GmM
L2
 Ep 


,
r
2mr 2
2mr 2
(4)
m 2r
.
2
Вид эффективной потенциальной кривой определяется значением L , которое можно вычислить из
начальных условий. На рис. качественно изображена
зависимость эффективной потенциальной энергии
U эфф от расстояния r для разных значений L
( L0  0, L1  L2  L3 ).
По значению механической энергии E
можно установить характер движения. Движение
происходит только в области, где E  U эфф , поскольку кинетическая энергия неотрицательна.
При E  0 движение финитное, то есть происходит в ограниченной области r , между точками поворота rmin и rmax . При E  0 движение инфинит-
U эфф
E 0
0
rmin
E0
rmax
r
7
ное, то есть после «точки поворота» точка уходит на бесконечность с кинетической энергией
E.
Первый закон Кеплера утверждает, что финитное движение (Е < 0) материальной
точки в центральном поле тяготения происходит по замкнутой траектории — эллипсу, в одном из фокусов которого находится центр силы притяжения (Солнце).
Дополним первый закон Кеплера утверждением, что инфинитное движение в центральном поле тяготения происходит либо по параболе (Е = 0), либо по гиперболе (Е > 0).
Второй закон Кеплера: за равные промежутки времени радиус-вектор, соединяющий
Солнце и планету, заметает равные площади.Этот закон относится к любому центральному
полю и является прямым следствием закона сохранения момента импульса.
Третий закон Кеплера утверждает, что квадраты периодов движения относятся как
кубы больших полуосей эллиптических орбит:
T12 a13

.
T22 a23