Геометрия/9 класс/2 триместр
реклама
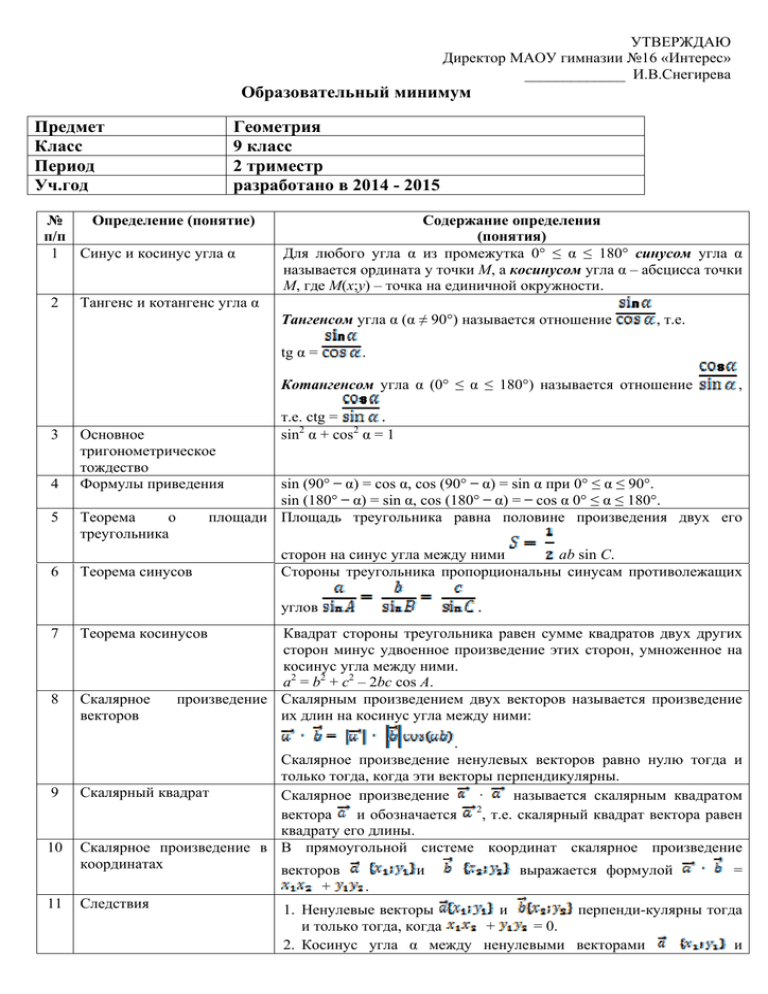
УТВЕРЖДАЮ Директор МАОУ гимназии №16 «Интерес» _____________ И.В.Снегирева Образовательный минимум Предмет Класс Период Уч.год Геометрия 9 класс 2 триместр разработано в 2014 - 2015 № Определение (понятие) п/п 1 Синус и косинус угла α 2 Содержание определения (понятия) Для любого угла α из промежутка 0° ≤ α ≤ 180° синусом угла α называется ордината у точки М, а косинусом угла α – абсцисса точки М, где М(х;у) – точка на единичной окружности. Тангенс и котангенс угла α Тангенсом угла α (α ≠ 90°) называется отношение tg α = , т.е. . Котангенсом угла α (0° ≤ α ≤ 180°) называется отношение 3 4 5 6 Основное тригонометрическое тождество Формулы приведения т.е. ctg = . 2 2 sin α + cos α = 1 sin (90° ̶ α) = cos α, cos (90° ̶ α) = sin α при 0° ≤ α ≤ 90°. sin (180° ̶ α) = sin α, cos (180° ̶ α) = ̶ cos α 0° ≤ α ≤ 180°. площади Площадь треугольника равна половине произведения двух его Теорема о треугольника Теорема синусов сторон на синус угла между ними ab sin C. Стороны треугольника пропорциональны синусам противолежащих . углов 7 Теорема косинусов 8 Скалярное векторов 9 10 Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними. a2 = b2 + c2 – 2bc cos A. произведение Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними: . Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. Скалярный квадрат Скалярное произведение · называется скалярным квадратом 2 вектора и обозначается , т.е. скалярный квадрат вектора равен квадрату его длины. Скалярное произведение в В прямоугольной системе координат скалярное произведение координатах и выражается формулой = векторов + 11 , Следствия . 1. Ненулевые векторы и перпенди-кулярны тогда и только тогда, когда + = 0. 2. Косинус угла α между ненулевыми векторами и выражается формулой . 12 Свойства скалярного Для любых векторов , , произведения векторов соотношения: 1. 2 ≥ 0, причем 2 > 0 при 2. 3. ) · 13 14 15 16 17 18 19 20 21 22 23 = = и любого числа k справедливы ≠ 0. (переместительный закон). · + (распределительный закон). =k( ) (сочетательный закон). 4. ) Определение правильного Правильным многоугольником называется выпуклый многоугольника многоугольник, у которого все углы равны и все стороны равны. Теорема об окружности, Около любого правильного многоугольника можно описать описанной около окружность, и притом только одну. правильного многоугольника Теорема об окружности, В любой правильный многоугольник можно вписать окружность, и вписанной в правильный притом только одну. многоугольник Следствия 1. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. 2. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. Эта точка называется центром правильного многоугольника. Формулы для вычисления площади правильного 1. . многоугольника, его ( = , = , = стороны и радиуса 2. вписанной окружности. 3. . Длина окружности Отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей (число π). C = 2πR. Длина дуги окружности · α. 2. Площадь круга Определение кругового Круговым сектором или просто сектором называется часть круга, сектора ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Площадь кругового сектора α. Отображение плоскости на Если каждой точке плоскости сопоставляется (ставится в себя соответствие) какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, тогда 24 Определение движения 25 Свойства движения 26 27 Определение наложения Свойства наложения 28 29 Следствие Определение параллельного переноса 30 Определение поворота говорят, что дано отображение плоскости на себя. Осевая симметрия представляет собой отображение плоскости на себя. Движение (или перемещение) плоскости – это отображение плоскости на себя, сохраняющее расстояние. Осевая и центральная симметрии плоскости являются движениями. При движении отрезок отображается на отрезок. При движении треугольник отображается на равный ему треугольник. Наложение – это отображение плоскости на себя. Прямое: Любое наложение является движением плоскости. Обратное: Любое движение является наложением. При движении любая фигура отображается на равную ей фигуру. Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что 1. Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что ОМ = ОМ1 и МОМ1= α.




