ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЭЛЕКТРОМАГНИТНОГО
реклама

ТУ
БН
ри
й
УДК 637.634
ит
о
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ
ЭЛЕКТРОМАГНИТНОГО ИМПУЛЬСА,
УПРАВЛЯЮЩЕГО ПРОЦЕССОМ КАПЛЕОБРАЗОВАНИЯ
ПРИ СВАРКЕ ПЛАВЯЩИМСЯ ЭЛЕКТРОДОМ
Канд. техн. наук ДЕМИДКОВ С. В., канд. физ.-мат. наук ЗАНКЕВИЧ В. А.,
БАЙЛУК Н. Д., канд. техн. наук СИЗОВ В. Д.
по
з
Белорусский государственный аграрный технический университет,
Белорусский национальный технический университет
Ре
В ряде технологических задач металлургии для управления течением
проводящих немагнитных струй используют осесимметричные, переменные во времени магнитные поля. При этом, как известно, аксиальное магнитное поле (м. п.) оказывает стабилизирующее воздействие на процесс
растяжения проводящей струи, а азимутальное магнитное поле, возникающее при пропускании по струе электрического тока, приводит к ускорению
распада струи на отдельные элементы [1–3]. Указанные эффекты механического воздействия магнитного поля на струю связаны с его перераспределением вдоль оси струи и соответственно магнитного давления при возмещении поверхности струи.
Данные закономерности воздействия магнитного поля на проводящую
среду можно успешно использовать для управления процессом каплеобразования при сварке плавящимся электродом.
47
БН
ТУ
Как известно, процесс сварки плавящимся электродом сопровождается
каплеобразованием, определяющим качество сварного соединения [4].
Для оптимизации параметров устройств, реализующих электромагнитное
управление параметрами процесса каплеобразования, требуется определение зависимостей параметров магнитного поля и размеров капли плавящегося электрода.
Из физических соображений будем считать,
B1 r
ζr
что динамика капли плавящегося электрода
в магнитном поле эквивалентна динамике элеz
мента жидкой струи, распадающейся на отλ
R
дельные элементы под действием перетяжечной неустойчивости в условиях воздействия
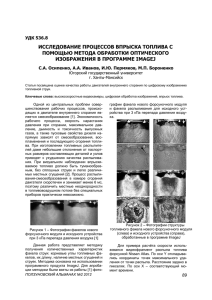
магнитного поля. Рассмотрим задачу о разРис. 1. Схема воздействия на витии неустойчивости типа «перетяжка» [1]
отделяющуюся каплю электрода продольным магнитным на поверхности струи (рис. 1), находящейся
в продольном магнитном поле:
полем
=
B1 {0, 0, B0 z } sin ω1t , –∞ < t < ∞,
ри
й
где ω 1 – частота изменения магнитного поля; материал струи считаем идеальной несжимаемой жидкостью, имеющей бесконечную проводимость.
Для описания процесса каплеобразования в условиях воздействия продольным м. п. используем систему линейных магнитогидродинамических
уравнений [1]:
∂ 2ξ
(1)
ρ 2 = −∇p1 ;
∂t
ит
о
∇B =
0;
∇ξ = 0,
(2)
(3)
где ξ = ⋅ ξ x , ξ y , ξ z – вектор смещения частицы среды; ρ – плотность сре
ды; B – вектор индукции магнитного поля; р 1 – возмущение гидродинамического давления (р = р 0 + р 1 , р – полное давление в материале струи;
р 0 – давление в материале невозмущенной струи).
}
по
з
{
Граничные условия: p (i )
S
= p(e)
S
(здесь p(i) – суммарное давление
Ре
внутри струи на ее поверхности S; p (e ) – суммарное внешнее давление на
S
поверхности материала струи, Bn = 0 ).
S
В начальный момент времени поверхность материала описывается
функцией ξ r =ξr ( R0 , z ,0) =ηeikz ; η – начальная амплитуда возмущения
поверхности материала; r, ϕ, z – координаты цилиндрической системы
(рис. 1); k – волновой вектор, k = 2π/λ; λ – длина волны возмущения.
Поскольку ускоренное движение среды определяет устойчивость ее
границы [1], положим, что поверхность струи движется с ускорением
48
БН
ТУ
< 0. В этом случае любое осесимметричное возмущение будет неустойR
чивым [1] и приведет к разрыву струи на отдельные элементы. Если принять, что разрыв струи происходит в результате развития поверхностной
неустойчивости, то реальные дестабилизирующие усилия, приводящие
к разрыву струи в каждом конкретном случае, можно заменить некоторыми эквивалентными гидродинамическими, возникающими внутри струи
при ускоренном движении ее поверхности, а это физически аналогично
, действующих вдоль
заданию поля гравитационных сил плотностью ρR
радиуса струи. Зная время разрыва струи t 0 в условиях, когда магнитное
поле отсутствует, можно, исходя из уравнения движения среды, оценить
величину сил, приводящих к разрыву струи, что позволяет провести исследование устойчивости растягивающейся струи в магнитном поле.
Задача устойчивости растяжения струи сводится к определению функции ξr =ξr ( R0 , z ,0). Используя метод вывода дисперсионного соотношения [1], проведем анализ устойчивости струи в магнитном поле для инте-
ресующих нас случаев. Из условия (2) следует, что м. п. реакции b
( B = B1 + b , где B – результирующее м. п.) имеет скалярный потенциал Ψ,
удовлетворяющий уравнению Лапласа [1]:
ри
й
∆ψ = 0.
При этом b = –∇ψ.
(4)
Решение (4), обращающееся в нуль на бесконечности, имеет вид
ψ = C(t)K 0 (kr)eikz,
ит
о
где K 0 (kr) – модифицированная функция Бесселя второго рода первого порядка.
Используя условие равенства нулю нормальной составляющей вектора
индукции на поверхности струи (в силу отсутствия магнитного поля внутри струи), получаем уравнение для определения C(t)
(5)
B1 + b ∇F =
0.
(
)
Ре
по
з
Здесь F = r – R 0 – ξr (R 0 , t) = ηeikz – функция, описывающая поверхность
струи.
Исключая из (5) слагаемые, содержащие произведение ξ r k в степени,
выше первой, получаем выражения компонент поля реакции:
K (kR )
br =
B0ik ξ r ( R0 , t ) 0 0 eikz sin ω1t ;
K1 (kR0 )
b ϕ = 0;
(6)
K (kR )
bz =
B0 k ξ r ( R0 , t ) 0 0 eikz sin ω1t.
K1 (kR0 )
Магнитное давление, действующее на поверхность струи, определяется
по формуле
49
=
pм
B12 B0bz
.
+
2µ0 2µ0
(7)
Условие равенства магнитного и гидродинамического давлений на поверхности струи приводит к соотношению
(8)
ТУ
B12 B0bz
+
=
p0 + p1.
2µ0 2µ0
Разлагая обе части (8) в ряд Тейлора и ограничиваясь линейными по
параметру ξ r /R 0 членами, получаем
(9)
БН
B0bz
=∇p R = R ξ r + p1.
0
2µ0
Применяя операцию дивергенции к уравнению (1) системы (1)–(3), получаем уравнение, определяющее поле гидродинамического давления:
∆p1 =
0.
(10)
Решение (10), ограниченное на оси струи, имеет вид
ри
й
p=
C1 (t )I0 (kr ),
1
(11)
где I0 ( kr ) – модифицированная функция Бесселя первого рода нулевого
ит
о
порядка; C1 (t ) – функция времени, подлежащая определению из граничных условий.
Подставляя (11) в (1), получаем
1 ∂ 2 ξr
C1 (t ) = −ρ
,
I1 (kR0 ) ∂t 2
где I1 ( kR0 ) – модифицированная функция Бесселя первого рода первого
по
з
порядка.
Подставляя C 1 (t) в (11), получаем
I0 (kR0 ) ∂ 2 ξr
.
ρ = −ρ
I1 (kR0 ) ∂t 2
(12)
Ре
, имеем
Подставляя (12), (6) в (9) и полагая ∇p0 = −ρR
I0 (kR0 ) ∂ 2 ξ r B02 k ξ r K 0 (kR0 )
ξ =
sin ω1t.
ρR
−
ρ
r
I1 (kR0 ) ∂t 2
µ0 K1 (kR0 )
(13)
Далее перегруппируем члены уравнения (13) и усредним обе части (13)
по периоду Т = 2πω 1 . Приходим к дифференциальному уравнению, описывающему возмущение поверхности ξ r :
50
I (kR ) B 2 k K 0 (kR0 )
∂ 2ξ
ρ 2r + k 0 0 0
+ R ξr =0.
I1 (kR0 ) 2µ0 K1 (kR0 )
∂t
(14)
Подставляя в (14) ξr ( R, t ) =
ξr ( R)eiωt , получаем дисперсионное уравнение
=
ω2 k
I1 (kR ) B02 k K 0 (kR0 )
+ R .
I0 (kR ) 2µ0 K1 (kR0 )
(15)
Тогда
)
(
I (kR )
1
=
k 1
R
,
2
I0 (kR ) R = R0
t0
R
R = R0
= −
БН
−
ТУ
i
, где t 0 – время разрушения на отдельные элементы
t0
в условиях отсутствия магнитного поля В 0 = 0, то, как следует из (15):
Поскольку ω −
I0 (kR )
.
I1 (kR )kt02
(16)
ри
й
Подставив (16) в (15), получаем выражение, определяющее время разрыва струи (отрыва капли) в условиях воздействия продольного магнитного поля:
t0
t=
.
(17)
I0 (kR0 ) K 0 (kR0 ) B02 k 2t02
1−
I1 (kR0 ) K1 (kR0 ) 2µ0ρ
Из (17) следуют выражение, определяющее критическую величину
начального магнитного поля:
I (kR ) K1 (kR0 )
1
2µ0ρ 1 0
,
kt0
I0 (kR0 ) K 0 (kR0 )
ит
о
B0∗
=
(18)
а также выражение коэффициента удлинения капли в том случае, когда
величина индукции начального магнитного поля меньше критической
по
з
n=
1
B
1 − 0∗
B
2
.
(19)
Ре
Расчеты, проведенные в соответствии с (18), (19), показывают, что при
характерной величине радиуса электрода R 0 ~ 10–3 м эффект увеличения
размера капли (порядка двукратного) реалиr
зуется в условиях воздействия магнитного
ζr
поля с амплитудами В 0 ~ 1Т.
J0z
z
Для того чтобы перейти к случаю азимуR
λ
тального магнитного поля (рис. 2), возникающего при протекании по струе тока, поло
жим J z {0,0, J 0 }sin ω1t. Тогда индукция
=
Рис. 2. Схема воздействия азимагнитного поля от координаты рассчитывамутальным магнитным полем
ется по формуле
51
J
Bϕ =
µ0 0 sin ω1t ,
2πr
а возмущение магнитного давления есть
pм =µ0
J 02
sin 2 ω1t ξ r .
4π2 R 3
(20)
J 02
I1 (kR )
,
−µ
0 2 3 +R
I0 (kR )
8π R0
БН
=
ω2 k
ТУ
Заменяя в (13) правую часть на (20), после усреднения по периоду колебаний тока и перегруппировки членов уравнения получаем дисперсионное соотношение
из которого получаем соотношение для определения времени разрыва
струи (отрыва капли)
где J x =
2πR0
t0
t0
J
1+ 0
Jх
2
,
(21)
ри
й
t=
2 R0ρ I0 (kR0 )
– характеристический ток.
µ0 k I1 (kR0 )
ит
о
Расчеты, проведенные в соответствии с (20), показывают, что при характерной величине J x ~ 10–3 A и радиусе электрода R 0 ~ 10–3 м реализуется
эффект двукратного уменьшения размера капли.
ВЫВОД
по
з
Предложены магнитогидродинамические механизмы управления процессом каплеобразования при сварке. Полученные соотношения параметров электромагнитного импульса и размеров капли позволяют рационально
подойти к проблеме создания источника электромагнитного воздействия.
ЛИТЕРАТУРА
Ре
1. Л а д и к о в, Ю. П. Гидродинамические неустойчивости в металлургических процессах / Ю. П. Ладиков, В. Ф. Ткаченко. – М., 1983. – 248 с.
2. Ш а ф р а н о в, В. Д. Об устойчивости цилиндрического газового проводника в магнитном поле / В. Д. Шафранов // Атомная энергия. – 1956. – № 5. – С. 85–92.
3. Т а к т а р о в, Н. Г. Распад струи магнитной жидкости / Н. Г. Тактаров // Магнитная
гидродинамика. – 1975. – № 2. – С. 35–38.
4. П р о х о р о в, Н. Н. Физические процессы в металлах при сварке / Н. Н. Прохоров. –
М.: Металлургия, 1968. – Т. 1. – 695 с.
Представлена кафедрой
энергетики БГАТУ
52
Поступила 07.07.2009