О поляризации колебаний оптического поля и поляризации пучка

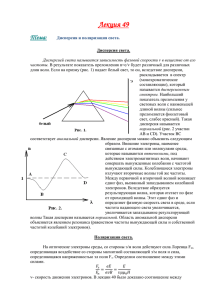
Физическое образование в вузах. 2009. №4. С.57-65
УДК 535.51; 535-6
О ПОЛЯРИЗАЦИИ КОЛЕБАНИЙ ОПТИЧЕСКОГО ПОЛЯ
И ПОЛЯРИЗАЦИИ ПУЧКА СВЕТА
ABОUT POLARIZATION OF OPTICAL FIELD VIBRATIONS
AND POLYARIZATION OF LIGHT BEAM
В.П. Рябухо
Саратовский государственный университет, Саратов, Астраханская 83
Институт проблем точной механики и управления РАН, Саратов, Рабочая 24
rvp@sgu.ru
Обсуждаются физические различия в понятиях поляризация колебаний оптического
поля и поляризация пучка света. Рассматривается поляризационная структура колебаний
оптических полей, образующихся при суперпозиции ортогонально линейно поляризованных
плоских и сферических монохроматических волн, рассеянных полей и лазерных пучков,
прошедших через многомодовое оптическое волокно. Обсуждаются пространственновременные
аналогии
в
пространственной
структуре
поляризации
рассеянной
монохроматической волны и во временной динамике поляризации колебаний частичнокогерентного волнового поля.
Ключевые слова: поляризация света, интерференция поляризованного света, многократное рассеяние,
спекл-структура, многомодовое оптическое волокно, хаотическая поляризация, частично-когерентный
свет
При изложении теории поляризации оптических волн в университетских учебных курсах и пособиях,
как правило, ограничиваются представлениями о поляризации плоских волн или о поляризации лучей
света. Понятие о плоско поляризованной волне непосредственно связано с этим представлением. Между
тем в оптике часто имеют дело с волновыми полями более сложного вида, например, с волновыми полями
протяженного некогерентного источника света или с рассеянными квазимонохроматическими полями. Для
полей более общего вида используется представление о поляризации колебаний, возбуждаемых в данной
точке пространства. Это более верный подход в теории поляризации света [1,2].
В оптических полях поляризация возбуждаемых колебаний может быть одинаковой во всех точках
пучка света. Тогда можно рассуждать о поляризации пучка света в целом. Однако, в оптике нередки
ситуации, когда в разных областях оптического поля состояние поляризации разное. В этом случае пучок
света в целом по его сечению может быть неполяризованным, тогда как в отдельных областях или точках
пространства имеет место полная поляризация колебаний.
58
Можно привести несколько примеров. Самый простой из них – поляризация поля, суперпозиции
двух монохроматических плоских волн с ортогональными направлениями линейной поляризации,
распространяющихся под некоторым углом
в поперечной плоскости
Δϕ 12  y  =
x, y
θ друг относительно друга (рис.1,а). Разность фаз этих волн
непрерывно изменяется вдоль одного из этих направлений,
2π
2sin  θ / 2  y , где λ – длина волны. Следовательно, в направлении оси y состояние
λ
поляризации
суммарных
  x , y , t = E
 1  x , y , t  
E
E2  x , y , t 
колебаний
будет
непрерывно
изменяться, принимая всевозможные формы – линейную, эллиптическую и круговую, в точках на прямых,
параллельных оси x (рис.1,б). Для появления круговой поляризации необходимо равенство амплитуд
складываемых колебаний,
 ∣=∣ 
∣E
E 2∣ .
1
а
б
Рис.1. Суперпозиция двух плоских линейно поляризованных монохроматических волн
с ортогональными направлениями колебаний: а – оптическая схема наложения волн;
б – поляризационная структура результирующей волны.
Пространственный период полного изменения состояния поляризации, например, от линейной до
линейной того же направления, равен
Λ y= λ/2 sin  θ /2  . Если поставить в такой пучок поляризатор-
анализатор, то мощность суммарного пучка света, прошедшего через анализатор, практически, не будет
зависеть от ориентации оси пропускания анализатора, если апертура пучка существенно превышает
период
Λy :
P=∬ I  x , y  dx dy≈const ,
SФ
Физическое образование в вузах. 2009. №4. С.57-65
(1)
59
2
S ф – площадь апертуры анализатора, I  x , y  ~ ⟨∣E  x , y ,t ∣ ⟩ τ – интенсивность суммарных
ф
где
τф
колебаний,
⟨.. .⟩ τ =τ
ф
−1
ф
∫ .. . dt
– усреднение по времени наблюдения. Следовательно, пучок света в
0
целом по достаточно большой апертуре
S ф оказывается неполяризованным, тогда как в отдельных
точках поля имеет место полная поляризация колебаний. Если амплитуды складываемых волн не равны,
 1∣≠∣ 
∣E
E 2∣ , то наблюдается зависимость мощности прошедшего пучка от угла α ориентации
анализатора,
P  α  . В этом случае можно говорить о частичной поляризации пучка света, при полной
поляризации колебаний поля в отдельных его точках.
Для интенсивности суммарных колебаний, прошедших анализатор, можно получить уравнение.
I  x , y , α =∣E 1∣2 cos2 α∣E 2∣2 sin 2 α2∣E 1∣∣E 2∣cos α sin α cos
[
]
2π
θ
2sin
y .
λ
2
(2)
При α≠mπ /2, m=0, ±1, ±2, . . . (иначе один из пучков не пропустит анализатор) формируется
система прямых интерференционных полос с периодом
(угла
Λ y . При изменении ориентации анализатора
α ) можно наблюдать эффект обращения картины полос – на месте светлых полос появляются
темные и наоборот.
Другой простой пример – суперпозиция двух квазисферических монохроматических волн с
ортогональными направлениями поляризации (рис.2).
Если квазиточечные источники этих волн находятся на различных расстояниях
z 1 и z 2 от
плоскости наблюдения x , y , то волны имеют разные радиусы кривизны волновых поверхностей и,
следовательно, имеют разность фаз, изменяющуюся осесимметрично в плоскости
Δϕ 12  x , y ≈
где


2π
π 1 1
z −z 
−
 x 2 y 2  ,
λ  1 2 λ z1 z 2
x,y
(3)
z 1 и z 2 – расстояния от источников S 1 и S 2 до плоскости наблюдения x , y . Результирующие
колебания будут иметь одинаковое состояние поляризации на окружностях (рис.2,б) – поляризация
суммарных колебаний осесимметрично изменяется в радиальных направлениях.
Физическое образование в вузах. 2009. №4. С.57-65
60
а
б
Рис.2. Суперпозиция сферических линейно поляризованных монохроматических волн с
ортогональными направлениями колебаний: а – схема наложения сферических волн; б –
поляризационная структура результирующего пучка света.
Если поставить анализатор с апертурой, в пределах которой окажется достаточно большое число
периодов изменения поляризации в отдельных точках поля, то мощность прошедшего пучка не будет
зависеть от ориентации анализатора,
P  α  =const . В прошедшем через анализатор поле будет
наблюдаться картина кольцевых интерференционных полос – колец Ньютона с распределением
интенсивности
2
2
2
2
I  x , y , α  =∣E 1∣ cos α∣E 2∣ sin α2∣E 1∣∣E 2∣ cos α sin α cos Δϕ12  x , y  . ,
где
(4)
Δϕ 12 определяется уравнением (3). При изменении угла ориентации оси анализатора, например, от
значения
α 1 =45 o
до
α 2 =−45 o
интерференционная картина обращается – светлые полосы
оказываются на месте темных, а темные на месте светлых.
Рассмотренные примеры, в определенном смысле, следует отнести к искусственным, поскольку на
практике такие монохроматические пучки могут формироваться только в специальных оптических
системах, в частности, в интерферометрах, например, в интерферометре Майкельсона или Маха-Цендера с
соответствующей фазовой пластинкой в
λ /4 или λ /2 в одном плече интерферометра.
В естественных условиях чаще всего приходится иметь дело с квазимонохроматическими, но
неполяризованными пучками света, образующимися при рассеянии света в объемных рассеивающих
средах. Монохроматическое поле после рассеяния в объемной статической рассеивающей среде остается
монохроматическим. Поэтому колебания рассеянного поля полностью поляризованы в отдельных его
точках, но рассеянный пучок по достаточно большой апертуре может оказаться в целом не
поляризованным. В отдельных точках рассеянного поля колебания имеют различные состояния
поляризации, что обусловлено многократностью процесса рассеяния света в объемной рассеивающей
среде (рис.3). В каждой точке пространства в рассеянном поле складываются взаимно когерентные
Физическое образование в вузах. 2009. №4. С.57-65
61
элементарные рассеянные волны с различным направлением колебаний и, что очень важно, с различными
фазами. В результате суммарное результирующее колебание в этой точке имеет случайное значение
амплитуды, а значит и интенсивности, и принимает то или иное состояние поляризации в зависимости от
разности фаз складываемых колебаний и их амплитуд. В рассеянном поле наблюдается спекл-эффект [3-6]
– случайное пространственное распределение интенсивности, которое выглядит в виде пятнистой картины
(рис.3,в-г). В отдельных спеклах рассеянного поля возникает то или иное состояние поляризации
колебаний, которое сохраняется (точнее, мало изменяется) в пределах области отдельного спекла. Поэтому
каждый спекл (пятно) этой картины следует рассматривать не только в качестве области амплитуднофазовой корреляции рассеянного поля, но и в качестве области корреляции поляризационной структуры
поля. Размер этой области корреляции
длиной волны
ε – поперечный размер спеклов, в среднем определяется [3-6]
λ и угловой апертурой θ рассеянного поля в плоскости наблюдения x , y (рис.3,а).
ε≈λ /θ .
а
(6)
б
в
г
д
Рис.3. Формирование оптического поля со случайным пространственным распределением состояния
поляризации колебаний при многократном рассеянии квазимонохроматической линейно поляризованной
волны в пространственно неоднородной среде: а – схема эксперимента: 1 – освещающий
квазимонохроматический линейно поляризованный пучок света; 2 – объемная рассеивающая среда; 3 –
диафрагма; 4 – рассеянный пучок света; 5 – плоскость наблюдения; б – спекл-структура и
поляризационная структура рассеянного пучка света; в, г, д – фотографии спекл-картин в рассеянном
пучке света, наблюдаемые без поляризатора (в) и с использованием поляризатора в двух скрещенных
положениях (г, д).
Физическое образование в вузах. 2009. №4. С.57-65
62
Если за рассеивающей средой поставить поляризатор-анализатор, то в прошедшем через него свете
появляется новая более контрастная, более четкая спекл-картина (рис.3,г,д). Если поляризатор-анализатор
повернуть на угол 90°, то он выделит (пропустит) в рассеянном поле другую ортогональную компоненту
поля с линейной поляризацией. В результате структура наблюдаемой спекл-картины полностью изменится
и будет не совпадать (не коррелировать) со спекл-структурой, образующейся при первоначальной
ориентации поляризатора-анализатора. Спекл-картины, наблюдаемые при ортогональных положениях
поляризатора-анализатора, пространственно некоррелированы, если в рассеивающей среде происходит
интенсивное многократное рассеяние. Спекл-картины на рис.3,г и рис.3,д полностью отличаются друг от
друга по структуре распределения интенсивности света в них.
Если же имеет место малократное
рассеяние, то в рассеянном пучке света наблюдается некоторое преимущественное состояние
поляризации. В этом случае при использовании линейно-поляризованного освещающего пучка полная
мощность пучка различна при ортогональных ориентациях поляризатора-анализатора, а спекл-картины
обнаруживают частичную корреляцию.
Пучок квазимонохроматического света (лазерного излучения), прошедший через многомодовое
оптическое волокно, также оказывается в целом (по полной апертуре) неполяризованным при
использовании линейно поляризованного лазерного пучка на входе волокна.. При использовании
поляроида на выходе из волокна мощность светового потока, прошедшего через поляроид не меняется при
изменении его ориентации. В вышедшем из волокна излучении имеет место когерентная суперпозиция
многих волновых полей, соответствующих различным типам (модам) волн, распространяющихся в
волокне. Эти волны, испытавшие многократное полное внутреннее отражение в волокне, имеют разные
состояния поляризации колебаний и различные фазовые сдвиги. В результате когерентной суперпозиции
таких волн на выходе волокна в дифракционной зоне формируется спекл-структура (рис.4) [5], подобная
спекл-структуре в рассеянном лазерном пучке. В отдельных спеклах этой структуры, которые можно
рассматривать в качестве областей корреляции волнового поля, колебания имеют различные состояния
поляризации - линейную, эллиптическую или (заметно реже) циркулярную. В различных спеклах
состояние поляризации различно – при переходе от спекла к спеклу состояние поляризации меняется
случайным образом.
На рис.4,б-г приведены фотографии спекл-структур, наблюдаемых в лазерном излучении, вышедшем
из многомодового волокна. Спекл-картины на рис.4,б получена без использования поляризатораанализатора на выходе волокна, а спекл-картины на рис.4,в и 4,г сфотографированы с использованием
поляроида на выходе волокна в двух его ортогональных ориентациях. Хорошо видно, что спекл-картины
на рис.4,в и 4,г имеют некоторые повторения на рис.4,б, но совершенно не похожи друг на друга.
При даже небольших изгибах многомодового волокна изменяются условия распространения
волновых мод, изменяются фазовые сдвиги полей, соответствующие этим модам и, как следствие,
изменяется спекл-структура и поляризационная структура в вышедшем излучении. Спекл-структура и,
соответственно, поляризационная структура изменяется также при изменении поляризации лазерного
пучка, входящего в волокно, в том числе и при повороте плоскости поляризации этого пучка.
Физическое образование в вузах. 2009. №4. С.57-65
63
а
б
в
г
Рис.4. Оптическая схема ввода линейно поляризованного лазерного пучка в многомодовое оптическое
волокно (а) и спекл-картины, наблюдаемые на выходе волокна (б-г) без использования поляризатораанализатора на выходе волокна (б) и при использовании поляроида в двух ортогональных ориентациях (в, г):
1 – линейно поляризованный лазерный пучок; 2 – собирающая линза; 3 – многомодовое оптическое
волокно; 4 – лазерный пучок, вышедший из волокна; 5 – плоскость наблюдения спекл-структуры.
Нельзя не отметить и не обсудить пространственно-временные аналогии в состоянии поляризации
оптических полей. Наблюдаемые пространственные поляризационные структуры в оптических полях
имеют соответствующие временные аналоги. Действительно, при суперпозиции двух монохроматических
волн различной частоты с ортогональными направлениями линейной поляризации, результирующая волна
будет иметь регулярно изменяющееся во времени состояние поляризации. Период изменения состояния
поляризации
T определяется разностью частот T =1 / Δν 12 .
Если имеет место суперпозиция множества волн разной частоты и различного направления
поляризации, как в естественном свете, то состояние поляризации результирующих колебаний будет во
времени хаотически (случайным образом) изменяться [7]. Характерное время этого изменения равно
времени когерентности колебаний
τ c=1/ Δν , где Δν ширина частотного диапазона колебаний [1,2].
Таким образом, в рассеянном монохроматическом свете имеем случайное изменение состояния
поляризации в пространстве, а в естественном свете для направленного пучка света – случайное изменение
во времени. Если имеем ненаправленный пучок естественного света, например, рассеянный, или пучок
света протяженного некогерентного источника, то имеет место случайное изменение состояния
поляризации колебаний и во времени и в пространстве. В течение времени когерентности
τc
приблизительно сохраняется состояние поляризации колебаний в отдельных точках поля. На расстояниях,
превышающих радиус поперечной пространственной когерентности
Физическое образование в вузах. 2009. №4. С.57-65
ρc= λ0 /θ [1,2,4], где λ 0 – средняя
64
длина волны,
θ – угловая апертура пучка, состояние поляризации изменяется случайным образом. С
течением времени вся эта пространственная поляризационная структура случайным образом изменяется.
Таким образом, с методической точки зрения в оптике целесообразнее рассматривать и говорить о
поляризации колебаний, возбуждаемых оптическим полем в той или иной точке пространства. При
одинаковом состоянии поляризации во всех точках волнового поля или во всех точках поперечного
сечения пучка света можно использовать представление о поляризации волны или пучка света в целом.
Такие пучки в оптике создаются известными способами и часто используются на практике. Вместе с этим
широко используются и часто встречаются в оптике квазимонохроматические волны с неоднородным
пространственным распределением состояния поляризации по полю. В таких волновых процессах
наблюдается полная поляризация колебаний в отдельных точках и отсутствие поляризации колебаний по
достаточно большой площади или пространству. Эти обстоятельства необходимо рассматривать при
обсуждении темы «Поляризация света» в общем и специальных курсах физики оптических явлений для
правильных представлениях о свойствах оптических полей.
Работа выполнена при поддержке грантов аналитической ведомственной целевой программы
«Развитие научного потенциала высшей школы», коды проектов 2.1.1/4364 и 2.2.1.1/2950 и гранта
Президента для поддержки ведущих научных школ РФ НШ-208-2008.2.
Литература
1. Борн М., Вольф Э. Основы оптики. Пер. с англ. /Под ред. Г.П. Мотулевич - М.: Наука, 1973. - 720 с.
2. Мандель Л., Вольф Э. Оптическая когерентность и квантовая оптика: Пер. с англ. М.: Наука. Физматлит,
2000. 896 с.
3. Франсон М. Оптика спеклов. Пер. с англ.- М.: Мир, 1980. 171 c.
4. Гудман Дж. Статистическая оптика. Пер. с англ. /Под ред. Г.В.Скроцкого - М.: Мир, 1988. – 528 с.
5. Gooman J.W. Speckle phenomena in optics. Theory and applications. Roberts & Company Publishers. 2007.
6. Рябухо В.П. Спекл-интерферометрия. Соросовский образовательный журнал. 2001. Т.7. №5. С.102-109.
7. Рябухо В.П. О графических формах отображения состояния поляризации оптических волн. Физическое
образование в вузах. 2008. Т.14. №3. с.88-93.
Физическое образование в вузах. 2009. №4. С.57-65