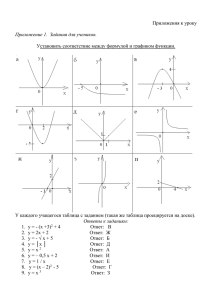
Построение графика функции прямо пропорциональной
реклама

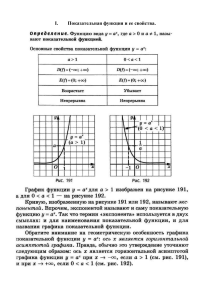
Построение графика функции прямо пропорциональной зависимости y = ax Графиком прямо пропорциональной зависимости является прямая, которая проходит через начало координат или точку О(0; 0) Для построения необходимо две точки, причем третья точка всегда будет с координатами (0; 0)Выбирают два любых значения х и вычисляют значения у, соответствующие выбранным значениям х. Рассмотрим построение графика прямо пропорциональной зависимости на примере. Дана функция у = –2х Выберем произвольно два значения х, а третье значение возьмем х = 0 Пусть х = -1, 2. Вычислим в этих точках значения у. Если х = –1, то у = –2(–1) = 2 Если х = 1, то у = –2·1 = –2 Если х = 0, то у = –2·0 = 0 Из этих значений составим таблицу: х –1 2 0 у 2 –2 0 Отметим эти точки на координатной плоскости и проведем через них прямую. Построение выполнено. Построение графика линейной функции y = ax + b Графиком линейной функции является прямая Для построения необходимо две точки. Во избежании ошибок при построении прямой берут три точки. Выбирают три любых значения х и вычисляют значения у, соответствующие выбранным значениям х. Рассмотрим построение линейной функции на примере. Дана функция у = 2х – 3 Выберем произвольно три значения х. Пусть х = 1, 0, 2. Вычислим в этих точках значения у. Если х = 1, то у = 2·1 – 3 = –1 Если х = 0, то у = 2·0 – 3 = 0 – 3 = –3 Если х = 2, то у = 2·2 – 3 = 4 – 3 = 1. Из этих значений составим таблицу: х 1 0 2 у –1 –3 1 Отметим эти точки на координатной плоскости и проведем через них прямую. Построение выполнено. Построение графика функции обратно пропорциональной a зависимости y x Графиком этой функции является гипербола. График имеет разрыв в точке х = 0, так как на ноль делить нельзя. Следовательно, график не пересекает ни ось ОХ, ни ось ОУ. Если a > 0, то ветви гиперболы расположены в I и III четвертях. Если a < 0, то ветви гиперболы расположены в II и IV четвертях. График функции строится по точкам. Чем больше значений х выберем, тем точнее будет график. Значения нужно взять как положительные (х > 0), так и отрицательные (х < 0). Обычно берут не меньше четырех положительных и четырех отрицательных значений. Рассмотрим построение графика обратно пропорциональной зависимости на примере. Дана функция y= 12 x Заполним таблицу: х 1 2 3 у 12 6 4 4 -1 -2 -3 -4 3 -12 -6 -4 -3 Отметим эти точки на координатной плоскости и соединим их кривыми линиями, помя, что график НЕ ПЕРЕСЕКАЕТ ось ОХ и ось ОУ