реклама
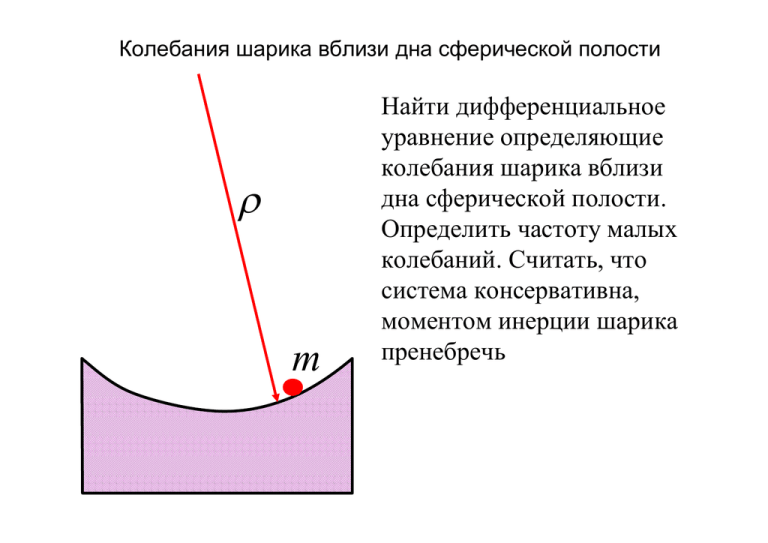
Колебания шарика вблизи дна сферической полости m Найти дифференциальное уравнение определяющие колебания шарика вблизи дна сферической полости. Определить частоту малых колебаний. Считать, что система консервативна, моментом инерции шарика пренебречь Сила F1 F2 F3 0 F1 sin F2 cos F3 0 2 F2 F3 F3 mg sin F3 F3 F1 mg Момент движения J M F3 mg sin g J m 2 m mg sin 2 0 2 F3 sin g 0 Линейное движение F1 F2 F3 0 ось x F1 0 F2 sin F3 0 F3 F2 sin F3 ось y F2 F1 F2 cos 0 sin F3 F3 mg cos F3 x F1 mg Линейное движение sin F3 mg mg cos x mx mg 1 x x 2 x 1 x 2 0 g x x 0 x g 2 0 Энергия T P const mV T 2 2 J T 2 2 2 LI LQ T 2 2 2 P mgh 2 x Pk 2 2 1Q P C 2 Энергия J T 2 2 J m 2 P mgh h cos h Энергия 2 m mg 1 cos const 2 2 g 1 cos const 2 2 g 2 sin 0 2 g 0 g sin 0 g 2 0 Крутильный маятник h Вид сверху L Однородный стержень подвешен за свои концы на нерастяжимых нитях. Определить частоту малых крутильных колебаний считая, что система консервативна. 1 2 J mL 12 Энергия P mgh1 cos h L 2 L 2h Энергия L P mgh1 cos 2h J 2 L mgh 1 cos C 2 2h L L J 2 mgh sin 0 2 2h 2h 2 1 L 2 mL mg 0 12 4h g 3 h 2 0 g 3 0 h Маятник l l m W Определить частоту малых колебаний бусины массы m, подвешенной на невесомой нерастяжимой нити. Движением груза M и потерями пренебречь. F2 l Маятник x l m F3 F1 W x l x l Mg Mg F1 y F2 y cos 2 F3 F1 x F2 x Mg sin ml Mg sin 0 Mg sin 0 ml Mg ml 2 0 шахта m R Определить частоту собственных колебаний груза, брошенного в шахту, проходящую через центр однородной сферической планеты m1m2 F 2 r q1q2 F 0 2 r x шахта 3 R 4R V 3 4R 3 m2 3 4mR 3 F 3x 2 x шахта 3 R х 4x V 3 4x 3 m2 3 4mx F 2 3x 3 3 4mx 4 F mx 2 3x 3 x шахта 4 mx mx 0 3 R х 4 x x 0 3 4 3 2 0 Трубка l Определить частоту собственных колебаний столба жидкости в U образной трубке. Считать, что система консервативна. S-сечение трубки -плотность жидкости l-длина столба шахта m Sl x l , S F 2 gSx Slx 2 gSx 0 2g x x0 l 2g l 2 0 Фазовый портрет Шарик движется горизонтально между двумя стенками в отсутствии гравитации. Построить фазовый портрет систему, считая что соударения со стенками абсолютно упруги, а сопротивление среды отсутствует. Указать особые точки Фазовый портрет x V V x -а а -V Фазовый портрет Решить предыдущую задачу в условии вязкого трения среды. Показать, что фазовые траектории представляют собой прямые линии. Фазовый портрет x x 0 x x C 0 Фазовый портрет x x -а а Фазовый портрет Шарик подпрыгивает над горизонтальной плитой. Построить фазовый портрет, считая, что сопротивление среды отсутствует, а удары абсолютно упруги. Фазовый портрет F mg x y y g 2 x g 0 mx mg 0 dy g dx y y gx C 2 ydy gdx 2 y x c 2g Фазовый портрет x x Два заряда m + + Груз математического маятника обладает зарядом. Одноименный заряд зафиксирован под маятником. Построить качественно фазовый портрет. (Маятник имеет два положения равновесия.) Фазовый портрет x x шахта m R Построить фазовый портрет системы. Учесть области когда груз вылетает за пределы планеты. x шахта 4mR F 3x 2 R х 3 4mx 3 4 F mx 2 3x 3 4 mx mx 0 3 4 3 2 0 x 02 x 0 3 R x 2 0 x 2 0 шахта x 02 x 0, x R 3 R 2 x 0, x R 0 2 x 0t x x 0, x R 3 R x 2 0, x R x окружность ??? шахта 3 x y 3 R y 2 x R x 2 0 x 3 R dx ydy 2 x R3 y 2 C x 3 dy R 2 dx x y 1 2 R3 y C 2 x шахта 3 R y 2 C x x 2R3 C<0 ; колебательный процесс C C>0 ; груз улетает в бесконечность С=0 ; сепаратриса асимптотически стремящаяся к нулю. Вторая космическая скорость y x R 2 R C 0 Фазовый портрет x x x шахта l r cos x r sin l х 2 2 2 r mr 2 sin 0 r cos x2 r 2 1 cos 2 1 ry x 2 1 r cos x r cos x 2 ry x r 2 1 y 2 3/ 2 dy 0 2 r 2 1 cos d


