1.19. Строение атомного ядра
реклама

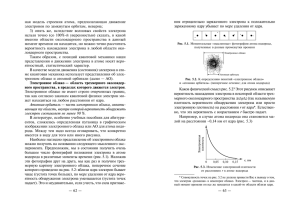
1.19. Ñòðîåíèå àòîìíîãî ÿäðà 1.19. Ñòðîåíèå àòîìíîãî ÿäðà  åðíåìñÿ ê ðàññìîòðåíèþ ïðîáëåìû ñòðîåíèÿ àòîìíîãî ÿäðà. Ïîñëå îïûòîâ Ðåçåðôîðäà ïî ðàññåÿíèþ àëüôà-÷àñòèö â òîíêèõ ïëåíêàõ ìåòàëëîâ, óñïåõîâ òåîðèè Áîðà, îòêðûòèÿ íåéòðîíà è ðàçâèòèÿ êâàíòîâîé ìåõàíèêè âñòàëà ïðîáëåìà âûÿñíåíèÿ âíóòðåííåé ñòðóêòóðû àòîìíîãî ÿäðà. Äî îòêðûòèÿ â 1932 ãîäó íåéòðîíà â ôèçèêå çíàëè òîëüêî äâå óñòîé÷èâûå àòîìíûå ÷àñòèöû – ïðîòîí è ýëåêòðîí, èç êîòîðûõ ìîæíî áûëî ïîñòðîèòü àòîìíûå ÿäðà. Òàê, ÿäðî ëåãêîãî èçîòîïà âîäîðîäà, ñîãëàñíî ïðèíÿòûì òîãäà ïðåäñòàâëåíèÿì, ñîñòîÿëî èç îäíîãî ïðîòîíà, ÿäðî òÿæåëîãî èçîòîïà âîäîðîäà – äåéòðîíà – èç äâóõ ïðîòîíîâ è îäíîãî âíóòðèÿäåðíîãî ýëåêòðîíà. Ñòðóêòóðà æå áîëåå ñëîæíûõ àòîìíûõ ÿäåð, íà÷èíàÿ ñ ãåëèÿ, ëèòèÿ è ò. ä. äî óðàíà, ñòðîèëàñü òàêæå èç äâóõ òèïîâ ìèêðî÷àñòèö – ïðîòîíîâ è ýëåêòðîíîâ. Ïðè ýòîì ÷èñëî ïðîòîíîâ ïîëàãàëè ðàâíûì àòîìíîìó âåñó, òî÷íåå åãî öåëî÷èñëåííîé ÷àñòè À, à ÷èñëî âíóòðèÿäåðíûõ ýëåêòðîíîâ ðàâíÿëîñü ðàçíîñòè ìåæäó À è ïîðÿäêîâûì íîìåðîì õèìè÷åñêîãî ýëåìåíòà Z, ò.å. âåëè÷èíå (À – Z). Âíóòðèÿäåðíûå ýëåêòðîíû íåéòðàëèçîâàëè «ëèøíèå» çàðÿäû ïðîòîíîâ, ñâåðõ ïîðÿäêîâîãî íîìåðà õèìè÷åñêîãî ýëåìåíòà Z, ïîñêîëüêó çàðÿä àòîìíîãî ÿäðà âñåõ èçîòîïîâ äàííîãî õèìè÷åñêîãî ýëåìåíòà äîëæåí áûë ðàâíÿòüñÿ +Ze. Íî ïðè áîëåå äåòàëüíûõ èññëåäîâàíèÿõ àòîìíûõ ÿäåð âîçíèê ðÿä ñóùåñòâåííûõ òðóäíîñòåé, èç-çà êîòîðûõ ïðèñóòñòâèå ýëåêòðîíîâ âíóòðè àòîìíûõ ÿäåð îêàçàëîñü ïðîòèâîïîêàçàííûì. Âî-ïåðâûõ, êàê ìû ïîìíèì, ñïèíîâûé ìàãíèòíûé ìîìåíò ýëåêòðîíà ðàâåí ýëåêòðîííîìó ìàãíåòîíó Áîðà, ò.å. µeB = e$/2mec, (19.1) à äëÿ ïðîòîíà â çíàìåíàòåëå ïðàâîé ÷àñòè âìåñòî ìàññû ýëåêòðîíà me ñòîèò ìàññà ïðîòîíà Ìð, êîòîðàÿ â 1836 ðàç áîëüøå ìàññû ýëåêòðîíà me, µpB = e$/2Mpc. (19.2) Îïûò ïîêàçàë, ÷òî â àòîìíûõ ÿäðàõ âî âñåõ íàáëþäàåìûõ ñëó÷àÿõ ìàãíèòíûå ìîìåíòû áûëè áëèæå ê âåëè÷èíå 136 1.19. Ñòðîåíèå àòîìíîãî ÿäðà (19.2). Ìîæíî, ïðàâäà, áûëî ïðåäïîëîæèòü, ÷òî ìàãíèòíûå ìîìåíòû ýëåêòðîíîâ âíóòðè àòîìíîãî ÿäðà ïîïàðíî êîìïåíñèðóþòñÿ èç-çà èõ àíòèïàðàëëåëüíîñòè. Îäíàêî â àòîìíûõ ÿäðàõ ñ íå÷åòíûì ÷èñëîì âíóòðèÿäåðíûõ ýëåêòðîíîâ êîìïåíñàöèè íåâîçìîæíî äîáèòüñÿ, è ìàãíèòíûé ìîìåíò òàêèõ àòîìíûõ ÿäåð âñå ðàâíî äîëæåí áûë áûòü áëèæå ê âûðàæåíèþ (19.1), ÷òî íèêîãäà íå íàáëþäàëîñü. Ïîýòîìó è âîçíèêàëà çàãàäêà – êóäà äåâàëñÿ ýòîò ìàãíåòîí Áîðà âíóòðèÿäåðíîãî ýëåêòðîíà? Âòîðàÿ «íåóâÿçêà» ñ ïðèñóòñòâèåì ýëåêòðîíîâ âíóòðè àòîìíûõ ÿäåð áûëà ñâÿçàíà ñ îïðåäåëåíèåì âåëè÷èíû ðåçóëüòèðóþùåãî ñïèíà àòîìíûõ ÿäåð. Ïðîòîí è ýëåêòðîí èìåþò îäèíàêîâûå ïî âåëè÷èíå ñïèíû, ðàâíûå $/2. Ïîýòîìó ðåçóëüòèðóþùèé ñïèí àòîìíîãî ÿäðà áóäåò ðàâåí ëèáî öåëîìó ÷èñëó $ (ïðè ÷åòíîì ÷èñëå ìèêðî÷àñòèö â àòîìíîì ÿäðå), ëèáî ïîëóöåëîìó ÷èñëó $ (ïðè íå÷åòíîì ÷èñëå ìèêðî÷àñòèö â àòîìíîì ÿäðå). Îïûò æå äàâàë äðóãîé ðåçóëüòàò, íàïðèìåð, â îñíîâíîì èçîòîïå õèìè÷åñêîãî ýëåìåíòà àçîòà 14N ïî ïðîòîííî-ýëåêòðîííîé ìîäåëè àòîìíîãî ÿäðà â åãî ÿäðå äîëæíî áûòü 14 ïðîòîíîâ è 7 ýëåêòðîíîâ (21 ìèêðî÷àñòèöà), è ðåçóëüòèðóþùèé ñïèí äîëæåí áûòü ïîëóöåëûì, à îïûò ïîêàçàë, ÷òî îí öåëûé. Òàêàÿ æå «íåóâÿçêà» íàáëþäàëàñü è äëÿ ðÿäà äðóãèõ èçîòîïîâ õèìè÷åñêèõ ýëåìåíòîâ. Íàêîíåö, òðåòüÿ «íåóâÿçêà» âîçíèêàëà â ñâÿçè ñ ïðèíöèïîì íåîïðåäåëåííîñòåé Ãåéçåíáåðãà. Äåëî â òîì, ÷òî ýëåêòðîí, çàïåðòûé â òåñíîì îáúåìå àòîìíîãî ÿäðà (åãî ðàäèóñ ðàâåí 10-13 ñì), ïðèîáðåòàåò ïðè ýòîì î÷åíü áîëüøóþ íåîïðåäåëåííîñòü â èìïóëüñå, ÷òî âëå÷åò çà ñîáîé ïîÿâëåíèå áîëüøîé êèíåòè÷åñêîé ýíåðãèè âíóòðèÿäåðíîãî ýëåêòðîíà, è àòîìíîå ÿäðî íå ñìîæåò óäåðæàòü â ñâîåì ìàëîì îáúåìå ñòîëü «ýíåðãè÷íîãî æèòåëÿ». Íóæíî áûëî ñîçäàòü íîâóþ ìîäåëü àòîìíîãî ÿäðà. Ãåéçåíáåðã è ñîâåòñêèé ôèçèê-òåîðåòèê Ä.Ä.Èâàíåíêî íåçàâèñèìî äðóã îò äðóãà ïðåäëîæèëè ñòðîèòü àòîìíûå ÿäðà òîëüêî èç òÿæåëûõ ìèêðî÷àñòèö ïðèáëèçèòåëüíî îäíîé ìàññû – ïðîòîíà è íåéòðîíà, êîòîðûå âìåñòå ñòàëè èìåíîâàòüñÿ íóêëîíàìè, ò.å. ÿäåðíûìè ÷àñòèöàìè. Îòìåòèì, ÷òî êîãäà ïîÿâèëàñü â ïå÷àòè ðàáîòà ×ýäâèêà îá îòêðûòèè íåéòðîíà, òî íà íàó÷íîì ñåìèíàðå â òåîðåòè÷åñêîì îòäåëå Ëåíèíãðàäñêîãî ôèçèêî-òåõíè÷åñêîãî èíñòèòóòà ó ß.È.Ôðåíêåëÿ îíà ïîäðîáíî îáñóæäàëàñü, è äîêëàä÷èê àêàäåìèê Àáðàì Ôåäîðîâè÷ Èîôôå ñêàçàë, ÷òî ìû ïîñëå 137 1.19. Ñòðîåíèå àòîìíîãî ÿäðà ýòîãî çàìå÷àòåëüíîãî îòêðûòèÿ íàõîäèìñÿ íà ïîðîãå íîâîé ýðû â ìèêðîôèçèêå. Îí îêàçàëñÿ ãëóáîêî ïðàâ. Ìàññà ïîêîÿ íåéòðîíà ðàâíà â ýíåðãåòè÷åñêèõ åäèíèöàõ 939,550 ÌýÂ, ÷òî íà 1,293 Ìý áîëüøå ìàññû ïðîòîíà â òåõ æå åäèíèöàõ, à ìàãíèòíûé ìîìåíò íåéòðîíà ðàâåí µn= – 1,9135µÿ, ãäå µÿ ÿäåðíûé ìàãíåòîí Áîðà, çíàê ìèíóñ ïîÿâèëñÿ ïîòîìó, ÷òî âåêòîð ñïèíîâîãî ìàãíèòíîãî ìîìåíòà íåéòðîíà àíòèïàðàëëåëåí âåêòîðó ìåõàíè÷åñêîãî ìîìåíòà. Ïî òåîðèè Äèðàêà ìèêðî÷àñòèöà ñî ñïèíîì $/2 äîëæíà îáëàäàòü ÿäåðíûì ìàãíåòîíîì Áîðà (19.2), åñëè îíà èìååò ýëåêòðè÷åñêèé çàðÿä å, è íóëåâûì ìàãíèòíûì ìîìåíòîì äëÿ íåéòðàëüíîé ýëåêòðè÷åñêè ìèêðî÷àñòèöû. Äëÿ íåéòðîíà ýòî ïîëîæåíèå òåîðèè, êàê ìû âèäèì, íå âûïîëíÿåòñÿ, ïîñêîëüêó åãî ñïèíîâûé ìàãíèòíûé ìîìåíò µn íå ðàâåí íóëþ, ñ ïðîòîíîì òîæå íå âñå â ïîðÿäêå, ïîñêîëüêó åãî ìàãíèòíûé ìîìåíò ðàâåí íå µÿ, à 2,79µÿ. Óêàçàííûé ôàêò ñâèäåòåëüñòâóåò î òîì, ÷òî ïðîòîí è íåéòðîí èìåþò ñëîæíóþ âíóòðåííþþ ñòðóêòóðó, ò.å. â íèõ ñóùåñòâóþò êàêèå-òî ýëåêòðè÷åñêèå òîêè, êîòîðûå è ñîçäàþò äîïîëíèòåëüíûå âêëàäû â ñïèíîâûé ìàãíèòíûé ìîìåíò.  èòîãå, ïî Ãåéçåíáåðãó è Èâàíåíêî, àòîìíîå ÿäðî ñîñòîèò èç íóêëîíîâ, ò.å. ïðîòîíîâ è íåéòðîíîâ. Ïî èõ ìîäåëè ÷èñëî ïðîòîíîâ ðàâíî ïîðÿäêîâîìó íîìåðó õèìè÷åñêîãî ýëåìåíòà Z, à ÷èñëî íåéòðîíîâ ðàâíî ðàçíîñòè (À – Z), ãäå À – öåëî÷èñëåííàÿ ÷àñòü àòîìíîãî âåñà. Òàêèì îáðàçîì, ðàçíûå èçîòîïû õèìè÷åñêîãî ýëåìåíòà îòëè÷àþòñÿ ïî ÷èñëó íåéòðîíîâ â èõ àòîìíûõ ÿäðàõ.  àòîìå æå â åãî îáîëî÷êó äîáàâëÿåòñÿ åùå Z îòðèöàòåëüíî çàðÿæåííûõ ýëåêòðîíîâ, áëàãîäàðÿ ÷åìó àòîì â íîðìàëüíîì íåâîçáóæäåííîì ñîñòîÿíèè ýëåêòðè÷åñêè âñåãäà íåéòðàëåí. Ïðîòîíû è íåéòðîíû â àòîìíûõ ÿäðàõ óäåðæèâàþòñÿ ñèëàìè ñöåïëåíèÿ, êîòîðûå äîëæíû ïðåâûøàòü êóëîíîâñêèå ñèëû, ðàñòàëêèâàþùèå ïðîòîíû âíóòðè àòîìíîãî ÿäðà. Êðîìå òîãî, îíè äîëæíû áîðîòüñÿ ñ ðàçðóøàþùèì äåéñòâèåì ïðèíöèïà Ïàóëè, ñïðàâåäëèâîãî íå òîëüêî äëÿ ýëåêòðîíîâ, íî òàêæå è äëÿ ïðîòîíîâ è íåéòðîíîâ. Îòìåòèì, ÷òî ñèëû ñöåïëåíèÿ ìåæäó íóêëîíàìè íàçûâàþòñÿ ÿäåðíûìè ñèëàìè. Ýíåðãèÿ ñâÿçè ñèñòåìû ìèêðî÷àñòèö (àòîìà èëè åãî ÿäðà) îïðåäåëÿåòñÿ ðàáîòîé, êîòîðóþ íóæíî çàòðàòèòü, ÷òîáû ðàçáèòü ñèñòåìó íà ñîñòàâëÿþùèå å¸ îòäåëüíûå ìèêðî÷àñòèöû è óäàëèòü èõ äðóã îò äðóãà íà òàêîå ðàññòîÿíèå, ÷òîáû îíè ïðàêòè÷åñêè íå âçàèìîäåéñòâîâàëè. Êðîìå òîãî, èñïîëü138 1.19. Ñòðîåíèå àòîìíîãî ÿäðà çóåòñÿ ïîíÿòèå óäåëüíîé ýíåðãèè ñâÿçè, ò.å. ýíåðãèè ñâÿçè ñèñòåìû, ïðèõîäÿùåéñÿ íà îäíó ñîñòàâëÿþùóþ å¸ ìèêðî÷àñòèöó. Èç îïûòà èçâåñòíû çíà÷åíèÿ óäåëüíîé ýíåðãèè ñâÿçè, ïðèõîäÿùèåñÿ íà îòäåëüíûé íóêëîí â àòîìíîì ÿäðå, äëÿ âñåõ àòîìíûõ ÿäåð õèìè÷åñêèõ ýëåìåíòîâ Òàáëèöû Ìåíäåëååâà. Íà ðèñ. 22 ïîêàçàíà çàâèñèìîñòü ýòîé âåëè÷èíû îò öåëî÷èñëåííûõ çíà÷åíèé àòîìíîãî âåñà À.  äåéòðîíå îíà ðàâíà 1 Ìýâ/íóêëîí, â ãåëèè (4Íå) óâåëè÷èâàåòñÿ äî 7 ÌýÂ/íóêëîí è çàòåì ñ íåáîëüøèìè êîëåáàíèÿìè äîñòèãàåò ìàêñèìóìà îêîëî 9 ÌýÂ/íóêëîí ó æåëåçà (60Fe), à çàòåì êðèâàÿ ìåäëåííî ïàäàåò âíèç. Àòîìíûå ÿäðà ñ À ìåæäó 30 è 80 ÿâëÿþòñÿ ñàìûìè óñòîé÷èâûìè. Ðèñ. 22. Êðèâàÿ çàâèñèìîñòè îïûòíûõ çíà÷åíèé óäåëüíîé ýíåðãèè ñâÿçè íóêëîíîâ â àòîìíûõ ÿäðàõ îò çíà÷åíèÿ ìàññîâîãî ÷èñëà À õèìè÷åñêèõ ýëåìåíòîâ. Òàêàÿ çàâèñèìîñòü ýíåðãèè ñâÿçè îò À ïîìîãàåò ñóäèòü î ïðîöåññàõ, ïðîèñõîäÿùèõ ïðè äåëåíèè è ñèíòåçå àòîìíûõ ÿäåð. Èçâåñòíî, ÷òî ïðè ñèíòåçå àòîìà âîäîðîäà (èç ïðîòîíà è ýëåêòðîíà) âûäåëÿåòñÿ ýíåðãèÿ 13,6 ýÂ, ïîñêîëüêó ìàññà ïîêîÿ àòîìà âîäîðîäà ìåíüøå ñóììû ìàññ ïîêîÿ îòäåëüíûõ 139 1.19. Ñòðîåíèå àòîìíîãî ÿäðà ýëåêòðîíà è ïðîòîíà (ìû óæå óêàçûâàëè, ÷òî, ñîãëàñíî òåîðèè îòíîñèòåëüíîñòè Ýéíøòåéíà, ìàññà ïîêîÿ mo è ýíåðãèÿ ïîêîÿ Åî ñâÿçàíû ñîîòíîøåíèåì Eo = moc2). Àíàëîãè÷íî ìàññà ïîêîÿ (èëè ýíåðãèÿ ïîêîÿ) äâóõ ëåãêèõ àòîìíûõ ÿäåð áîëüøå ìàññû ýòèõ àòîìíûõ ÿäåð, êîãäà îíè îáúåäèíåíû â îäíî àòîìíîå ÿäðî. Òàêèì îáðàçîì, ïðè èõ ñèíòåçå âûäåëÿåòñÿ ýíåðãèÿ, ñâÿçàííàÿ ñ ðàçíîñòüþ ìàññ ïîêîÿ ñèíòåçèðîâàííîãî àòîìíîãî ÿäðà è ñóììû ìàññ ïîêîÿ åãî ñîñòàâëÿþùèõ.  ñëó÷àå æå òÿæåëûõ àòîìíûõ ÿäåð ñ âûäåëåíèåì ýíåðãèè áóäåò ïðîèñõîäèòü äðóãîé ïðîöåññ – ðàñùåïëåíèå èëè äåëåíèå èñõîäíîãî àòîìíîãî ÿäðà íà äâå áîëåå ëåãêèå ÷àñòè. Ñóììà èõ ìàññ ïîêîÿ áóäåò ìåíüøå ìàññû ïîêîÿ èñõîäíîãî àòîìíîãî ÿäðà, à ðàçíîñòü ìàññ è ïðèâåäåò ê âûäåëåíèþ ýíåðãèè. Ýòà êèíåòè÷åñêàÿ ýíåðãèÿ ðàçëåòàþùèõñÿ îáëîìêîâ èñõîäíîãî àòîìíîãî ÿäðà èñïîëüçóåòñÿ â ÿäåðíûõ ðåàêòîðàõ ëèáî â àòîìíîé áîìáå, à ñèíòåç ëåãêèõ àòîìíûõ ÿäåð – â òåðìîÿäåðíûõ ðåàêòîðàõ èëè â âîäîðîäíîé áîìáå.  ñòðóêòóðå àòîìíûõ ÿäåð åùå íàäî ó÷èòûâàòü, ÷òî íóêëîíû ÿâëÿþòñÿ ôåðìèîíàìè (íàïîìíèì, ÷òî òàê íàçûâàþòñÿ ìèêðî÷àñòèöû ñî ñïèíîì $/2), è äëÿ íèõ, òàê æå êàê è äëÿ ýëåêòðîíîâ, ñïðàâåäëèâ ïðèíöèï Ïàóëè. Îí çàñòàâëÿåò íóêëîíû çàíèìàòü â íîðìàëüíîì ñîñòîÿíèè âñå âîçìîæíûå ýíåðãåòè÷åñêèå óðîâíè âíóòðè àòîìíîãî ÿäðà, íà÷èíàÿ îò ñàìîãî íèæíåãî è äî íåêîòîðîãî ïðåäåëüíîãî, êîòîðûé, åñòåñòâåííî, çàâèñèò îò ÷èñëà ôåðìèîíîâ â ñèñòåìå. Òàêîé ïðåäåëüíûé óðîâåíü íîñèò íàçâàíèå óðîâíÿ Ôåðìè (ýòî î÷åíü âàæíàÿ âåëè÷èíà è â ìèêðîôèçèêå, è â ôèçèêå òâåðäîãî òåëà). Áåç âûâîäà ïðèâåäåì âûðàæåíèå äëÿ ýíåðãèè Ôåðìè íóêëîíîâ â çàâèñèìîñòè îò èõ ïëîòíîñòè (ò.å. ÷èñëà íóêëîíîâ n â îáúåìå â 1ñì3), êîòîðàÿ ðàâíà EF = – ($2/8M)×(3n/π)2/3, (19.3) ãäå Ì – ìàññà íóêëîíà. Îöåíèì ÷èñëåííî ýòó ýíåðãèþ Ôåðìè íóêëîíîâ. Äëÿ ýòîãî ïðåæäå âñåãî íàäî îïðåäåëèòü ïëîòíîñòü íóêëîíîâ â àòîìíîì ÿäðå n, à òàêæå èõ ìàññîâóþ ïëîòíîñòü â ã/ñì3. Îïûò ïîêàçûâàåò, ÷òî â àòîìíîì ÿäðå ñ ìàññîâûì ÷èñëîì À ïî÷òè âñå íóêëîíû óïàêîâàíû â îáúåìå ñôåðè÷åñêîé ôîðìû ñ ðàäèóñîì R, êîòîðûé ðàâåí R = 1,2×10-13×A1/3 ñì. 140 (19.4) 1.19. Ñòðîåíèå àòîìíîãî ÿäðà Ïîñêîëüêó îáúåì V ïðîïîðöèîíàëåí R3, òî îí ïðîïîðöèîíàëåí è À. Òàêèì îáðàçîì, âñå àòîìíûå ÿäðà, íåçàâèñèìî îò èõ ðàçìåðà, èìåþò ïðàêòè÷åñêè îäèíàêîâóþ ïëîòíîñòü. Âû÷èñëèì ïëîòíîñòü ÿäåðíîãî âåùåñòâà â âèäå ÷èñëà A íóêëîíîâ â 1 ñì3 è â ã/cì 3.  ïåðâîì ñëó÷àå: n = , íî V ñîãëàñíî (19.4) îáúåì ÿäðà V: V = (4π/3)×R3 = (4π/3)×(1,2×10-13)3×A (19.5) è ñëåäîâàòåëüíî n = A/(4π/3)×R3×(1,2)3×10-39 = 1,38×1038 (19.6) íóêëîíîâ â 1 ñì3. Óìíîæàÿ (19.6) íà ìàññó ïîêîÿ îäíîãî íóêëîíà, êîòîðàÿ èìååò âåëè÷èíó ïîðÿäêà 1,67×10-24 ã, ïîëó÷àåì äëÿ ïëîòíîñòè ÿäåðíîãî âåùåñòâà ñëåäóþùåå çíà÷åíèå: ρ = 2,3×1014 ã/ñì3, (19.7) ò.å. 1 ñì3 ÿäåðíîãî âåùåñòâà âåñèë áû 230 ìèëëèîíîâ òîíí! Ðàññìîòðèì îòäåëüíûé íåéòðîí, íàõîäÿùèéñÿ âíóòðè òÿæåëîãî àòîìíîãî ÿäðà. Îí èñïûòûâàåò íåêîå óñðåäíåííîå ïðèòÿæåíèå ñî ñòîðîíû âñåõ îñòàëüíûõ íóêëîíîâ àòîìíîãî ÿäðà. Òî åñòü äëÿ íåãî ñóùåñòâóåò íåêàÿ ïîòåíöèàëüíàÿ ýíåðãåòè÷åñêàÿ ÿìà è â íåå ïîïàäàþò âñå íåéòðîíû àòîìíîãî ÿäðà, êîòîðûå, â ñîîòâåòñòâèè ñ òðåáîâàíèÿìè ïðèíöèïà Ïàóëè, çàñåëÿþò ïî äâà íåéòðîíà ñ ïðîòèâîïîëîæíûìè ñïèíàìè êàæäûé ýíåðãåòè÷åñêèé óðîâåíü. Ãëóáèíà ýòîé ÿìû, î÷åâèäíî, ïî ïîðÿäêó âåëè÷èíû äîëæíà ðàâíÿòüñÿ ñóììå óäåëüíûõ ýíåðãèé ñâÿçè, êîòîðàÿ èçîáðàæåíà íà ðèñ. 23 è ýíåðãèè Ôåðìè ÅF. Ïîñëåäíþþ ìû ìîæåì âû÷èñëèòü ïî ôîðìóëå (19.3), åñëè ïðèìåì äëÿ ÷èñëà íåéòðîíîâ â àòîìíîì ÿäðå ñ àòîìíûì âåñîì À âåëè÷èíó, ðàâíóþ À/2: ÅF = (3$2/8πM)×(0,69×1038)2/3 = 33,7 ÌýÂ. (19.8) Äëÿ ãëóáèíû ïîòåíöèàëüíîé ÿìû äëÿ íåéòðîíîâ â àòîìíîì ÿäðå ïîëó÷àåì: Å = ÅF + Åñâ = 33,7 + 8,5 = 42,2 ÌýÂ, (19.9) ÷òî èçîáðàæåíî íà ðèñ. 23 â âèäå óñðåäíåííîé ïîòåíöèàëüíîé ÿìû äëÿ íåéòðîíîâ. Íà ðèñ. 24à, á èçîáðàæåíû äâå ïî141 1.19. Ñòðîåíèå àòîìíîãî ÿäðà Ýíåðãèÿ, Ìýâ R=1,2æ10-13 A1/3 ñì Ýíåðãèÿ ñâÿçè }Âîçáóæäåííûå ñîñòîÿíèÿ Îñíîâíîå ñîñòîÿíèå Ðèñ. 23. Óñðåäíåííûé ÿäåðíûé ïîòåíöèàë äëÿ íåéòðîíîâ â àòîìíîì ÿäðå ðàäèóñà R. Ñïëîøíûå ëèíèè ñîîòâåòñòâóþò çàíÿòûì ñîñòîÿíèÿì, à ïóíêòèðíûå – ñâîáîäíûì ñîñòîÿíèÿì, êîòîðûå çàíèìàþòñÿ ïðè âîçáóæäåíèè àòîìíîãî ÿäðà. òåíöèàëüíûå ÿìû, äëÿ íåéòðîíîâ è ïðîòîíîâ ïî îòäåëüíîñòè, ò.ê. ïðè ðàñ÷åòå ýíåðãèè äëÿ ïðîòîíîâ, êðîìå ýíåðãèè Ôåðìè è ÿäåðíîé ýíåðãèè ñâÿçè, íàäî åùå ó÷èòûâàòü èõ êóëîíîâñêîå âçàèìîäåéñòâèå. Êàê ýòî âèäíî èç ðèñ. 24à,á, îáå ÿìû èìåþò O Êóëîíîâñêèé áàðüåð O / -B V0 Óðîâåíü Ôåðìè Ef,p Ef,n Ec Íåéòðîíû à ïðîòîíû á Ðèñ. 24. Ïîòåíöèàëüíûå ÿìû: à) äëÿ íåéòðîíîâ, á) äëÿ ïðîòîíîâ. Å – îïûòíûå çíà÷åíèÿ ýíåðãèè ñâÿçè. E(c) – êóëîíîâñêàÿ ýíåðãèÿ ïðîòîíîâ, Å(f,n) è Å(f,p) – ñîîòâåòñòâåííî – ýíåðãèè Ôåðìè äëÿ íåéòðîíîâ è ïðîòîíîâ, V(0) – ãëóáèíà íåéòðîííîé ïîòåíöèàëüíîé ÿìû. ðàçíóþ ôîðìó è ðàçíóþ ãëóáèíó, à äíî ïîòåíöèàëüíîé ÿìû äëÿ ïðîòîíîâ ïðèïîäíÿòî îòíîñèòåëüíî äíà íåéòðîííîé ÿìû 142 1.19. Ñòðîåíèå àòîìíîãî ÿäðà íà âåëè÷èíó êóëîíîâñêîé ýíåðãèè îòòàëêèâàíèÿ ìåæäó ïðîòîíàìè, êîòîðàÿ ðàâíà: Åêóë = (3/5)×(Ze)2/R (19.10) Òàêàÿ âåëè÷èíà ïîëó÷àåòñÿ, åñëè ñ÷èòàòü, ÷òî ýëåêòðè÷åñêèé çàðÿä ïðîòîíîâ ðàâíîìåðíî ðàñïðåäåëåí ïî âñåìó îáúåìó àòîìíîãî ÿäðà, êîòîðîå èìååò âèä ñôåðû ðàäèóñà R. Êðîìå òîãî, ÿìà äëÿ ïðîòîíîâ èìååò êóëîíîâñêèé ïîòåíöèàëüíûé áàðüåð, îêðóæàþùèé àòîìíîå ÿäðî. Ïðîòîíû, êîòîðûå ïûòàþòñÿ ïðîíèêíóòü èçâíå âíóòðü àòîìíîãî ÿäðà, îòòàëêèâàþòñÿ ïîëîæèòåëüíûì çàðÿäîì +Ze ýòîãî ÿäðà. Ýíåðãåòè÷åñêèå óðîâíè, íà÷èíàÿ ñî äíà ïîòåíöèàëüíûõ ÿì, ïëîòíî çàíÿòû â íîðìàëüíîì ñîñòÿíèè àòîìíîãî ÿäðà: íà êàæäîì óðîâíå «ñèäèò» ïî äâà íóêëîíà ñ àíòèïàðàëëåëüíûìè ñïèíàìè. Òåîðèÿ ñòðóêòóðû àòîìíûõ ÿäåð ñåé÷àñ ïîëó÷èëà äîñòàòî÷íî ïîëíîå è ðåçóëüòàòèâíîå ðàçâèòèå, íî ìû íå áóäåì áîëüøå îñòàíàâëèâàòüñÿ íà äåòàëÿõ ýòîé òåîðèè è å¸ ìàòåìàòè÷åñêîì àïïàðàòå. 143