КАЛЕНДАРНЫЙ ПЛАН - Кафедра систем телекоммуникаций РУДН
реклама
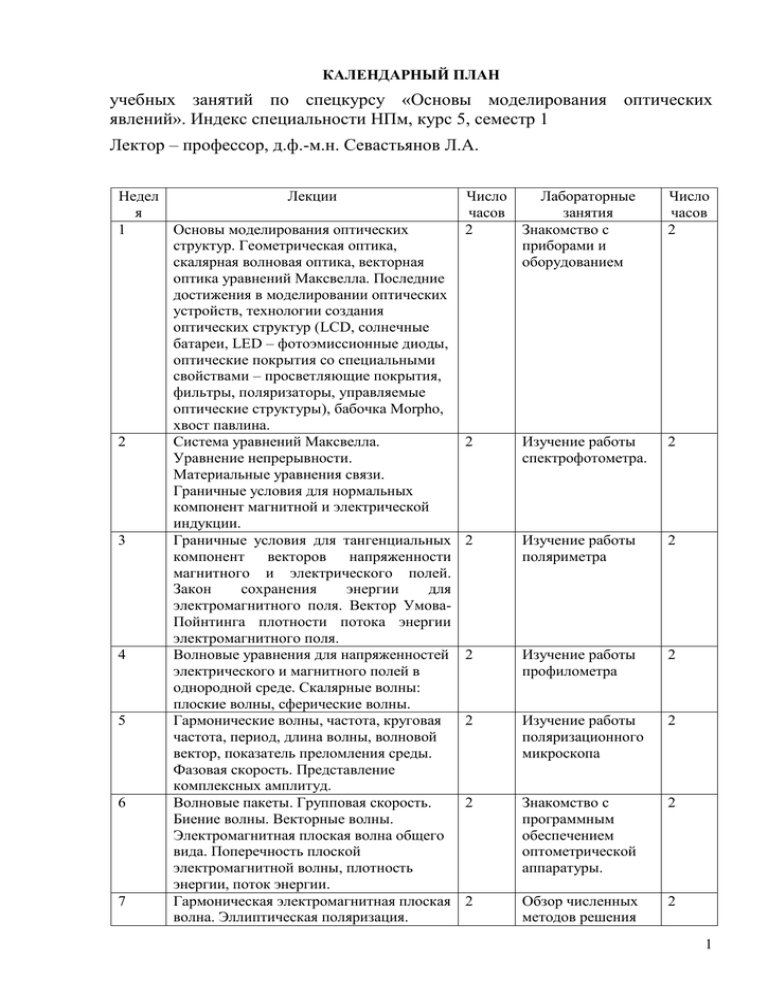
КАЛЕНДАРНЫЙ ПЛАН учебных занятий по спецкурсу «Основы моделирования оптических явлений». Индекс специальности НПм, курс 5, семестр 1 Лектор – профессор, д.ф.-м.н. Севастьянов Л.А. Недел Лекции я 1 Основы моделирования оптических структур. Геометрическая оптика, скалярная волновая оптика, векторная оптика уравнений Максвелла. Последние достижения в моделировании оптических устройств, технологии создания оптических структур (LCD, солнечные батареи, LED – фотоэмиссионные диоды, оптические покрытия со специальными свойствами – просветляющие покрытия, фильтры, поляризаторы, управляемые оптические структуры), бабочка Morpho, хвост павлина. 2 Система уравнений Максвелла. Уравнение непрерывности. Материальные уравнения связи. Граничные условия для нормальных компонент магнитной и электрической индукции. 3 Граничные условия для тангенциальных компонент векторов напряженности магнитного и электрического полей. Закон сохранения энергии для электромагнитного поля. Вектор УмоваПойнтинга плотности потока энергии электромагнитного поля. 4 Волновые уравнения для напряженностей электрического и магнитного полей в однородной среде. Скалярные волны: плоские волны, сферические волны. 5 Гармонические волны, частота, круговая частота, период, длина волны, волновой вектор, показатель преломления среды. Фазовая скорость. Представление комплексных амплитуд. 6 Волновые пакеты. Групповая скорость. Биение волны. Векторные волны. Электромагнитная плоская волна общего вида. Поперечность плоской электромагнитной волны, плотность энергии, поток энергии. 7 Гармоническая электромагнитная плоская волна. Эллиптическая поляризация. Число Лабораторные часов занятия 2 Знакомство с приборами и оборудованием Число часов 2 2 Изучение работы спектрофотометра. 2 2 Изучение работы поляриметра 2 2 Изучение работы профилометра 2 2 Изучение работы поляризационного микроскопа 2 2 Знакомство с программным обеспечением оптометрической аппаратуры. 2 2 Обзор численных методов решения 2 1 8 9 10 11 12 13 14 15 16 Линейная и круговая поляризации. (прямых) Характеристика состояния поляризации с оптических задач. помощью параметров Стокса. Промежуточный контроль знаний (Контрольная работа №1) Условия на бесконечности. Законы 2 Методы отражения и преломления Снеллиуса. сопряжения Формулы Френеля для параллельной и программного перпендикулярной линейных обеспечения с поляризаций. Отражательная и приборами. пропускательная способности; Форматы и поляризация при отражении и структура преломлении. Угол полной поляризации измеренных (угол Брюстера). Полное внутреннее данных отражение. Теория диэлектрических пленок. Система 2 Комплексная уравнений Максвелла в слоистой арифметика диэлектрической среде. Система двух компилятора дифференциальных уравнений второго Delphi. порядка для двух независимых поляризаций. Характеристическая матрица для слоистой среды. Решение системы с помощью определителя Вронского. Характеристическая матрица однородной диэлектрической пленки. Характеристическая матрица слоистой 2 Методы решения среды, состоящей из тонких однородных СЛАУ над полем пленок. Коэффициенты отражения и комплексных чисел пропускания. Отражательная и пропускательная способности. Определение анизотропной среды. 2 Определение Тензоры диэлектрической и магнитной собственных проницаемостей. Уравнения Максвелла значений и для анизотропной среды. Уравнения собственных Максвелла для плоских векторов монохроматических волн в анизотропной комплекснозначны среде. х матриц Взаимная ориентация всех векторов, 2 Визуализация характеризующих процесс результатов распространения электромагнитной измерений и волны в анизотропной среде. Волновое и расчетных дисперсионное уравнения. характеристик. Промежуточный контроль знаний (Контрольная работа №2) Дисперсионное уравнение для плоской 2 Произведение электромагнитной волны в анизотропной комплексных среде (уравнение Френеля). Две волны с матриц и различными фазовыми скоростями, комплексной обладающие ортогональными линейными матрицы на поляризациями, распространяющиеся в комплексный заданном направлении. вектор Электромагнитные волны в одноосной анизотропной среде, поляризации 2 Метод LUразложения для 2 2 2 2 2 2 2 2 2 2 обыкновенной и необыкновенной волн. Произвольная ориентация кристаллографических осей анизотропной среды. решения комплексных систем линейных алгебраических уравнений 17 Дифракционный интеграл Кирхгофа, приближения дифракционного интеграла. Принцип Гюйгенса, дифракция Френеля, дифракция Фраунгофера. Двумерная дифракция. Одномерная дифракционная решетка. 2 18 Амплитудная решетка, фазовая решетка. Волны в периодических структурах, уравнение Матье, теорема Флоке, уравнение Хилла. Дисперсионное уравнение решетки. 2 Метод Якоби для решения комплексных систем линейных алгебраических уравнений 2 Метод Якоби для 2 отыскания собственных векторов и собственных значений комплексных матриц. Заключительный обзор курса. Консультации по подготовке к итоговому контролю знаний. Итоговый контроль знаний Зав. кафедрой систем телекоммуникаций, проф. К.Е. Самуйлов 3

