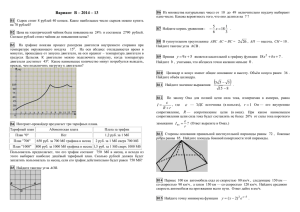
- RGR

Министерство образования Российской Федерации
Пермский государственный технический университет
Кафедра электротехники
Утверждено
на заседании кафедры
9 ноября 1999 г.
Электротехника и электроника
Программа, методические указания и контрольные задания для студентов заочного
отделения
Пермь 2000
Составитель: канд. техн. наук, доцент В.В.Тиунов.
УДК621.313
Электротехника и электроника: Программа, методические указания и контрольные задания
для студентов / Сост. В.В.Тиунов; ПГТУ, Пермь, 2000. Программа, методические указания и
контрольные задания по курсам «Электротехника», «Электротехника и электроника»
предназначаются для студентов-заочников технического университета.
Содержание пособия соответствует действующим типовым пособиям, программам и
государственным
образовательным
стандартам
по
соответствующим
курсам
для
неэлектротехнических специальностей высших учебных заведений.
В пособии представлены краткие теоретические сведения по основным видам электрических
цепей, электронных элементов и устройств, а также по основным типам электрических машин и
аппаратов. Приводится значительное количество детально разобранных примеров по расчету
параметров электрических цепей, электронных устройств и характеристик электрических машин.
Пособие может быть рекомендовано для самостоятельной и индивидуальной работы не
только студентам заочного отделения, но и для студентов всех других форм обучения, проходящих
электротехническую подготовку, а также может быть полезным для лиц, занимающихся
самоподготовкой в соответствующих областях.
ПРОГРАММА
Цели и задачи дисциплины, ее место в учебном процессе
Цели изучения дисциплины
Курс «Электротехника и электроника» имеет существенное значение в инженерной
подготовке студентов технического университета. Он обеспечивает условия для успешного
усвоения последующих профилирующих дисциплин. Целью данной дисциплины является
теоретическая и практическая подготовка дипломированных специалистов, чтобы выпускники
изучили основные процессы, происходящие в типовых электрических цепях и электронных
элементах, освоили принципы их расчета, разобрались в устройстве и принципе действия основных
типов электрических машин и аппаратуры для их управления. Итогом изучения курса должна стать
совокупность теоретических знаний и практических навыков, позволяющая выпускаемым
специалистам понимать принципы работы, эксплуатации, разработки и совершенствования
электроустановок по профилю своей профессиональной инженерной деятельности.
Задачи изучения дисциплины
Главные задачи изменил вышеуказанного курса сводится к следующему:
•ознакомиться с ролью электрических цепей, машин и устройств промышленной электроники
в жизни современного общества, с состоянием основ их теории, практического использования и
перспективами совершенствования в нашей стране и за рубежом;
•научиться ясно понимать основные физические процессы, происходящие в основных типах
электрических цепей, машин и электронных устройств;
•получить необходимые навыки расчетов основных параметров и характеристик
электрических цепей и машин, а также простейших электронных устройств с целью
квалифицированного выбора и использования этих элементов в электроустановках по профилю своей
профессиональной деятельности;
•освоить базовые методики экспериментального исследования основных видов электрических
цепей, машин и устройств промышленной электроники;
•научиться грамотно, в соответствии с требованиями государственных и отраслевых
стандартов, оформлять отчеты о выполнении контрольных заданий, проведенных лабораторных
исследований и формулировать выводы по полученным результатам.
Перечень дисциплин, изученных ранее, знание основ которых необходимо для изучения
данного курса:
•высшая математика;
•физика;
•прикладная механика.
Содержание дисциплины Введение
Электрическая энергия, ее особенности и области применения. Значение электрификации и
компьютеризации в научно-технической революции на современном этапе развития общества. Роль
электротехники и электроники в развитии передовых систем горнодобывающей промышленности.
Значение электротехнической подготовки для инженеров-механиков и нефтяников
неэлектротехнических специализаций. Содержание
промежуточным и итоговой аттестациям обучаемых.
и
структура
курса.
Требования
к
Электрические цепи постоянного тока
Области применения электротехнических устройств постоянного тока в современных
производствах добычи и переработки полезных ископаемых. Структура электрической цепи.
Генерирующие и приемные устройства. Стандартные графические обозначения электротехнических
устройств постоянного тока. Схемы замещения электротехнических устройств. Линейные резистивные
элементы, идеальные источники ЭДС и тока, их свойства и вольт-амперные характеристики. Условные
графические обозначения, применяемые на схемах замещения
Линейные неразветвленные и разветвленные электрические цепи с одним источником ЭДС.
Условные положительные направления ЭДС, токов и напряжений на схемах замещения.
Пассивный и активный двухполюсники. Режимы работы электрической цепи. Энергетический баланс
в электрических цепях. Определение эквивалентных сопротивлений разветвленных пассивных
линейных цепей. Взаимное преобразование схем соединений треугольником и звездой пассивных
элементов. Анализ электрического состояния неразветвленной и разветвленной линейных
электрических цепей с несколькими источниками ЭДС путем непосредственного применения законов
Кирхгофа. Методы контурных токов и узлового напряжения. Принцип суперпозиции.
Основные свойства и области применения четырехплечих мостовых цепей.
Нелинейные элементы и их характеристики (диод, стабилитрон, терморезистор). Анализ
электрического состояния неразветвленных и разветвленных электрических цепей с нелинейными
элементами.
Электрические цепи переменного тока
Особенности электромагнитных процессов в цепях с изменяющимися во времени токами.
Генерирующие устройства переменного тока промышленной и высоких частот. Области применения и
причины широкого распространения электротехнических устройств синусоидального тока
промышленной частоты.
Однофазные цепи. Принцип действия простейшего однофазного электромашинного
генератора синусоидальной ЭДС промышленной частоты. Основные параметры, характеризующие
синусоидальную величину. Начальная фаза. Сдвиг фаз. Мгновенное, амплитудное, действующее и
среднее значения синусоидально изменяющихся электрических величин. Представление
синусоидальных величин тригонометрическими функциями, графиками изменений функций во времени,
вращающимися векторами и комплексными числами.
Электротехнические устройства переменного тока: источники ЭДС, резисторы, индуктивные
катушки и конденсаторы. Стандартные графические обозначения на схемах электротехнических
устройств переменного тока. Схемы замещения электротехнических устройств переменного тока.
Идеальные элементы: резистивные, индуктивные и емкостные. Параметры (активное сопротивление,
индуктивность, емкость) и характеристики (вольтамперные, вебер-амперные, кулон-вольтные)
идеальных элементов. Условные графические обозначения, применяемые на схемах замещения для
изображения идеальных и реальных элементов. Законы Ома и Кирхгофа для цепей синусоидального
тока.
Уравнение электрического состояния для неразветвленной цепи. Активное, реактивное и полное
сопротивления двухполюсника. Комплексное сопротивление. Треугольник сопротивлений. Векторные
диаграммы. Фазовые соотношения между токами и напряжениями. Понятие о потенциальных
(топографических) диаграммах. Колебание энергии и мгновенная мощность элементов цепи.
Активная, реактивная и полная мощности. Треугольник мощностей. Коэффициент мощности и его
технико-экономическое значение. Выражение мощности в комплексной форме. Резонанс
напряжений, условия его возникновения и практическое значение.
Цепи с параллельным соединением ветвей. Уравнения электрического состояния цепи.
Векторные диаграммы. Активная, реактивная и полная проводимости. Треугольник проводимостей.
Комплексная проводимость. Резонанс токов, условия его возникновения и практическое значение.
Компенсация реактивной мощности для повышения коэффициента мощности. Анализ
электрического состояния разветвленных цепей с применением комплексных чисел. Регулируемые
и нерегулируемые фазовращающие устройства. Особенности и области применения четырехплечих
мостовых устройств в цепях синусоидального тока. Магнитосвязанные электрические цепи.
Анализ простейших цепей с учетом явления взаимоиндукции.
Трехфазные цепи. Области применения трехфазных устройств. Простейший трехфазный
генератор. Способы соединения трехфазной обмотки генератора. Представление электрических
величин трехфазных систем тригонометрическими функциями, графиками, вращающимися векторами
и комплексными числами. Условные положительные направления электрических величин в
трехфазной системе. Фазные и линейные напряжения. Векторные диаграммы.
Способы включения в трехфазную сеть однофазных и трехфазных приемников.
Четырехпроводная и трехпроводная трехфазные цепи. Соотношение между фазными и линейными
напряжениями, фазными и линейными токами.
Мощность трехфазной цепи Понятие о работе трехфазной цепи при несимметричной
нагрузке в четырехпроводной и трехпроводной цепях. Назначение нейтрального провода.
Напряжение между нейтралями. Компенсация реактивной мощности для повышения коэффициента
мощности трехфазной установки. Измерение активной мощности (энергии) трехфазной системы
методом двух и трех ваттметров (счетчиков). Однолинейное изображение трехфазной цепи на
электрических схемах.
Переходные процессы в линейных электрических цепях. Причины возникновения
переходных процессов в электрических цепях и их значение для работы цепей. Дифференциальные
уравнения электрического состояния цепи. Установившиеся и свободные составляющие токов и
напряжений. Законы коммутации и их использование для определения начальных условий. Влияние
параметров цепи на длительность переходного процесса. Постоянная времени.
Переходные процессы при включении на зажимы источника постоянного напряжения
неразветвленных цепей: с резистором и индуктивной катушкой, с резистором и конденсатором, с
резистором, индуктивной катушкой и конденсатором. Понятие о характере протекания переходных
процессов в цепи, содержащей индуктивную катушку и резистор, включаемых на зажимы источника
синусоидального напряжения.
Разряд конденсатора на резистор. Простейший генератор пилообразного напряжения.
Возникновение перенапряжения и дугового разряда на контактах при размыкании цепи,
содержащей индуктивную катушку. Назначение разрядного резистора. Понятие о характере
протекания переходных процессов при разряде конденсатора на цепь с резистором и индуктивной
катушкой. Практическое использование переходных процессов.
Применение цепей с резисторами, индуктивными катушками и конденсаторами для
электрического моделирования процессов в механических, гидравлических и других системах.
Периодические несинусоидальные токи в электрических цепях. Причины возникновения
периодических несинусоидальных ЭДС, токов и напряжений. Электрические цепи с вентилями.
Представление периодических несинусоидальных величин рядами Фурье. Частотный спектр
периодической несинусоидальной величины. Максимальное, среднее и действующее значения
периодической несинусоидальной величины. Коэффициенты амплитуды, формы и искажения.
Анализ линейных электрических цепей при несинусоидальном напряжении источника питания.
Активная и полная мощности. Влияние индуктивных и емкостных элементов цепи на форму
кривых токов и напряжений. Резонансные фильтры. Электрические схемы и принцип работы
выпрямителей и сглаживающих фильтров. Понятие о дифференцирующих, интегрирующих и
избирательных цепях.
Электромагнитные устройства и трансформаторы
Применение электромагнитных устройств постоянного и переменного токов в технике.
Назначение магнитопровода. Свойства ферромагнитных материалов, используемых для
изготовления магнитопроводов электромагнитных устройств с постоянными и переменными
магнитными полями. Неразветвленные и разветвленные магнитные цепи.
Магнитные цепи с постоянной магнитодвижущей силой (МДС). Реальная и идеальные
магнитные цепи. Применение закона полного тока для анализа идеальной магнитной цепи.
Магнитное сопротивление и проводимость. Схема замещения магнитной цепи. Вебер-амперные
характеристики. Аналогия методов анализа электрических и магнитных цепей. Магнитные цепи
при наличии воздушного зазора в магнитопроводе. Расчет тягового усилия электромагнита
постоянного тока. Электромагнитные устройства постоянного тока: подъемные электромагниты
контакторы, реле и т.п. Их характеристики, свойства и области применения. Неразветвленная цепь
с постоянным магнитом. Понятие о ее расчете. Область применения.
Магнитные цепи с переменной магнитодвижущей силой. Особенности магнитной цепи с
переменной МДС. Реальная и идеальная катушки с магнитопроводом. Катушка с
магнитопроводом как нелинейный индуктивный элемент и ее вольт-амперная характеристика.
Способы уменьшения мощности потерь энергии на гистерезис и вихревые токи. Зависимости
мгновенных значений магнитного потока и тока во времени при синусоидальном напряжении на
катушке.
Эквивалентный синусоидальный ток. Уравнение электрического состояния, векторная
диаграмма и схема замещения катушки. Влияние воздушного зазора магнитопровода на вольтамперную характеристику катушки. Полное сопротивление катушки. Электромагнитные
устройства переменного тока с изменяемым воздушным зазором: дроссели, контакторы и т.п.
Зависимость полного сопротивления от величины зазора. Понятие о ферромагнитном
стабилизаторе напряжения.
Трансформаторы. Назначение и области применения трансформаторов. Однофазный
трансформатор. Устройство и принцип действия трансформатора. Основной магнитный поток,
потокосцепление рассеяния. Коэффициент трансформации. Условные положительные
направления напряжений, токов, ЭДС и магнитных потоков. Условные графические обозначения,
применяемые для изображения трансформатора на электрических схемах. Уравнения
электрического и магнитного состояния трансформатора. Реальный трансформатор. Идеальный
трансформатор. Приведенный трансформатор. Векторная диаграмма и схема замещения. Опыты
холостого хода и короткого замыкания, назначение и условия поведения. Потери энергии и КПД.
Изменение вторичного напряжения при нагрузке и внешняя характеристика трансформатора.
Устройство, принцип действия и области применения трехфазных трансформаторов.
Понятие о группах соединений обмоток. Устройство, принцип действия и области применения
автотрансформаторов. Понятие о многообмоточных трансформаторах. Измерительные
трансформаторы тока и напряжений, назначение и свойства. Схемы включения измерительных
трансформаторов и приборов. Погрешности измерений при использовании измерительных
трансформаторов. Классы точности. Определение цены деления шкал измерительных приборов,
включаемых с использованием измерительных трансформаторов.
Магнитные цепи с постоянной и переменной магнитодвижущими силами. Дроссель
насыщения как управляемый нелинейный индуктивный элемент. Устройство и принцип действия
простейшего магнитного усилителя. Схемы включения, рабочих обмоток и обмоток управления.
Характеристика управления. Коэффициенты усиления по току, напряжению и мощности.
Назначение обмоток обратной связи и смещения. Понятие о магнитных усилителях с
самонамагничиванием. Понятие о дифференциальных магнитных усилителях. Области
применения магнитных усилителей.
Основы электроники
Полупроводниковые приборы: диоды (выпрямительные, туннельные, стабилитроны), свето и
фотодиоды; биполярные транзисторы, полевые транзисторы и тиристоры. Электровакуумные
диоды, триоды тетроды, пентоды и тиратроны. Основные характеристики и параметры.
Полупроводниковые и электронные усилители. Классификация; усилителей. Однокаскадные
усилители. Графический анализ работы усилителя с коллекторной нагрузкой. Основные
параметры усилителя. Режимы работы усилителей (классы усиления А, В, С, и др.).
Температурная стабилизация режима работы усилителя. Влияние внутреннего сопротивления
источника сигнала и сопротивления нагрузки на коэффициент усиления. Особенности усилителя
на полевом транзисторе. Усилители на электровакуумном триоде и пентоде. Многокаскадные
усилители. Двухкаскадный усилитель с RC-связью. Понятие о частотной характеристике.
Усилители постоянного тока (УПТ). Основные свойства и характеристики. Дрейф нуля и способы
его устранения. Балансные схемы УПТ.
Обратные связи в электронных устройствах. Влияние отрицательной обратной связи на
параметры усилителей. Усилительный каскад с эмиттерной нагрузкой (эмиттерный повторитель).
Усилители мощности (УМ). Однотактные и двухтактные УМ. Понятие об избирательных
усилителях LC- и RC-типов.
Генераторы и импульсные устройства. Автогенераторы гармонических колебаний. Понятие
об автогенераторах LC- и RC-типов. Использование импульсных устройств в промышленной
электронике. Работа транзистора в режиме ключа. Электронные реле. Триггеры. Понятие о
пересчетных устройствах.
Интегральные схемы (ИС) и микроэлектроника. Необходимость перехода современной
электроники к ИС. Принципы построения ИС.
Электрические измерения и приборы
Расширение понятия измерительного процесса. Сочетание измерений с функциями
автоматического контроля, сигнализации и управления. Преимущества электрических методов
измерения неэлектрических величин. Понятие, об электрическом преобразователе. Методы
измерения: прямые и косвенные. Меры. Измерительные приборы непосредственного отсчета и
приборы сравнения. Понятие об аналоговом и цифровом приборах.
Основные показатели качества измерительного устройства: точность, чувствительность,
потребления энергии. Случайная и систематические погрешности в электрических измерениях.
Погрешности метода в электрических измерениях. Погрешности косвенных измерений.
Измерительная цепь и измерительный механизм показывающего прибора. Устройство,
принцип действия, основные свойства и области применения показывающих приборов
магнитоэлектрической, электромагнитной, электродинамической и выпрямительной систем.
Логомстры. Счетчики электрической энергии. Обозначения на шкалах приборов. Определение
цены деления шкалы. Погрешности и классы точности показывающих приборов.
Измерение токов, напряжений, сопротивлений, активной мощности и энергии. Общая оценка
достижимых в настоящее время пределов чувствительности и точности измерений постоянных и
переменных токов и напряжений. Понятие о мостовом методе измерений. Уравнение равновесия
четырехплечевого моста постоянного тока. Понятие об уравновешенных и неуравновешенных
мостах. Области применения мостов для измерения электрических величин. Мосты переменного
тока и их применение для измерения неэлектрических величин с помощью параметрических
преобразователей. Понятие о компенсационном методе измерений.
Особенности электронных измерительных приборов. Электронный осциллограф.
Функциональная схема осциллографа и его применение. Электронный вольтметр. Функциональная
схема вольтметра.
Электрические машины
Машины постоянного тока. Устройство машины постоянного тока. Коллектор и его
назначение. Простейшие обмотки якоря. Возможность работы машины в режимах генератора и
двигателя. Схема замещения цепи якоря. Преобразование энергии. ЭДС якоря и
электромагнитный момент машины постоянного тока. Понятие о реакции якоря и коммутации.
Потери энергии и КПД машин постоянного тока.
Работа машины в режиме генератора. Генераторы постоянного тока независимого
возбуждения и самовозбуждения. Характеристика холостого хода. Уравнение электрического
состояния цепи якоря. Внешняя и регулировочная характеристики. Сравнительная оценка свойств
и области применения генераторов постоянного тока различных способов возбуждения.
Тахогенераторы.
Работа машины в режиме двигателя. Классификация двигателей постоянного тока по
способу возбуждения. Уравнение электрического состояния цепи якоря. Пуск двигателя.
Назначение пускового реостата. Зависимости магнитного потока и электромагнитного момента
двигателей разных способов возбуждения от тока якоря. Механические характеристики
двигателей. Регулирование скорости вращения. Понятие о тормозных режимах двигателей
постоянного тока. Реверсирование. Сравнительная оценка свойств двигателей постоянного тока
разных способов возбуждения и области применения. Особенности устройства исполнительных
двигателей постоянного тока. Понятие; об универсальных
коллекторных двигателях.
Асинхронные машины. Устройство трехфазной асинхронной машины. Возбуждение
вращающегося магнитного поля трехфазной симметричной системой токов. Скорость вращения
поля. Направление вращения.
Принцип действия трехфазного асинхронного двигателя и области применения.
Конструкция фазного и короткозамкнутого роторов. Графическое изображение асинхронного
двигателя на электрических схемах. Скорость вращения ротора и его поля. Скольжение.
Зависимость частоты и величины ЭДС и тока в фазе обмотки ротора от скольжения. Схема
замещения фазы трехфазного асинхронного двигателя. Преобразования энергии, происходящие в
асинхронном двигателе. Активная, электромагнитная и полезная мощности двигателя. Потери
энергии и КПД двигателя. Реактивная мощность и коэффициент мощности двигателя.
Электромагнитный момент двигателя и его зависимость от величин скольжения и напряжения
сети. Механическая характеристика двигателя. Перегрузочная способность двигателя. Пуск
двигателя. Рабочие характеристики двигателя. Асинхронные двигателя с улучшенными
пусковыми свойствами. Регулирование скорости вращения. Понятие о работе асинхронных машин
в качестве тормоза и генератора Области применения трехфазных асинхронных двигателей.
Понятие о линейных асинхронных двигателях.
Принцип действия, механические характеристики, свойства и области применения
однофазных асинхронных двигателей. Однофазные двигатели с пусковыми элементами и
конденсаторные двухфазные двигатели. Двигатели с расщепленными полюсами. Двухфазные
исполнительные двигатели с полым немагнитным ротором. Асинхронный тахогенератор. Понятие
об устройстве, принципе действия и области применения поворотных трансформаторов.
Понятие об устройстве, принципе действия и области применения однофазных сельсинов с
трехфазной обмоткой синхронизации.
Синхронные машины. Устройство трехфазных синхронных машин с электромагнитным
возбуждением. Области применения синхронных машин. Графическое изображение синхронной
машины на электрических схемах.
Работа синхронной машины в режиме генератора Работа генератора на автономную
нагрузку. Магнитное поле машины ЭДС и электромагнитный момент. Схема замещения фазы
обмотки статора неявнополюсного синхронного генератора Уравнение электрического состояния
фазы обмотки статора: Векторная диаграмма. Электромагнитная мощность. Внешние
характеристики синхронного генератора. Работа трехфазного синхронного генератора
параллельно с сетью. Включение генератора на параллельную работу с сетью. Регулирование
активной мощности. Угловые характеристики. Предел устойчивости и выпадение их синхронизма.
Регулирование реактивной мощности генератора, U-образные характеристики.
Работа синхронной машины в режиме двигателя. Схема замещения. Пуск двигателя.
Уравнение электрического состояния и векторная диаграмма фазы обмотки статора.
Электромагнитный момент двигателя. Механическая и U-образная характеристики двигателя.
Влияние величины тока возбуждения на коэффициент мощности двигателя. Понятие о принципе
действия и назначении синхронного компенсатора.
Устройство, принцип действия и области применения синхронных двигателей малой
мощности: реактивных, гистерезисных и шаговых.
Принципы выбора электродвигателей.
Аппаратура управления и защиты
электротехнических устройств
Определение понятия электропривода. Значение электропривода в автоматизации
производственных процессов. Понятие об установившихся и переходных процессах электроприводов.
Типовые режимы работы электропривода. Технико-экономическое значение правильного выбора
мощности электродвигателя. Условия, определяющие выбор мощности двигателя Нагрев и охлаждение.
Классы изоляции. Понятие о нагрузочных диаграммах и принципе их построения. Продолжительность
включения. Приближенные методы выбора мощности при длительном и повторно-кратковременном
режимах работы электродвигателя. Особенности выбора мощности электродвигателя по нагреву и
перегрузочным способностям при его работе с постоянной и переменной нагрузками. Выбор
электродвигателя по каталогу.
Понятие об управлении электроприводами. Аппаратура управления и защиты электротехнических
устройств. Контакторы, конечные выключатели и реле. Условнее графические обозначения аппаратуры
на схемах. Типовые схемы управления. Общие принципы релейно-контакторного и бесконтакторного
управления электротехническими устройствами.
Понятие о схемах электроснабжения, выборе сечения проводов и тепловой защите электроустановок .
УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО ДИСЦИПЛИНЕ
Основная и дополнительная литература
Основная литература
1.Электротехника // Под ред. В.Г.Герасимова. М.: Высшая школа, 1985.
2.Борисов ЮМ, Липатов Д.Н., Зорин Ю.Н. Электротехника. - М.: Энергоатомиздат, 1985, 1999.
3.Основы промышленной электроники // Под ред. В.Г Герасимова. - М.: Высшая школа, 1986.
4.Волынский Б.А., Зейн Е.Н., Шатерников В. Е. Электротехника, - М: Энергоатомиздат, 1987.
5.Касаткин А.С., Немцов М.В., Электротехника. М.: учеб. для вузов - 6-е изд., перераб. Высшая
школа, 1999.
6.Сборник задач по электротехнике и основам электроники // Под ред. В.Г.Герасимова. М:
Высшая школа, 1987.
Дополнительная литература
7.Липатов Д.Н. Вопросы и задачи по электротехнике для программированного обучения. М:
Энергоатомиздат, 1984.
8.Данилов И.А., Иванов П.М. Общая электротехника с основами электроники: Учеб. пособ. - 3-е
изд., стер. М: Высшая школа,1998.
9.Промышленная электроника. Авт. Котлярский А.И. и др. М.: Недра, 1984.
10.Криштафович А.К. Промышленная электроника. М.: Высшая школа, 1984.
11.Гершунский Б.С. Основы электроники. Киев: Высшая школа, 1977.
12.Сборник задач по электротехнике и основам электроники // Под ред. В.С.Пантюшина. М:
Высшая школа, 1979.
13.Сборник задач с решениями по общей электротехнике // Под ред. В.К.Пономаренко. М.:
Высшая школа, 1972.
14.Васин В.М Электрический привод. М.: Высшая школа, 1984.
15.Справочное пособие по электротехнике и основам электроники // Под ред. А.В.Нетушила. М.:
Высшая школа, 1986.
16.Забродин Ю.С. Промышленная электроника, - М.: Высшая школа, 1982.
17.Иванов Й.И., Равдоник В.С. Электротехника. М: Высшая школа, 1984.
18. Гершунский Б.С. Основы электроники и микроэлектроники. Киев: Высшая школа, 1989. 423с.
Перечень методических указаний по проведению лабораторных занятий
1.Электрические цепи. Руководство к лабораторным работам по курсу «Электротехника», часть 1.
ПермГТУ. Пермь, 1990,1999.
2.Электрические машины. Методические указания к проведению лабораторных работ по курсу
«Электротехника», часть 1,2, ПермГТУ, Пермь, 1988.
3.Промышленная электроника. Методическое руководство к лабораторным работам. Часть 1,2,
ПермГТУ, Пермь, 1991.
РАЗДЕЛ I
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ТЕМАМ КУРСА
Электрические цепи постоянного тока
Приступая к изучению данного раздела, необходимо иметь представление о тинах генерирующих
устройств, их внешних характеристиках и режимах работы, а также об основных видах приемных
устройств и их условных обозначениях. Следует знать основные законы и понимать свойства
линейных электрических цепей. Необходимо уметь анализировать электрическое состояние цепей с
нелинейными резистивными элементами. В результате изучения данного раздела студенты должны:
1)знать области применения электротехнических устройств постоянного тока, способы
соединения электрических устройств, методику составления уравнений электрического состояния
линейных цепей, примеры нелинейных элементов и их вольт-амперные характеристики;
2)понимать эквивалентность схем источников ЭДС и источника тока, смысл вольт-амперных
характеристик, приемных и внешних
характеристик генерирующих устройств, сущность энергетических процессов, происходящих в
генерирующих пассивных и активных приемных устройствах, возможность осуществления взаимных
преобразований схем соединении пассивных элементов треугольником и звездой, возможность
замены нелинейного элемента эквивалентной схемой замещения с линейными элементами,
возможность проведения анализа линейных электрических цепей методами контурных токов,
суперпозиции, пропорциональных величин;
3)уметь проводить анализ линейных электрических цепей методами свертывания,
непосредственного применения законов Кирхгофа узлового напряжения, составлять уравнения баланса
электрической мощности, определять ток любой ветви сложной электрической цепи методом
эквивалентного генератора, применять метод пересечения характеристик для определения тока в
нелинейной цепи.
Приступая к расчету электрических цепей, необходимо иметь четкое представление о схемах
соединения (последовательное, параллельное, смешанное) как приемников, так и источников
электрической энергии. В ряде случаев приходится иметь дело и с более сложными соединениями, к
которым относятся многоугольники и звезды. Наиболее часто встречаются соединения
треугольником и трехлучевой звездой. При расчете электрических цепей обычно пользуются
законами Ома и Кирхгофа. Электрические цепи, разделяются на простые и сложные. К простым
относятся цепи, состоящие только из последовательных, параллельных и смешанных соединений
приемников электрической энергии. Если в электрической цепи, до того как произведен ее расчет,
можно указать направление тока во всех ее участках, то она является простой, К сложным
электрическим цепям относятся такие цепа, которые не удовлетворяют условиям простой цепи.
Расчет простых целей, проводится двумя методами: методом свертывания схемы (определение
входного или эквивалентного сопротивления) и методом пропорциональных величин.
При расчете сложных цепей используются метод непосредственного применения законов
Кирхгофа, методы контурных токов (ячеек), суперпозиции (наложения), узлового напряжения (если
в схеме имеется два узла) и эквивалентного генератора (для нахождения тока в одной из ветвей
схемы).
В большинстве случаев при расчете электрических цепей известными (заданными)
величинами являются электродвижущие силы (э. д. с.), напряжения или токи источников
электрической энергии и сопротивления, неизвестными (рассчитываемыми) величинами являются
токи и напряжения приемников.
Расчет простых электрических цепей постоянного тока
Рассмотрим электрическую цепь, изображенную на рис. 1. Пусть известны величины
сопротивлений резисторов r1 , r2 , r3 , r4 , r5 , r6 , э. д. с. E и ее внутреннее сопротивление r0 . Требуется
определить токи во всех участках цепи и напряжение, которое покажет вольтметр (сопротивление
его бесконечно велико), включенный между точками схемы a и d .
Такие задачи решаются методом свертывания схемы, по которому отдельные участки схемы
упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному)
сопротивлению относительно зажимов источника питания. Схема упрощается с помощью замены
группы последовательно или параллельно соединенных сопротивлений одним эквивалентным
сопротивлением. Так, сопротивления r4 и r5 соединены последовательно и их эквивалентное
сопротивление
r45  r4  r5
Сопротивления r45 и r6 соединены параллельно и, следовательно, их эквивалентное
сопротивление
r456 
r45  r6
r45  r6
Рис. 1 Рис. 2
После произведенных преобразований цепь принимает вид, показанный на рис. 2, а
эквивалентное сопротивление всей цепи найдем из уравнения
rэкв  r0  r1 
r2 r3  r456 
r2  r3  r456
Ток I 1 в неразветвленной части схемы определим по закону Ома:
I1  E rэкв
Воспользовавшись схемой на рис. 2, найдем токи I 2 и I 3 :
I 2  I1 
r3  r456
r2
; I 3  I1 
.
r2  r3  r456
r2  r3  r456
Переходя к рис. 1, определим токи I 4 ; I 5 и I 6 по аналогичным уравнениям:
I4  I5  I3 
r6
r4  r5
; I6  I3 
r4  r5  r6
r4  r5  r6
Зная ток I 1 можно найти ток I 2 другим способом. Согласно второму закону Кирхгофа,
U ab  E  (r0  r1 ) I1 тогда
I 2  U ab r2
Показание вольтметра можно определить, составив уравнение по второму закону Кирхгофа,
например, для контура acdc :
r3 I 3  r4 I 4  U ad .
Для проверки решения можно воспользоваться первым законом Кирхгофа и уравнением
баланса мощностей, которые для схемы, изображенной на рис. 1, примут вид
I1  I 2  I 3 ; I 3  I 4  I 6
EI1  r0  r1 I12  r2 I 22  r3 I 32  r4  r5 I 42  r6 I 62
Простые электрические цепи можно рассчитывать методом подобия (метод
пропорциональных величин), который применим только для расчета линейных цепей, т. е. цепей с
неизменными величинами сопротивлений. Воспользуемся свойством линейных цепей для
определения токов схемы, изображенной на рис. 1, в следующей последовательности. Задаемся
произвольным значением тока I 6 ' в сопротивлении r6 , наиболее удаленном от источника
питания. По заданному I 6 ' и сопротивлению определяем напряжение U 'cb :
U cb'  r6 I 6'
Далее определяем:
U cb'
'
'
'
 r3 I 3' ; U ab
 U ac
 U cb'
I I 
; I 3'  I 4'  I 6' ; U ac
r4  r5
'
4
'
5
'
I 2'  U ab
r2 ; I 1'  I 2'  I 3'
Наконец, находим величину э. д. с. E ' :
E '  r0  r1 I 1'  r2 I 2'
Рис. 3
Однако найденное значение э. д. с. E ' в общем случае отличается от заданной величины э. д.
с. E . Поэтому для определения действительных значений токов и напряжений вычисляем так
называемый коэффициент подобия K  E / E' . Умножив на него полученные при расчете
значения токов и напряжении, находим действительное значение токов схемы. Метод
пропорциональных величин особенно эффективен при расчете разветвленных линейных
электрических цепей с одним источником.
Рассмотрим электрическую цепь, изображенную на рис. 3. К источнику тока I  0,1A
подключены резисторы с сопротивлениями r1  r2Oм,
r2  10Ом, r3  16Ом, r4  40Ом,
r5  60Ом . Определить напряжение U ab источника тока и все токи. Составить баланс
мощностей. Задача решается методом свертывания схемы.
Находим входное сопротивление rab схемы относительно зажимов источника тока:

rr 
40  60 

r2  r3  4 5 
1016 

r4  r5 
100 


rab  r1 
 12 
 20 Ом
r4 r5
40  60
10  16 
r2  r3 
100
r4  r5
Находим напряжение на зажимал источника тока U ab :
U ab  rab I  20  0,1  2 В
По закону Ома находим ток I 2 :
I2 
U ab  r1 I 2  0,1 12

 0,08 А
r2
10
Ток I 3 определяем из уравнения первого закона Кирхгофа:
I 3  I  I 2  0,1  0,08  0,02 А
Этот ток распределяется обратно пропорционально сопротивлениям r4 и r5 :
I4  I3
r5
r
 0,012 А; I 5  I 3 4  0,008 А.
r4  r5
r4  r5
Уравнение баланса мощностей отражает равенство мощностей, отдаваемой источником и
расходуемой приемниками, т. е.
U ab I  r1 I 2  r2 I 22  r3 I 32  r4 I 42  r5 I 52  2  0,1 
 0,12 12  0,08 2 10  0,02 2 16  0,012 2  40  0,008 2  60  0,2 Вт
Следовательно,
PИ  PН  0,2Вт
Методы общего анализа линейных электрических цепей
Важным вопросом этого раздела является расчет распределения токов в сложных линейных
цепях с несколькими источниками. Классическим методом расчета таких цепей является
непосредственное применение законов Кирхгофа. Все остальные методы расчета исходят из этих
фундаментальных законов электротехники.
Рассмотрим сложную электрическую цепь (рис. 4), которая содержит 6 ветвей. Если будут
заданы величины всех э. д. с. и сопротивлений, а по условию задачи требуется определить токи в
ветвях, то мы будем иметь задачу с шестью неизвестными. Такие задачи решаются при помощи
законов Кирхгофа. В этом случае должно быть составлено столько уравнений, сколько
неизвестных токов.
Порядок расчета:
1. Если цепь содержит последовательные и параллельные соединения, ее упрощают, заменяя
эти соединения эквивалентными.
2. Произвольно указывают направления токов во всех ветвях. Если принятое направление
тока не совпадает с действительным, то при расчете такие токи получаются со знаком «минус».
3. Составляют (n—1) уравнений по первому закону Кирхгофа (n—число узлов).
4. Недостающие уравнения составляют по второму закону Кирхгофа, при этом обход
контура можно производить как по часовой стрелке, так и против нее. За положительные э.д.с. и
токи принимаются такие, направление которых совпадает с направлением обхода контура.
Направление действия э. д. с. внутри источника всегда принимают от минуса к плюсу (см. рис.4).
Рис. 4 Рис. 5
5. Полученную систему уравнений решают относительно неизвестных токов. Составим
расчетные уравнения для электрической цепи изображенной на рис. 4. Выбрав произвольно
направление токов в ветвях цели, составляем уравнения по первому закону Кирхгофа для узлов a ,
b и c.
I 1  I 2  I 3  0

I 5  I1  I 4
 (1)
I4  I2  I6 

Приняв направление обхода контуров по часовой стрелке, составляем уравнении но второму
закону Кирхгофа для трех произвольно выбранных контуров:
для контура adkba
E1  r1 I1  r3 I 3  r01 I 5 (2)
для контура bacldkb
E1  E2  r1 I1  r2 I 2  r01 I 5  r02 I 6 (3)
для контура bmncab
0  r1 I1  r2 I 2  r4 I 4 (4)
Решая совместно уравнения (1), (2), (3) и ( 4), определяем токи в ветвях электрической
цепи.
Легко заметить, что решение полученной системы из шести уравнений является весьма
трудоемкой операцией. Поэтому при расчете сложных электрических цепей целесообразно
применить метод контурных токов (метод ячеек), который позволяет уменьшить число уравнений,
составляемых по двум законам Кирхгофа, на число уравнений, записанных по первому закону
Кирхгофа. Следовательно, число уравнений, составляемых по методу контурных токов, равно
m  n  1. При решении методом контурных токов количество уравнений определяется числом
ячеек. Ячейкой будем называть такой контур, внутри которого отсутствуют ветви. B нашем
случае таких контуров-ячеек три:
badkb , aclda и mncabm .
Расчет сложных электрических цепей методом контурных токов ведется следующим
образом:
1.Вводя понятие «контурный ток», произвольно задаемся направлением этих токов в
ячейках. Удобнее все токи указать в одном направлении, например по часовой стрелке (рис.5).
2.Составляем для каждого контура-ячейки уравнение по второму закону Кирхгофа. Обход
контуров производим по часовой стрелке:
первый контур:
E1  r01  r1  r3 I k1  r3 I k 2  r1 I k 3 (5)
второй контур:
 E1  r3 I k1  r02  r2  r3 I k 2  r2 I k 3 (6)
третий контур:
0  r1 I k1  r2 I k 2  r1  r2  r4 I k 3 (7)
3.Решая совместно уравнения (5), (6), (7) , определяем контурные токи. В том случае когда
контурный ток получается со знаком «минус», это означает, что его направление противоположно
выбранному на схеме.
4.Токи во внутренних ветвях схемы определяются как сумма или разность соответствующих
контурных токов. В том случае, когда контурные токи в ветви совпадают, берут сумму, а когда
направлены навстречу — из большого тока вычитают меньший.
5.Токи во внешних ветвях схемы равны по величине соответствующим контурным токам.
Задача1. Рассчитать сложную цепь постоянного тока для схемы, изображенной на рис. 5,
Задано: E1  100B , E2  120B , r01  r02  0,5Ом , r1  5Ом , r2  10Ом , r3  2Ом , r4  10Ом .
Определить токи в ветвях цепи.
Решение. Используя уравнения (5), (6) и (7 ) , получаем:
100  7,5I k1  2 I k 2  5I k 3 ,


 120  2 I k1  12,5I k 2  10 I k 3 ,

0  5I k1  10 I k 2  25I k 3 .

Выразив I k 3 через I k1 и I k 2 :
Ik3 
5
10
I k1 
Ik2
25
25
и произведя соответствующие подстановка, получаем:
100  6,5I k1  4 I k 2 ,


 120  4 I k1  8,5I k 2 
Совместное решение полученных уравнений дает:
I k1  5,2 А; I k 2  33,5 А; I k 3  14,4 А.
Определяем токи в ветвях:
I1  I k1  I k 3  5,2  14,4  9,2 А; I 2  I k 3  I k 2  14,4  33,5  19,1 А;
I 3  I k1  I k 2  5,2  33,5  28,3 А; I 4   I k 3  14,4 А;
I 5   I k1  5,2 А; I 6   I k 2  33,5 А.
Задача 2. Определить токи и составить баланс мощностей для схемы, изображенной на рис.
6. Дано: I  50 мА , E  60В , r1  5кОм , r2  4кОм , r3  16кОм , r4  2кОм , r5  8кОм .
Решение. Схема содержит шесть ветвей (m  6) и четыре узла ( n  4) . Число уравнений,
составляемых по методу контурных токов, равно m  n  1  1  2 , так как в схеме имеется
источник тока, ток которого может быть принят равным контурному току. Зададимся
произвольным направлением контурных токов I k1 и I k 2 , как показано на рис.6. Там же нанесён
известный контурный ток источника тока I . Составим систему уравнений для первого и второго
контуров:
Рис. 6
r1  r2  r5 I k1  r5 I k 2  r1 I  E,

r5 I k1  (r3  r4  r5 ) I k 2  r3 I  0.
Подставляя числовые значения и решая эти уравнения, найдем контурные токи:
I k1  30 мА; I k 2  40 мА.
Искомые токи будут равны:
I1  I  I k1  20 мА; I 2   I k1  30 мА;
I 3  I  I k 2  10 мА; I 4  I k 2  40 мА;
I 5  I k1  I k 2  10 мА.
Составляем баланс мощностей:
PИ   EI 2  U cd I   EI 2  r1 I1  r3 I 3 I ;
PН  r1 I 12  r2 I 22  r3 I 32  r4 I 42  r5 I 52
Подставляя числовые значения, получим: Pu  Pн  11,2 Вт.
Метод наложения, основанный на принципе суперпозиции, позволяет свести расчет
разветвленной цепи с несколькими источниками к нескольким расчетам этой же цепи, но с одним
источником. Порядок расчета:
1.Поочередно рассматривают действие в цепи только одного источника, а все остальные
источники исключаются (остаются только их внутренние сопротивления).
2.Рассчитывают токи в ветвях от действия каждого источника,
3.Алгебраическим суммированием находят токи в ветвях от действия каждого источника; в
отдельности.
Метод является особенно эффективным при расчете токов от изменения величины только
одного источника.
На практике часто используются цепи, в которых параллельно включены несколько
источников энергии и приемных устройств. Такие цепи удобно анализировать с помощью метода
узлового напряжения (напряжения между двумя узлами).
Рис. 7 Рис. 8
Задача. Найти токи цепи (рис.7) и показание вольтметра, если r1  r2  r3  r4  10Ом .
Р е ш е н и е . Изобразим схему в ином виде (рис. 8): E1  20B , E2  18B , E3  10 B .
Найдем узловое напряжение U ab (показание вольтметра):
U ab 
g1 E1  g 2 E2  g 3 E3 0,1  20  0,1 18  0,1 10

 3 В.
g1  g 2  g 3  g 4
0,4
Токи в ветвях определяются но закону Ома:
I1 
E1  U ab
E  U ab
 1,7 А; I 2  2
 2,1 А;
r1
r2
I3 
E3  U ab
U
 0,7 А; I 4  ab  0,3 А.
r3
r4
Частичный анализ электрических цепей. Метод эквивалентного
генератора
На практике часто бывает необходимо изучить режим работы только одной из ветвей
сложной электрической схемы. При этом не следует возводить громоздкий расчет всей схемы, а
целесообразно воспользоваться методом эквивалентного генератора. Соваться методом
эквивалентного генератора. Согласно этому методу воздействие всех источников сложной
электрической цепи на исследуемую ветвь можно заменить воздействием последоватёльно
включённого с ветвью эквивалентного источника (генератора), имеющего э. д. с. E э , равную
напряжению холостого хода U x на зажимах разомкнутой исследуемой ветви, и внутреннее
сопротивление rэ , равное входному сопротивлению схемы со стороны зажимов исследуемой
ветви.
Порядок расчета:
1.Произвольно выбирают направление тока в исследуемой ветви.
2.Отключают исследуемую ветвь, осуществляя режим холостого хода.
3.Определяют напряжение холостого хода U x на зажимах разомкнутой ветви.
Рис. 9 Рис. 10
4.Находят входное (эквивалентное) сопротивление схемы со стороны зажимов разомкнутой
ветви.
5.В общем случае находят ток и исследуемой ветви по выражению
I
Uх  E
(8)
rэ  r
где r — сопротивление ветви, в которой определяется ток; rэ — входное сопротивление
схемы со стороны зажимов выделенной ветви; U x — напряжение холостого хода на зажимах
разомкнутой выделенной ветви; E — э. д. с, находящаяся и исследуемой ветви. Если ветвь не
содержит э. д. с, то она принимается равной нулю.
Знаки «плюс» или «минус» выбираются в соответствии с законом Ома для ветви с
источником, т. е., если направление э. д. с. совпадает с направлением тока, то берется знак «плюс»,
в противном случае — знак «минус».
Рассмотрим применение
изображенной на рис. 9.
метода
эквивалентного
генератора
на
примере
схемы,
Задача. Определить ток в ветви bc , если E2  E3  E4  20 B , E5  30B , E6  60B ,
r1  r2  r3  r4  2Ом , r5  3Ом , r6  6Ом .
Решение задачи распадается на два этапа.
1.Определение напряжения холостого хода U xbc
на зажимах разомкнутой ветви bc . Схема в этом случае имеет вид, показанный на рис.10.
Для нахождения U xbc следует найти ток I 1 и напряжение U ac :
I1 
E2
20

 5 А.
r1  r2 2  2
Напряжение Uac находим по формуле узлового напряжения:
1
1
1
30   20   60 
g E  g 4 E 4  g 6 E6
3
2
6  10 B
U ac  5 5

1
1
1
g 4  g5  g6
 
2 3 6
U xbc найдем по второму закону Кирхгофа, обходя контур bacb :
U хbc  r1 I1  U ac  2  5  10  0
2.Определение эквивалентного сопротивления rэbc . Схема в этом случае имеет вид,
показанный на рис. 11:
rэbc 
r1 r2
1
22
1



 2 Ом.
r1  r2 1 1 1 2  2 1 1 1
 
 
r4 r5 r6
2 3 6
Рис. 11
Подставляя найденные величины в (8), получим:
I bc 
0  20
 5 А.
22
т. е. истинный ток в схеме имеет направление, противоположное выбранному.
Метод эквивалентного генератора находит применение при расчете нелинейных цепей
постоянного тока с одним нелинейным элементом. Например, широко распространены мостовые
схемы измерения неэлектрических величин электрическими методами, в которых с помощью
нелинейного элемента (преобразователя), включенного в одно из плеч или диагональ мостовой
схемы, происходит преобразование неэлектрического воздействия в электрический сигнал (ток
или напряжение), который фиксируется измерительным прибором.
При расчете нелинейных цепей постоянного тока также используется метод свертывания,
который сводится к графическому определению результирующей вольт-амперной характеристики
нескольких нелинейных элементов, и метод пересечения характеристик, когда к источнику
напряжения подключено не более двух резистивных элементов.
Электрические цепи переменного тока
Однофазные цепи
В результате изучения данного раздела студенты должны:
1)знать содержание терминов: резистор, сопротивление, индуктивная катушка,
индуктивность, индуктивное сопротивление, конденсатор, емкость, емкостное сопротивление,
фаза, начальная фаза, угол сдвига фазы, период, частота, угловая частота мгновенное,
действующее и среднее значения гармонических величин, полное, активное, реактивное,
комплексное сопротивления и проводимость; полная, активная, реактивная, комплексная
мощность; характеристики и параметры элементов схем замещения цепей однофазного тока;
условия достижения резонансов напряжении, и токов;
2)понимать особенности электромагнитных процессов в электрических цепях
синусоидального тока, энергетические соотношения в цепях синусоидального тока,
экономическое значение коэффициента мощности; особенности простейших электрических цепей
с магнито-связанкыми элементами;
3)уметь составлять дифференциальные и комплексные уравнения состояния линейных
цепей; представлять гармонически изменяющиеся величины тригонометрическими функциями,
графиками, изображающими величинами и комплексными числами; строить векторные
диаграммы неразветвленных цепей и цепей с параллельным соединением ветвей; определять
опытным путем параметры схем замещения пассивных двухполюсников; с помощью
электроизмерительных приборов измерять токи, напряжения и мощности в электрических цепях;
строить потенциальные (топографические) диаграммы для неразветвленных цепей и цепей с
параллельным соединением ветвей.
При изучении явлений резонанса в цепях переменного тока необходимо знать условия их
возникновения, а также обратить внимание на практическое применение резонанса токов для
искусственного повышения коэффициента мощности в промышленных электроустановках. В то
же время возникновение резонанса напряжений в электрических устройствах может представлять
опасность как для самих устройств, так и для обслуживающего персонала.
Изучая явления резонанса, необходимо усвоить следующее. При резонансе напряжение и ток
на зажимах цепи всегда совпадает по фазе. Настройка же цепи на резонанс зависит от схемы
соединений индуктивности и емкости. Для последовательной цепи условием резонанса является
равенство индуктивного и емкостного сопротивлений: x L  xC . Для цепи, содержащей
параллельный контур, в одной из ветвей которого находится индуктивность, а в другой —
емкость, условием резонанса является равенство реактивных проводимостей ветвей: bL  hC .
При расчете цепей синусоидального тока приходится совершать различные математические
операции, которые удобно производить над действующими значениями токов и напряжений,
рассматривая их как векторы. Величины векторов при этом равны действующим значениям тока и
напряжения, а начальная фаза определяет положение вектора относительно положительной
горизонтальной оси координат. При положительной (опережающей) начальной фазе вектор
повернут на соответствующий угол против движения часовой стрелки, а при отрицательной
(отстающей)— по направлению движения часовой стрелки. Совокупность векторов,
изображающих синусоидальные э. д. с, напряжения и токи одной частоты, выходящих из общей
точки, называют векторной диаграммой.
Для цепей синусоидального тока обычно строят потенциальную (топографическую)
диаграмму, каждая точка которой соответствует определенной точке электрической цепи. Чтобы
осуществить это соответствие точек диаграммы и цепи, построение потенциальной диаграммы
ведут в той же последовательности, в какой обходят электрическую цепь. Обычно направление
обхода выбирают противоположный принятому направлению тока в цепь. Для наглядности в
некоторых случаях векторные и потенциальные диаграммы объединяют в одну. Необходимо
обратить особое внимание на направление векторов на потенциальных диаграммах. Векторы
напряжений направлены относительно точек потенциальной диаграммы противоположно
положительным направлениям напряжений относительно соответствующих точек цепи. Ценность
потенциальной диаграммы состоит в том что она позволяет определять напряжения между
любыми точками цепи. Для этого следует соединить соответствующие точки потенциальной
диаграммы отрезком прямой и придать этому отрезку соответствующее направление.
При помощи потенциальной диаграммы удобно производить сложение напряжений,
возникающих на отдельных участках последовательной цепи (второй закон Кирхгофа), и
сложение токов, протекающих в ветвях параллельной цепи (первый закон Кирхгофа).
При построении векторных диаграмм одни из векторов принимают за основной (опорный),
располагая его обычно по положительному направлению горизонтальной оси. В этом случае
начальная фаза тока или напряжения в зависимости от того, что данный вектор изображает, равна
нулю. Для последовательной цепи за основной вектор принимают вектор тока, а для параллельной
— вектор напряжения.
На рис. 12 показаны последовательная цепь (рис. 12,а) и ее векторная (рис. 12,б) и
потенциальная (рис. 12, в) диаграммы. На рис. 13 в той. же последовательности, что- и на рис. 12,
показана параллельная цепь и ее векторная и потенциальная диаграммы.
В том случае, когда сложение или вычитание вектора требуется производить не графически,
а математически (например, при расчете электрической цепи), векторы раскладывают на две
составляющие, одна из которых называется активной, а вторая — реактивной. Активной
составляющей напряжения является та, которая совпадает по фазе c током, а реактивная —
которая опережает ток или отстает от него по фазе на 90°. .Активной составляющей тока является
та, которая совпадает по фазе с напряжением, а реактивной — которая опережает напряжение пли
отстает от него по фазе на 90°. Зная сдвиг фаз между током и напряжением и величины векторов
тока и напряжения, легко определить соответствующие составляющие этих векторов. Например,
если нам задан синусоидально изменяющийся ток уравнением вида i  Im sin( wt   ) , то его
активная и реактивная составляющие для действующего значения будут соответственно равны:
I а  I cos , I р  I sin 
где I  I m
2
Аналогично для напряжении:
U а  U cos  ; U р  U sin  .
На диаграмме, изображенной на рис. 13,б, показаны активные
и реактивные составляющие токов.
Рис. 12
Рис. 13
В том случае, когда необходимо произвести сложение двух или более векторов,
выражающих собой токи или напряжения, определяют их активные и реактивные составляющие и
модуль результирующего вектора:
I
 I    I   I 
2
2
а
L
c
;U 
U   U  U 
2
2
а
L
c
,

где индексы L и С указывают на характер реактивной составляющей (индуктивности или
емкость). Начальная фаза результирующего вектора определяется через tg: 
tg 
I
L
  IC
I
а

U  U
U
L
C
а
Для практических расчетов удобнее выражать векторы тока и напряжения, а также
сопротивления и проводимости комплексными числами, в которых активные составляющие
являются действительными величинами, а реактивные — мнимыми. Причем знак у мнимой
величины зависит от характера активной составляющей. При расчете электрических цепей
переменного тока с помощью комплексных чисел могут быть использованы методы расчета,
применяемые для цепей постоянного тока. Уравнения Кирхгофа в этом случае записываются как
составляющие геометрические суммы.
При выполнении расчетов по методу комплексных чисел следует иметь в виду, что
вещественная и мнимая части комплексного сопротивления, комплексной проводимости и
комплексной мощности всегда представляют собой соответственно активную и реактивную
составляющие этих величин; что же касается комплексного напряжения и комплексного тока, что
такое положение имеет место, лишь в частных случаях. Вещественная и мнимая части
комплексного напряжения и комплексного тока определяются начальными фазами величии, иначе
говоря, зависят от расположения соответствующих векторов относительно осей комплексной
плоскости, тогда как их активная и реактивная составляющие определяются углом сдвига по фазе
 между этими двумя векторами,
При анализе магнитосвязанных электрических цепей необходимо иметь в виду, что при
составлении уравнения по второму закону Кирхгофа, при учете напряжения от взаимоиндукции
сравнивается направление обхода рассматриваемой катушки и направление тока во влияющей на
нес катушке относительно одноименных зажимов катушек. Если эти направления совпадают, то
напряжение взаимоиндукции учитывается в уравнении со знаком плюс, в противном случае — с
минусом.
Задача 1. Рассчитать электрическую цепь синусоидального тока со смешанным соединением
приемников.
Для схемы, изображенной на рис. 13,г (на рис. 13,г ток i2 направлен по часовой стрелке, ток
i3 — против часовой стрелки), известно, что
U  120B , r1  10Ом , r2  24Ом , r3  15Ом ,
L1  19,1мГ , L3  63,5 мГ , С2  455 мкФ , f  50 Гц .
Определить токи I1 , I 2 , I 3 о ветвях цепи, напряжения па участках цепи U ab , U bc
активную, реактивную и полную мощности и построить векторную диаграмму.
Решение. Выражаем сопротивления ветвей цепи в комплексной форме:
Z  r  jx  ze  j
Z1  r1  jL1  10  j 2  50 19,1 10 3  10  j 6 Ом.
Переходя от алгебраической формы записи комплексного числа к показательной, получаем:
Z1  z1e j1  11,6e j 31 Ом,
где z1  r12  L1  ; tg1 
2
Z 2  r2  j
L1
r1
1
10 0
 24  j
 24  j 7Ом  25e  j1615' Ом ;
C2
2  50  455
Z 3  r3  jL3  15  j 2  50  63,5  10 3  15  j 20Ом  25e j 5305' Ом
Рис. 14
Выражаем заданное напряжение U в комплексной форме. Если начальная фаза напряжения
не задана, то ее можно принять равной нулю и располагать вектор напряжения совпадающим с
положительным и направлением действительной оси. В этом случае мнимая составляющая
комплексного числа будет отсутствовать (рис. 14):
U =U = 120 В.
Полное комплексное сопротивление цепи
Z2Z3

24  j 7 15  j 20
25e  j1615'  25e j 5310'
Z  Z1 
 10  j 6 
 10  j 6 

Z2  Z3
39  j13
41e j1825'
 24,4  j10,8  26,7e j 2355' Ом
Определяем ток I1 в неразветвленной части цепи:
U
120
I1  
 4,5e  j 2355' А.
j 2355'
Z 26,7e
Токи I 2 и I 3 в параллельных ветвях могут быть выражены через ток в неразветвленной
части цепи:
I2  I1
Z3
15  j 20
 4,5e  j 2355' 
 2,74e j1045' А;
Z 2  Z3
39  j13
I3  I1
Z2
24  j 7
 4,5e  j 2355' 
 2,74e  j 5635' А.
Z 2  Z3
39  j13
Токи I 2 и I 3 можно найти и по-другому:
24  j 7 15  j 20  4,5e  j 2355'  68,4e  j 530' В;
Z Z
U bc  Z bc I1  2 3 I1 
Z 2  Z3
39  j13
U
68,4e  j 530'
I2  bc 
 2,74e j1045' А;
 j1615'
Z2
25e
U
68,4e  j 530'
I3  bc 
 2,74e  j 5835' А.
Z3
25e j 5305'
Найдем мощности всей цепи и отдельных ее ветвей:

~
S  U I  120  4,5e j 2355'  540e j 2355' В  А
Для определения активной и реактивной мощностей полную мощность, выраженную
комплексным числом в показательной форме, переводим в алгебраическую форму. Тогда
действительная часть комплекса будет представлять собой активную мощность, а мнимая —
реактивную:
~
S  540 cos 2355' j 540 sin 2355'  494  j 218В  А ,
откуда
P  494 Вт; Q  218 вар.
Активную и реактивную мощности можно найти и по-другому:


 
P  Re U I1   Re 120  4,5e j 2355'  120  4,5 cos 2355'  494 Вт;


P1  r1I12  10  4,52  202 Вт; P2  r2 I 22  180 Вт;
P3  r3 I 32  112 Вт.
Проверка показывает, что P  P1  P2  P3 .


 
Q  Im U I1   Im 120  4,5e j 2355'  120  4,5 sin 2355'  218 вар;


Q1  x1I12  6  4,52  122 вар; Q2  x2 I 22  52,5 вар;
Q3  x3 I 32  150 вар.
Учитывая, что Q1 и Q3 положительны (реактивная мощность индуктивных катушек), a Q2
отрицательно (реактивная мощность конденсатора), получим Q  Q1  Q2  Q3  218вар .
На рис.15 приведена векторная диаграмма токов и напряжений, построенная но расчетным
данным. Порядок ее построения следующий: по результатам расчетов отложены векторы токов I 1
I 2 и I 3 затем по направлению I1 отложен вектор r1 I1 и перпендикулярно к нему в сторону
опережения — вектор jxI1 . Их сумма дает вектор Z1 I1 . Далее в фазе с I 2 построен вектор r2 I 2 и
перпендикулярно к нему в сторону отставания вектор jx2 I 2 , а их сумма даст вектор напряжения
на параллельном участке U bc . Тот же вектор может быть получен, если в фазе с I 3 отложить. r3 I 3
и к нему прибавить вектор jx3 I 3 , опережающий I 3 на 90°. Сумма векторов Z1 I1 и U bc дает
вектор приложенного напряжения U .
Рис. 15
Рис.16
Задача2. Определить эквивалентное комплексное сопротивление цепи (рис.16,а), ток и
напряжение между точками a и b , c и d , если U  130B , r1  2Ом , r2  3Ом , wL1  3Ом ,
wL2  7Ом , wM  1Ом .
Р е ш е н и е . Из рис.16,а следует, что при заданном направлении тока в каждой катушке
потоки самоиндукции и взаимной индукции одинаково направлены, Следовательно, катушки
включены согласно. Заданная Цепь может быть представлена схемой замещения, показанной на
рис.16,б. Составим для нее уравнение по второму закону Кирхгофа:
U  r1 I  jL1 I  jMI  r2 I  jL2 I  jMI .
Эквивалентное комплексное сопротивление цепи
Z  r1  jL1  r2  jL2  2 jM  5  j12  13e j 6720' Ом.
Искомый ток
I  U Z  130 13e j 6720'  10e  j 6720' А.
Комплексные напряжения между точками а и b, с и d равны:
U ab  r1  jL1  jM I  2  j 4  10e  j 6720'  44,7e  j 350' В;
U cd  r2  jL 2  jM I  3  j8  10e  j 6720'  85,5e j 205' В.
На рис, 16,в. представлена векторная диаграмма. По действительной оси отложен вектор
напряжения, от него в сторону отставания на 67°20' направлен вектор тока, затем отложены
векторы падения напряжения в каждой из катушек.
Трехфазные цепи
При изучении трехфазных цепей особое внимание необходимо обратить на преимущества,
которые дает трехфазная система по сравнению с однофазной. Рассматривая схемы соединения
обмоток генераторов, надо уяснить связь между фазными и линейными напряжениями в схеме
соединения звездой, а также связь между фазными и линейными токами в схеме соединения
треугольником.
Необходимо четко представить, что в трехфазной цепи могут быть два режима:
симметричный и несимметричный. Расчет трехфазной, цепи в симметричном режиме сводится к
расчету для одной фазы и производится аналогично расчету обычной цепи однофазного тока.
Трехфазная цепь может, рассматриваться как разветвленная цепь с тремя источниками питания и
для ее расчета применяются методы, используемые при расчете сложных электрических цепей.
Например, если несимметричный приемник соединен звездой без нейтрального провода, то для
расчета трехфазной цепи можно применить метод узлового напряжения в комплексной форме.
После изучения настоящего раздела студенты должны:
1)знать основные элементы трехфазных цепей, способы соединения фаз обмотки генератора
а включения в трехфазную цепь приемников; способы изображения трехфазной симметричной
системы
э. д. с;
2)понимать роль нейтрального провода; принципы построения потенциальных диаграмм;
влияние рода и схемы включения нагрузки на величину тока в нейтральном проводе; схемы
электроснабжения предприятий;
3)уметь анализировать различные режимы симметричных и не симметричных цепей; читать
схемы соединения трехфазных и одно фазных приемников; предвидеть последствия
коммутационных изменений в цепи на ее электрическое состояние.
Задача1. В трехфазную сеть с линейным напряжением U Л  220B включен приемник,
соединенный треугольником, сопротивление каждой фазы которого Z  (10  j10)Ом (рис. 17).
Найти токи в каждой фазе нагрузки и ляпни и показания каждого ваттметра. Построить,
векторную диаграмму. Найти те же величины в случае обрыва цепи в точке d.
Решение. Расчет токов в трехфазных целях производится комплексным методом. Примем,
что вектор линейного напряжения U AB направлен по действительной оси, тогда
U AB  U ab  220 В; U BC  U bc  220e  j120 В;
U CA  U ca  220e j120 В.
Рис. 17
Определяем фазные токи:
U
220
Iab  ab 
 15,6e  j 45  11  j11 А;
Z
10  j10
U
220e  j120
Ibc  bc 
 15,6e  j165  15  j 4,03 А;
Z
10  j10
U
220e j120
Ica  ca 
 15,6e j 75  4,03  j15 А.
Z
10  j10
Находим линейные токи:
IA  Iab  Ica  6,97  j 26  26,9e  j 75 А;
IB  Ibc  Iab  26  j 6,97  26,9e j165 А;
IC  Ica  Ibc  19  j19  26,9e j 45 А.
Определим, показания ваттметров:





P1  Re U AB I A   Re 220  26,9e j 75  220  26,9 cos 75  1530 Вт;









P2  Re U CB I C   Re  220e  j120  26,9e  j 45  Re 220e j 60  26,9e  j 45 


 220  26,9 cos15  5730Вт.
Активная мощность цепи (алгебраическая сумма показаний ваттметров) P равна:
P  P1  P2  1530  5730  7260Вт ,
или
P  3U Л I Л cos  3  220  26,9 cos 45  3rI Ф2  7260Вт .
Рис. 18
На рис. 18 приводится векторная диаграмма напряжений и ков. При обрыве в точке 4; тока в
фазах нагрузки будут:
 j120

I  U bc  220e
 15  j 4,03
bc
Z
10  j10
U
220e  j120
Iab  I ca  cb  
 7,5  j 2,02 A
2Z
2(10  j10)
Вычислим линейные токи:
IA  0 ; I   I  I  I  22,5  j 6,05  23,3e j15 A .
C
B
ca
bc
Находим показания ваттметров:



P1  0 ; P2  Re U CB I C   Re 220e j 60  23,3e  j15   220  23,3 cos 45  3630Вт.


Задача 2. В четырехпроводную трехфазную сеть с линейным, напряжением U Л  220B
включен звездой приемник, активные и индуктивные сопротивления фаз которого соответственно
равны: ra  3Ом , ха  4Ом , rb  3Ом , xb  5,2Ом , rc  4Ом , хс  3Ом (рис.19). Определить
токи в линейных и нейтральном проводах и построить векторную диаграмму.
Решение. Считаем, что вектор фазного напряжения U a направлен по действительной оси,
тогда
U a  U Л
3  127 В, U b  127e  j120 В, U c  127e j120 В.
Рис. 19 Рис. 20
Находим линейные токи:
U
127
127
Ia  a 
 j 53  25,4e  j 53 А;
Z a 3  j 4 5e
U
127e  j120 127e  j120
Ib  b 

 21,2e  j180 А;
j 60
Zb
3  j 5,2
6e
j120

127e j120
I  U c  127e

 25,4e j 83 А.
c
j 37
Zc
4  j3
5e
Ток в нейтральном проводе определяется как геометрическая сумма линейных токов:
IN  Ia  Ib  Ic  25,4e  j 53  21,2e  j180  25,4e j 83  5,9e j124 А.
Векторная диаграмма показана на рис.20.
При несимметричной нагрузке для определения активной мощности находят мощность
каждой фазы отдельно:
PФ  U Ф I Ф cos  ,
а мощность всей трехфазной системы получают как сумму мощностей всех фаз или
используют схему включения двух ваттметров.
Задача 3. В трехфазную сеть с линейным напряжением U Л  380B включен звездой
приемник;
активное, индуктивное
r  xL  xC  22Ом (рис. 21).
и
емкостное
сопротивление
фаз
которого
равны:
Рис. 21 Рис. 22
Р е ш е н и е . Расчет токов производит комплексным методом. Находим фазные напряжения:
UФ  U Л
3  380 1,73  220 В;
U a  220 В; U b  220e  j120   110  j191 В;
U c  220e j120   110  j191 В.
Определяем напряжение между нейтральными точками приемника и источника питания:
U nN
1
1
1
 220  j  110  j191  j  110  j191
YaU a  YbU b  YcU c 22
22
22


 602 В.
1
1
1
Ya  Yb  Yc
j
j
22
22
22
Определяем напряжения на зажимах фаз приемника:
U an  220  602  382 В;
U bn   110  j191  602   712  j191 В;
U cn   110  j191  602   712  j191 В.
Определяем фазные (линейные) токи:
Ia  U an r   382 22  17,3
А;
U
 712  j191
Ib  bn 
 8,68  j32,4
 jxC
 j 22
А;
U
 712  j191
Ic  cn 
 8,68  j32,4
jxL
j 22
А.
Векторная диаграмма изображена на рис. 22.
Для подсчета активной мощности в данной схеме можно воспользоваться уравнениями,
записанными для схемы включения двух ваттметров. Из рассмотрения этой задачи следует, что
напряжения на зажимах фаз приемника получаются неодинаковыми. Поэтому несимметричные
приемники (Оптовые и др.) соединяют либо четырехпроводной звездой, либо треугольником.
Переходные процессы в линейных электрических цепях
После изучения данного раздела студенты должны:
1)знать законы изменения токов и напряжений в простейших электрических цепях при
переходном процессе решение уравнений электрического состояния цепи при переходном
процессе;
2)понимать причины возникновения переходных процессов в электрических цепях; законы
коммутации; характер изменения токов и напряжений в электрических цепях при переходных
процессах; смысл и значение постоянной времени;
3)уметь составлять уравнения электрического состояния линейных электрических цепей при
переходных процессах; определять постоянную времени простейших электрических цепей;
определять закон изменения токов и напряжений в простейших линейных электрических цепях
при переходных процессах.
Переходный (неустановившийся) процесс возникает в электрической цепи как в результате
изменения параметров цепи, так и при негармоническом изменении величины приложенного
напряжения.
Изучая переходные процессы, мы определяем закономерности изменения тока и напряжения
в элементах электрических цепей в функции временя при переходе от одного установившегося
состояния к другому. Переход от одного установившегося состояния к другому сопровождается
изменением энергии магнитного поля в индуктивности WL  L
i2
и энергии электрического поля
2
u2
. Эти энергии не могут изменяться скачком, так как мощность, равная
2
dW
производной энергии по времени P 
, должна в этом случае достигнуть бесконечно
dt
в емкости WC  C
большого значения, что практически невозможно. Следовательно, если не могут скачком
изменяться энергии WL , и WC , то не могут изменяться скачком ток i в индуктивности L и
напряжение u на емкости C , что в обусловливает законы коммутации.
Для последовательной цели, содержащей r , L , и C , уравнение, составленное по второму
закону Кирхгофа, для мгновенных значений имеет следующий вид:
uL
di
1
 ri   idt (9)
dt
C
Это уравнение справедливо для любого момента времени, следовательно, оно справедливо
как для установившегося состояния так и для переходного процесса. Уравнение (9) является
неоднородным и его решение можно представить как сумму частного решения данного уравнения
и общего решения однородного уравнения, которое получается из основного уравнения путем
замены напряжения и нулем.
Решением уравнения для переходного процесса являются показательные и
тригонометрические функции, играющие главенствующую роль при исследовании переходных
процессов. Представим себе, что уравнение (9) рассматривается для установившегося состояния.
Назовем ток установившегося состояния «установившимся» током и будем обозначать через i yc .
тогда уравнение (9) примет вид
uL
di yc
dt
 ri yc 
1
i yc dt (10)
C
Вычитая уравнение (10) из уравнения (9), получаем
0L
d (i  i yc )
dt
 r (i  i yc ) 
1
(i  i yc )dt (11)
C
В полученном уравнении разность токов (i  i yc ) является ничем иным, как некоторым
током, который существует в электрической цепи только во время переходного процесса;
напряжение и равно нулю и ток (i  i yc ) существует как бы независимо от приложенного к цепи
внешнего напряжений. В силу сказанного этот ток называют «свободным» и обозначают через icb :
iСВ  i  iУС .
Откуда
i  iУС  iСВ . (11а)
Как показывает, выражение (11а), ток переходного процесса может быть получен как сумма
двух токов, одним из которых является, ток установившегося состояния i yc , определяемый как
частное решение дифференциального уравнения (9), а вторым — ток, который определяется как
общее решение соответствующего однородного уравнения.
Заменяя (i  i yc ) в уравнении (11) на icb , получаем однородное дифференциальное уравнение
для Определения свободного тока:
0L
diСВ
1
 riСВ   iСВ dt . (11б)
dt
C
Таким образом, для исследования переходного процесса в последовательной цепи
составляется дифференциальное уравнение описывающее переходный процесс (9), уравнение,
определяющее собой ток установившегося состояния (10), и однородное дифференциальное
уравнение для свободного тока (116).
Для решения однородного дифференциального уравнения свободного тока составляется
характеристическое уравнение, для чего однородное дифференциальное уравнение свободного
тока записывается в алгебраической форме путем замены производной
интеграла
 dt через 1 / p .
Произведя указанные операции над уравнением (116), получаем
0  pLiСВ  riСВ 
Вынося за скобку icb , получаем
1
iСВ .
pC
d
через оператор p , а
dt

1 
iСВ .
0   pL  r 
pC 

Так как здесь icb не равен нулю, то
pL  r 
1
 0.
pC
Откуда получаем искомое характеристическое уравнение
p2 
r
1
p
 0.
L
LC
Показатель степени p определяет порядок дифференциального уравнения свободного тока.
Как видно в последовательной цепи, содержащей r , L и C , мы имеем дифференциальное
уравнение второго порядка.
Определяем корни характеристического уравнения:
2
p1, 2
r
1
 r 

   
.
2L
LC
 2L 
В зависимости от значения корней характеристического уравнения (соотношения между
параметрами цепи r , L и C ) будут получены частные решения однородного дифференциального
уравнения свободного тока:
2
1
 r 
, решение для свободного тока имеет вид
 
LC
 2L 
1.Если 
iСВ  A1e p1t  A2 e p2t .
2
1
 r 
, решение для свободного тока имеет вид
 
LC
 2L 
2.Если 
iСВ  A1e p1t  A2 te p2t
2
1
 r 
3.Если 
, решение для свободного тока имеет вид
 
LC
 2L 
iСВ  e t  A1 sin  ' t  A2 cos  ' t  ;

где
r
; ' 
2L
2
1  r 

 ,
LC  2 L 
A1 и A2 — постоянные интегрирования; p1 и p2 — корни характеристического
уравнения.
Корни характеристического уравнения в последнем случае соответственно равны:
p1    j' , p2    j'
Рассмотрим несколько задач.
Задача.1. Определить ток переходного процесса при подключении
(последовательная цепь r и L) как па постоянное, так и на синусоидальное напряжения.
катушки
Дано: r  10Ом , L  0,1Г , для постоянного напряжения U  100B , для синусоидального
напряжения u  100 sin( wf  30) B , f  50 Гц .
1. Постоянное напряжение. Определяем ток установившегося положения:
iУС  U r  100 10  10 А.
Уравнение свободного тока
0  riСВ  L
diСВ
.
dt
Его характеристическое уравнение
0  r  Lp ,
откуда корень характеристического уравнения
p   r L  10 0,1  100 .
Свободный ток
iСВ  Ae pt  Ae 100t А.
Ток переходного процесса
i  iУС  iСВ  10  Ae100t А.
Определяем постоянную интегрирования A . Полагая t  0 и учитывая, что ток в
индуктивности скачком возникнуть не может (цепь до начала переходное процесса была
разомкнута i  0 ), получим
it 0   iУС t 0   iСВ t 0   10  A  0 .
откуда A = —10.
Таким образом, ток переходного процесса будет равен
i  10  10e 100t А.
2. Синусоидальное напряжение. Определяем установившийся ток:
Z  r  jL  10  j 2  50  0,1  10  j31,4  33e j 72 Ом;
ImУС  U m Z  100e j 30 33e j 72  3e  j 42 Ом;
iУС  3 sin t  42 А.
Так как свободный ток не зависит от напряжения, то воспользуемся его выражением,
полученным в предыдущей задаче. Тогда ток переходного процесса
i  iУС  iСВ  3 sin t  42  Ae 100t А.
Определяем постоянную интегрирования A :
it 0   3 sin  42  A  2  A  0 ,
откуда A  2 .
Таким образом, ток переходного процесса будет равен
i  3 sin t  42  2e 100t А.
Задача 2. Определить ток переходного процесса в последовательной цепи с активным
сопротивлением и емкостью при подключении ее как к постоянному, так и к синусоидальному
напряжениям.
Дано: r  10Ом , C  200 мкФ , для постоянного напряжения U  100В , для
синусоидального напряжения u  100 sin t  30 В, f  50 Гц .
1. Постоянное напряжение. Установившийся ток в цепи с емкостью, подключенной к
постоянному напряжению, равен нулю, так как конденсатор, зарядившись до величины
питающего напряжения, размыкает цепь.
Следовательно, ток переходного процесса определяется только
свободным током. Уравнение свободного тока
0  riСВ 
1
iСВ dt .
С
Дифференцируя уравнение свободного тока, получаем
0r
diСВ iСВ
,

dt
C
тогда характеристическое уравнение
0  rp 
1
,
C
откуда корень характеристического уравнения
p
Ток переходного процесса
1
10 6

 500 .
rC
10  200
i  iСВ  Ae pt  Ae 500t А.
Определяем постоянную интегрирования А. Полагая t  0 и учитывая, что напряжение на
емкости скачком возникнуть не может (конденсатор до начала переходного процесса не был
заряжен, u c  0 ), получаем
it 0   A  U r  100 10  10 А.
Таким образом, ток переходного процесса будет равен
i  10e 500t А.
1. Синусоидальное напряжение. Определяем установившимся ток :
Z r j
1
10 6
 10  j
 10  j16  19e  j 58 Ом;
C
2  50  200
U m 100e j 30
I

 5,3e j 88 А;
mУС 
 j 58
Z
19e
iУС  5,3 sin t  88 А.
Воспользуемся выражением для свободного тока из предыдущей задачи. Тогда ток
переходного процесса
i  iУС  iСВ  5,3 sin t  88  Ae 500t А.
Определяем постоянную интегрирования A :
it 0   5,3 sin 88  A  5,3  A ,
откуда A  it 0   5,3 .
Найдем ток it 0  в момент включения:
it  0  
u t  0 
r

100 sin 30
 5 А,
10
следовательно, A  5  5,3  0,3 .
Таким образом, ток .переходного процесса будет равен
i  5,3 sin t  88  0,3e 500t А.
Задача 3. Определить емкость C конденсатора в схеме с последовательным соединением
резистора и конденсатора, включенной на постоянное напряжение U 0  200 B , из условия, что
через время t  T1  30 мс после включения напряжение на конденсаторе при заряде его через
резистор с сопротивлением r  5мОм достигнет значения U C1  30 B . Найти значение тока ic в
момент t  T1 .
Р е ш е н и е . Выражение для напряжения, на конденсаторе во время переходного процесса в


рассматриваемой цепи имеет вид u C  U 0 1  e  t rC . Из этого выражения определим значение
емкости

конденсатора

C.
t  T1  30 мс ,
При
uC T1   U C1  30 B
следовательно,
30  200 1  e T1 rC ,откуда e T1 rC  170 200  0,85 .Отсюда
 T1 rC  ln 0,85  ln 8,5  ln 10  2,14  2,3  0,16 , т.е. T1  0,16rC  30 мс.
Окончательно
C
30 10 3
 0,037 мкФ.
0,16  5 10 6
Выражение для тока в цепи запишем в виде
iC  C
duC U 0 t rC
.

e
dt
r
Подставляя в это выражение значения U 0 , r , C и t  T1  30 мс , найдем
iC1 
U 0 T1 rC
200 0,16
e

e
 34,2 мкА.
r
5 10 6
Периодические несинусоидальные токи в электрических цепях
После изучения данного раздела студенты должны:
1)знать значение терминов: электрический фильтр, амплитудно-частотный и фазочастотный
спектры, коэффициент пульсаций, коэффициент искажения формы кривой; назначение
сглаживающего, полосового, заградительного избирательного фильтров;
2)понимать причины возникновения несинусоидальных токов; принцип работы
дифференцирующих и интегрирующих цепей; влияние формы кривой тока и напряжения на
показания приборов различных систем;
3)уметь анализировать электрическое состояние линейной цепи несинусоидального тока
методом суперпозиции, работу простейших фильтров.
При изучении настоящего раздела необходимо усвоить, что источников с абсолютно
постоянной или синусоидальной э.д.с. не существует. Различные источники энергии в силу ряда
причин создают пульсирующие, медленно меняющиеся или незначительно отличающиеся от
синусоидальной формы напряжения.
Причинами появления несинусоидальных токов являются:
1)несовершенство источников постоянной и синусоидальной э.д.с.;
2)подключение к линейной цепи генераторов, создающих специальную форму напряжения;
3)наличие различного рода нелинейных элементов в электрической цепи.
При расчете цепей, находящихся под воздействием периодических несинусоидальных
Величин, необходимо знать способы их представления:
1)графики зависимости мгновенных значений, несинусоидальных токов и напряжений от
времени;
2)аналитический способ разложения периодических функций в ряд Фурье, из которого для
практических целей берут ограниченное число первых членов ряда. В разложении в ряд Фурье в
общем случае представлены постоянная составляющая, основная (первая) гармоническая
составляющая, имеющая период, равный периоду данного несинусоидального воздействия,
высшие гармонические составляющие и их начальные фазы. Основную и высшие гармонические
составляющие обычно называют просто гармониками Амплитуды и начальные фазы гармоник
определяют спектральный состав несинусоидальной кривой, который может быть представлен в
виде диаграмм амплитудно-частотного и фазо-частотного спектров.
При анализе электрических цепей с несинусоидальными напряжениями и токами частот
имеют дело с действующими значениями этих-величин:
U  U 02  U12  U 22  ...  U n2 ;
I  I 02  I12  I 22  ...  I n2 .
Таким образом, действующее значение несинусоидального напряжения или тока равно
корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех
гармоник несинусоидального напряжения или тока.
Действующее значение каждой гармоники
U k  U km
2.
Среднее значение мощности при несинусоидальных напряжениях и токе равно сумме
средних значений мощностей от постоянных составляющих и каждой гармоники тока и
напряжения:
P  U 0 I 0  U1 I1 cos 1  U 2 I 2 cos  2  ...  U n I n cos  n .
Форму периодических несинусоидальных кривых принято характеризовать некоторыми
коэффициентами: амплитуды Ка, формы КФ, искажения Ки и др. Разложение в ряд Фурье позволяет
заменить на основании принципа суперпозиции реальный источник несинусоидального
напряжения совокупностью последовательно включенных
Рис. 23
источников. Таким образом, мгновенные значения искомых токов и напряжений определяют
путем суммирования найденных и результат те расчета постоянных и гармонических
составляющих тока или напряжения. При расчете цепей следует учитывать, что сопротивления
емкостного и индуктивною элементов зависят от частоты: сопротивление индуктивного элемента
возрастает с увеличением номера к гармоники, т.е. x L ( k )  kwL , а сопротивление емкостного
элемента уменьшается с увеличением порядкового номера гармоники, т. е. xc ( k )  1 / kwC . В тех
случаях, когда это требуется по условиям работы электрических цепей для изменения формы
кривой тока или напряжения, применяются специальные устройства, содержащие индуктивные
катушки и конденсаторы. Эти устройства называются электрическими фильтрами.
Задача 1. Для кривой напряжения однополупериодного выпрямления u  ( wt )  U m sin wt
(рис. 23). Найти действующее значение напряжения путем непосредственного интегрирования.
Сравнить найденный результат с расчетом по гармоникам ряда Фурье, учитывая только: а) первый
член ряда, б) первые три члена ряда. Оценить погрешность  в процентах. Определить
коэффициенты K a , K ф , K н .
Разложение в ряд Фурье:
u t  
2U m  1 
1

cos 2t  ...  .
  cos t 
 2 4
1 3

Р е ш е н и е . Находим действующее и среднее значения напряжения непосредственным
интегрированием:

U

U m2  1
U m2  U m
1
1 2

2
2
U
sin

td

t


t

sin
2

t


;


m
2 0
2  2
4
2 2
2
0

U ср

U
U
1

U m sin tdt   m cos t  m .

2 0
2

0
Учитывая только первый член разложения в ряд Фурье, оценим погрешность  :
U' Um  ;
Um Um

U U '
 100%  36,3% .
 '
100%  2
U
U
m
2
С учетом первых трех членов разложения получим
2
U '' U m
2
2
1  1   2 
 
  0,499U m ;
  
    2 2   3 2 
Um
 0,499U m
U U ''
2
 ''
100% 
100%  0,2% .
Um
U
2
Получаем погрешность, вполне допустимую при инженерных расчетах. Таким образом,
остальными членами разложения в ряд Фурье можно пренебречь.
Определим коэффициенты, характеризующие форму кривой напряжения:
Ka 
Um
Um
U  
U
 m   1,57 ;

 2 ; KФ 
U ср 2U m 2
U Um 2
KИ 
2U m
U1

 0,707 .
U 2 2U m
Задача 2. Определить индуктивности L1 и L2 резонансного фильтра (рис. 24), являющегося
бесконечно большим сопротивлением для тока первой гармоники и не представляющего
сопротивления для тока седьмой гармоники. Дано; C  50 мкФ , f1  50 Гц .
Р е ш е н и е . Чтобы исключить первую гармонику в нагрузке, необходимо выполнить
условие резонанса токов: 1/ w1 L1  w1C , отсюда
L1 
1
1

 203 мГ.
2
2
1 C 314  50  10 6
Чтобы выделить седьмую гармонику в нагрузке ZH , следует обеспечить условие резонанса
напряжений для седьмой гармоники:
1
71C 
1
 71 L2 ,
71 L1
Рис. 24
Рис. 25
Отсюда
L2 
L1

49 L1C  1
2
1
1
1
49 C 
L1
1

49  314  50  10
2
1
2
6
1

0,203
 4,23 мГ.
Задача 3. Найти показания приборов электромагнитной системы (рис. 25), записать
выражения для мгновенных значений всех токов и определить их коэффициенты искажения. Дано:
r  6Ом , xL (1)  2Ом , xС (1)  18Ом , u (t )  180 sin wt  60 sin( 3wt  20) B .
Решение. Находим токи в ветвях от первой гармоники:
I11 
U 1
r

180
6 2

30
2 А;
U 1
180
90  j 90
I21 


e
jxL 1
2 j2
2
А;
I31 
U 1

 jxC 1
180
2  j18
I1  Y1U 1
Y1 
где

10
2
e j 90
А;
,
1
1
1
1 1
1
8,55  j 6930'


 


e
r jxL1 jxC 1 6 j 2 j18 18
1/Ом;
180  8,55  j 6930' 85,5 j 6930'
I1 
e

e
2  18
2
А.
Определяем токи в ветвях от третьей гармоники:
j 20

10  j 20
I  U 3  60e

e
13 
r
2 6
2
А;
U 3
60e j 20 10  j 70
I23 


e
jxL 3
2  j6
2
А;
I33 
U 3
 jxC 3

60e j 20
2  j 6

10
2
e j110
На третьей гармонике в параллельном контуре резонанс токов
I3  Y3U 3
Y3 
где
1
1
1
1 1
1 1


 


r jxL 3 jxC 3 6 j 6 j 6 6
,
1/Ом;
А.
60e j 20 10 j 20
I3 

e
2 6
2
А.
Показания приборов будут иметь следующие значения:
I1  I121  I123 
900 100

 22,4 А;
2
2
I 2  I 221  I 223 
8100 100

 64 А;
2
2
I 3  I 321  I 323 
I  I 21  I 23 
100 100

 10 А;
2
2
7310,25 100

 60,8 А.
2
2
Мгновенные значения токов имеют вид:
i1  30 sin t  10 sin 3t  20 А;
i2  90 sin t  90  10 sin 3t  70 А;
i3  10 sin t  90  10 sin 3t  110 А;
i  85,5sin t  6930'  10 sin 3t  20 А.
Коэффициенты искажения, токов:
K И1 
I 11
K И2 
I 21
I1
I2


30
2  22,4
 0,95 ;
90
 0,995 ;
2  64
K И3 
KИ 
I 31
I3
I 1
I


10
 0,707 ;
2 10
85,5
 0,995 .
2  60,8
Наиболее искажена кривая тока на емкостном элементе.
Магнитные цепи
Магнитные цепи с постоянной магнитодвижущей силой
Магнитной цепью называется совокупность источников магнитодвижущей силы и
магнитопроводов (ферромагнитных тел или сред), предназначенных для создания в определенном
месте электротехнического устройства магнитного поля требуемой интенсивности, определенной
конфигурации и надлежащей направленности. Магнитные цепи бывают простые и сложные
(разветвленные), однородные и неоднородные (состоящие из различных материалов).
Различие свойств неферромагнитного и ферромагнитного материалов наглядно
иллюстрируется зависимостью B  f (H ) . Для неферромагнитного материала это линейная
зависимость, а для ферромагнитного — существенно нелинейная и изображается кривой
намагничивания или задается в форме таблицы. Различные ферромагнитные материалы обладают
различной способностью намагничиваться. Так, например, при одинаковой напряженности
магнитного поля H величина магнитной индукции B для электротехнической стали во много раз
больше, чем для чугуна.
Магнитные цепи играют важную роль в электрических машинах и аппаратах, так как при их
помощи создаются магнитные потоки, необходимые для работы этих аппаратов.
В основу расчета магнитных цепей положен закон полного тока, математическое выражение
которого для магнитных цепей, выполняемых из ферромагнитных материалов имеет вид
 Hl   I ,
где H —напряженность магнитного поля; l — длина средней силовой
магнитной линии; I — ток.
При расчете магнитных цепей встречаются две задачи — прямая и обратная. Если задан
магнитный поток и требуется определить магнитодвижущую силу, то задача является прямой. B
том случае, когда задана магнитодвижущая сила и требуется определить магнитный поток, задача
— обратная.
Задача 1. На рис. 26 даны геометрические размеры сердечника магнитной цепи в
миллиметрах, выполненного из электротехнической стали марки Э11. Требуется определить
магнитодвижущую силу F  wI , которая необходима для создания магнитного потока
  2  10 3 Вб, величину тока в катушке I , содержащей w  1000 витков, и индуктивность
катушки L .
Р е ш е н и е . Магнитную цепь делим на участки так, чтобы в пределах каждого участка
материал и сечение сердечника оставались неизменными. В нашем случае таких участков три.
Контур, по которому составляем уравнение, пользуясь законом полного тока, проходит по средней
магнитной линии:
l1  150  25  125 мм;
l2  l2  l2  125  2 107,5  2  338 мм.
Определяем магнитную индукцию в каждом участке цепи, для чего находим сечения
сердечника S1 и S 2 :
S1  40  50  2000мм 2  2 10 3 м 2 ;
S 2  50  25  1250мм 2  1,25 10 3 м 2 .
Магнитная индукция равна:
B1 
 2  10 3

 1 Т;
S1 2  10 3

2  10 3
B2  B0 

 1,6 Т.
S 2 1,25  10 3
Напряженность магнитного поля для ферромагнитных материалов определяем по кривым
намагничивания B  f (H ) , которые приводится в справочной и учебной литературе. В нашем
случае дли электротехнической стали марки Э11 имеем: H1  502 A / м и H 2  4370 A / м . Для
воздушного зазора l 0 напряженность магнитною поля определяется из равенства
H 0  8  10 5 B0  8  10 5  1,6  1280000 А/м.
Искомая магнитодвижущая сила, равная произведению тока на число витков катушки, по
которой он протекает, согласно закону полного тока будет равна:
F  wI  H 1l1  H 2 l 2  H 0 l0  502  0,125  4370  0,338  1280000  2  10 3  4000 А.
Рис.26 Рис. 27
Ток в катушке
I  F w  4000 1000  4 А.
Индуктивность катушки
L
 w 1000  2  10 3


 0,5 Гн,
I
I
4
где  — потокосцепление.
Задача 2. На рис. 27 изображен тороидальный сердечник, выполненный из
электротехнической стали марки Э42. Заданы размеры: l  30см , l0  0,1см , магнитодвижущая
2
сила F  wI  1000 А; w  1000 ; витков; S  4см . Определить, какой поток будет замыкаться
по сердечнику.
Р е ш е н и е . Задача является обратной. Поэтому для ее решения необходимо построить
кривую зависимости магнитного потока от магнитодвижущей силы   f wI  , а затем по
заданной магнитодвижущей силе определить графически магнитный поток Ф. Для построения
зависимости   f wI  , необходимо задаться несколькими значениями магнитного потока и для
всех этих значений определить магнитодвижущую силу, т. е. решить несколько прямых задач
(обычно достаточно 3—5 значений). Первое значение магнитного потока выбирается из расчета,
что магнитное сопротивление стали RM СТ  0 , а основное сопротивление представляет
сопротивление воздушного зазора R0 . Полученное значение потока будет несколько завышенным,
поэтому далее задаемся меньшими значениями потока. Если пренебречь RM СТ , то закон полного
тока для рассматриваемой цепи запишется в виде
wI  H 0 l0 ,
откуда
H 0  wI l 0  1000 10 3  10 6 А/м.
Магнитная индукция
B0  H 0 8  10 5  10 6 8 10 5  1,25 Т.
Магнитный поток
 0  B0 S  1,25  4  10 4  5  10 4 Вб.
Напряженность магнитного поля определяем для В=1,25 Т по кривым намагничивания
B  f (H ) для стали Э42, которые приводятся в литературе. В нашем случае lcт Н ст  600 А / м ,
H ст lcm  180 A , H 0 l0  10 3 A .
wI  H СТ lСТ  H 0 l0  180  10 3  1180 А.
Далее задаемся меньшими значениями потока Ф . Результаты вычислений сводим в таблицу:
Ф, Вб
В, т
Нст,А/м Нст lст.A
5 10 4
4,5  10 4
1,25
1,25
600
300
4  10 4
1.0
200
Но, А/м
Hоlо, А
wI, А
180
90
10 6
9  10 5
103
900
1180
990
60
8  10 5
800
860
По полученным данным строим зависимость
  f wI  (рис. 28). По заданной
магнитодвижущей силе находим
 иск  4,53 10 4 Вб.
Рис. 28
Задача может быть решена с помощью построения так называемой опрокинутой
характеристики (рис. 28). Для этого строится зависимость   f H cm lcm  и в точке пересечения
ее с опрокинутой характеристикой (прямая линия), которая строится при Rмст  0 , находим
искомое значение потока  иск .
Электромагнитные устройства с постоянной магнитодвижущей силой широко используются
в подъемных электромагнитах, контакторах, реле и т. и. Создание магнитного поля в этих
устройствах преследует цель создать условия для возникновения сил, действующих на проводник
Стоком либо на ферромагнитные тела. В последнем случае сила; пропорциональна изменению
энергии магнитного поля при изменении объема, занимаемого этим полем. Для того чтобы
определить работу сил в магнитном поле, необходимо определить величину индукции
эквивалентного однородного ноля, т. е. cследует решить обратную магнитную задачу.
Магнитные цепи с переменной магнитодвижущей силой
Необходимо обратить внимание на то, что при работе на линейном участке вебер-амперной
характеристики и синусоидальном напряжении амплитуда магнитного потока зависит только от
приложенного напряжения, частоты и числа витков обмотки и не зависит от свойств сердечника и
величины тока ( U  4,44 fw m ). Ток в катушке с ферромагнитным сердечником представляется
периодической несинусоидальной кривой i (t ) , которая при учете потерь на гистерезис и вихревые
токи опережает кривую Ф(t ) на угол магнитных потерь. Необходимо понимать, что изменение
воздушного зазора приводит к увеличению тока в катушке, но магнитный поток при этом остается
неизменным (если неизменно приложенное напряжение). Нужно четко уяснить алгоритм
определениятока, параметров последовательной и параллельной электрической схем замещения
катушки с ферромагнитным сердечником и их физический смысл, уметь строить векторную
диаграмму.
Введение в цепь синусоидального тока нелинейной индуктивности, какой является катушка
со стальным сердечником, даст возможность осуществить феррорезонанс напряжений и токов.
Это явление находит широкое практическое применение в феррорезонансных стабилизаторах
напряжения, в которых при значительных колебаниях напряжения на входе напряжение на выходе
остается почти неизменным.
Задача. На рис. 29 даны геометрические размеры сердечника магнитной цепи в
миллиметрах, выполненного из электротехнической стали марки Э42. Сердечник набран из листов
толщиной d  0,5 мм . Толщина изоляции между листами 0,05 мм Удельный вес стали
  7,8 г см 3 . Напряжение сети U  220 В, индукция Вm  1,4T , частота f  50 Гц . Требуется
определить ток I , параметры последовательной и параллельной схем замещения, если можно
пренебречь активным сопротивлением обмотки и потоком рассеяния.
Р е ш е н и е . Определяем длину средней магнитной линии и сечения сердечника:
lст  80  2  120  2  400мм  40см ;
Sсерд  30  20  600мм 2  6см 2 .
Считаем, что изоляция занимает 10 0 0 площади сердечника, т.е.
S ст  0,9S серд  5,4см 2 .
Находим активную и реактивную составляющие тока I (они определяются мощностью
потерь и намагничивающей мощностью):
I а  PСТ U  pСТ G U ; I р  QСТ U  qСТ G U .
Масса сердечника G  l ср S СТ  7,8  40  5,4  1,68 кг.
Рис. 29 Рис. 30
По кривым зависимостей удельной активности и намагничивающей мощности pcт ( Bт ) и
qcт ( Bт ) , .которые приводятся в справочной и учебной литературе, находим: pcт  2,8Bт / кг ;
qcт  26вар / кг , тогда:
Pст  pст G  2,8 1,68  4,7 Вт;
Qст  qст G  26 1,68  43,8 вар;
I а  4,7 220  0,0214А  21,4мА ;
I р  43,8 220  0,199А  119мА ;
I  I а2  I р2  201 мА.
Параметры параллельной и последовательной схем замещения (рис. 30) определяются
следующим образом:
g ст  I а U  0,0214 220  0,0973 10 3 1/Ом;
bст  I р U  0,199 220  0,905 10 3 1/ОМ;
z ст  U I  220 0,201  1095 Ом;
cos   I а I  0,0214 0,201  0,106 ;
rст  zст cos  1095  0,106  116 Ом;
2
xст  zст
 rст2  10952  116 2  1090 Ом.
Электрические измерения
После изучения данного раздела студенты должны:
1)знать устройство и области применения основных типов электроизмерительных, приборов
непосредственной оценки; основные показатели этих приборов; способы расширения пределов
измерения приборов;
2)понимать устройство и работу электрических схем при измерении неэлектрических
величин; принципы мостового и компенсационного методов измерения электрических и
неэлектрических величин; принцип работы электронных измерительных приборов;
3)уметь выбрать электроизмерительный прибор по пределу измерений и точности в
соответствии с каталогом; пользоваться электронным осциллографом; представлять результаты
измерений с учетом точности.
Рис. 31
Особое внимание следует обратить на измерение неэлектрических величин (например,
скорость, давление, температура, влажность, концентрации растворов, газовых смесей и т.п.)
электрическими методами, так как в условиях современного производства, когда контроль и
управление ходом технологических процессов осуществляется дистанционно или автоматически,
электрические методы часто оказываются единственно возможными.
Рассмотрим несколько примеров решения задач.
Задача l. При измерении напряжения на выходе схемы (рис. 31) используют вольтметр
магнитоэлектрической системы М366 с пределом измерения 150В, класса точности 1,0 и током
потребления 1,1мА. Задано U1  300B , r1  6кОм , r2  4кОм . Определить максимальную
абсолютную погрешность измерения напряжения U 2 таким прибором и оценить точность
измерения.
Решение.
Максимальная абсолютная погрешность измерения ( A ) определяется
погрешностью метода ( A1 ) и погрешностью прибора ( A2 ), т.е.
A  A1  A2 .
Погрешность метода A1 — это разность значений измеряемой величины без учета и с
учетом влияния из мерительного прибора, т.е.
A1  Aист  Aизм ;
Aист  U 2 x 
Aизм  U 2 
U1
300
 r2 
 4  120 В;
r1  r2
10
rr
U1
300
4 136
 2V 

 117 В,
r2 rV r2  rV
4 136 140
6
r1 
140
r2  rV
3
где rV  150 1,1  10  136 кОм — внутреннее сопротивление прибора.
Таким образом,
A1  Aист  Aизм  120  117  3 В.
Погрешность прибора ( A2 ) определяется классом точности и пределом измерения
измерительного прибора:
A2  KAном 100  1 150 100  1,5 В.
Погрешность метода может быть много больше, чем погрешность прибора. Максимальная
абсолютная погрешность измерения составит:
Рис. 32
A  A1  A2  3  1,5  4,5 В.
Точность измерения определяется относительной погрешностью:
% 
A
4,5  100
 100 
 3,84% .
AИЗМ
117
Задача 2. В трехфазную сеть, нагрузка которой симметрична, включено два ваттметра через
измерительные трансформаторы тока и напряжения (рис. 32). Коэффициенты трансформации
трансформаторов тока и напряжения: KTT  200 / 5  40 ; KTН  6000 / 100  60 . Определить
активную и реактивную мощности, коэффициент мощности
cos  
и ток нагрузки при
следующих показаниях ваттметров: P1  30Bт , P2  20Bт .
Решение. Как известно, активная мощность цепи, измеряемая по схеме двух ваттметров,
равна P  P1  P2 . Учитывая, что измерительные приборы включены через измерительные
трансформаторы, мощность, полученная по показаниям ваттметров, должна быть умножена на
коэффициент трансформации измерительных трансформаторов:
P  P1  P2 K ТТ K ТН  30  20  40  60  120000Вт  120кВт .
Реактивная мощность для симметричной нагрузки, определяемая по показаниям двух
ваттметров, равна Q  3 P1  P2  .С учетом коэффициентов трансформации измерительных
трансформаторов
Q  3 P1  P2 K ТТ K ТН  3 30  2040  60  41600вар  41,6квар .
Для определения коэффициента мощности cos  найдем тангенс угла сдвига фаз:
tg  Q P  41,6 120  0,347 ;   1910' ,
что соответствует cos   0,94 .
Ток нагрузки найдем из равенства P1  U Л I Л cos30    :
IЛ 
P1 K ТТ K ТН
30  40  60

 12,3 А.
U Л cos30    6000  0,98
Можно определить ток и на равенства
P2  U Л I Л cos30    .
Задача3. Вольтметр, номинальное напряжение которого U н  100В , а сопротивление
обмотки rB  10000Ом , необходимо включить в сеть постоянного тока для измерения
напряжения до U  600B . Определить величину добавочного сопротивления, которое надо
включить последовательно с вольтметром.
Решение. Определяем рабочий ток вольтметра:
I В  U Н rВ  10 10000  0,01 А.
Определяем падение напряжения на добавочном сопротивлении:
U Д  U  U Н  600  100  500 В,
откуда величина добавочного сопротивления rД  U Д I В  500 0,01  50000 Ом.
Задача4. Для измерения тока I  4 A имеются два амперметра: один класса точности 0,5
имеет предел измерения 20А, другой класса точности 1,5 имеет предел измерения 5А. Определить,
у какого прибора меньше предел допускаемой основной относительной погрешности и какой
прибор лучше использовать для измерения тока I  4 A .
Решение. Наибольшие относительные погрешности прибора равны: при измерении
заданного тока амперметром класса 0,5
1% 
K1 Ak1
0,5  20
100 
100  2,5% ;
AИЗМ
4
при измерении заданного тока амперметром класса 1,5
2% 
K 2 Ak 2
1,5  5
100 
100  1,9% .
AИЗМ
4
Таким образом, при измерении тока I  4 A лучше использовать прибор класса 1,5 с
пределом измерения 5А.
Так как по теме «Электрические измерения» контрольной работы нет, приводим несколько
задач для самоконтроля:
1. В сеть постоянного тока напряжением и U  500В включили последовательно два
вольтметра, каждый из которых рассчитан на напряжение U П  300В . Первый вольтметр дает
полное отклонение стрелки при токе 10мА, второй — при токе 20мА; Определить показания
вольтметров.
2. Для определения расхода энергии предприятия в трехфазную сеть через измерительные
трансформаторы включены два счетчика. Коэффициент трансформации трансформатора тока
равен KTT  200 / 5 , трансформатора напряжении — KTH  600 / 100 . Определить расход,
энергии за месяц, если счетчики показали 400 и 300 кВт ч.
3.Для выявления внешней характеристики источника ( E  100 B ) имеются два вольтметра
магнитоэлектрической системы: а) М330, класса 1,5, U ном  100 B ; б)М366, класс 1,0,
U ном  250B . Определить, каким прибором следует воспользоваться для получения большей
точности измерения.
4.Для измерения тока I в последовательной цепи включается микроамперметр типа М95
класса точности 1,5, имеющий предел измерения 1,5мкА и внутреннее сопротивление
ra  7300Ом . При U  15мВ и r  10кОм найти: а) относительную методическую погрешность
измерения тока микроамперметром; б) наибольшую относительную погрешность результата
измерения тока микроамперметром класса 1,5 с пределом измерения 1мкА .
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Электрические цепи постоянного тока
1.Какое соединение
треугольником, звездой?
называется
последовательным,
параллельным,
смешанным,
2.Сформулируйте обобщенный закон Ома и запишите его для участка цепи, содержащего
источник э. д. с.
3.Сформулируйте закон Кирхгофа и запишите их выражения.
4.Изложите сущность методов расчета электрических цепей с несколькими источниками:
методы непосредственного применения законов Кирхгофа, контурных токов и узлового
напряжения.
5.Когда применяется метод эквивалентного генератора и в чем он заключается?
6.Какими методами производится расчет нелинейных цепей постоянного тока?
7.Как перейти от схемы с источником э. д. с. к эквивалентной схеме с источником тока?
Электрические цепи синусоидального тока
1.Сформулируйте понятия мгновенного, амплитудного, среднего и действующего значений
синусоидального тока.
2.Что называется периодом, частотой, угловой частотой, начальной фазой и сдвигом фаз?
3.Напишите выражение для мгновенного значения тока в цепи, состоящей из соединенных
последовательно элементов r и L, если к зажимам цепи приложено напряжение
u  U m sin t   И  .
4.Условия возникновения резонанса напряжений и способы его достижения. Векторная
диаграмма.
5.Условия возникновения резонанса токов и способы его достижения. Векторная диаграмма.
6.Комплексный (символический) метод расчета электрических цепей синусоидального тока.
7.От чего зависит коэффициент мощности cos   и для чего стремятся его повысить?
Трехфазные цепи
1.В чем состоит преимущество трехфазной системы перед однофазной?
2.Напишите выражения для активной, реактивной и полной мощностей трехфазной системы.
3.Начертите схему включения трех приемников, соединенных в «треугольник», и введите в
нее измерительные приборы для измерения линейных и фазных токов и напряжений.
4.Какие существуют соотношения (для симметричной нагрузки) между фазными и
линейными значениями напряжения и тока для соединений звездой и треугольником?
5.Какими уравнениями связаны линейные и фазные напряжения и токи для несимметричной
нагрузки, соединенной звездой и треугольником?
6.Схемы измерения активной мощности для симметричной и несимметричной нагрузок,
соединенных звездой и треугольником.
Магнитные цепи
1.Для чего необходима кривая намагничивания?
2.Начертите петлю гистерезиса ферромагнитного материала и обозначьте на ней
характерные точки: остаточная магнитная индукция, коэрцитивная сила.
3.Что такое магнитный поток, магнитная индукция, напряженность магнитного поля и в
каких единицах они измеряются?
4.Сформулируйте закон полного тока и поясните его применение при расчете.
5.Изложите метод расчета симметричной разветвленной магнитной цепи.
6.Прямая и обратная задачи. Способы расчета.
7.Объясните принцип работы стабилизатора напряжения.
Электрические измерения
1.Какие системы электроизмерительных приборов вы знаете? Устройство и принцип работы
приборов, основанных на этих системах.
2.На какие группы делятся электроизмерительные приборы но роду измеряемой величины?
3.Почему прибор магнитоэлектрической системы не может измерять переменный ток или
переменное напряжение, а приборы электромагнитной и электродинамической системы могут
измерять и постоянный, и переменный токи?
4.Как устроен электрический счетчик индукционной системы?
5.Способы измерения мощности и электроэнергии в трехфазных цепях.
6.Способы расширения пределов измерения амперметров, вольтметров и ваттметров
постоянного и переменного токов.
7.Назначение датчика при измерении неэлектрических величин. Какие датчики вы знаете?
8.Чем определяется абсолютная погрешность прибора?
9.Чем определяется точность измерения?
КОНТРОЛЬНАЯ РАБОТА 1
Задача 1. Для электрической схемы, изображенной на рис. 1  1  1  50 , по заданным в
табл.1.сопротивлениям и э.д.с, выполнить следующее: 1) составить систему уравнений,
необходимых для определения токов по первому и второму законам Кирхгофа; 2) найти все токи,
пользуясь методом контурных токов; 3) проверить правильность решения, применив метод
узлового напряжения. Предварительно упростить схему, заменив
Рис. 1-1 Рис. 1-2
Рис. 1-3 Рис.1-4
треугольник сопротивления r4 , r5 и r6 эквивалентной звездой. Начертить расчетную схему с
эквивалентной звездой и показать на ней токи; 4) определить ток в резисторе r6 методом
эквивалентного генератора; 5) определить показание вольтметра и составить баланс мощностей
для заданной схемы; 6) построить в масштабе потенциальную диаграмму для внешнего контура.
Задача 2. Для электрической схемы изображенной на рис. 2-1 -2-10, по заданным в табл. 2
параметрам и э.д.с. источника определить токи во всех ветвях цепи и напряжения на отдельных
участках. Составить баланс активной и реактивной мощностей. Построить в масштабе на
комплексной плоскости векторную диаграмму токов и потенциальную диаграмму напряжений по
внешнему контуру. Определить показание вольтметра и активную мощность, показываемую
ваттметром.
r3 V
W
c1
r1
c2
L3
W
L1
r1
r2
r2
E
r3
L3
c3
V
L2
E
Рис. 2 - 1
Рис. 2 - 2
r3 V
W
r1
c1
r2
L3
W
L2
E
L1
r1
r2
V
E
Рис. 2 - 3
Рис. 2 - 4
c2
r3
L3
V
r2
W
r1
W
c2
c1
L3
r1
L1
c3
c4
V
E
r2
L2
E
Рис. 2 - 5
W
Рис. 2 - 6
r3
L1
W
c2
r1
V
r3
r1
L3
E
Рис. 2 - 7
V
W
r1
Рис. 2 - 9
V
Рис. 2 - 8
L1
c2
r2
E
c2
r2
E
L3
W
r3
V
L1
r1
L3
c2
E
Рис. 2 - 10
r2
Вариант
Рисунок
E,В
f , Гц
C1 ,
C2 , мкф
C 3 , мкф
C4 , мкф
L1 , мГн
L2 , мГн
L3 , мГн
r1 , Ом
r2 , Ом
r3 , Ом
мкф
0
2-1
150
50
637
300
-
-
-
-
15,9
2
3
4
1
2-1
100
50
637
300
-
-
-
-
15,9
8
3
4
2
2-1
120
50
637
300
-
-
-
-
15,9
8
3
4
3
2-1
200
50
637
300
-
-
-
-
15,9
8
3
4
4
2-1
220
50
637
300
-
-
-
-
15,9
8
3
4
5
2-2
50
50
-
-
100
-
15,9
1000
115
10
4
100
6
2-2
100
50
-
-
100
-
15,9
1000
115
10
4
100
7
2-2
120
50
-
-
100
-
15,9
1000
115
10
4
100
8
2-2
200
50
-
-
100
-
15,9
1000
115
10
4
100
9
2-2
220
50
-
-
100
-
15,9
1000
115
10
4
100
10
2-3
50
50
637
-
-
-
-
15,9
6,37
5
10
8
11
2-3
100
50
637
-
-
-
-
15,9
6,37
5
10
8
12
2-3
120
50
637
-
-
-
-
15,9
6,37
5
10
8
13
2-3
200
50
637
-
-
-
-
15,9
6,37
5
10
8
14
2-3
220
50
637
-
-
-
-
15,9
6,37
5
10
8
15
2-4
150
50
-
1600
-
-
31,8
-
95
10
2
10
16
2-4
100
50
-
1600
-
-
31,8
-
95
10
8
10
17
2-4
120
50
-
1600
-
-
31,8
-
95
10
8
10
18
2-4
200
50
-
1600
-
-
31,8
-
95
10
8
10
19
2-4
220
50
-
1600
-
-
31,8
-
95
10
8
10
20
2-5
50
50
637
159
-
-
-
-
95
15
10
-
21
2-5
100
50
637
159
-
-
-
-
95
15
10
-
22
2-5
120
50
637
159
-
-
-
-
95
15
10
-
23
2-5
200
50
637
159
-
-
-
-
95
15
10
-
24
2-5
220
50
637
159
-
-
-
-
95
15
10
-
25
2-6
150
50
-
-
637
159
25
9
-
6
4
-
26
2-6
100
50
-
-
637
159
25
9
-
6
4
-
27
2-6
100
50
-
-
637
159
25
9
-
6
4
-
28
2-6
200
50
-
-
637
159
25
9
-
6
4
-
29
2-6
220
50
-
-
637
159
25
9
-
6
4
-
30
2-7
50
50
-
637
-
-
19,1
-
31,8
40
-
40
31
2-7
100
50
-
637
-
-
19,1
-
31,8
40
-
10
32
2-7
120
50
-
637
-
-
19,1
-
31,8
40
-
10
33
2-7
200
50
-
637
-
-
19,1
-
31,8
10
-
40
34
2-7
220
50
-
637
-
-
15,9
-
31,8
40
-
10
35
2-8
50
50
-
318
-
-
15,9
-
-
8
10
4
36
2-8
100
50
-
318
-
-
15,9
-
-
8
10
4
37
2-8
150
50
-
318
-
-
15,9
-
-
8
10
4
38
2-8
200
50
-
318
-
-
15,9
-
-
8
10
4
39
2-8
220
50
-
318
-
-
15,9
-
-
8
10
4
40
2-9
50
50
-
318
-
-
9,55
-
-
4
40
40
41
2-9
100
50
-
318
-
-
9,55
-
-
4
40
4
42
2-9
120
50
-
318
-
-
9,55
-
-
4
40
4
43
2-9
200
50
-
318
-
-
9,55
-
-
40
10
40
44
2-9
220
50
-
318
-
-
9,55
-
-
40
10
40
45
2-10
50
50
-
159
-
-
15,9
-
31,8
35
20
-
46
2-10
100
50
-
159
-
-
15,9
-
31,8
35
20
-
47
2-10
120
50
-
159
-
-
15,9
-
31,8
35
20
-
48
2-10
200
50
-
159
-
-
15,9
-
31,8
35
20
-
49
2-10
220
50
-
159
-
-
15,9
-
31,8
35
20
-
50
2-10
50
50
-
318
-
-
15,9
-
31,8
5
10
-
Задача 3.Для электрической схемы изображенной на рис. 3-1 – 3-17, по заданным в табл. 3
параметрам и линейному напряжению определить фазные и линейные токи в нейтральном
проводе (для четырехпроводной схемы), активную мощность всей цепи и каждой фазы отдельно.
Построить векторную диаграмму токов и напряжений на комплексной плоскости.
a
a
ra
ra
xa
xa
c
xc
xb
n
rc
c
rb
b
xc
xb
n
rc
rb
b
Рис. 3 - 2
Рис. 3 - 1
a
a
ra
xa
n
rb
c
b
xa
n
xb
xc
rc
ra
xc
rc
Рис. 3 - 4
a
a
xсa
ra
n
xb
c
b
rb
c
b
Рис. 3 - 3
xb
xc
rab
rca
c
xab
xbc
b
Рис. 3 - 5
Рис. 3 - 6
rbс
a
a
xсa
xсa
rab
rca
rca
xab
c
xbc
c
rbс
rab
xab
xbc
rbс
b
b
Рис. 3 - 8
Рис. 3 - 7
a
a
xсa
rab
rca
c
xсa
xab
rbс
xbc
rab
c
xbc
b
b
Рис. 3 - 10
Рис. 3 - 9
a
a
ra
ra
xc
n
xc
xb
xb
c
b
c
b
n
Рис. 3 - 11
Рис. 3 - 12
a
a
xсa
xсa
rab
xab
rca
rca
c
b
xbc
rbс
c
xbc
b
Рис. 3 - 13
Рис. 3 - 14
rbс
Вариант Рисунок
Uл , В
ra ,Ом
rb , Ом
rc , Ом
x a , Ом
x b , Ом
xс , Ом
rab ,
rbc ,
rca ,
Ом
Ом
Ом
x ab , Ом
x bc ,
x ca ,
Ом
Ом
0
3-1
127
8
8
8
6
6
6
-
-
-
-
-
-
1
3-1
220
8
8
8
6
6
6
-
-
-
-
-
-
2
3-1
380
8
8
8
6
6
6
-
-
-
-
-
-
3
3-2
127
3
4
6
4
3
8
-
-
-
-
-
-
4
3-2
220
8
4
6
4
3
8
-
-
-
-
-
-
5
3-2
380
8
4
6
4
3
8
-
-
-
-
-
-
6
3-3
127
4
8
6
3
4
8
-
-
-
-
-
-
7
3-3
220
4
8
6
3
4
9
-
-
-
-
-
-
8
3-3
380
4
3
6
8
4
8
-
-
-
-
-
-
9
3-4
127
16,8
8
8
14,2
6
4
-
-
-
-
-
-
10
3-4
220
16,8
8
8
14,2
6
4
-
-
-
-
-
-
11
3-4
380
16,8
8
8
8
6
4
-
-
-
-
-
-
12
3-5
127
10
-
-
-
10
10
-
-
-
-
-
-
13
3-5
220
10
-
-
-
10
10
-
-
-
-
-
-
14
3-5
380
10
-
-
-
10
10
-
-
-
-
-
-
15
3-6
127
-
-
-
-
-
-
8
8
8
6
6
6
16
3-6
220
-
-
-
-
-
-
8
8
8
6
6
6
17
3-6
380
-
-
-
-
-
-
8
8
8
6
6
6
18
3-7
127
-
-
-
-
-
-
8
4
6
4
3
8
19
3-7
220
-
-
-
-
-
-
8
4
6
4
3
8
20
3-7
380
-
-
-
-
-
-
8
4
6
4
3
8
21
3-8
127
-
-
-
-
-
-
4
8
6
3
4
8
22
3-8
220
-
-
-
-
-
-
4
8
6
3
4
8
23
3-8
380
-
-
-
-
-
-
4
8
6
3
4
8
24
3-9
127
-
-
-
-
-
-
16,8
8
3
14,2
6
4
25
3-9
220
-
-
-
-
-
-
16,8
8
3
14,2
6
4
26
3-9
380
-
-
-
-
-
-
16,8
8
8
14,2
6
4
27
3-10
127
-
-
-
-
-
-
10
-
-
-
10
10
28
3-10
220
-
-
-
-
-
-
10
-
-
-
10
10
29
3-10
380
-
-
-
-
-
-
10
-
-
-
10
10
30
3-11
127
10
-
-
-
10
10
-
-
-
-
-
-
31
3-11
220
10
-
-
-
10
10
-
-
-
-
-
-
32
3-11
380
10
-
-
-
10
10
-
-
-
-
-
-
33
3-12
127
15
-
-
-
5
5
-
-
-
-
-
-
34
3-12
220
15
-
-
-
5
5
-
-
-
-
-
-
35
3-12
380
15
-
-
-
5
5
-
-
-
-
-
-
36
3-13
127
-
-
-
-
-
-
-
3
8
4
6
8
37
3-13
220
-
-
-
-
-
-
-
3
8
4
6
8
38
3-13
380
-
-
-
-
-
-
-
3
8
4
6
8
39
3-14
127
-
-
-
-
-
-
8
4
8
-
6
10
40
3-14
220
-
-
-
-
-
-
8
4
8
-
6
10
41
3-14
380
-
-
-
-
-
-
8
4
8
-
6
10
42
3-15
127
-
-
-
-
-
-
-
5
6
5
8
4
43
3-15
220
-
-
-
-
-
-
-
5
6
5
8
4
44
3-15
380
-
-
-
-
-
-
-
5
6
5
3
4
45
3-16
127
-
-
-
-
-
-
5
-
6
-
8
4
46
3-16
20
-
-
-
-
-
-
5
-
6
-
8
4
47
3-16
380
-
-
-
-
-
-
5
-
6
-
8
4
48
3-17
127
-
3
-
15
-
10
-
-
-
-
-
-
49
3-17
220
-
3
-
15
-
10
-
-
-
-
-
-
50
3-17
380
-
3
-
15
-
10
-
-
-
-
-
-
a
a
xсa
xсa
xab
xab
rca
rca
c
xbc
c
rbс
rab
xbc
b
b
Рис. 3 - 15
Рис. 3 - 16
a
xa
xc
n
xb
c
b
Рис. 3 - 17
РАЗДЕЛ II
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ТЕМАМ КУРСА
Трансформаторы.
Данную тему целесообразно начинать с изучения электрической цепи однофазного тока,
содержащей катушку со стальным сердечником, а затем переходить непосредственно к изучению
трансформатора.
Рассматривая физические процессы, возникающие в трансформаторе, необходимо обратить
особое внимание на то положение, что при изменении нагрузки трансформатора в широком
диапазоне (от холостого хода до номинального режима) магнитный поток может, считаться
практически постоянным: и разным магнитному потоку в режиме холостого хода. Это в свою
очередь определяет постоянство потерь в стали, которые легко определяются из режима
холостого хода.
При рассмотрения режима «нормального», короткого замыкания получается, что магнитный
поток в сердечнике трансформатора настолько мал, что им можно пренебречь, а, следовательно,
при этом режиме потери в стали трансформатора практически равны нулю, а потери в меди (в
обмотках трансформатора) равны потерям при номинальной нагрузке трансформатора. Величины
токов, напряжений и мощностей, полученные из режимов холостого хода и «нормального»
короткого замыкания, позволяют определить основные параметры трансформатора.
В паспорте трехфазных трансформаторов дается номинальная, мощность и мощность потерь
всех трех фаз; под номинальными напряжениями понимаются линейные напряжения па зажинах
трансформатора в режиме холостого хода, а под номинальными токами — линейные токи
независимо от схемы соединения обмоток.
После изучения настоящего раздела студенты должны:
1) знать основные элементы конструкции трансформатора; выражение для коэффициента
трансформации; уравнения электрического и магнитного состояний трансформатора;
2) понимать назначение опытов холостого хода и короткого замыкания; сущность
«приведения» параметров вторичной обмотки трансформатора к первичной; различие опыта
короткого замыкания и режима короткого замыкания трансформатора; причины изменения
напряжения на вторичной обмотке трансформатора; принципы построения векторных диаграмм
для различных нагрузок;
3) уметь анализировать различные режимы работы трансформатора; читать паспорт
трансформатора; включать приемники и электроизмерительные приборы для определения
напряжений, токов и мощностей; предвидеть последствия коммутационных изменений в цепи
нагрузки на электрическое состояние трансформатора.
Теория трансформатора полностью распространяется на автотрансформаторы и
измерительные трансформаторы. Поэтому при их изучении следует обратить внимание на
область их применения и особенности работы.
Задача. Для трехфазного трансформатора мощностью S н =100 кВ·А, соединение обмоток
которого Y Y0 —0, известно: номинальное напряжение на зажимах первичной обмотки
трансформатора U1н = 6000 В, напряжение холостого хода на зажимах вторичной обмотки
трансформатора
U 2 o = 400 В, напряжение короткого замыкания
u к = 5,5%, мощность короткого
замыкания Pк = 2400 Вт, мощность холостого хода P0 = 600 Вт, ток холостого хода I 0 = 0,07 I1н .
Определить: 1) сопротивление обмоток трансформатора r1 , x1 , r2 и x 2 ; эквивалентное
сопротивление z 0 (сопротивление намагничивающей цепи) и его составляющие r0 и x 0
которыми заменяется магнитная цепь трансформатора. 2) угол магнитных потерь  .
Построить характеристики трансформатора: 1) зависимость U 2 = f1 (  ) напряжения U 2 от
нагрузки (внешняя характеристика), 2) зависимость  = f (  ) коэффициента полезного действия
от нагрузки,  — коэффициент нагрузки трансформатора (коэффициент мощности нагрузки
принять cos  2 = 0,75).
Построить векторную диаграмму трансформатора при нагрузке, составляющей 0,8 от
номинальной мощности трансформатора S н и cos  2 = 0,75
Составить Т-образную схему замещения трансформатора.
Решение. Определяем номинальный ток первичной обметки:
I1н 
Sн
100 1000

 9,6 А.
3U1н
3  6000
Определяем ток холостого хода и cos  0 :
I 0  0,07 I1н  0,07  9,6  0,67 А;
cos 0 
P0
600

 0,086;0  85 .
3U1н I 0
3  6000  0,67
Определяем угол магнитных потерь:
  90  0  90  85  5 .
Определяем сопротивления обмоток.
1) Сопротивления короткого замыкания:
0,055  6000
 19,9 Ом;
3  9,6
zк 
U к .ф
rк 
Pк
2400

 8,7 Ом;
2
3I к 3  9,6 2
I к .ф

xк  z к2  rк2  19,6 2  8,7 2  17,9 Ом.
2) Сопротивления первичной обмотки:
r1  r2  rк 2  8,7 2  4,35 Ом;
x 1  x 2  xк 2  17,9 2  8,95 Ом.
3) Сопротивления вторичной обмотки:
r2  r2 K 2  4,35 225  0,0193 Ом;
x 2  x 2 K 2  8,95 225  0,0398 Ом,
где K= U 1н U 20  6000 400  15.
Определяем сопротивления намагничивающей цепи:
z0 
Uн.ф
6000

 5180 Ом;
I о.ф
3  0,67
r0 
P0
600

 447 Ом;
2
3I 0 3  0,67 2
x0  z 02  r02  5180 2  447 2  5160 Ом.
Для построения внешней характеристики U 2  f1 (  ) определяем потерю напряжения во
вторичной обмотке трансформатора:
U 2 %   ( u a % cos  2  u р % sin  2 ),
где u a % , u р % - соответственно активное и реактивное падение напряжений;
u a %  u k % cos  k ; cos k  rk z k ;
u a %  5,5
uр % 
8,7
 2,4% ;
19,9
u k %2  u a %2
 5,5 2  2,4 2  4,95%.
Напряжение на зажимах вторичной обмотки трансформатора определяем по формуле
U2 
U 20
100  U 2 %.
100
Задаваясь различными значениями  , по формулам (12) и (13) определяем напряжение U 2
(см. табл. 4).
Для построения зависимости   f 2   расчет коэффициента полезного действия
произведем по формуле:

S н cos  2
.
S н cos  2  P0   2 Pн
номер
p
U 2 ,%
U2 , В
1
0,1
-
-
2
0,025
-
-

0,555
3
0,05
-
-
0,757
4
0,1
0,507
397,97
0,904
5
0,2
1,104
395,94
0,924
6
0,3
1,521
393,92
0,956
7
0,4
2,028
391,89
0,965
8
0,5
2,535
389,86
0,967
9
0,6
3,042
387,83
0,969
10
0,7
3,549
385,80
0,967
11
0,8
4,056
383,78
0,966
12
0,9
4,563
381,75
0,964
13
1,0
5,070
379,72
0,963
0,962

U,В

1,0
0,9
0,8 400
0,7
0,6
0,5
0,4 200
0,3
0,2
0,1
0
0,1 0,2
Uz
 МАКС
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0

Рис. 33
Результаты расчета сведены в табл. 4. Полученные характеристики показаны на рис. 33.
Определим при какой нагрузке трансформатор имеет максимальный к.п.д.:
 м  P0 Pк  600 2400  0,5 ;  м  0,969
Построение векторной диаграммы начнем с вектора фазного напряжения U 2 ф , величина
которого для   0,80 и cos  2  0,75 будет равна:
U2ф  383,78
3  222 В.
Приведенное значение вторичного напряжения:
  U 2ф K  222  15  3330 В.
U 2ф
  на заданный угол  и равен:
Вектор тока I2 отстает по фазе от вектора U
2ф
2
U 1
jx1 I1
z1 I1
r1 I1
jx2 I2
z 2 I2
r2I2
E 2   E1
U 2
2
90
I2
I

I 2  0,8I 2н  0,8
Sн
3U 2н
 0,8
I0
I1


m
Рис. 34
100  1000
 115,6 А.
1,73  400
Падения напряжения во вторичной обмотке:
r2I 2  4,35  7,72  33,6 А;
x 2 I 2  8,95  7,72  68,3 А.
Электродвижущую силу E 2 находим из уравнения электрического состояния,
составленного по второму закону Кирхгофа, для вторичной цепи:
E 2  U 2  r2I 2  jx 2 I2
r1
I1
U1
r2
x1
I0
r0
x2 
I2
U 2
zн
x0
Рис. 35
  на 90 ; а ток холостого хода I опережает поток
Вектор тока Фm отстает от вектора E
2
1
 на угол потерь  .
Ф
m
Ток в первичной обмотке трансформатора I1 получаем из уравнения намагничивающих
магнитодвижущих сил:
I1  I0  I2 , где I2   I2 K .
Вектор напряжения первичной обмотки трансформатора U1 определяем из
уравнения электрического состояния, составленного по второму закону Кирхгофа для
первичной цепи:
U 1   E 1  r1 I1  jx 1 I1 .
Током холостого тока I0 можно пренебречь (так как он мал) и принять I1  I2 или
определить I1 по диаграмме. Тогда падения на первичной обмотке будут:
r1 I1  4,35  7,76  33,8 В.
x 1 I1  8,95  7,76  69,4 В.
Векторная диаграмма трансформатора приведена на рис. 34. Т-образная схема
замещения трансформатора изображена на рис. 35.
Магнитные цепи с постоянной и переменной
магнитодвижущими силами.
Большое распространение в современной технике получили магнитные усилители.
Магнитный усилитель представляет собой устройство, предназначенное для усиления слабых
электрических сигналов по мощности. Основным элементом магнитного усилителя является
дроссель с подмагничиванием, сердечник которого одновременно находится под воздействием
постоянного и переменного магнитных полей. При отсутствии подмагничивающего тока (Iу = 0)
дроссель не насыщен, а поэтому индуктивность его велика и ток в нагрузке мал. При подаче
небольшого управляющего тока значение магнитной проницаемости и, следовательно,
индуктивности дросселя уменьшается, и ток нагрузки значительно возрастает. Меняя значение небольшого тока I у , можно получить значительно большие изменения тока нагрузки I н . В этом и
состоит принцип действии магнитного усилителя. Ясно, что такое усиление происходит за счет
расхода энергии из сети, к которой подключена цепь рабочих обмоток. В основе действия
магнитного, усилителя лежит нелинейный характер магнитной характеристики ферромагнитного
сердечника, зависимость его магнитной проницаемости от напряженности магнитного поля.
Магнитные усилители подразделяются на две группы.
1.
Нереверсивные,
в
которых
зависит от полярности входного сигнала.
полярность
выходного
сигнала
не
2. Реверсивные, в которых полярность выходного сигнала изменяется при изменения
полярности входного (управляющего) сигнала. Магнитные усилители обеих групп могут быть без
обратной связи или с обратной связью (внешней и внутренней). При этом обратную связь
используют как положительную, так и отрицательную.
Асинхронные двигатели.
После изучения настоящего раздела студент должен: 1) знать содержание терминов:
скольжение, синхронна, скорость, круговое вращающееся магнитное поле, короткозамкнутый
ротор, контактные кольца, поток полюса, глубокопазный ротор, двойная “беличья клетка”;
способы изменения направления вращения магнитного поля; устройство и области применения
двух типов трехфазных асинхронных двигателей; условные обозначения трехфазных асинхронных
двигателей на схемах; вид механических характеристик; способы регулирования скорости
вращения двигателя;
2) понимать принцип возбуждения многополюсного вращающегося магнитного поля;
принцип действия трехфазной асинхронной машины в режимах двигателя, генератора и
электромагнитного тормоза; факторы, влияющие на частоту вращения ротора трехфазного
асинхронного двигателя; возможность замены трехфазного асинхронного двигателя с
вращающимся ротором эквивалентным асинхронным двигателем с неподвижным ротором;
аналогию физических явлений в трехфазном асинхронном двигателе с неподвижным ротором и в
трансформаторе с резистивной нагрузкой; энергетические преобразования в трехфазном
асинхронном двигателе;
3)уметь осуществлять пуска синхронного двигателя; измерять скольжение с помощью
стробоскопического устройства, частоту вращения; оценивать величины номинального, пускового
и максимального моментов, пускового тока и номинального скольжения по данным каталога.
Приступая к изучению этой темы, необходимо понять условия возбуждения вращающегося
магнитного поля.
Изучение асинхронного двигателя надо начинать с его устройства и принципа работы.
Необходимо обратить особое внимание на электромагнитные процессы, возникающие в
двигателе, как при его пуске, так и в процессе работы. Векторная диаграмма и эквивалентная схема асинхронного двигателя облегчают изучение его работы и используются при выводе основных
уравнений. Эксплуатационные параметры асинхронного двигателя наглядно демонстрируются
при помощи механических и рабочих характеристик;
Механические характеристики M  f s  и n  f M  могут быть построены по расчетной
формуле вращающего момента:
M 
m1 pU 12ф
r2
s
2


r2 
2
2f1  r1     x1  x 2  
s


,
где М - вращающий момент двигателя в Н·м; r1 , x1 , r2 , x 2 - сопротивления статорной и
роторной обмоток; m1 - число фаз статора; p – число пар полюсов;
U 1ф - фазное напряжение статорной обмотки; s – скольжение.
По зависимости M  f (s ) легко построить характеристику n = f(M). Механические
характеристики могут быть построены и по данным каталога. Известно, что
M 
2M k
sk
s

s sk
,
где M k - критический (максимальный) вращающийся момент двигателя; s k - скольжение,
при котором двигатель развивает критический момент.
Зная отношение критического момента к номинальному M к M н   и определив
номинальный момент как
M н  9550
Pн
, где Pн - номинальная мощность двигателя; nн nн
номинальная скорость вращения ротора, легко получить выражение для sк .
Рассматривая уравнение (15) для номинального режима и учитывая, что
получим:
1


2
s к sн

sн sк
.
Mн 1
 ,
Mк 
а)
б)
M
n
nн
nк
Mк
Mн
0 Sн
Mк
Mн
Mn
Sк
1
S
0
Mn
M
Рис. 36
Решая уравнение (16) относительно критического скольжения , получаем:
s к  s н (  2  1) .
Зная M к и sк и задаваясь значениями s в пределах от 0 до 1, легко построить
механическую характеристику M  f (s ) , данные для которой получаются из
уравнения (15).
Характеристика n  f (M ) получается из характеристики M  f (s ) , учитывая при
этом что
n  n0 (1  s) .
где n 0 об/мин – скорость вращения магнитного поля.
Механические характеристики асинхронного двигателя, изображенные на рис. 36, а и 36, б,
показывают свойства двигателя в системе электропривода; пусковые свойства, перегрузочную
способность, устойчивость работы.
Для более полного выявления свойств двигателя служат рабочие характеристики, которые
показывают зависимость скорости вращения ротора n, вращающего момента М, к. п. д.  , тока
статора и коэффициента мощности cos  от мощности на валу двигателя P2 . Эти характеристики
могут быть рассчитаны по данным каталога или получены в процессе испытания двигателя в
лабораторных условиях.
I1 , M , ,cos  , n
I1 M

cos 
n
0
PНОМ
P2
Рис. 37
Рабочие характеристики асинхронного двигателя изображены на рис. 37.
Рассмотрим примеры решения задач по асинхронным двигателям.
Задача 1. номинальная мощность трехфазного асинхронного двигателя с короткозамкнутым
ротором Pн  10 кВт, номинальное напряжение U н  380 В, номинальное число оборотов
ротора nн  1420 об/мин, номинальный к.п.д.  н  0,84 и номинальный коэффициент мощности
cos н  0,85 . Кратность пускового тока I п I н  6,5 , а перегрузочная способность двигателя
  1,8 . Определить:
1) потребляемую мощность;
2) номинальный и максимальный (критический) вращающие моменты; 3) пусковой ток; 4)
номинальное и критическое скольжения. Построить механические характеристики M  f (s ) и
n  f (M ) .
Решение. Потребляема мощность.
P1н 
Pн
н

10
 11,9
0,84
кВт.
Номинальный и максимальный моменты:
M н  9550
Pн
10
 9550
 67,3 Н·м.
nн
1420
M M  M н  1,8  67,3  121 Н·м.
Номинальный и пусковой токи:
Iн 
P1н
11,9  1000

 21,2 А;
3U н cos н 1,73  380  0,84
I п  6,5I н  6,5  21,2  138 А.
Номинальное и критическое скольжения:
sн 
n 0  nн 1500 - 1420

 0,053 ;
n0
1500
sк  sн (  2  1)  0,53(1,8  1,82  1)  0,175 .
Механические характеристики
M
M  f (s )
строятся по уравнению (15):
242
.
0,175
s

s
0,175
б)
n, об мин
а)
1500
1400
1300
1200
1100
1000
900
800
700
600
500
400
300
200
100
M , Нм
120
110
100
90
80
70
60
50
40
30
20
10
0
M  f (S )
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
0
S
Рис. 38
n  f (M )
10 20 30 40 50 60 70 80 90 100 110 120
M , Нм
номер
s
nн , об/мин
MM
1
0,053
1420
67,3
2
0,4
1350
104,3
3
0,175
1238
121,0
4
0,2
1200
120,5
5
0,3
1050
105,3
6
0,4
900
88,8
7
0,5
750
75,5
8
0,6
600
65,2
9
0,7
450
57,0
10
0,8
300
50,5
11
0,9
150
45,5
12
1,0
0
41,2
Н·м
Задаваясь скольжением s от 0 до 1, подчитываем вращающий момент. Скорость
вращения ротора определяем из уравнения (17). Расчетные данные приведены в табл.
5. Характеристики, построенные по данным табл. 6, изображены на рис. 38, а, б.
Задача 2. Трехфазный асинхронный двигатель с фазным ротором, сопротивление фаз
обмоток которого r1 = 0,46 Ом, r2 = 0,02 Ом, x1 = 2,24 Ом, x 2 = 0,08 Ом, соединен треугольником
и работает при напряжение U н = 220 В с частотой f = 50 Гц. Число витков на фазу обмоток 1 =
192, 2 = 36. Обмоточные коэффициенты K1 = 0,932, K 2 = 0,955. Число пар полюсов p = 3.
Определить: 1) Пусковые токи статора и ротора, пусковой вращающий момент, коэффициент
мощности (cos  ) при пуске двигателя с замкнутым накоротко ротором; 2) токи ротора и статора
и вращающий момент при работе двигателя со скольжением s = 0,03; 3) критическое скольжение
и критический (максимальный) момент; 4) величину сопротивления фазы пускового реостата для
получения пускового момента, равного максимальному, а также пусковые токи статора и ротора
при этом сопротивление.
Решение. Для приведения сопротивления обмотки ротора к обмотке статора определяем
коэффициент трансформации:
K
m11 K1 3  192  0,932

 5,2 .
m2  2 K 2
3  36  0,955
Приведенные значения сопротивлений роторной обмотки:
r2  r2 K 2  0,02  5,2 2  0,54 Ом;
x2  x2 K 2  0,08  5,2 2  2,16 Ом.
Сопротивления короткого замыкания:
rк  r1  r2  0,46  0,54  1,0 Ом;
xк  x1  x2  2,24  2,16  4,4 Ом;
z к  rк2  xк2  12  4,4 2  4,51 Ом.
Пусковые токи, пусковой момент и cos  п при пуске двигателя с замкнутым накоротко
ротором:
I 1п 
Uф
zк

220
 48,8 А;
4,51
I 2п  KI1п  5,2  48,8  254 А;
MП
где
2
m2 r2 I 2п
3  0,02  254 2


 37 Н·м.
0
104,5
m2 - число фаз ротора;  0 - угловая скорость вращения магнитного поля:
0 
2n0
60 f1
; n0 
60
p
.
Определяем коэффициент мощности:
rк
1,0

 0,222 .
z к 4,51
cosп 
Токи и вращающий момент при работе двигателя со скольжением s = 0,03:
z  (r1 
I1 
Uф

z
r2 2
0,54 2
)  ( x1  x2 )  (00,46 
)  4,4 2  18,9 Ом;
s
0,03
220
 11,6 А;
18,9
I 2  KI1  5,2  11,6  60,3 А;
M 
r2 2 3  0,02  60,32
I2
0,003
s

 70
0
104,5
m2
Н·м
Критическое скольжение и критический (максимальный) момент:
sк 
MM
r2
r x
2
1
2
к

0,54
0,46  4,4
2
2
 0,122 ;
m1U ф2
P
3
3  220 2




 141 Н  м
2f1 2 r1  r12  xк2
2  3,14  50 2 0,46  0,46 2  4,4 2




Определяем сопротивление пускового реостата. Известно, что пусковой вращающий момент
достигает максимального значения при условии, что
sк 
r2  rp
xк
 1,0 ,r
где r p - приведенное значение сопротивления пускового реостата:
rp  xк  r2  4,4 - 0,54  3,86 Ом;
rp 
rp
K2

3,68
 0,143 Ом.
5,22
Пусковые токи при пуске двигателя с реостатом:
zп  (rк  rp ) 2  xк2  (1  3,68) 2  4,4 2  6,55 Ом;
I1п 
Uф
zп

220
 33,6 А;
6,55
I 2п  KI1п  5,2  33,6  174,7 А.
Задача 3. из каталога на асинхронные двигатели с фазным ротором известны: номинальная
мощность двигателя
Pн
= 11 кВт, номинальное напряжение
Uн
= 220 В, номинальное число
оборотов ротора n = 920 об/мин, к.п.д.:  н = 81%, номинальный коэффициент мощности
= 0,78, перегрузочная способность двигателя
MM MН
cos н
= 3,4, активное сопротивление фазы
статора r1 = 0,422 Ом. Определить:
1) номинальный ток статора; 2) номинальный и максимальный моменты; 3) сопротивления
r2 и xк
ветви приведенного тока
I 2
в Г – образной схеме замещения (рис. 39); 4) приведенный
I 2 ; 5) ток в статоре в режиме холостого хода I10
6) сопротивления r10 и x10 в Г – образной схеме замещения.
ток ротора
и коэффициент мощности
cos10 ;
Решение. По каталогу находим номинальный ток статора:
I1н 
Pн
11  1000

 26,4 А.
3U н н cos н 3  220  0,81  0,78
Для определения реактивного сопротивления воспользуемся формулой максимального
электромагнитного момента:
I1
I2 r
1
r10
U н
I10
r2 S н
x10
Рис. 39
MM 
1,46U н2
n 0 (r1  r  x )
2
1
из которой следует, что
xк  rм2  r12 ,
2
к
xк
,
где rм - расчетное сопротивление:
1,46U н2
rм 
 r1 .
M M n0
r2 найдем из формулы, выражающей
зависимость номинального электромагнитного момента M н от номинального скольжения sн :
Приведенное активное сопротивление ротора
2,92U н2 r2
,
Mн 


r2 2
n0 sн (r1  )  xк2 
sн


из которой следует, что
r2  sн (rн  rн2  rм2 ) ,
где rн - расчетное сопротивление:
1,46U н2
rн 
 r1 ,
M н n0
По каталогу номинальный момент
M н  9550
Pн
11
 9550 
 114 Н·м.
nн
920
Максимальный момент
M M  3,4Mн  3,4  114  389 Н·м.
Расчетные сопротивления:
1,46U н2
1,46  220 2
rм 
 r1 
 0,422  1,36
M M n0
39,6  1000
Ом;
1,46U н2
1,46  220 2
rн 
 r1 
 0,422  5,64 Ом;
M н n0
11,65  1000
где
MM
= 39,6 кг·м;
M н = 11,65 кг·м;
Реактивное сопротивление
xк  rм2  r12  1,362 - 0,4222  1,29 Ом.
Приведенное активное сопротивление ротора
r2  sн (rн  rн2  rм2 )  0,08(5,64  5,642  1,362 )  0,888 Ом.
Определяем приведенный ток I 2 при номинальном режиме работы двигателя:
I 2 
Uн
220

 19 А.
r2 2
0
,
888
(r1  )  xн2
(0,422 
) 2  1,29 2
s
0,08
Для Г – образной схемы замещения (см. рис. 39) составим два уравнения баланса активных
реактивных мощностей при номинальном режиме работы двигателя:
U н I1 cos н  (r1 
r2
)(I 2 ) 2  r10 I102 ;
sн
U н I1 cos  н  xн ( I 2 ) 2  x10 I102 .
Активная мощность двигателя в режиме холостого хода, отнесенная к одной фазе обмотки
статора,
P10  r10 I102  U н I1 cos  н  (r1 
 220  26,4  0,78  (0,422 
r2
)  ( I 2 ) 
sн
0,888
)  19 2  330 Вт.
0,08
Реактивная мощность двигателя в режиме холостого хода, отнесенная к одной фазе
обмотки статора,
Q10  x10 I102  U н I1 sin  н  xк ( I 2 ) 2 .
Величина
cos н = 0,78 соответствует sin н = 0,625, поэтому
Q10  220  26,4  0,625  1,29  19 2  3165 вар.
Полная мощность двигателя в режиме холостого хода, отнесенная к одной фазе обмотки
статора,
s10  P102  Q102  3302  31652  3170 В·А.
Ток холостого хода
I10 
s10 3170

 14,4 А.
Uн
220
Коэффициент мощности при холостом ходе двигателя
cos 10 
P10 330

 0,1 .
s10 3170
Сопротивления при холостом ходе:
r10 
Uн
220
cos 10 
 0,1  1,52 Ом;
I10
14,4
x10 
Uн
220
sin 10 
 0,995  15,2 Ом.
I10
14,4
Электрические машины постоянного тока.
После изучения данного раздела студент должен: 1) знать основные конструктивные
элементы машин постоянного тока: статор, обмотка статора, якорь, обмотка якоря; термины:
щеточно-коллекторный узел, геометрическая и физическая нейтрали, реакция якоря, коммутация,
противо-э.д.с.; классификацию машин постоянного тока по способу возбуждения; внешние
характеристики генераторов постоянного тока всех способов возбуждения; механические
характеристики двигателей постоянного тока всех способов возбуждения; способы пуска
двигателей постоянного тока; способы регулирования скорости вращения двигателей постоянного
тока;
2) понимать назначение основных конструктивных элементов машин постоянного тока;
принцип действия генератора и двигателя постоянного тока; уравнения электрического состояния
генератора и двигателя постоянного тока; назначение пусковых и регулировочных сопротивлений;
энергетические диаграммы генератора и двигателя, постоянного тока;
3) уметь включать в сеть, регулировать скорость и реверсировать двигатель постоянного
тока; отличать до внешнему виду машину постоянного тока от других типов электрических машин;
ориентироваться в паспортных данных машины и определять номинальный момент; выбирать
двигатель применительно к заданным технически условием.
Изучение электрических машин постоянного тока надо начинать с их принципа работы и
устройства. Учитывая, что машина постоянного тока обратима, т.е. может работать как в режиме
генератора, так и в режиме двигателя, изучение таких вопросов, как коллектор, реакция якоря,
электромагнитный момент, возбуждение и ряд других необходимо рассматривать в
сопоставлении для обоих режимов! Очень важно правильно понимать связь между напряжением
на зажимах машины U , ее э.д.с. E и падением напряжения rя I я в обмотке якоря для
генераторного и двигательного режимов:
для генератора
E  U  rя I я ;
для двигателя U
 E  rя I я .
Изучая работу машин постоянного тока в режиме двигателя, надо обратить особое
внимание на пуск, регулирование скорости вращения и вращающий момент двигателя, а в режиме
генератора — на самовозбуждение. Характеристики генераторов и двигателей дают наглядное
представление об эксплуатационных свойствах электрических машин.
Рассмотрим несколько примеров решения задач.
Задача 1. Дан генератор параллельного возбуждения с номинальными данными:
кВт, U н = 230 В и скорость вращения
Pн = 5,2
rя = 0,75
nн = 2860 об/мин. Сопротивление обмотки якоря
Ом, сопротивление цепи возбуждения rв = 154 Ом, механические и магнитные потери составляют
4% от номинальной мощности генератора. Определить момент на валу первичного двигателя.
Р е шени е. Номинальный ток нагрузки
Iн 
Pн 5,2  1000

 22,6 А.
Uн
230
Ток возбуждения
Iв 
U н 230

 1,5 А.
rн 154
Ток якоря при нормальной нагрузке
I я.н  I н  I в  22,6  1,5  24,1 А.
Э.д.с. генератора
E  U н  rя I я.н  230  0,75  24,1  248 В.
Потери в обмотке якоря и в цепи возбуждения
Pя  rя I я2.н  0,75  24,12  435 Вт;
Pв  rв I в2  154  1,52  346 Вт.
Сумма механических и магнитных потерь
Pмех  Pмаг 
4
 5,2  103  208 Вт.
100
Суммарные потери при номинальной нагрузке
 P  435  346  208  989 Вт  0,989 кВт.
Мощность на валу первичного двигателя
Pмех.н   P  Pн  0,989  5,2  6,189 кВт.
К.п.д. генератора при номинальной нагрузке
Pн
н 
Pмех.н
 100 
5,2
 100  84 %.
6,189
Момент на валу первичного двигателя при номинальной нагрузке генератора
M Д  9550
Pмех.н
6,189
 9550
 20,7
nн
2860
Н·м.
Задача 2. Двигатель параллельного возбуждения, присоединяется к сети с напряжением
Uн
= 220 В, потребляет при номинальной нагрузке ток
2,35 А. Сопротивление обмотки якоря
Номинальная скорость вращения
nв
rя
Iн
= 20,5 А, а при холостом ходе -
= 0,75 Ом, а в цепи возбуждения
rв
I0
=
= 258 Ом.
= 1025 об/мин. Определить номинальную мощность
двигателя (на валу), номинальный к.п.д., номинальный вращающий момент, пусковой ток при
пуске двигателя без пускового реостата, сопротивление пускового реостата для условия
I п  2,5I н
и пусковой момент при пуске двигателя с реостатом. При решении принять, что
магнитные и механические потери не зависят от нагрузки.
Решение. Номинальная мощность на валу двигателя
Pн  P1н   P ,
где
 P - потери в двигателе; P1н - потребляемая мощность;
P1н  U н I н  220  20,5  4510 Вт.
Для определения потерь в цепи якоря и цепи возбуждения надо знать ток в цепи якоря
и ток возбуждения I в :
Iв 
U н 220

 0,85 А;
rв
258
I я.н  I н  I в  20,5  0,85  19,65 А.
Потери в обмотке якоря и в цепи возбуждения
2
Pя.н  rя I я.н
 0,75  19,652  290 Вт;
I я.н
Pв  rв I в2  258  0,85  186 Вт.
Магнитные и механические потери
Pм  P0  Pя.0  Pв ,
где
P0  U н I0  220  2,35  517
Вт;
Pя.0
- потребляемая мощность при холостом
ходе двигателя:
Pя.0  rя ( I 0  I н ) 2  0,75  (2,35  0,85) 2  1,7 Вт;
Pм  517  1,7  186  329,3 Вт;
 Pн  290  186  329,3  805,3 Вт;
Pн  4510  805,3  3704,7
Вт;
Номинальный к.п.д.
Pн
3,71
 100 
 100  82,2 %
P1н
4,51
y 
Номинальный вращающий момент
M н  9550
Pн
3,71
 9550
 34,6
nн
1025
Н·м.
Пусковой ток двигателя при пуске без реостата
Iп 
U н 220

 293 А.
rя
0,75
Сопротивление пускового реостата определяется из равенства
I п  2,5 I я.н 
Uп
rя  rр
,
откуда
rр 
Uн
220
 rя 
 0,75  3,73 Ом.
Iн
2,5  19,65
Определяем пусковой момент двигателя при пуске с реостатом. Известно, что вращающий
момент двигателя определяется уравнением
M  Cм I я .
Для режима номинальной нагрузки выражение (18) принимает вид
M н  Cм I я.н ,
а для пускового режима
M п  Cм I п .
Полагая магнитный поток в двигателе постоянным, возьмем отношение моментов
M н I я.н
,

Mп
Iп
откуда
Mн  Mп
I я.н
2,5  19,65
 34,6
 86,5 Н·м.
Iп
19,65
Задача 3. Двигатель последовательного возбуждения работает от сети с напряжением 220 В.
Номинальный вращающий момент двигателя и номинальная скорость вращения соответственно
равны
Mн
= 75 Н·м,
nн
= 1020 об/мин, сопротивления обмоток якоря и возбуждения rя = 0,4
Ом, rв = 0,3 Ом. Номинальный к.п.д.  н = 81,5 %. Определить: 1) мощность на валу двигателя и
мощность, потребляемую из сети при номинальной нагрузке; 2) ток двигателя; 3) противо-э.д.с. и
электромагнитную мощность (мощность передаваемую на якорь); 4) потери в двигателе при
номинальной нагрузке и сопротивление пускового реостата, при котором пусковой ток превышает
номинальный в два раза.
Решение. Нормальная мощность двигателя.
Pн 
M н nн 75  1020

 8 кВт.
9550
9550
Потребляемая мощность
P1н 
Pн
н

8
 9,8 кВт.
0,815
Номинальный ток двигателя
Iн 
P1н 9,8  1000

 44,5 А.
Uн
220
Полученный ток является током обмотки якоря и обмотки возбуждения
I я.н  I в  44,5 А.
Противо-э.д.с., наводимая в обмотке якоря
E  Uн  (rя  rв ) I н  220  (0.4  0,3)  44,5  188,5 В.
Электромагнитная мощность
Pэм  EI я.н  188,8  44,5  8400 Вт.
Магнитные и механические потери
Pм  Pэм  Pн  8,4  8  0,4 кВт.
Потери в обмотке якоря и обмотки возбуждения
Pя.н  rя I я2.н  0,4  44,52  792 Вт.
Pв  rв I в2  0,3  44,52  595 Вт.
Проверим полученный результат
 Pн  P1н  Pн  9,8  8  1,8 кВт.
Суммарные потери в двигателе
 Pн  400  792  595  1787 Вт.
Сопротивление пускового реостата
rр 
Uн
220
 (rя  rв ) 
 0,7  1,77 Ом.
2I я.н
2  44,5
Принципы выбора электродвигателей.
Аппаратура управления и защиты
электротехнических устройств.
После изучения настоящего раздела студент должен:
1) знать области применения электропривода и его преимущества перед другими типами
приводов; основаны, электротехнические и механические устройства, входящие в состав
электропривода; режимы работы электропривода; типы электропривода; механические
характеристики основных производственных механизмов; основные аппараты ручного и
автоматического управления электроприводом; условные графические обозначения двигателей и
элементов устройств управления; основные аппараты защиты электротехнических устройств;
2) понимать нагрузочные диаграммы и их построение; влияние температуры окружающей
среды на нагрузочную способности двигателя; сущность методов эквивалентного тока, момента
мощности для расчета мощности приводного электродвигателя; назначение и принцип действия
аппаратов управления; работу типовых схем управления электроприводом; назначение
принцип действия аппаратуры защиты;
и
3) уметь определять по механическим характеристикам двигателя и рабочего механизма
частоту вращения и момент в установившемся режиме; рассчитывать мощность двигателя по
нагрузочной диаграмме рабочего механизма; выбирать по каталогу двигатель нужного
исполнения, соответствующего условиям окружающей среды и режиму работы
производственного механизма, проверить выбранную мощность двигателя по пусковым условиям
и перегрузочной способности; читать несложные схемы управления электроприводами;
приводить в действие устройстве электропривода общепромышленных механизмов; выбирать
соответствующие аппараты управления и защиты.
Основными вопросами, которые нужно изучить, в данной теме, являются: сравнительная
оценка свойств и область применения электрических двигателей как постоянного, так и
переменного токов, выбор мощности двигателя для различных режимов работы; аппаратура
управления электродвигателями; схемы электроснабжения предприятия; внутризаводские
силовые и осветительные сети, их устройства и расчет.
Электропривод (выбор мощности двигателя).
Выбор двигателя — один из ответственных этапов проектирования электропривода, так как
именно двигатель в значительной степени определяет технические и экономические качества
привода в целом. Из многочисленных типов двигателей переменного и постоянного токов для
привода той или иной производственной, машины должен быть выбран такой, который наиболее
полно удовлетворял бы технико-экономическим требованиям. Это значит, что двигатель должен
быть наиболее простым по управлению, надежным в эксплуатации и иметь наименьшую
стоимость, массу и габариты, а также высокие энергетические показатели. В сравнении со всеми
существующими типами двигателей этим требованиям в наибольшей мере отвечают асинхронные
двигатели с короткозамкнутым ротором. При выборе двигателя такого типа необходимо
выяснить, Удовлетворяются ли технические требования: допустимое уменьшение скорости при
увеличении нагрузки, допустимая величина повторных включений, возможность быстрого и
надежного пуска,
В напряженных режимах работы привода, с большой частотой включений, где требуется
повышенный или ограниченный пусковой момент, а также регулирование частоты вращения в
узких пределах, применяют асинхронные двигатели с контактными кольцами. Для
нерегулируемых приводов средней и большой мощности, работающих в продолжительном
режиме с редкими пусками, рекомендуется применять синхронные двигатели. Они отличаются
более высоким к.п.д. и допускают регулирование коэффициента мощности за счет компенсации
реактивной мощности. При необходимости плавного, и глубокого регулирования скорости, а
также при большой частоте включений применяются двигатели постоянного тока. При выборе
мощности двигателя основными исходными данными являются требуемые моменты, которые
должны быть приложены к валу механизма, т.е. необходимо иметь нагрузочные диаграммы
электропривода P  f (t ) или M  f (t ) которые могут быть заданы как в виде графика, так и в
виде таблицы.
P, кВт
0
5
P3  6кВт
P1
P2  8кВт
P1  12кВт
12
11
10
9
8
7
6
5
4 t  20с
3 1
2
1
t 2  30с
tц
10
15
20
25
30
35
40
45
50
55
t3  15с
60
t1
65
70
t, с
Рис. 40
Задача 1. Определить необходимую мощность двигателя для привода механизма, режим
работы которого задан нагрузочной диаграммой на рис. 40. По технологическим условиям
следует использовать асинхронный двигатель с короткозамкнутым ротором. Двигатель должен
развивать частоту вращения n = 980 об/мин. Помещение, где будет установлен двигатель, - сухое,
без пыли и грязи.
Решение. В нашем случае режим работы представляет собой длительную переменную
нагрузку. Мощность двигателя подбирается при подобных режимах работы по эквивалентной
мощности, которая равна
n
Pэ 
 (Pк2tк )
к 1
tц
,
где t ц - время цикла работы
tц  t1  t 2  t3  20  30  15  65 с;
12 2  20  8 2  30  6 2  15
Pэ 
 9,05 кВт.
65
По данным каталога в качестве приводного двигателя может быть использован асинхронный
короткозамкнутый двигатель в защищенном исполнении типа А2-61-6; Pн = = 10 кВт, nн = 965
об/мин,  н = 0,870, M п M н = 1,2, M м M н = 1,8.
В ряде случаев момент нагрузки на отдельных участках может оказаться больше
максимально допустимого момента двигателя, и синхронный двигатель может остановиться.
Поэтому после выбора двигателя его необходимо проверить по перегрузочной способности
исходя из условия M макс  M макс.д , где M макс — максимальный момент на валу двигателя;
M макс.д
— максимально допустимый момент двигателя.
Для
асинхронного
двигателя
M макс.д  0,9M к Здесь M к — критический (максимальный) момент двигателя; В вашем примере:
номинальный момент двигателя
Mн 
9550  P1 9550  10

 99 Н·м
nн
965
максимальный (критический) момент
M к  M н  1,8  99  178 Н·м
максимальный статический момент
Mс 
9550  P1 9550  12

 117 Н·м
n
980
По перегрузочной способности двигатель проходит, так как выполняется условие
0,9M н  0,9  178  160  M 0  117 .
В том случае, когда нагрузочные диаграммы заданы моментом M  f (t ) или током
I  f (t ) , мощность двигателей выбирают либо по эквивалентному моменту:
n
 (M k2t k )
Mэ 
k 1
tц
n
, либо по эквивалентному току I э 
 (I
k 1
2
k k
t )
tц
.
Задача 2. Определить необходимую мощность0 двигателя для привода механизма,
работающего в повторно-кратковременном режиме, который задан нагрузочной диаграммой,
изображенной на рис. 41. Двигатель должен развивать частоту вращения n  720 об мин.
Решение. Определяем эквивалентный момент за рабочее время:
n
 (M
M раб 
k 1
2
k k
t )
tp
100 2  10  70 2  30  60 2  20  40 2  10

 63,2 Н  м .
10  30  20  10
Определяем мощность, соответствующую эквивалентному моменту за рабочее время:
Pраб 
M раб n
9550

63,2  720
 4,75кВт .
9550
Определяем относительную продолжительность включения:
ПВ 
tp
Tц

tp
t p  t0

70
 0,54.
130
В каталогах для двигателей повторно-кратковременного режима номинальная мощность
указывается для следующих стандартных относительной продолжительности включения ПВ:
0,15; 0,25; 0,4 и 0,6. В том случае, когда расчетная ПВ отличается от стандартного значения,
рассчитанная по нагрузочной диаграмме мощность пересчитывается по формуле:
ПВ раб
  Pраб
Pраб
ПВном
.
Для ПВном  0,6 получим
0,54
 4,5кВт .
0,6
  4,75
Pраб
По данным
каталога по аналогии с задачей 1, может быть подобран двигатель для
расчетной мощности 4,5 кВт и ПВном  0,6 .
M ,Нм
100
M1
90
80
70
60
50
40
30 t
20 1
10
0
M1
M2
M3
t2
10
20
t01
tц
30
40
50
M4
t4
t3
60
70
80
90
t02
t1
100 110 120 130 140 150 t , с
Рис. 41
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Трансформаторы.
1. Назначение и принцип работы трансформатора.
2. Начертите векторную диаграмму трансформатора в режиме холостого хода.
3. Почему обмотки высшего и низшего напряжений размещают на общем стержне?
4. Напишите уравнение магнитодвижущих сил в трансформаторе.
5. Объясните, почему магнитный поток трансформатора практически не зависит от
нагрузки?
6. Какие потери в трансформаторе являются постоянными и какие переменными?
7. Напишите уравнения электрического состояния для первичной и вторичной обмоток и
объясните смысл каждого из членов этих уравнений.
8. Как устроен трехфазный трансформатор?
9. Каковы преимущества и недостатки автотрансформатора?
10. Какие погрешности возникают при использовании трансформаторов напряжений и тока
для измерения напряжении и тока?
Магнитные цепи с постоянной и переменной магнитодвижущими
силами.
1. Перечислите достоинства и недостатки магнитных усилителей.
2. Как изменяются вольт-амперные характеристики, дросселя с подмагничиванием при
увеличении тока в управляющей обмотке  y ?
3. В чем заключается принцип действия магнитного усилителя?
4. Как влияют на характеристику вход — выход изменения нагрузки, напряжения и частоты
источника питания?
5. От чего зависят постоянная времени и коэффициент усиления магнитного усилителя?
6. Что такое «обратная связь», как она реализуется в магнитных усилителях и какие
изменения в работе она, вызывает?
7. Нарисуйте характеристики управления магнитного усилителя без обратной и с обратной
связями и объясните их разницу.
8. Какими способами можно регулировать коэффициент обратной связи?
9. Объясните принцип действия магнитного усилителя с внутренней обратной связью.
10. Для чего применяется смещение в магнитном усилителе?
11. Составьте уравнение электрического состояния рабочей цепи магнитного усилителя.
12. Что такое коэффициент усиления и как его можно определить?
Электрические машины переменного тока.
1. Объясните принцип работы асинхронного двигателя.
2. Как образуется вращающееся магнитное поле?
3. Объясните, в чем заключается аналогия между асинхронным двигателем и
трансформатором?
4. От каких величин зависит вращающий момент асинхронного двигателя?
5. Какая часть кривой n  f (M ) соответствует устойчивой работе двигателя и какая –
неустойчивой?
6. Перечислите возможные способы регулирования скорости вращения асинхронного
двигателя.
7. Почему при увеличении нагрузки на валу асинхронного двигателя растут токи статора и
ротора?
8. Объясните работы однофазных асинхронных двигателей и их недостатки.
9. Изложите устройство синхронной машины.
10. Начертите характеристику холостого хода синхронного генератора.
11. Как осуществляется пуск синхронных двигателей?
12. Начертите механическую и угловую характеристики синхронного двигателя.
13.Объясните явление выпадения из синхронизма синхронного двигателя.
14. Почему ток холостого хода асинхронного двигателя больше, чем у трансформатора?
15. Почему cos  асинхронного двигателя при холостом ходе значительно ниже, чем при
номинальной нагрузке?
16. Почему при введении реостата в цепь ротора асинхронного двигателя с контактными
кольцами пусковой ток уменьшается, а пусковой момент возрастает?
17. Объясните, как отличаются токи короткозамкнутого асинхронного, двигателя при
соединении обмотки статора звездой и треугольником при пуске от одной и той же сети. Как
отличаются при этом вращающие моменты?
18.
Чем
определяется
величина
активной
мощности
генератора при работе в системе? Как она регулируется на электростанции?
синхронного
19. Как изменить режим работы синхронной машины?
20. От чего зависит максимальный момент синхронного двигателя?
21. При каких условиях синхронный двигатель работает в качестве синхронного
компенсатора?
Электрические машины постоянного тока.
1. Объясните устройство машины постоянного тока.
2. Объясните принцип работы машины постоянного тока в качестве генератора и двигателя.
3.Объясните назначение и устройство щеточно-коллекторного узла.
4. От каких величин зависит э. д. с. обмотки якоря?
5. От каких величин зависит вращающий момент двигателя постоянного тока?
6. Каковы условия самовозбуждения генераторов постоянного тока?
7. Напишите уравнения электрического состояния для генератора и двигателя.
8. Какие двигатели постоянного тока применяются в станках и крановых механизмах?
9. Какие существуют способы регулирования частоты вращения двигателей постоянного
тока?
10. Объясните образование постоянного напряжения на зажимах якоря генератора.
11. Чем отличаются схемы и обмотки генераторов различных способов возбуждения?
12. Почему при одном и том же токе якоря напряженно шунтового генератора ниже, чем
ври независимом возбуждении?
13. Как отражается на работе шунтового двигателя снижение подведенного напряжения?
14. Как происходит процесс саморегулирования двигателя при изменении момента на валу?
15. Сопоставьте три способа регулирования частоты вращения двигателя и дайте их оценку.
Принципы выбора электродвигателей.
1. Какие типы электроприводов вы знаете?
2. Напишите уравнение движения электропривода.
3. Как осуществляется приведение моментов и сил к валу электродвигателя?
4. Изобразите механические характеристики широко распространенных производственных
механизмов.
5. Какие вы знаете режимы работы производственных механизмов?
6. От каких причин зависит выбор приводного электродвигателя по типу и роду тока?
7. Как производится расчет мощности и выбор двигателя для длительного режима работы?
8. Как производится расчет мощности и выбор двигателя для кратковременного и повторнократковременного режимов работы?
КОНТРОЛЬНАЯ РАБОТА 2.
Задача 1. Для трехфазного трансформатора, параметры которого приведены в табл. 6,
определить коэффициент мощности холостого хода cos  0 коэффициент мощности cos  при
нагрузках   0,7 и cos  2 ,   0,7 и cos  2  0,75 , сопротивления первичной и вторичной
обмоток
r1 ,
x1
r2
и
x2 ,
расчетные
сопротивления
z0 ,
r0
и
x0 ,
угол магнитных потерь  . Построить векторную диаграмму трансформатора для нагрузки
  0,8 и cos  2  0,75 . Построить внешнюю характеристику U 2  f1 ( ) и зависимость к.п.д. от
нагрузки   f 2 ( ) для cos  2  0,75 . Начертить Т-образную схему замещения трансформатора.
Задача 2. варианты 0—25. Двигатель параллельного возбуждения, номинальное
напряжение которого U н при номинальной нагрузке потребляет ток I н , а при холостом ходе —
I 0 Номинальная скорость вращения nн , сопротивление обмотки якоря rя , сопротивление цепи
возбуждения rв . Магнитные и механические потери принять постоянными при всех режимах
работы двигателя (табл. 7). Определить: номинальную мощность двигателя Pн , номинальный
вращающий момент M н , номинальный к.п.д.  н , ток I м , при котором мощность, на валу
двигателя достигнет максимального значения, величину этой мощностей P2м и к.п.д.  м .
Данные для расчета
Вариант
Группа соединений
0
1
2
3
4
Y Y0  0
Y   11
Y Y0  0
Y Y0  0
Номинальная
мощность
Номинальное напряжение
S н , кВ  А
U 1н , В
U 2н , В
10
6300
20
Напряжение
короткого
замыкания
Мощность
короткого
замыкания
Мощность
холостого хода
Ток холостого
Pо , Вт
хода I о , %
uк , %
Pк , Вт
400
5,0
335
105
10,0
6300
230
5,0
600
180
9,0
30
10000
400
5,0
850
300
9,0
50
10000
400
5,0
1325
440
8,0
75
10000
230
5,0
1875
590
7,5
100
10000
525
5,0
2400
730
7,5
180
10000
525
5,0
4100
1200
7,0
240
10000
525
5,0
5100
1600
7,0
320
35000
10 500
6,5
6200
2300
7,5
420
10000
525
5,5
7000
2100
6,5
25
6000
230
4,5
600
125
3,0
25
10000
230
4,7
690
125
3,0
Y Y0  0
5
6
7
8
9
Y Y0  0
Y   11
Y Y0  0
Y   11
Y Y0  0
10
11
Y Y0  0
12
Y Y0  0
25
6000
400
4,5
600
125
3,0
13
Y   11
25
10000
400
4,7
690
125
3,0
14
Y   11
40
10000
230
4,5
880
180
3,0
40
6000
230
4,5
880
180
3,0
Y Y0  0
15
16
Y Y0  0
40
6000
400
4,7
1000
180
3,0
17
Y Y0  0
40
10000
400
4,0
690
125
3,2
18
Y   11
63
6000
230
4,5
1280
260
2,8
19
Y   11
63
6000
400
4,5
1280
260
2,8
20
Y   11
63
10000
230
4,7
1470
260
2,8
21
Y   11
63
10000
400
4,7
1470
260
2,8
22
Y Y0  0
63
2000
400
4,7
1470
260
2,8
23
Y Y0  0
63
20000
230
4,7
1470
260
2,8
24
Y Y0  0
63
2000
400
4,5
1280
260
2,8
100
10000
230
4,7
2270
365
2,6
100
10000
400
4,7
2270
365
2,6
25
Y Y0  0
26
Y   11
Y   11
27
100
6000
230
4,5
1970
365
2,6
28
Y   11
100
6000
400
4,5
1970
365
2,6
29
Y Y0  0
100
20000
230
4,7
2270
465
2,6
30
Y   11
100
20000
400
4,7
2270
465
2,6
31
Y Y0  0
100
35000
230
4,7
2270
465
2,6
100
35000
400
4,7
2270
465
2,6
33
160
6000
230
4,5
2650
540
2,4
34
160
6000
400
4,5
2650
540
2,4
160
10000
230
4,5
3100
540
2,4
160
10000
400
4,5
3100
540
2,4
160
6000
690
4,5
2650
540
2,4
250
6000
230
4,5
3700
780
2,3
250
6000
400
4,5
3700
780
2,3
250
10000
230
4,7
4200
780
2,3
250
10000
690
4,7
4200
780
2,3
32
Y   11
Y Y0  0
Y   11
35
Y   11
36
37
38
Y Y0  0
Y Y0  0
Y   11
39
Y   11
40
41
Y   11
42
Y Y0  0
400
3000
400
4,5
5500
1080
3,2
43
Y Y0  0
400
6000
400
4,5
5500
1080
3,2
Y Y0  0
Y Y0  0
Данные для расчета
Вариант
Uн, В
I н, А
I 0, А
rя , Ом
rв , Ом
nн , об мин
0
220
15
1,6
1,2
180
1025
1
220
53
5,3
0,212
33
1225
2
115
100
9,5
0,11
50
1000
3
110
267
5
0,04
27,5
1100
4
220
16,3
1,78
1,16
75
1025
5
110
7,8
0,7
0,8
210
1240
6
220
19,8
2,0
1,5
150
960
7
110
35
3,2
0,6
60
1400
8
220
32
2,8
0,94
120
1600
9
220
34
3,0
0,45
110
1100
10
110
9,5
0,9
1,9
200
850
11
110
20
1,8
0,7
80
940
12
220
15
1,5
0,82
200
1350
13
110
8,2
0,8
1,4
220
1450
14
220
20,5
2,35
0,74
258
1025
15
220
40
4,2
0,52
190
1420
16
110
10,5
1,2
1,2
160
960
17
110
18,6
2,0
0,9
120
825
18
220
16
1,8
0,6
270
1600
19
220
32
3,5
0,62
200
1350
20
110
28
3,2
0,55
80
875
21
110
25
2,6
0,58
90
1110
22
220
60
6,8
0,40
130
935
23
220
50
5,7
0,40
150
1340
24
220
102
9,5
0,12
110
750
25
220
151
15
0,07
75
1000
Указание. Для определения тока, при котором мощность на валу двигателя достигает
максимального
значения;
необходимо
найти
первую производную
P  U н  rя ( I м  I в )( I м  I в )  Pм и приняв ее к нулю, определить I м .
dp
dI м
выражения
Задача 2, варианты 26—50. Двигатель параллельного возбуждения, номинальное
напряжение которого U н , развивает номинальную мощность Pн . Номинальная скорость
вращения якоря n н и номинальный к.п.д.  н . Потери мощности в цепи якоря Pя и в цепи
возбуждения Pв , заданы в процентах от потребляемой мощности двигателя P1н (табл. 8).
Определить: ток в цепи возбуждения, ток якоря при номинальной нагрузке, номинальный
вращающий момент при пуске двигателя с пусковым реостатом.
При определении пускового момента воспользоваться указаниями к предыдущей задаче.
Задача 3, варианты 0-25. Трехфазный асинхронный двигатель с фазным ротором, обмотки
статора и ротора которого соединены звездой, включен в сеть под номинальное напряжение
U н с частотой f  50Гц.
Данные для расчета
Вариант
Pв , %
nн , об мин
 н ,%
4,8
980
86,5
5,2
4,8
2250
86,0
4,0
5,0
4,2
1025
82,2
220
6,6
6,2
4,1
2400
85,5
220
4,4
6,2
4,8
2100
84,5
4,8
1000
85,0
4,4
2250
83,0
Uн, В
Pн, кВт
26
110
60
27
220
10
28
220
29
30
Pя , %
6,5
31
220
2,5
32
220
10
5,8
33
110
77
5,3
4,2
1050
85,5
34
110
80
5,0
4,5
1150
85,8
35
110
92
5,4
4,1
970
86,5
5,0
1050
85,5
5,3
36
110
66
37
110
35
6,2
5,2
2200
84,5
38
110
45
6,3
4,6
1500
85,5
39
220
15
5,7
4,0
1000
84,5
40
220
10
5,0
4,2
970
85,5
5,0
2200
84,0
5,2
41
220
5,8
42
220
19
6,0
4,5
980
86,5
43
220
29
4,8
4,3
2520
86,0
44
220
46,5
5,0
4,8
1025
82,2
45
220
14
5,4
4,6
2400
84,0
4,2
2100
85,5
4,0
46
220
20,5
47
220
33,5
5,1
4,0
1000
84,5
48
220
8,5
5,5
4,1
2250
85,5
49
220
13,5
4,0
4,2
1050
85,0
50
110
60
4,8
4,0
1150
84,5
5,0
Определить: номинальный ток статора I 1н , номинальный M н и максимальный M м
моменты, сопротивления r2 , x н , r10 и x10 в Г-образной схеме замещения (см. рис. 39),
приведенный ток ротора I 2 , ток в статоре в режиме холостого хода I 10 и коэффициент
мощности cos 10 . Данные для расчета приведены в табл. 9.
Задача 3, варианты 26-50. Трехфазный асинхронный двигатель с короткозамкнутым
ротором номинальная мощность которого Pн включен в сеть под, номинальное напряжение
U н с частотой I  50 Гц . Определить: номинальный I н и пусковой I п токи, номинальный M н
пусковое M п и максимальный M м моменты, полные потери в двигателе при номинальной
нагрузке Pн . Как изменится пусковой момент двигателя при снижении напряжения на его
зажимах на 15% и возможен ли пуск двигателя при этих условиях с номинальной нагрузкой?
Данные для расчета приведены в табл. 10.
Задача 4, для заданного в табл. 11 режима нагрузки производственного механизма
построить нагрузочную диаграмму P  f (t ) и выбрать мощность асинхронного
короткозамкнутого двигателя.
Данные для расчета
вар.
Uн, В
Pн , кВт
nн , об мин
 н ,%
cos  н
Mм Mн
r1 , Ом
m1  m2
p
0
220
40
1440
90,0
0.84
2,0
0,072
3
2
1
220
55
1440
90,5
0,84
2,0
0,039
3
2
2
220
75
1450
90,5
0.85
2,0
0,032
3
2
3
220
100
1450
90,5
0,85
2,0
0,021
3
2
4
220
30
960
89,0
0,84
1,8
0,092
3
3
5
220
40
960
89,0
0,85
1,8
0,060
3
3
6
220
55
960
89,0
0,86
1,8
0,059
3
3
7
220
75
960
90,5
0,86
1,8
0,035
3
3
8
220
22
720
87,5
0,79
1,7
0,157
3
4
9
220
30
720
87,5
0,79
1,7
0,093
3
4
10
220
40
720
87,5
0,81
1,7
0,086
3
4
11
220
55
720
90,0
0,081
1,7
0,051
3
4
12
220
10
1420
85,0
0,82
2,0
0,270
3
2
13
220
7,5
960
84,0
0,82
1,8
0,495
3
3
14
220
10
960
85,0
0,83
1,8
0,340
3
3
15
220
5,5
710
82,0
0,72
1,7
0,645
3
4
16
220
2,2
875
64,0
0,72
2,3
0,750
3
3
17
220
3,5
910
70,5
0,73
2,5
0,740
3
3
18
220
5,0
940
74,5
0,68
2.9
0,685
3
3
19
220
7,5
945
78,5
0,69
2,8
0,490
3
3
20
220
11,0
953
82,5
0,71
3,1
0,325
3
3
21
220
7,5
720
77,5
0,69
2,6
0,450
3
4
22
220
11,0
720
81.0
0,70
2,9
0,475
3
4
23
220
16,0
710
82,5
0,74
3,0
0,355
3
4
24
220
22,0
710
84,5
0,67
3,0
0,180
3
4
25
220
30,6
720
86,0
0,71
3,0
0,095
3
4
Данные для расчета
вар.
26
Uн, В
Pн , кВт
220
0,8
S н ,%
н
cos  н
p
Mм Mн
Mп Mн
Iп Iн
0,78
0.86
1
2,2
1,9
7,0
0,795
0,87
1
2.2
1,9
7,0
0,805
0,88
1
2,2
1,8
7,0
0,83
0,89
1
2,2
1,8
7,0
0,845
0,89
1
2,2
1,7
7,0
0,855
0,89
1
2,2
1,7
7,0
0,86
0,89
1
2,2
1,7
7,0
0,87
0,89
1
2,2
1,6
7,0
0,88
0,89
1
2,2
1,5
7,0
0,88
0,89
1
2,2
1,5
7,0
0,88
0,90
1
2,2
1,2
7,0
3,0
27
220
0,1
3,0
28
220
1,5
4,0
29
220
2.2
4,5
30
220
3,0
3,5
31
220
4,0
2,0
32
220
5.5
3.0
33
220
7.5
3,5
34
220
10
4,0
35
220
13
3,5
36
220
17
3,5
37
220
22
0,88
0,90
1
2,2
1,1
7,0
0,89
0,90
1
2.2
1,1
7,0
0,89
0,91
1
2,2
1,0
7,0
0,90
0,92
1
2,2
1,0
7,0
0,90
0,92
1
2,2
1,0
7,0
0,915
0,92
1
2,2
1,0
7,0
0,885
0,87
2
2,0
1,4
7,0
0,885
0,889
2
2,0
1,3
7,0
0,89
0,89
2
2,0
1,3
7,0
0,90
0,90
2
2.0
1,2
7,0
0,91
0,91
2
2,0
1,2
7,0
0,925
0,92
2
2,0
1,1
7,0
3,5
38
220
30
3,0
39
220
40
3,0
40
220
55
3,0
41
220
75
3,0
42
220
100
2,5
43
380
10
3,0
44
380
13
3,0
45
380
17
3,0
46
380
22
3,0
47
380
30
3,0
48
380
40
49
380
55
3,0
0,925
0,92
2
2,0
1,1
7,0
50
380
75
3,0
0,925
0,92
2
2,0
1,1
7,0
3,0
Данные для расчета
Вариант
t, с
0
P , кВт
50
15
25
10
0
13,5
8
1
20
10
10
20
23,5
8
5
0
25
10
2
18
30
10
20
30
8
4
15
10
25
3
60
100
60
45
10
25
10
0
18
30
4
30
15
40
60
45
0
4
8
0
5
5
50
20
20
50
30
15
4
30
15
10
15
25
10
30
5
0
15
25
6
35
60
7
10
75
15
50
12
6
20
3
15
30
8
7
3
2,5
4
1,5
8
6
0
4
3,5
9
1
1,5
2,5
1,5
3
20
10
6
8
8
10
1,5
4
50
3,5
15
20
10
6
8
8
20
10
23,5
8
6
0
4
3,5
11
10
10
12
18
30
10
20
3,0
8
4
15
10
25
13
60
100
60
45
10
6
20
3
15
30
14
30
15
40
60
45
30
5
0
4
25
15
30
20
10
50
30
8
6
0
4
3,5
15
25
10
15
4
30
15
10
16
35
60
17
10
75
15
50
20
0
4
8
0
5
18
7
3
2,5
4
1,5
10
10
0
18
30
19
1
1,5
2,5
1,5
3
8
4
15
10
25
20
1
4
50
3,5
15
8
6
0
4
3,5
20
10
21
10
10
23,5
20
10
6
8
8
22
18
30
10
20
30
26
20
13
15
30
23
60
100
60
45
10
30
5
0
15
25
24
30
15
40
60
45
15
4
30
15
10
25
50
20
10
50
30
0
4
8
0
5
15
25
10
30
5
0
15
25
26
35
60
27
20
75
15
50
2
25
10
0
13,5
8
28
7
3
2,5
4
1,5
8
5
0
25
10
29
1
1,5
2,5
1,5
3
0
4
8
0
50
30
1
4
30
3,5
20
8
5
0
25
10
30
45
40
20
10
6
8
8
31
15
20
32
10
15 10
10
40
30
8
5
0
25
10
33
20
10
15
20
35
8
4
15
10
25
34
50
10
15
20
20
30
5
0
15
25
35
20
20
20
15
30
20
10
6
8
8
25
8
6
0
4
3,5
15
36
30
15
15
37
20
20
20
15
15
8
6
10
6
5
38
10
5
50
15
10
30
5
0
15
25
39
25
45
50
5
60
0
4
8
0
5
40
10
3
30
60
10
25
10
0
18
30
40
15
Данные для расчета
Вариант
t, с
P , кВт
41
20
15
15
10
5
8
6
0
6
5
42
8
8
10
10
12
8
4
15
10
25
43
16
5
3
2
12
15
10
0
10
8
44
15
15
20
25
15
20
10
6
8
8
45
20
35
35
25
25
30
0
25
25
10
46
10
25
10
15
20
6
0
0
6
5
47
15
30
35
40
40
8
6
0
4
3,5
48
40
30
30
20
15
20
10
6
8
8
49
20
15
15
10
5
0
4
8
0
5
50
35
35
20
15
10
15
4
30
15
10
ЭЛЕКТРОНИКА.
Изучение данного раздела целесообразно проводить, базируясь на курс физики и
руководствуясь программой курса.
Транзисторные усилители.
Усилители являются одними из самых распространенных электронных устройств,
применяемых в системах автоматики и радиосистемах. Усилители подразделяются на усилители
предварительные (усилители напряжения) и усилители мощности. Предварительный
транзисторные усилители, как и ламповые, состоят из одного или нескольких каскадов
усиления. При этом все каскады усилителя обладают общими свойствами, различие между
ними может быть только количественное: разные токи, напряжения, разные значения
резисторов, конденсаторов и т. д.
Для каскадов предварительного усиления наибольшее применение получили
резистивные схемы (с реостатно-емкостной связью). В зависимости от способа подачи входного
сигнала и получения выходного усилительные схемы получили следующие названия:
1. С общим эмиттером — ОЭ (рис. 42).
2. С общей базой—ОБ (рис. 43).
3. С общим коллектором (эмиттерный повторитель) — ОК (рис, 44).
"Наиболее распространенной является каскад ОЭ. Схема с ОБ в предварительных
усилителях встречается редко. Эмиттерный повторитель обладает наибольшим из всех трех
схем входным наименьшим выходным сопротивлениями, поэтому его применяют в тех случаях,
когда эта особенность позволяет согласовать те или иные звенья усилителя в целях улучшения
качества усиления. В табл. 12 дается сопоставление различных схем включения транзисторов.
Рассмотрим усилительный каскад с ОЭ. При расчете каскада усилителя обычно являются
известными: 1) Rн - сопротивление нагрузки, на которую должен работать рассчитываемый
каскад. Нагрузкой может являться и аналогичный каскад; 2) I н. м или U н. м - необходимое
значение амплитуды тока или напряжения нагрузки; 3) допустимые частотные искажения; 4);
диапазон рабочих температур; 5) в большинстве случаев является заданным напряжение
источника питания коллекторной цепи.
В результате расчета должны быть определены: 1) тип транзистора; 2) режим работы"
выбранного транзистора; 3} параметры каскада; 4) значения всех элементов схемы (резисторы,
конденсаторы), их параметры и типы.
Схема включения
№
Параметр
с общей базой (ОБ)
с общим эмиттером
(ОЭ)
с общим
коллектором (ОК)
1
Коэффициент
усиления по
напряжению
30  40
30 1000
2
Коэффициент
усиления по
току
1
10  200
10  200
3
Коэффициент
усиления по
мощности
30  40
3000  30000
10  200
4
Входное
сопротивление
50  100Ом
200  2000Ом
10  500кОм
5
Выходное
сопротивление
0,1  0,5 мОм
30  70кОм
50  100Ом
Eп
- +
R1
Eп
+ Rк
Rк
Т
1
Cp
Cp
R1
Т
U вых
U вх
R2
R3
C3
Rн
U вх
Rн
Cp
R2
Rвх
Рис. 42
Рис. 43
R3
Eп
- +
R1
Т
Cp
U вх
R2
R3
Rн
Рис. 44
Расчет усилителей.
Расчет каскада транзисторного усилителя напряжения
низкой частоты с реостатно-емкостной связью.
Последовательность расчета приводится для транзистора, включенного по схеме ОЭ
(общий эмиттер). На рис. 42 дана схема каскада усилителя.
Исходные данные: 1) напряжение на выходе каскада U вых. м (напряжение на нагрузке); 2)
сопротивление нагрузки Rн 3) нижняя граничная частота
f н 4) допустимое значение
коэффициента частотных искажений каскада в области нижних частот M н ; 5) напряжение
источника питания Et п .
Примечание.
Считать,
что
каскад
работает
в
стационарных
условиях
(
Tмин  15C; Tм  25C  ). При расчете влиянием температуры на режим транзистора
пренебрегаем.
Определить: 1) тип транзистора; 2) режим работы транзистора 3) сопротивление
коллекторной нагрузки Rк 4) сопротивление в цепи эмиттера R э 5} сопротивления делителя
напряжения R1 стабилизирующие режим работы транзистора; 6) емкость разделительного
конденсатора C р ; 7) емкость конденсатора в цепи эмиттера C э 8) коэффициент усиления
каскада по напряжению KU .
Порядок
расчета:
1.
Выбираем
тип
транзистора,
руководствуясь
следующими
соображениями: а) U кэ.доп  (1,1  1,3) Eп , U кэ.доп - наибольшее допустимое напряжение между
коллектором и эмиттером, приводится в справочниках; б) I к.доп  2
U вых. м
, I н. м -наибольшая
Rн
возможная амплитуда тока нагрузки; I к .доп - наибольший допустимый ток коллектора,
приводится в справочниках.
Примечания: 1) Заданному диапазону температур удовлетворяет любой транзистор.
2) Для выбранного типа транзистора выписать из справочника значения коэффициентов,
усиления по току для ОЭ  м ин и  м . В некоторых справочниках дается коэффициент усиления
 по току для схемы ОБ и начальный ток коллектора I к.н . Тогда  

1
(при выборе режима
работы транзистора необходимо выполнять условия I к. мин  I к. м ).
3) Для каскадов усилителей напряжения обычно применяют маломощные транзисторы
типа ГТ-108, ГТ-109, МП20, МП21, МП25,МП40, МП41, МП42, МП111, МП113 и др. (Справочник
по полупроводниковым диодам, транзисторам и интегральным схемам /Под ред. Н. Н.
Горюнова. - М.: Энергия, 1972; Справочник - транзисторы/ Под ред. Н. Ф. Николаевского.- М:
Связь, 1969; Лавриненко В. Ю. Справочник по полупроводниковым приборам. – Киев: Техника,
1980; Справочник радиолюбителя-конструктора. - М.: Энергия, 1977).
2. Режим работы транзистора определяем по нагрузочной прямой, построенной на
семействе входных статических (коллекторных) характеристик для ОЭ. Построение нагрузочной
прямой показано на рис. 45. Нагрузочная прямая строится по двум точкам: т. 0 - точка покоя
(рабочая) и т. 1, которая определяется величиной напряжения источника питания E п .
Координатами т. 0 являются ток покоя I к.0 и напряжение покоя U кэ 0 (т. е. ток и напряжение,
соответствующие U вых = 0).
Можно принять I к 0  (1,05  1,2) I вых  (1,05  1,2) I н. м .
Напряжение покоя U кэ 0
U кэ 0  U вых. м  U ост  U кт  U ост .
где U ост - наименьшее допустимое напряжение U кв .
При U кв  U ост возникают значительные нелинейные искажения, так как в рабочую зону
попадают участки характеристик, обладающие большой кривизной. Для маломощных
транзисторов можно принять U ост  0,15  1,0 В .
3. Определяем величины сопротивлений Rн и R э .
Iк 
Iк
Pк.доп
U кэ
I б5
I б4
4
3
I кт
I б3
I к.м
I
I б
I б2
5
I б1
I к0
2
1
I к.мин
I к.мин.доп
U ост
U кт
U кт
U к30
U кэ.м  Eп
Рис. 45
U кт
По выходным характеристикам (см. рис. 45) определяем
Rоб  Rн  Rэ . Общее
сопротивление в цепи эмиттер – коллектор:
Rоб  Eп I ,
где I - ток, определяемый т. 1, т.е. точкой пересечения нагрузочной прямой, с осью токов.
Принимая Rэ  (0,15  0,25) Rн , получим
Rн 
Rоб
; Rэ  Rоб  Rн .
(0,15  0,25)
4. Определяем наибольшие амплитудные значения входного сигнала тока I в х. м и
напряжения U в х. м , необходимые для обеспечения заданного значения U вых. м . Задавшись
наименьшим значением коэффициента усиления транзистора по току  м ин , получим
I вхт  I бт  I кт  мин ,
Причем I вхт не должен превышать величины
I  .м  I  .мин
, где для маломощных
2
транзисторов I бм  1  2 мА; , I б / мин  0,05 мА.
По входной статической характеристике для схемы ОЭ (рис. 46) и найденным значениям
I б . м ин и I бм находят, величину 2U вх. м .
5. Определяем входное сопротивление Rв х каскада переменному току (без учета делителя
напряжения R1 и R2 ):
Rвх ~ 
2U вх.м 2U вх.m
.

2I вх.m
2I .м
6. Определяем сопротивления делителя R1 и R2 . Для уменьшения шунтирующего
действия
делителя
на
входную
R12  (8  12) Rвх ~ , где R12 
цепь
R1 R2
.
R1  R2
каскада
по
переменному
току
принимают
Тогда
Eп R1а Eп R12
;

Rэ I э
Rэ I ко
R1 
R2 
R1 R12
R1  R12
.
7. Определяем коэффициент нестабильности работы каскада:
S
Rэ ( R1  R2 )  R1 R2
RR
Rэ ( R1  R2 )  1 2
1 м
,
где  м - наибольший возможный коэффициент усиления по току выбранного типа
транзистора.
Для нормальной работы каскада коэффициент нестабильности S не должен превышать
нескольких единиц.
8. Определяем емкость разделительного конденсатора C р :
Cр 
где.
1
2f н Rвых M н2  1
Rвых.Т
; Rвых 
Rвых.Т Rк
 Rн ,
Rвых.Т  Rк
- выходное сопротивление транзистора, определяемое по выходным
статическим характеристикам для схемы ОЭ. В большинстве случаев Rвых.Т  Rк поэтому
можно принять Rвых  Rк  Rн .
9. Определяем емкость конденсатора C э 
10
.
2f н Rэ
10. Определяем коэффициент усиления каскада по напряжению КU  U вых.м / U вх. м .
Примечание. Приведенный порядок расчета не учитывает требований на стабильность
работы каскада.
Задача. Рассчитать Каскад транзисторного усилителя напряжения для схемы с общим
эмиттером, (см. рис. 42):
U вых.м  4В , Rн  500Ом , f н  100 Гц;
М н  1,2 , Eп  12В .
Решение. 1. U  1,2E  1,2  f2  14,4 В ;
I к .доп  2 I н. м  2
U в ых. м
4
 2
 0,016 А  16 мА .
Rн
500
Выбираем транзистор МП42А, для которого I к .доп  30мА , U кэ.доп  15В ,  мин  30 ,
 м  50 , I к.мин.доп  25 мк. А .
2. Для построения нагрузочной прямой находим (рабочую) точку покоя (т. 0), для этого
определяем
I  1,2 I н.м  1,2  8  9,6мА ;
U кэ0  U вых. м  U ост  4  1  5В .
Вторая точка нагрузочной прямой U эк  Eп  12В . По полученным величинам строится
нагрузочная прямая.
3. По статическим выходным характеристикам и нагрузочной прямой находим I  18мА ,
откуда
U кэ  5В
I б.м
2I бm
Iб
I б.мин
U бэ
U бэ.мин
U бэ.м
Рис. 46
Rоб 
12
 670 Ом .
18  10 3
Следовательно,
Rк 
Rоб 670

 560Ом ;
1,2
1,2
Rэ  Rоб  Rк  670  560  110Ом .
2U вх.м
4. Наименьший коэффициент усиления по току (для схемы ОЭ) для транзистора МП42А
 мин  30 ,тогда I вх.мин  I б. мин  I к. мин . Из-за малого значения I к. м ин можно принять I к. м ин  0 и
следовательно, I б . м ин  0 .
I к. м
I б. м 
 мин

14
 0,47мА .
30
Амплитуда входного тока
I бт 
I б. м  I б . мин 0,47

 0,253мА.
2
2
По входной статической характеристике (для схемы ОЭ)
U бэ.мин  0,11В; U бэ.м  0,33В;
2U вх.м  U бэ.м  U бэ.мин  0,33  0,11  0,22В.
5. Находим входное сопротивление транзистора переменному току
Rвх ~ 
2U вх.м
0,22

 470Ом.
2 I б.м
0,47  10 3
6. Для определения R1 и R2 находим R12  8Rвх ~  8  470  3800Ом . Отсюда
R1 
Eп R12
12  3800

 43000Ом;
Rэ I ко
110  9,6  10 3
R2 
R1 R12
43000  3800

 4200Ом.
R1  R12 43000  3800
7. Определяем, будет ли схема достаточно стабильна
S
Rэ R1  R2   R1 R2
110  43000  4200  4300  4200

 2,66.
R1 R2
43000  4200
110  43000  4200 
Rэ R1  R2  
1  50
1  м
Следовательно, работа рассчитанного каскада достаточно стабильна.
8. Определяем емкость C р
Cр 
1
2f н Rк  Rн  M  1
2
н
Принимаем C р  3,0мкФ.
Определяем емкость C э

1
2  3,14  100560  500 1,2  1
2
 2,28  10 6 Ф.
Cэ 
10
10

 159  10 6 Ф  159к59
2f н Rэ 2  3,14  100  100
Для
полного
устранения
отрицательной
обратной
связи
необходимо
включить
C р  159мкФ . Эта емкость слишком велика. Обычно используют C э  10  30мкФ.
Принимаем Cэ  20мкФ.
10. Коэффициент усиления каскада по напряжению будет равен
KU 
U вых.м
4

 36,4.
U вх.м
0,11
Расчет каскада однотактного транзисторного усилителя мощности.
Последовательность расчета приводится для транзистора, включенного по схеме с общим
эмиттером (ОЭ). На рис. 47 дана принципиальная схема каскада однотактного усилителя
мощности.
Исходные данные: 1.) мощность на выходе каскада Pвых 2) сопротивление нагрузки Rн . 3)
нижняя граничная частота f н . 4) коэффициент частотных искажений каскада на нижних частотах
M и . 5) напряжение источника: питания Eu .
Примечание, Принимая Tмин  15С и Tм  25С , влиянием температуры на режим
работы транзистора пренебрегаем.
Определить: 1) тип транзистора; 2) режим работы транзистора; 3) сопротивление в цепи
эмиттера Rэ . 4) емкость конденсатора C э . 5) сопротивления делителя R1 и R2 . 6) коэффициент
усиления каскада по мощности K р . 7) коэффициент трансформации трансформатора K . 8)
сопротивления первичной и вторичной обмоток трансформатора rт1 и rт 2 . 9) индуктивность
первичной обмотки трансформатора L1 10) площадь поверхности охлаждающего радиатора,
если он необходим, S ох .
- Eп +
Тр
R1
Rн
Т
R2
Rэ
Рис. 47
Cэ
Порядок расчета. 1. Для выбора типа транзистора необходимо определить мощность P0 ,
которая будет выделяться на транзисторе: P0 
P~
к
где  к - коэффициент использования
транзистора к  0,035  0,45 чем больше напряжение питания Eп , тем больше  к ); P~ мощность, отдаваемая транзистором: P~ 
Pвых
т
. К. п. д. трансформатора  т принимают
равным 0,7  0,9.
Ориентировочно
определяют
падения
напряжений
на
активном
сопротивлении
первичной обмотки трансформатора rт1 и .на сопротивлении Rэ :
U  U rT 1  U Rэ  0,2  0,3Eп .
Тогда наибольшее возможное напряжение на транзисторе
U кэ.м 
E п  U
к
.
По найденным значениям P0 и U кэ.м подбирают транзистор.
Примечание. Для выбранного транзистора выписать из справочника: а) допустимый ток
коллектора
I к.доп . б) допустимое напряжение на коллекторе U кэ.доп . в) наибольшую
рассеиваемую мощность на транзисторе Pдоп . г) наименьший коэффициент усиления по току
 мин . д) начальный ток коллектора I к.н е) тепловое сопротивление rтт . ж) наибольшую
допустимую температуру коллекторного перехода Tт.м .
2. На выходных статических характеристиках (для ОЭ) находят положение точки покоя
(рабочей) т. 0 (рис. 48), для этого определяют напряжение на коллекторе при U вх  0 и ток покоя
коллектора
U кэо  Eп  U ; I ко  U ко 
Pо
.
U кэо
Через т. О и 4 ( U кэ  U кэ.м ; I к  0 ) проводят нагрузочную прямую. Для определения
рабочего участка нагрузочной прямой задаются величиной остаточного напряжения U ост (часто
принимают U ост  1В ) и наименьшим током коллектора I к.мин  I к.н ( I к.н - начальный ток
коллектора, дается в справочнике). По величине U ост определяют I к.м (т. 2); необходимо, чтобы
I к.м  I к.доп .
I вых  I нт
I б5
Iк
1
I б
2
I б4
0
I к.м
I б2
I к0
I
En
Tоб
I б3
I б1
I к.мин.  I кн
I к.мин
U ост
U вых.м
U к30
U вых.м
3 I б
4 U кэ
U кэ.м
Рис. 48
Без существенной ошибки можно принять I к.мин  0 . Таким образом, рабочий участок
находится между т. 2 и 3. Наибольшая возможная амплитуда, напряжения выходного сигнала
U вых.м  U кэ.о  U ост .
Наибольшая амплитуда тока I к.м определяется т. 0 и 3 (или т. 0 и 2). После этого
проверяют, обеспечит ли выбранный режим заданную мощность Pвых .
В соответствии с построенной нагрузочной прямой находят p ~ 
выбранном режиме p ~ 
Pвых
т
U км I км
. При правильно
2
.
Если это условие, не выполняется, то увеличивают наклон нагрузочной прямой (значение
I берут большим).
Необходимо иметь в виду, что нагрузочная прямая не должна выходить из области,
ограничиваемой гиперболой допустимых мощностей:
Iк 
Pк.доп
U кэ
( Pк.доп - берется из справочника).
Затем рассчитывают наибольшее и наименьшее значения входного тока:
I б.м 
I к.м
 мин
; I б.мин 
I к.мин
 мин
.
и фиксируют их величину на входной статической характеристике схемы ОЭ (рис. 49).
По т. 1 и 2 входной характеристики находят наибольшее и наименьшее напряжения
U бэ.мин и U бэ.м и наибольшую амплитуду напряжения входного сигнала. Далее определяют
мощность входного сигнала
Pвх 
U б.м I б.м
2
и входное сопротивление транзистора переменному току
2U б.м
.
2 I б.м
Iб
2I бm
U кэ  5В
U бэ
I б.мин
I б.м
Rвх 
U бэ.мин
2U бm
U бэ.м
Рис. 49
3. Сопротивление цепи эмиттера Rэ определяется по падению напряжения на этом
сопротивлении. Приняв U Rэ  0,3  0,5U , получаем Rэ 
U Rэ
I ко
.
4. Емкость конденсатора, шунтирующего Rэ определяется из выражения C э 
1
2f н Rэ
(при Cэ  100мкФ блокировочный конденсатор не ставят).
5. Сопротивление делителя переменному току R12 
условию R12  8  12Rвх ~ , тогда R1 
R1 R2
должно удовлетворять
R1  R2
Eп R12
R1 R12
; R2 
.
R1  R12
I ко Rэ
6. Коэффициент усиления каскада по мощности
K р  Pвых Pвх .
7. Для расчета коэффициента трансформации трансформатора по наклону нагрузочной
прямой (см. рис. 48) определяют величину сопротивления коллекторной нагрузки переменному
току
Rк ~ 
U кэ.м
.
I
Тогда коэффициент трансформации трансформатора будет равен
K
Rн
Rк ~ т
.
8. Сопротивления обмоток выходного трансформатора
rт1  0,5Rк~ 1  т  ; rт2  0,5 Rн
1  т
т
.
9. Индуктивность первичной обмотки
L1 
Rн  rт2
2f н K 2 M н2  1
.
10. При необходимости определяют площадь поверхности охлаждающего радиатора
S ох 
1100  1300Pо
Tт.м  Tср.м  Pо rтт
,
где Tт.м - наибольшая допустимая температура коллекторного перехода (дается в
справочнике); Tср.м - наибольшая возможная температура окружающей среды.
Задача. Рассчитать каскад транзисторного усилителя мощности для схемы ОЭ (см, рис. 47),
если известны Pвых  1В , Ru  5Ом , f н  1кГц , M н  1,3 , Eп  10В .
Решение.
1. P~ 
Pвых
т

P 1,43
1
 1,43Вт ; Pо  ~ 
 3,56Вт .
0,7
 к 0,4
Падение напряжения на rт1  Rэ принимаем равным
U  0,25Eп  0,25 10  2,5В ,
тогда
U кэ.м 
E п  U 10  2,5

 18,8В .
0,4
0,4
Полученными значениями Pо и U кэ.м соответствует транзистор ГТ430А, у которого
I к.доп  1,25А ,
U кэ.доп  30В ,
Pодоп  4Вт ,
мин  20 ,
I к.м  0,05мА ,
rтт  15 C Вт ,
Tт.м  85С .
2. определяем положение точки покоя (т. 0)
U кэо  Eп  U  10  2,5  7,5В ;
I ко 
Pо
3,56

 0,48А .
U кэо
7,5
Принимаем
U ост  1В .
Воспользовавшись
характеристиками,
которые
даны
в
справочнике, нагрузочную прямую проводим через точки U кэо  7,5В , I ко  0,48А
и
U кэ.м  18,8В , I к  0 .
Наибольшее значение напряжения
U к.м  U кэо  U ост  7,5  1  6,5В
•Такой амплитуде напряжения выходного сигнала будут соответствовать напряжения:
U кэ.м  U кэо  U к.м  7,5  6,5  14В ;
U кэ.мин  U кэо  U к.м  7,5  6,5  1В .
Для этих напряжений находим
I к.м  0,75А ; I к.мин  0,2А .
Тогда удвоенная амплитуда тока выходного сигнала
2I кm  I к.м  I к.мин  0,75  0,2  0,55А .
Проверим правильность выбора режима:
P~ 
2U кm I кm 2  6,5  0,55
P

 0,89  вых  1,43Вт .
8
8
т
Следовательно, необходимо выбрать новую точку покоя и, возможно, изменить наклон
нагрузочной прямой. Так как I к.мин велик, то, перемещая точку покоя по построенной
нагрузочной прямой вправо будем увеличивать U кm , при этом возрастет и P~ . Для нового
положения точки покоя (рабочей) принимаем U кэо  10В ; I ко  0,36А .
Тогда
U к.м  U кэо  U ост  10  1  9В ;
U кэ.м  10  9  19В ; U кэ.мин  10  9  1В ;
I к.м  0,75А ; I к.мин  0 ;
2 I кm  I к.м  I к.мин  0,75А /
Проверяем новый режим:
P~ 
2U кm I кm 2  9  0,75

 1,7Вт ,что вполне достаточно.
8
8
Определяем наибольшее и наименьшее значения входного тока
I б.м 
I к.м
 мин

I
0,75
0
 0,04А ; I б.мин  к.мин 
 0А .
20
 мин 20
По входной статической характеристике для схемы ОЭ находим
U бэ.м  0,72В ; U бэ.мин  0,6В .
Находим удвоенные амплитудные значения входного сигнала
2 I бm  I б.м  I б.мин  0,04А ;
2U бm  U бэ.м  U бэ.мин  0,72  0,6  0,12В ;
Pвх 
2U бm 2I бm 0,12  0,04

 0,0006Вт  0,6м,6 ;
8
8
Rвх 
2U бm 0,14

 3,0Ом /
2 I бm 0,04
3. Приняв U Rэ  0,4U  0,4  2,5  1В найдем
Rэ 
U Rэ
I ко

1
 2,1Ом .
0,48
4. Определим емкость конденсатора
Cэ 
10
10

 0,007Ф .
2f н Rэ 6,28  1000  2,1
Так как требуемая емкость чрезмерно велика, то ее не ставят.
5. найдем значения сопротивлений делителя. Приняв R12  10Rвх ~  10  3,0  30Ом ,
получим
R1 
Eп R12
10  30

 300Ом ;
I ко
0,75  2.1
R2 
R1 R12
300  30

 33,5Ом .
R1  R12 300  30
Принимаем ближайшие стандартные значения: R1  300Ом , R2  35Ом .
6. Коэффициент усиления каскада по мощности
KP 
Pвых
1

 1670 .
Pвх
0,0006
7. для расчета параметров трансформатора определим величину сопротивления
коллекторной нагрузки:
Rк ~ 
U кэ.м
19

 25,4Ом ,
I
0,75
тогда
K
Rн

Rк~ т
5
 0,53 .
25,4  0,7
8. rт1  0,5Rк~ 1   т   0,5  25,41  0,7  3,82Ом ;
rт2  0,5Rн
9. L1 
1 т
т
 0,5  5
Rн  rт2
2f н K
2
M 1
2
н
1  0,7
 1,07Ом .
0,7

5  1,07
6,28  1000  0,53
2
1,3  1
2
 4,15  10 3 Гн .
Принимаем L1  0,004мГн .
10.Так как P0  2 Вт , то необходим радиатор охлаждения площадью
S ох 
Tт.м
1200 Pо
1200  3,56

 660см 2 .
 Tср.м  Pо rтт 85  25  3,56  15
При анализе транзисторных усилителей широкое распространение получили h-параметры.
Электрическое состояние транзистора, включенного по схеме с общим эмиттером
характеризуется четырьмя величинами: I б , U бэ , I к и U кэ . Из практических соображений
удобно выбирать в качестве независимых величин U кэ и I б тогда U бэ  f1 I б ,U кэ  и
I к  f 2 I б ,U кэ  .
В усилительных схемах входным и выходным сигналами являются приращения входных и
выходных напряжений и токов. В пределах линейной части характеристик для приращений
U бэ и I к справедливы равенства
U бэ  h11э I б  h12э U кэ ;
I к  h21э I б  h22э U кэ ,
где hiкэ - соответствующие частные производные, которые легко могут быть найдены по
семейству входных и выходных характеристик транзистора, включенного по схеме ОЭ:
h11э 
U бэ
при U кэ  const U кэ  0 ;
I б
h12э 
U бэ
при I б  const I б  0 ;
U кэ
h21э 
I к
при U кэ  const U кэ  0 ;
I б
h22э 
I к
при I б  const I б  0 .
U кэ
h11э представляет собой входное сопротивление транзистора. Безразмерный параметр
h12э является коэффициентом обратной связи по напряжению. Как показывает анализ схем на
транзисторах, величина h12э  0,002  0,0002 поэтому при практических расчетах его можно
полагать равным нулю: h21э - безразмерный коэффициент передачи по току, характеризующий
усилительные свойства (по току) транзистора при постоянном напряжении на коллекторе; h22э
имеет размерность проводимости и характеризует выходную проводимость транзистора при
постоянной токе базы.
ПОНЯТИЕ ОБ ИНТЕГРАЛЬНЫХ МИКРОСХЕМАХ.
Применение электронных устройств для решения современных технических задач
приводит к существенному усложнению их электрических схем. Анализ развития электронной
техники показывает, что примерно в течение 10 лет сложность электронных устройств
возрастает приблизительно в 10 раз. Такой рост приводит к возникновению в первую очередь
проблемы надежности как элементов схем, так и электрических соединений между ними.
Усложнение электронной аппаратуры приводит к увеличению вероятности отказов из-за
увеличения отказов комплектующих элементов: и отказов в цепях электрических соединений.
Существенное увеличение надежности возможно только при значительном уменьшении
числа комплектующих элементов за счет увеличения их функциональной сложности при
повышении надежности их работы. Создание новых комплектующих изделий стало возможным
на основе внедрения в электронную технику принципов элементной интеграции, т.е.
объединения в одном сложном миниатюрном элементе многих простых элементов (резисторов,
диодов, транзисторов и т.п.). Полученный в результате такого объединения сложный
микроэлемент называют интегральной микросхемой. Таким образом, интегральные
микросхемы - это микроэлектронные изделия, состоящие из активных элементов (транзисторов,
диодов), пассивных элементов, (резисторов, конденсаторов, дросселей) и соединительных
проводов, которые изготавливаются в едином технологическом процессе, электрически
соединены между собой, заключены в общий корпус и представляют единое целое. По
технологии изготовления интегральные микросхемы делятся на полупроводниковые, в которых
все элементы формируются в полупроводниковом материале, и гибридные, которые
выполняются в виде пленок, наносимых на поверхность диэлектрического материала, и
навесных бескорпусных элементов (транзисторов, конденсаторов и т.п.), прикрепляемых к
основанию. В отличие от гибридных интегральных микросхем, которые состоят из двух
различных типов элементов: тонкопленочных резисторов, конденсаторов, соединительных
проводов и навесных транзисторов, дросселей я конденсаторов большой емкости,
полупроводниковые интегральные микросхемы состоят, как правило, из отдельных областей
кристалла, каждая из которых выполняет функцию резистора, конденсатора, диода или
транзистора. Дроссели в таких микросхемах создавать очень трудно; поэтому большинство схем
проектируется так, чтобы исключить применение индуктивных элементов. Все эти элементы
схемы получают в едином технологическом цикле в кристалле полупроводника. Это позволяет
существенно усложнять микросхему и увеличивать число активных и пассивных элементов
практически без повышения трудоемкости изготовления. При этом можно создавать весьма
сложные микросхемы с большой (содержащей более 150 элементов) степенью интеграции при
вполне удовлетворительной себестоимости.
Полупроводниковые интегральные микросхемы могут рассеивать мощности порядка 50 —
100 мВт; работать до частот 20 — 100 мГц, обеспечивать время задержки не более 2--5 нс.
Надежность этих схем весьма высока: в пределах нагруженных режимов среднее время
безотказной работы может достигать (1  2)  10 6 ч. Электронные устройства, выполненные на
полупроводниковых интегральных микросхемах, могут иметь плотность монтажа до 500
элементов (резисторов, конденсаторов, транзисторов, диодов) на кубический сантиметр. Это
позволяет увеличить плотность элементов в 20 — 50 раз посравнению с микромодульными
схемами. Среднее время безотказной работы устройства, содержащего 10 7  10 8 элементов,
может достигать 10 — 20 .тыс. ч. Преимуществом интегральных микросхем являются также
высокое быстродействие, так как малые размеры схем обеспечивают снижение таких
паразитных параметров, как междуэлектродные емкости и индуктивности соединительных
проводов; высокая экономичность (даже большие интегральные схемы обычно потребляют не
более 100-200 мВт). Такая малая величина потребляемой мощности позволяет снизить расход
электроэнергии и уменьшить массу источников питания устройств, выполненных с применением
интегральных схем. Некоторым недостатком интегральных микросхем является небольшая
величина их выходной мощности (обычно 50 — 100 мВт), что обусловлено в основном малыми
габаритами и сложностью отвода тепла от микросхем. Общетехнические параметры
интегральных микросхем — механическая прочность, диапазон рабочих температур,
устойчивость к. пониженным и повышенным давлениям и влагоустойчивость, как правило, не
хуже, чем у диодов и транзисторов. Основными функциональными параметрами интегральных
микросхем являются: коэффициент усиления K U , входное сопротивление Rвх , выходное
сопротивление Rвых , максимальная величина выходного напряжения U вых.м , рабочий диапазон
частот f н и f в , где f н — нижняя рабочая частота; f в — верхняя рабочая частота.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.
1. Принцип устройства электроннолучевых трубок. Назначение трубок, их маркировка.
2. Расскажите о прохождении электрического тока через пространство, заполненное
разреженным газом.
3. Формы (виды) газового разряда.
4. Устройство и работа тиратрона тлеющего разряда.
5. Почему после зажигания тиратрона его сетка теряет свое управляющее действие?
6. Внутриатомное строение чистого полупроводника.
7. Как влияют примеси на проводимость полупроводника?
8. Электронная (типа n) проводимость полупроводников.
9. Дырочная (типа p) проводимость.
10. Процесс прохождения тока через электронно-дырочный переход.
11. Устройство и свойства точечных и плоскостного диодов.
12.Полевые транзисторы и тиристоры.
13. Устройство и работа полупроводникового триода.
14. Что называется коэффициентом усиления по току? напряжению? Каковы их значения
для транзисторов?
15. Принцип выпрямления переменного тока.
16. По каким признакам классифицируются усилители низкой частоты и каковы их
особенности?
17. Как определяется коэффициент усиления усилительного каскада?
18. В каких случаях используют многокаскадные усилители?
19. Каким образом осуществляется связь между каскадами в многокаскадном усилителе?
20. Что такое амплитудная характеристика усилителя?
21. Что такое частотная характеристика усилителя?
22. Чем определяется максимальное значение коэффициента усиления усилителя?
23. Что такое обратная связь в усилителях? Какие виды обратной связи вы знаете?
24. Как изменяется коэффициент усиления с увеличением глубины отрицательной
обратной связи?
25. При каких условиях происходит переход усилителя в режим самовозбуждения?
26. Как влияет отрицательная обратная связь на стабильность работы усилителя?
27 Принципиальное отличие усилителя мощности от усилителя напряжения.
28. Назначение усилителя напряжения.
29. Принцип работы усилителя напряжения на сопротивлениях с автоматическим
смещением. Назначение элементов схемы.
30. Принцип действия схемы усилителя напряжения на полупроводниковом триоде с
общим эмиттером.
31. Какие характеристики являются входными и выходными каждой из схем включения
транзистора?
32. Что такое h-параметры транзистора?
33. Что такое рабочая точка транзистора?
34. Почему для усилителя с общим коллектором коэффициент усиления по напряжению
меньше единицы?
35. В чем преимущество усилителя по схеме с общим коллектором перед другими
схемами усилителей?
36. За счет чего достигается усиление мощности в схемах с полупроводниковым триодом?
37. Начертите схему и объясните принцип работы генератора с автотрансформаторной
(индуктивной) обратной связью.
38. Сравнение LC-генераторов с RC-генераторами.
39. Какие параметры диодов ограничивают величину мощности, которую необходимо
получить на нагрузке?
40. Принцип работы импульсных устройств.
41. Чем вызвана необходимость перехода на интегральные схемы?
42. Особенности микроэлектронных устройств.
КОНТРОЛЬНАЯ РАБОТА 3.
Задача 1, варианты 0 – 25. Рассчитать каскад транзисторного усилителя напряжения,
принципиальная схема которого изображена на рис. 42. Данные для расчета приведены в табл.
13.
Таблица 13
Данные для расчета
Вариант
U вых. м , В
Rн , Ом
f , Гц
Eп , В
0
3,0
600
100
12
1
2,0
400
90
6
2
1,0
250
120
9
3
5,0
450
200
27
4
8,0
350
150
12
5
2,4
600
180
3
6
3,4
550
140
12
7
1,6
280
160
6
8
4,0
590
170
27
9
2,2
440
110
9
10
3,4
600
150
12
11
1,5
200
60
3
12
1,7
250
70
6
13
1,8
300
80
9
14
2,0
350
90
12
15
2,1
400
120
15
16
2,3
450
140
18
17
2,5
480
150
24
18
2,7
500
160
27
19
2,8
520
170
24
20
3,0
540
180
20
21
3,1
550
200
18
22
3,2
580
220
15
23
3,5
560
230
12
24
3,6
480
250
9
25
3,8
320
270
6
Задача 2, варианты 26 – 50. Рассчитать каскад транзисторного усилителя напряжения,
принципиальная схема которого изображена на рис. 47. Данные для расчета приведены в табл.
14.
Таблица 14
Данные для расчета
Вариант
Pвых. м , Вт
Rн , Ом
f , Гц
Mн
Eп , В
26
1,8
9
70
1,20
12
27
1,0
3
90
1,25
9
28
3,0
5
100
1,22
27
29
2,0
6
110
1,16
6
30
0,9
10
50
1,12
12
31
2,5
4
120
1,18
12
32
0,5
12
140
1,14
9
33
0,1
20
160
1,26
27
34
1,5
8
180
1,28
27
35
4,0
4
200
1,30
27
36
2,5
10
100
1,12
12
37
2,5
11
100
1,12
12
38
2,5
12
100
1,15
12
39
2,0
13
160
1,15
12
40
2,0
14
160
1,5
12
41
2,0
15
160
1,20
24
42
2,0
16
200
1,20
24
43
1,5
17
200
1,20
24
44
1,5
18
200
1,25
24
45
1,5
19
120
1,25
24
46
1,5
20
120
1,25
24
47
4,0
3
140
1,20
9
48
4,0
6
140
1,22
9
49
4,0
9
140
1,28
9
50
3,0
6
140
1,30
9
Список использованной литературы
Г. Копылов И.П. Электрические машины: Учебник для ВУЗов. М.: Энергоатомиздат, 1986.
360 с.
2. Общая электротехника с основами электроники: Контрольные задания для учащихсязаочников всех технических специальностей, кроме электротехнических и некоторых
энергетических специальностей средних специальных учебных заведений/ Ю.А. Михеев, М.И.
Григоревский - М.: Высш. школа. 1989. - 176 с.: ил.
3. Электротехника: Программа, методические указания и контрольные задания для
студентов-заочников инженерно-технических (не электротехнических) спец. ВУЗов./ Волынский
Б.А. - 4-е изд. - М.: Высш. школа. 982.-95с.
4. Электротехника и основы электротехники: Методические указания и контрольные
задания для студентов-заочников инженерно-технических специальностей ВУЗов. / Соколов
Б.Л.. Соколов В.Б. - 3-е изд. - М.: Высш. школа, 1981. -127 с.