Лекция №4 СМА Часть 2 2015

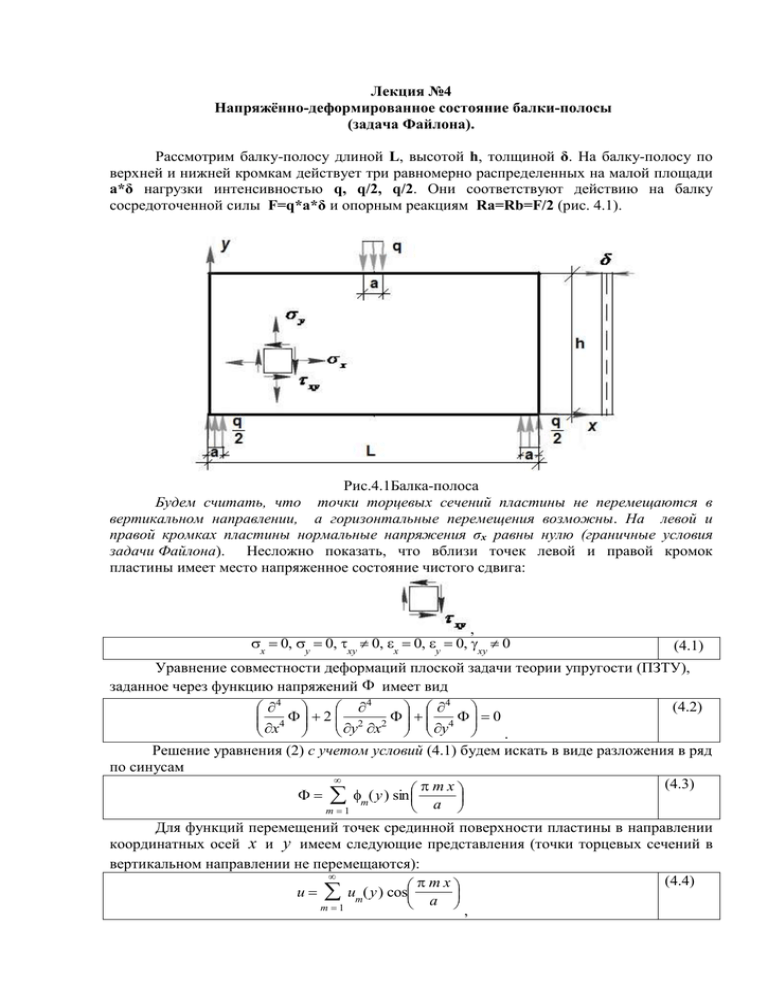
Лекция №4
Напряжённо-деформированное состояние балки-полосы
(задача Файлона).
Рассмотрим балку-полосу длиной L, высотой h, толщиной δ. На балку-полосу по
верхней и нижней кромкам действует три равномерно распределенных на малой площади
a*δ нагрузки интенсивностью q, q/2, q/2. Они соответствуют действию на балку
сосредоточенной силы F=q*a*δ и опорным реакциям Ra=Rb=F/2 (рис. 4.1).
Рис.4.1Балка-полоса
Будем считать, что точки торцевых сечений пластины не перемещаются в
вертикальном направлении, а горизонтальные перемещения возможны. На левой и
правой кромках пластины нормальные напряжения σx равны нулю (граничные условия
задачи Файлона). Несложно показать, что вблизи точек левой и правой кромок
пластины имеет место напряженное состояние чистого сдвига:
,
x0, y0, xy0, x0, y0, xy0
(4.1)
Уравнение совместности деформаций плоской задачи теории упругости (ПЗТУ),
заданное через функцию напряжений  имеет вид
(4.2)
 4 
 4
  4 

2 
 



 x4 
 y2 x2  y4  0



 

.
Решение уравнения (2) с учетом условий (4.1) будем искать в виде разложения в ряд
по синусам

(4.3)
mx
  m( y ) sin 

 a 
m1
Для функций перемещений точек срединной поверхности пластины в направлении
координатных осей x и y имеем следующие представления (точки торцевых сечений в
вертикальном направлении не перемещаются):

(4.4)
mx
u  um( y ) cos

 a ,
m1

mx
v  vm( y ) sin 

 a  .
m1
(4.5)
Алгоритм решение поставленной задачи будет изложен в последующих лекциях. В
данной лекции
представлены результаты вычислений по этому алгоритму и их
графическая иллюстрация, полученные с помощью системы компьютерной алгебры
Maple.
Приведем результаты анализа напряженного состояния балки–полосы при
следующих исходных данных: L=120 см, h=30 см, δ=1 см, a= 2 см (L, h>> δ).
Интенсивность равномерно распределенной нагрузки на участке малой площади по
верхней кромке равна qB=500 МПа, а интенсивности опорных реакций qH=250 МПа.
Для сравнения результатов расчета балки-полосы с расчетами по обычной
балочной теории укажем величины сосредоточенной силы и опорных реакций.
Распределенные нагрузки на малой площади a* δ=2 см2, соответствуют действию на
балку-полосу сосредоточенной силы F=100 кН и опорных реакций Ra=Rb= 50кН.
Нагрузки, действующие на балку-полосу, разложим в ряд Фурье
mm
(4.6)
mx
q( x )  qm sin 

 a ,
m1
где коэффициенты разложения определяются по формулам
a
2
qm
a

mx

q( x ) sin 
 dx


 a 

0
(4.7)
Результаты аппроксимации функции нагрузки (приложенной по верхней и нижней
кромкам пластинки рис. 4.1) для нечетных значений m=1,3,…, 301 представлены на рис.
4.2.
Рис.4.2 Аппроксимация функции нагрузки
Горизонтальные линии на рис. 4.2 соответствуют заданным величинам
интенсивности нагрузки, приложенной по верхней и нижней кромкам пластинки.
Отметим, что приближение отрезком ряда Фурье дает хорошие результаты для
периодической функции. В случае непериодической функции имеет место так
называемый эффект Гиббса, который состоит в том, что значение аппроксимации на
некоторых интервалах всегда превосходит значение исходной функции и вблизи точек
разрыва имеют место колебания аппроксимации и рост погрешности. Оценка
погрешности проводилась сравнением величин сосредоточенных сил F, Ra+Rb с
соответствующими равнодействующими аппроксимированной нагрузки по верхней FB и
a
a
qB( x ) dx FH
qH( x ) dx ).
нижней FH кромкам ( FB




0
0
,
Разложение нагрузки в ряд Фурье производилась с целью перехода от
уравнения в частных производных (4.1) с помощью представления (4.3) к
обыкновенным дифференциальным уравнениям.
Для каждой амплитуды нагрузки с номером m записываем
условия на
поверхности. На верхней кромке пластинки (y=h)
y qv , xy 0
(4.8)
m
m
m
на нижней кромке пластинки (y=0)
y qn , xy 0
m
m
(4.9)
m
Из условий (4.8), (4.9) находим константы интегрирования, которые используются
для определения амплитуд функции напряжений, нормальных и касательных напряжений
и перемещений.
Проведем анализ напряженно-деформированного состояния балки-полосы. На
рис.4. 3 показана поверхность нормальных напряжений  x в точках срединной
плоскости балки-полосы. На рис.4.4 представлены сечения поверхности напряжений
(эпюры) вблизи места приложения нагрузки (х=58см) и на достаточном удалении от нее.
Рис. 4.3 Поверхность напряжений
x
Рис. 4.4а ПЗТУ. Сечение х=58см.
Напряжения  x
Рис.4.4 Эпюры напряжений
x
Рис. 4.4б ПЗТУ и балочная теория. Сечение
х=58см. Напряжения  x
Решения плоской задачи теории упругости и решения по формулам сопротивления
материалов представлены на рис.4.4а, 4.4б и в таблице 4.1 (длина пролета балки L=120
см, высотой сечения h=30 см, (h/L=1/4)). Начало координат в левом нижнем углу балкиполосы (рис. 4.1). Сравнение показывает, что
вблизи места приложения нагрузки,
решения сопротивления материалов и теории упругости имеют существенные различия
(рис. 4.4а, 4.4б), а на достаточном удалении решения близки (Табл.4.1, принцип СенВенана).
Таблица 4.1
Решение теории
Балочная теория
Координата x
Координата y точки
упругости
σx (МПа)
сечения
по высоте
σx
(МПа)
по длине балки (см) поперечного сечения
(см)
30
0
97.8
100
30
30
-94.7
-100
На рис.4.5,4.6 представлена поверхность нормальных напряжений
 y и ее сечения
вблизи места приложения нагрузки. В теории плоского изгиба стержней нормальные
напряжения  y  0 , т.е. используется гипотеза о ненадавливании продольных волокон.
Результаты вычислений, представленные на рис.4.5, 4.6 показывают, что на достаточном
удалении от места приложения внешних сил σy →0. Эти результаты наглядно
подтверждают обоснованность принятой гипотезы.
Рис.4.5 Напряжения
y
Рис.4.6 Эпюры напряжений
На рис.4.7 показана поверхность касательных напряжений
y
 xy , а на рис. 4.8а,4.8б,
4.8в, соответствующие эпюры. Вблизи места приложения нагрузки закон изменения
напряжений существенно отличается от квадратной параболы (в опорных зонах
касательные напряжения изменяют направление рис 4.8б,в). Сравнения решений задачи
теории упругости и решений по формулам сопротивления материалов представлены в
табл. 4.2. Максимальное значение напряжений в сечении пластины x=60.5 см достигается
в точке с координатой y=29.2 см (вблизи верхней кромки пластины) и равно  xy =79.7
МПа. По формуле Журавского касательные напряжения по высоте сечения изменяются по
закону квадратной параболы и наибольших значений достигают в точке с координатой
у=15 см. Соответствующее напряжение τxy =25.0 МПа . На достаточном удалении от места
приложения нагрузки в сечении x=75 см  xy =25.5 МПа (y=15 см) т.е имеет место
хорошее совпадение с результатами, полученными
материалов..
Рис.4.7 Напряжения  xy
Рис. 4.8б Эпюры напряжений xy
по формуле сопротивления
Рис. 4.8а Эпюры напряжений  xy
Рис. 4.8в Эпюры напряжений  xy (х=58см)
Таблица 4.2.
Координата точки по
Решение теории
Балочная теория
высоте поперечного
упругости
τxy (МПа)
сечения (см)
τxy (МПа)
60.5
29.2
79.7
75
15
25.5
25.0
По известным значениям нормальных и касательных напряжений вычисляем
главные напряжения в точках срединной плоскости пластины (по балочной теории σy=0)
2
2
2
1
1
1
m ax x y
x 2 x yy 4 xy
2
2
2
2
2
2
1
1
1
m in x y
x 2 x yy 4 xy
(4.10)
2
2
2
.
Координата сечения
балки (см)
Поверхности главных напряжений в точках срединной плоскости балки - полосы
представлены на рис.4. 9, 4.10.
Рис.4.9 Напряжения
m ax
Рис.4.10
Напряжения
m in
Напряжения m ax , m in характеризуются не только своей интенсивностью, но и
направлением. Угол между осью x и внешней нормалью к сечению, в котором действует
напряжение m ax определяется из уравнения
,
xy
tan( m ax)
m axx
(4.11)
.
Положительное направление угла отсчитывается против хода часовой стрелки.
Сечения (главные площадки), на которых действуют напряжения m ax , m in взаимно
перпендикулярны.
Векторное поле главных напряжений строится следующим образом. Срединная
плоскость пластинки разбивается на
квадратные элементы (при
симметричном
загружении разбиение выполняется для половины пластинки). В окрестности центра
каждого элемента строится квадрат,
направление сторон которого совпадает с
направлением главных площадок. Вектор главного напряжения направляется по
внешней нормали к главной площадке, если напряжение растягивающее (положительное
- красный цвет) и по внутренней, если напряжение сжимающее (отрицательное - синий
цвет). Построенное таким образом векторное поле в дальнейшем будем называть
картиной напряженного состояния (КНС). На (рис. 4.11). КНС представлена для
половины пластики на сетке 20*10.
Из рис.4.11видно, что в точках вблизи приложения силы вдоль верхней кромки
имеет место
напряженное состояние - двухстороннее сжатие. По формулам
сопротивления материалов в окрестности точек верхней кромки балки одностороннее
сжатие (продольные волокна друг на друга не давят)
Рис.4.11 Картина напряженного состояния
На рис. 4.12 выделены векторные поля растягивающих напряжений
Рис.4.12 Векторное поле главных (растягивающих) напряжений
По направлению максимальных главных напряжений (растягивающих)
выполняется армирование железобетонной балки (рис.4.13)
Рис.4.13 Траектории главных напряжений при изгибе и схема армирования
железобетонной балки.
Перейдем к задаче проверки прочности материала по теориям прочности.
Рис. 4.13 Опыты на плоское напряженное состояние (ПНС)
Рассмотрим особенности, которые имеют место при оценке наступления
катастрофического состояния материала пластинки по различным теориям прочности. В
точках срединной плоскости пластинки возникает плоское напряженное состояние. При
вычислении эквивалентного напряжения по теориям прочности используются главные
напряжения пространственного состояния, удовлетворяющие условию
(4.12)
1   2   3 .
Вариант 1-й - двустороннее растяжение (рис. 4.14)
Рис.4.14 Двустороннее растяжение
0m ax, 0m in ; ( 1max, 2min, 30 ) .
Первая теория прочности i( 1m ax) , вторая
(4.13)
теория прочности
( i1 ( 23 ) )max min По 2-й теории эквивалентное
.
меньше.
Вариант 2-й - растяжение-сжатие (рис. 4.15)
 i напряжение
Рис. 4.15 Растяжение-сжатие
( 0m ax, m in0 ), ( 1max, 20, 3min ).
(4.14)
Первая теория прочности i( 1m ax) . Вторая im ax m in По 2-й теории
.
эквивалентное напряжение
 i больше.
Вариант 3-й - двустороннее сжатие (рис.4.16)
Рис.4.16 Двухстороннее сжатие


0
,

0 ),( 10, 2max, 3min ).
( m ax
m in
(4.15)
Первая теория прочности i( 3min ) . Вторая теория прочности
( i1 ( 23 ) ) ( maxmin )
. Эквивалентное напряжение по 2-й теории
положительное, т.е. растягивающее. Это противоречит здравому смыслу.
Момент наступление течения в материале можно оценить по 3-й теории прочности
(4.16)
  3
i  1
,
2
или по 4-ой теории прочности
2
2
2
i 1 1 22 1 33 2 3
(4.17)
Третья теория прочности не содержит  2 . Поэтому результаты расчетов по 3-й и
4-й теориям для случаев двустороннего растяжения и двустороннего сжатия будут
различаться. На рис. 4.17, 4.18 и 4.19 показаны поверхности главных напряжений
1   2   3
Рис. 4.19  3
Рис. 4.17  1
Рис.4.18  2
На рис. 4.20 показаны эквивалентные напряжения по 3-й и по 4-ой теориям
прочности. Наибольшее расхождение в зоне двухстороннего сжатия
Рис. 4.20 Эквивалентные напряжения по 3-ей и 4-ой теориям прочности
Эпюры эквивалентных напряжений по 3-ей теории прочности представлены на рис.
4.21
Результаты вычислений,
полученные по формулам сопротивления
материалов хорошо согласуются в сечениях балки, находящихся на достаточном
удалении от места приложения сосредоточенных сил и имеют существенное
качественное и количественное отличие вблизи их приложения.
Рис. 4.21 Эквивалентные напряжения по 3-ей теории прочности
Отметим, что проведенный анализ напряженного состояния через функцию
напряжений
не зависят от упругих свойств изотропного линейно-упругого
материала (E,μ-модуля упругости и коэффициента Пуассона). Это означает, что
полученное напряженное состояние можно переносить на геометрически подобные и
аналогично загруженные детали конструкций, выполненные из другого материала.
Анализ деформированного состояния балки – пластины проведем при
5
следующих упругих постоянных материала:  =0.3; Е  2,06  10 МПа .
На рис. 4.22 показан деформированный вид балки-полосы. На рис 4.23. показаны
перемещения точек вертикальных торцевых волокон и волокон вблизи места приложения
внешних сил. Торцевые сечения остаются плоскими и после деформации балки, а сечения
вблизи приложения сил искривляются, т.е. гипотеза плоских сечений, принимаемая в
сопротивлении материалов, не выполняется.
Рис.4.22 Деформированный вид балкиполосы
Рис. 4.23 Перемещения точек
вертикальных торцевых волокон и волокон
вблизи места приложения внешних сил
На рис.4.24 показаны вертикальные перемещения верхней и нижней кромок балки,
а также ее оси. Из рис. 4.24 видно, что наибольшие перемещение получает точка верхней
кромки балки в месте приложения силы. Перемещения нижней кромки меньше чем
перемещения оси. В сопротивлении материалов, балка закрепляется на уровне оси и
считается, что перемещения точек верхней и нижней кромок балки одинаковые и равны
перемещениям соответствующих точек оси. На достаточном удалении от места
приложения силы решение линейного дифференциального уравнения оси изогнутой
балки хорошо согласуется с решением плоской задачи теории упругости.
Рис. 4.24 Вертикальные перемещения верхней и нижней кромок балки, а также ее оси
Рассмотрим балку-полосу длиной L, высотой h, толщиной δ. На балку-полосу по
нижней кромке действуют три равномерно распределенных на малой площади a*δ
нагрузки интенсивностью q, q/2, q/2. Они соответствуют действию на балку
сосредоточенной силы F=q*a*δ и опорных реакций Ra=Rb=F/2 (рис.4.25)
Рис.4.25 Балка – полоса загружена силами по нижней кромке
В курсе сопротивления материалов считается, что нагрузка к балке
прикладывается на уровне ее оси и загружения по схемам рис. 4.1 и рис. 4.25 не
различаются. Однако, НДС балки – полосы при загружении по схемам рис. 4.1 и
рис. 4.25 различаются и весьма существенно.
Рис.4.26 Нормальное напряжение
x
Рис.4.27 Нормальное напряжение
y
Рис. 4.28 Касательные напряжения xy
На рис. 4.26, рис.4.27 и рис. 4.28 показаны поверхности напряжений
 x , y , xy
(сравниваем с рис. 4.3, рис. 4.5, рис. 4.7). В местах резкого изменения напряжений (зона
концентрации напряжений) значения напряжений вычислены на более мелкой сетке. На
рис. 4.29 и рис.4.30 представлены поверхности главных напряжений (сопоставляем с
рис.4.9,4.10).
Рис. 4.29 Главные напряжения
Рис.4.30. Главные напряжения
Чтобы сопоставить величины растягивающих напряжений в одних и тех же точках,
на рис. 4.31 поверхности  max , min совмещены в одном объеме. На рис. 4.32 показана
поверхность эквивалентных (приведенных) напряжений по 3-ей теории прочности
(сравниваем с рис.4.20).
Рис. 4.31 Главные напряжения  max , min
Рис. 4.32 Приведенное напряжение
На рис.4.33 показана картина напряженного состояния, а на рис. 4.34 потоки
наибольших растягивающих напряжений. Вблизи места приложения нагрузки в центре
полосы имеет место двустороннее растяжение (для нагрузки поверху рис.4.11 двухстороннее сжатие).
Для пластичного материала в точках
двустороннего
растяжения
0m ax, 0m in ; ( 1max, 2min, 30 ) необходимо использовать 4-ю теорию
прочности (4.17), так как 3-я теория прочности (4.16)  2 не содержит.
Рис.4.33 Картина напряженного состояния
Рис. 4.34 Потоки растягивающих напряжений
На рис. 4.35 показан деформированный вид срединной плоскости балки-полосы
(сравнение с рис 4.22).
Рис.4.35 Деформированный вид срединной плоскости балки-полосы
На рис. 4.36 представлены перемещение верхней кромки, оси и нижней кромки.
Наибольшие перемещения в точках нижней кромки (сравнение с рис. 4.24).
Рис. 4.36 Перемещения верхней кромки, оси, нижней кромки
На рис.4.37 показаны перемещения точек вертикальных торцевых волокон и
волокон вблизи места приложения внешних сил. Сечения вблизи места приложения
нагрузки не остаются плоскими, а искривляются (сравнение с рис. 4.23).
Рис. 4.37 Сечения вблизи места приложения нагрузки не остаются плоскими
(искривляются)
Внимание! При ответе на экзамене данных вопросов весь графический материал
студенту предоставляется. Студент дает описание графического материала и
приводит расчеты по балочной теории сопротивления материалов.