Получение наночастиц аэрозольными методами. Часть 1
реклама
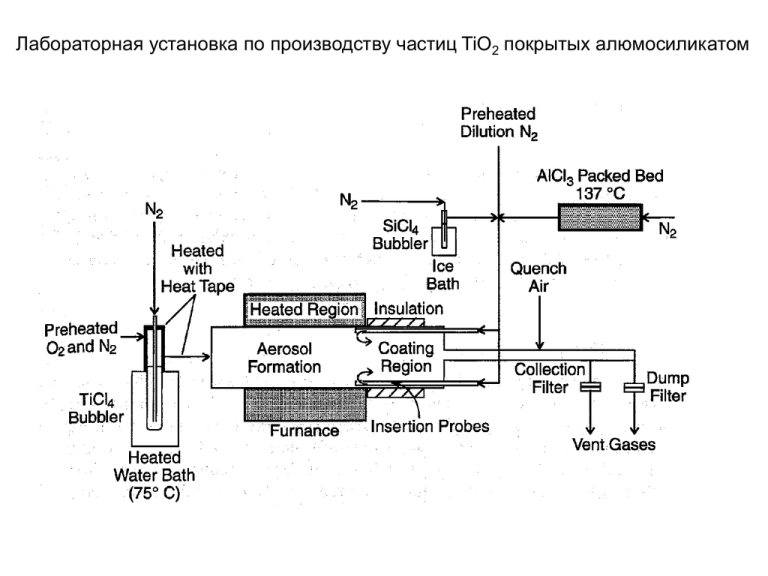
Лабораторная установка по производству частиц TiO2 покрытых алюмосиликатом Основные процессы протекающие при распылительной сушке Аэрозоль определение: твердые частицы и/или жидкость распределенные в газе. Примеры: пыль, дым Различные варианты получения частиц методом аэрозольного распыления Процесс Пленки Частицы Преобразование газа в частицу за счет физического воздействия Ионизованный или незаряженный пучок частиц Сверхкритический синтез Распылительная сушка под давлением Преобразование газа в частицу за счет химической реакции Реакция внутри частицы Гибридный процесс Прямой процесс Лазерное испарение/осаждение Реакция на горячей стенке Реакция инициированная лазерным излучением Реакция на горячей стенке Распыление в плазму Реакция в плазме Распыление в пламя Реакция в пламени Образование частицы с возможным осаждением Аэрозольное химическое осаждение Распылительная сушка Конденсация после протекания реакции на частице Лазерное распыление Соотнесение длинны свободного пробега молекулы и размеров частиц 2.00 / c вязкость газа, плотность газа с средняя скорость молекулы газа K n 2 / d p Kn 1 частица движется в непрерывном пространстве Kn 1 частица движется в режиме отдельных молекул Диффузия частиц в газовом потоке J– количество частиц пересекающих определенное пространство за определенный промежуток времени, (количество/(см2*сек)). N∞ - концентрация частиц х – координата D– коэффициент диффузии, (см2/сек) kB – константа Больцмана, (эрг/К) Т– температура, (К) μ – вязкость, (г/см*сек) dp – диаметр частицы Сс – фактор коррекции используемый когда частицы сопоставимы по размерам или меньше длинны свободного пробега молекулы газа А1, А2, А3 – эмпирические константы Значения факторов коррекции для частиц различного диаметра Влияние диффузии и условий течения газового потока на потери частиц в Ламинарный поток, число Рейнольдса меньше 2100 Турбулентный поток, число Рейнольдса больше 2100 U – скорость газового потока, ρ – плотность газа, μ – вязкость газа, dt – диаметр трубы, D – скорость диффузии, Q – скорость потока аэрозоля, L – длина трубы, к – коэффициент переноса массы. Диффузия вызванная внешними факторами Общая формула миграции частиц под воздействием внешнего поля J – Степень осаждения, Vt – скорость осаждения, N∞ - количество частиц Сила гравитации, действующая на частицу Где mp – масса частицы, dp – диаметр частицы ρ – плотность газа, ρp – плотность частицы Сила противодействующая седиментации Где Cd – коэффициент скорости перемещения частицы зависящий от числа Рейнольдса, Cc – фактор Каннингема, Vs – скорость осаждения Коэффициент скорости перемещения частицы в среде при различных условиях потока Фактор несферичности частицы, который определяет насколько движение данной частицы в среде отличается от движения идеально сферичной частицы de – эквивалентный диаметр частицы того же объема Движение частиц в электрическом поле Сила действующая на частицу в электрическом поле Где Z – заряд частицы, E – интенсивность электрического поля Максимальный заряд твердой частицы Где dp – диаметр частицы, EL – энергия спонтанной эмиссии электрона или иона Максимальный заряд капли жидкости определяется пределом Релея Где γ – величина поверхностного натяжения Когда движение частицы под воздействием электрического поля сбалансировано движением всего потока, скорость миграции частицы может быть описана теми же выражениями что и для миграции под воздействием гравитации В том случае если число Рейнольдса меньше 0.1, миграция частицы под воздействием электрического поля описывается следующим выражением Движение частиц при градиенте температур Общее название процесса – термофорез. Самая часто встречающаяся причина диффузии частиц при аэрозольном распылении, поскольку любой реактор имеет некоторый температурный градиент от стенки реактора в глубину реактора. Более того сам процесс аэрозольного распыления подразумевает наличие температурного градиента, когда в термостатированный реактор впускают газовый поток или аэрозоль с другой температурой. Поток частиц движущихся под воздействием градиента температур сбалансирован с противодействующей ему силой беспорядка действующей на флюид, определяемой тем же уравнением что и для процесса седиментации. Сложение этих сил дает следующие выражения: Где α – термофоретический коэффициент, Kn – число Кнудсена, k – теплопроводность газа, kp – теплопроводность частицы, μ – вязкость газа, ρ – плотность газа Эффективность осаждения частиц SiO2 пролетающих через трубу с холодными стенками Движение частиц при столкновении со стенкой реактора Способ получения различных тонких пленок, способ сортировки частиц по размерам Останавливающая дистанция для частиц разных размеров St – число стокса, определяет соотношение между кинетической энергией частиц и энергией их взаимодействия с жидкостью. Схема части реактора с изменением направления потока Где ρp – плотность частицы, μ – вязкость среды, L – характеристика геометрии потока (для аэрозоля в цилиндре с радиусом R, L=R ), U – скорость флюида Эффективность улавливания частиц в зависимости от стадии улавливания в мультистадийном процессе. Каждая последующая стадия проходит с меньшим диаметром сопла и меньшим давлением газа Образование и пост частиц размером меньше свободного пробега молекулы Kn>>1 Введя некий коэффициент αs соударения частицы с молекулами того же состава что и частица, учтя процессы осаждения и испарения мы можем вывести изменение размеров частицы во времени Для частиц размером порядка 10 нм, молекулы газа ударяют частицу меняя ее направление. Поток частиц в потоке газа можно описать следующим образом: средняя скорость молекул газа, Где n1 – концентрация молекул, p1 – парциальное давление газа Общее количество столкновений молекул с поверхностью частицы определяется следующим соотношением: Изменение размера частицы можно определить следующим образом: Где p1 – парциальное давление газа, pd – парциальное давление частиц или капель, ν1 – объем частицы, m1 – масса молекулы, F1 – корректирующий коэффициент, вычисляемый по формуле: Рост частиц в режиме непрерывной среды В условиях когда размер частицы превышает длину свободного пробега молекулы (Kn<<1), процессы испарения и осаждения молекул с поверхности частицы определяются исключительно скоростью диффузии молекул по поверхности частицы Скорость изменения размеров частицы определяется следующим соотношением: Где D – коэффициент диффузии, p1 – парциальное давление газа, pd – парциальное давление частиц или капель, ν1 – объем частицы, m1 – масса молекулы, F2 – корректирующий коэффициент, вычисляемый по формуле: Определение характеристического времени конденсации или испарения Kn<<1 Kn>>1 Где dp0 – начальный диаметр частицы, pd = pe Рост частицы за счет химической реакции Рост частицы за счет реакции протекающей в объеме частицы Рассмотрим случай взаимодействия молекул с неким веществом растворенным в капле жидкости, тогда скорость реакции в капле описывается следующим выражением: Где H – константа Генри, которая связывает концентрацию (CL) вещества в жидкости с парциальным давлением вещества Рост частицы за счет реакции протекающей на поверхности частицы Скорость реакции для реакции первого порядка описывается следующим образом: ks – константа реакции Исходя из скорости реакции, можно определить увеличение размеров молекулы для такой реакции: Соответственно скорость роста частицы определяется: Или в упрощенном варианте время необходимое для удвоения размеров частицы: Или в упрощенном варианте время необходимое для удвоения размеров частицы: Образование частиц лимитированное скоростью реакции Визуализация зарождения частицы Наиболее простая, классическая теория описания скорости зарождения частиц из молекул и их роста до стабильного состояния предлагает следующую зависимость: Что по сути является обобщением уравнений описывающих скорость роста частицы в режиме свободного пробега молекулы, уравнения описывающего стабильность начального кластера и уравнения Кельвина связывающего зависимости парциального давления на плоской поверхности и изогнутой поверхности для одного вещества. Уравнение описывает размер стабильного кластера в зависимости от поверхностного натяжения (σ), объема молекулы или атома (ν) и степени насыщения пара (S) Образование частиц лимитированное процессом диффузии вещества из среды Реализуется в случае когда нет термодинамического барьера образования частиц, т.е. размер стабильной частицы определяемый уравнением Кельвина меньше размера мономера Заменив это выражение на уравнение Кельвина с тем условием, что размер стабильной частицы меньше мономера получим следующую зависимость Скорость роста частицы определяется подвижностью мономеров (т.е. температурой и вязкостью среды) и их парциальным давлением, которые могут быть объединены как коэффициент насыщения (Пример получения оксида титана). Графическое изображение процесса коагуляции TiO2 в зависимости от температуры и конверсии компонентов (С0 – концентрация TiCl4, С – концентрация TiO2).
