математическая модель прогнозирования качества атмосферы
реклама

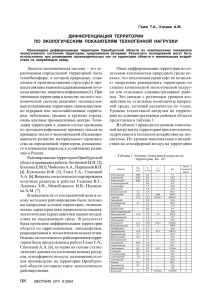
Хазова С.В. Оренбургский государственный университет МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОГНОЗИРОВАНИЯ КАЧЕСТВА АТМОСФЕРЫ ПРОМЫШЛЕННЫХ ГОРОДОВ В данной статье рассматриваются основные проблемы, возникающие при оценке качества атмосферы промышленных городов. Предлагается модель позволяющая учитывать уровень загрязнения атмосферы и прогнозировать возникновение той или иной экологической ситуации с учетом ряда факторов влияющих на изменение концентрация загрязняющих веществ в атмосфере промышленных городов. Àòìîñôåðíûé âîçäóõ ÿâëÿåòñÿ ñâîåãî ðîäà ïîñðåäíèêîì àíòðîïîãåííîãî çàãðÿçíåíèÿ âñåõ äðóãèõ ýëåìåíòîâ ïðèðîäû, îí ñïîñîáñòâóåò ðàñïðîñòðàíåíèþ çàãðÿçíÿþùèõ âåùåñòâ íà çíà÷èòåëüíûå ðàññòîÿíèÿ. Íàèáîëåå îñòðî ïðîáëåìà àíòðîïîãåííîãî è òåõíîãåííîãî çàãðÿçíåíèé ñòîèò â êðóïíûõ ãîðîäàõ ñ âûñîêîé êîíöåíòðàöèåé ïðîìûøëåííûõ ïðåäïðèÿòèé, òðàíñïîðòà è íàñåëåíèÿ. Äëÿ ïðîãíîçèðîâàíèÿ âîçíèêíîâåíèÿ òîé èëè èíîé ýêîëîãè÷åñêîé ñèòóàöèè áîëüøîå çíà÷åíèå èìååò ñòåïåíü êîíöåíòðàöèè (Ñi) çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðíîì âîçäóõå, åå ïðåâûøåíèå íàä ïðåäåëüíî äîïóñòèìîé êîíöåíòðàöèåé (ÏÄÊ) è ïðè èõ ïðåâûøåíèè ìîãóò áûòü äàíû ðåêîìåíäàöèè ïî óìåíüøåíèþ âðåäíûõ âûáðîñîâ èëè ïðîäîëæèòåëüíîñòè âðåìåíè ðàáîòû ïðåäïðèÿòèé. Ïî äàííûì ìíîãèõ àâòîðîâ, íàñ÷èòûâàåòñÿ îò 100 äî 250 ìåòîäîâ ïðîãíîçèðîâàíèÿ êà÷åñòâà àòìîñôåðû, îäíàêî âåäóùèå ñïåöèàëèñòû (Èçðàýëü Þ.À., Ãàñèëèíà Í.Ê., Ðîâèíñêèé Ô.ß., Áåðëÿíä Ì.Å.) ñ÷èòàþò, ÷òî èìååò ñìûñë ãîâîðèòü âñåãî ëèøü î òðåõ ìåòîäàõ: ýêñïåðòíîì, ýêñòðàïîëÿöèè è ìîäåëèðîâàíèÿ. À âñå îñòàëüíûå ÿâëÿþòñÿ ëèøü ðàçíîâèäíîñòÿìè ýòèõ ìåòîäîâ. Ìåòîä ýêñïåðòíîãî ïðîãíîçèðîâàíèÿ ïðèìåíÿåòñÿ â òîì ñëó÷àå, åñëè äàííûå ïðîãíîçà íå ïîääàþòñÿ îáðàáîòêå ïîëíîñòüþ èëè õîòÿ áû ÷àñòè÷íî. Îí îñíîâûâàåòñÿ íà ñèñòåìå ïîëó÷åíèÿ è ñïåöèàëèçèðîâàííîé îáðàáîòêè îöåíîê ïðîãíîçà òîé èëè èíîé ñèòóàöèè ïóòåì îïðîñà ýêñïåðòîâ â äàííîé îáëàñòè íàóêè. Ìåòîä ýêñòðàïîëÿöèè è èíòåðïîëÿöèè ïðèìåíÿåòñÿ ÷àùå âñåãî äëÿ êðàòêîâðåìåííûõ ïðîãíîçîâ.  åãî îñíîâó ïîëîæåíî èçó÷åíèå äàííûõ (êàê êîëè÷åñòâåííîå òàê è êà÷åñòâåííîå) çà íåñêîëüêî ïðåäøåñòâóþùèõ ëåò è åñëè èçìåíåíèå ýêîëîãè÷åñêîé ñèòóàöèè íå ïðåòåðïåâàåò ðåçêèõ ñêà÷êîâ, ïðåäïîëàãàåòñÿ òåíäåíöèÿ èçìåíåíèÿ ñèòóàöèè íà ñëåäóþùèé ïðîãíîçèðóåìûé ïåðèîä.  ïðàêòèêå íàèáîëüøåå ðàñïðîñòðàíåíèå ïîëó÷èë ìåòîä ìîäåëèðîâàíèÿ. Äëÿ ñîñòàâëåíèÿ ìîäåëè òðåáóåòñÿ âûïîëíåíèå òðåõ îñíîâíûõ óñëîâèé: – âûÿâëåíèå ôàêòîðîâ, èìåþùèõ ñóùåñòâåííîå çíà÷åíèå äëÿ ïðîãíîçà; – îïðåäåëåíèå äåéñòâèòåëüíîãî îòíîøåíèÿ ôàêòîðîâ ê ïðåäñêàçóåìîìó ÿâëåíèþ; – ðàçðàáîòêà àëãîðèòìà è ïðîãðàììû. Äàííûé ìåòîä õîðîø òåì, ÷òî äëÿ îáðàáîòêè äàííûõ ïîçâîëÿåò èñïîëüçîâàòü ÝÂÌ. Äàëåå, êàê áû íå áûëà ñëîæíà ìîäåëü, – îíà âñåãäà óïðîùàåò îáúåêò ïðîãíîçèðîâàíèÿ. Ê òîìó æå, ïðè èñïîëüçîâàíèè äàííîãî ìåòîäà, íå òðåáóåòñÿ ïðèâëå÷åíèå âûñîêîêâàëèôèöèðîâàííûõ ñïåöèàëèñòîâ. Êðîìå òîãî, îí ïîçâîëÿåò ó÷èòûâàòü ôàêòîð âåðîÿòíîñòè âîçíèêíîâåíèÿ òîé èëè èíîé ýêîëîãè÷åñêîé ñèòóàöèè. Èç âûøåèçëîæåííîãî ñëåäóåò, ÷òî äëÿ îöåíêè ñîñòîÿíèÿ àòìîñôåðíîãî âîçäóõà íåîáõîäèìî ñîâåðøåíñòâîâàòü ìåòîäû ïðîãíîçèðîâàíèÿ, óñëîæíÿòü ìîäåëè è óòî÷íÿòü áàçó äàííûõ. ×òîáû ïîëó÷èòü èíôîðìàöèþ îá èçìåíåíèè êîíöåíòðàöèé âðåäíûõ âåùåñòâ â âîçäóõå è ïî ýêñïåðèìåíòàëüíûì äàííûì ñîñòàâèòü êàðòó çàãðÿçíåíèÿ âîçäóøíîãî áàññåéíà, íåîáõîäèìî ïðîèçâîäèòü ñèñòåìàòè÷åñêèå çàìåðû óðîâíÿ êîíöåíòðàöèè çàãðÿçíÿþùèõ âåùåñòâ â âîçäóõå, ïðè÷åì îòáîðû ïðîá âîçäóõà äîëæíû ïðîèçâîäèòüñÿ â «óçëàõ ðåãóëÿðíîé ñåòêè ñ øàãîì íå áîëåå 2 êì» [1]. Òàêàÿ çàäà÷à ïðàêòè÷åñêè íå âûïîëíèìà. Ïðè ñîçäàíèè ìîäåëè ïðîãíîçà âîçíèêíîâåíèÿ òîé èëè èíîé ýêîëîãè÷åñêîé ñèòóàöèè íåîáõîäèìî ó÷èòûâàòü òðè îñíîâíûõ óñëîâèÿ: «à) âûÿâëåíèå ôàêòîðîâ, èìåþùèõ ñóùåñòâåííîå çíà÷åíèå äëÿ ïðåäñêàçàíèÿ; á) îïðåäåëåíèå äåéñòâèòåëüíîãî îòíîøåíèÿ ôàêòîðîâ ê ïðåäñêàçóåìîìó ÿâëåíèþ; â) ðàçðàáîòêà àëãîðèòìà è ïðîãðàììû.» [1] Êðîìå òîãî íàäî ó÷èòûâàòü, ÷òî â ëþáûõ ïðèðîäíûõ ïðîöåññàõ îáÿçàòåëüíî ïðèñóòñòâóþò òðè ñîñòàâëÿþùèå: «à) äåòåðìèíèðîâàííàÿ, êîòîðàÿ ïîääàåòñÿ òî÷íîìó ðàñ÷åòó íà ïåðèîä, äîñòàòî÷íûé äëÿ öåëåé ïðîãíîçèðîâàíèÿ; á) âåðîÿòíîñòíàÿ, êîòîðàÿ âûÿâëÿåòñÿ â ïðîöåññå èçó÷åíèÿ ïðîãíîçèðóåìîãî îáúåêòà èëè ÿâëåíèÿ; â) ñëó÷àéíàÿ, êîòîðàÿ íà ñîâðåìåííîì óðîâíå çíàíèé ïðàêòè÷åñêè íå ïîääàåòñÿ ïðåäñêàçàíèþ.» [1] Íî, êàê ýòî íå ïàðàäîêñàëüíî ïðè ïðîãíîçèðîâàíèè ñîñòîÿíèÿ îêðóæàþùåé ñðåäû, â äàííîì ñëó÷àå àòìîñôåðíîãî âîçäóõà, íàì ïðèõîäèòñÿ ВЕСТНИК ОГУ 10`2005 Том 2. Естественные и технические науки 85 Естественные науки ñòàëêèâàòüñÿ ñ âåðîÿòíîñòíûìè è ñëó÷àéíûìè ñîñòàâëÿþùèìè. Äëÿ ñîñòàâëåíèÿ ìàòåìàòè÷åñêîé ìîäåëè îæèäàåìîãî èçìåíåíèÿ ñîñòîÿíèÿ àòìîñôåðíîãî âîçäóõà òðåáóåòñÿ îïðåäåëèòü êàêèå ïîêàçàòåëè íåîáõîäèìû äëÿ àíàëèçà ïðîöåññà ðàññåèâàíèÿ çàãðÿçíÿþùèõ âåùåñòâ è ó÷åñòü âñå ñîñòàâëÿþùèå, îêàçûâàþùèå çíà÷èòåëüíîå âëèÿíèå íà äàííûé ïðîöåññ. Òàêæå ñëåäóåò ó÷åñòü, ÷òî ïðèìåñè â àòìîñôåðå íàõîäÿòñÿ â ðàçëè÷íûõ àãðåãàòíûõ ñîñòîÿíèÿõ: ãàçîîáðàçíûõ, â âèäå àýðîçîëåé, òâåðäûõ. Íåîáõîäèìî ó÷åñòü êàêîå åñòåñòâåííîå èëè àíòðîïîãåííîå çàãðÿçíåíèå îêàçûâàåò íàèáîëüøåå âëèÿíèå íà îæèäàåìóþ ýêîëîãè÷åñêóþ ñèòóàöèþ. Íà èçìåíåíèå ñîñòàâà çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðå â çíà÷èòåëüíîé ñòåïåíè âëèÿþò ìåòåîðîëîãè÷åñêèå (ÌÏÀ – ìåòåîðîëîãè÷åñêèé ïîòåíöèàë ðàññåèâàþùåé ñïîñîáíîñòè àòìîñôåðû) è êëèìàòè÷åñêèå (ÏÇÀ ìåòåîðîëîãè÷åñêèé ïîòåíöèàë çàãðÿçíåíèÿ àòìîñôåðû) óñëîâèÿ äàííîé ìåñòíîñòè. Èñïîëüçóÿ ìíîãîëåòíèå ñòàòèñòè÷åñêèå äàííûå ìîæíî ñïðîãíîçèðîâàòü óñëîâèÿ, îöåíèòü èõ è ó÷åñòü â äàëüíåéøåì ïðè ïðîãíîçèðîâàíèè óðîâíÿ àíòðîïîãåííîãî çàãðÿçíåíèÿ àòìîñôåðû.  íàøåì ñëó÷àå íàñ èíòåðåñóåò ðîëü àíòðîïîãåííîãî çàãðÿçíåíèÿ äëÿ ñîçäàíèÿ ìîäåëè ïðîãíîçà ñîñòîÿíèÿ àòìîñôåðíîãî âîçäóõà. Ðàçâèòèå ìåòîäîâ ïðîãíîçà âîçíèêíîâåíèÿ òîé èëè èíîé ýêîëîãè÷åñêîé ñèòóàöèè âîçìîæíî ïî äâóì íàïðàâëåíèÿì. Îäíî áàçèðóåòñÿ íà îñíîâå ìàòåìàòè÷åñêîãî îïèñàíèÿ ðàñïðîñòðàíåíèÿ ïðèìåñåé ñ ïîìîùüþ ðåøåíèÿ ñîîòâåòñòâóþùèõ óðàâíåíèé äèôôóçèè. Äðóãîå æå îñíîâûâàåòñÿ íà àíàëèçå ñòàòèñòè÷åñêèõ äàííûõ ïî ðàñïðîñòðàíåíèþ çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðå. Ïåðâîå íàïðàâëåíèå áîëåå ïðåäïî÷òèòåëüíî, ïîñêîëüêó ïîçâîëÿåò ó÷èòûâàòü âñå ôàêòîðû âëèÿþùèå íà ñïîñîáíîñòü àòìîñôåðû ê ðàññåèâàíèþ çàãðÿçíÿþùèõ âåùåñòâ è ó÷èòûâàòü êîýôôèöèåíò âåðîÿòíîñòè îæèäàåìîé ñèòóàöèè.  íàøåé ñòðàíå íàèáîëüøåå ðàñïðîñòðàíåíèå ïîëó÷èëà ìîäåëü ïðîôåññîðà Ì.Å. Áåðëÿíäà. «Â ñîîòâåòñòâèè ñ ýòîé ìîäåëüþ ñòåïåíü çàãðÿçíåíèÿ àòìîñôåðíîãî âîçäóõà âûáðîñàìè âðåäíûõ âåùåñòâ èç íåïðåðûâíî äåéñòâóþùèõ èñòî÷íèêîâ îïðåäåëÿåòñÿ ïî íàèáîëüøåìó ðàññ÷èòàííîìó çíà÷åíèþ ðàçîâîé ïðèçåìíîé êîíöåíòðàöèè âðåäíûõ âåùåñòâ (Ñm), êîòîðàÿ ó÷èòûâàåòñÿ íà íåêîòîðîì ðàññòîÿíèè (Õm) îò ìåñòà âûáðîñà ïðè íåáëàãîïðèÿòíûõ ìåòåîðîëîãè÷åñêèõ óñëîâèÿõ, êîãäà ñêîðîñòü âåòðà äîñòèãàåò îïàñíîãî çíà÷åíèÿ (Um) è â ïðèçåìíîì ñëîå ïðîèñõîäèò èíòåíñèâíûé òóðáóëåíòíûé îáìåí». [3] Íî äàííàÿ ìî- 86 äåëü äîñòàòî÷íî ñëîæíà, òàê êàê òðåáóåò ñïåöèàëüíîé ôèçèêî-ìàòåìàòè÷åñêîé ïîäãîòîâêè. Ñëåäîâàòåëüíî, âîçíèêàåò íåîáõîäèìîñòü â ïîëó÷åíèè ìîäåëè èçìåíåíèÿ ñîñòàâà àòìîñôåðíîãî âîçäóõà â òå÷åíèå îïðåäåëåííîãî âðåìåííîãî èíòåðâàëà, ñ ó÷åòîì âñåõ ôàêòîðîâ, âëèÿþùèõ íà èçìåíåíèå êîíöåíòðàöèè çàãðÿçíÿþùèõ âåùåñòâ, íå òðåáóþùåé ñïåöèàëüíîé êâàëèôèêàöèè. Íà èçìåíåíèå êîíöåíòðàöèè (Ñi) çàãðÿçíÿþùèõ âåùåñòâ â âîçäóõå, êàê èçâåñòíî, îêàçûâàþò âëèÿíèå: à) êà÷åñòâåííûå è êîëè÷åñòâåííûå õàðàêòåðèñòèêè âûáðîñîâ ïðîìûøëåííûõ ïðåäïðèÿòèé è òðàíñïîðòà. Ñòåïåíü çàãðÿçíåíèÿ àòìîñôåðíîãî âîçäóõà çàâèñèò òàêæå îò âûñîòû âûáðîñà. «Ñ óâåëè÷åíèåì âûñîòû âûáðîñà ñòåïåíü ðàññåèâàíèÿ çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðå âîçðàñòàåò, èõ êîíöåíòðàöèÿ ñíèæàåòñÿ è â îòäåëüíûõ ñëó÷àÿõ ìîæåò áûòü óìåíüøåíà äî ÏÄÊ». [2]; á) àðõèòåêòóðà ãîðîäîâ è èõ âåëè÷èíà; â) ðåëüåô ìåñòíîñòè; ã) âåòðÿíàÿ íàãðóçêà; ä) òåìïåðàòóðà îêðóæàþùåé ñðåäû è âðåìÿ ãîäà; å) îñàäêè, êàê òàêîâûå (äîæäü, ñíåã, òóìàí) èëè îòñóòñòâèå èõ; æ) ôîíîâàÿ èëè îñòàòî÷íàÿ êîíöåíòðàöèÿ çàãðÿçíÿþùèõ âåùåñòâ â âîçäóõå; ç) óðîâåíü ñîëíå÷íîé ðàäèàöèè. Âñå ýòè ôàêòîðû î÷åíü òðóäíî ó÷åñòü â îäíîé ìîäåëè, íî â ýòîì íåò è íåîáõîäèìîñòè. Äëÿ ñóùåñòâåííîãî óïðîùåíèÿ ðàñ÷åòîâ ìîæíî ðàññìàòðèâàòü ðÿä äîïóùåíèé. Òàê êàê, ðàñ÷åò âåäåòñÿ äëÿ îïðåäåëåííîé òåððèòîðèè, òî ìîæíî ââåñòè ðÿä äîïóùåíèé: à) â ëþáîé ñèòóàöèè ïðè ñîñòàâëåíèè ïðîãíîçà ïðîöåññà ðàññåèâàíèÿ çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðå ïðèñóòñòâèå ôîíîâîé êîíöåíòðàöèè íå èãðàåò ñóùåñòâåííîé ðîëè, è åå óñëîâíî ìîæíî ïðèíÿòü ≅ const . á) âëèÿíèå ðåëüåôà ïîâåðõíîñòè çåìëè, çàñòðîéêè çäàíèÿìè è ñîîðóæåíèÿìè íà èçìåíåíèå êîíöåíòðàöèè çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðå, òîæå íå îêàçûâàåò çíà÷èòåëüíîãî âëèÿíèÿ è èõ òàêæå ìîæíî ñ÷èòàòü ≅ const .  ñâÿçè ñ ýòèì ñàìà ìîäåëü çíà÷èòåëüíî óïðîùàåòñÿ è ñâîäèòüñÿ ê ðàñ÷åòó èçìåíåíèÿ êîíöåíòðàöèé çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðå ñ ó÷åòîì âðåìåíè, îñàäêîâ, òåìïåðàòóðû îêðóæàþùåé ñðåäû è âåòðÿíîé íàãðóçêè.  êà÷åñòâå îñíîâíûõ êðèòåðèåâ îöåíêè çàãðÿçíåíèÿ àòìîñôåðíîãî âîçäóõà ÿâëÿþòñÿ Ïðåäåëüíî Äîïóñòèìûå Êîíöåíòðàöèè (ÏÄÊ) âðåäíûõ ïðèìåñåé.  êà÷åñòâå îñíîâíîãî ïîêàçàòåëÿ îïàñíîñòè çàãðÿçíåíèÿ âîçäóõà ïðèíèìàåòñÿ ñóììàðíàÿ âåñîâàÿ êîíöåíòðàöèÿ ïðèìåñåé. Ïðè÷åì ВЕСТНИК ОГУ 10`2005 Том 2. Естественные и технические науки Хазова С.В. Математическая модель прогнозирования качества атмосферы... äàííûé ïîêàçàòåëü ñïðàâåäëèâ êàê äëÿ ãàçîâ, òàêæå è äëÿ ïûëè è àýðîçîëåé, õîòÿ â íåêîòîðûõ ñëó÷àÿõ íà èçìåíåíèå êîíöåíòðàöèè çàãðÿçíÿþùèõ âåùåñòâ ìîæåò âëèÿòü è èõ äèñïåðñíîñòü. Íî â ëþáîì ñëó÷àå òðåáóåòñÿ âûïîëíåíèå ñëåäóþùåãî ñîîòíîøåíèÿ: n C ∑ ÏÄÊi ≤ 1 (1) I i =1 Ïðè ñîñòàâëåíèè ìàòåìàòè÷åñêîé ìîäåëè íåîáõîäèìî ó÷èòûâàòü ðÿä êðèòåðèåâ è ïàðàìåòðîâ, èñïîëüçóåìûõ äëÿ õàðàêòåðèñòèêè àíòðîïîãåííîãî âîçäåéñòâèÿ ÷åëîâåêà íà îêðóæàþùóþ ñðåäó: êàòåãîðèÿ îïàñíîñòè ïðåäïðèÿòèÿ (ÊÎÏ), êîòîðàÿ ó÷èòûâàåò ñóììàðíóþ ìàññó âûáðîñîâ âðåäíûõ âåùåñòâ â àòìîñôåðó îò ïðåäïðèÿòèÿ, ïðèâåäåííóþ ê îäíîìó êëàññó îïàñíîñòè;  ñâÿçè ñ òåì, ÷òî ìû èìååì äåëî ñ áîëüøîé òåððèòîðèåé, ãäå ðàñïîëîæåíèå ïðåäïðèÿòèé è àâòîìîáèëüíûõ äîðîã êðàéíå íåðàâíîìåðíî. Êðîìå òîãî ñàìè ïðåäïðèÿòèÿ ìîãóò áûòü ðàçíîãî íàçíà÷åíèÿ è, â ñâÿçè ñ ýòèì èìåòü ðàçíûå ÊÎÏ, à àâòîìîáèëüíûå äîðîãè èìåòü ðàçëè÷íóþ ñòåïåíü çàãðóæåííîñòè, à ñëåäîâàòåëüíî, êîýôôèöèåíò îïàñíîñòè äîðîã (ÊÎÄ) ó íèõ òîæå áóäåò ðàçëè÷åí, òî äëÿ áîëåå ïîëíîé îöåíêè ñîñòîÿíèÿ çàãðÿçíåíèÿ îêðóæàþùåé ñðåäû íåîáõîäèìî ââåñòè òàêîé ïàðàìåòð êàê êîýôôèöèåíò îïàñíîñòè ðàéîíà ãîðîäà (ÊÎÐ), êîòîðàÿ äàåò íåêîòîðûé óñëîâíûé îáúåì çàãðÿçíåííîãî âîçäóõà îò âñåõ ïðåäïðèÿòèé è äîðîã ðàéîíà ãîðîäà, ðàçáàâëåííûé äî ñàíèòàðíî-ãèãèåíè÷åñêèõ íîðì è ïðèâåäåííûé ê îäíîé òîêñè÷íîñòè. Îíà îöåíèâàåòñÿ êàê ñóììà îïàñíîñòè ïðåäïðèÿòèé (ÊÎÏ) + ñóììà îïàñíîñòåé àâòîìîáèëüíûõ äîðîã (ÊÎÄ): m m n i =1 i=1 j=1 ÊÎÐ = Σ ÊÎÏ + Σ ÊÎÓ = Σ ÊΠ; (2) ãäå m ÷èñëî ïðåäïðèÿòèé íà òåððèòîðèè ãîðîäà èëè íàñåëåííîãî ïóíêòà; ÊΠêàòåãîðèÿ îïàñíîñòè âåùåñòâà âûáðàñûâàåìîãî â àòìîñôåðó ãîðîäà èëè íàñåëåííîãî ïóíêòà, ì3/ñ; n êîëè÷åñòâî çàãðÿçíÿþùèõ âåùåñòâ; Êàòåãîðèÿ îïàñíîñòè ïðåäïðèÿòèé, â ñâîþ î÷åðåäü, îïðåäåëÿåòñÿ ÷åðåç ñóììàðíîå êîëè÷åñòâî âûáðîñîâ âðåäíûõ âåùåñòâ â àòìîñôåðó: α n Mi ; ÊÎÏ = ∑ (2.1) i =1 ÏÄÊ I ãäå Mi êîëè÷åñòâî âûáðîñîâ i-é ïðèìåñè â àòìîñôåðó, ò/ãîä; ÏÄÊi ñðåäíåñóòî÷íàÿ ÏÄÊ i-ãî âåùåñòâà â àòìîñôåðå íàñåëåííîãî ïóíêòà, ìã/ì3; α i – áåçðàçìåðíàÿ êîíñòàíòà, ïîçâîëÿþùàÿ ñîîòíåñòè ñòåïåíü âðåäíîñòè i-ãî âåùåñòâà ñ âðåä- íîñòüþ äèîêñèäà ñåðû (III êëàññ îïàñíîñòè). Çíà÷åíèÿ äëÿ òîêñèêàíòîâ 1; 2; 3 è 4 êëàññîâ îïàñíîñòè ñîîòâåòñòâåííî ðàâíû 1,7; 1,3; 1,0 è 0,9. Åñëè ìàññó âûáðîñîâ çàãðÿçíÿþùèõ âåùåñòâ âûðàçèòü ÷åðåç èõ ìàññîâóþ êîíöåíòðàöèþ â ïîòîêå: (2.11) m=Ci*Vi; ãäå Vi îáúåì ãàçîâîãî ïîòîêà, çàãðÿçíåííîãî i-ì òîêñè÷íûì âåùåñòâîì. Óðàâíåíèå (2.1) áóäåò âûãëÿäåòü ñëåäóþùèì îáðàçîì: α i n Cm V ÊÎÏ = ∑ i * i ; (2.12) ÏÄÊ t i i =1 ãäå Vi îáúåì âîçäóøíîé ñðåäû â ïðèçåìíîì ñëîå, ì3. m ÊÎÓ=ÊÎÄ+ ∑ ÊÎÀ i =1 (2.2) ãäå m êîëè÷åñòâî àâòîìîáèëåé íà óëèöàõ ãîðîäà; ÊÎÄ êàòåãîðèÿ îïàñíîñòè äîðîãè ðàéîíà ãîðîäà èëè íàñåëåííîãî ïóíêòà, ì3/ñ. Ìn ÑV y ÊÎÄ = = (2.21) ÏÄÊ n ÏÄÊ n ãäå Ñ êîíöåíòðàöèÿ ïûëè â âîçäóõå óëèöû; Vy îáúåì àòìîñôåðíîãî âîçäóõà, â êîòîðîì ðàññåÿíà ïûëü. n Ñ = ∑ Ñ m + C Σo (2.22) j=1 ãäå Ñm – êîíöåíòðàöèÿ ïûëè â âîçäóõå óëèöû îò âûáðîñîâ àâòîìîáèëåé íà òåêóùèé ìîìåíò; ΨlS Al N l t (2.23) Vy ó ãäå V – îáúåì ñðåäû â ïðèçåìíîì ñëîå àòìîñôåðû óëèöû â êîòîðîì ðàñïðåäåëÿåòñÿ ïûëü; Ψl – ñäóâàåìîñòü ïûëè, ìã/ñì2ñ.; S Àl – ïëîùàäü ïðîåêöèè àâòîìîáèëÿ íà ïîâåðõíîñòü äîðîãè, ì2; N l – êîëè÷åñòâî àâòîìîáèëåé l-êëàññà, ïðîõîäÿùèõ íàä îïðåäåëåííîé ïîâåðõíîñòüþ äîðîãè; t âðåìÿ âçàèìîäåéñòâèÿ àâòîìîáèëÿ ñ ïîâåðõíîñòüþ äîðîãè; L t= A (2.24) VA ãäå LA – äëèíà àâòîìîáèëÿ, ì; VA ñêîðîñòü åãî äâèæåíèÿ, êì/÷. Ñ= Ñ Σo – îñòàòî÷íàÿ (ðàâíîâåñíàÿ) êîíöåíòðàöèÿ ïûëè â âîçäóõå óëèöû; äëÿ óñëîâèé øòèëÿ (V ≈ 0 ì/ñ): Ñ Σo = ΨlS Al N l te − ∆G RT (2.25) Vy äëÿ âåòðåíîé ïîãîäû (V>5 ì/ñ), êîãäà îñåäàíèå − ∆G ïûëè íå íàáëþäàåòñÿ ( e RT → 1 ) ïðîèñõîäèò ðàññåÿíèå ïûëè â àòìîñôåðå: ВЕСТНИК ОГУ 10`2005 Том 2. Естественные и технические науки 87 Естественные науки C Σo = C o Voy = C o Voy (2.26) Vy Voy + ∆V ïîñòîÿííûé îáúåì ñðåäû â ïðèçåìíîì ñëîå àòìîñôåðû, îïðåäåëÿåìûé ïëîùàäüþ óëèöû (S) è âûñîòîé ïðèçåìíîãî ñëîÿ (h); V îy Voy = B * L * h (2.27) ãäå  è L õàðàêòåðèñòèêè àâòîäîðîãè ( ñðåäíÿÿ øèðèíà äîðîãè, L äëèíà äîðîãè êàæäîé óëèöû); h âûñîòà çàñòðîåê. ∆V – ïðèðîñò ïîñòîÿííîãî îáúåìà ñðåäû â ïðèçåìíîì ñëîå àòìîñôåðû, ñîçäàâàåìûé äèôôóçèîííûìè ïðîöåññàìè : Äëÿ ñëó÷àÿ, êîãäà â àòìîñôåðå íàáëþäàþòñÿ çàñòîéíûå ÿâëåíèÿ (V < 3 ÷ 5 ì/ñ), ðàññåÿíèå ïðèìåñè áóäåò ïðîèñõîäèòü ïî ìåõàíèçìó ìîëåêóëÿðíîé äèôôóçèè. Ñíèæåíèå êîíöåíòðàöèè ïðèìåñè â âîçäóõå çà ñ÷åò ìîëåêóëÿðíîé äèôôóçèè ïðîèñõîäèò â îñíîâíîì ïðè âåðòèêàëüíîì ïåðåíîñå (Läèô= ∆ h). Äëÿ ýòîãî ñëó÷àÿ ∆V îïðåäåëÿåòñÿ ÷åðåç óâåëè÷åíèå âûñîòû ïðèçåìíîãî ñëîÿ: (2.28) ∆V =[2(L*h)+S]*Väèô*t Ïðè ñêîðîñòè âåòðà > 5 ì/ñ ñàìûì íåáëàãîïðèÿòíûì ñëó÷àåì áóäåò, åñëè íàïðàâëåíèå âåòðà ïåðïåíäèêóëÿðíî ðàñïîëîæåíèþ óëèöû: (2.29) ∆V =Lh Väèôt Êàòåãîðèÿ îïàñíîñòè ãîðîäà (ÊÎÃ), êîòîðàÿ äàåò íåêîòîðûé óñëîâíûé îáúåì çàãðÿçíåííîãî âîçäóõà ãîðîäà, ðàçáàâëåííûé äî ñàíèòàðíî-ãèãèåíè÷åñêèõ íîðì è ïðèâåäåííûé ê îäíîé òîêñè÷íîñòè. Îíà îöåíèâàåòñÿ êàê ñóììà îïàñíîñòè ðàéîíîâ ãîðîäà (ÊÎÐ): m ÊÎà = ∑ ÊÎÐ ; (3) i=1 Óðîâåíü çàãðÿçíåíèÿ àòìîñôåðû (ÈÇÀ–j), êîòîðûé ïîêàçûâàåò, âî ñêîëüêî ðàç ñóììàðíûé óðîâåíü çàãðÿçíåíèÿ âîçäóõà ïðåâûøàåò ïðåäåëüíî äîïóñòèìûå çíà÷åíèÿ:[6] n j = ∑( i =1 αi Ci ) ÏÄÊ i ; (4) ãäå n êîëè÷åñòâî ïðèìåñåé â âîçäóõå íàñåëåííîãî ïóíêòà. α i – áåçðàçìåðíàÿ êîíñòàíòà ïîçâîëÿþùàÿ ñîîòíåñòè ñòåïåíü âðåäíîñòè i-ãî âåùåñòâà ñ âðåäíîñòüþ äèîêñèäà ñåðû. Èçìåíåíèå êîíöåíòðàöèè Ç â àòìîñôåðå âîçìîæíî ïî äèôôóçèîííûì ïðîöåññàì (ïðè V âåòðà < 3-5 m/c) è ïî èíâåðñèè. Ðàññìîòðèì òåððèòîðèþ îäíîãî ðàéîíà ãîðîäà êàê åäèíóþ òåðìîäèíàìè÷åñêóþ åäèíèöó, ÿâëÿþùóþñÿ ñîñòàâíîé ÷àñòüþ êðóïíîãî ïðî- 88 ìûøëåííîãî ìåãàïîëèñà. Äëÿ èíâåðñèîííûõ óñëîâèé, â ñëó÷àå, åñëè àòìîñôåðíóþ ñðåäó åäèíè÷íîãî ðàéîíà ïðîìûøëåííîãî ãîðîäà ðàññìàòðèâàòü êàê çàìêíóòóþ åäèíóþ òåðìîäèíàìè÷åñêóþ ñèñòåìó, êîíöåíòðàöèþ ïðèìåñè â ïîòîêå C im ìîæíî ïðèðàâíÿòü ê ìàêñèìàëüíîé ìàññîâîé êîíöåíòðàöèè C im = C imax âðåäíîãî âåùåñòâà â ïðèçåìíîì ñëîå, à îáúåì ãàçîâîãî ïîòîêà ñ÷èòàòü ðàâíûì îáúåìó âîçäóøíîé ñðåäû â ïðèçåìíîì ñëîå ðàéîíà ãîðîäà, â ýòîì ñëó÷àå ÈÇÀ ìîæíî ïðåäñòàâèòü â ñëåäóþùåì âèäå: j= ÊÎÐ * t ; Vc/ (5) , 2 ãäå Vc = Vc − π * L * U * t – îáúåì àòìîñôåðíîãî âîçäóõà, â êîòîðîì ðàññåèâàþòñÿ ïðèìåñè. Ýòîò îáúåì óìåíüøàåòñÿ çà ñ÷åò íèñõîäÿùåé (âåðòèêàëüíîé) ñîñòàâëÿþùåé âîçäóøíîãî ïîòîêà. ÈÇÀ ïðè ýòîì íàðàñòàåò, ÷òî óêàçûâàåò íà óâåëè÷åíèå êîíöåíòðàöèé â âîçäóõå.  ñëó÷àå äèôôóçèîííûõ ïðîöåññîâ ìû èìååì: j= t t ÊÎÐ = α* ; * 2 h π * L H(t ) (6) ãäå α = ÊÎÐ π * L2 – âåëè÷èíà ïîñòîÿííàÿ äëÿ äàííîãî ðàéîíà ãîðîäà,  ñëó÷àå âûñîêîé âåòðîâîé àêòèâíîñòè (U>5 ì/ñ) ÈÇÀ áóäåò èçìåíÿòüñÿ ïî ñëåäóþùåé çàâèñèìîñòè. ÊÎÐ j= ; (7) L*H*U ãäå L ðàçìåð ðàéîíà; H âûñîòà òåìïåðàòóðíûõ èíâåðñèé U ñêîðîñòü âåòðà Ïîäñòàâèì â ôîðìóëó 5 óðàâíåíèå 2.1 ó÷èòûâàÿ, ÷òî ÊÎÐ – ýòî ñóììàðíîå çíà÷åíèÿ ÊÎÏ è ÊÎÄ M ∑∑ ÏÄÊi I i =1 j=1 j= ` Vc m n α I * t ; (8) Èç âûøå èçëîæåííîãî âèäíî, ÷òî íàèáîëüøåå âëèÿíèå íà ñêîðîñòü ðàññåèâàíèÿ ïðèìåñåé â âîçäóõå îêàçûâàåò âåòåð, âåðíåå åãî ñêîðîñòü. Òàê êàê ïðè V ≤ 3-5 m/c íàáëþäàþòñÿ çàñòîéíûå ÿâëåíèÿ â àòìîñôåðå è ñîçäàþòñÿ íåáëàãîïðèÿòíûå óñëîâèÿ äëÿ ðàññåèâàíèÿ ïðèìåñåé. Äàëåå íà èçìåíåíèå êîíöåíòðàöèè çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðå ñóùåñòâåííî âëèÿåò è íàëè÷èå îñàäêîâ. Íàïðèìåð: âî âðåìÿ òóìàíà ðàñòâîðèìûå ïðèìåñè ïî÷òè ïîëíîñòüþ ïîãëîùàþòñÿ âîäÿíûìè êàïëÿìè. Îñóùåñòâëÿåòñÿ ðåàêöèÿ îáðàçîâàíèÿ êèñëîò. Òàê ñåðíèñòûé ВЕСТНИК ОГУ 10`2005 Том 2. Естественные и технические науки Хазова С.В. Математическая модель прогнозирования качества атмосферы... Ðèñóíîê 1. ãàç â óñëîâèÿõ òóìàíà òðàíñôîðìèðóåòñÿ â ñåðíóþ êèñëîòó.  òîæå âðåìÿ ïðè âûïàäåíèè îñàäêîâ > 0,05 ìì â ñóòêè ïðîèñõîäèò ïðîöåññ âûìûâàíèÿ çàãðÿçíÿþùèõ èç àòìîñôåðíîãî âîçäóõà, ÷òî ñïîñîáñòâóåò åãî î÷èùåíèþ. Êðîìå ýòîãî çàìå÷åíî, ÷òî èçìåíåíèå êîíöåíòðàöèè çàãðÿçíÿþùèõ âåùåñòâ â àòìîñôåðíîì âîçäóõå âåäåò ñåáÿ ïî ðàçíîìó ïðè Ò> è < 0. Ïðè ñîñòàâëåíèè ìàòåìàòè÷åñêîé ìîäåëè íåîáõîäèìî òàêæå ó÷èòûâàòü óðîâåíü çàãðÿçíå- íèÿ àòìîñôåðû, êîòîðûé îïèñûâàåòñÿ ðÿäîì ñòàòèñòè÷åñêèõ õàðàêòåðèñòèê äëÿ èçìåðÿåìûõ âðåäíûõ âåùåñòâ (ÈÇÀ èíäåêñ çàãðÿçíåíèÿ àòìîñôåðû). ÈÇÀ ÿâëÿåòñÿ êîìïëåêñíîé îöåíêîé âëèÿíèÿ âðåäíûõ âåùåñòâ íà îêðóæàþùóþ ñðåäó è ðàññ÷èòûâàåòñÿ ÷åðåç ìàññó ïðèìåñåé â àòìîñôåðå. Ïðåäïîëàãàåìóþ ìîäåëü ìîæíî ïðåäñòàâèòü â âèäå ñõåìû (ðèñ 1.) (ïðèíèìàÿ, ÷òî âûáðîñ óæå ïðîèçîøåë). Ñïèñîê èñïîëüçîâàííîé ëèòåðàòóðû: 1. Áåêêåð À.À., Àãàåâ Ò.Á. Îõðàíà è êîíòðîëü çàãðÿçíåíèÿ ïðèðîäíîé ñðåäû. Ë.: Ãèäðîìåòåîèçäàò, 1989. 2. Êóøåëåâ Â.Ï. Îõðàíà ïðèðîäû îò çàãðÿçíåíèé ïðîìûøëåííûìè âûáðîñàìè. Ì.: Õèìèÿ, 1979. 3. Áåðëÿíä Ì.Å. Ïðîãíîç è ðåãóëèðîâàíèå çàãðÿçíåíèÿ àòìîñôåðû. Ë.: Ãèäðîìåòåîèçäàò, 1985. 4. Öûöóðà À.À., Áîåâ Â.Ì., Êóêñàíîâ Â.Ô., Ñòàðîêîæåâà Å.À. Êîìïëåêñíàÿ îöåíêà êà÷åñòâà àòìîñôåðû ïðîìûøëåííûõ ãîðîäîâ Îðåíáóðãñêîé îáëàñòè: Ìîíîãðàôèÿ Îðåíáóðã, Èçäàòåëüñòâî ÎÃÓ, 1999. ВЕСТНИК ОГУ 10`2005 Том 2. Естественные и технические науки 89