1 Линейная алгебра
реклама
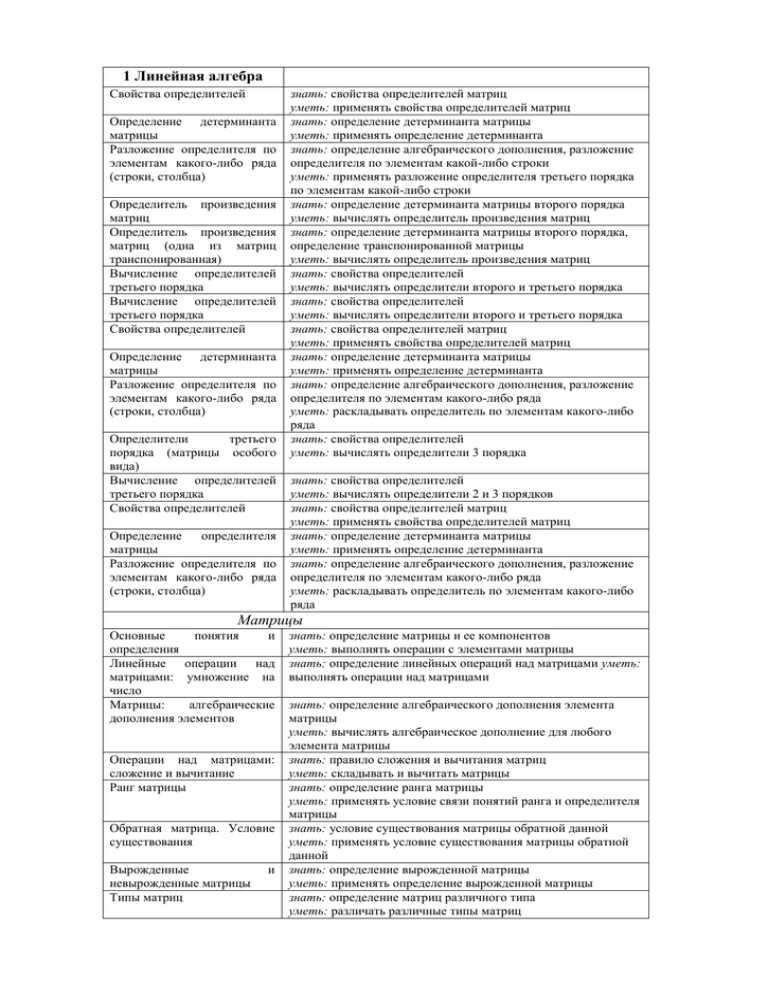
1 Линейная алгебра Свойства определителей Определение детерминанта матрицы Разложение определителя по элементам какого-либо ряда (строки, столбца) Определитель произведения матриц Определитель произведения матриц (одна из матриц транспонированная) Вычисление определителей третьего порядка Вычисление определителей третьего порядка Свойства определителей Определение детерминанта матрицы Разложение определителя по элементам какого-либо ряда (строки, столбца) Определители третьего порядка (матрицы особого вида) Вычисление определителей третьего порядка Свойства определителей Определение определителя матрицы Разложение определителя по элементам какого-либо ряда (строки, столбца) знать: свойства определителей матриц уметь: применять свойства определителей матриц знать: определение детерминанта матрицы уметь: применять определение детерминанта знать: определение алгебраического дополнения, разложение определителя по элементам какой-либо строки уметь: применять разложение определителя третьего порядка по элементам какой-либо строки знать: определение детерминанта матрицы второго порядка уметь: вычислять определитель произведения матриц знать: определение детерминанта матрицы второго порядка, определение транспонированной матрицы уметь: вычислять определитель произведения матриц знать: свойства определителей уметь: вычислять определители второго и третьего порядка знать: свойства определителей уметь: вычислять определители второго и третьего порядка знать: свойства определителей матриц уметь: применять свойства определителей матриц знать: определение детерминанта матрицы уметь: применять определение детерминанта знать: определение алгебраического дополнения, разложение определителя по элементам какого-либо ряда уметь: раскладывать определитель по элементам какого-либо ряда знать: свойства определителей уметь: вычислять определители 3 порядка знать: свойства определителей уметь: вычислять определители 2 и 3 порядков знать: свойства определителей матриц уметь: применять свойства определителей матриц знать: определение детерминанта матрицы уметь: применять определение детерминанта знать: определение алгебраического дополнения, разложение определителя по элементам какого-либо ряда уметь: раскладывать определитель по элементам какого-либо ряда Матрицы Основные понятия и определения Линейные операции над матрицами: умножение на число Матрицы: алгебраические дополнения элементов Операции над матрицами: сложение и вычитание Ранг матрицы Обратная матрица. Условие существования Вырожденные невырожденные матрицы Типы матриц и знать: определение матрицы и ее компонентов уметь: выполнять операции с элементами матрицы знать: определение линейных операций над матрицами уметь: выполнять операции над матрицами знать: определение алгебраического дополнения элемента матрицы уметь: вычислять алгебраическое дополнение для любого элемента матрицы знать: правило сложения и вычитания матриц уметь: складывать и вычитать матрицы знать: определение ранга матрицы уметь: применять условие связи понятий ранга и определителя матрицы знать: условие существования матрицы обратной данной уметь: применять условие существования матрицы обратной данной знать: определение вырожденной матрицы уметь: применять определение вырожденной матрицы знать: определение матриц различного типа уметь: различать различные типы матриц Линейные операции над матрицами: сложение (вычитание) матриц, умножение на число Ранг матрицы, имеющей пропорциональные строки или столбцы Собственные значения матрицы Операции над матрицами: умножение матриц (одна из матриц – вектор-столбец) Основные понятия и определения Операции над матрицами: умножение матриц Вырожденные и невырожденные матрицы Ранг матрицы Алгебраические дополнения элементов матрицы (определителя) третьего порядка Типы матриц Операции над матрицами: умножение матриц (одна из матриц – вектор-столбец) Ранг матрицы Обратная матрица Матрицы: основные понятия Вырожденные невырожденные матрицы и знать: определение операций над матрицами уметь: выполнять операции над матрицами знать: определение ранга матрицы уметь: вычислять ранг матрицы знать: вид характеристического уравнения уметь: составлять характеристическое уравнение для вычисления собственных значений знать: определение операции умножения матриц уметь: выполнять операцию умножения матриц знать: определение матрицы и ее компонентов уметь: выполнять операции с элементами матрицы знать: правило умножения матриц уметь: умножать матрицы знать: определение вырожденной матрицы уметь: применять определение вырожденной матрицы, вычислять определители второго порядка знать: определение ранга матрицы уметь: приводить матрицу к ступенчатому виду; вычислять ранг матрицы знать: определение алгебраического дополнения элемента матрицы уметь: вычислять алгебраическое дополнение для любого элемента матрицы третьего порядка знать: определение матриц различного типа уметь: различать различные типы матриц знать: определение операции умножения матриц уметь: выполнять операцию умножения матриц знать: определение ранга матрицы уметь: вычислять ранг матрицы знать: определение обратной матрицы уметь: находить обратную матрицу знать: определение транспонированной матрицы уметь: определять элементы транспонированной матрицы знать: определение вырожденной матрицы уметь: применять определение вырожденной матрицы, вычислять определители второго порядка Системы линейных уравнений Матричная запись систем линейных уравнений Системы линейных уравнений Основная и расширенная матрицы системы линейных уравнений Системы линейных уравнений (формы записи) Системы линейных уравнений. Метод Гаусса. Системы линейных уравнений. Определитель основной матрицы системы. Системы линейных уравнений Системы линейных знать: матричную форму записи системы линейных уравнений уметь: представлять данную систему в матричной форме знать: методы решения систем линейных уравнений уметь: находить решение системы линейных уравнений знать: определение основной матрицы системы линейных уравнений уметь: находить основную матрицу системы знать: определение основной матрицы системы линейных уравнений уметь: находить систему линейных уравнений по основной матрице системы и вектору-столбцу свободных членов знать: метод Гаусса для решения систем линейных уравнений уметь: выделять систему линейных уравнений, подготовленную для обратного хода метода Гаусса. знать: определение детерминанта основной матрицы системы. уметь: записывать определитель основной матрицы системы - вычислять определитель третьего порядка знать: методы решения систем линейных уравнений уметь: находить решения системы линейных уравнений знать: методы решения систем линейных уравнений уметь: уравнений: правило Крамера Системы линейных уравнений: свободные переменные Системы линейных уравнений: базисные переменные Системы линейных уравнений с параметром Системы линейных уравнений Системы линейных уравнений с параметром находить решения системы линейных уравнений по правилу Крамера знать: понятия базисных и свободных переменных уметь: выделять свободные переменные в системе, приведенной к ступенчатому виду знать: понятия базисных и свободных переменных уметь: выделять базисные переменные в системе, приведенной к ступенчатому виду знать: определение совместности и несовместности систем линейных уравнений уметь: вычислять определители второго порядка знать: методы решения систем линейных уравнений уметь: находить решение системы линейных уравнений знать: определение совместности и несовместности систем линейных уравнений уметь: вычислять определители второго порядка Квадратичные формы Определение квадратичной формы типа Определение квадратичной формы типа Квадратичные канонический вид формы: Квадратичные матричная квадратичных форм Обратная матрица формы: запись Обратная матрица Операции над матрицами: умножение Вычисление определителей второго порядка Матрицы: элементарные преобразования Собственные значения матрицы Матричная запись систем линейных уравнений Системы линейных уравнений. Теорема Кронекера-Капелли знать: определение квадратичной формы, знакоопределенные квадратичные формы уметь: различать знакоопределенные квадратичные формы знать: определение квадратичной формы, знакоопределенные квадратичные формы уметь: различать знакоопределенные квадратичные формы знать: канонический вид квадратичной формы уметь: приводить квадратичную форму к каноническому виду с помощью ортогональных преобразований и собственных векторов знать: определение матрицы квадратичной формы уметь: выписывать матрицу квадратичной формы знать: определение обратной матрицы и свойства определителей знать: формулы для вычисления обратной матрицы уметь: вычислять обратную матрицу знать: определение операции умножения матриц знать: определение определителя второго порядка уметь: вычислять определители второго порядка знать: определение элементарных преобразований матрицы уметь: приводить матрицу к ступенчатому виду знать: вид характеристического уравнения уметь: вычислять собственные значения матрицы знать: матричную форму записи систем линейных уравнений уметь: представлять систему линейных уравнений в матричной форме знать: теорему Кронекера-Капелли уметь: вычислять ранг матрицы 2. Абстрактная алгебра Алгебраические операции. Основные алгебраические структуры. Основные алгебраические структуры. Замкнутость множества относительно операции Определение бинарной алгебраической операции Свойства бинарных алгебраических операций Основные алгебраические знать: понятие замкнутости множества относительно данной операции уметь: проверять выполнимость заданных операций на конкретном числовом множестве знать: определение бинарной операции уметь: проверять выполнимость операции на конкретном числовом множестве знать: свойства алгебраических операций уметь: определять свойства алгебраических операций знать: понятие замкнутости множества относительно данной структуры. Замкнутость множества относительно операции Определение бинарной алгебраической операции Свойства бинарных алгебраических операций Основные алгебраические структуры: группы Определение бинарной алгебраической операции Основные алгебраические структуры: кольца Свойства бинарных алгебраических операций операции уметь: проверять выполнимость заданных операций на конкретном числовом множестве знать: определение бинарной операции уметь: проверять выполнимость и однозначность операции на конкретном числовом множестве знать: свойства алгебраических операций уметь: определять свойства алгебраических операций знать: определение группы уметь: проверять аксиомы определения группы в различных формах его записи знать: определение бинарной операции уметь: проверять выполнимость и однозначность операции на конкретном числовом множестве знать: определение кольца уметь: применять определение кольца знать: свойства алгебраических операций уметь: определять свойства алгебраических операций Линейные отображения Линейные отображения Линейные отображения Линейные (операторы) отображения знать: определение линейного отображения уметь: выделять линейное отображение из заданных знать: зависимость между координатами вектора и его образа в данном базисе уметь: определять координаты образа вектора в линейном отображении, заданном матрицей знать: вид характеристического уравнения уметь: составлять характеристическое уравнение для вычисления собственных значений Векторные пространства Векторное пространство Векторные пространства Векторные пространства знать: основные понятия, используемые в векторных пространствах уметь: находить линейную комбинацию заданных векторов знать: определение линейной комбинации векторов уметь: находить линейную комбинацию векторов в данном базисе знать: определение координат вектора в данном базисе уметь: находить координаты вектора в его разложении по базису Алгебра многочленов Алгебра многочленов: корни многочленов Алгебра многочленов: корни многочленов Алгебра многочленов: корни многочленов Алгебра многочленов: теорема Виета Многочлены над числовыми полями знать: определение корня многочлена, определение кратного корня многочлена уметь: находить корни многочлена по его разложению на множители, определять кратность корня знать: определение корня многочлена, заданного над числовым полем уметь: - находить корни многочлена по его разложению на множители; - определять принадлежность корня заданному числовому множеству знать: теоретический материал разложения многочлена на неприводимые множители над числовыми полями уметь: по заданным корням находить коэффициенты искомого многочлена знать: теорему Виета уметь: применять теорему Виета для заданного многочлена знать: связь между степенью многочлена и количеством его корней над полем комплексных чисел (основная теорема алгебры); определение корня n-ой степени из комплексного числа уметь: находить корни многочлена, заданного над полем комплексных чисел Размерность пространства Векторные базис векторного пространства: знать: основные понятия, используемые в векторных пространствах уметь: определять размерность конкретных векторных пространств знать: определение базиса векторного пространства уметь: выделять вектора, образующие базис векторного пространства 3. Аналитическая геометрия Аналитическая геометрия на плоскости Основные задачи аналитической геометрии на плоскости: расстояние между двумя точками Основные задачи аналитической геометрии на плоскости: деление отрезка в данном отношении. Кривые второго порядка Полярная система координат Основные задачи аналитической геометрии на плоскости: расстояние между двумя точками Основные задачи аналитической геометрии на плоскости: деление отрезка в данном отношении. Кривые второго порядка Условие коллинеарности и перпендикулярности векторов Полярная система координат Основные задачи аналитической геометрии на плоскости: деление отрезка в данном отношении. Основные задачи аналитической геометрии на плоскости: площадь треугольника Кривые второго порядка Угол между векторами Полярная система координат знать: формулу для нахождения расстояния между двумя точками на плоскости уметь: решать основные задачи аналитической геометрии на плоскости знать: формулу для нахождения координат середины отрезка уметь: находить координаты середины отрезка знать: определения кривых второго порядка уметь: представлять уравнения кривых второго порядка в каноническом виде знать: полярную систему координат уметь: записывать уравнение кривой в полярных координатах. знать: формулу вычисления расстояния между двумя точками на плоскости уметь: применять формулу вычисления расстояния между двумя точками для определения координат одной из точек знать: формулу для нахождения координат середины отрезка уметь: находить координаты середины отрезка знать: канонические уравнения кривых 2-го порядка уметь: использовать канонические уравнения кривых 2-го порядка при решении задач знать: условия коллинеарности (перпендикулярности) векторов уметь: использовать условия коллинеарности (перпендикулярности) векторов при решении задач знать: полярную систему координат уметь: переводить декартовы координаты точки плоскости в полярные. Знать: формулу для нахождения координат середины отрезка уметь: применять формулу координат середины отрезка знать: формулы вычисления площади треугольника уметь: вычислять площадь треугольника знать: канонические уравнения кривых второго порядка уметь: по виду кривой составить ее уравнение знать: определение скалярного произведения векторов уметь: определять угол между векторами знать: полярную систему координат уметь: переводить декартовы координаты точки плоскости в полярные. Прямая на плоскости Типы уравнений прямой Прямая на плоскости: угловой коэффициент знать: типы уравнений прямой на плоскости уметь: использовать различные виды уравнения прямой на плоскости при решении задач знать: определение уравнения прямой на плоскости уметь: определять угловой коэффициент по данному Общее уравнение прямой Условие параллельности двух прямых Условие перпендикулярности двух прямых Типы уравнений прямой Условие параллельности двух прямых Условие перпендикулярности двух прямых Расстояние от точки до прямой Уравнение прямой в отрезках Условие параллельности двух прямых Условие перпендикулярности двух прямых Расстояние прямой от точки до уравнению прямой знать: общее уравнение прямой уметь: применять общее уравнение прямой при решении задач знать: условие параллельности двух прямых уметь: применять условие параллельности при решении задач знать: условие перпендикулярности двух прямых уметь: применять условие перпендикулярности при решении задач знать: типы уравнений прямой на плоскости уметь: использовать различные виды уравнений прямой на плоскости при решении задач знать: условие параллельности двух прямых уметь: применять условие параллельности при решении задач знать: условие перпендикулярности двух прямых уметь: применять условие перпендикулярности при решении задач знать: понятии расстояния от точки до прямой уметь: вычислять расстояние от точки до прямой знать: уравнение прямой «в отрезках» уметь: записывать общее уравнение прямой на плоскости знать: условие параллельности двух прямых уметь: применять условие параллельности при решении задач знать: условие перпендикулярности двух прямых уметь: применять условие перпендикулярности при решении задач знать: понятии расстояния от точки до прямой уметь: вычислять расстояние от точки до прямой Аналитическая геометрия в пространстве Поверхности второго порядка Поверхности второго порядка. Канонические уравнения Поверхности второго порядка. Канонические уравнения Основные задачи аналитической геометрии в пространстве: деление отрезка в данном отношении Основные задачи аналитической геометрии в пространстве: расстояние между точками знать: канонические уравнения поверхностей второго порядка уметь: находить координаты центра сферы знать: канонические уравнения поверхностей второго порядка уметь: по уравнению поверхности устанавливать ее вид знать: канонические уравнения поверхностей второго порядка уметь: определять уравнение поверхности второго порядка по ее графическому изображению знать: формулу для нахождения координат середины отрезка уметь: применять формулу координат середины отрезка знать: формулу для вычисления расстояния между двумя точками в пространстве уметь: применять формулу для вычисления расстояния между двумя точками в пространстве Плоскость и прямая в пространстве Условие принадлежности точки заданной плоскости Общее уравнение плоскости Канонические прямой уравнения Положение плоскости относительно координатных осей Положение плоскости знать: условие принадлежности точки заданной плоскости уметь: проверять условие принадлежности точки заданной плоскости знать: общее уравнение плоскости уметь: использовать общее уравнение плоскости при решении задач знать: - канонические уравнения прямой в пространстве - условие перпендикулярности прямой и плоскости уметь: - использовать канонические уравнения прямой в пространстве - использовать условие перпендикулярности прямой и плоскости при решении задач знать: - общее уравнение плоскости в пространстве уметь: - определять положение плоскости в пространстве относительно координатных осей знать: - общее уравнение плоскости в пространстве относительно координатных плоскостей Взаимное расположение прямой и плоскости в пространстве (условие параллельности) Расстояние от точки до плоскости Прямая и плоскость. Взаимное расположение точки и плоскости Условие перпендикулярности двух плоскостей Канонические прямой уравнения Взаимное расположение прямой и плоскости в пространстве Расстояние от точки плоскости Уравнение плоскости отрезках Декартовы координаты плоскости до в на Основные задачи аналитической геометрии: координатная ось Декартовы координаты в пространстве Взаимное расположение прямой и плоскости в пространстве Уравнение прямой с угловым коэффициентом Полярная система координат: уравнение линии Условие принадлежности точки заданной прямой на плоскости Расстояние между двумя точками в пространстве Взаимное расположение прямой на плоскости Условие принадлежности точки заданной плоскости Поверхности порядка второго уметь: - определять положение плоскости в пространстве относительно координатных плоскостей знать: условие параллельности прямой и плоскости, геометрический смысл коэффициентов в уравнении прямой и плоскости уметь: вычислять скалярное произведение знать: понятие расстояния от точки до плоскости уметь: находить расстояние от точки до плоскости знать: условие принадлежности заданной плоскости уметь: проверять условие принадлежности точки заданной плоскости знать: условие перпендикулярности двух плоскостей уметь: использовать условие перпендикулярности двух плоскостей при решении задач знать: каноническое уравнение прямой, проходящей через точку с направляющим вектором уметь: составить каноническое уравнение прямой, проходящей через данную точку с заданным направляющим вектором знать: условие параллельности прямой и плоскости уметь: применять условие параллельности прямой и плоскости для вывода уравнения прямой, вычислять скалярное произведение знать: понятие расстояния от точки до плоскости уметь: находить расстояние от точки до плоскости знать: уравнение плоскости в отрезках уметь: составлять уравнение плоскости в отрезках знать: определение декартовых координат точки на плоскости уметь: оценивать расположение точки на плоскости по знакам ее координат знать: декартовы координаты на прямой уметь: определять положение точки на координатной оси знать: определение декартовых координат в пространстве уметь: оценивать расположение точки в пространстве по знакам ее координат знать: возможные варианты взаимного расположения прямых и плоскостей в пространстве уметь: находить пересечение прямых и плоскостей в пространстве знать: определение углового коэффициента прямой уметь: вычислять значение углового коэффициента прямой линии по ее графику знать: уравнение линии в полярных координатах уметь: определять вид линии по ее уравнению в полярных координатах знать: условие принадлежности точки данной прямой уметь: определять условие принадлежности точки данной прямой знать: формулу расстояния между двумя точками в пространстве уметь: вычислять расстояние между двумя точками в пространстве знать: условия параллельности и перпендикулярности прямых на плоскости уметь: по уравнениям определять параллельные и перпендикулярные прямые знать: условие принадлежности точки заданной плоскости уметь: проверять условие принадлежности точки заданной плоскости знать: определение канонического уравнения сферы уметь: составлять уравнение сферы с заданным центром Основные задачи аналитической геометрии в пространстве: деление отрезка в данном отношении Прямая на плоскости: угловой коэффициент знать: формулу для нахождения координат середины отрезка в пространстве уметь: находить координаты одного из концов отрезка по координатам другого конца и координатам середины этого отрезка знать: определение уравнения прямой на плоскости уметь: определять угловой коэффициент по уравнению прямой 4. Дифференциальная геометрия Дифференциальная геометрия кривых Дифференциальная геометрия поверхностей Элементы топологии Дифференциальная геометрия кривых. Кривизна плоской кривой Дифференциальная геометрия кривых Дифференциальная геометрия поверхностей Элементы топологии Кривизна линии знать: свойства центральных кривых 2-го порядка уметь: использовать свойства центральных кривых 2-го порядка при решении задач знать: типы поверхностей 2-го порядка уметь: по виду уравнения поверхности 2-го порядка определять ее тип знать: геометрическую иллюстрацию операций над множествами уметь: использовать теоретико-множественную символику знать: определение кривизны плоской линии уметь: вычислять кривизну плоской линии знать: теоретический материал для вычисления кривизны плоских линий уметь: вычислять кривизну плоских линий знать: уравнение касательной плоскости к поверхности уметь: составлять уравнение касательной плоскости к поверхности знать: геометрическую иллюстрацию операций над множествами уметь: использовать теоретико-множественную символику знать: определение радиуса кривизны плоской линии уметь: вычислять радиус кривизны 5. Математический анализ Введение в анализ Область функции Область функции определения определения Предел функции: вычисление предела дробно-линейной функции Предел функции: вычисление предела (раскрытие 0 неопределенности ) 0 Окрестность точки (окрестность) Предел функции: первый замечательный предел Основные элементарные функции: область значений функции Непрерывность функции. Точки разрыва. Предел функции: вычисление предела знать: область определения основных элементарных функций уметь: решать рациональные неравенства знать: понятие области определения функций уметь: находить область определения элементарных функций на числовой прямой. знать: определение предела функции уметь: вычислять предел дробно-линейной функции 0 знать: способы раскрытия неопределенности вида 0 уметь: использовать способы раскрытия неопределенностей при вычислении пределов знать: определение «-окрестности» точки на числовой прямой уметь: находить «-окрестность» точки на числовой прямой знать: первый замечательный предел уметь: вычислять пределы функций, применяя знание первого замечательного предела знать: понятие области значений функции уметь: находить множество значений функции знать: понятия непрерывной и разрывной функции уметь: находить точки разрыва дробно-рациональной функции, содержащей в знаменателе линейные сомножители знать: основные приемы раскрытия неопределенностей вида Область определения функции Предел функции: второй замечательный предел Основные элементарные функции: область значений функции Непрерывность функции: точки разрыва. Асимптоты кривых Предел функции: вычисление предела Область определения функции Предел функции: второй замечательный предел Предел функции: первый замечательный предел Основные элементарные функции: область значений функции Непрерывность функции: точки разрыва. Асимптоты кривых уметь: вычислять предел функции знать: область определения основных элементарных функций уметь: решать рациональные неравенства знать: второй замечательный предел уметь: вычислять пределы функций, применяя знание второго замечательного предела знать: понятие области значений функции уметь: находить множество значений функции знать: понятия непрерывной и разрывной функции уметь: находить точки разрыва дробно-рациональной функции знать: определения асимптот графика функции уметь: - находить точки разрыва дробно-рациональной функции - находить предел функции на бесконечности знать: основные приемы раскрытия неопределенностей; основные правила и формулы дифференцирования уметь: вычислять предел функции в точке знать: область определения основных элементарных функций уметь: решать рациональные неравенства знать: второй замечательный предел уметь: вычислять пределы функций, применяя знание второго замечательного предела знать: - основные свойства пределов - первый замечательный предел уметь: вычислять пределы функций, применяя знание первого замечательного предела знать: понятие области значений функции уметь: находить множество значений функции знать: понятия непрерывной и разрывной функции уметь: находить точки разрыва элементарных функций знать: - определения асимптот графика функции - условия существования асимптот уметь: находить вертикальные и горизонтальные асимптоты. Дифференциальное исчисление ФОП Геометрический производной Геометрический производной смысл смысл Физический смысл производной Правила дифференцирования Производная произведения Производная частного Приложения дифференциального исчисления ФОП: экстремумы функции Производные высших порядков Геометрический смысл производной знать: геометрический смысл производной функции уметь: находить угловой коэффициент прямой знать: геометрический смысл производной функции уметь: - по графику функции определять дифференцируемость функции знать: физический смысл производной уметь: дифференцировать основные элементарные функции знать: основные правила и формулы дифференцирования уметь: дифференцировать основные элементарные функции знать: правило дифференцирования произведения функций уметь: дифференцировать функции, применять правило дифференцирования произведения функций знать: правило дифференцирования частного функций уметь: дифференцировать функции, применять правило дифференцирования частного функций знать: достаточное условие существования экстремума функции уметь: использовать достаточное условие существования экстремума функции, заданной графиком ее производной знать: основные правила и формулы дифференцирования уметь: дифференцировать сложные функции знать: геометрический смысл производной функции уметь: находить угловой коэффициент прямой Физический производных смысл Производная произведения Производная частного Производная сложной функции Приложения дифференциального исчисления ФОП: экстремумы функции Приложения дифференциального исчисления ФОП: исследование функции с помощью графиков Приложения дифференциального исчисления ФОП: наибольшее и наименьшее значение функции на отрезке Производные высших порядков Физический смысл производной второго порядка Физический смысл производной Производная произведения Производная частного Производная сложной функции Приложения дифференциального исчисления ФОП: исследование функций с помощью графиков Производные высших порядков Физический смысл производной второго порядка знать: физический смысл производной уметь: применять правила дифференцирования сложной функции знать: правило дифференцирования произведения функций уметь: дифференцировать функции, применять правило дифференцирования произведения функций знать: правило дифференцирования частного функций уметь: дифференцировать функции, применять правило дифференцирования частного функций знать: основные правила и формулы дифференцирования уметь: дифференцировать сложные функции знать: достаточное условие существования экстремума функции уметь: использовать достаточное условие существования экстремума функции, заданной графиком ее производной знать: - достаточные условия монотонности функции - достаточные условия выпуклости (вверх, вниз) графика функции уметь: применять производные функции для исследования свойств функции по заданному графику знать: основные правила и формулы дифференцирования уметь: - дифференцировать элементарные функции - находить наименьшие (наибольшие) значения функции на отрезке знать: основные правила и формулы дифференцирования уметь: дифференцировать сложные функции знать: физический смысл производной второго порядка уметь: применять правила дифференцирования знать: физический смысл производной уметь: применять правила дифференцирования сложных функций знать: правило дифференцирования произведения функций уметь: дифференцировать функции, применять правило дифференцирования произведения функций знать: правило дифференцирования частного функций уметь: дифференцировать функции, применять правило дифференцирования частного функций знать: основные правила и формулы дифференцирования уметь: дифференцировать сложные функции знать: - достаточные условия монотонности функции - достаточные условия выпуклости (вверх-вниз) графика функции - основные правила и формулы дифференцирования уметь: использовать производные для исследования свойств функции по заданному графику знать: основные правила и формулы дифференцирования уметь: дифференцировать сложные функции знать: физический смысл производной второго порядка уметь: применять правила дифференцирования Дифференциальное исчисление ФНП Частные производные первого порядка Частные производные первого порядка Частные производные первого и второго порядка Экстремум нескольких функции переменных: знать: основные правила и формулы дифференцирования уметь: - дифференцировать элементарные функции - находить частные производные ФНП знать: основные правила и формулы дифференцирования уметь: дифференцировать сложные функции - находить частные производные ФНП знать: основные правила дифференцирования уметь: находить частные производные функции двух переменных знать: определение условного экстремума уметь: находить условные экстремумы функции двух условный экстремум переменных Интегральное исчисление Неопределенный интеграл Интегрирование показательных функций Интегрирование тригонометрических функций Геометрические приложения определенного интеграла: вычисление площадей Неопределенный интеграл Интегрирование показательных функций Интегрирование тригонометрических функций Геометрические приложения определенного интеграла: вычисление площадей Основные методы интегрирования: метод замены переменной Основные методы интегрирования: метод интегрирования по частям Интегрирование рациональных функций Свойства интеграла определенного Упрощение подынтегральной функции Определенный вычисление интеграл: Двойной интеграл: геометрический смысл (произвольная область) Двойной интеграл: геометрический смысл (прямоугольная область) Несобственные интегралы Метод замены переменной при интегрировании Неопределенный интеграл (свойства неопределенных знать: таблицу простейших интегралов уметь: находить первообразную функции знать: основные правила интегрирования элементарных функций уметь: находить первообразные показательных функций знать: основные методы вычисления неопределенных интегралов уметь: находить первообразные тригонометрических функций знать: геометрический смысл определенного интеграла уметь: вычислять площадь криволинейной трапеции с помощью определенного интеграла знать: основные правила интегрирования элементарных функций уметь: находить первообразные элементарных функций знать: методы вычисления неопределенных интегралов уметь: применять метод замены переменных в неопределенном интеграле знать: основные методы вычисления неопределенных интегралов уметь: находить первообразные тригонометрических функций знать: геометрический смысл определенного интеграла уметь: записать формулу площади криволинейной фигуры с помощью определенного интеграла знать: основные методы интегрирования уметь: вычислять простейшие интегралы, использовать метод замены переменной знать: основные методы интегрирования уметь: вычислять простейшие интегралы, метод интегрирования по частям знать: разложение дробно-рациональной функции на элементарные дроби уметь: интегрировать дробно-рациональные функции знать: свойства определенного интеграла уметь: применять свойства определенного интеграла при решении задач знать: правило разложения дробно-рациональной функции на элементарные дроби уметь: применять правило разложения дробно-рациональной функции на элементарные дроби знать: методы интегрирования, формулу Ньютона-Лейбница, правила нахождения первообразных уметь: вычислять определенные интегралы, применяя различные методы интегрирования знать: вид произвольной области по заданным пределам интегрирования уметь: строить область по заданным пределам интегрирования знать: вид прямоугольной области по заданным пределам интегрирования уметь: строить область по заданным пределам интегрирования знать: формулу вычисления несобственных интегралов с бесконечным верхним пределом уметь: - применять формулу вычисления несобственных интегралов с бесконечным верхним пределом - вычислять первообразные и пределы функций знать: метод замены переменной при интегрировании функций уметь: применять метод замены переменной при интегрировании функций знать: таблицу основных интегралов; - свойства неопределенных интегралов интегралов) Неопределенный интеграл (замена переменной, интегрирование по частям) Интегрирование показательных функций Интегрирование тригонометрических функций Геометрические приложения определенного интеграла: вычисление площадей Основные методы интегрирования Кратные интегралы Криволинейные интегралы Интегрирование рациональных функций Определенный интеграл: интегрирование тригонометрических функций. Формула НьютонаЛейбница. Определенный интеграл. Формула Ньютона-Лейбница. Свойства интеграла определенного Приложения интегралов: длина дуги кривой в декартовой системе координат Приложения интегралов: длина дуги кривой в полярной системе координат Приложения интегралов: длина дуги кривой в параметрическом виде Двойной интеграл (сведение двойного интеграла к повторному в полярной системе координат) Сложная функция Предел числовой последовательности Несобственные интегралы Приложения уметь: вычислять простейшие интегралы знать: таблицу основных интегралов, методы интегрирования уметь: - вычислять простейшие интегралы - использовать метод интегрирования по частям знать: методы вычисления неопределенных интегралов уметь: применять метод замены переменных в неопределенном интеграле знать: основные методы вычисления неопределенных интегралов уметь: находить первообразные тригонометрических функций знать: геометрический смысл определенного интеграла уметь: записать формулу площади криволинейной фигуры с помощью определенного интеграла знать: - основные правила и формулы дифференцирования формулы простейших интегралов уметь: использовать прием подведения выражения под знак дифференциала при нахождении первообразной знать: таблицу простейших интегралов уметь: вычислять повторные интегралы знать: таблицу простейших интегралов уметь: вычислять криволинейные интегралы 2 рода знать: разложение дробно-рациональной функции на элементарные дроби уметь: интегрировать дробно-рациональные функции знать: - определение определенного интеграла - формулу Ньютона-Лейбница уметь: - вычислять значение определенного интеграла от простейших тригонометрических функций знать: - определение определенного интеграла - формулу Ньютона-Лейбница уметь: - вычислять значение определенного интеграла для простейших функций знать: свойства определенного интеграла уметь: применять свойства определенного интеграла при решении задач знать: формулу для вычисления длины дуги кривой в декартовой системе координат уметь: вычислять длину дуги кривой в декартовой системе координат знать: формулу для вычисления длины дуги кривой в полярных координатах уметь: вычислять длину дуги кривой в полярных координатах знать: формулу для вычисления длины дуги кривой в параметрическом виде уметь: вычислять длину дуги кривой в параметрическом виде знать: формулу сведения двойного интеграла к повторному в полярной системе координат уметь: применять формулу сведения двойного интеграла к повторному в полярной системе координат знать: определения сложной функции, четной и нечетной функции уметь: определять четность и нечетность сложной функции знать: свойства сходящихся последовательностей знать: метод вычисления несобственных интегралов с бесконечным верхним пределом уметь: - применять метод вычисления несобственных интегралов с бесконечным верхним пределом - вычислять первообразные и пределы функций знать: основные правила и формулы дифференцирования дифференциального исчисления ФОП: наибольшее и наименьшее значение функции на отрезке Тройной интеграл (сведение тройного интеграла к повторному в цилиндрической системе координат) Приложения тройного интеграла: объем тела Приращение функции Производная порядка График функции первого Геометрический производной Неопределенный свойства смысл интеграл: Предел функции: односторонние пределы Основные методы интегрирования: метод замены переменной Приложения тройного интеграла: физический смысл Двойной интеграл (сведение двойного интеграла к повторному в декартовой системе координат) уметь: - дифференцировать элементарные функции - находить наименьшие (наибольшие) значения функции на отрезке знать: формулу сведения тройного интеграла к трем однократным интегралам в цилиндрической системе координат уметь: сводить тройной интеграл к повторному интегралу в цилиндрической системе координат знать: формулу нахождения объема тела с помощью тройного интеграла уметь: находить объем тела, ограниченного поверхностями в цилиндрической системе координат знать: определение приращения функции уметь: вычислять приращение функции знать: определение производной функции уметь: дифференцировать основные элементарные функции знать: основные характеристики функции уметь: исследовать функцию по ее графику знать: геометрический смысл производной уметь: находить уравнение касательной к кривой знать: незнание свойств неопределенного интеграла уметь: неумение использовать свойства неопределенного интеграла знать: определение предела функции одной переменной уметь: определять односторонние пределы функции знать: основные методы интегрирования уметь: применять метод замены переменных в неопределенном интеграле знать: формулу для нахождения массы тела через тройной интеграл уметь: вычислять тройной интеграл в декартовых координатах знать: формулу сведения двойного интеграла к повторному уметь: применять формулу сведения двойного интеграла к повторному 6. Векторный анализ Векторы и операции над ними Линейные операции над векторами Условие перпендикулярности векторов Условие векторов Скалярное векторов коллинеарности произведение Длина вектора Скалярное векторов произведение Смешанное векторов произведение Норма вектора в евклидовом пространстве Норма вектора в евклидовом пространстве: нормирование векторов знать: определения линейных операций над векторами уметь: находить линейную комбинацию векторов знать: условия перпендикулярности векторов уметь: вычислять скалярное произведение векторов, заданных в координатной форме знать: определение коллинеарных векторов уметь: находить координаты коллинеарного вектора знать: формулу для нахождения скалярного произведения векторов в координатной форме уметь: находить скалярное произведение двух векторов знать: формулу для нахождения длины вектора уметь: находить длину (модуль) вектора знать: определение скалярного произведения векторов уметь: применять понятие скалярного произведения для вычисления угла между векторами знать: определение смешанного произведения уметь: вычислять смешанное произведение с помощью определителя третьего порядка знать: определение нормы вектора в евклидовом пространстве уметь: вычислять норму вектора в евклидовом пространстве знать: определение нормы вектора в евклидовом пространстве уметь: - вычислять норму вектора - нормировать векторы Векторное произведение Геометрический смысл смешанного произведения векторов Векторное произведение Применение произведения векторного Применение смешанного произведения векторов Норма вектора в евклидовом пространстве знать: формулу вычисления векторного произведения в координатном виде уметь: находить векторное произведение с помощью определителя третьего порядка знать: геометрический смысл смешанного произведения векторов уметь: вычислять смешанное произведение с помощью определителя третьего порядка знать: определение векторного произведения уметь: вычислять векторное произведение знать: -определение векторного произведения векторов -геометрическую интерпретацию векторного произведения уметь: - находить векторное произведение векторов, заданных в координатной форме - находить длину вектора знать: формулу для вычисления объема параллелепипеда с помощью смешанного произведения уметь: применять смешанное произведение для вычисления объема параллелепипеда знать: определение нормы вектора в евклидовом пространстве уметь: вычислять норму вектора в евклидовом пространстве Элементы скалярного и векторного поля Векторная функция скалярного аргумента Градиент скалярного поля Производная поля скалярного Векторная функция скалярного аргумента Градиент скалярного поля Элементы векторного поля (дивергенция) Производная поля скалярного Координаты вектора Базис пространства векторного Длина вектора Скалярное произведение векторов Коллинеарность векторов Координаты пространстве вектора в знать: основные правила и формулы дифференцирования уметь: находить значение производной 1 и 2 порядков векторной функции скалярного аргумента в точке знать: - основные правила и формулы дифференцирования - определение градиента функции уметь: находить частные производные ФНП знать: - основные правила и формулы дифференцирования - формулу для нахождения производной скалярного поля в заданном направлении уметь: находить значение производной скалярного поля в заданном направлении знать: основные правила и формулы дифференцирования уметь: находить значение производной векторной функции скалярного аргумента знать: - определение градиента функции - основные правила и формулы дифференцирования уметь: находить частные производные ФНП знать: - определение дивергенции векторного поля - основные правила и формулы дифференцирования уметь: вычислять частные производные ФНП знать: - основные правила и формулы дифференцирования - формулу для нахождения производной скалярного поля в заданном направлении уметь: находить значение производной скалярного поля в заданном направлении знать: связь между координатами вектора и координатами его начала и конца уметь: находить координаты вектора по координатам начала и конца этого вектора знать: определение базиса векторного пространства уметь: применять определение базиса векторного пространства знать: определение длины вектора уметь: вычислять длину вектора знать: определение скалярного произведения векторов уметь: вычислять скалярное произведение векторов знать: определение коллинеарных векторов уметь: находить координаты коллинеарных векторов знать: связь между координатами вектора и координатами его начала и конца Линейные операции векторами Коллинеарность перпендикулярность векторов над и уметь: находить координаты вектора по координатам начала и конца этого вектора знать: определение линейных операций над векторами уметь: находить линейную комбинацию векторов знать: условия коллинеарности и перпендикулярности векторов уметь: применять условия коллинеарности и перпендикулярности векторов 7. Функциональный анализ Элементы теории множеств Мера плоского множества Отображение множеств «Эпсилон-окрестность» точки Элементы теории множеств Мера плоского множества Метрические пространства «Эпсилон-окрестность» точки Отображение множеств знать: - способ задания множества с помощью характеристического свойства - определения основных числовых множеств уметь: относить число к заданному множеству знать: определение меры плоского множества уметь: вычислять меру плоского множества знать: основные свойства отображений множеств уметь: находить образ множества при заданном отображении знать: определение «-окрестности» точки на числовой прямой уметь: находить «-окрестность» точки на числовой прямой знать: - определения операций над множествами - определение подмножества уметь: выполнять операции над множествами знать: определение меры плоского множества уметь: вычислять меры плоских множеств знать: определение метрического пространства уметь: проверять аксиомы определения метрического пространства знать: определение « – окрестности» точки на числовой прямой уметь: находить « – окрестность» точки на числовой прямой знать: основные свойства отображений множеств уметь: находить образ множества при заданном отображении 8. Комплексный анализ Алгебраическая и тригонометрическая формы комплексного числа. Операции над комплексными числами. Комплексные числа: модуль комплексного числа Геометрическая интерпретация комплексных чисел Комплексно-сопряжённые числа Операции над комплексными числами: сложение, вычитание Операции над комплексными числами: возведение в степень Комплексные числа: модуль комплексного числа Комплексные числа: аргумент комплексного числа Тригонометрическая форма комплексного числа Комплексно-сопряженные числа: умножение знать: определение модуля комплексного числа уметь: вычислять модуль комплексного числа знать: геометрическую интерпретацию комплексного числа уметь: представлять комплексные числа в алгебраической форме по их геометрической интерпретации знать: определение комплексно-сопряжённых чисел уметь: определять число, комплексно-сопряжённое данному знать: определение операций над комплексными числами уметь: выполнять действия с комплексными числами знать: определение комплексного числа в алгебраической форме уметь: - возводить в степень комплексное число - выделять действительную часть комплексного числа знать: определение модуля комплексного числа уметь: вычислять модуль комплексного числа знать: определение аргумента комплексного числа уметь: вычислять аргумент комплексного числа знать: геометрическую иллюстрацию комплексных чисел на плоскости уметь: записывать комплексное число в тригонометрической форме знать: определение комплексно-сопряженных чисел уметь: - определять число, комплексно-сопряженное данному Комплексно-сопряженные числа: деление Операции над комплексными числами: сложение, вычитание Операции над комплексными числами: умножение Операции над комплексными числами: деление Операции над комплексными числами: возведение в степень Комплексные числа: модуль комплексного числа Комплексные числа: аргумент комплексного числа Тригонометрическая форма комплексного числа Операции над комплексными числами: деление Операции над комплексными числами: возведение в степень (в тригонометрической форме) - умножать комплексные числа знать: определение комплексно-сопряженных чисел уметь: - определять число, комплексно-сопряженное данному - находить частное комплексных чисел знать: определение операций сложения и вычитания комплексных чисел уметь: выполнять операции сложения и вычитания комплексных чисел, заданных в алгебраической форме знать: определение операций над комплексными числами уметь: выполнять действия с комплексными числами знать: - определение операции деления комплексных чисел - определение комплексно- сопряженных чисел уметь: выполнять операцию деления комплексных чисел в алгебраической форме знать: определение комплексного числа в алгебраической форме уметь: - возводить в степень комплексное число - выделять действительную (мнимую) часть комплексного числа знать: определения модуля комплексного числа уметь: вычислять модуль комплексного числа знать: определение аргумента комплексного числа уметь: вычислять аргумент комплексного числа знать: геометрическую иллюстрацию комплексных чисел на плоскости уметь: записывать комплексное число в тригонометрической форме знать: - определение операции деления комплексных чисел - определение комплексно- сопряженных чисел уметь: выполнять операцию деления комплексных чисел в алгебраической форме знать: формулу возведения в степень комплексного числа, заданного в тригонометрической форме уметь: применять формулу возведения в степень комплексного числа, заданного в тригонометрической форме Теория функций комплексного переменного Определение функции комплексного переменного Определение функции комплексного переменного Дифференцирование функций комплексного переменного Конформные отображения Дифференцирование функции комплексного переменного Особые точки функций комплексного переменного Вычеты и их применение Показательная комплексной функция в области. знать: определение функции комплексного переменного уметь: находить значение функции комплексного переменного в заданной точке знать: определение функции комплексного переменного уметь: находить значение функции комплексного переменного в заданной точке знать: определение производной функции комплексного переменного уметь: вычислять производную функции комплексного переменного в заданной точке знать: свойства элементарных функций при конформных отображениях уметь: находить образы точек при заданных отображениях знать: определение производной функции комплексного переменного уметь: вычислять производные функций комплексного переменного знать: определение особой точки функции комплексного переменного уметь: определять особые точки функций комплексного переменного знать: определение вычета функции в изолированной особой точке и формулы для его нахождения уметь: находить вычет функции в изолированной особой точке знать: показательную форму записи комплексного числа. Формулу Эйлера Формулы Эйлера Основные элементарные функции в комплексной плоскости Отображение в комплексной плоскости Мнимая и действительная части функции комплексного переменного Операции над комплексными числами: извлечение корня Интегральная формула Коши Операции над комплексными числами: сложение, вычитание, умножение Геометрическая интерпретация комплексных чисел уметь: выписывать показательную форму комплексного числа знать: формулу Эйлера для вычисления тригонометрических функций комплексной переменной уметь: применять формулу Эйлера для вычисления значений тригонометрических функций комплексной переменной знать: правило отображения в комплексной плоскости уметь: отображать комплексное число знать: мнимую и действительную часть функции комплексного переменного уметь: определять мнимую и действительную часть функции комплексного переменного знать: формулу нахождения корней комплексного числа уметь: находить корни комплексного числа и, соответственно, число не являющееся корнем комплексного числа знать: интегральную формулу Коши уметь: применять интегральную формулу Коши; определять особую точку знать: определение операций сложения, вычитания и умножения комплексных чисел уметь: выполнять операции сложения, вычитания и умножения комплексных чисел, заданных в алгебраической форме знать: геометрическую интерпретацию комплексного числа уметь: изображать на плоскости множества комплексных чисел 9. Гармонический анализ Элементы гармонического анализа Определение периодической функции Определение периода функции Элементы гармонического анализа Элементы анализа гармонического знать: определение периодической функции уметь: выделять из заданных функций периодические знать: определение периода функции уметь: применять определение периода функции знать: определение периодической функции уметь: применять определение периодической функции для исследования свойств функции по заданному её графику знать: определение периодической функции уметь: применять определение периодической функции для исследования свойств функции по заданному графику Гармонические колебания. Ряды Фурье. Определение гармонического колебания Ряд Фурье. Теорема Дирихле Определение гармонического колебания Ряд Фурье. Теорема Дирихле Коэффициенты ряда Фурье Разложение в ряд Фурье четных и нечетных функций Определение гармонического колебания Ряд Фурье. Теорема Дирихле Коэффициенты ряда Фурье знать: определение гармонического колебания уметь: записать уравнение гармонического колебания знать: условия теоремы Дирихле уметь: записать ряд Фурье для функции, удовлетворяющей условиям ее разложения в ряд Фурье знать: определение гармонического колебания уметь: записать закон гармонического колебания знать: вид ряда Фурье для произвольной, четной и нечетной функций уметь: записать ряд Фурье для функции, удовлетворяющей условиям ее разложения в ряд Фурье знать: определение ряда Фурье уметь: вычислять коэффициенты ряда Фурье знать: разложение в ряд Фурье четных и нечетных функций уметь: определять вид ряда Фурье для четных и нечетных функций знать: определение гармонического колебания уметь: записать уравнение гармонического колебания знать: вид ряда Фурье для произвольной, четной и нечетной функций уметь: записать ряд Фурье для функции, удовлетворяющей условиям ее разложения в ряд Фурье знать: определение рядов Фурье Разложение в ряд Фурье четных и нечетных функций уметь: вычислять коэффициенты ряда Фурье знать: разложение в ряд Фурье четных, нечетных функций уметь: определять вид ряда Фурье для четных и нечетных функций 10. Ряды Числовые ряды Последовательности Числовые последовательности: рекуррентные последовательности Суммирование числового ряда. Частичная сумма ряда Сходимость числовых рядов. Признак Даламбера Знакочередующиеся ряды Последовательности Числовые последовательности: рекуррентные последовательности Признаки сходимости числового ряда Суммирование числовых рядов Признаки сходимости знакопеременных (знакочередующихся) рядов (абсолютно сходящиеся и условно сходящиеся ряды) Сходимость числовых рядов. Признак Даламбера Признаки числового ряда сходимости Последовательности Суммирование числовых рядов Знакочередующиеся ряды Суммирование числового ряда. Частичная сумма ряда Числовые последовательности: рекуррентные последовательности знать: определение числовой последовательности уметь: вычислять члены числовой последовательности по формуле общего числа знать: определение рекуррентной последовательности уметь: вычислять элементы числовой последовательности знать: определение частичной суммы ряда уметь: находить частичную сумму ряда знать: признак Даламбера сходимости числового ряда уметь: применять условие сходимости числового ряда по признаку Даламбера знать: понятия знакоположительного, знакочередующегося и степенного рядов уметь: выделять знакоположительные, знакочередующиеся и степенные ряды знать: определение числовой последовательности уметь: записывать формулу общего члена числовой последовательности знать: определение рекуррентной последовательности уметь: вычислять элементы числовой последовательности знать: - определение сходимости числовых рядов - достаточные признаки сходимости числовых рядов уметь: применять достаточные признаки сходимости числовых рядов знать: определение сходимости числового ряда уметь: вычислять сумму сходящегося числового ряда знать: понятия абсолютной, условной сходимости знакочередующихся рядов уметь: выделять абсолютно и условно сходящиеся ряды знать: признак Даламбера сходимости числового ряда уметь: применять условие сходимости числового ряда по признаку Даламбера знать: - определение сходимости числовых рядов - признаки сходимости числовых рядов уметь: применять признаки сходимости знать: определение числовой последовательности уметь: записывать формулу общего члена последовательности знать: определение сходящегося числового ряда уметь: вычислять сумму сходящегося числового ряда знать: понятия абсолютной, условной сходимости знакочередующихся рядов уметь: выделять абсолютно и условно сходящиеся ряды знать: определение частичной суммы и суммы числового ряда уметь: находить сумму ряда с помощью предела последовательности частичных сумм знать: определение рекуррентной последовательности уметь: вычислять элементы числовой последовательности Степенные ряды Ряды Тейлора Область сходимости степенного ряда Ряды Тейлора Область сходимости степенного ряда Ряды Тейлора (Маклорена) Радиус сходимости степенного ряда Область сходимости степенного ряда Сходимость числовых рядов знать: определение ряда Тейлора уметь: вычислять коэффициенты ряда Тейлора знать: определение области сходимости степенного ряда уметь: находить интервал сходимости знать: определение ряда Тейлора уметь: вычислять коэффициенты ряда Тейлора знать: определение области сходимости степенного ряда уметь: находить интервал сходимости знать: определение ряда Тейлора уметь: вычислять коэффициенты ряда Тейлора знать: формулы для вычисления радиуса сходимости степенного ряда уметь: вычислять радиус сходимости степенного ряда знать: определение области сходимости степенного ряда уметь: находить интервал сходимости степенного ряда знать: необходимый признак сходимости числового ряда уметь: вычислять пределы числовых последовательностей 11. Дифференциальные уравнения Понятие о дифференциальном уравнении Дифференциальные уравнения с разделяющимися переменными Дифференциальные уравнения 2 порядка: основные понятия Линейные дифференциальные уравнения 2 порядка Типы дифференциальных уравнений Дифференциальные уравнения 1 порядка Дифференциальные уравнения 1-порядка с переменными коэффициентами Дифференциальные уравнения первого порядка: геометрическая интерпретация решения задачи Коши Линейные однородные дифференциальные уравнения 2 порядка Линейные неоднородные дифференциальные уравнения 2 порядка Типы дифференциальных уравнений Дифференциальные уравнения 1 порядка знать: определение порядка дифференциального уравнения уметь: по виду дифференциального уравнения определять его порядок знать: таблицу простейших интегралов уметь: находить общий интеграл дифференциального уравнения с разделяющимися переменными знать: - определение решения дифференциального уравнения - дифференцировать элементарные функции уметь: решать алгебраические уравнения знать: определение характеристического уравнения линейного дифференциального уравнения II порядка уметь: составлять характеристическое уравнение линейного однородного дифференциального уравнения II порядка знать: типы дифференциальных уравнений уметь: по виду дифференциальных уравнений определять тип дифференциального уравнения знать: определение решения дифференциального уравнения уметь: решать дифференциальные уравнения 1 порядка знать: таблицу простейших интегралов уметь: находить общий интеграл дифференциального уравнения с разделяющимися переменными знать: геометрическую интерпретацию решения задачи Коши для дифференциального уравнения 1-го порядка уметь: решать задачу Коши для дифференциального уравнения 1-го порядка знать: определение линейных однородных дифференциальных уравнений 2-го порядка уметь: находить решение линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами знать: определение частного решения линейного неоднородного дифференциального уравнения второго порядка уметь: находить общий вид частного решения со специальной правой частью знать: типы дифференциальных уравнений уметь: определять тип дифференциального уравнения по его виду знать: определение дифференциального уравнения с разделяющимися переменными уметь: - разделять переменные в дифференциальном уравнении - находить частное решение дифференциального уравнения Дифференциальные уравнения первого порядка с разделяющимися переменными (общий интеграл) Дифференциальные уравнения первого порядка с разделяющимися переменными (общее решение) Дифференциальные уравнения первого порядка: геометрическая интерпретация решения задачи Коши Системы линейных однородных дифференциальных уравнений 1 порядка Линейные однородные дифференциальные уравнения 2 порядка Линейные неоднородные дифференциальные уравнения 2 порядка Уравнения производных в частных Определение типа линейного дифференциального уравнения с частными производными второго порядка Одномерное волновое уравнение Уравнение теплопроводности Задача Коши Дифференциальные уравнения первого порядка с разделяющимися переменными (частные решения) Линейные однородные дифференциальные уравнения 2 порядка знать: таблицу простейших интегралов уметь: находить общий интеграл дифференциального уравнения с разделяющимися переменными знать: таблицу простейших интегралов уметь: находить общее решение дифференциального уравнения с разделяющимися переменными знать: геометрическую интерпретацию решения задачи Коши для дифференциального уравнения 1-го порядка уметь: решать задачу Коши для дифференциального уравнения 1-го порядка знать: метод исключения неизвестных уметь: применять метод исключения неизвестных при решении системы дифференциальных уравнений знать: определение линейного однородного дифференциального уравнения 2 порядка уметь: находить общее решение линейного однородного дифференциального уравнения 2 порядка с постоянными коэффициентами знать: определение частного решения неоднородного дифференциального уравнения второго порядка уметь: находить общий вид частного решения со специальной правой частью знать: основные правила и формулы дифференцирования уметь: находить частные производные ФНП – решать алгебраические уравнения знать: типы линейных дифференциальных уравнений с частными производными второго порядка уметь: определять тип линейного дифференциального уравнения с частными производными второго порядка знать: решение одномерного волнового уравнения уметь: находить решение одномерного волнового уравнения знать: определение краевой задачи для уравнения теплопроводности уметь: определять краевые условия для уравнения теплопроводности знать: определение задачи Коши уметь: представлять задачу Коши в виде интегрального уравнения знать: определение частного решения дифференциального уравнения первого порядка уметь: решать задачу Коши для дифференциального уравнения первого порядка с разделяющимися переменными знать: определение линейного однородного дифференциального уравнения 2-го порядка уметь: находить частные решения и составлять определитель Вронского для линейного однородного дифференциального уравнения 2-го порядка 12. Операционное исчисление Преобразование Лапласа Оригинал изображения Операторный метод решения дифференциальных знать: определение преобразования Лапласа уметь: находить изображение оригинала знать: изображения основных оригиналов уметь: находить оригинал по известному изображению знать: определение решения дифференциального уравнения уметь: решать дифференциальные уравнения 1-го порядка уравнений Преобразование Лапласа для тригонометрических функций Операторный метод решения систем дифференциальных уравнений операторным методом знать: определение преобразования Лапласа уметь: находить изображение оригинала для тригонометрических функций знать: таблицу изображений основных функций уметь: составлять операторные системы уравнений 13. Теория вероятностей Понятия теории вероятностей. Теоремы сложения и умножения вероятностей. Основные понятия вероятностей теории Классическое определение вероятности Теоремы сложения и умножения вероятностей: вероятность произведения Теоремы сложения и умножения вероятностей Формула полной вероятности (вычисление) Формула полной вероятности Теория вероятностей: основные понятия Основные понятия теории вероятностей: виды случайных событий Основные понятия и теоремы теории вероятностей Основные понятия теории вероятностей: аксиомы теории вероятностей Классическое определение вероятности Теоремы сложения и умножения вероятностей: вероятность произведения Теоремы сложения и умножения вероятностей: вероятность появления хотя бы одного события Формула полной вероятности Классическое определение вероятности Теоремы сложения и умножения вероятностей: вероятность произведения Теоремы сложения и умножения вероятностей: вероятность появления хотя бы одного события Формула полной вероятности знать: определение достоверного (невозможного) события уметь: определять вероятность достоверного (невозможного) события знать: классическое определение вероятности уметь: вычислять вероятность случайного события знать: теорему умножения вероятностей уметь: вычислять вероятность произведения случайных событий знать: теоремы умножения и сложения вероятностей уметь: вычислять вероятность событий знать: формулу полной вероятности уметь: вычислять условные вероятности событий и полную вероятность знать: формулу полной вероятности уметь: использовать формулу полной вероятности знать: определение достоверного (невозможного) события уметь: определять вероятность достоверного (невозможного) события знать: понятия несовместных и независимых событий уметь: определять зависимость – независимость и совместность – несовместность событий знать: - понятия несовместных и независимых событий - основные теоремы теории вероятностей уметь: определять зависимость – независимость и совместность – несовместность событий в простом случайном эксперименте знать: - основные понятия и аксиомы теории вероятностей уметь: определять правильность соотношений между вероятностями случайных событий знать: классическое определение вероятности уметь: вычислять вероятность случайного события знать: теоремы умножения вероятностей событий уметь: использовать теоремы умножения вероятностей событий знать: определение вероятности противоположенного события уметь: вычислять вероятность наступления хотя бы одного из нескольких независимых в совокупности событий знать: формулу полной вероятности уметь: использовать формулу полной вероятности знать: классическое определение вероятности уметь: вычислять вероятности случайных событий знать: знать формулы сложения и умножения вероятностей уметь: использовать теоремы сложения и умножения вероятностей знать: определение вероятности противоположенного события уметь: вычислять вероятность наступления хотя бы одного из нескольких независимых в совокупности событий знать: формулу полной вероятности уметь: использовать формулу полной вероятности Распределение дискретных случайных величин Числовые дискретных величин характеристики случайных Законы распределения вероятностей дискретных случайных величин Законы распределения вероятностей дискретных случайных величин: формула Пуассона Числовые характеристики дискретных случайных величин Законы распределения вероятностей дискретных случайных величин Биномиальный закон распределения вероятностей дискретных случайных величин Числовые характеристики дискретных случайных величин Законы распределения вероятностей дискретных случайных величин Биномиальный закон распределения вероятностей дискретных случайных величин Формулы Байеса знать: - определение закона распределения вероятностей дискретной случайной величины - определение математического ожидания дискретной случайной величины уметь: уметь вычислять математическое ожидание дискретной случайной величины знать: определение закона распределения вероятностей дискретных случайных величин уметь: вычислять вероятности возможных значений дискретных случайных величин знать: асимптотические приближения схемы Бернулли уметь: выбрать тип асимптотического приближения схемы Бернулли знать: определение математического ожидания дискретной случайной величины уметь: - находить закон распределения вероятностей функции одного случайного аргумента - вычислять математическое ожидание дискретной случайной величины знать: определение закона распределения вероятностей дискретной случайной величины уметь: вычислять вероятности возможных значений и математическое ожидание дискретной случайной величины знать: биномиальный закон распределения вероятностей уметь: вычислять числовые характеристики биномиального закона распределения вероятностей знать: определение математического ожидания дискретной случайной величины уметь: - находить закон распределения функции случайного аргумента - вычислять математическое ожидание случайной величины знать: определение закона распределения вероятностей дискретной случайной величины уметь: вычислять вероятности возможных значений и математическое ожидание дискретной случайной величины знать: биномиальный закон распределения вероятностей уметь: вычислять вероятности при повторных независимых испытаниях знать: формулу Байеса уметь: применять формулу Байеса для вычисления условных вероятностей Распределение непрерывных случайных величин Законы распределения вероятностей непрерывных случайных величин: равномерное распределение Законы распределения вероятностей непрерывных случайных величин: равномерное распределение (свойство равномерного распределения) Законы распределения вероятностей непрерывных случайных величин: нормальное распределение Законы распределения знать: определение плотности распределения вероятностей непрерывной случайной величины, свойства плотности распределения вероятностей непрерывной случайной величины уметь: использовать свойство плотности распределения вероятностей непрерывной случайной величины знать: понятие равномерного распределения уметь: применять свойство равномерного распределения знать: определение нормального закона распределения случайной величины уметь: вычислять числовые характеристики нормально распределённой непрерывной случайной величины знать: асимптотические приближения схемы Бернулли вероятностей дискретных случайных величин: интегральная формула Муавра – Лапласа Законы распределения вероятностей непрерывных случайных величин: равномерное распределение Законы распределения вероятностей непрерывных случайных величин: нормальное распределение Законы распределения вероятностей непрерывных случайных величин: равномерное распределение Законы распределения вероятностей непрерывных случайных величин: нормальное распределение Теоремы сложения и умножения вероятностей: вероятность суммы уметь: выбрать тип асимптотического приближения схемы Бернулли для параметров, заданных в условии знать: определение плотности распределения вероятностей непрерывной случайной величины, свойства плотности распределения вероятностей непрерывной случайной величины уметь: использовать свойство плотности распределения вероятностей непрерывной случайной величины знать: определение нормального закона распределения случайной величины уметь: вычислять числовые характеристики нормально распределённой непрерывной случайной величины знать: определение закона распределения вероятностей непрерывных случайных величин уметь: вычислять числовые характеристики непрерывных случайных величины знать: определение нормального закона распределения случайной величины уметь: вычислять числовые характеристики нормально распределённой непрерывной случайной величины знать: теоремы сложения и умножения вероятностей уметь: вычислять вероятность суммы случайных событий 14. Математическая статистика Статистическое распределение выборки Характеристики вариационного ряда Точечные оценки параметров распределения Проверка статистических гипотез Интервальные оценки параметров распределения Статистическое распределение выборки Непрерывное распределение признака Точечные оценки параметров распределения: оценка математического ожидания Элементы корреляционного анализа Проверка статистических гипотез знать: - определение статистического распределения выборки - определение полигона частот уметь: вычислять частоты статистического распределения выборки знать: определения характеристик вариационного ряда уметь: определять моду вариационного ряда знать: определения точечных оценок параметров распределения уметь: вычислять несмещенную оценку математического ожидания знать: - определение статистической гипотезы - определение конкурирующей гипотезы уметь: выдвигать конкурирующую гипотезу знать: определение интервальной оценки параметров распределения уметь: использовать определение интервальной оценки для записи доверительного интервала знать: определение вариационного ряда уметь: вычислять частоты вариант выборки знать: - определение вариационного ряда для непрерывного признака Х - определение гистограммы частот уметь: вычислять частоты статистического распределения выборки знать: определения точечных оценок параметров распределения уметь: вычислять несмещенную оценку математического ожидания знать: определение коэффициента корреляции, определение коэффициента регрессии уметь: вычислять выборочный коэффициент корреляции знать: - определения статистической гипотезы - определение конкурирующей гипотезы уметь: выдвигать конкурирующую гипотезу Интервальные оценки параметров распределения знать: определение интервальной оценки параметров распределения уметь: использовать определение интервальной оценки для записи доверительного интервала Характеристики вариационного ряда Точечные оценки параметров распределения: оценка дисперсии знать: определение характеристик вариационного ряда уметь: определять моду вариационного ряда знать: определения точечных оценок параметров распределения уметь: вычислять несмещенные оценки параметров распределения знать: определение вариационного ряда уметь: вычислять частоты вариант выборки знать: определение характеристик вариационного ряда уметь: определять моду вариационного ряда знать: определение интервальной оценки параметров распределения уметь: использовать определение интервальной оценки для записи доверительного интервала знать: определение коэффициента корреляции, определение коэффициента регрессии уметь: вычислять выборочный коэффициент корреляции знать: - определение статистической гипотезы - определение конкурирующей гипотезы уметь: выдвигать конкурирующую гипотезу знать: определения точечных оценок параметров распределения уметь: вычислять несмещенные оценки параметров распределения знать: - определение вариационного ряда для непрерывного признака Х - определение гистограммы частот уметь: вычислять частоты статистического распределения выборки знать: определения точечных оценок параметров распределения уметь: вычислять несмещенную оценку математического ожидания Статистическое распределение выборки Характеристики вариационного ряда Интервальные оценки параметров распределения Элементы корреляционного анализа Проверка статистических гипотез Точечные оценки параметров распределения: оценка дисперсии Непрерывное распределение признака Точечные оценки параметров распределения: оценка математического ожидания 15. Дискретная математика Элементы математической логики. Операции. Элементы алгебры высказываний Операции высказываниями Операции высказываниями логики над над знать: элементы алгебры логики высказываний уметь: записывать высказывания на языке алгебры логики знать: определения логических операций уметь: составлять таблицу истинности для операций над высказываниями знать: определение логических операций уметь: составлять таблицу истинности для формулы алгебры логики Элементы теории множеств Операции над множествами Способы задания множеств Операции над множествами (объединение, пересечение, разность) Декартово произведение множеств Элементы комбинаторики знать: определение основных операций над множествами уметь: выполнять операции над конечными множествами знать: основные способы задания множеств; операции над множествами уметь: устанавливать способ задания множеств; - находить результат операций над конечными множествами, заданными перечислением знать: определение операций над множествами уметь: выполнять операции над конечными числовыми множествами знать: определение декартова произведения множеств уметь: находить декартово произведение множеств знать: основные элементы комбинаторики Декартово произведение множеств Элементы комбинаторики Бинарные отношения: свойства Операции над множествами (объединение, пересечение, разность) Декартово произведение множеств Элементы комбинаторики Бинарные свойства отношения: уметь: находить число перестановок конечного множества знать: определение декартова произведения множеств уметь: находить декартово произведение множеств знать: основные формулы комбинаторики уметь: решать простейшие комбинаторные задачи знать: свойства бинарных отношений уметь: определять свойства бинарных отношений знать: определение операций над множествами уметь: выполнять операции над числовыми множествами знать: определение декартова произведения множеств уметь: находить декартово произведение множеств знать: основные формулы комбинаторики уметь: решать простейшие комбинаторные задачи знать: свойства бинарных отношений уметь: определять свойства бинарных отношений Элементы теории графов и групп Основные понятия Ориентированные графы Основные графов понятия теории Ориентированные графы Матрица смежности Основные понятия Матрица смежности Свойства операций алгебраических Элементы алгебры логики высказываний: необходимые и достаточные условия Операции над высказываниями: двойственные функции Элементы алгебры логики высказываний: необходимые и достаточные условия знать: определение вершины графа уметь: по заданному графу находить количество его вершин знать: - определение ориентированного графа - определение полного пути уметь: выделять полные пути знать: определение вершин и ребер графа уметь: по заданным вершинам и отношению инцидентности ребер и вершин представлять граф в виде геометрических объектов знать: - определение ориентированного графа - определение полного пути уметь: выделять полные пути знать: определение матрицы смежности уметь: строить матрицу смежности знать: определение вершин и ребер графа уметь: по заданным вершинам и отношению инцидентности ребер и вершин представлять граф в виде геометрических объектов знать: определение матрицы смежности уметь: строить матрицу смежности знать: свойства алгебраических операций, заданных на числовом множестве уметь: определять обладают ли алгебраические операции соответствующими свойствами знать: понятия необходимого и достаточного условия уметь: определять необходимость и достаточность условий в формулировках утверждений знать: определение и принцип двойственной функции, основные эквивалентности функции алгебры логики уметь: по определению или принципу двойственности находить двойственную функцию знать: понятия необходимого и достаточного условия уметь: определять необходимость и достаточность условий в формулировках утверждений 16. Численные методы Численные методы решения алгебраических уравнений: отделение корней Численные методы анализа Численные методы решения дифференциальных уравнений знать: методы определения корней алгебраических уравнений уметь: отделять корни алгебраических уравнений знать: методы решения трансцендентных уравнений уметь: применять методы решения трансцендентных уравнений знать: приближенные методы решения дифференциальных уравнений с использованием рядов уметь: использовать приближенные методы решения Численное дифференцирование и интегрирование Численные методы решения алгебраических уравнений: метод половинного деления Численные методы решения алгебраических уравнений: интерполирование функций Численные методы решения алгебраических уравнений: отделение корней Численные методы анализа Численные методы решения дифференциальных уравнений Интерполирование функций: интерполяционный многочлен Лагранжа Численные методы решения алгебраических уравнений: метод половинного деления Численные методы решения дифференциальных уравнений: метод Эйлера Интерполирование функций: многочлены второго порядка Численное дифференцирование и интегрирование дифференциальных уравнений знать: определение дифференциала функции уметь: применять дифференциал для приближенного вычисления значений функции знать: метод половинного деления для решения алгебраического уравнения уметь: применять метод половинного деления для решения алгебраического уравнения знать: определение интерполяционного многочлена уметь: строить интерполяционный многочлен второго порядка знать: методы отделения корней алгебраических уравнений уметь: отделять корни алгебраических уравнений знать: графический метод решения трансцендентных уравнений уметь: использовать графический метод при решении трансцендентных уравнений знать: приближенные методы решения дифференциальных уравнений с использованием рядов уметь: использовать приближенные методы решения дифференциальных уравнений знать: определение интерполяционного многочлена Лагранжа уметь: строить интерполяционный многочлен Лагранжа второго порядка знать: метод половинного деления для решения алгебраического уравнения уметь: применять метод половинного деления для решения алгебраического уравнения знать: метод Эйлера приближенного решения задачи Коши обыкновенных дифференциальных уравнений первого порядка уметь: использовать метод Эйлера решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка знать: определение интерполяционного многочлена уметь: строить интерполяционный многочлен второго порядка знать: определение дифференциала функции уметь: применять дифференциал для приближенного вычисления значений функции 17. Экономико-математические методы Линейное программирование: графическое задание области допустимых решений Линейное программирование: аналитическое задание области допустимых решений Нелинейное программирование Теория игр: матричные игры Теория игр: игры с природой Транспортная задача Сетевое планирование и знать: методы решения задач линейного программирования уметь: решать задачи линейного программирования графическим (симплексным) методом знать: методы решения задач линейного программирования уметь: решать задачи линейного программирования графическим (симплексным) методом знать: определение решения задачи нелинейного программирования уметь: находить условные экстремумы функции двух переменных знать: - методы решения матричных игр - определение нижней (верхней) цены матричной игры уметь: вычислять нижнюю (верхнюю) цену матричной игры знать: - методы решения игр с природой - принцип оптимальности Байеса решения игр с природой уметь: применять принцип оптимальности Байеса для решения игр с природой знать: постановку транспортной задачи уметь: выделять открытые и закрытые транспортные задачи знать: определение критического пути управление Марковские процессы Теория массового обслуживания Динамическое программирование Модели межотраслевого баланса Линейное программирование: графическое задание области допустимых решений Линейное программирование: аналитическое задание области допустимых решений Теория игр: матричные игры Теория игр: транспортная задача Сетевое планирование и управление уметь: вычислять длину критического пути знать: уметь: знать: уметь: знать: уметь: знать: уметь: знать: методы решения задач линейного программирования уметь: решать задачи линейного программирования графическим (симплексным) методом знать: методы решения задач линейного программирования уметь: решать задачи линейного программирования графическим (симплексным) методом знать: - методы решения матричных игр - определение нижней (верхней) цены матричной игры уметь: вычислять нижнюю (верхнюю) цену матричной игры знать: постановку транспортной задачи уметь: выделять открытые и закрытые транспортные задачи знать: определение критического пути уметь: вычислять длину критического пути 18. Экономико-математические модели Функции полезности Кривые безразличия Функции спроса и предложения: равновесная цена Функции выпуска продукции Производственные функции Коэффициенты эластичности Функции спроса и предложения: равновесный объем знать: - аксиомы рационального поведения потребителя - определение бюджетного ограничения потребителя уметь: вычислять оптимальный набор благ потребителя знать: определение функции полезности уметь: определять кривую безразличия знать: определение положения равновесия уметь: вычислять равновесную цену знать: определение предельных издержек производства уметь: вычислять предельные издержки производства знать: определение предельного продукта труда (капитала) уметь: вычислять предельный продукт труда (капитала) знать: определение эластичности уметь: определять эластичность по капиталу и труду знать: определение положения равновесия уметь: вычислять равновесный объем «спроса-предложения» 19. Вариационное исчисление Вычисление значений функционала Вычисление расстояний между кривыми в пространстве С0([0;1]) Вычисление глобального максимума, минимума функционала на классе кривых Нахождение - окрестности функции Основные задачи вариационного исчисления. знать: определение функционала уметь: вычислять значения функционала от заданных функций знать: определение расстояния между кривыми в пространстве С0 уметь: вычислять расстояния между кривыми в С0 знать: определение глобального минимума (максимума) функционала уметь: вычислять глобальный минимум (максимум) функционала на заданных кривых знать: определение окрестности нулевого и первого порядка для кривой x*(t) уметь: определять условие попадания заданной функциональной последовательности в окрестность заданной функции знать: основные задачи вариационного исчисления уметь: сопоставлять условия задачи с ее названием Уравнение Эйлера Нахождение экстремали функционала знать: определение экстремали уметь: применять свойства экстремали