ОПРЕДЕЛЕНИЕ МАГНИТНЫХ И ДИЭЛЕКТРИЧЕСКИХ СВОЙСТВ

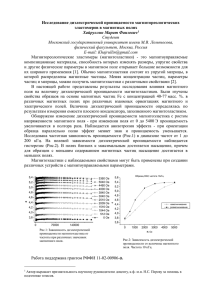
160
ВЕСТНИК
Людила Петровна СЕМИХИНАдоцент кафедры механики многофазных
систем физического факультета, кандидат физико–математических наук
УДК 546.212
ОПРЕДЕЛЕНИЕ МАГНИТНЫХ И ДИЭЛЕКТРИЧЕСКИХ
СВОЙСТВ ВЕЩЕСТВ С ПОМОЩЬЮ ИНДУКТИВНЫХ L-ЯЧЕЕК
АННОТАЦИЯ. Разработан способ одновременного определения магнитных и диэлектрических параметров веществ с помощью L-ячеек. Показана
возможность парамагнитного состояния воды в поверхностных слоях некоторых сорбентов за счет селекции молекул воды по спиновым состояниям.
The inductive method for investigation dielectric and magnetic property of
objects has been developed. The author demonstrates the possibilities of paramagnetic state of water in the surface layers of some sorbents as a result of molecule
selection according to spin modification.
Для магнито-мягких материалов, используемых в качестве сердечников, а также ферромагнитных жидкостей (стабильные суспензии магнетита в
углеводороде) важно знать их динамические магнитные проницаемости µ. В
диапазоне частот до 50 МГц значения µ находятся по изменениям индуктивности измерительных катушек (L–ячеек). В [1] отмечается, что определенные
таким способом значения µ больших магнитных образцов в области низких
частот искажаются из-за возникновения в образцах вихревых токов.
Этими же вихревыми токами в [2-5] объясняется причина изменения
параметров соленоидальных L–ячеек при вводе в них растворов солей. Поскольку величина вихревых токов пропорциональна электропроводности
жидкости, то L–ячейки более 50 лет пытались использовать как метод бесконтактной кондуктометрии. Однако определяемые таким способом значения
электропроводности жидкостей были неоднозначны, теории метода плохо
согласовывались с экспериментом. В [6-7] впервые показано, что изменение
параметров L–ячеек при вводе в них немагнитных диэлектриков с удельной
электропроводностью æ<10мСм/см обусловлено не вихревыми токами, а токами смещения, зависящими от диэлектрической проницаемости вещества.
На основании данного факта в [6-7] разработан способ определения с помощью L–ячеек диэлектрических параметров немагнитных материалов.
К настоящему времени в литературе описаны методики определения с
помощью L–ячеек магнитных характеристик у магнитных материалов и диэлектрических − у немагнитных. Однако для повышения точности определения этих характеристик необходимо учитывать наличие диэлектрических
свойств у магнитных материалов и магнитных свойств − у диэлектриков.
С целью разработки способа одновременного определения магнитной
и диэлектрической проницаемости материалов, рассмотрим изменения параметров колебательного контура куметра, состоящего из калиброванного конденсатора переменной емкости C, а также измерительной L-ячейки с индук-
ТЮМЕНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
161
тивностью L и активным сопротивлением R. Условием резонанса колебательного контура с добротностью Q = ωL / R является соотношение:
ω2 =
1
R2
− 2 =
LC 4 L
1
(1)
LC(1 + 1 / 4Q2 )
Ввод в L-ячейку любого вещества, магнитного
или немагнитного, снижает доброт1
ность колебательного контура с Q1 до Q2 и
200
уменьшает резонансную емкость на величину
∆C
∆С= С1 − С2 - рис. 1, таблица 1.
100
Из (1) следует, что при Q > 20 (этому
2
условию соответствуют все эксперименты)
С, пФ
0
влияние изменения добротности контура на
150
155
160
165
условие резонанса не превышает 0,1%. ПоэтоРис. 1. Пример резонансных
му вполне справедливо соотношение
кривых колебательного кон(2)
ω2 = 1 / L(C + С о )
тура куметра до (1) и после
В (2) учтено, что измерительная L-ячейка
(2) введения вещества
в L-ячейку
имеет собственную емкость Со. Тогда условие
резонанса контура на частоте ω до и после ввода
магнитного вещества в L-ячейку, увеличивающего ее индуктивность µ раз, при
Q>20 можно записать в виде:
(3)
ω2 = 1/ Lo (С1 +С0) = 1/ µ Lo (С2 +С0)
где Lo - индуктивность пустой ячейки. Из (3) получаем, что для магнитного
вещества должно выполняться соотношение:
(4)
∆С/(С1+С0)= ∆С/(С1-∆С +С0)= µ-1=const
Обозначив сдвиг резонансной емкости ∆С=С1-С2 за счет магнитных
свойств вещества как ∆Сµ, из (4) получаем, что
(5)
∆Сµ=(С1+С0)(µ-1)/µ≈(µ-1)/µLoω2
Таким образом, величина сдвига резонансной емкости после ввода магнитных веществ в L-ячейку примерно обратно пропорциональна индуктивности
этой ячейки. Однако, согласно (4), отношение ∆С/(С1+С0) для магнитных веществ должно определяться величиной их магнитной проницаемости и не зависеть от индуктивности ячейки. Справедливость этого вывода на примере концентрированной ферромагнитной жидкости (ФМЖ) подтверждают данные таблицы 1, для которой разброс значений ∆С/(С1+С0)=µ-1, найденных на трех измерительных L-ячейках, укладывается в 3% экспериментальную погрешность.
Таблица 1 на примере воды также демонстрирует, что особенностью
веществ, у которых можно пренебречь магнитными свойствами, является независимость сдвига резонансной емкости при их вводе в L-ячейку от индуктивности ячейки.
Как показано в [6-7], величина С1-С2=∆Сε немагнитных веществ определяется значением их диэлектрической проницаемости ε:
(6)
∆Сε=ε/α ,
где α − постоянная комплекта L-ячеек одинакового геометрического размера,
определяемая по калибровочным экспериментам.
300
Q
ВЕСТНИК
162
Таблица 1
Изменения параметров L-ячеек одинакового размера
(диаметр 22мм, высота 90мм) с разной индуктивностью на частоте 100 кГц
после ввода в них воды и ФМЖ
Lо
мГн
C0
(пФ)
Q1
33
11,6
4,3
10
8
6
148
176
162
33
11,6
4,3
10
8
6
148
176
162
C2
∆С
102⋅
(пФ)
(пФ)
∆С/(С2+Со)
Вода (бидистиллят)
55,1
80
53,32
1,78
2,73
174,47
135
172,7
1,77
0,97
545,6
148
543,8
1,8
0,33
1,78±0,02
Ферромагнитная жидкость (ФМЖ)
55,1
52
50,65
4,45
7,68
174,47
55
160,7
13,8
7,56
545,6
55
500,3
45,3
8,2
7,82 ± 0,26
C1
(пФ)
Q2
102⋅tgδ
16,9
17,1
16,9
17,0±0,2
14,7
15,1
14,9
14,9±0,2
Разная зависимость ∆Сε и ∆Сµ от индуктивности L-ячеек позволяет
найти обе эти величины с помощью двух L-ячеек одинакового размера с разной индуктивностью, настраиваемых на резонанс на исследуемой частоте.
Для полного сдвига резонансной емкости, обусловленного и магнитными и
диэлектрическими параметрами вещества, для двух таких L-ячеек имеем:
(7.а)
∆ C = (С1 + Со ) ⋅ (µ − 1) / µ + ∆ Cε
∆ C * = (С1* + С*о ) ⋅ (µ − 1) / µ + ∆ C ε ,
(7.б)
где «*»− отмечены измеряемые параметры для второй измерительной ячейки.
Из (7) находим магнитную µ и диэлектрическую ε проницаемость исследуемого вещества:
∆С * −∆С
(8)
µ −1 =
(С1* − С1 ) − ( ∆С * −∆С ) + (С о* − С о )
∆С * −∆С
]
ε = α∆Сφ = α [∆С −(С1 + С о ) ⋅ *
(С1 − С1 ) + (С о* − С о )
(9)
Для используемых в работе куметров TESLA BM-311 и BM-311 погрешность определения ∆С составляла ±0,02пф. Тогда из (4) находим, что
вклад от магнитных свойств вещества оказывается порядка точности эксперимента при µ-1<10-4. Таким образом для веществ с µ-1<10-4 параметры
L-ячеек определяются только их диэлектрическими свойствами. Величину
магнитной проницаемости данным методом можно находить для веществ
с µ-1>10-4.
Из разработанного метода определения µ следует, что замеченное в
[1] искажение значений µ больших образцов в области низких частот связано
не с вихревыми токами, а с увеличением вклада от диэлектрических свойств,
поскольку величина ∆Сε растет пропорционально сечению образца [6-7].
То, что не учет диэлектрических или магнитных свойств образца может
существенно исказить вид частотных зависимостей ε и µ массивных образцов, демонстрирует рис. 2 на примере гравия (объем образца 120 см2, диаметр
3 см), содержащего 3,5% магнетита. Однако рассчитанные по соотноше-
ТЮМЕНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
163
ниям (8-9) частотные зависимости ε и µ на рис. 2 являются классическими и
типичными для магнитных образцов [1].
2,4
10 2 (µ−1)
Б
ε
А
1
2,2
120
2
2
80
2
1,8
3
40
1,6
1
lgν (кГц)
1,4
1,3
1,7
3
2,1
0
1,3
1,7
lgν(кГц)
2,1
Рис. 2. Частотные зависимости магнитной µ (А) и диэлектрической ε (Б)
проницаемости образца сухого гравия, найденные с помощью двух измерительных L-ячеек: 1-2 – без учета вклада от ∆Сε (А) или ∆Сµ (Б);
3 – расчет по соотношениям 8-9.
Разработанный метод определения ε и µ в данной работе использован
для исследования состояния связанной воды в поверхностных слоях порошкообразных или пористых твердых тел. Интерес такого исследования обусловлен тем, что согласно [8-9] в зависимости от ориентации ядерных спинов
двух протонов, входящих в состав молекулы воды, по аналогии с орто- и пара- модификациями водорода, возможны две модификации молекул воды:
орто- (спины протонов параллельны) и пара- (спины протонов антипараллельны). Молекулы орто-воды обладают магнитным моментом, а в молекулах пара-воды он отсутствует. В статистически равновесной фазе воды содержится ¼ часть пара- и ¾ орто-воды. В [9] экспериментально установлено,
что вероятность образования димерных молекул и кластеров зависит от вращательных состояний молекул воды, которые, в свою очередь, определяются
их спиновым состоянием. Например, в состав димера вода-углекислый газ
преимущественно входят молекулы пара-воды. В результате появляется возможность разделения молекул воды по спин-модификациям.
Селекция молекул воды по спин-модификациям может происходить и
на поверхности большинства твердых тел. Именно путем адсорбции и последующей десорбции с поверхности твердых тел в [8] произведено разделение
спин-модификаций водорода.
Очевидна гипотеза, что если при контакте водяного пара с поверхностью твердых частиц будут преимущественно адсорбироваться ортомолекулы воды с ненулевым магнитным моментом, то это должно сопровождаться увеличением магнитной проницаемости сорбента. С целью выявления
возможности регистрации данного эффекта предложенным способом, были
исследованы образцы песка, монтмориллонитовой глины и нескольких цеолитов с различным содержанием воды. Для повышения чувствительности
использовались достаточно большие образцы сорбентов объемом ~120 см3.
Значения ε и µ определялись у образцов:
а) находящихся в контакте с воздухом 40-45% влажности и содержащих примерно монослой воды;
ВЕСТНИК
164
б) выдержанных в насыщенных парах воды в течение 3 суток и содержащих 2-3 монослоя воды;
в) содержащих 40-45% пленочной воды в пространстве между частицами.
ε
4
160
10 (µ -1)
110
ε
4
10 ( µ -1)
1
120
2'
120
2
120
100
80
1
90
2
80
80
80
40
1'
40
40
1'
0
0
0
1,3
1,4
70
lg( ν , кГц)
1,5
1,6
lg(ν1,7
, кГц)
Рис. 3. Частотные зависимости
µ (1-2) и ε (1′) для образца
монтмориллонитовой глины (1, 1′)
и цеолита после выдержки в
насыщенных парах воды.
60
1,3
1,4
1,5
1,6
1,7
Рис. 4. Частотные
зависимости
µ (1-2) и ε (1′-2′) для образца
цеолита после выдержки в
насыщенных парах воды(1, 1′)
Характерные частотные зависимости ε и µ образцов сорбентов с адсорбированной водой показаны на рис. 3-4 на примере цеолита и монтмориллонитовой глины. Сопоставляя рис. 2-4 видим, что особенностью таких образцов является наличие экстремумов ε и µ на частоте ~35кГц (максимум µ и
минимум ε). При повышении содержания воды в образце наблюдается увеличение значений µ на частоте 35кГц - рис. 3-4. Этот факт свидетельствует, что
данный максимум обусловлен водой. То, что повышенные значения µ влажного цеолита обусловлены именно водой, доказывают также диаграммы на
рис. 5, на котором сопоставлены значения ε и µ смоченных водой двух образцов цеолитов, сразу после заливки его водой и через сутки.
4
10
150(µ−1)
А
1
120
90
60
30
0
Б
ε
120
2
100
а
б
80
а
б
Рис. 5. Значения ε на частоте 20 кГц и µ на частоте 35 кГц смоченных водой
двух образцов цеолитов (а, б), сразу после заливки его водой (1)
и через сутки (2).
Итак, сначала состояние воды вблизи частиц цеолита близко к обычному состоянию связанной воды с высоким значением ε и малым µ (лишь
чуть выше нижнего предела чувствительности метода). Однако с течением
ТЮМЕНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
165
времени происходит существенное изменение состояния воды, контактирующей с поверхностью частиц цеолита: происходит резкое увеличение µ и
снижение ε. Данный факт обусловлен тем, что магнитный и дипольный момент молекулы воды не коллинеарны. Кроме того, не коллинеарны и вектора
напряженности электрического и магнитного поля в L-ячейке. Поэтому повышение в воде доли орто-молекул с ненулевым магнитным моментом и их
ориентирование по направлению магнитного поля L-ячейки, сопровождающееся увеличением µ, снижает возможность ориентирования дипольных моментов по направлению электрического поля, что приводит к уменьшению ε.
Отметим, что подобный эффект не наблюдается в водных растворах
солей железа вплоть до концентрации 1моль/л. Поэтому представленный на
рис. 5 эффект не объясняется переходом каких-то парамагнитных примесей в
воду. Более того, оказалось, что переход каких-либо примесей из сорбента в
воду не повышает, а, наоборот, резко снижает максимум µ связанной воды на
частоте ∼35кГц. Данный факт был установлен в результате промывания частиц цеолитного сорбента дистиллированной водой. Промывка сорбента велась до тех пор, пока электропроводность сливаемой промывочной воды не
снизилась до значения в дистиллированной воде. После такой промывки максимум µ образцов цеолитов с 40% воды увеличился от 1,5 до 5 раз.
То, что максимум значений µ веществ на частоте ∼35 кГц обусловлен
присутствием в них воды, ранее было показано в [10] на примере порошкообразных магнитных материалов. Установлено, что данный экстремум исчезает
на обезвоженных образцах путем их вакуумирования и, наоборот, растет по
величине в процессе выдержки в насыщенных парах воды. Характерная частотная зависимость µ сорбентов с пренебрежимо малым содержанием воды и
магнитной примесью в данной работе представлена на рис. 2(А) на примере
гравия (влияние адсорбированной воды на свойства этого сорбента пренебрежимо мало из-за достаточно крупных его гранул и отсутствия пористости).
Причина появления максимума значений µ на частоте ∼35 кГц у содержащих воду веществ впервые была рассмотрена в [10]. Показано, что данный эффект является аналогом эффекта Ханле [11], который наблюдается в
малых полях Н < Н гео и заключается в сильной зависимости поляризации
рассеянного света от напряженности магнитного поля. Эффект Ханле имеет
простую интерпретацию. Накачка светом резонансной частоты переводит
атом в возбужденное состояние с временем жизни τ. При наличии внешнего
магнитного поля Но магнитные моменты (спины) возбужденного атома прецессируют с частотой Ω = γ H o вокруг направления поля Но. В сильном поле, когда Ω τ >> 1 , спины за время τ успевают сделать много оборотов, и их
распределение становится изотропным. Максимальный эффект Ханле наблюдается при условии:
(10)
Ω τ ≅ 1 или g р τ e µ o H o / m ≅ 1
При выполнении данного условия прецессирующие в поле Но спины
дают максимальный вклад в намагниченность атома по направлению Но [11].
Принимая в соотношении (10) величину Но равной геомагнитному полю
( Н гео ≅ 0,5Э), а g р , e, m − равными g-фактору, заряду и массе протона, най-
166
ВЕСТНИК
дем время жизни возбужденного состояния протона, при котором проекция
его спина на направление геомагнитного поля максимальна
τ = τ гео =3⋅10-5сек, f гео =1/ τ гео =33 кГц
(11)
Величина f гео практически совпадает с частотой, на которой обнаружен максимум µ на содержащих воду сорбентах. Таким образом, переменное магнитное поле вертикально расположенной соленоидальной L-ячейки на
такой частоте усиливает поляризацию спинов протонов молекул воды во
внешнем геомагнитном поле, что приводит к увеличению значений µ. В
обычной объемной воде данный эффект пренебрежимо мал. То, что в связанной воде этот эффект может резко возрастать, обусловлено, по-видимому,
двумя факторами: во-первых, снижением подвижности молекул в такой воде,
и, во-вторых, повышением доли орто-молекул воды в приповерхностных
слоях. Следует отметить, что данный эффект наблюдается не на любых сорбентах. Например, он отсутствует на обычном песке и частицах ионообменной смолы, для которой µ-1<0, т.е. на ней преимущественно сорбируется уже
не орто-, а пара-вода. Полученные результаты указывают на перспективность
применения разработанной методики определения диэлектрических и магнитных характеристик веществ для исследования специфических особенностей связанной воды.
СПИСОК ЛИТЕРАТУРЫ
1. Смит Я., Вейн X. Ферриты. М.: Иностранная литература, 1962. 504 с.
2. Лопатин Б. А. Теоретические основы электрохимических методов анализа. М.:
Высшая школа, 1975. 295 с.
3. Лопатин Б.А. Высокочастотное титрование с многозвенными ячейками. М.:
Наука, 1980. 207 с.
4. Тонконогов М. П., Векслер В А., Биржанов К. Ж. Диэлектрическая релаксация
в водных растворах и суспензиях // Изв. вузов. Физика.1975. № 2. С. 81-84
5. Андреев В. С. Кондуктометрические методы и приборы в биологии и медицине.
М.: Медицина. 1973. 336 с.
6. Семихина Л. П. Способ определения диэлектрических параметров воды и ее
растворов в низкочастотной области с помощью L-ячейки. Патент РФ № 2234102 //
БИПМ. 2004. № 6.
7. Семихина Л. П. Разработка индуктивного метода измерения диэлектрических
параметров жидкостей // Вестник ТюмГУ. 2002. С. 94-100.
8. Фаркас А. Ортоводород, параводород и тяжелый водород. М.: ОНТИ, 1936.
9. Конюхов В. Е, Тихонов В. И., Тихонова Т. Л. Разделение спин-модификаций
молекул воды и тяжелой воды // Письма в ЖТФ. 1986. Т. 12. С. 1438-1441.
10. Семихина Л. П., Семихин В. И. Влияние адсорбированной воды на магнитные
свойства магнитных частиц и ФМЖ // Сборник трудов 10-й международной конференции по магнитным жидкостям. Иваново, 2002. С. 168-175.
11. Новиков Л. Н., Скроцкий Г. В., Соломахо Г. В. Эффект Ханле // УФН. Т. 113.
1974. С. 597-625.