http://www.zachet.ru/ Задача 1. Брокерская фирма предлагает

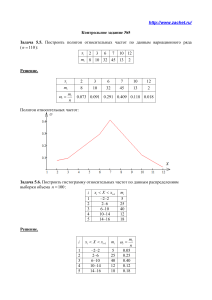
http://www.zachet.ru/
Задача 1. Брокерская фирма предлагает акции различных компаний. Акции 10 из них
продаются по наименьшей среди имеющихся акций цене и обладают одинаковой
доходностью. У трех компаний в следующем году ожидается наибольший рост цены. Клиент
собирается приобрести акции 5 таких компаний – по одной от каждой компании. Какова
вероятность того, что в число случайно отобранных попадут хотя бы две акции, рост цен на
которые будет наибольшим в следующем году?
Решение.
Вероятность того, что в число случайно отобранных попадут хотя бы две акции, рост цен на
которые будет наибольшим в следующем году, равна P  P X  2  P X  3 
7! 3!
7! 3!


3
2
2
3
C7  C3 C7  C3 3!4! 2!1! 2!5! 3!0! 1




  0.5 .
10!
10!
C105
C105
2
5!5!
5!5!
Задача 2. Вероятность того, что в страховую компанию в течение года обратится с иском о
возмещении ущерба первый клиент, равна 0.008 , для второго клиента эта вероятность равна
0.005 , а для третьего клиента 0.002 . Определите вероятность того, что в течение года
обратится только два клиента, если обращения клиентов – события независимые.
Решение.
Вероятность того, что в течение года обратится только два клиента, равна
P  p1 p2 1  p3   p1 1  p2  p3  1  p1  p2 p3 
P  0.008  0.005  1  0.002  0.008  1  0.005  0.002  1  0.008  0.005  0.002  0.00006576 .
Задача 3. Менеджер ресторана по опыту знает, что 70% людей, сделавших заказ на вечер,
придут в ресторан поужинать. В один из вечеров менеджер решил принять 20 заказов, хотя в
ресторане было лишь 15 свободных столиков. Чему равна вероятность того, что более 15
посетителей придут на заказанные места?
Решение.
Вероятность того, что более 15 посетителей придут на заказанные места, равна
P  P X  16  P X  17  P X  18  P X  19  P X  20 
16
17
18
19
 C20
 p16  1  p   C20
 p17  1  p   C20
 p18  1  p   C20
 p19  1  p   p 20 
20!
20!
20!
20!

 0.716  0.34 
 0.717  0.33 
 0.718  0.32 
 0.719  0.3  0.7 20  0.2375 .
16!4!
17!3!
18!2!
19!1!
4
3
2
http://www.zachet.ru/
Задача 4. В магазине имеется 15 автомобилей определенной марки. Среди них – 7 черного
цвета, 6 – серого и 2 – белого. Представители фирмы обратились в магазин с предложением о
продаже им 4 автомобилей этой марки, безразлично какого цвета. Составьте ряд
распределения случайной величины X , равной числу проданных автомобилей черного цвета
при условии, что автомобили отбирались случайно. Найдите числовые характеристики этого
распределения: математическое ожидание M  X  ; дисперсию D X  ; функцию распределения
FX x  , постройте график функции распределения. Найдите закон распределения случайной
величины Y  X 2  1 и математическое ожидание M Y  .
Решение.
Найдем вероятности:
8!
C84
2
P X  0  4  4!4! 
– 0 проданных черных автомобилей;
15!
C15
39
4!11!
8! 7!

C83  C71 3!5! 1!6! 56
P X  1 


– 1 проданный черный автомобиль;
15!
C154
195
4!11!
8! 7!

C82  C72 2!6! 2!5! 28
P X  2 


– 2 проданных черных автомобиля;
15!
C154
65
4!11!
8! 7!

C81  C73 1!7! 3!4! 8
P X  3 


– 3 проданных черных автомобиля;
15!
C154
39
4!11!
7!
C74
1
P X  4  4  4!3! 
– 4 проданных черных автомобиля.
15!
C15
39
4!11!
Ряд распределения:
X
0
2
39
1
56
195
2
28
65
3
8
39
4
1
39
ZACHET.RU
P
5
Математическое ожидание M  X    X i Pi  0 
i 1
2
1 28
 4  
 1.867 .
39
39 15
2
2
28  2
28  1 176


2
 0.782 .
Дисперсия D X     X i  M  X  Pi   0        4    
15  39
15  39 225


i 1
5
http://www.zachet.ru/
Функция распределения:
P X

P X

P X

F x   
P X


P X

P X

 x   0, если x  0,
2
 x   , если 0  x  1,
39
2 56 22
 x 

 , если 1  x  2,
39 195 65
22 28 10
 x 

 , если 2  x  3,
65 65 13
10 8 38
 x  
 , если 3  x  4,
13 39 39
38 1
 x 

 1, если x  4.
39 39
Найдите закон распределения случайной величины Y  X 2  1 и математическое ожидание
M Y  .
Закон распределения случайной величины Y  X 2  1:
Y  X 2 1
P
5
–1
2
39
0
56
195
Математическое ожидание M Y    Yi Pi  1 
i 1
3
28
65
8
8
39
15
1
39
2
1 49
   15  
 3.267 .
39
39 15
http://www.zachet.ru/
Задача 5. Плотность распределения непрерывной случайной величины X имеет вид
0, x  3

f X x   cx  36  x , 3  x  6 . Найдите нормирующую константу c , функцию
0, x  6

распределения, математическое ожидание, дисперсию, среднеквадратичное отклонение,
вероятность того, наблюденное значение X попадает в интервал 1; 4 .
Решение.

6
 9x2
x3 
Так как  f X x dx  1 , то получим,  cx  36  x dx  c  9 x  18  x dx  c
 18 x   
3 3
 2
3
3

6
6

2

 9  62
63   9  32
33 
9
9
2
 c
 18  6    с
 18  3    с  , с   1 , с  .
3  2
3
2
2
9
 2
Математическое ожидание M  X  

6
2
9
 x  f x dx   x  9 x  36  x dx  2  4.5 .
X

Дисперсия D X  

3
9

2
 x  M  X   f X xdx    x  
6

3

Среднеквадратичное отклонение  X  D X  
4
2
2

2
x  36  x dx  9  0.45 .
9
20
9
 0.671 .
20
4
P1  X  4   f X x dx  
1
2
x  36  x dx  7  0.259 .
9
27
3
Задача 6. По таблице распределения двумерной случайной величины
X Y
–1
1
4
1
2
5
0.1 0.2 0
0 0.3 0.1
0 0.2 0.1
Найдите частные законы распределения случайных величин X и Y ; математическое
ожидание M  XY  , M  X  , M Y  ; дисперсию D XY  , D X  , DY  , вычислите
корреляционный момент K  XY  и коэффициент корреляции r  XY  .
ZACHET.RU
Решение.
Закон распределения случайной величины X :
4
X –1 1
P 0.3 0.4 0.3
Закон распределения случайной величины Y :
1
2
5
Y
P 0.1 0.7 0.2
3
3
M  XY    Pi , j X iY j  0.1   1 1    0.1  4  5  4.2 .
i 1 j 1
http://www.zachet.ru/
3
3
M  X    Pi X i  1.3 . M Y    PjYi  2.5 .
i 1
3
i 1
D XY    Pi , j X iY j  M  XY   39.76 .
3
2
i 1 j 1
3
3
D X    Pi  X i  M  X   3.81 . DY    Pj Yi  M Y   1.65 .
2
i 1
2
i 1
Корреляционный момент K  XY   M  XY   M  X   M Y   0.95 .
K  XY 
0.95

 0.379 .
Коэффициент корреляции r  XY  
D X   DY 
3.81 1.65
Задача 7. За отчетный год себестоимость единицы продукции (тыс. руб.) предприятий одной
из отраслей промышленности характеризуется данными: 21 33 24 26 21 23 23 23 26 26 30 26
30 28 26 28 26 30 28 28.
1) Постройте ряд распределения предприятий по себестоимости продукции, начертите
полигон распределения и определите среднюю себестоимость единицы продукции,
дисперсию, среднеквадратичное отклонение и коэффициент вариации. Объясните
полученные данные.
2) Разбив все данные по предприятиям на 6 равных интервалов, постройте группированный
ряд распределения предприятий по себестоимости. С помощью гистограммы оцените
плотность
распределения.
Постройте
доверительный
интервал
(точный
или
асимптотический) для математического ожидания с уровнем доверия 0.95.
Решение.
1) Ряд распределения:
X
n
21 23 24 26 28 30 33
2 3 1 6 4 3 1
Полигон распределения:
1 7
1
X i ni  21  2    33 1  26.3 тыс. руб.

N i1
20
2
1
21  26.32  2    33  26.32 1  9.61 тыс. руб.2.
X i  x ni 
20
Средняя себестоимость x 
Дисперсия DX 
1 7

N i1




Среднеквадратичное отклонение  X  DX  9.61  3.1 тыс. руб.

3.1
100%  11.8% .
Коэффициент вариации V  X 100% 
26.3
x
Таким образом, средняя себестоимость единицы продукции по предприятиям составляет 26.3
тыс. руб. со среднеквадратическим отклонением 3.1 тыс. руб. Так как V  33 %, то выборка
однородная.
http://www.zachet.ru/
2) Ряд распределения:
интервал
середина интервала, x
n
21; 23 23; 25 25; 27 27; 29 29; 31 31; 33
22
2
24
4
26
6
28
4
30
3
32
1
Гистограмма:


2
1
1
xi ni  26.5 ; дисперсия: S 2   xi  x ni  7.15 .

N
N
Доверительный интервал для оценки математического ожидания с надежностью   0.95 :
Математическое ожидание: x 
 U  S 2
U  S 2
U 
~
xx 
 x ,       0.95 , U   1.96 .
n
n
 2
1.96  7.15
1.96  7.15
Получим, 
 26.5  ~
x
 26.5 , 25.33  ~
x  27.67 .
20
20
Задача 8. По 6 магазинам имеются следующие данные:
Товарооборот (тыс. р)
670 560 580 630 650 520
Издержки обращения (тыс. р) 40 30 25 36 35 20
Вычислите ранговый коэффициент корреляции Спирмена, установите зависят ли издержки
обращения от товарооборота. Оцените значимость этого коэффициента. Принять уровень
значимости 0.01.
Решение.
Проранжированная выборка:
Товарооборот (тыс. р)
1 5 4 3 2 6
Издержки обращения (тыс. р) 1 4 5 2 3 6
http://www.zachet.ru/
10
Коэффициент ранговой корреляции Спирмена   1 

6 D1  D2 
i 1
2


.
n n2 1

6 1  1  5  4  4  5  3  2  2  3  6  6
Тогда получим   1 
 0.886 .
6 62  1
2
2
2

2

Оценим значимость коэффициента Спирмена: tнабл  
tкр 1   , n  2  tкр 0.99, 4  3.747 .
2
2
n 1
6 1
 0.886
 4.266 .
2
1 
1  0.8862
Т.к. tнабл  tкр , то значение коэффициента Спирмена можно считать существенным, т.е. между
признаками очевидна положительная связь.
Задача 9. На основе исследований главных показателей экономики за 1980 год было
установлено, что валовой национальный продукт на человека в США составил 2334$, а в
Англии 998$; внешнеторговый оборот у США достиг 26836 млн.$, в то время как в Англии
он составил 18667 млн.$. По имеющимся данным постройте таблицу сопряженности и по ней
при уровне значимости   0.05 проверьте гипотезу о независимости признаков:
внешнеторговый оборот и валовой национальный продукт.
Решение.
Пусть признак A – внешнеторговый оборот; признак B – валовый национальный продукт.
Тогда, согласно условию, таблица сопряженности имеет вид:
США Англия Итого
A 26836 18667 45503
998
3332
B 2334
Теоретические значения:
США Англия
22751,5
22751,5
A
1666
1666
B
Наблюдаемое значение
2
2
2
2

26836  22751.5 18667  22751.5 2334  1666 998  1666
2
 набл 



 2002 .
22751.5
22751.5
1666
1666
Критическое значение  кр2 0.05, 2  5.991 .
2
  кр2 , то признаки зависимы.
Так как  набл
http://www.zachet.ru/
Задача 10. В ходе социологического исследования, касающегося проблемы разводов среди
молодых семей было установлено, что из 100 нуклеарных семей (живущих отдельно от
родителей) в течение первых 3 лет совместной жизни развелось 19 семей, за тот же период
времени из 108 сложных семей (живущих совместно с родителями) развелось 23 семьи.
Проверьте гипотезу о равенстве вероятностей разводов для молодых нуклеарных и сложных
семей при уровне значимости 0.1.
Решение.
Нулевая гипотеза H 0 : p1  p2 . В качестве конкурирующей гипотезы выберем H1 : p1  p2 .
Вычислим наблюдаемое значение критерия по формуле:
m1 m2
19
23


n1 n2
100 108
U набл 

 0.412 .
19  23 
19  23  1
1 
m1  m2  m1  m2  1 1 

1 
  
1 


100  108  100  108  100 108 
n1  n2 
n1  n2  n1 n2 
Критическое значение U кр 0.1  1.645 .
Так как U набл  U кр , то нулевая гипотеза принимается, т.е. вероятности развода для молодых
нуклеарных и сложных семей не отличаются.
Если данная работа оказалась полезной для вас, то мы были бы признательны вам
за небольшую финансовую поддержку нашего проекта http://www.zachet.ru/donate/