Отчет по лабораторной работе № 4 «Компьютерное моделирование» «Символьные вычисления MatLab»
реклама

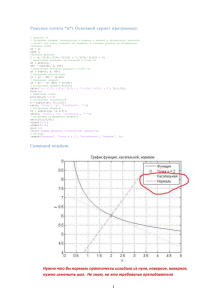
Отчет по лабораторной работе № 4 по дисциплине: «Компьютерное моделирование» на тему: «Символьные вычисления MatLab» Вариант 1. Выполнил: Батищев Д.С. Проверила: Голощапова В.А. Урсол Д.В. Белгород 2012 1 (1+x)2 ax3+bx2+cx+d Задание 1. Выполнить развертку и свертку аналитического выражения. Ввести выражение f1 (x). Вывести в командное окно выражение f1 (x) в естественном виде (команда pretty). Развернуть выражение f1 (x). Полученное выражение свернуть. Сравнить результат c f1(x). Рис. 1. Решение задачи 1. На рис. 1 видно, что метод сворачивания функции возвращает значение аналогичное введенному в начале выполнения. Задание 2. Выполнить дифференцирование и интегрирование аналитическое выражение. Ввести выражение f1 (x) и найти производную по х. Вывести в командное окно выражение f1 (x) в естественном виде (команда pretty). Рис. 2. Решение задачи 2. Из рис. 2 видно, что метод интегрирования корректно нашел первообразную для дифференцированного выражения. Задание 3. Разложить в ряд Тейлора функцию, заданную аналитическим выражением. Ввести выражение f2(x) и найти его разложение в ряд Тейлора. Построить XY график для f2(x) и его разложения в ряд Тейлора F2(x). Рис. 3. Решение задачи 3. На рис. 3 видно, что разложение в ряд Тейлора прошло успешно, но графики построить невозможно, так как в обоих функциях более одной переменной используется. Это баг встроенного метода ezplot(). Задача 4. Работа с командой funtool Задать функцию f1 и выполнить с ней операции задачи 2. Задать функцию f2 и выполнить с ней операцию символьного дифференцирования. Рис. 4. Решение задачи 4а. На рис. выше представлены два графика исходной и дифференцированной функции. Рис. 5. Решение задачи 4б Из рис. 5 видно, что возникла проблема аналогичная заданию 3. Из-за наличия нескольких переменных в функциях графики не могут быть построены. Задача 5. Исследование скорости роста символьной функции, описывающей некоторые параметры модели объекта в точке X0=0 и в диапазоне [X0-1,X0+1]. Необходимо написать следующие файл-функции: а) файл-функция, входными аргументами которой являются: - строка с символьным представлением функции f1(x) одной переменной х, - числовое значение абсциссы точки, в которой следует провести касательную. б) файл-функция анимации процесса построения касательной в точках диапазона [X0-1,X0+1]. function res = task5diffx(f, x0) res = ''; syms x; f = sym(f); y0 = subs(f, 'x', x0); yt = sym( 'y0 + k * (x - x0)' ); f = diff(f, 'x', 1); k = subs(f, 'x', x0); yt = subs(yt, 'k', k); yt = subs(yt, 'x0', x0); yt = subs(yt, 'y0' ,y0); res = yt; end Листинг 1. Нахождение производной в точке. Файл task5diffx.m function res = task5pp( yt ) res = ''; x = -1 : 0.1 : 1 ; x1 = -1.5 : 0.1 : 1.5 ; x0 = x(1) y0 = subs(yt, 'x', x0); mg = line(x0, y0); set(mg,'Marker', 'o'); set(mg,'color', 'b'); set(mg,'EraseMode', 'xor'); ygt = subs(yt, 'x', x); gt = line(x, ygt); set(gt, 'color', 'r'); y0t = y0 + 2 * x0 * (x1 - x0); g0t = line(x1, y0t); set(g0t, 'color', 'g'); set(g0t, 'EraseMode', 'xor'); axis( [-2 2 -1 4] ); axis manual; pause(0.1); k = length(x); while 1 for i = 1 : 1 : k x0 = x(i); y0 = subs(yt, 'x', x0); y0t=y0+2*x0*(x1-x0); set(mg, 'XData', x0, 'YData' ,y0); set(g0t, 'XData', x1, 'YData', y0t); pause(0.1); end; end; end Листинг 2. Построение графика функции и касательной к нему. Файл task5pp.m Рис. 6. Решение задачи 5.