11.4.2. Моделирование трехслойных оболочек

11.4.2. Моделирование трехслойных оболочек - конструкций с заполнителем
Идея повышения изгибной жесткости и устойчивости оболочек реализуется в виде трехслойных панелей,
состоящих из двух несущих слоев и заполнителя. Несущие слои выполняются либо из металла, либо из
композита, и между ними помещается пенопластовый или сотовый заполнитель. Несущие слои воспринимают
нормальные и касательные усилия в плоскости панели, а заполнитель поперечную нагрузку.
Возможно несколько вариантов моделирования трехслойных оболочек:
• элементами типа Laminate, где каждый слой задается в явном виде со своими характеристиками
материала. При этом обеспечивается получение исчерпывающих результатов во всех компонентах
расчетной модели;
• элементами типа Plate с толщиной, равной сумме толщин несущих слоев. Изгибная жесткость,
обусловленная заполнителем, учитывается с помощью свойства 12I/t^3. Этот способ обеспечивает
простую расчетную модель, но напряжения в несущих слоях и заполнителе не вычисляются, поскольку
компоненты отсутствуют в модели .
• несущие слои моделируется элементами Plate или Laminate, а заполнитель моделируется объемными
элементами типа Solid. Такой способ обеспечивает наглядность модели и отображения результатов, но
для того, чтобы включить в работу несущие слои в местах приложения нагрузки в модель необходимо
добавлять поперечные стенки. При создании модели нужно задавать толщину элементов Solid равную
расстоянию между серединными поверхностями несущих слоев, что приводит к незначительному
увеличению жесткости заполнителя.
Применим эти три способа при задании свойств трехслойной панели размером 500 × 50 × 22 мм, с
металлическими несущими слоями толщиной 1 мм, и сотовым заполнителем толщиной 20 мм.
Модель из элементов Laminate
Модуль упругости материала несущих слоев E = 72000 МПа.
Сотовый заполнитель моделируется пластиной из ортотропного материала, имеющего такую же
поперечную жесткость как пакет сот, заданной ориентации. Характеристики ортотропного материала можно
вычислить из модели, учитывающей разный удельный объем материала сот, работающий на сдвиг в
направлении осей X и Y. Предположим, что соты изготовлены из фольги с модулем сдвига G0 , и
ориентированы так, как показано на рис. 11.19, тогда:
3δ
3δ
E z = kE ; E1 = E2 << E ≈ 1.0 ; Gxy << G0 ≈ 1.0 ; Gxz = G0
; G yz = G0
,
4r
4r cos 30o
где x и y – оси в плоскости панели; z – ось нормали; δ – суммарная толщина фольги; r – радиус ячейки сот; k –
коэффициент объемного заполнения сот, который вычисляется, как отношение плотности сот к плотности
материала, из которого изготовлены соты. Модуль E z определяется в том случае, если для задания свойств
заполнителя используется трехмерный ортотропный материал.
Рис. 11. 19
В данном случае будем использовать двумерный ортотропный материал с модулями сдвига
G xz = 1385 МПа, G yz = 1600 МПа.
Задание материала: Model ⇒ Material;
• несущих слоев: Title=Alumin; <Type> ; Isotrotropic=Yes; <OK>;
E=72000; Poisson Ratio (nu)=0.3; Mass Density=1e-8; <OK>;
• ортотропного материала сот: Title=Honey; <Type> ; Orthotropic (2D)=Yes; <OK>;
Stiffness (E): 1=1.0, 2=1.0; Shear (G): 12=1.0, 1z=1385, 2z=1600;
<OK>; <Cancel>;
Создание пакета слоев укладки элемента Laminate: Model ⇒ Layup;
Title= Layup;
Material ={1..Alumin}; Thickness=1, Angle=0; <New Ply>;
Material ={2..Honey}; Thickness=20, Angle=0; <New Ply>;
Material ={1..Alumin}; Thickness=1, Angle=0; <New Ply>;
<OK>; <Cancel>;
Создание свойств элемента Laminate: Model ⇒ Property; Title=Lamin;
выбор типа элемента: <Elem/Property Type>; Laminate=Yes;
задание ориентации осей материала: <Element Material Orientation>;
Coordinate Direction=Yes; X=Yes; <OK>; <OK>;
Layup={1..Layup};
<OK>; <Cancel>;
Модель из элементов Plate
В свойстве (Property) элемента Plate нужно задать:
• разные материалы, определяющие жесткость при работе элемента в своей плоскости и на поперечную
нагрузку:
o модуль упругости материала однородной оболочки E = 72000 МПа;
o модули материала поперечного сдвига: Gxz = 1385 МПа, G yz = 1600 МПа;
коэффициент увеличения изгибной жесткости: 12 I / δ3 =330.75,
здесь изгибная жесткость панели I = δ( H − δ) 2 / 2 =220.5 мм3 ( δ - толщина несущего слоя, H – толщина
панели);
• отношение толщины, работающей на изгиб, к толщине однородной оболочки δ s / δ =16.66666.
Задание материалов выполняется так же, как в предыдущем варианте.
Создание свойств элемента Plate: Model ⇒ Property;
выбор типа элемента: <Elem/Property Type>; Plate=Yes; <OK>;
Title=Plate; Material ={1..Alumin};
Thickness, Tavg or T1=2.0;
Bend Stiffness, 12I/T**3 = 330.75;
TShear/Mem Thickness, ts/t = 16.66666;
Bending={0..Plate Material};
Tranverse Shear={2..Honey};<OK>;<Cancel>;
Модель из элементов Plate и Solid
Задание материалов выполняется так же, как в первом варианте.
Создание свойств элемента Plate: Model ⇒ Property;
выбор типа элемента: <Elem/Property Type>; Plate=Yes; <OK>;
Title=Plate; Material ={1..Alumin};
Thickness, Tavg or T1=1.0;
Bend Stiffness, 12I/T**3 = 1.0;
TShear/Mem Thickness, ts/t = 0.833333;
Bending={0..Plate Material};
Tranverse Shear={0..Plate Material };<OK>;
Создание свойств элемента Solid:
выбор типа элемента: <Elem/Property Type>; Solid=Yes; <OK>;
Title=Solid; Material ={2..Honey};
<OK>;<Cancel>;
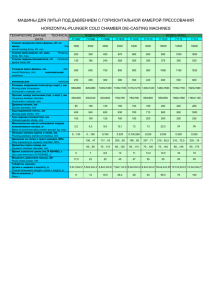
В таблице 11.2 и на рис. 11.20 приведены собственные частоты и формы колебаний пластины для
расчетных моделей, созданных различными способами. Из сравнения этих результатов видно, что при
втором способе моделирования поперечная жесткость панели завышается, о чем говорит завышенное
значение крутильной частоты колебаний.
•
Рис. 11. 20 Формы колебаний трехслойной панели
Таблица 11.2. Частоты колебаний трехслойной панели (Гц).
Номер
Форма колебаний
Способ моделирования
тона
Laminate
Plate
Plate+Solid
1
Изгиб в плоскости XZ
63.0
63.2
63.1
2
Изгиб в плоскости XY
168.7
168.6
168.4
3
Изгиб в плоскости XZ, 2-й тон
380.1
385.5
383.2
4
Кручение вокруг оси X
500.9
526.1
494.9