L15-1

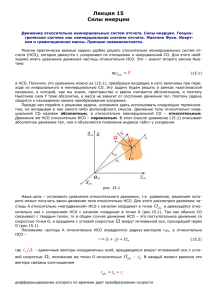
Лекция 15
Силы инерции
Движение относительно неинерциальных систем отсчета. Силы
инерции. Геоцентрическая система как неинерциальная система
отсчета. Маятник Фуко. Инертная и гравитационная массы. Принцип
эквивалентности.
Многие практически важные задачи удобно решать относительно неинерциальных
систем отсчета (НСО), которые движутся с ускорением по отношению к инерциальной
СО. Для этого необходимо иметь уравнение движения частицы относительно НСО. Это –
аналог второго закона Ньютона
maабс  F
(15.1)
в НСО. Получить это уравнение можно из (15.1), преобразуя входящие в него величины
при переходе из инерциального в неинерциальную СО. Эту задачу будем решать в
рамках ньютоновской механики, в которой, как мы знаем, пространство и время
считаются абсолютными, и поэтому Ньютонов сила F тоже абсолютна, а масса не
зависит от состояния движения тел. Поэтому задача сводится к нахождению закона
преобразования ускорения.
Прежде чем перейти к решению задачи, условимся здесь использовать следующую
терминологию, не вкладывая в нее какого-либо философского смысла. Движение тела
относительно инерциальной СО назовем абсолютным, а относительно неинерциальной
СО – относительным. Движение же НСО относительно ИСО – переносным. В этом
смысле уравнение (15.1) описывает абсолютное движение тел, чем и объясняется
появление индекса «абс» у ускорения.
рис. 15.1
Наша цель – установить уравнение относительного движения, т.е. уравнение,
решением которого можно получить закон движения тела относительно НСО. Для этого
рассмотрим движение частицы А относительно «неподвижной» ИСО с началом
координат в точке
Oабс
и движущейся относительно нее с ускорением НСО с началом
координат в точке О (рис.15.1). Так как обычно СО связывают с твердым телом, то в
общем случае движение НСО – это поступательное движение со скоростью точки О, и
вращение с угловой скоростью  вокруг мгновенной оси, проходящей через О
(рис.15.1).
Положение частицы А относительно ИСО определится радиус-вектором rабс, a
относительно НСО –
r  ix  jy  kz,
(15.2)
где
i, j , k
- единичные векторы координатных осей, вращающиеся вокруг мгновенной
оси с угловой скоростью
,
положение же точки О относительно
Oабс
-
r0 .
В каждый
момент времени эти вектора связаны соотношением
rабс  r0  ri
дифференцирование которого по времени дает преобразование скорости
Вычислим
vабс  v0  r
(15.3)
r  i x j y  k z  i x  j y  k z  vотн  [r ] ,
(15.4)
r:
где учитывали, что единичные векторы
i, j , k
вращаются с угловой скоростью
i  [i], j  [j ], k  [k ].
 , т.е.
(15.5)
В формуле (15.4) член
vотн  i x j y  k z
есть скорость частицы в той СО, относительно которой орты
(15.6)
i, j , k
покоятся, т.е. НСО.
Поэтому (15.6) есть относительная скорость частицы. Подставляя (15.4) и (15.6) в
(15.3), получим преобразование скорости в окончательном виде:
vабс  vотн  vo  [r ]  vотн  vпер .
Здесь
vпер  vo  [r ]
(15.7)
есть скорость НСО в точке А, т.е. является переносной
скоростью. Следовательно, абсолютная скорость равна векторной сумме
переносной и относительной скоростей частицы.
Для получения закона преобразования ускорения, продифференцируем (15.7) по
времени:
v абс  аабс  vотн  v пер .
(15.8)
Вычислим производные в правой части в отдельности:
v пер  vo  [ r ]  [ r ]  ao  [ r ]  [vотн ]  [[r ]] .
Здесь пользовались формулой (.4). С учетом (.5) и (.6) получим
vотн  i x j y  k z  i x j y  k z  aотн  [vотн ] ,
где
аотн  i x  j y  k z
(15.9)
- относительное ускорение частицы, в котором орты i,j,k считаются неизменными.
Подставляя полученные представления в (17.8), окончательно получим следующий
закон преобразования ускорения:
aабс  ao  [ r ]  2 r  aотн  2[vотн ]  aпер  аотн  аkор ,
где
двойное
векторное
произведение
раскрыто
по
правилу
(15.10)
«бац-цаб»,
перпендикулярная к мгновенной оси вращения составляющая радиус-вектора,
r ао  v0 -
ускорение поступательного движения НСО, ε – ее угловое ускорение,
апер  ao  [ r ]  2 r
(15.11)
- переносное ускорение, которая бы имела покоящаяся относительно НСО частица.
Последний член –
аkор  2[vотн ] ,
(15.12)
называется кориолисовым ускорением в честь французского ученого Кориолиса
(1792-1843).
Преобразование (15.10) выражает теорему Кориолиса: абсолютное ускорение
равно векторной сумме относительного, переносного и кориолисова
ускорений.
Подставим теперь выражение (15.10) в уравнение (15.1) и перенесем члены,
содержащие
апер и акор , в правую часть:
mаотн  F  mапер  mакор .
(15.13)
Это и есть искомое уравнение движения частицы относительно произвольной НСО.
Для физического истолкования полученного результата, обобщим понятие силы,
считая, что сила - причина ускорения частицы относительно любой системы
отсчета (а не только инерциальной, как считали до сих пор). При такой трактовке, всю
правую часть уравнения (15.13) следует считать силой, действующей на частицу в
НСО. Она состоит из двух совершенно разных составляющих. Первая – Ньютонов сила
F, которая действует на частицу и в ИСО и является результатом взаимодействия тел.
Мы показали, что в рамках абсолютности пространства и времени, будучи зависящей от
относительного положения и относительной скорости взаимодействующих тел, эта сила
инвариантна при переходе в другие системы отсчета. Совершенно иной представляется
вторая составляющая:
mапер  mакор ,
которая возникает не из-за взаимодействия
тел, а из-за ускоренного движения системы отсчета и называется силой инерции. Она
представляет сумму переносных сил инерции: Fпер
кориолисовой силы инерции:
 mапер ,
и так называемой,
Fкор   mакор .
Силы инерции не подчиняются третьему закону Ньютона. Если на тело действует
сила инерции, то не следует искать другое тело, на которое приложена
противодействующая сила. В этом смысле движение под действием сил инерции
аналогично движению во внешних силовых полях. Сила инерции является всегда
внешней силой по отношению к любой движущейся системе материальных тел.
Другая особенность силы инерции заключается в том, что она меняется при
переходе в другие НСО и, в частности, исчезают в ИСО, т.е. силы инерции не
инвариантны относительно переходам в другие СО.