теоретические основы адсорбции

Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Северный (Арктический) федеральный университет имени М . В . Ломоносова»
Н.А. М а к а р е в и ч , Н.И. Богданович
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АДСОРБЦИИ
Учебное
пособие
Архангельск
САФУ
2015
Рекомендовано
к изданию редакционно-издателъским
советом
Северного (Арктического)
федерального
университета
имени М.В.
Ломоносова
Авторы:
Н.А. Макаревич, Н.И. Богданович
Рецензенты:
Кафедра химической технологии древесины Уральского
государственного лесотехнического университета;
Комаров B.C. академик Н А Н Беларуси, доктор химических наук,
профессор;
Макаревич Н.А..
Теоретические основы адсорбции: учебное пособие / Н.А. Макаревич,
Н.И.
Богданович;
Архангельск:
Сев.
(Арктич.)
федер.
ун-т
им.
М.В.
Ломоносова.
-
САФУ, 2015. - 362 с : ил.
Изложены основы теории физической адсорбции и капиллярной
конденсации. Приведены элементы термодинамики межфазовых процессов и
методы моделирования пористых материалов. Рассмотрены уравнения и методы
расчета дифференциальных теплот адсорбции в рамках теории полимолекуляной
адсорбции в различных модельных представлениях. Описаны адсорбционные
методы исследования пористых материалов.
Пособие предназначено для студентов, обучающихся по программам
бакалавриата и магистратуры по направлениям «Химическая технология», а
также для аспирантов и научных работников.
© Макаревич Н.А.,
Богданович Н.И., 2015
© Северный (Арктический)
федеральный университет
им. М.В. Ломоносова, 2015
Оглавление
ВВЕДЕНИЕ
6
1. ВВЕДЕНИЕ В ТЕОРИЮ ДИСПЕРСНЫХ СИСТЕМ И
ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ
8
1.1. Поверхностные явления
15
1.2. Адсорбция и адсорбционные силы
18
1.2.1. Количественное описания адсорбционных процессов
32
1.2.2. Термодинамика поверхностного слоя
35
1.3. Элементы классической термодинамики
44
1.3.1. Объединенное уравнение первого и второго начал (законов)
термодинамики
54
1.4. Объединенное уравнение первого и второго законов термодинамики
поверхностных избытков Гиббса
57
1.5. Количественное описание адсорбции
63
1.6. Модели адсорбции на основе уравнений состояния адсорбционного
слоя
74
Приложение к разделу 1.6. Ассоциативно-ионизационный множитель как
фактор неидеальности систем
88
1.7. Термодинамика поверхностных явлений на границе газ, жидкость,
твердое тело
99
СПИСОК ЛИТЕРАТУРЫ
108
2. АДСОРБЦИЯ НА ТВЕРДЫХ ПОВЕРХНОСТЯХ
111
2.1. Термодинамика поверхности твердого тела
111
2.2. Элементы моделирования твердого тела
120
2.2.1. Модельные представления твердого тела
123
2.2.2. Неидеальность и неоднородность поверхности твердого тела
132
2.2.3. Пористая структура адсорбентов
157
2.3. Классическая теория капиллярной конденсации
173
2.4. Динамика адсорбции
187
2.4.1. Адсорбция на границе газ/твердое тело
187
2.4.2. Процессы на поверхности адсорбента
189
2.4.3. Изотермы адсорбции
194
2.4.4. Изотермы полимолекулярной адсорбции
208
2.5. Адсорбция в микропористых адсорбентах
225
2.5.1. Теория объемного заполнения микропор
225
СПИСОК ЛИТЕРАТУРЫ
233
3. ТЕРМОДИНАМИКА В ТЕОРИИ ПОЛИМОЛЕКУЛЯРНОЙ
АДСОРБЦИИ И ТЕОРИИ ОБЪЕМНОГО ЗАПОЛНЕНИЯ
236
3.1. Теплоты адсорбции на основе двух и более экспериментальных
изотерм адсорбции
238
3.2. Термодинамика в теории объемного заполнения микропор
242
3.3. Термодинамика в теории полимолекулярной адсорбции
246
3.4. Приложение термодинамической теории полимолекулярной
адсорбции к адсорбции из газовой и жидкой фаз на твердой гладкой и
пористой поверхности
255
СПИСОК ЛИТЕРАТУРЫ
261
4. ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ПОВЕРХНОСТИ ТВЕРДЫХ ТЕЛ ИЗ
ИЗОТЕРМ АДСОРБЦИИ ПАРОВ
262
4.1. Метод Гаркинса-Юра
264
4.2. Метод Грегга
269
4.3. Метод Киселева
270
4.4. Измерение удельной поверхности по методу БЭТ
273
4.5. Метод Хюттига
280
4.6. Сравнительные адсорбционные методы
281
4.7. Сравнительный адсорбционный метод Комарова
285
4.8. Сравнительный метод определения объема микропор и поверхности
мезопор
289
4.9. Современная практика определения удельной поверхности методом
БЭТ
292
СПИСОК ЛИТЕРАТУРЫ
296
5. РАСПРЕДЕЛЕНИЕ ПОР ПО РАЗМЕРАМ
298
5.1. Методы определения пористости
302
5.2. Типы гистерезисных петель
308
5.3. Традиционные методы расчета PSD (роге size distribution)
313
5.4. Методы расчета пористых систем на современном оборудовании .... 318
СПИСОК ЛИТЕРАТУРЫ
326
6. МЕТОДЫ ИЗМЕРЕНИЯ ВЕЛИЧИН АДСОРБЦИИ И ТЕПЛОТ
АДСОРБЦИИ
328
СПИСОК ЛИТЕРАТУРЫ
339
7. ОБЩАЯ ХАРАКТЕРИСТИКА НЕКОТОРЫХ ПОРИСТЫХ
АДСОРБЕНТОВ
340
СПИСОК ЛИТЕРАТУРЫ
360
ЗАКЛЮЧЕНИЕ
362
ВВЕДЕНИЕ
Исходя из агрегатных состояний веществ (газообразное, жидкое,
твердое) выделяют пять типов поверхностей раздела фаз: газ
жидкость
(Г-Ж), газ - твердое тело (Г-Тв) жидкость
(Ж-Ж), жидкость
тело
(Тв-Тв).
- твердое
Говоря
о
тело (Ж-Тв), твердое
«поверхностном
слое»
-
-
жидкость
тело -
твердое
имеют
в
виду
межфазовую область, где заканчивается одна фаза и начинается
другая.
Существенным
отличием
жидких
и твердых
состояний
является относительная подвижность молекул (большая у жидких и
малая у твердых). Для сравнения, среднее «время жизни» молекул т
на поверхности
воды «10 с, а на поверхности
твердого
тела,
32
например, вольфрама, « 1 0 с [ 1 ] .
Поверхность раздела между двумя фазами (межфазовый
слой)
это особое состояние вещества, зависящее от объемных состояний
контактирующих фаз. Межфазовый слой существенно отличается от
фаз (газ, жидкость, твердое тело), которые его образуют, а его
свойства,
как
правило,
определяются
молекулярной
(атомной,
ионной) природой контактирующих фаз.
Поверхностные процессы, протекающие на границах раздела
фаз,
является
главной
технологических
ареной
процессов.
И
практически
как
частный
всех
природных
случай
-
и
прямые
процессы адсорбции частиц из газовой фазы или растворов
на
твердых телах, реакции адсорбированных частиц между собой и с
молекулами в газовой фазе или растворе, процессы растворения и
проницаемости пленок и т.д. То есть в общем случае эти процессы
реализуются в конденсированных фазах на границах раздела газ жидкость - твердое тело.
Изучение межфазовых процессов в конечном итоге сводится к
исследованию
природы
взаимодействий.
В
свою
определяют
равновесное
динамические
и
кристаллов
межчастичных
очередь
и аморфных
межчастичные
поведение
статические
(межмолекулярных)
свойства
взаимодействия
неидеальных
жидких
систем,
фаз,
соединений, разнообразные
структуру
химические
взаимодействия и т.д. Одной из форм проявления межмолекулярных
взаимодействий является адсорбция.
Поэтому сама адсорбция, как
физико-химический процесс, может служить
важным, и к тому же
очень удобным, средством изучения межфазовых явлений.
Теория адсорбции базируется на знании математики, физики,
химии, супрамолекулярной химии, биологии, химической технологии
и является составной частью физической и коллоидной
химии,
называемой
химией
в
современной
литературе,
дисперсных систем и поверхностных явлений.
физической
1. ВВЕДЕНИЕ В Т Е О Р И Ю Д И С П Е Р С Н Ы Х С И С Т Е М И
ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ
Дисперсность.
Дисперсные
которых одно вещество
системы
распределено
это - такие системы, в
в другом
в виде
частиц
различных размеров. Дисперсность (лат. dispersus) — рассеянный,
рассыпанный).
Понятие
«дисперсность»
широкую область размеров тел: от 10
распространяется
до 10
на
см. Дисперсность
охватывает коллоидные (грубо- и высокодисперсное) состояния, в
котором обычно существуют все реальные тела. Поэтому говорят о
коллоидном
состоянии,
как
об
Особенностью этого состояния —
особом
состоянии
ведущая роль
материи.
поверхностных
явлений. Это можно проследить на простом примере: дробя
и
измельчая твердое тело, мы непрерывно увеличиваем его суммарную
поверхность, сохраняя неизменными массу и объем его. Иными
словами
увеличиваем удельную поверхность, приходящаяся на 1
2
массы, которая может достигать сотен и даже тысячм /г.
Высокая дисперсность и огромная поверхность характерны не
только для множества малых частиц, диспергированных в жидкой,
твердой
или
газообразной
средах,
а
и
для
тел
пронизанных
тончайшими порами (почвы, грунты, горные породы, адсорбенты
(поглотители), катализаторы, спрессованные порошки и т. д. Этот
класс частиц называют связнодисперсными.
Предельным состоянием
этого класса дисперсных систем являются мембраны и гели, у
которых
матрица
(сплошная
пространственная
сетка)
окружает
ячейки, заполненные газами или жидкостью. Размер таких «пор»
приближается
к
молекулярным
грубодисперсные
размерами
системы
частиц
размерам.
(суспензии,
более
1 мкм
Наука
изучает
эмульсии,
(10 -10
м.
высокодисперсные с размерами меньше 1 мкм (< 10
как
порошки)
с
(),
и
так
м), то есть от
1 мкм до 1нм. В современной науке понятие наноразмерные частицы,
т.е. частицы с размерами 1-100 нм, прочно связано с получением
веществ, обладающих уникальными свойствами. В этом диапазоне
радикально изменяются многие физические и химические свойства,
образуются нанокластеры. В настоящее время в этой области науки
накоплен
значительный
теоретический
и
экспериментальный
материал, поэтому ее стали выделять в отдельную науку: наука о
нанокластерах.
С
этой
наукой
связаны
высокие
достижения
в
кибернетике, в компьютерных технологиях, в технологии получения
новых
материалов
практически
для
всех
областей
техники,
в
медицине и т.д.
Для высоко- или, как их часто называют, ультрадисперсных
систем
характерны
два
общих
дисперсность [2]. Гетерогенность
признака:
гетерогенность
и
или многофазность, выступает в
высокодисперсных системах как признак (на рассмотрении которого
мы выше подробно останавливались), указывающий
поверхностного
слоя
-важнейшего
объекта
на
наличие
исследований
таких
систем.
Дисперсность
(раздробленность) -
дисперсных
систем.
Дисперсность
геометрией
частиц
самой
второй признак ультра¬
определяется
различной
формы:
размерами
и
сферической,
цилиндрической, прямоугольной, а чаще — неправильной. В общем
виде, раздробленность
определяется размером тела по той
оси,
уменьшением которого она достигнута, т. е. наименьшим размером R
и часто характеризуют величиной, обратной размеру R, т. е. 1/R. Эта
величина носит название дисперсности D. Понятие «диспергировать»
означает
уменьшать
тело
в
размерах,
измельчать.
Численно
дисперсность, как правило, выражают в виде: отношения поверхности
индивидуальной частиц s к ее объему V
D
s
s
= vV =
kcv
1
1
С-)
^7>
а
где s = k a;
V = ka;
k и k , - коэффициенты формы, определяющие поверхность и объем через
общий характерный размер частицы а;
к
k v = — - поверхностно-объемный коэффициент формы;
k.
s
3
v
s
V
s
v
V - поверхностно-объемным соотношением, в котором
s =
2/3
4nR^n
3
V = 3 ( ^ п)
Я
0
R - радиус атомов или молекул;
N - их число в частице, кластере.
0
В простейшем случае, если частицы имеют сферическую форму,
то k
sV
= 6, близкую к сферической.
При
простейших
моделировании
форм
(куб,
кристаллических
октаэдр,
структур
кубооктаэдр,
частиц
тетраэдр
и
др.)
дисперсность выражают как отношение числа поверхностных атомов
Ns к общему числу атомов N в структуре: D
N
Простейшая
кубическую
модель -
упаковку
=
.
кристаллы твердой
атомов,
подобную
фазы,
упаковке
имеющие,
ионов
в
минеральных кристаллах сильвинитовой руды (сильвин - КС1, галит
- N a d ) . Допустим, эти кубические
кристаллы состоят из N атомов
размера а. Если длина ребра куба l , а ее относительная длина
/
о т н
= - , то для любого кубического кристалла /
объеме такого
куба
координационное
имеют
число
по шесть
1/3
о т н
= N .
ближайших
(к.ч.) объемной решетки n
v
Атомы в
соседей, т.е.
= 6.
Восемь
поверхностных атомов в вершинах куба имеют "поверхностное"
к.ч.
n = 3, атомы, расположенные на гранях куба n = 5 и на ребрах куба
s
s
n = 4. Расчеты
показывают,
s
1/3
2
что число
атомов
на гранях
куба
1/3
6 ( N - 2 ) , а на ребрах - 1 2 ( N - 2 ) . Отсюда
N
s
D
Изменяя
= ¥
форму
(6ЛП3 -
+ 8)
= "
N
частиц
6
-
~= -
при одном
12
-
8
(
+ N
и том же объеме
1
2
)
можно
регулировать соотношение ^, т.е. изменять свойства поверхности. По
мере приближения к сфере ~ = ~ величина поверхности убывает.
Отношение поверхности многогранника к поверхности сферы
для тетраэдра «
1,49,
s /s^
MTi
для куба «1,24, для октаэдра ~1,18, для
икосаэдра (с 20 треугольными гранями) «1,06.
Модельными
дисперсность
расчетами
Д^^-^«й Д .
а
5
установлено,
Здесь
d
a
=
что
а
-
при
5
N>10 ^10
размер
6
атомов,
образующих кристаллическую решетку.
С уменьшением размеров частиц менее 1 nm величина
D >0,5.
N
Это означает, что большая доля атомов находится в таких структурах
на поверхности частиц. Структуры, образованные такими частицами,
и будут называться ультрадисперсными
размеров частиц 1^100
или кластерными.
Область
nm называют наноразмерной, а материалы,
образованные такими кластерами наноматериалами. В этой области
вещество обладает особыми поверхностно-избыточными свойствами
и одновременно свойствами объемной фазы, что приводит
качественно
новым
физико-химическим
свойствам.
В
к его
этом
и
заключена уникальность свойств наносистем. Особенностью веществ
в нанокристаллическом состоянии наносистем является проявления в
них эффектов размерного квантования, которые могут кардинально
изменять свойства материалов. К тому же
с позиций классической
физики следует, что в результате уменьшения
размеров
частиц
наблюдается увеличение удельной поверхности вещества s ,
что
yd
ведет к увеличению вклада избыточной поверхностной энергии в
общую свободную энергию системы. Свободная энергия кластеров G
складывается
из
отрицательной
положительной
свободной
поверхностной
объемной энергии
G.
V
энергии
Например,
G
s
и
для
кластера, образующегося из газовой фазы и включающего n атомов
или молекул, поверхностная энергия [3]
2
G = 4по ( — )
s
п
3
(1.3)
где о — поверхностное натяжение (поверхностная энергия, Дж
площади, м ) ;
s — площадь поверхности;
и — объем атома или молекулы.
на единицу
2
Допуская, что частицы в газовой фазе находятся в идеальном
состоянии,
т.е.
не
взаимодействуют
между
собой,
свободную
объемную энергию можно приближенно выразить в виде
G = -пк Т1п(£)
v
где к — константа Больцмана;
Б
в
(1.4)
Т - абсолютная температура;
Р, P - давление пара и давление насыщенного пара при температуре Т.
s
Следовательно, свободная энергия образования кластера
2
'3г;\з
G
/Р
n -nk Tln(j)
(1.5)
B
B
1
1 / 1
При условии ^
2
3
4па(—)
'
1
= 0 из уравнения (1.36) можно рассчитать
минимальное число частиц в кластере n
min
кластера
_
и минимальный размер
r .
min
2
2
32na v
Р
(квТ1п( ))
SS
/свПп(р-)
Из
уравнений
(1.5)
и
(1.6)
можно
3
энергетического барьера: G*
1б7гег г;
определить
высоту
2
2
р
Увеличение
относительного
давления P/P
s
ведет к снижению
высоты энергетического барьера, а следовательно, к
уменьшению
r , т.е. критического размера кластера.
min
Из уравнений 1.6 -1.7 видим, что для ультрадисперсных систем
кроме
двух
общих
признаков
(гетерогенность
добавляется важнейшая характеристика — удельная
Удельная
поверхность
определяется
межфазной поверхности к объему тела s/V.
и
дисперсность)
поверхность $> .
отношением
удк
площади
Гетерогенность, дисперсность и удельная поверхность связаны
между собой: с уменьшением характеристического размера частица
увеличиваются дисперсность D и удельная поверхность s .
yA
Дисперсность
является
характеризует
степень
поверхности,
а
характеристикой
количественным
раздробленности
гетерогенность
и
и
размер
межфазовой
с
качественной
связана
объектов. При этом
параметром
изменение дисперсности —
количественной характеристики — может приводить к изменению ряда
качественных
характеристик
веществ,
что
мы
и
наблюдаем
у
нанокластерых структур.
Дисперсные системы классифицируют [2]:
по
дисперсности,
микроскопе)
выделяя
грубо
- и ультрадисперсные
(видимые
в
оптическом
(не видимые
в
оптическом
микроскопе);
по агрегатному
состоянию,
компонентов в которых
рассматривая системы, один из
— дисперсная
фаза или дисперсная
среда
находиться в твердом, жидком, газообразном состоянии;
по
структуре,
связанные
выделяя
между
собой
свободнодисперсные
—
суспензии,
частицы
эмульсии,
(не
золи)
и
связнодисперсные (одна из фаз связана, т.е. структурно закреплена);
по межфазовому
взаимодействию,
рассматривая
действие
межмолекулярных сил между дисперсной фазой и дисперсной средой
и
в
зависимости
лиофильные
лиофобные
от
(сильное
степени
их
взаимодействия
межмолекулярное
и,
выделяя
взаимодействие)
(слабые межмолекулярное взаимодействие);
и
по
фазовой
соединений являющиеся
различимости,
рассматривая
высокомолекулярные
истинными
особый
класс
соединения (ВМС), по сути,
растворами,
но
обладающие
многими
признаками дисперсных систем
Отличительной
особенностью
дисперсных
высокоразвитая поверхность, выступающая в
которой
протекают
взаимодействием
поверхностными
поверхностные
качестве
процессы,
контактирующих
явлениями.
систем
фаз
является
арены, на
связанные
и
с
называемые
Поверхностные явления вызваны тем,
что на межфазовых границах в тонких поверхностных слоях атомы и
молекулы образуют из-за различия связей в сопряженных
особую
структуру,
Поверхностный
отличающуюся
от структур
в объемах
фазах
фаз.
слой - неоднородный тонкий слой, разделяющий
объемные фазы и обладающий
конечной толщиной и объемом.
Условием существования межфазной поверхности является наличие
твердой Т или жидкой Ж фазы, при чем
их объемная структура
существенно влияет на свойства поверхностного слоя. В дисперсных
системах
более
инертная
фаза
определяет
форму
и
строение
поверхностного слоя. Для систем Ж/Г и Г/Ж структурообразующей
является жидкая фаза, для других типов систем - твердая фаза.
1.1. Поверхностные явления
Основное условие стабильности существования
поверхности
раздела между фазами является положительное значение свободной
энергии образования поверхности (AG >0).
s
Для AG <0
s
случайные
флуктуации приводят к разрушению межфазового слоя в результате
естественного
диспергирования
одной
из
фаз
внутри
другой.
Примеры тому — отсутствие границы раздела между разреженными
газами
(воздух),
смешивающимися
жидкостями
(этанол—вода),
расплавы различных металлов. Несмешивающиеся жидкости так же
можно диспергировать и превратить в устойчивую эмульсию, если
между ними окажется дифильное вещество — поверхностно активное
вещество (ПАВ), способное уменьшить AG до значений близких к
s
нулю.
Изменение
площади
свободной
поверхности
энергии,
раздела
фаз
отнесенное
As
будет
к
изменению
эквивалентна
коэффициенту поверхностного натяжения о
AG
0 = -^
S
(1.8)
As
2
измеряемому в системе Си в Дж/м .
В записи:
AG = °As
(1.9)
S
видно, что о выступает в роли коэффициента пропорциональности
между AG
s
и As. Это означает, что увеличивая поверхность
As
жидкости или твердого тела молекулы поверхностного слоя будут
совершать работу против сил,
действующих внутри жидкости или
твердого тела. Работа, совершаемая над жидкостью или твердым
телом
при
постоянной
температуре,
полностью
совпадает
с
изменением их свободной поверхностной энергии. Из (1.8) следует,
что коэффициент
поверхностного
натяжения
представляет
собой
свободную энергию единицы площади поверхности. На классическом
примере мыльной пленки (водный раствор ПАВ), помещенный
в
кольцо и выдуваемой из кольца в виде пузырей, легко доказывается,
что с мыльного раствора, находящегося в кольце, определяется силой
ЛF, действующей на единицу длины Л1, т.е. размерность с - н/м. Обе
размерности Дж/м
и н/м одинаковы. Для каждой жидкости или
твердого тела < является основной характеристикой их поверхности.
Например,
при
температуре
0
20
С
с
гексана
составляет
18,42-10 Дж/м , этанола - 22,03-10 Дж/м , воды - 72,8-10 Дж/м ,
-3
2
-3
2
-3
2
ртути - 4 8 4 - 1 0 Д ж / м , расплава платины при температуре 2000°С -3
1819-10
2
Дж/м . По величине с можно констатировать: чем выше
поверхностное натяжения индивидуального вещества или раствора,
тем сильнее энергия межчастичного
взаимодействия.
Для
жидких органических веществ поверхностное натяжение
поверхностного натяжения воды.
всех
меньше
Отметим, что в отличие от
жидкостей, прямых надежных методов определения поверхностного
натяжения
твердых
тел
(большое
нет, поэтому их с
поверхности)
«время
жизни»
приближенно
частиц
оценивают
на
либо
косвенными, либо расчетными методами.
Поверхностное
натяжение
жидкостей,
включая
растворы,
определяют статическими и динамическими методами: взвешивания
или счета
капель (сталогмометрический), висячей или лежащей
капли, отрыва кольца (Дю Нуи) или тонкой пластинки (Вильгельми),
максимального давления в газовом пузырьке, движущейся струи и
др.[1]. При этом измеряют статическое или близкое к статическому и
динамическое значение поверхностного натяжения. Из современных
приборов
для
измерения
с
наиболее
простым,
доступным
и
достаточно точным является автоматизированный метод Вильгельми.
Статическое значение а одного и того же вещества всегда ниже
динамического. Учет разности Да между этими значениями можно
успешно использовать при регулировании и оптимизации многих
технологических
процессов,
в
частности
при
флотационном
обогащении руд. Данные о поверхностном натяжении жидкостей, как
правило, приводятся в справочниках физико-химических величин.
Дисперсные системы и поверхностные явления— теоретическая
основа,
на
заданными
сплавов,
которой
держится
свойствами:
смазочных
получение
сорбентов
и
новых
материалов
и катализаторов,
лакокрасочных
цементов
материалов,
с
и
пищевых
продуктов и лекарственных веществ.
В химической технологии нет такой отрасли, где бы ни имели
решающего значения поверхностные явления и дисперсные системы:
процессы
обогащения
руд,
в
особенности
флотация,
сгущение,
отстаивание, фильтрация, процессы конденсации и кристаллизации,
брикетирование,
спекание,
гранулирования.
В
этих
процессах
большое значение имеют поверхностные явления (адсорбция, адгезия,
смачиваемость, капиллярность, коагуляция и пр.).
1.2. Адсорбция и адсорбционные силы
Основные
термины.
К
поверхностным
явлениям,
сопровождающимся самопроизвольным уменьшением поверхностной
энергии
ДG<0,
поверхностного
т.е.
уменьшением
натяжения,
межфазовой
относится
поверхности
адсорбция
sor^co-поглощение, концентрирование с приставкойаа-на).
(от
и
лат.
Адсорбцию можно определить не только как явление, но и как
процесс,
вызванный
перераспределением
компонентов
системы
между поверхностным слоем и объемной фазой. Если коротко, то
«адсорбция
—концентрирование веществ на границе раздела фаз или
в порах твердого тела». Обратный процесс перехода вещества из
поверхностного слоя в сопредельную гомогенную фазу называют:
«десорбция».
Более
называют:
плотную
адсорбент.
фазу,
определяющую
Адсорбент
может
форму
быть
поверхности
жидкостью
или
твердым телом.
Вещество, которое перераспределяется на границе фаз, т.е. на
поверхности,
называют: адсобат.
Вещество, находящееся в менее
плотной фазе (не на поверхности), но способное адсорбироваться
называют: адсорбтив.
жидкостью
«Адсорбтив,
Адсорбат, адсорбтив может быть газом или
(в общем
случае это
адсорбируясь
на
— флюид).
адсорбенте,
Для
запоминания:
превращается
в
адсорбат».
В
отличие
объемной
фазой
от
адсорбции,
называют
процесс
«абсорбция».
поглощения
Его
вещества
синоним
—
«растворение», т.е. равномерное распределение вещества в газовой
(воздух), жидкой (соль в воде) или твердой (сплавы металлов) фазах.
В сомнительных случаях, когда нет уверенности в определении
«адсорбция» это, или «абсорбция»,
осторожно используют термин
«сорбция». Возможны термины: «сорбат», «сорбтив»,
«гость»/«хозяин».
«сорбент»,
Классификация
зависимости
от
адсорбции по агрегатному
агрегатного
состояния
состоянию
фаз. В
сопредельных
фаз
различают следующие типы адсорбционных процессов:
- адсорбция из растворов на границе раздела жидкость - газ (Ж /Г).
- адсорбция из растворов на границах раздела жидкость - жидкость
(Ж/Ж).
- адсорбция из растворов на границах раздела жидкость -твердое
тело (Ж/Т);
- адсорбция из газовой фазы на твердых адсорбентах (Г/Т);
Классификация
адсорбата
и
адсорбции
адсорбента.
по
Если
механизму
адсорбцию
взаимодействия
рассматривать
как
результат взаимодействия молекул адсорбата с активными центрами
поверхности адсорбента, то по механизму их взаимодействия можно
выделить следующие виды адсорбции:
-физическая
адсорбция
(физадсорбция) - взаимодействие между
молекулами адсорбата и адсорбента за счет сил Ван-дер-Ваальса с
энергией
адсорбционного
взаимодействия
«10
кДж/моль.
Физадсорбцию из-за очень малой величины потенциального барьера
называют неактивированной
-химическая
адсорбция
адсорбцией;
(хемосорбция) - реакция взаимодействия
молекул адсорбата с активными центрами адсорбента с образованием
устойчивых
химических
соединений
различного
исключением реакций ионного обмена). Энергия
взаимодействия
может
достигать
сотен
типа
(за
адсорбционного
кДж/моль.
Хемосорбция
может быть как активированной, так и неактивированной, но всегда
локализованной
адсорбцией
из-за прочной связи между молекулами
(атомами) адсорбата и адсорбента.
Физическая адсорбция. Типичная физадсорбция протекает без
переноса
или
обобществлении
электронов,
т.е.
за
счет
межмолекулярного взаимодействия.
Межмолекулярные
взаимодействия
-
очень
сложный
процесс взаимодействия электронов
и
ядер
атомов,
молекулы.
составляющих
Представления
адсорбции
связаны
об
с понятием
о
короткодействии и дальнодействии
адсорбционных
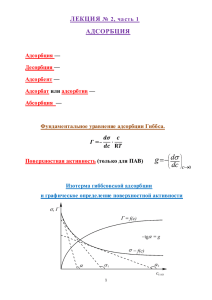
Рисунок
1.1.
Зависимость
потенциала сил взаимодействия (1)
и его составляющих сил (2) притяжения и (3) - отталкивания
от
межмолекулярного
(межатомного) расстояния.
Результирующая
взаимодействия-
глубина
определяет
которой
глубже яма, тем прочнее
электрически
Силы
заряженных
являются
отталкивания
молекулами
условии
некотором
одновременно
взаимного
быстрее,
определенном
силы
(2) и
силы
отталкивания
(3).
кривая (1) с потенциальной
энергию
частиц,
ямой,
связи между молекулами
связь). Эти силы обусловлены
с
(рис.1.1)
действуют
притяжения
взаимного
входящих
увеличением
чем силы
могут
Между
вещества
короткодействующими.
убывают
молекулы
молекулами
сил.
действием
в состав
При
молекулы.
этом
расстояния
притяжения.
Только
находиться
в устойчивом
равновесном
расстоянии
(чем
силы
между
при
равновесии
друг от
этом
на
друга.
Если равновесное
310
расстояние
см (средний
преобладают
порядок
r между молекулами
диаметра
силы отталкивания,
силы притяжения.
На расстоянии
силы практически
перестают
силы это -
молекул),
составляет
то при r < 310
а при r > 310
r « 1,510
действовать.
см
см
около
см
преобладают
межмолекулярные
Короткодействующие
силы, действующие между частицами на расстоянии
нескольких атомных радиусов.
Дальнодейсвующие
силы - это силы притяжения, обусловленные
действием трех типов сил слабых электромагнитных взаимодействий
Ван-дер-Ваальса: ориентационных,
индукционных
и
дисперсионных
[4].
Силы,
которые
удерживают
молекулы
жидких
и
твердых
веществ вместе, называют ван-дер-ваальсовыми. Они отличаются от
сил, обеспечивающих химические связи, не только количественно
(обычно в десятки раз меньшей величиной), но и качественно, а
именно,
своей
универсальностью
и
ненасыщаемостью.
Они
действуют на сравнительно больших расстояниях в сопоставлении с
расстояниями между атомами в молекулах и распространяются на
любое
число
Вандерваальсовы
молекул,
силы
попавших
-
это
силы
в
поле
действия
притяжения,
этих
сил.
обусловленные
движением электронов в атомах, и они в 10...20 раз слабее, чем силы
притяжения между ионами. Например, силы, удерживающие атомы
азота в молекуле азота в десяток раз больше, чем силы, связывающие
молекулы N 2 между собой. Но без этого слабого межмолекулярного
притяжения нельзя получить жидкий азот.
Ориентационное
которых
«центры
взаимодействие.
тяжести»
Полярные
положительного
и
молекулы,
в
отрицательного
зарядов не совпадают- называют диполями, например HCl, H O , N H ,
2
3
ориентируются таким образом, чтобы рядом находились дипольные
молекулы с противоположными зарядами. Характеристикой таких
молекул служит величина, называемая дипольным
моментом
ju. Для
простейшей системы зарядов, с не зависящим от выбора начала
координат ненулевым дипольным моментом:
[I
= q • I
где q - величина заряда;
l - длина диполя (вектор с началом в центре отрицательного
концом в центре положительного).
заряда
и
Для системы из N частиц электрический дипольный момент
М= ^
Ш
где q - заряд частицы с номером /;
г - её радиус-вектор.
t
;
При суммировании отдельно по положительным и отрицательным
зарядам:
М = 2 +q+iTi - 2 - \ q - i \ n = Q R
+
+
-
\Q-\R-
где N± - число положительно/отрицательно заряженных частиц (N±=N++N-);
q±,- - их заряды;
Q+, R+, Q-, R- - суммарные заряды положительной и отрицательной подсистем и
радиус-векторы их «центров тяжести».
Электрический дипольный момент нейтральной системы зарядов не
зависит от выбора начала координат, а определяется относительным
расположением
определений
(и
величинами)
зарядов
в
системе.
видно, что дипольный момент обладает
Из
этих
свойством
аддитивности , т.е. дипольный момент наложения нескольких систем
зарядов равен векторной сумме их дипольных моментов, а в случае
нейтральных систем это свойство приобретает еще более простую
форму ft=q-l. Электрический дипольный момент молекул принято
30
измерять в дебаях: в системе Си 1Д=3,33564 1 0 " К л м .
Между постоянными диполями молекул возникает кулоновское
притяжение.
Электростатическая
составляющая
проявляется
при
адсорбции полярных молекул на поверхности, несущей постоянные
электростатические
квадруполи.
При
заряды,
этом
т.
е.
потенциал
разноименных ионов (р (г)
с
ионы
(монополи),
кулоновского
диполи,
взаимодействия
с зарядами q i и q выражается: <р (г) =
2
с
Q.lQ.2
Г
Для взаимодействия двух диполей потенциал притяжения
между
ними (потенциал Кеезома) определяется как:
где ц и ц - моменты взаимодействующих диполей;
r - расстояние между ними (радиус - вектор).
1
2
Притяжение диполь-диполь
может осуществляться
только
тогда,
когда энергия притяжения превышает тепловую энергию молекул,
равную
kT,
здесь
k-постоянная
Больцмана,
Т-абсолютная
температура, °К. Результат взаимодействия проявляется в полярных
жидкостях (H O, HF, N H ) .
2
Индукционное
3
взаимодействие
-
межмолекулярное
взаимодействие, вызванное поляризацией нейтральной молекулы под
действием постоянного диполя. Наведение диполя - индуцирование
молекул,
благодаря наличию у них свойства поляризуемости
а.
Постоянный диполь может индуцировать дипольное распределение
зарядов в неполярной молекуле. Неполярная молекула становится
полярной, и молекулы притягиваются друг к другу, только слабее,
чем две полярные молекулы.
Потенциал притяжения между постоянным и наведенным диполем
(потенциал Дебая) определяется выражением:
2
<р(г)
где р.
Мнав^
(1.11)
- момент наведенного диполя.
нав
Притяжение постоянного и наведенного диполей, как правило, очень
слабое
из-за
веществ.
Оно
невысокой
действует
поляризуемости
на
очень
молекул
малых
большинства
расстояниях
между
диполями. Этот вид взаимодействия проявляется, главным образом, в
растворах полярных соединений в неполярных растворителях.
Дисперсионные
взаимодействия
- взаимодействия, вызванные
между мгновенно наведенными диполями в неполярных молекулах в
результате
флуктуаций
при
движении
электронов
в
атомах,
составляющих молекулы. Это вызывает перераспределение зарядов в
соседних
молекулах,
кратковременные связи:
и
между
ними
устанавливаются
Потенциал
такого
взаимодействия
(энергия
Лондона)
дается
соотношением
^
где р.
мгн
( Г )
=
( 1 . 1 2 )
—
= аЕ — момент мгновенного диполя;
а
— электронная поляризуемость, см с величиной, близкой к
значению объема сферической электронной оболочки молекулы;
Е — напряженность электрического поля.
Следовательно, величина потенциала такого притяжения зависит от
размеров
частиц
Дисперсионные
и
числа
электронов
взаимодействия
в
—самые
наведенных
слабые
диполях.
из
всех
межмолекулярных взаимодействий. Однако, именно они являются
наиболее
универсальными,
молекулами,
включая
так
и
как
возникают
полярные.
между
Дальнодействие
любыми
играет
важнейшую роль в механизмах формирования самоорганизующихся
структур.
Межмолекулярное
отталкивание.
Если бы молекулы только
притягивались друг к другу, это привело бы к их слиянию. Но на
очень малых расстояниях их электронные оболочки отталкиваются.
Потенциал отталкивания дается выражением
г
ч
+ / С
где к — постоянная отталкивания;
n — принимает различные целые значения (5 ^15).
Силы межмолекулярного отталкивания действуют на очень малых
расстояниях.
В
расчетах
потенциалов
парного
межатомного
или
межмолекулярного дисперсионного взаимодействия при постоянной
температуре часто используют потенциала
)
=
<Kr
-
^
Леннард - Джонса
( 1 . 1 4 )
+ ^2
который носит название потенциала 6 - 12, поскольку
притяжения
6
(—) пропорциональна
(LD)
1/г ,
а
энергия
энергия
отталкивания
12
(+)—1/г . Для
моделирования
межмолекулярных
часто используют эмпирические
(отталкивание
описывается
потенциалы
двенадцатой
взаимодействий
Леннард
-
степенью
Джонса
обратного
расстояния, притяжение— шестой) и Бакингема (с более физически
обоснованным
экспоненциальным
отталкиванием)
[4].
В
конденсированной фазе, где мультипольное разложение для молекул
плохо применимо из-за близости молекул друг к другу, используется
метод
атом-атомных
взаимодействий
потенциалов,
атомов,
но
с
основанный
добавкой
на
парных
кулоновских
членов,
описывающих взаимодействие их эффективных зарядов. На практике
уравнение Леннард - Джонса записывают в форме [4]
(
^ г
где
с = cr = (-) —
ф(г)=0,
LD
а
глубина
расстоянию л - и ^
)
-
= 4 [(-)
£
+ { - ) \
( 1 . 1
5
)
расстояние между атомами или молекулами, на котором
потенциальной
= —.
ямы
е
— соответствует
межатомному
Размеры
RWW
и
i
R
ww
соотношением
связаны
а
2б « 1,22
и
рассчитываются
дифференцированием
уравнения
(1.15).[Фенелонов]
Rww
Рисунок 1.2 Кривая потенциала L D
парного взаимодействия ф(г) как
функции
от
межмолекулярного
расстояния
r,
а^и
Rww-
равен
сумме
а
ваальсовых,
sили
кинетических
соответственно,
ж
о
н
с
о
в
ы
х
сумма
и
в
а
н
-
д
е
р
-
в
а
радиусов
ленарда
л
ь
С
О
В
^1
Х
в з а и м о д е
радиусов, s-глубина потенциальной
я м ы [Фен.]
минимальному
й
с т в
ующ
молекул
атомов
или
и х
и
соответствует
при
физических
взаимодействиях могут самопроизвольно сближаться,
дальнейшее
сближение
межмолекулярному
сумме
леннард-
джонсовых
д
ван-дер¬
требует
преодоления
расстоянию
сил
отталкивания.
При
этом
принимается, что каждое парное взаимодействие не зависит от других
парных
взаимодействий,
соответственно,
ф(г)
суммарного
взаимодействия молекул адсорбата с поверхность адсорбента равен
сумме потенциалов всех парных взаимодействий.
Заметим,
что
вандрваальсовы
взаимодействия
относят
к
неспецифическим взаимодействия, однако, по классификации А.В.
Киселева
[5]
ориентационные,
частично
индукционные
взаимодействия, вызванные электростатическим взаимодействием, и
водородную
связь
взаимодействия-это
относят
типичные
к
специфическим.
Дисперсионные
неспецифические
взаимодействия.
Методика оценки специфической и неспецифической составляющих
межчастичных взаимодействий по теплотам
адсорбции полярных
молекул и неполярных (парафиновых углеводородов) на твердых
поверхностях
детально
[6/7]Макаревич
Дисс,
В
исследованиях
межмолекулярных
физическую
в
работах
Н.А.Макаревича
ВМС].
современных
измерение
рассмотрены
адсорбцию,
сил
стало
возможным
взаимодействия,
благодаря
прямое
вызывающих
созданию
уникальных
микроскопов: сканирующий туннельный микроскоп (STM) -1980г. и
атомно-силовой микроскоп ( A F M ) - 1 9 8 5 R
Разрешение
STM при
сканировании рельефа поверхности составляет около 0,1-5-1,0 нм, а
A F M при измерении ультрамалых сил - о к о л о 1мкН. Создатели этой
уникальной техники Г. Бинниг и Х Рохрер (Швейцария, I B M ) в 1986г
удостоены Нобелевской премии. Сегодня эти микроскопы широко
применяются при исследовании поверхностей различных материалов,
включая адсорбенты и катализаторы [3]. В частности с помощью
AFM
возможно
прямое
измерение
поверхностного
натяжения
твердых тел, что до недавнего времени было практически не реально.
Химическая
(неактивированной
является
адсорбция.
и
образовала
отличие
нелокализованной)
активированной
адсорбата
В
физической
адсорбции,
(локализованной).
«адсорбционный
центром адсорбента и вступила с ним
от
Чтобы
комплекс»
в
хемособция
с
молекула
активным
химическую связь она
должна преодолеть потенциальный барьер, высота которого будет
равна энергии активации Е
ас1
на
кривой
расположен
(справа)
реакции (Рис.1.3). Пологий мининимум
соответствует
на расстоянии
z,
w
физической
равном
сумме
адсорбции
и
вандерваальсовых
радиусов
поверхностного
(активного
атома
центра)
и
адсорбированной молекулы.
Чтобы
приблизиться
молекуле
адсорбата
к
поверхности на расстояние z и
преодолеть
барьер,
потенциальный
она
должна
обладать
энергией, равной или больше
Но
Рисунок 1.3 Совмещенные кривые
потенциальной
энергии
неактивированной
(физической)
и
активированной
(химической)
адсорбции.(см. справа налево)
это
тот
случай,
Е .
ас(
когда
способна
молекула
диссоциировать на два атома. На
графике
изображена
ситуация,
когда молекула адсорбтива (например, Н ) вдали от поверхности
2
(например Pt) продиссоциировала.
Энергии диссоциации
обычно
достаточно для преодоления сил отталкивания электронных оболочек
и
сближения
продиссоциированных
атомов
адсорбтива
с
поверхностными атомами адсорбента и образования двух прочных
химических
связей
металл—водород.
Энергии
такой
связи
E
B
соответствует глубокий минимум на кривой (слева). Эта энергия
пропорциональна теплоте хемосорбции, достигающей 300 кДж/моль
и
выше.
Десорбция
возможна
лишь
при условии
преодоления
атомами адсорбата потенциального барьера высотой E .
А для этого
des
обычного ваакуумирования недостаточно.
Поэтому хемосорбция — это локализованная адсорбция. Как
будет рассмотрено выше, такой тип адсорбции газов и паров на
твердой поверхности является, как правило, монослойной адсорбцией
(адсорбция Ленгмюра, изотермы с формой кривой I типа). Для
физической
(нелокализованной)
адсорбции
набор
кривых
на
изотермах значительно шире, но он включает и кривые I типа.
Для наглядности предлагается
(Табл.1.1) сравнить и
оценить
различие между физадсорбцией и химадсорбцией.
Таблица 1.1.
Сравнительная упрощенная характеристика физической и химической
адсорбции
Физическая
адсорбция
Хемосорбция
Обусловлена физическими силами
Обусловлена химическими силами
(силами Ван-дер-Ваальса)
Теплота адсорбции мала,
Теплота адсорбции велика,
« 10 -г 20 кДж/моль
« 40 - 400 кДж/моль
С повышением температуры часто
Повышение температуры
уменьшается (десорбция выше
способствуетдостижению Е ,
адсорбции)
т.е.хемоадсорбции
Мало специфична, слабо зависит от
Специфична, образуется поверхностное
природы адсорбата
химическое соединение
Обратима (адсорбция ^ д е с о р б ц и я )
Как правило, необратима
Нелокализованная (молекулы адсорбата Локализованная (молекулы адсорбата
способны перемещаться по поверхности связаны с адсорбентом за счет прочных
химических связей)
адсорбента)
а
Из термодинамики адсорбции следует, что различие теплот
адсорбции физической и химической адсорбции влечет за собой
к
существенному различию и энтропии адсорбции, т.е. к уменьшению
степеней
свободы
адсорбции
адсорбированных
молекула
поступательному
адсорбата
движению
молекул.
может
При
терять
перпендикулярно
физической
способность
к
к поверхности,
но
сохранять вращательные и колебательные степени свободы. В то
время
как
при
хемосорбции
колебательной
степени
свободы.
«возмущение»
приповерхностного
возможно
ограничение
При хемосорбции
слоя
атомов
даже
наблюдается
адсорбента,
что
может привести к структурной перестройке поверхности, поэтому
систему адсорбент - адсорбат рассматривают как единую квантовомеханическую
систему.
приповерхностный
При
слой
физической
адсорбента
в
первом
адсорбции
приближении
рассматривают как инертную систему, а ее участников - как две
независимые системы. Однако, заметим, что четкого различия между
физической и химической адсорбции на практике не всегда удается
выяснить. Для этого проводят прецизионные
измерения
теплот
адсорбции,
либо
калориметрические
применяют
высокоточные
экспериментальные методы прямого измерения сил межчастичного
взаимодействия, типа STM, A F M , полевую микроскопию в сочетании
с современными спектроскопическими методами и др.
1.2.1. Количественное описания адсорбционных процессов
Полная
адсорбция
-
полное
количество
адсорбата
в
поверхностном слое, отнесенное к единице площади поверхности или
массы адсорбента. Обозначение - а; размерность: моль/м , моль/кг.
Гиббсовская
количество
(избыточная)
адсорбция
-
избыточное
адсорбата в поверхностном слое по сравнению с его
количеством в объемной фазе того же объема, что и поверхностный
слой, отнесенное к единице площади поверхности
адсорбента.
Обозначение -
Г
(гамма);
или
массы
размерность:
моль/м ,
2
моль/кг.
Степень
заполнения
поверхности
6
-
доля
поверхности,
заполненная адсорбатом, относительно максимально упакованного
молекулами этого адсорбата мономолекулярного
адсорционного
слоя:
а
где a
m
Г
и Г,
- соответственно, максимальная полная и избыточная величины
адсорбции;
6 - безразмерная величина, изменяющаяся в интервале от 0 до 1.
т
Формально
связь
между
абсолютной
и
избыточной
адсорбцией можно проиллюстрировать с помощью уравнения:
а = Г + ск ,
(1.16)
где с - равновесная молярная концентрация вещества в объеме гетерогенной
фазы, моль/м ;
h - толщина поверхностного слоя, м, которую на практике не всегда удается
оценить.
3
Основные зависимости, определяемые
изотермы адсорбции a=f(p)
эксперимента различают:
изостеры p=f (T),
или а=/(с).
-
В зависимости от условий
изобары a=f (T),
P
или c=f (T)
a
экспериментально,
изопикны a=f (T
c
)
и
адсорбции (Рис.1.4). Их получают из
a
экспериментальных изотерм путем взаимного перестроения.
Р
Т
т
Т
Рисунок 1.4. Типичные графики изотермы, изобары, изопикны, изостеры
Из
общей
термодинамики
известно,
что
любой
параметр
системы однозначно может быть определен как минимум через два
других. Относительно адсорбции этими параметрами могут быть
давление p (концентрация c), адсорбата и температура T. Тогда в
общем
виде
записывают
уравнение
системы: а=f(p,T), или а=/(с,7).
состояния
адсорбционной
Уравнение
состояния
термодинамические
- уравнение, связывающее между собой
(макроскопические,
т.е. с огромным
числом
частиц) параметры системы, такие, как температура, давление, объём,
химический потенциалы др. Уравнение состояния записывают для
термодинамического
описания
явлений.
При
этом
реальные
уравнения состояний реальных веществ могут быть очень сложными.
Уравнение
состояния
системы
не
содержится
в
постулатах
термодинамики и не может быть выведено из неё. Его составляют на
основе эксперимента или модели, созданной в рамках статистической
физики. Термодинамика же не рассматривает проблемы внутреннего
устройства веществ.
В
общей
(феноменологической)
термодинамике
различают
следующие виды уравнений состояния систем:
термическое
уравнение
состояния,
которое
связывает
макроскопические параметры системы и для системы с постоянным
числом частиц N его общий вид f(P,V,T)
термическое
уравнение
состояния
= 0, а чтобы
необходимо
задать
еще
конкретизировать вид функции f
калорическое
уравнение,
в котором внутренняя энергия U системы
выражается через давление, объем и температуру и для системы с N
= const U = U(P,V,T),
или с учетом того, что давление можно выразить
из термического уравнения:
Каноническое
выражение
для
U=U(V,T);
уравнение
одного
состояния
из
представляет
термодинамических
собой
потенциалов
(внутренней энергии U , энтальпии H, свободной энергии Гельмгольца
F
или
потенциала
Гиббса
G)
через
независимые
переменные,
относительно
U=U(S,V),
которых
H=H(S,P\
записывается
F=F(T,V),
его
G=G(T,P).
полный
дифференциал:
Каноническое уравнение,
независимо от того, в каком из видов оно представлено, содержит
полную
информацию
о термических
и калорических
свойствах
поверхностным
явлениям,
термодинамической системы.
Заметим,
что
применительно
к
включая адсорбцию, во всех записанных видах уравнений из общей
термодинамики параметры -
объем V и давление p могут быть
заменены, соответственно,
на параметры
-
поверхность s и
поверхностное натяжение о.
1.2.2. Термодинамика поверхностного слоя
Для описания термодинамики поверхностного слоя используют
два метода: метод
избыточных
величин
Гиббса
и метод
слоя
конечной толщины [8].
Фаза а
Фаза
<Uk
Фаза р
Фаза а
Фаза р
Рисунок 1.5. Схема, иллюстрирующая принцип термодинамических методов:
слоя конечной толщины (а) и избыточных величин (б). Стрелками показаны
межфазовый слой ар толщиной 8 (а) и межфазовый слой нулевой толщины.
В методе слоя конечной толщины рис 1.5, а между гомогенными
контактирующими
фазами
а
и
р
выделен
особый
тонкий
гетерогенный слой ар с реальной толщиной 8 (слой неоднороден в
перпендикулярном к поверхности направлении), границы которого
проходят через области с плотностями
каждой из фаз р
а
и рр,
равными их плотностям в объемах соответствующих фаз а и b вдали
от границы. Метод слоя конечной толщины нагляден, позволяет
проводить
описание
неоднородной
фазы
ab
и
получать
термодинамические уравнения, в которых будут содержаться полные
термодинамические характеристики. Это детально рассмотрено
в
монографии академика физико-химика Анатолия Ивановича Русанова
[8].
А.И.Русанов
предложил
новые
методы
исследования
поверхностных явлений: определение толщины поверхностных слоев,
измерение поверхностной плотности вещества и другие, позволившие
сделать
ряд
позволяет
экспериментальных
характеризовать
открытий.
состав
Метод
межфазового
Русанова
слоя
при
распределении в нем смесей компонентов путем введения их средних
мольных долей, однако, их величины будут зависеть от выбора
границ слоя ab. Метод слоя конечной толщины и его различные
модельные
приближения,
например,
модель
монослоя,
широко
применяются при адсорбции из растворов на поверхности твердых
тел для определения полного содержания вещества в слое конечной
толщины [8 Русанов, 9 Гугенгейм, 10 Толмачев].
Метод
Гиббса
основан
на
термодинамике
поверхностных
избытков. В методе избыточных величин (рис.1.5 б) гомогенные фазы
а и b разделены гипотетической поверхностью нулевой толщины.
Рассмотрим
простейшую
однокомпонентную
жидкость-пар,
систему:
разделенную плоской
межфазовой
поверхностью
Абстрактное
понятие
поверхность
н
е
о
д
н
о
р
о
д
н
~
имеющей
s
разделяющая
(математическая
поверхность)
Рисунок
1.6а.
Схема
распределения
плотности
на
границе
Ss жидкость/пар
F
F
(1.6а).
о
вместо
й
р
е
а
л
ь
н
о
й
некоторую
физически
п
о
в
е
р
х
н
о
с
т
толщину
впервые ввел выдающийся американский физико-химик
и
,
с
о,
Джозайя
Уиллорд Гиббс (1839-1903).
По
методу
Гиббса
сопоставляются
реальная
двухфазная
и
модельная
(воображаемая)
двухфазная система, в которой фазы
разделены
математической
(геометрической) поверхностью S. В
модельной системе сравнения с нулевым уровнем
(плотность
р,
адсорбция
Г,
все
свойства фаз
термодинамические
функции)
неизменны вплоть до математической границы раздела.
В реальной
свойства
фаз
межфазной
системе
в
(рис 1. 6б)
приближении
границе,
к
меняются.
Например, плотность жидкой фазы (I)
р
ж
Рисунок
1.6б.
Схема,
демонстрирующая
избыток
свободной энергии в жидкой
фазе G (1) по сравнению в
паровой G (2) на границе
жидкость/пар
II
до воображаемой границы S будет
уменьшаться,
s
а
плотность
газообразной-пар (II) р
пар
Разделяющую
- возрастать.
(математическую)
I
поверхность
Ss можно
проводить
в
произвольном
сечении
параллельно
различными способами,
реальной
поверхности
но как показано на рис.1.6а,
величина
адсорбции Гиббса Г = 0 только в одном случае, когда алгебраическая
сумма равных площадей заштрихованных «профилей плотностей»,
I(-)
- отрицательный избытоки
равны
нулю.
эквимолярной
В
Такая
- положительный избыток,
разделяющая
поверхность
называется
поверхностью.
других
случаях
разделяющую
поверхность
S
можно
s
располагать так, чтобы:
-
в фазе пара мольное содержание компонента в реальной
системе было больше, чем в модельной. Это будет соответствовать
положительному
избытку компонента (+) в фазе пара,
а фазе
жидкости отрицательному избытку ( - ) . Алгебраическая сумма при
равенстве избытков окажется равной нулю;
- избыток компонента был только (+), а отрицательный избыток
обнулять;
-
избыток
компонента
был только
(-),
а
положительный
обнулялся
Из рис. 1.6б следует, что
поверхностный избыток G
s
равен
разности площадей G жидкой и паровой фаз: G =G#-G/.
s
Принципиальным в методе Гиббса является то, что величина
поверхностного
избытка
будет
определяться
положением
разделяющей поверхности, но в любом случае не будет зависеть от
толщины пограничного слоя.
Отношение величины избыточного содержания компонента n к
s
величине
поверхности?
Гиббс
назвал
абсолютной
удельной
адсорбцией,
в
обозначают
^njs
поверхность
литературе
ее
(моль/м).
проводить
называют
Гиббс
таким
адсорбцией
предложил
образом,
Гиббса
и
математическую
чтобы
поверхностный
избыток одного из компонентов в двух- или многокомпонентной
системе равнялся нулю. Обычно при исследовании растворов на
поверхности
жидкой
фазы
за
нулевой
уровень
принимают
избыточное содержание растворителя и тогда поверхностный избыток
/компонента по отношению к растворителю, т.е. к нулевому уровню,
определяют, используя уравнение Гиббса
-da
= ^
(1.7)
где ц - х и м и ч е с к и й потенциал (определение ц будет дано ниже).
Для
двухкомпонентной
системы,
подставляя
в
(1.17)
выражение химического потенциала через активность компонента
(а=ус):
/u=RTlna
исследовании
получают уравнение, широко используемое
адсорбциив
изобарно-изотермических
при
условиях
из
растворов П А В [2]
Г
-
И
= Rf\da)
Л
И
PiT
Величину
Г
Г
=
-
( 1 . 1 8 )
~Rf\dc)
cT
рассчитывают
по
уравнению
(1.18)
из
экспериментальной изотермы поверхностного натяжения o=f(a) или
в менее строгой форме сг = Дс), предварительно определяя величины
поверхностной активности dc/da или dcd
где а -
активность,
концентрация.
у -
(например, графически),
коэффициент активности,
с-молярная
Из (1.18) видно, что
положительная
адсорбция Г >0 наблюдается, если dc/da или
dcd
< 0. В этом случае с увеличением
концентрации
Рисунок
1.7.
ПАВ
поверхностное
Схема
упаковки молекул П А В в
натяжение раствора П А В снижается от с
-
плотном монослое
поверхностное натяжение растворителя до с
< со, принимая минимальное значение при достижении состояния
насыщения
поверхностного
слоя
молекулами
ПАВ
(мономолекулярная или монослойная адсорбция Ленгмюра (Рис.1.7)).
Отрицательная адсорбция Гиббса Г < 0 наблюдается, если dc/da или
dcd
> 0. В этом случае с увеличением концентрации
поверхностное
веществ
натяжение
(ИПАВ)
С!
растет
раствора
от
с0
ИПАВ
поверхностно-инактивных
-
поверхностное
С
натяжение
с
Рисунок 1.8. (слева) Типичная зависимость поверхностного натяжения с от
концентрации С 1,2 - И П А В
и 3 - П А В в растворе, с - поверхностное
натяжение растворителя;
Рисунок 1.9.(справа) зависимость гиббсовской адсорбции Г=ДС) для П А В ,
построенная с п о м о щ ь ю уравнению (1.18) с получением dc/dс графическим
дифференцированием
экспериментальной c=f(C) методом касательных, Г предельная адсорбция.
0
0
растворителя до о
> оо, принимая максимальное значение
при
достижении состояния насыщения И П А В в объёме раствора.
На рис.
1.8
поверхностного
(слева) показаны три возможных
натяжения
от концентрации
зависимости
раствора
(изотермы
поверхностного натяжения).
Если
экспериментальную
изотерму
поверхностного
натяжения ст=/(С) нельзя представить в аналитическом виде, то
поверхностную активность П А В -do/dC при некоторой выбранной
концентрации С определяют графически, проводя касательную к
1
изотерме
поверхностного
натяжения
в
точке
С;
при
1
этом
поверхностная активность численно равна тангенсу угла наклона
касательной к оси концентраций: - ~~ =
К
ПАВ
относятся
высокомолекулярных
tga
молекулы
соединений
мономеров
(ВМС),
и
имеющих
даже
дифильное
строение, т.е. полярные и неполярные части крупных и даже малых
молекул с различием сродства к жидкой, газообразной и твердой
фазам. Типичными П А В по отношению к воде, как растворителю,
являются
линейные
молекулы,
углеводородную и гидрофильную отрицательно
заряженную
имеющие
гидрофобную
-
полярную положительно или
составляющие.
Такие
молекулы
в
поверхностном слое «частоколом» выстраиваются в поверхностном
монослое водного раствора, строго ориентируясь углеводородными
радикалами в сторону газовой фазы, а полярными (функциональными
-
-
группами-карбокси - С О О , сульфо - H S O , аминокислая -1ЧН +и
3
3
т.д.) - в сторону водной. При этом с увеличением концентрации
значительно понижают поверхностное натяжение воды и тем сильнее,
чем длиннее углеводородный радикал (правило Траубе). Достигнув
состояния насыщения в поверхностном монослое, часть избыточного
количества молекул П А В способна образовывать второй монослой на
поверхности первого, но уже
взаимодействуя
меняя ориентацию в пространстве и
своими углеводородными «хвостами» с «хвостами»
предыдущего слоя (подобное с подобным). Для остающихся молекул
ПАВ
в объеме
раствора термодинамически
выгодным
является
образование ассоциатов со структурами, называемыми в коллоидной
химии мицеллами. Мицеллы - это заряженные коллоидные частицы
(+ или - в зависимости от заряда функциональной группы ПАВ), в
которых
молекулы П А В ориентированы друг к другу
своими
углеводородными радикалами, а полярными группами к молекулам
воды.
Мицеллы
способны
(солюбилизировать-
относиться
растворять
с
внутри
любовью
к
себя
подобному)
углеводороды, жиры, гидрофобные частицы. В принципе, на этом
свойстве основано моющее действие натуральных (мыла, шампуни) и
синтетических моющих средств (СМС), называемых в англоязычной
литературе детергентами. П А В в больших объёмах используются при
флотационном обогащении руд в качестве «коллекторов», способных
избирательно закрепляться полярными группами на
целевых
минеральных
частиц
(гидрофобизация),
поверхности
размельченных
(классифицированных) до оптимального размера (около 0,2-2мм), а
углеводородными
«хвостами»
ориентироваться
в
газовую
фазу
воздушного пузырька. Таким образом, гидрофобизированная частица
минерала
закрепляется
на
поверхности
малых
пузырьков
и
выноситься
на
поверхности
огромного
движущегося
потока,
поступающего на обезвоживание, сушку, при необходимости
на
грануляцию и т.д. Смачиваемая водой гидрофильная масса частиц
руды, проходя через процессы осаждения, сгущения, отстаивания
др.
поступает
компонентом
в
в
отвал.
ПАВ
служит
охлаждающих
металлообработке
режущими
так
же
жидкостях
инструментами,
и
обязательным
при
при
скоростной
этом
снижает
кратно энергию, затрачиваемую на обработку поверхности металла. И
таких
примеров
множество.
К
природным
ПАВ
различной
поверхностной активности относятся практически все биологически
активные вещества (биологическая активность веществ напрямую
связана с их поверхностной активностью, на что не всегда обращают
внимание
исследователи
при
препаратов и биологически
парфюмерной
и
создании
новых
фармацевтических
активных добавок
косметической
-
БАД).
промышленности,
как
Товары
правило,
включают один из обязательных компонентов в виде ПАВ. Бытовой и
производственный спектр использования П А В необычайно широк.
Знание коллоидно-химических свойств натуральных и синтетических
ПАВ, прежде всего, их поверхностной
условие
на
пути
производство
ПАВ
получения
это
-
активности
качественного
обязательное
товара.
многотоннажное
Мировое
производство,
достигающее около биллиона тон/г. Однако, в этом есть и оборотная
сторона
медали
-
например,
синтетические
ПАВ
(в
основном
детергенты), губительно действуют на окружающую среду, угнетают
множество биологических процессов.
Возвращаясь
к
методу
поверхностных
избытков
Гиббса
отметим, что при исследовании избыточной адсорбции компонента на
поверхности
твердой
фазы
за
нулевой
уровень
принимают
поверхностный избыток твердой фазы. Но в этом случае из-за низкой
подвижности
частиц
твердой
поверхностного
натяжения
поверхности
напрямую
измерить
коэффициент
невозможно,
а,
следовательно, и рассчитать адсорбцию Гиббса, поэтому используют
другие адсорбционные уравнения, отличающиеся от «гиббсовского»,
которые будут рассмотрены далее.
В методе поверхностных избытков Гиббса рассматриваются
поверхностные избытки термодинамических функций:
внутренняя
энергия - U , свободная энергия Гиббса - G и Гельмгольца s
s
F,
s
энтропия - S , химический потенциал -ц и др.
s
1.3. Элементы классической термодинамики
Для понимания поверхностных явлений необходимо знание
элементов классической термодинамики, детально разработанной для
однородных
(гомогенных
систем).
Несмотря
на то, что
общая
термодинамика изучается в учебных курсах по общей, физической и
коллоидной химии, ниже (мелкий шрифт) в справочной
приведены
основные
сведения
по
химической
форме
термодинамике,
которые послужат полезным и необходимым отправным материалом
для перехода к термодинамике поверхностных избытков Гиббса.
Классическая
термодинамика
является
исследования естественных и искусственных
фундаментальная
научная
дисциплина,
методом
теоретического
процессов. Термодинамика это
изучающая
взаимные
превращения
различных видов энергии. Термодинамика базируется на трех законах, из них
первые
два, ввиду
особого
их значения, называют
началами:
1-е
начало
термодинамики, 2-е начало термодинамики. Начала термодинамики являются,
по сути, постулатами, так как были сформулированы в результате длительного
наблюдения людей за явлениями и процессами, протекающими в природе и
технике.
Отсутствие
исключений
для
наблюдаемых
закономерностей
и
подтверждение на опыте логических следствий, вытекающих из них, придают
особую надежность фундаменту, на котором построена термодинамика.
Существует несколько различных формулировок каждого из
законов
термодинамики, позволяющих путем логических рассуждений перейти от одной
к другой. Например, 1-й закон термодинамики - невозможен вечный двигатель
1-го рода, П-й закон термодинамики - невозможен вечный двигатель 2-го рода,
Ш-й закон термодинамики - невозможен вечный двигатель 3-го рода:
вечный двигатель 1-го рода - машина, производящая работу без затраты
энергии;
вечный
двигатель
2-го
рода
-
непрерывно
действующая
машина,
способная полностью превращать тепло в работу;
вечный двигатель 3-го рода - машина, позволяющая охладить тело до
абсолютного нуля.
Жизнь показала, что множество попыток создания вечного
двигателя
оказались бессмысленными.
Для математической формулировки законов термодинамики необходимо
ввести некоторые основные понятия и определения.
Система.
реального
Под системой в термодинамике понимают выделенную часть
физического
мира.
Следовательно,
термодинамическая
система
обязательно должна иметь границы. Всё, что не входит в систему, находится за
её границами, называют окружающей средой. Через границы система может
взаимодействовать
с
окружающей
средой.
Границы
системы
могут
быть
реальными и мыслимыми. Если система обменивается с окружающей средой
энергией и веществом, она называется открытой.
невозможен,
Если обмен
веществом
а обмен энергией происходит, то система называется
закрытой.
Если же системаимеет границы, через которые невозможен обмен энергией и
веществом, то такая система называется изолированной,
и хотя такие системы
реально не существуют, в термодинамике они используются.
Термодинамическая система обязательно должна быть макроскопической,
т.е. состоять из большого числа частиц. Это условие определяется тем, что
состояние системы в термодинамике выражается через такие понятия, например,
как температура, давление, теплота и др., которые имеют смысл только для
макросистем. Нет смысла говорить о температуре и давлении одной молекулы.
Таким
образом,
для
термодинамической
системы
существуют
ограничения как "сверху", так и "снизу". Система не может иметь бесконечное
число частиц, так как обязательно д о л ж н ы быть границы, и система не может
состоять из малого числа частиц, так как при этом невозможно использование
таких параметров, как давление, температура и т.д.
По структуре термодинамическая система может быть однородной, или
гомогенной (состоять из одной фазы), и неоднородной - гетерогенной (состоять
из нескольких фаз).
Состояние
системы
термодинамических
задается
параметров
с
помощью
состояния.
Опыт
свойств,
или
показывает,
что
иначе
для
однозначной характеристики данной системы в данных условиях достаточно
задать лишь некоторое число определенных термодинамических параметров,
которые
поддаются
непосредственному
измерению.
В
качестве
таких
параметров чаще всего выбирают температуру (Т), давление (Р), объем (V), их
называют основными термодинамическими параметрами.
Параметры
состояния
системы связаны между собой
соотношением,
которое называется уравнением состояния. Если система состоит из одного
вещества и в качестве параметров выбраны P,V,T,
то уравнение состояния в
общем виде можно записать: _ДР,У.Т)=0. Например, для n молей идеального
газа
уравнением состояния является известное уравнение Менделеева - Клапейрона
PV = nRT
где Р VR T -
(1.19)
давление;
объем;
газовая постоянная;
температура.
В
термодинамике
кроме
основных
термодинамических
параметров
широко используются другие свойства системы (также параметры состояния,
которые могут быть выражены через Р,У.Т), называемые функциями состояния
- внутренняя энергия системы (U), энтальпия (H), энергия Гиббса (G), энергия
Гельмгольца (F), энтропия (S), химический потенциал (//) и др.
Параметры состояния системы могут быть:
внутренние,
определяемые только координатами тел системы (плотность
P,U);
внешние,
определяемые пространственными координатами (V);
экстенсивные
если
(аддитивные),
значение
параметра
пропорционально размеру части системы, т.е. прямо пропорциональные
числу частиц (V, U, S, теплоемкость C, электрический
интенсивные
(неаддитивные),
потенциал
ф);
имеющие одно и то же значение, не
зависящее от размера любой выделенной части равновесной системы, т.е.
не зависящие от числа частиц, (T, р , Р, заряд q). И м е ю т смысл «в точке».
Отношение
любых
двух
экстенсивных
параметров
становится
интенсивным параметром: парциальные - объем или мольная доля.
Для описания состояние равновесия системы, в которой совершается не
одна, а несколько видов работ, вводят термодинамические параметры в виде
обобщенных
сил и обобщенных
обобщенные
силы-
координат:
интенсивные параметры. К ним относят давление Р , ц,
поверхностное натяжение О ;
обобщенные
координаты-экстенсивные
параметры. Они изменяются под
действием соответствующих обобщенных сил. Это -V, n, площадь 5,заряд е.
В
зависимости
изотермические,
Изотермическими
от
изобарные,
процессы
-
протекания
изохорные
называются
температуре. Изобарные
Изохорные
условий
и
процессы,
процесса
различают
адиабатические
процессы.
протекающие
при
постоянной
процессы протекают при постоянном
протекают
при
постоянном
объеме.
давлении.
Адиабатические
процессы протекают без обмена энергией с окружающей средой
(E=const).
Отметим, что все эти термодинамические свойства характеризуют лишь
то состояние, в котором система находится в данный момент, и не дают
представления о её предшествующих состояниях. Поэтому изменение свойства
(обозначается знаком А) при переходе системы из одного состояния в другое
определяется только исходным и конечным состоянием и не зависит от пути
перехода системы из одного состояния в другое.
Если, например, система, имеющая в исходном состоянии температуру Т ,
н
перешла в конечное состояние с температурой Т , то изменение температуры АТ
к
определяется только температурами Т и Т , т.е. АТ = Т - Т , и не зависит от
н
к
к
н
того, как осуществлялся процесс изменения температуры: медленно, быстро, с
остановками или непрерывно и т.д. Также и для любого другого свойства
системы.
Изменение какого-либо свойства системы (АТ, АР, AV, AS, AG и т.д.)
можно
рассчитать
для
конкретной
химической
реакции.
Но,
вследствие
независимости изменения свойства от пути перехода, м ы при таком расчете, к
сожалению, не получим никакой информации о том, каким путем исходные
вещества превратились в продукты реакции, т.е. каков механизм превращения
веществ. Однако, определяя знак и величину некоторых термодинамических
параметров (функций состояния) системы, можно указать на принципиальную
возможность или невозможность протекания процесса.
Кроме термодинамических свойств системы в уравнения термодинамики
входят теплота (Q) и работа (A), которые в отличие от первых определяются не
состоянием системы, а путем перехода системы из одного состояния в другое.
Представим
физический
смысл
используемых
в
химической
термодинамике параметров состояния.
Температура
(Т)
-
физическая
величина,
характеризующая
степень
нагретости тела. Температура равновесной системы отражает интенсивность
теплового движения микрочастиц, образующих систему. Для газа температура
является мерой средней кинетической энергии движения молекул. Единица
измерения температуры - градус Кельвина (К).
Давление
(Р)
характеризует
взаимодействие
системы
с
окружающей
средой и определяется силой, действующей на единицу площади поверхности.
Давление газа определяется натиском молекул на стенки заключающего этот газ
сосуда. Е д и н и ц ы измерения давления - паскаль (Па), атмосфера (атм), 1 атм =
101 323 Па.
Объем (V) является пространственной характеристикой макроскопической
3
системы. Единица измерения объема - м .
Внутренняя
которой
энергия
стало
возможным
математического
совокупность
внутреннюю
(U) - важная характеристика системы, с помощью
выразить
уравнения.
всех
видов
энергию
не
1 -й
Внутренняя
энергии
входят
частиц,
закон
термодинамики
энергия
представляет
составляющих
потенциальная
энергия,
в
виде
собой
систему.
Во
обусловленная
положением системы в пространстве, и кинетическая энергия движения системы
как целого. Следует заметить, что нельзя определить абсолютное
значение
внутренней энергии (так как нельзя получить состояние, лишенное энергии), но
можно
определить
изменение
энергии
при
переходе
системы
из
одного
состояния в другое. Такое изменениеявляется мерой теплоты, поглощенной или
выделенной системой в изохорном процессе. Внутренняя энергия измеряется в
джоулях (Дж) или эквивалентных единицах.
Энтальпия
(H)
-
широко
используемая
в
термодинамике
функция
состояния, связанная с внутренней энергией системы
Н = U + PV
Поскольку
энтальпия
определяется
(1.20)
через
внутреннюю
энергию,
ее
абсолютное значение также определить нельзя. Определяется только изменение
энтальпии
(ЛЯ).
Энтальпия
больше
внутренней
энергии
на
величину
произведения PV. Произведение PV можно отождествить с потенциальной
энергией
системы
расширении).
По
(работой,
этой
которую
причине
может
энтальпию
совершить
иногда
система
называют
при
энергией
расширенной системы. Энтальпия является мерой теплоты п р и изобарном
процессе теплообмена системы и о к р у ж а ю щ е й среды.
Для изменения энтальпии используют выражение
AH = AU + PAV
(1.21)
Единица измерения для ЛН та же, что для Ли и для работы (A = РЛ V), - Дж.
Энтропия
(S).
Для
математического
описания
второго
закона
термодинамики потребовалось введение функции состояния, которую назвали
энтропией.
Понятие энтропии впервые 1865 году ввел в термодинамику немецкий
физик Рудольф Юлиус Эмануэль Клаузиус (1822-1888) для определения меры
необратимого рассеивания энергии (диссипации), меры отклонения реального
процесса
от
идеального.
Постулат
Клаузиуса:
«Невозможен
процесс,
единственным результатом которого являлась бы передача тепла от более
холодного тела к более горячему».
Математически энтропия определяется как функция состояния системы,
равная в равновесном процессе количеству теплоты, сообщённой системе и л и
отведённой от системы, отнесённому к абсолютной
температуре
системы:
dS=8Q/T, где d S - приращение энтропии; 8 Q - минимальная теплота, подведённая
к с и с т е м е ; Т - абсолютная температура процесса.
Энтропия устанавливает связь между макро- и микро-состояниями.
В статистической физике энтропия
расположении
системы.
частиц,
составляющих
определяется
систему,
как мера беспорядка
или мера
в
неупорядоченности
Энтропия S связана с числом соответствующих микросостояний W
термодинамической системы —принцип Людвига Больцмана (1865—1906)
S = MnW
(1.22)
где к = 1,3806488-10 Д ж / К - коэффициент пропорциональности - постоянная
Больцмана;
W - термодинамическая вероятность состояния системы, определяемая к а к
число всех в о з м о ж н ы х способов реализации данного состояния.
В реальных системах W - это очень большое число. Величину этого числа
можно представить, если в качестве системы взять некоторое количество газа,
находящегося п р и заданных Р, V, Т, и вспомнить, что молекулы газа в результате
движения и столкновений могут занимать очень большое число положений
(координат) и иметь различные скорости движения. И если для всех молекул
газа подсчитать все возможные положения молекул в пространстве и все
возможные скорости и х движения для состояния с д а н н ы м и Р , V, то можно
определить W.
Л ю б о й фактор, который увеличивает беспорядок в системе, увеличивает и
энтропию. П о в ы ш е н и е температуры, увеличение объема приводят к увеличению
энтропии системы.
Любой
процесс,
протекающий
в
системе
с
изменением
порядка
в
расположении частиц, приводит к соответствующему изменению энтропии. Так,
в процессе испарения жидкости энтропия увеличивается, п р и кристаллизации
жидкости энтропия уменьшается.
Если в системе протекает химическая реакция с увеличением объема,
например:
СО2(г.) + С (к.) = 2 С О (г.),
то изменение энтропии такого процесса положительно (AS > 0). П р и протекании
реакции с у м е н ь ш е н и е м объема AS < 0:
2NO (г.) + О2(г.) = 2 N 0 2 (г.).
В отличие от U и Н можно определять абсолютную энтропию вещества
(существуют методы определения S).
Единицей измерения энтропии моля вещества является Дж/(моль-град)
(размерность энтропии такая же, как у теплоемкости С).
Свободная
энергия Гиббса
(G)- это свойство системы, которое выражается
через уже известные нам свойства уравнением
С = Я - Г5
С
помощью
свободной
энергии
(1.23)
Гиббса
получаются
удобные
для
практического использования выражения 2-го закона термодинамики.
Физический смысл этой функции состояния формально может
быть
представлен исходя из так называемого определительного уравнения для Н, если
записать его следующим образом:
Я = G + Г5
(1.24)
Отсюда следует, что энтальпия системы Н может быть представлена в
виде двух частей: первую часть (G) назвали свободной энергией
(прежнее
название
изобарно-изотермический
энтальпии, равную произведению
(TS),
потенциал);
Гиббса
вторую
часть
назвали связанной энергией.
На
основании 2-го закона термодинамики было доказано, что в работу может быть
превращена первая часть энтальпии, равная G, а вторая часть, равная TS, в
работу принципиально превращена быть не может.
Единица измерения свободной энергии Гиббса в системе С И - Дж/моль.
Свободная
энергия
Гельмгольца
(F)
(прежнее
название
изохорно-
изотермический потенциал) выражается уравнением
F = U - Г5
По
аналогии
с
G
свободная
энергия
(1.25)
Гельмгольца
может
быть
представлена как часть внутренней энергии, которая может быть превращена в
работу.
Это
свойство
системы,
выражаемое
через
другие
свойства
определительным уравнением
U = F + Г5
(1.26)
Термодинамический
Термодинамическим
процесс,
процессом
термодинамическое
равновесие.
называется изменение во времени хотя бы
одного из параметров, характеризующих систему.
Если же параметры состояния сохраняют постоянные значения, то такая
система
находится
в
состоянии
равновесия.
В
зависимости
от
условий
протекания процессы могут быть: изобарические ( Р = const), изотермические (Т
= const), изохорические (V= const).
В открытых системах энергия может изменяться в результате обмена со
средой веществом.
Все процессы, встречающиеся в природе, подразделяются на обратимые,
необратимые и самопроизвольные, несамопроизвольные.
Самопроизвольный
процесс
- это такой процесс, который не требуют
затраты энергии извне (например, растворение соли в воде, смешение газов
и т.д.). Протекают самопроизвольные
процессы
одном направлении: теплота
переходит от горячего тела к холодному, а не наоборот; газ стремится занять
весь предоставляемый ему объем, и самопроизвольно не сжимается; газы и
жидкости
проникают
друг
в
друга
и
смешиваются.
То
есть,
все
самопроизвольные процессы ведут к уменьшению и исчезновению разности
температур, разности давлений и разности концентраций. Д л я получения ж е
полезной работы, всегда необходимо иметь разность потенциалов (градиент)
какой-либо величины - температуры, давления и т. д.
Несамопроизвольный
процесс
требуют для своего протекания
затраты
энергии.
Самопроизвольные
и несамопроизвольные
процессы
подразделяются на
термодинамически обратимые и необратимые.
Обратимый
процесс
-
это равновесный термодинамический
процесс,
который может проходить как в прямом, так и в обратном направлении. П р и
этом
система
Равновесные
возвращается
состояния
в
системы
исходное
могут
состояние
изучаться
без затрат
на
основе
энергии.
принципа
существования энтропии. О н утверждает, что существует функция состояния
системы - энтропия, изменение которой в равновесных процессах происходит
только п о д действием энергии в форме теплоты. Равновесные процессы в
природе и технике никогда не встречаются и представляют собой предельное
состояние процесса. Н а практике обратимый процесс реализовать невозможно.
О н протекает бесконечно медленно, и можно только приблизиться к нему.
Термодинамическая
обратимость
процесса
отличается
от
химической
обратимости. Химическая обратимость характеризует направление процесса, а
термодинамическая
—
способ
его проведения.
В состоянии
химического
равновесия скорость прямой реакции равна скорости обратной реакции.
Необратимый
процесс
-
процесс,
который
нельзя
провести
в
противоположном направлении. Все реальные процессы необратимы. Например
диффузия, теплопроводность,
энергии макроскопического
вязкое течение и др. Переход
кинетической
движения через трение в теплоту, то есть во
внутреннюю энергию системы, является необратимым процессом.
Достижением
термодинамики
является
установление
критериев,
позволяющих определить, является ли д а н н ы й процесс самопроизвольным и л и
несамопроизвольным.
1.3.1. Объединенное уравнение первого и второго начал (законов)
термодинамики
Для термодинамической равновесной гомогенной системы п р и обратимом
изменении ее состояния, согласно I I закона термодинамики по Клаузиусу
аЬ = —,
количество
теплоты,
поглощаемое
системой,
выражают
через
изменение ее энтропии
SQ = TdS
(1.27)
Объединив выражения для первого и второго законов термодинамики
TdS = dU + SA
с учетом
SA = pdV
получаем
обобщенное
уравнение,
(1.28)
справедливое для
равновесных процессов
TdS = dU + pdV
(1.29)
следовательно, внутренняя энергия
dU = TdS - pdV
(1.30)
Выражения для свободной энергии Гиббса (Р и Т=сош1)
и Гельмгольца (У и
T=const) dG и dF легко получаются после дифференцирования (1,9) и (1,11) и
подстановки в (1.16).
Свободная энергии Гиббса
dG = -SdT - Vdp
(1.31)
а свободной энергии Гельмгольца
dF = -SdT - pdV
(1.32)
Это дифференциалы G и F для процессов, происходящих в системах, в которых
отсутствуют
химические
превращения.
Если
же
в
системе
химические процессы, то необходимо учесть изменение
вызванное
изменением
количества
вещества.
возможны
внутренней энергии,
П р и изменении
количеством
вещества dni одного из компонентов i системы пропорционально произойдет
изменение
внутренней
энергии
dU ^^ dn ,
i
i
i
где
fi
t
-
пропорциональности, который называют химический
потенциал.
Изменение
изменением
внутренней
энергии,
вызванное
коэффициент
количества
веществавсех компонентов системы, выразится формулой:
^ dn
1
1
+ \i dn
2
2
+ pi dn
3
3
+ —+ Hkdn
= V ^idn
k
t
(1.33)
Тогда полное изменение внутренней энергии в системе
dU = TdS - pdV + V
^ dn
t
t
(1.34)
По аналогии для других функций:
dF = -SdT - pdV + V Hidn
t
(1.35)
dG = -SdT + Vdp + V Hidn
t
(1.36)
Для большого термодинамического потенциала Д , связывающего свободную
энергию с химическим потенциалом П = F - /in = -PV
dn = -SdT - PdV + V n d^
Sii
t
(1.37)
Химический
потенциал
(//)
вещества
в
выражениях
(1.33
-
1.37)
-
термодинамическая_ функция, применяемая п р и описании состояния систем с
переменным
числом
частиц.
Определяет
изменение
термодинамических
потенциалов (энергии Гиббса, внутренней энергии, энтальпии и т. д.) п р и
изменении числа частиц в системе. Представляет собой энергию добавления
одной частицы в систему без совершения работы. Если / - параметр системы, то
как интенсивная величина, подобно температуре Т и давлению P, характеризует
фазу. Химический потенциал может быть определен по массе вещества m, его
количеству n, либо числу частиц N. Соответственно, в зависимости от величины
по которой берется производная от энергии Гиббса, химический потенциал
называется удельным (Дж/кг), молярным (Дж/моль) и химическим потенциалом,
отнесенным к одной частице (Дж).
Исходя из выражений
химический потенциал f
i
1.34 -
1.36, п р и соответствующих
компонента i , находящегося в объеме
условиях,
гомогенной
фазы, определяется как
/dU\
/dF\
/dG\
где fij - парциальная мольная внутренняя энергия, свободная энергия
Гельмгольца либо Гиббса (подстрочная запись означает условие постоянства
переменных S, V,P,T, а для nj#i — постоянство всех nj кроме n ).
Условием
равновесия
является
равенство
химических
потенциалов
i
контактирующих гомогенных фаз: р. — р. , либо,/ж — /ж,либо р. — [л , либо р. —
г
ж
г
тв
ж
.
Мтв
И наконец, из (1.34) и (1.36) вытекает важное уравнение Гиббса-Дюгема,
связывающее приращения (дифференциалы) интенсивных параметров Р,Т, Мгомогенных систем:
+SdT - VdP + ^
Заканчивая
краткий
экскурс
в
ц^щ
= 0
термодинамику
гомогенных
(1.39)
систем
отметим, что состояние термодинамического равновесия в системах достигается
при минимальных значениях потенциалов. В этом случае равновесие является
устойчивым.
П р и фиксированных
может принимать
различные
значениях
значения,
своих переменных
одно из которых
и
потенциал
соответствует
состоянию термодинамического равновесия. Н и ж е приведена сводная таблица,
показывающая,
(P,T,V,N,S,ju)
при
каких
постоянных
значениях
параметров
может достигаться минимальное значение
системы
термодинамического
потенциала (U,H,F, G, Q, TS).
Таблица 1.2.
Условия (фиксированные параметры), при которых достигается
устойчивое термодинамическое равновесие в системе (минимальное
значение термодинамического потенциала)
Фиксированные
параметры
S,V,N
S,P,N
T,V,N
T,P,N
T,V,M
S,P,ju
После
сведений
из
Термодинамический потенциал
Внутренняя энергия, U
Энтальпия, H
Свободная энергия Гельмгольца, F
Потенциал Гиббса,0
Большой термодинамический потенциал,Г2
Связанная энергия, TS
«лирического»
отступления
классической
термодинамики,
термодинамику
поверхностных
поверхностных
избытков
термодинамикой
адсорбции.
явлений,
Гиббса,
(мелкий
в
перенесем
частности
теснейшим
Продолжим
шрифт),
в виде
эти
на
сведения
на
термодинамику
образом,
рассмотрение
общих
связанных
с
фенименалогической
термодинамики, применительно к адсорбции, термодинамикой поверхностных
избытков Гиббса, сравнивая термодинамические уравнения для гомогенных фаз
с аналогичными уравнениями для гетерогенных фаз.
1.4. Объединенное уравнение первого и второго законов
термодинамики поверхностных избытков Гиббса
В методе поверхностных избытков Гиббса
поверхностные
избытки
термодинамических
рассматриваются
функций:
внутренняя
энергия- U ,
s
энтропия-S^,
Гельмгольца -F
свободная
энергия
Гиббса
-G
и
s
, химический п о т е н ц и а л - ш др. В разделе 1.2.3.
s
рассмотрены варианты положения эквимолярной
разделяющей
поверхности
компонентов
исследуемой
с
занулением
системы
(гипотетической)
избытка
(например,
одного
из
растворителя
в
системе Г-Ж, или твердой поверхности вблизи границы раздела Г-Т
или Ж-Т).Эта модель позволяет определить поверхностные избытки
всех функций состояния системы: U , S , G , F , и т.д. Гиббс дал эти
s
s
s
s
определения. Так поверхностный избыток внутренней энергии
U = Т5 + аз + ^
s
(140)
№s,i
5
или в дифференциальной форме
dU = TdS
s
+ ads + ^
^idn
si
(1.41)
- sda + ^
^idn
si
1.42
s
Аналогично для H
s
dH
= TdS
s
s
То же, для других функций в дифференциальной форме:
dF = -S dT
+ ads + ^
H-idn
dG = -S dT
— ads + ^
H-idn
s
s
s
s
+ ads + ^
(1.44)
si
И для большого термодинамического потенциала
dH = -S dT
(1.43)
si
n d^i
si
Q=F-/un
(1.45)
В свою очередь аналогом уравнения Гиббса-Дюгема для гомогенных
систем (1.23), связывающее приращения интенсивных параметров
будет
S dT
+ sda + ^
s
n
s,i^^i
Уравнение (1.46) называется: адсорбционное
= 0
(1.43)
уравнение
Гиббса,
а его
аналог, уравнения Гиббса-Дюгема для гомогенных систем (1.39),
полученное формально (в приближении аддитивности) не только для
гомогенной, но и
для всей гетерогенной системы в целом, будет
выступать в роли системы
сравнения.
По уравнению (1.46) Алексей Анфимович Лопаткин [11] в своем
фундаментальном
термодинамической
труде,
и
посвященном
глубокому
анализу
молекулярно-статистической
теории
равновесной физической адсорбции, делает принципиально важные
замечания: 1) "значения, входящих в него (адсорбционное
Гиббса)
уравнение
избыточных экстенсивных величин зависят от того, как
проведены математические границы раздела между фазами в системе
сравнения; 2) .. .однородные фазы, для которых написано уравнение
(1.39) и которые на самом деле не существуют, имеют те же свойства,
что и объемы реальной гетерогенной системы, расположенные вдали
от фазовых границ принимается, что влияние поверхности раздела
распространяется на очень малые расстояния вглубь прилегающих
фаз. Это допущение не следует из термодинамики, но очень широко в
ней
используется.
поверхности
Если
считать,
распространяется
что возмущение
на
бесконечные
от
реальной
расстояния,
то
избыточные величины в (1.46), а так же поверхностное натяжение
будут зависеть от объема и формы прилегающих фаз ' ' Э т о ключевые
моменты, от которых зависит правильность получаемых на практике
адсорбционных характеристик различными методами, но формально
рассчитанных
по методу
избытков
Гиббса".
(Этой
не
простой
проблеме
посвящено
ряд
теоретических
и
экспериментальных
исследований, некоторых из которых коснемся ниже).
Сопоставляя систему уравнений термодинамических функций
для гомогенных систем (1.34-1.39) и систему уравнений избыточных
термодинамических
функций
Гиббса для
гетерогенных
систем
(1.40-1.46), а также из сводной (Табл. 1.2) видим, что формально в
методе избытков объем
V заменен
на площадь
поверхности
s,
давление Р - н а поверхностное натяжение У, а элементарная работа по
уменьшению объема в изотермическом процессе -PdV
yds
заменена на
(здесь знак ( - ) указывает, что в гомогенной системе работа
связана с уменьшение V, а в гетерогенной системе с увеличением
поверхности s. При этом обобщенная координата V заменена на s , а
обобщенная сила Р - н а У.
Таблица 1.3
Сравнительная характеристика фундаментальных уравнений для
гомогенных фаз и межфазовой поверхности (гетерогенные системы)
Гомогенные
Потенциал
Гетерогенные системы
системы
Внутренняя энергия
U=TS-PV+I u n
U =TS +os
+Ziw j
Энтальпия
H=TS + Ijun
Изохорно-изотермич.
F=-PV+Iju n
Fs = Os + IjUinsj
Изобарно-изотермич.
G=U-S+PV+Ijun
GS=US-TSS-OS
+Zjunis,i,
Большой термодинамический Q=F-IjUini
Q=F-IjUinsi
Важным следствием уравнения (1.46) является то, что в
J
i
изотермическом
процессе
^^const
i
i
s
s
S
i
и
dT=0)
sdo-+Zn d^ =0,
si
i
при
почленном делении выражения на s, приходим к уравнению Гиббса
-da=SP d// (1.3),
i
i
с
которого
мы
начинали
рассмотрение
термодинамики Гиббса, а так же
к частному
уравнению
двухкомпонентных
Гиббса
(1.4)
для
адсорбционному
систем,
исключительно
широко применяемому в научных
исследованиях
растворов ПАВ. К тому же при экспериментальном исследовании
границы раздела фаз Г-Ж легко измеряемым параметром, например,
по методу Вильгельми, является величина поверхностного натяжения
а (в русской
величину
и зарубежной
<7 чаще обозначают
однако, А.И. Русанов
на
разницу
натяжения,
обращал
литературе
не
как у, а величину поверхности
формальных
обозначениях
а в принципиальном
механическому
избытков
в своих трудах [12] особо обращает
в
внимание
при рассмотрении
и Гиббс),
различии
механическое
(у)
и
поверхностного
натяжения
внимание
поверхностного
между а и у (на
если их применяют
состоянию
s как A,
твердых
по отношению
поверхностей.
к
Тогда
термодинамическое
(а)
не совпадают,
но это особый
Легко измеряется и величина поверхностного
это
определения
давления
случай).
%, равная
разности текущего равновесного значения поверхностного натяжения
раствора а и поверхностного натяжения растворителя <т \
0
п = а-а
= f Vid^i,
0
(1.47)
из которого рассчитывают адсорбцию Г [1].
При исследовании адсорбции на твердых поверхностях также
можно
измерять
избыточные
и полные
величины
адсорбции,
а
двумерное давление рассчитывать по уравнению Гиббса:
п = RT f*Td(lnP)
Заканчивая
явлений
отметим,
рассмотрение
что
их удобно
термодинамики
(1.47 а)
поверхностных
классифицировать,
исходя
из
объединенного уравнения первого и второго законов термодинамики
для любой гетерогенной системы [2], в которое входят основные
виды
энергии
(свободная
механическая
VdP,
энергия
Гиббса
поверхностная
dG,
ods,
тепловая
химическая
SdT,
Uidn ,
t
электрическая <pdq):
= - S d T + VdP + <rds + £ Hidn
t
Уравнение
замечательно
тем,
что
в
+ <pdq
(1.48)
лаконичной
форме
демонстрирует важнейший принцип термодинамики, как науки,
сохранении материи
и возможности превращения
о
одного вида
энергии в другой. Превращение поверхностной энергии ods в какой
либо
вид
энергии
(1.48)
соответствует
поверхностному
явлению:
капиллярность,
электрические
явления,
адсорбция,
определенному
смачивание,
включая
адгезия,
реакционную
способность вещества, связанную с изменением его дисперсности.
Дисперсные
основа,
на
заданными
системы и поверхностные
которой
держится
свойствами:
явления— теоретическая
получение
сорбентов
новых
материалов
и катализаторов,
цементов
с
и
сплавов, смазочных и лекарственных материалов, пищевых продуктов
и лекарственных веществ.
В химической технологии нет такой отрасли, где бы ни имели
решающего значения дисперсные системы и поверхностные явления:
процессы
обогащения
руд,
в
особенности
флотация,
сгущение,
отстаивание, фильтрация, процессы конденсации и кристаллизации,
брикетирование,
спекания,
гранулирования.
В
этих
процессах
большое значение имеют поверхностные явления (адсорбция, адгезия,
смачиваемость, капиллярность, коагуляция и пр.).
1.5. Количественное описание адсорбции
На практике для описания
две
ее
количественных
адсорбции применяют в основном
характеристики
Г
и
a,
получаемых,
соответственно, по методу избытков Гиббса и методу слоя
толщины
[8], получившего
содержания
свое
развитие
в методе
конечной
полного
[10].
Термодинамическая теория поверхностных явлений один из
самых сложных
разделов феноменологической термодинамики. В
приложении к адсорбционным процессам наилучшей монографией, в
которой приведен обстоятельный критический анализ обоих методов
и показаны пути возможного практического использования
избытков Гиббса и метода полного содержания
метода
для количественного
описания адсорбции, считается монография классика
современной
теории адсорбции Алексея Анфимовича Лопаткина [11]. Из ниже
приведенных цитат этого фундаментального труда достаточно ясно
видны проблемы и подходы
при анализе
опытно измеряемого
межфазового слоя, макроскопической толщины: "Термодинамическая
теория адсорбции должна строится на непосредственной связи с
конкретным
типом
трудностью
построения
адсорбционных
адсорбционного
систем
эксперимента"."...основной
строгой термодинамической
модели
является проблема разделения системы на
две фазы, точнее определение координат поверхности, разделяющей
объемную
и
адсорбционную
фазы".
"Точное
проведение
разделяющей поверхности невозможно [8], поэтому в теоретических
работах рассматриваются два подхода: термодинамически строгий,
но мало информативный метод
избытков
Гиббса,
не разделяющий
систему
на
объемную
и
адсорбционную
фазы
и
позволяющий
анализировать лишь свойства системы в целом, и метод
содержания
способом
полного
Ленгмюра, основанный на выбираемой тем или иным
модели
(размеров, емкости) адсорбционной фазы и
использовании реальных (абсолютных) концентраций компонентов в
этой фазе.
Хотя последний метод менее
более информативен, т.к. рассматривает
строг,
он
существенно
адсорбционную
систему,
как двухфазную и позволяет анализировать свойства каждой из фаз в
отдельности...".
Метод избытков
Гиббса в термодинамическом смысле строг и
был разработан для анализа поверхностных
явлений
на
границах
раздела газ—жидкость и жидкость—жидкость. Преимущество метода
избытков состоит в том, что он не связан ни с какими модельными
представлениями. Заметим, что на сегодняшний день предложено
множество адсорбционных моделей, но любая модель это —лишь
некоторое приближение к реальности. С помощью метода избытков
можно
выстраивать
включать
термодинамическую
теорию,
которая
только экспериментальные величины. В
исследованиях
метод
сохранил
свое
будет
современных
значение
поскольку
поверхностное натяжение o, входящее в адсорбционное уравнение
Гиббса
(1.3-1.4),
является
легко
экспериментально
измеряемой
величиной.
Метод избытков применяться при исследовании адсорбции и на
твёрдых
поверхностях.
Если
ограничиться
простейшим
системы флюид—инертный адсорбент с однородной
случаем
поверхностью
(рис.1.10) и рассмотреть две сообщающиеся между собой системы
сравнения a -реальную и б-идеальную с общей площадью адсорбента
s и одинаковыми объемами V при одинаковой температуре Т, то при
0
достижении состояния равновесия в системах в результате адсорбции
в системе а вблизи
поверхности
создается
адсорбата [5]. Определим в общем виде
некоторый
избыток
адсорбцию i компонента
флюида по Гиббсу как
П д = П;
—
5
где n и n -число
i
g>i
( 1 .
п^,
49)
молей флюида в реальной a и гипотетической б
системе сравнения. При известной удельной поверхности адсорбента
Б
уд
избыточная адсорбция Гиббса Г, отнесенная к единице площади
поверхности выразится как
Рисунок 1.10. Схема, поясняющая количественное определение
гиббсовской адсорбции Г на инертном адсорбенте (заштрифован) при сравнении
реальной а и идеальной б систем
Для определения абсолютной адсорбции a
i
(средней
объему адсорбционной фазы) в реальной системе на
расстоянии
от
разделяющую
адсорбирующей
поверхность
(делая
поверхностиусловно
допущение,
что
по
всему
некотором
проводят
разделяющая
поверхность находится на расстоянии в несколько вандерваальсовых
радиусов от твердой поверхности) так, чтобы отдельно выделить в
системе объемную и адсорбционную
фазы. В этом случае можно
рассчитать абсолютную величину адсорбции по формуле
Щ = nf + п
(1.51)
дХ
При небольших (до нескольких атмосфер) давлениях газа (или
разбавленных растворах) n
малая величина
g>i
по
избыточной адсорбцией, поэтому не делают
абсолютными
и
различия
заметными.
адсорбции
с
между
избыточными величинами щ = nf. Однако, в
экспериментах с высокими давлениями адсорбтивов
становятся
сравнению
растут
эти
Но при этом, абсолютные
различия
величины
с увеличением давления, стремясь к некоторому
пределу, а избыточная
адсорбция
проходит
через
максимум,
затем уменьшается до нуля, т.к. молярная концентрация
а
объемной
фазы становится такой же, как и вблизи поверхности.
На рисунке 1.11 приведен пример
изотерм полного содержания а, в
порах цеолита NaX и избыточной
адсорбции rfi н-октена-1 из
его
раствора
Это
в
н-октане
классический
Рисунок 1.11. Изотермы избыточной
адсорбции n и полного содержания
s
специфического
[5].
пример
(квадруполь-
t
а н-октена-1
г
из
раствора
в
н-
ионного)
межчастичного
октанецеолитом NaX
притяжения
молекулы
непредельного углеводорода (по двойной связи) к ионной решетке
цеолита,
при
практически
полной
взаимной
компенсации
дисперсионной составляющей взаимодействий обоих углеводородов с
цеолитом.
При адсорбции из растворов возможна и положительная, и
отрицательная адсорбция молекул, ионов, более сложных частиц, а
так же возможно изменение состава функциональных поверхностных
групп в результате их сольватации под воздействием растворителя и
др.
Традиционно,
измерение
равновесных
величин
адсорбции
проводят по изменению концентрации одного из компонентов при
контакте раствора с адсорбентом (для ускорения процесса адсорбции,
дополнительно встряхивая). Расчет поверхностных избытков ведут по
разнице равновесных концентраций раствора вблизи
твёрдой фазы и вдали от нее. Величину
компонента
af
выражают
в
моль/г
поверхности
гиббсовской адсорбции
адсорбента
(если
известна
молярная масса компонента).
5
Уо(С()Д
-
Q)
г л
а- =
гол
(1.52)
т
где V - объем раствора;
т - масса адсорбента;
С ; и С; - равновесные начальная и конечная концентрации i компонента.
0
а
При известном значении величины удельной поверхности адсорбента
Буд проводят пересчет величины af на единицу площади поверхности
s и получают значение избыточной адсорбции Гиббса выраженную в
2
моль/м .
Г,- =
Ситуация
(максимум
ростом
и л и Г,- =
с
положительным
на изотерме
концентрации
(1.53)
адсорбции)
компонента
избытком
адсорбции
часто возникает,
в
растворе
его
когда с
избыточная
адсорбция сначала растет, а затем убывает и при
компонента, равной единице, величина адсорбция
мольной доле
равна нулю (рис.
1.12, верхняя кривая) [13]. Это проявляется, когда сродство одного из
компонентов в растворе к поверхности адсорбента выше, чем других
(другого) компонентов. В рассматриваемом случае сродство толуола
к силикагелю (поверхность гидрофильная) выше, чем у н-гептана. В
другой
ситуации,
когда
в
некоторой
области
концентраций
происходит адсорбция преимущественно одного компонента, а при
более высоких концентрациях — другого, то
на адсорбционной
кривой (рис.1.12, нижняя кривая) можно наблюдать два экстремума
(максимум
и
минимум,
т.е.
положительный
и
отрицательный
избытки). Здесь поверхность графитизированной сажи гидрофобна и
сродство
н-гептана
к ней выше
(более высокая
дисперсионная
составляющая взаимодействий), чем у толуола, поляризуемость
а
которого уступает поляризуемости н-гептана [13].
Если
при
низких
абсолютные
и
давлениях
избыточные
величины адсорбции неразличимы,
то при адсорбции из газовой фазы в
Мольная доля
Рисунок
1.12
Изотерма
избыточных величин адсорбции
т
о
л
у
о
л
а
в
г
е
(верхняя
г
р
а
ф
и
т
и
з
п
т
а
н
е
н
а
с
и
кривая)
и
р
о
в
кривая) при
Фенелонов)
а
н
н
о
20
й
с
л
и
к
а
г
е
л
а
ж
е
°С.(по
(
д
а
в
л
е
н
и
я
м
и
температурах
е
и
экспериментах
а
д
с
с
о
р
б
т
и
высокими
в
о
эти
в
и
н
и
з
к
и
х
различия
на
н
и
ж
н
я
я
становятся заметными: абсолютные
данным
величины
адсорбции
растут
с
увеличением давления, стремясь к некоторому пределу. Избытки
(максимумы на кривых) на изотермах проявляются при высоких
давлениях и относительно низких температурах (рис 1.13).
По оси абсцисс отложены
значения
относительной
фугитивности, f M P a , а по
ординате
удельная
адсорбция, ммоль/г
Детальная
и
разработка
подробный
метода
слоя
толщины,
конечной
был
А.И. Русановым
основе
И.
анализ
проведен
[8]. На
метода Гиббса
Русанов,
А.
используя
полные концентрацие компонентов в слое вывел термодинамические
соотношения для анализа поверхностных явлений
и
свойств
слоя
конечной толщины для плоских и искривленных поверхностей.
Из-за того, что метод Гиббса для твердых поверхностей имеет
формальные трудности, большинство исследователей предпочитают
пользоваться
другими
определением
определениями
адсорбции,
в
частности
«полное содержание». Хотя, само понятие «полное
содержание»-не достаточно строго, поскольку привязано к какому
либо модельному приближению, например, модели
адсорбции
Ленгмюра,
модели
(Брунауэра-Эмметта-Теллера),
полислойной
теории
монослойной
адсорбции
объемного
БЕТ
заполнения
микропор
заполнения
и
др.,
позволяющих
измерение
адсорбции.
«Полным
проводить
содержанием»
макропористых и мезопористых твердых тел
монослойной
адсорбция)
адсорбции
и для
микропорах.
(предельная
микропористых
Каждая
из
этих
для
гладких,
служит
адсорбция
тел
прямое
«емкость»
^-максимальная
-«емкость»
характеристик
адсорбции
требует
в
особого
методического подхода, на которых остановимся далее.
Метод полного
содержания
принципиально не отличается от
метода слоя конечной толщины, но опирается на
разработанные
методы определения «размеров» (емкости) адсорбционной фазы и
на уравнения для термодинамических
метода
полного содержания
известные
уравнения
были
потенциалов. В
получены
изотерм
рамках
практически
адсорбции
из
все
одно-
и
многокомпонентных объемных фаз.
По мнению А. М. Толмачава [10], активно
метод
полного
содержания,
предлагающего
"попытки использования
во
всех
случаях, включая адсорбцию из газовой и жидкой фаз на твердой
поверхности, только
Гиббса
избыточной
адсорбции
поставило
метод
в противоречие с активно развиваемыми методами прямого
измерения
адсорбции,
уравнении
величин
состояния
адсорбционной
опирающихся
представления,
участвуют
Поскольку,
в
например, простейшем уравнении
Фрумкин),
реальных
адсорбции.
используется
молекул.
не
Очевидно,
только
фазы
на
не
любой
модели
Ленгмюра,
(Фаулер,
или
Гугенгейм,
молекулярно-кинетические
избыточное, а
что
избыточные,
в
полное
межфазовых
а
все
число
процессах
адсорбированные
молекулы. К тому же, в применяемом
описания
адсорбционных
термодинамики,
никогда
в статистической физике для
явлений,
не
методе
учитывалось
статистической
«избыточное
число
молекул»".
Метод полного содержания. И так, метод полного содержания
- э т о метод слоя конечной толщины, но связанный к конкретными
адсорбционными моделями (Ленгмюра, Брунауэра-Эммета -Теллера,
теории
объемного
возможность
отдельной
фазы
и
определения
фазы
содержания
заполнения
и
«емкости»
адсорбционной
[8, 10, 14],
описании
др.),
из
которых
адсорбционной
системы.
Метод
вытекает
фазы, как
полного
основан на разделении системы на две
ее свойств,
как
гетерогенной
системы
с
использованием абсолютных концентраций компонентов в каждой
из равновесных фаз. Термодинамически этот метод менее строг,
чем
«метод
избытков»,
поскольку
основан
на
модельном
приближении, устанавливающем границу раздела между объемной и
адсорбционной фазами. Однако,
метод
Рисунок
1.13.
Изотермы
адсорбции
углеводородов и C O на активном угле
Nuxit п р и 293К.
Обозначения: о метан, • - этилен, А - этан, V - пропилен, •
- пропан, Ч - CO2. фазы. (по данным [10])
достаточно
2
информативен,
т.к.
позволяет
получать
J
характеристики адсорбционной фазы, что важно с практической
точки
зрения.
изотермы
Примером
адсорбции
полного
содержания
углеводородов
и
могут
служить
CO2 на активном
угле
(Рис.1.13).
Метод
позволяет
использовать
различные
молекулярные
конкретного
расположения
Значительная
часть
в компьютерных
модели,
молекул
современной
связанные
у
избытков
используется
информации и, как
заданием
поверхности адсорбента.
информации
представляется в рамках, именно, метода полного
метод
с
расчетах
об адсорбции
содержания,
для получения
критериальный, при
выборе
а
первичной
модели
для
перехода к методу полного содержания [10].
И так, для количественного выражение величин адсорбции на
практике используют следующие определения:
абсолютная
адсорбция
(а) - количество вещества (моль)
в
поверхностном слое, приходящееся на единицу площади поверхности
адсорбента (моль/м ) и адсорбция
или масса вещества (г)
(а) - количество вещества
в поверхностном слое, приходящееся на
единицу массы адсорбента (моль/г,
адсорбента
не
(моль)
известна.
Из
г/г), если величина поверхности
этих
двух
величин
а,
кроме
геометрической характеристики поверхности, дает дополнительную
информацию
о
природе
адсорбента
и
позволяет
сравнивать
различные адсорбенты между собой по «методу слоя
конечной
толщины h » [8] и методу полного содержания [10,14];
s
а = — = ^
s
sh
(1.54)
s
гиббсовская
(избыточная)
адсорбция
(Г-гамма)
-
избыточное
количество молей адсорбата в поверхностном слое определенной
толщины h
s
по сравнению с тем его количеством, которое бы
находился в адсорбционном объеме в отсутствие а д с о р б ц и и - «метод
Гиббса»
Г = (побщ - c V)s
v
В
случае
(
s
больших
поверхностном слое O
S
объемной фазе C V
)
= (V c
- c )s
s
= —
s
v
избытках
- —
s
= a - ch
концентрации
v
s
(1.55)
адсорбата
в
по сравнению концентрации адсорбтива в
( С >> C ), концентрацией адсорбтива C , следуя
V
V
(1.16) и (1.55), можно пренебречь, т.к. величины а « Г. Тогда
экспериментально определяют величину Г.
При исследованиях адсорбции
на поверхности
твердых
тел
проще измерять непосредственно избыточные или полные величины
адсорбции, поскольку измерения поверхностного натяжения сильно
затруднены из-за отсутствия простых методик, да и просто, из-за
неоднородности поверхности твердых адсорбентов. Для измерения
избыточных
предложено
состояния
величин
ряд
-
на
плоских
адсорбционных
уравнение
однородных
моделей
поверхностях
на основе
Менделеева-Клапейрона
для
уравнений
идеальных
систем, или уравнений типаВан дер Ваальса для реальных систем.
1.6. Модели адсорбции на основе уравнений состояния
адсорбционного слоя
Исходя из
особых термодинамических свойств поверхности
раздела фаз (адсорбционный слой), кроме широко применяемого в
экспериментальных
исследованиях
поверхностных
явлений
основного уравнения Гиббса и связывающего избыточную адсорбцию
Г с поверхностным натялением С и поверхностным давлением
л
(1.17-1.18, 1.47), на основе уравнений состояния было выведено ряд
уравнений
изотерм
адсорбции
(моделей
адсорбции)
таких,
как
уравнение Фольмера, Хилла—де Бура, Фаулера—Гугенгейма, Киселева
и др. При выводе авторы использовали
идеальных
систем
— уравнение
уравнение состояния для
идеального
газа
Менделеева-
Клапейрона (1.18) и для реальных систем — уравнение Ван дер
Ваальса.
Оба уравнения
(ограничения
для
термодинамическое
состояния
применения),
состояние
имеют
лишь
систем
свои
приближения
качественно
и поэтому
отражают
адсорбционные
уравнения (модели), вытекающие из уравнений состояния
иметь
аналогичные
приближения.
Это
желательно
будут
помнить,
используя то или иное уравнение на практике. Вообще
следует
заметить, что на сегодняшний день получено более сотни уравнений
состояния
различной
теоретических
сложности[15],
исследованиях
и
которые
для расчетов
используют
составоа
в
смесей
флюидов в самых различных технологических процессах. И каждый
из читателей, выбрав при желании одно из них, в принципе, может
вывести
новое
адсорбционное
получения подобных уравнений [1]
уравнение,
следуя
алгоритму
При исследовании адсорбции на жидких поверхностях удобно
измеряемым
параметром
является
натяжения а, а следовательно,
величина
поверхностного
величина двумерного давления к,
определяемая как
n = a-e
при
условии,
что
=
0
fr ,
= RTJr (lnc)
id i
(1.56)
id
начальная
концентрация
с =0.
Здесь
0
а 0
поверхностное натяжение чистого растворителя. Для твердых и для
жидких
поверхнностей
при
адсорбции
газов
концентрацию
с
заменяют на давление p . Из уравнения (1.56) следует, что при
положительной адсорбции величина к - отрицательна, что создает
условия
для самопроизвольного
распределения
молекул
по поверхности, достигающего
адсорбированных
со временем
состояния
термодинамического равновесия.
В
гомогенных
неэлектролитов)
системах
взаимодействие
между
(разбавленные
растворы
молекуламирастворенного
вещества не существенно. В таких растворах выполняется закон Генри
и
зависимость
поверхностного
натяжения
от концентрации
-
линейная.
о = о — ЪС или л = ЬС
(1.57)
0
Согласно уравнению Гиббса (1.18),
da
TRT
ас
с
Как следует из уравнений (1.56-1.58)
( 1 . 5 8 )
-
да/дс
равно b, и
уравнение (1.58) принимает вид
7г = TRT или тш = RT
(1.59)
где
площадь,
приходящаяся
на
мольрастворенного
соответственно;
G0 - площадь, приходящаяся на одну молекулу
со
вещества,
и тогда
ла)
0
Уравнение
(1.59-1.59а)
идеального газа: PV=nRT,
пленка
= кТ
(1.59а)
аналогично
уравнению
состояния
и очевидно, что в разбавленных растворах
адсорбированного
вещества
подчиняется
уравнению
состояния двумерного идеального газа.
Если
использовать
уравнение
(1.59-1.59а)
для
концентрированных растворов, то в нем можно сделать поправку на
размер самих молекул [1], тогда это двумерное уравнение примет вид
л(а) - (X)Q) = nRT
(1.60)
где а> - исключенная площадь в расчете на один моль
вещества;
n - количество молей адсорбата.
0
растворенного
Одной из форм уравнения Менделеева- Клапейрона является
уравнение для осмотического давления: 7 V= nRT. Напомним, что
os
осмотическое давление обычного раствора — это давление, которое
необходимо
приложить
к
раствору,
чтобы
давление
растворителя увеличилось до давления паров чистого
паров
растворителя
(см. в общей химии законы Рауля и Вант Гоффа), тогда для
двумерного аналога
7^05,5^
= nRT или n
0s>s
= c RT
(1.61)
m>s
где, 7 - осмотическое давление в поверхностном слое;
oss
V - объем самого адсорбционного слоя;
s
c
m , - молярная концентрация вещества в поверхностном слое.
s
Если толщина этого слоя h известна, то давление 7 в пленке равно
s
произведению
осмотическому
давления 7t ,
os>s
приложеного
к
полупроницаемому барьеру (мембране) на h . Если вести эксперимент
s
с разбавленными растворами (например, методом Вильгельми по а,
или на весах Ленгмюра по 7i[1]), то получая изотерму 7t =j(c )
os
можно
m !
приближенно оценивать молярную массу вещества, распределяемого
в поверхностном слое.
Естественно,
гомогенных
применяя
систем
уравнение
и заменяя
в
нем
Ван
дер
объмное
Ваальса
для
давление p
на
поверхностное п„ а объем V на величину поверхности со, то получим
полный двумерный
аналог
уравнения Ван дер Ваальса, в котором
учитывается собственнаяплощадкамолекул (исключенная площадь) и
/
а \
V +
ЯГ
я
—
= ^
и
л
и
7 1
=
Ь
Э
(
1
—
Э
)
аЭ
-j-Г
—
2
(
1
.
6
2
,
1
.
6
2
б
)
где а - к о н с т а н т а дальнодействующего двумерного притяжения адсорбат адсорбат;
а>=1/Г - средняя площадь поверхности, занимаемая одной адсорбированной
молекулой;
Ь=1/Г - константа отталкивания, равная площади со , занимаемой молекулой в
предельно заполненном монослое со—>а> ,
(со-а> ) - площадь поверхности, не занятой молекулами адсорбата;
0=Г/Г =Ь/а>, ( Г и Г - соответственно, поверхностная концентрация молекул
адсорбата и «емкость» монослоя).
т
0
0
0
т
т
Формально
величину
адсорбции
можно
оценить
по
поверхностному давлению адсорбированного слоя или уменьшению
свободной
поверхностной
энергии жидкости
или твердого
тела,
непосредственно связанных с интегралом (1.56). С другой стороны,
рассматривая адсорбированный слой как двумерную пленку типа
монослойных
пленок на жидких поверхностях (1.59-1.62) через
соответствующие
адсорбционные
уравнения
уравнения,
состояния,
удовлетворительно
экспериментальные изотермы адсорбции.
можно
получить
описывающие
Как
указано
подобных
выше,
уравнениям
существует
ряд уравнений
для идеальных
состояния,
(Менделеев-Клапейрон)
и
реальных (Ван дер Ваальс) газов в равной мере применимых как к
газам, жидкостям и твердым телам, так и к их двумерным аналогам.
Простейшие
из
этих
уравнений
состояния
используются
для
получения соответствующих изотерм адсорбции газов (паров) на
жидких, твердых поверхностях и изотерм адсорбции из растворов.
Идеальный
адсорбированного
результате
двумерный
слоя
получаем
представляющего
газ.
В
описывается
линейное
этом
случае
уравнением
уравнение
состояние
(1.59—1.59а).
изотермы
собой адсорбционный слой в виде
В
Генри,
идеального
«двумерного газа».
Кр
н
где К — константа
н
заполнения
= в
адсорбционного
поверхности
(1.63)
равновесия
p—равновесное
Генри,
давление.
6—степень
Уравнение
описывает состояние адсорбированного слоя лишь при очень низких
степенях заполнения поверхности, т. е. в случае очень разреженного
двумерного газа. При более высоких степенях заполнения в это
уравнение необходимо ввести поправку на собственную площадь
молекул
адсорбата (1.60). Используя уравнения
(1.60) и (1.56),
представленные в виде,
1С
l n p
=
w }
С
a
d
n
=
de
}e(T-ey
c учетом, что в = у получено уравнение изотермы адсорбции [1],
представляющего
собой адсорбционный слой в виде
идеального
«двумерного газа», но уже с учетом площади, занимаемой собственно
молекулами адсорбата
Кр =
т4^
е(1-Щ
(1-65)
или в логарифмической форме
е
е
InKp = In
+
(1.65а)
Аналогичное уравнение получено Фольмером в виде
InKp = Inn + —
(1.656)
удобное при изучении адсорбции из растворов по а или %. Здесь К и
b-консганты адсорбции, зависящие от природы адсорбата.
Реальный двумерный газ. Состояние
адсорбированного слоя
описывается уравнением (1.62а - 1.62б). В этом случае учитывается
дальнодействующее
двумерное
притяжение
адсорбат
-
адсорбат
через константу a - латеральные (боковые) взаимодействия, а через
Ь=1/Г т
отталкивание. Принимая все допущения и подстановки,
сделанные
в
(1.62б)
необходимо
продифференцировать
это
уравнение, чтобы подставить его в уравнение Гиббса, записанное в
форме dine = dlnp -
при условии е = ТЬ, придем к известному
уравнению Хилла - де Бура [16]
е
к
г»
=
\n(pK )
H
1-е
/
е
х
е
= In-—-
р
е
\
2ае
-
{т-е) т
е
2ае
+-—--——
или в относительных давлениях для паров
(
1
-
6
6
)
(1.66а)
^
1
= (K
)- i — e
e x p
HVO
[т~в
-
Клат
6
в]
(1.66 )
где К — константа Генри учитывает межчастичное взаимодействие адсорбатадсорбент,
а константа К =2а/ЬЯТ
характеризует межмолекулярное
взаимодействие
адсорбат-адсорбат,
р—текущее
довление,
p —даление
насыщенного пара п р и данной температуре.
н
лат
0
Уравнение
(1.66—1.66
мономолекулярной
поверхности.
а,б)
— это
нелокализованной
уравнение
адсорбции
на
однородной
Если латеральные взаимодействия малы К
лат
уравнение Хилла - де Бура переходит в уравнение
уравнение
изотермы
мономолекулярной
нелокализованной
= 0, то
Фольмера —
адсорбции
(1.65а,б).
Общий вид семейства кривых для уравнений типа(1.65а, б)(1.66а,
б) подобен тому, который изображен на рис. 1.14. Штриховой линией
0,01
1
0,1
10
кР
Рисунок 1.14. Изотермы адсорбции, соответствующие уравнению состояния
двумерной адсорбированной фазы типа уравнения Ван-дер-Ваальса. Здесь
константа с=К =2а/ЬЯТ
[1].
лат
(субмонослойная
область)
показан
фактическийход
изотермы
в
области конденсации двумерного газа в жидкость. Приведенные
уравнения
довольно
хорошо
описывают
отдельные
экспериментальные изотермы адсорбции в субмонослойной области.
Так, Росс и Уинклер [17], выбрав уравнение состояния в виде (1.62,
1.62б) установили, что в области 0,1 < в < 0,5 адсорбция азота на
саже с однородной поверхностью
при 77,8 К хорошо описывается
уравнением Хилла-де Бура (1.66а, б).
Существует
множество
вариантов
уравнения
состояния
неидеального двумерного газа [1]. Например, с поправкой для ж,
взятой в виде а/со3
[и + ^ ) (о) - о) ) = RT
(1.67)
0
получено уравнение изотермы, отличающееся от уравнения Хилла-де
2а
2
Бура только в при К
= —
лат
в
2
Г в
2ав 1
или в линейной форме
в
в
К в2
(1.676)
InKp = In+
лат
1 - в
1- в
Если уравнение состояния берут с поправкой для ж в виде а/со
л
в
3
и для со с поправкой соо/со
•°) = RT
(1.68)
О)
то уравнение принимает форму
в
в
exp
1-в
т
2
2ав
в
(1.68а)
ьяг
-I
в
=
1 - в
в
+
л
1- в
лат
в
(1.686)
Уравнения (1.66б - 1.68б), представленные в линейной форме, удобны
для определения значений констант K и Ki .
H
Анализ величин К .
лат
at
показывает [16], что они могут изменяться
(рис.1.12) в диапазоне 0 + 10, где 0 -И соответствуют очень слабым, а
область
значений
взаимодействиям.
=10
Обычно,
-
сильным
с ростом K
lat
межмолекулярным
изотермы
обращаясь выпуклостью к оси давлений. При K =6
изгибаются,
сначала также
lat
выпуклы, а затем становятся вогнутыми к оси давлений, напоминая
по виду кривые состояния для трехмерных газов при температуре
выше критической. И далее при 7-10 имеют участки, отвечающие
мета-стабильному
область),
неустойчивому
аналогично
состоянию
получаемым
на
(субмонослойная
диаграммах
состояния
трехмерных газов ниже критической точки в области их конденсации
в жидкую фазу. Если исключить возможность пересыщений, то,
исходя
из
формы
скачкообразный
значениях
рост
давления.
полученных
адсорбции
Этот
кривых,
при
скачок
следует
некоторых
соответствует
конденсации сорбата, а область скачка -
ожидать
постоянных
двумерной
сосуществованию двух
поверхностных фаз - "двумерного газа" и "двумерной жидкости".
Аналогичные расчеты показывают, что увеличение значений K
lat
Р
0
смещает зоны двумерной конденсации вправо - в область более
высоких давлений в газовой фазе.
Все
рассмотренные
изотермы
с
двумерными
фазовыми
переходами рассчитаны для адсорбции на однородной поверхности,
наиболее характерной для границы жидкость-пар, например, для
адсорбции анионо-активных и катионо-активных ПАВ. В частности,
для алифатических аминов, применяющихся в больших масштабах в
качестве коллектора при флотации калийных руд или солевых форм
алифатических
сульфокислот,
применяющихся
как
детергенты
(моющие средства).
Для твердых тел достаточно однородня поверхность может быть
получена в редких случаях, например, на графитированных сажах и
монокристаллах,
либо
на
гомотактических
(лоскутковых однородных и гомогенных)
поверхностях
в виде
мозаики
на
участках поверхности.
Основное
достоинство
рассмотренных
выше
уравнений
применительно к адсорбции на реальной неоднородной
плоской
поверхности пористых тел заключается, прежде всего в том, что они
дают
достаточно
достоверную
качественную
картину
адсорбционного процесса, где при малых заполнениях важнейшей
энергетической характеристикой является константа Генри, а при
больших заполнениях проявляется межмолекулярное взаимодействие
адсорбат
-
адсорбат,
и
ассоциативная
адсорбция
может
сопровождаться двумерными фазовыми переходами.
Если на минуту
переключиться
с двумерного
газообразного
состояния на трехмерное в виде растворов, и, например, в результате
измерений понижения температуры замерзания раствора AT, будет
обнаружено хорошее соблюдение закона Рауля, то раствор близок к
идеальному (аналогично закону Генри), описываемому в рамках
чисто физической модели. Когда это установлено, для физики
явление
это
можно считать достаточным. Однако в реальных системах
наблюдается отклонение от аддитивности как признак проявления
химизма. И тогда, в случае неидеальных систем, как правило,
используют
аддитивные
неидеальность
в
виде
приближения,
коэффициентов
вводя
поправки
активности
на
компонентов
раствора. Если при этом участвует реальная твердая фаза с ее
неоднородностью и дефектами структуры, то можно
дополнительные
квазихимические
использовать
уравнения,
учитывающие
ассоциацию точечных дефектов в твердом теле. Однако, отклонение
от
идеальности,
как
результат
сложных
межчастичных
взаимодействий, в реальных гетерогенных системах можно провести
иначе.
Макаревич Н.А. [18] предлагает новый подход в получении
уравнений
изотерм
адсорбции
на
основе
известных
уравнений
адсорбции (адсорбционных моделей) путем введения в эти уравнения
ассоциативно-ионизационного множителя ias (фактора неидеальности
g), при этом сохранив все достоинства и приближния, присущие
оригиналу. Что касается рассматриваемых выше изотерм адсорбции,
вытекающих
из
уравнений
состояния,
то
можно
рассмотреть
некоторые из них, в частности, уравнение изотермы ассоциативнодиссоциативной адсорбции [19], пригодное как для адсорбции паров
на границе растворов неэлектролитов и электролитов, так и на
твердых
поверхностях
рассмотренных
в данном
[19].
Принципиальным
разделе
1.6
уравнений
отличием
от
стало то,
что
Макаревич Н.А. ввел в уравнения состояния, предложенный им ранее
[18], универсальный ассоциативно-ионизационный
ias (фактор неидеальности g) отслеживать
одновременно
множитель А И М
коэффициент, который способен
в
системах
любые
взаимно
противоположные процессы (+) <-> ( - ) : притяжение <-> отталкивание,
ассоциация о
случае,-
диссоциация, испарение о
упорядочение
конденсация,
(ordnung-(3ord)
и
в общем
разупорядочение
(nonordnung-onord) элементов системы
t
= 1- a
a 5
он же-обобщенный
a 5
+ а ; О - 1)
фактор неидеальности
9 =
1
—
+
/?ord
(1.70)
систем GNF
( 1 . 7 0 а )
°nord
где ias =
o Оv a s
Pord
o„ordj
g;
степень ассоциации;
степень ионизации;
число ионов, на которое распадается нейтральная частица (молекула);
- доля (вероятность) упорядоченных элементов системы;
- доля (вероятность) разупорядоченных элементов системы.
В общем случае, под множителем
показывающая,
во
(концентрация)
ассоциации
сколько
частиц
реальной
и диссоциации
числом (концентрацией)
не вступивших
раз
в эти
(ионизации)
единичных
состоянии
- отношение
N% (реальная
практике
сравнением
система
значения
изотерм
например, Г =/(с)
экс
понимается
величина,
изменится
общее
системе,
в результате
по сравнению
число
их
с
исходным
частиц N в идеальной
системе,
( 1 . 7 1 )
= ^
числа
(молекул) - идеальная система
На
as
превращения
^
Проще, las^g
i
частиц
c N i)
rea
Ndeai,
(молекул)
к исходному
т.е. ias^g=
АИМ^ОТ
адсорбции:
в
равновесном
числу
частиц
Nrea/Ndeai-
легко
экспериментально
определяются
полученной,
и теоретически построенной изотермы
Г =/(с),
теор
или
а =/(р)
и
экс
а =Лр)
при
теор
одинаковых
фиксированных
переменных, входящих в уравнение.
Автор
[18-19]
показал,
что
широко
применяемые
в
термодинамических расчетах множители - коэффициенты активности
у и фугитивности ф Льюиса, осмотический коэффициент Бьеррума Гуггенгейма ф, изотонический коэффициент Вант Гоффа i, а так же
коэффициент сжимаемости z являются частным случаем АИМ.
В
отличие от формул для у, ф, i и z в формулу для А И М входит
характеристика, от которой напрямую зависит отклонение системы от
идеальности - степень ассоциации (кластеризации) a
as
Для начала при
[18].
выводе изотерм адсорбции с А И М (GNF),
выбрав для записи g, воспользуемся уравнениями состояния (1.59) и
(1.60), представленными в виде
n = gTRT или nod = gRT
(1.72)
n((x) - о) ) = gnRT
(1.73)
0
И по тому же алгоритму
[9, 13], по которому
получены
изотермы Генри и Фольмера запишем соответствующие изотермы
адсорбции
с ассоциативно-ионизационом
множителем
(фактором
неидеальности)
1/
Кр з
н
1/
= е
1
inKp ' а = in
1
InKp /9
уравнения
получены
=
(1.74)
е
+ 1 - е
+ 1-е
- ^ла^е
2
с допущением, что при низких
(1.74а)
давлениях
(концентрациях адсорбтива) g=const по тому же алгоритму, что и
оригинальные - Генри, Фольмера, де Бура [16]. В действительности,
g-величина
переменная,
адсорбтива.
В
этом
неидеальности
-
Следовательно,
т.е.
принципиальное
он
в
изменяется
отслеживает
каждом
с
ростом
давления
преимущество
изменения
конкретном
случае
в
фактора
системе.
g=f(p)=f(c),
по
возможности, можно представить в аналитическом виде, что позволит
аппроксимировать
экспериментальную
максимальной
достоверностью
математические
компьютерные
изотерму
2
R,
адсорбции
используя
редакторы,
с
стандартные
например,
в
Excel,
MatCad, Matematica и др.
Практически,
чтобы
воспользоваться
предлагаемыми
уравнениями для обработки экспериментальных изотерм адсорбции
необходимо:
линейной
1)
форме
максимальной r
m
выбрать
уравнение
без множителя
изотермы
g или
i;
as
в
оригинальной
2) найти
величину
монослойной адсорбции и рассчитать 6=Г/ r ; 3) по
m
линейной зависимости найти K , если по Хиллу де Буру, то и К ;
H
построить
теоретическую
зависимость
Г(6)=Дс) с заданными К
(и К
н
экспериментальную
лат
изотермы
значениях p (для паров р/р ),
0
л а т
изотерму
T(6)=f(p)
4)
или
) ; 5) сравнить теоретическую и
адсорбции
при
найти g=f(p/p )
0
Excel, подставить в выбранное уравнение
разных
текущих
и аппроксимировать в
g=f(p/p )
0
вместо g и
уравнение изотермы с фактором неидеальности для исследуемой
системы
готово;
6)
снова
построить
теоретическую
кривую
зависимости T(6)=f(p), но уже по полученному уравнению изотермы,
и сравнить с экспериментальной изотермой.
Поскольку, введение А И М (GNF) в классические уравнения,
пригодные для описания идеальных систем, значительно расширяет
возможности
использования
адсорбционные
реальных
классических
уравнений
уравнения) с новым множителем для
систем,
систем,
читателю
предлагается
(включая
описания
детальнее
ознакомиться с этим термодинамическим фактором.
Приложение к разделу 1.6. Ассоциативно-ионизационный множитель как
фактор неидеальности систем.
К ассоциированным системам не п р и м е н и м ы классические законы для
идеальных газов и жидкостей [20,21]. Применительно к
ассоциированному
раствору возможно рассмотрение двух случаев: первый - когда агрегаты частиц
выделяются как отдельный компонент раствора[18]; второй - не выделяются.
В первом - раздельно вводятся концентрации мономерных частиц и
агрегатов (димеров, тримеров и т.д.). Тогда отклонение системы от идеальности,
изучаемое с п о м о щ ь ю
размеру) агрегата,
метода, чувствительного
к свойствам (например,
к
определяется взаимодействием растворенных частиц друг с
другом под действием потенциальных сил, т.е. через дальнодействующие силы
[22].
Во втором - отклонение системы
числом
частицы
от идеальности определяется только
растворенных частиц (мономеров, димеров, тримеров и т.д.). Все
независимо
от
их
природы
и
размера
будут
называться
ассоциатами[ 18,19].
Мерой
отклонения
системы
от идеальности
могут
выступать
две
характеристики: коэффициент активности y , отнесенный безразлично ко всем
as
частицам и степень ассоциации
a.
as
Рассмотрим ассоциированный раствор неэлектролита (первый
случай),
известный в коллоидной х и м и и [22]. Для этого случая допускается, что числа
агрегации п постоянны, а сами агрегаты N
ю
состоят из мономерных частиц
n
одного сорта N , общее количество которых в процессе ассоциации не меняется,
j
тогда по закону сохранения масс
N = N? + п Ы
±
ш
п
(6а)
N = N f+nJNn-
(6а)
или через концентрации
mj = mj + n m
w
(66)
n
0
где N i или m - число или концентрация свободных мономеров, не в о ш е д ш и х в
1
агрегаты.
Из (6б) вытекает определение «числа агрегации»
= ^
и степени агрегации a ,
as
w
(7)
[22]
a
(
as,w = ~ "
7
а
)
В дополнение к предлагаемым определениям [22] от себя добавим, что степень
агрегации можно представить и в таком виде:
1 — т
0
(
=
7
6
)
Из (6 -7) и далее следует, что характеристики, которым приписан индекс " со",
являются
средневесовыми,
точнее,
среднемассовыми
величинами,
т.е.
их
экспериментальное определение возможно только методами, чувствительными к
размеру частиц, например, с п о м о щ ь ю светорассеяния.
В теории ассоциированных растворов второй
растворенного
вещества,
включая
единичные
случай,
частицы
когда все частицы
и агрегаты
являются ассоциатами (коллигативные свойства) не рассматривается.
частиц,
Поэтому
для второго случая автором [18] даны не тривиальные определения степени
ассоциации a
as
и
числа ассоциации n, а именно, сохраняя все принятые
приближения и допущения [22] о том, что числа ассоциации ппостоянны, а сами
агрегаты Nn состоят из мономерных частиц
одного сорта, общее количество
которых в процессе ассоциации не меняется, по закону сохранения масс:
= (т
0
+ m )n = m
n
a s
n
(8)
где m/- концентрация свободных мономеров, не в о ш е д ш и х в агрегаты;
m,
n
m
- общая концентрация ассоциатов, включающая кроме концентрации
as
агрегатов;
m - концентрацию всех свободных единичных частиц
n
При
использовании
методов
осмометрии,
m/.
крио-
и
эбулиоскопии,
изотермической дистилляции, изопиестического метода и др., чувствительных
только
к
числу
рассматривать
частиц
в виде
в
растворе,
ассоциатов.
все
частицы
в растворе
следует
«Число ассоциации» для этого случая
определено как
п =
—
=
- л -
1
(9)
Обратим особое внимание на следующее определение. Степень
определим так, чтобы при m = m
i
степень
ассоциации
независимо
as
системы
a=
0, а п р и m »m a =l.
as
i
(газа,
раствора),
от их природы
являются
ассоциатами
выражается
отношением
разности
между
единичных
частиц
ассоциатов
N
в которой
состояние)
частиц
все
(коллигативные
числом
N
as
частицы
свойства),
(концентраций)
и числом
i
a
Таким образом,
as
(сумма мономеров и агрегатов) к числу
as
(мономерных)
(идеальное
as
ассоциации
исходных
(концентраций)
исходных
единичных
N:
i
« =^ = 1 — ^
(10а)
as
или через концентрации
a =—
^ = 1 — ^
as
т
т
1
1
Во втором случае индекс «со»
асоциированного
10б)
опущен и в дальнейшем все характеристики
раствора,
согласно
этому
подходу,
будем
называть
«численными». Сравнивая, например, (7а,б) и (10а,б), видим, что определения
степеней ассоциации принципиально отличаются:
по (7а,б) для среднемассовых
равна
доле
отношению
величин
агрегатов,
образованными
разности
между
a , — степень ассоциации раствора
as 0
мономерными
исходным
числом
частицами,
мономерных
и л и же
частиц
0
неэлектролита M i числом свободных м о н о м е р о в ^ (не вошедших в агрегаты) к
общему числу исходных молекул неэлектролита N;
по (10а,б) для среднечисленных
величин
a — степень ассоциации раствора,
as
в котором все частицы, независимо от их природы являются ассоциатами, равна
отношению
неэлектролита
разности
между
исходным
N i числом ассоциатов N
числом
мономерных
частиц
к общему числу исходных молекул
as
неэлектролита N.
Из (9-10) следуют простые, но информативные соотношения:
(
m
= mi 1
as
— a)
1
as
(11а)
(11б)
п =
1
—
а
П—1
(11в)
O-as =
П
П р и необходимости все численные характеристики ассоциированных растворов
можно выразить через соответствующие массовые и наоборот:
a
as
=
- =
(12а)
( 1 2 б )
n
А
теперь
рассмотрим
^
w
—
раствор
(12в)
электролита,
в
котором
может
одновременно протекать и ассоциация, и диссоциация (ионизация) частиц. Для
таких
систем
(множитель)
число,
и
i .,
as
предложен
коэффициент
частиц)
конкурентных
процессов:
ассоциацию
и
.
Определение:
показывающая,
в общем случае под множителем
во сколько раз изменится
Nj, в реальной
системе,
по сравнению
с исходным
идеальной
[18,19] -универсальный
одновременно отслеживающий в системе результат (общее
концентрацию
диссоциацию
АИМ
системе,
в результате
числом
не вступивших
i
as
величина,
общее число (концентрация)
их ассоциации
и диссоциации
(концентрацией)
в эти
понимается
единичных
частиц
(ионизации)
частиц
Nj
в
превращения.
N.
—
to,
ж
Для ассоциированной системы (газа, раствора) неэлектролита, исходя
из коллигативных свойств растворов Nj=N ,
согласно
as
(13) и (10а),
следуют
формулы для ассоциативного множителя (АМ):
N
ta—^T
( 1 4 а )
t
ИЛИ a — 1 - a
as
(14б)
Используя выражение (12а), А М , так же легко определяется и через
степень агрегации а
т
1
=
Для
ассоциированного
-
М
раствора
п
.
-
1
)
электролита
(15)
необходимо
записать,
подобно изотоническому коэффициенту Вант Гоффа i (5), свое выражение
коэффициента i , учитывающего общее число частиц в растворе: свободных
a s
недиссоциированных частиц и свободных ионов, а также ассоциированных
частиц и ионов. В ы в о д ы формул для i , включающих a
a s
as
и л и а , м о г у т быть
ю
проведены согласно закону сохранения массы частиц в ассоциированном
растворе электролита для брутто молярной концентрации электролита [19],
либо путем рассмотрения реального раствора слабого электролита с общих
позиций теории электролитической диссоциации и теории ассоциации [20,21].
И так, по определению изотонического коэффициента Вант-Гоффа
[21],
суммарное число частиц после диссоциации
N^ — iN
(16)
где i - изотонический коэффициент Вант-Гоффа.
В результате ассоциации суммарное число частиц уменьшится и станет
равным N j
a s
%
= % i — JVa
a s
as
= iiV — JVa
(
= JV i — a
as
)
(17)
a s
Следуя определению для ассоциативно-ионизационного множителя i
= N;
a s
a s
(13): i
a s
/ N с учетом (5) и (17), получим
i
)
= 1 + a^i; — 1 — a
a s
(18)
a s
Далее подстановкой (12а) в (18) приходим к выражению
;
= 1 + а,(г;—1)—
а 5
(19)
Здесь, как и в (5) a - степень диссоциации, v-число ионизированных частиц, на
i
которое распадается молекула электролита.
Из (12а), (14б) и (15), а также (18) (19) вытекает важное следствие, что
расчетные значения i
ш' , получаемые методами чувствительными к числу
a
аз
частиц через a , и значения i ш , получаемые методами чувствительными к
as
a
аз
размеру (природе) частиц через a и n ,
w
АИМ
является
универсальным
совпадают.
w
термодинамическим
множителем.
С
его
помощью можно отслеживать изменение концентрации частиц в растворе в
результате действия конкурентных по своей природе процессов -
ионизации
(распада молекул на ионы) и ассоциации (увеличения размеров молекул и ионов
в результате физического или химического взаимодействия между собой и
другими частицами). Однако, из (18) и (19) наглядно видно, что в реальных
системах в результате
диссоциации,
действия конкурентных
значение
АИМ
может
процессов -
оказаться
ассоциации
равным
и
единице.
Подтверждением тому может быть множество примеров, в частности, поведение
концентрированных коллоидных растворов электролитов становится идеальным
при добавлении к ним простых электролитов (типа NaCl) за счет сжатия
двойного электрического слоя, образованного мицеллами [22].
Ассоциативно-ионизационный
экспериментально
Р
о с м э к с
множительможно
найденные
величины
, д а в л е н и я насыщенного пара А Р
кипения А Г
к и п э к с
э к а
найти,
сравнивая
осмотического
давления
, температур кристаллизации А Т
и
з а м э к с
с теоретическими, в ы т е к а ю щ и м и из законов Вант-Гоффа и
Рауля [6,7] и др.
Р
.
f
_
as
=
i
_
ДР
' осм.экс. _
р
=
Р
_
Р
±
о с м
, А Р , АТ ,
зам
АТ
к и п
ДР
АР
осм.экс. _
as
где Р
экс _
ДТ
ДТ
^зам.экс. _
^кип.экс. _
=
экс. _
_
~
АР
ДТ
AT
ДТ
АТ
зам.экс. _
_
- - зам.
i
L
=
кип.экс. _
АТ
L
осм
=
гпг\\
(
L
i
(20)
,
АТ
)
""
(
)
L
- - кип.
- теоретические величины.
Тогда для растворов электролитов основные законы выражаются следующим
образом. Законы Рауля [20,21]:
топометрический АР = i P °N ,
as
криоскопический
АТ
з а ж
1
2
= i Km,
as
(21)
ДР = i P ° W
as
1
(22) ДГ = i / O n
a s
2
(21)
(22)
эбулиоскопический
Закон
АГ
к и а
= i iEm.
(23) AT — i iEm
as
Вант-Гоффа[20,21]:
осмотический
^осм — i cRT
Изотонический
(24)
коэффициент
универсального
ассоциативно-ионизационного
as
(23)
as
Вант-Гоффа
Р
=
осм
является
i cRT.
(24)
as
частным
случаем
множителя. Частным
будут коэффициент активности у и осмотический коэффициент ф,
случаем
связанные
между собой приближенным выражением [20]:
lny+
ф —1+^- -±^
ln(1-N*)
J
(25)
w
v
J
здесь N* - мольная доля электролита.
Резюме: коэффициенты активности отражают природу межчастичных
взаимодействий (обусловленных действием потенциальных сил); осмотический
коэффициент отслеживает число частиц в системе, связанное с межчастичными
взаимодействиями,
но не связанное
с ионизацией частиц;
изотонический
коэффициент - число частиц, связанное только с ионизацией; универсальный
ассоциативно-ионизационный множитель отслеживает общее число частиц в
системе, связанное и с
межчастичными взаимодействиями, и с ионизацией
(диссоциацией) частиц.
Пример: пусть в единице объема раствора находится 100 единичных
молекул растворенного электролита, условная мольная доля которого составляет
0,35.
В результате
агрегации
и диссоциации
этих
молекул
образовался
ассоциированный раствор, в котором стало, например, мономеров-33, димеров0
15, тримеров-5, тетрамеров-3, пентамеров-2, т.е. N =100, N = 3 3 , N =25, N = 5 8 ,
1
1
n
из н и х часть распалась на ионы, например, в мономерах-10,
тримерах-8, тетрамерах-5, пентамерах-5 (в сумме
40).
определениями для степеней агрегации а и а с с о ц и а ц и и a
ю
a s
as
димерах-12,
В соответствии с
и для чисел агрегации
п и ассоциации n получим: а = 0 , 6 7 ; n =2,68; a =0,42; п=1,72-среднее значение;
ю
ю
а =0,40; А И М t
1
as
ro
—1+ a - a
t
as
a
as
—1+ a - »
( n
t
»
- 1 )
— 0,98 t — 1 + a — 1,40,
t
n
a>
осмотический коэффициент ф — 1 - ^
(i
a sm -N )
e
a
2
— 0,7, коэффициент активности у± —
— 0,834 Д л я сравнения, коэффициент активности по формуле (25)
равен 0,761, т.е. д л я условно принятой мольной доли электролита N =0,35
2
погрешность определения у± по (25) составит 8,74%. Если принять N =0,2, то
2
погрешность определения у± по (25) у ж е составит 0,98%, а д л я N = 0 . 1 - всего
2
0,21%. ^ - м о л ь н а я доля электролита. Д л я рассматриваемого гипотетического
ассоциированного раствора средняя степень полидисперсности растворенных
частиц s — — — 1,56 .
п
Ассоциативные множители (18)
и (19) - важные
термодинамические
характеристики реальных систем неэлектролитов и электролитов и как
отклонения реальных системах
от идеальности четко расставляют
мера
методы
исследования в иерархии при изучении этих систем. Как видно из физической
сущности и универсальности А И М его действие может быть распространено не
только на растворы. Для этого приведем формулы (18), (19) к общему виду
и
введем в них новые обозначения. П р и рассмотрении любых противоположно
протекающих процессов, например, из (18) вытекает формула (26). В ней
- на jB
заменена на g,
ord
и a(v-1)9
=
1
на
—
i
as
a„ .
ord
a
/?ord +
nord
(26)
(26)Условимся называть g - обобщенный фактор неидеальности систем (GNF),
РоЫ - мера упорядоченности (доля упорядоченных элементов) системы, a„
-
ord
мера неупорядоченности (доля разупорядоченных элементов) системы. Эти два
терма в (26) можно трактовать иначе:
- усредненная суммарная доля
fi
ord
(вероятность состояния) упорядоченных (связанных между собой) элементов
системы,
-
an
ord
разупорядоченных
усредненная
суммарная
(несвязанных
между
доля
собой)
необходимости, вместо средних величин fi
и a„ ,
ord
ord
(вероятность
элементов
состояния)
системы.
При
для учета полидисперсности
состава системы с элементами i и j сорта корректно записывать: /? =
, а
ord
+
£=l - 2 &
Фактор
g
является
важнейшей
Z
a
i
27
;
( )
относительной
термодинамической
характеристикой, связывающей идеальную и реальную модели л ю б ы х систем, в
которых можно выделить два конкурентных (противоположных по знаку и
действию)
процесса: порядок <-> хаос; объединение <-> распад; притяжение ( - )
<-» отталкивание (+); уплотнение <-» разрежение; сжатие ( - ) <-» расширение (+);
сжижение
<-» разжижение;
(выделение),
кластеризация,
иррадиация,
поглощение,
растворение;
рекомбинация)
концентрирование
ассоциация
<->
<-» рассеивание
(агрегация,
диссоциация
молизация,
(ионизация);
развертывание<-»свертывание; конденсация <-» испарение; кристаллизация <-»
плавление; смачивание <-» несмачивание; минимум <-» максимум; симметрия
(цис-)<->
асимметрия
(транс-);
ламинарность
<-» турбулентность;
и
т.
д.
Численное значение g будет зависеть от того, какой из конкурентных процессов
преобладает и изменяться в интервале:
0<g>1, при g = 1 поведение элементов
реальной системы будет таким же, что и идеальной, прототипом которой она
служит.
Физический смысл g, как относительной
характеристики реальной Ф* и
Ф*
идеальной
д = — g= Ф*/Ф
Ф систем:
виден,
например,
из
рассмотрения
уравнений состояния идеального
Ф <-> рV = пRТ
(28а)
и реального газа
Ф* <-> p*V = n*RТ = gnRТ
(28б)
изохорно-изотермического процесса. Здесь, соответственно, Ф и Ф* — функции
состояния, P и P* — давление, n и n* - количество молей идеального и реального
газа;
V,
R,
T
-
объем,
P*V
универсальная
газовая
постоянная,
абсолютная
П*
температура. д = — = — — обобщенный фактор (коэффициент) неидеальности,
как функция относительной работы реального и идеального газа, а также
относительного реального и идеального количества молей в системе. Количество
молей в системе может меняться в результате протекания реальных процессов
межчастичного
взаимодействия
(ассоциация,
кластеризация,...,
т.е.
упорядочения элементов системы) и межчастичного отталкивания (диссоциация,
распад,.
т.е. разупорядочения элементов системы). В реальных системах g
отслеживает конкурентные (противоположные по знаку) процессы: порядок <г->
хаос;
т.д.,
притяжение
и
(—) <-+ отталкивание
определяется
(+); сжатие
(—) <-+ расширение(+)
отношениемфактического
(реального)
и
числа
упорядоченных и неупорядоченных элементов системы к теоретическому.
Таким образом, фактор g— полный эквивалент i
as
как универсальный
(обобщенный)
множитель
следует рассматривать,
с помощью
которого
(легко
провести построение общей теории реальных систем) на основе классических
уравнений,
с их ограниченными
возможностями.
Идея метода
построения
теории реальных систем (процессов) сводится к простой процедуре — к введению
фактора g в известные классические уравнения физики для идеальной систем с
последующим
описанием
соответствующего
поведения
модифицированного
реальных
систем
уравнения.
При
способный отслеживать любые отклонения от идеальности,
с
помощью
этом
фактор
g,
может принимать
как постоянные, так и переменные значения, выполняя роль функции от числа
(концентрации)
элементарные
макрочастицы,
элементов
частицы,
системы.
молекулы,
Элементами
ионы,
системы
ультрадисперсные
могут
быть:
частицы
и
а в космическом масштабе — космическая пыль, планеты,
звездные системы и даже галактики.
Множитель g может быть введен не только в уравнения, отвечающим
законам Генри
д Em);,
Вант
=
Гоффа
(Росм.эксп
, Рауля (LP = дP%N , ДГзам. = дKm, АТ
(Росм = 9 cRT),
Гиббса
Г =
ттйг\ ,
9^осм)
2
КИП
5
9RT
VdMc)
TiV
=
где
ст-поверхностное
натяжение раствора, моно и полимолекулярной адсорбции, и
во многие другие уравнения (математические модели), описывающие поведение
реальных
физических
систем
любого
масштаба
в естественно
-
научных
областях познания. П р и этом сам множитель также может выступать в виде
уравнения
единицы
любой
оно
сложности,
включало
но
разные
с обязательным
по
знаку,
условием, чтобы
математически
обоснованные, относительные характеристики противоположно
процессов -p
ord
= ZPi и a
n o r d
Дифференциальные
и
кроме
физически
протекающих
= I a
t
и
интегральные
термодинамические
функции. В термодинамике поверхностных явлений, как и в обычной
химической
интегральные
термодинамике,
значения
дифференциальные
используются
функций
значения
дифференциальные
состояния.
обычно
относят
При
к
избыточной адсорбции. Например, дифференциальная
и
этом
гиббсовской
избыточная
энтропия адсорбции записывается как
дифференциальная избыточная внутренняя энергия как
/dU \
(dU \
s
s
или в более общем случае
^
где
Ys,di«p
состояния.
- дифференциальная
—
[mr)
—
TiA
избыточная
btl
величина
(
какой либо
1
7
5
функции
б
)
Формально
такое
определение
дифференциальных
избыточных
величин сходно с обычным определением парциальных
мольных
величин
/dY\
у
;,диф
,
=ЬН
г
д
е
1
*1
XUU
^T,P,nj
но обычные условия
постоянства
n и P=const
заменены
из-за
неопределенности объема адсорбированной фазы на s=const [13].
Необходимо отметить, что определенные так парциальные
величины
поверхностных функций отличаются от соответствующих
среднемольных
значений,
определяемых
Y s
обстоятельство
величин,
'
c p
=
n
обусловлено
а его игнорирование
соотношениями
типа
Y
-
Y
Это
мольные
s
использованием
является
наиболеее
избыточных
характерной
причиной различных недразумеий. Можно показать (подробнее см.,
например, в [13]), что
^ ,
д
и
ф
-
Химический
-
Ъ„ + n
s
потенциал
Ъ„ + Г
адсорбированного
1.76)
компонента,
определяется как
/dF\
»
-
/dU.\
{ 1 Г )
Т
/dS,\
Ы
Т
Т
-
Ь Г )
-
-
Т
Из уравнения (1.77) следует
dAF
RTlnP
s
—
-
A
l
l
l
l
l
l
0
—
r
( 1 . 7 7 )
где индекс (s) означает стандартное состояние, в качестве которого
обычно выбирают состояние жидкости с давлением насыщенных
паров P при температуре Т. В работах школы М.М.Дубинина [23]
s
величину AF в уравнениях типа (1.78) называют
изменением
свободной
дифференциальной
адсорбции,
а
энергии
работой
взятую
при
адсорбции,
адсорбции
с
обратным
разницу
или
знаком
интегральным
Л/и -
просто
-
работой
адсорбционным
потенциалом (по [23] адсорбционный потенциал s = - Л / ).
Дифференцируя
уравнение
(1.78)
по
Т,
можно
получить
выражение для дифференциальной энтропии адсорбции
d(AS )
ds
s
=
а
(
ds
d6
)
=
(d/л)
d6
(
Р
=
Р Л п
)
П
s
( )
P
(
)
dlnP
| RT( )
d6
(
+
)
R
T
d
l
n
P
dT
s
(1.79)
Это
уравнение
включает
равновесного
давления
называемый
изостерическим
температурный
при постоянной
адсорбции
температурным
коэффициент
ВГ(с1пР/дТ)г,
коэффициентом,
определяемый из изостер адсорбции. Совместное решение уравнений
(1.79) и (1.78) позволяет получить уравнение для расчета изменений
дифференциальной
избыточной
d(AU )
s
0
внутренней
энергии при адсорбции
(dlnP\
RT dlnP
2
0
Правая часть этого уравнения представляет разницу двух очень
похожих
выражений,
одно
из
которых
включает
равновесное
давление Р адсорбтива, т.е. пара, а другое - давление того же пара Р
над
чистой
жидкой
фазой
адсорбтива.
При
0
этом
RT^ dlnP
— — — = Я - теплоте испарения чистого адсорбтива, определяемой
уравнением
2
RT
Клаузиуса-Клайперона,
= Qst
-
так называемой
а
величина
изостерической
теплоте
адсорбции, определяемой из изостер адсорбции. Разницу (Л - Q)
называют чистой теплотой
энергию
адсорбции.
взаимодействия
адсорбат
Эта разница характеризует
-
адсорбент
за
вычетом
составляющей взаимодействия адсорбат - адсорбат. Интегральная
теплота адсорбции определяется уравнением
Г
Qz =
1
J Qstds
(1.81)
о
Экспериментально
в
калориметрах
измеряется так называемая дифференциальная
постоянного
объема
теплота адсорбции
q,
которая связана с величиной изостерической теплоты адсорбции Q
st
уравнением
Qst = Q + RT
Анализ
различных
способов
выражения
(1.82)
теплот
адсорбции
проведен в [2, 11].
1.7. Термодинамика поверхностных явлений на границе газ,
жидкость, твердое тело
Замкнутые формы и конечные размеры реальных фаз приводят
к непрерывному или локальному искривлению межфазовой границы.
Кривизна поверхности влияет на условия равновесия и требует
особого
подхода к изучению
термодинамики
поверхностных
явлений на искривленных границах раздела фаз[2, 8].
Капля
на
ЖИДКОСТИ
плоской
поверхности.
Классическим
примером трехфазной системы является система, состоящая из капли
жидкости, помещенной на идеально плоскую гладкую поверхность,
находящуюся в паровой среде (Закон Юнга).
Рисунок 1.13. Капли жидкости
поверхности твердого тела.
о
ж - г
на
смачиваемой
(а)
и
несмачиваемой
- сила, направленная по касательной к поверхности раздела
фаз «жидкость - газ»;
о
т - ж
- сила, направленная параллельно поверхности раздела фаз
«твердое
тело -
жидкость», стремящаяся
сократить
площадь
контакта этих фаз и препятствующая растеканию капли;
о
фаз
т - г
- сила,
«твердое
направленная
тело
-
газ»,
параллельно
стремящаяся
поверхности
растянуть
раздела
каплю
по
поверхности твердого тела и увеличить площадь контакта «твердое
тело - жидкость».
В
состоянии
смачивания
или
равновесия
несмачивания
между
о ,
т - г
соблюдаются
о
т - ж
,
о
ж - г
в
соотношение
случае
Юнга
(1.83) или (1.84):
ст = а
тг
тж
+ а соБО
жг
(1.83)
отсюда
со sQ =—
—
(1.84)
где © - краевой угол смачивания, который легко
экспериментально. При смачивании поверхности несмачивании - ©>90 .
определяется
©<90 , при
0
0
Предостережем, что в уравнении Юнга © - равновесный краевой
угол смачивания, который объективно не отражает смачиваемость не смачиваемость на реальных поверхностях, т.к. в реальности и з - з а
неидеальности (например, шероховатости) поверхности можно снять
только так называемый гистерезисный
краевой угол.
Гистерезис
-
задерживание, исключительно широко распространенное явление в
природе и технике. Типичный пример гистерезиса
смачивания
задерживание капли дождя на нечистой поверхности стекла.
К
сожалению,
с
в
огромном
количестве
публикаций,
связанных
измерением краевых углов смачивания этот факт игнорируется, что
приводит к искаженной интерпретации результатов эксперимента.
Различают два типа поверхностей: гидрофильные
которые хорошо смачиваются
смачиваются
неполярными
6
6
смачиваются
полярными (например, водой) и не
жидкостями
бензолом C H ) , и гидрофобные
(олеофобные),
(например,
(олеофильные),
маслом
которые
или
хорошо
неполярными (например, маслом или бензолом) и не
смачиваются
полярными
Гидрофильной
является
жидкостями
поверхность
(например,
оксидов,
H O).
2
гидроксидов,
силикатов, карбонатов и многих других минералов. Эти материалы
хорошо смачиваются водой. Гидрофобными являются поверхности
многих
пластмасс, сульфидов металлов, углеродных адсорбентов.
Самая высокая гидрофобность у тефлона, у которого 0=180°.
Работа
когезии
и адгезии.
Количественной
характеристикой
когезионных и адгезионных сил, связанных с уравнение
Юнга,
является работа когезии и адгезии.
Работа когезии и когезии по Дюпре равна энергии, затрачиваемой
на обратимый изотермический разрыв тела по сечению, равному
единице площади (рис. 1.14).
5-1м
:
5-1м
:
Рисунок 1.14. Определение работы когезии(слева) и адгезии (справа).
При разрыве цилиндра образуется поверхность, которая в 2 раза
превышает
разрываемую,
удвоенному
значению
т.е.
работа
поверхностного
когезии
натяжения
^У
ког
равна
разрываемой
конденсированной фазы (жидкости или твердого тела) на границе
с воздухом (формула Дюпре):
Жсог = 2ст ж _ г ,
М^ог = 2стт_г, Д ж / м
2
Для идеального твердого тела работа когезии
представляет
собой прочность тела на разрыв или когезионную прочность ( W ) .
KII
Когезионная
прочность реальных твердых
тел из-за
наличия
дефектов в их структуре в десятки и сотни раз меньше \ У .
к п
Для работы адгезии ^ У
уравнение
адг
Юнга-Дюпре,
формулу Дюпре (1.85) преобразуют в
удобное
экспериментально измеренным о
W
= а _ (1
aAr
ж
г
Кривизна
характеризует
ж - г
для
расчета
по
адг
и ®.
+ cosQ)
(1.86)
поверхности.
меру
^У
Кривизна
отклонения
этой
линии
линии
на
от
плоскости
прямой.
Если
произвольная линия на плоскости задана в виде функции f (х), то
f"
кривизна этой линии С определяется как С =
2
2
3
С = f"/ х[1
2
2
X[l + (f') ]2
2
3/2
+ (f ') ] ,
где f и f
— первая и вторая производные функции f(x).
Величину, обратную кривизне К , называют радиусом кривизны r.
2
Для f"
= 0 кривизна
равна
бесконечности. Кривизна
нулю, а радиус
поверхности
кривизны
равен
- мера отклонения формы
какой-либо поверхности от плоскости.
Кривизну
поверхности
в
данной
точке
определяют
путем
построения нормали к поверхности в рассматриваемой точке и
пересечения
поверхности
(ортоганальными)
двумя
плоскостями,
взаимоперпендикулярными
включающими
эту
нормаль.
Положение секущих плоскостей выбирается так, чтобы радиусы
кривизны линий пересечения rj и r
2
принимали наибольшее
и
наименьшее значения из всех возможных. Эти радиусы называют
главными
радиусами
пересечения
кривизна
кривизны
С >0
2
ги
1
r.
2
принимается
Для
выпуклых
положительной
линий
и
для
вогнутых
—
С <0.
В
2
адсорбции
кривизна
рассматривается как средняя величина C =0,5(1/
поверхности
r +1/ r ) = 1/r.
H
j
2
Радиус кривизны сферы как простейшей поверхности постоянной
кривизны: 2/R = 1/r + l/r
= 2/r,
оба главных радиуса кривизны
имеют одинаковые знаки и значения, поэтому радиус кривизны равен
геометрическому радиусу сферы R.
Для определения радиуса кривизны поверхности прямого
цилиндра
одна из плоскостей проводится перпендикулярно оси цилиндра
и
вырезает круг радиуса r , равный радиусу цилиндра Ru (r = Ru), а
1
1
вторая проводится в плоскости вдоль оси цилиндра, пересечение дает
прямую линию поэтому
соответствующий r
радиус кривизны цилиндрической поверхности
2
= да. В результате
Г = 2 Г т. е. равен
ц
ц
удвоенному геометрическому радиусу цилиндра
Аналогично
определяют
среднюю
кривизну
и радиус
кривизны
других поверхностей.
В дифференциальной геометрии и топологии часто используется
так
называемая
полная
или
гауссова
кривизна
К,
к
которая
определяется значениями тех же главных радиусов кривизны r и r :
1
2
1
=
. Эллиптическая
поверхность
кривизны r и r , имеющие одинаковые
1
2
или седловидная
радиусы
с главными
знаки, С > 0;
к
радиусами
гиперболическая
поверхность, для которой С < 0, так как главные
кривизны
К
имеют
разные
знаки;
и
параболическая
поверхность, для которой С =0, но одна из величин 1/r
к
1
или 1/r
2
не
равна нулю.
Если вместо кривизны поверхности
некоторая
область,
тогда
вместо
в точке рассматривается
дифференциальных
значений
кривизны поверхности
гаусовой
кривизне.
вводят интегральную кривизну области по
Для элементов
поверхности
со средней
C
H
выполняется соотношение
Usi
US
2 = 11
2
11
w = r = 7
( 1 . 8 7 )
+ 7,
где ds и dV — приращения поверхности и объема п р и малом изменении R.
Используем
уравнения
соотношение
Лапласа,
(1.87)
на котором
для
простейшего
вывода
основные
законы
основаны
поверхностных и капиллярных явлений.
Уравнения
Лапласа
и Кельвина.
радиусом кривизны г, находящаяся
Пусть капля жидкости с
на межфазовой поверхностьи с
площадью s, образует вместе с собственным паром изолированную
систему с полным постоянным объемом V = V
n
+ У . Согласно
ж
первого начала термодинамики [13]
dQ = dU + P dV
n
n
+ Р йУ - a _ ds
ж
ж
n
7K
(1.88)
где Р и Р — давление в газовой и ж и д к о й фазах.
п
ж
При бесконечно малом отклонении этой системы от равновесия
теплосодержание Q и энергия U системы не меняются, т. е. dQ = dU =
0, а изменения объема паровой и жидкой фаз связаны уравнением
i
—dy = dy .
n
M
Из ссотношения
(1.87) йУ =
ж
г
Б
2^ ж
и (1.88) при
условии dQ = dU = 0 следует
2
о = -р &у
п
ж
+ р ау
ж
ж
—
ау
ж
(1.89)
г
И тогда в интегральной форме
2
ж — Рп = —Р
г
р
или
-
ж
,
(1.90)
2(7 _
п
ж
АР =
= 2а,
(1.91)
г
В
капле
жидкости
собственным
радиуса
паром,
r,
находящейся
возникает
избыточное
в
условия
механического
с
гидростатическое
давление AP. Уравнение (1.91) называется законом
определяет
равновесии
равновесия
Лапласа.
на
Закон
искривленной
межфазовой поверхности, например, столба жидкости в капилляре,
пузырька пара в жидкости, мембран при их равномерном натяжении
и т. д.
Согласно уравнению Лапласа, давление всегда больше со
стороны
выпуклой
положительной,
фазы,
вогнутые
кривизна
поверхности
которой
имеют
принимается
отрицательную
кривизну. В пузырьке пара радиуса r давление больше, чем в
окружающей его среде, на величину АР и чем меньше пузырек, тем
выше в нем давление. Например, на искривленной границе вода/пар
при радиусе кривизны мениска 1 мкм величина АР = 1,4 атм, но при
радиусе 10 нм АР = 145 атм, а при радиусе 1 нм расчетная величина
АР = 1450 атм [13].
Из
уравнения
Лапласа
выразим
зависимость
величины
химического потенциала ц от кривизны поверхности
li = li ±
0
2
о _жУ г
П
т
= /л ±
0
а _жУ
П
т
[— + —)
\r
rf
1
(1.91а)
2
где ц
и ц - значения химического потенциала для фаз с плоской и искрив­
ленной поверхностями раздела;
0
<т
V
- поверхностное натяжение;
- мольный объем рассматриваемой фазы, который принимается не
зависящим от давления. Знак (+) относится к фазам с выпуклой,
знак ( - ) - с вогнутой поверхностью,
r и r - главные радиусы кривизны.
п-ж
1
m
2
При сопоставлении давлений внутри и вне сферической капли
жидкости Р
к - ж
- Р
0 - ж
(с индексами п и ж относятся соответственно к
пару и жидкости, с индексом г - к искривленной и индексом 0 - к
плоской границе раздела) радиуса R уравнение можно переписать
А д = ±2а _ У
ж
Из
определения
п
ж
(-
т
химического
1
+
(1.92)
ii=RTlna
потенциала
аналогичное
приращение химического потенциала в газовой фазе, считая газ
идеальным, примет вид:
р
А/1 = RTln-^-
(1.93)
п
В условиях равновесия ц = ц и Ац = Ац
Tln-^ =
±
ж
п
ж
nn
п
п
ж
ж
(1.94)
R
где Р = Р , - равновесное давление пара над плоской поверхностью ж и д к о с т и
при температуре Т. Здесь, знак (+) относится к фазам с выпуклой,
знак ( - ) — с вогнутой поверхностью.
0
0
п
Уравнение называется (уравнением) Кельвина, его чаще записывают
в виде
(
j
Р = Р0вхр
( 1 . 9 5 )
Итак, для искривленных поверхностей раздела фаз основными
фундаментальными термодинамическими уравнениями являются: 1)
уравнение
cosQ),
Юнга
а =а +а Со8б
тп
тж
определяющие
жп
условие
трехфазной границе; 2) уравнения
и Юнга-Дюпре
W
механического
равновесия
Гаусса
agr
1
изменениями
постоянной
поверхности
г
+
на
г
2
с радиусами
и
ж
С=1/г + г =2/г = I dA/dV I ,
которое связывает среднюю кривизну
объема
= а _ (1
кривизны
кривизны;
и
3)
уравнение
Лапласа
АР=2а/г=Са,
определяющее
механического равновесия в фазе флюида; 4) уравнение
условие
Кельвина
RT
ln P/P = 2 a V ^ r , определяющее условия равновесия в паровой фазе
0
или
равновесную
химического
растворимость;
потенциала
5) уравнение
ц =ц +2а
ж
для
выражения
у /г, определяющее
о ж
ж
связь
химического потенциала с кривизной поверхности и ряд других
важных уравнений
уравнениями,
отсутствие
[13]. Эти уравнения являются
которые
выполняются
межчастичных
в
условиях
взаимодействий.
классическими
равновесия
И несмотря
в
на это,
уравнения с соответствующими оговорками широко используются в
адсорбционной практике для описания капиллярных явлений на
искривленых поверхностях, включая пористые материалы, в которых
при
адсорбции
наблюдается
капиллярная
конденсация
паров.
Анализ адсорбции и капиллярной конденсации в пористых телах
будет рассмотрен в последующих разделах книги.
СПИСОК ЛИТЕРАТУРЫ
1. Адамсон
А. Физическая химия поверхностей. - М.: Мир, 1979.
568с.
2. Фролов, Ю.Г. Курс коллоидной химии.- М.: Химия, 1988.- 464 с.
3. Елисеев А.А., Лукашин А.В. Функциональные наноматериалы /
Под ред. Ю.Д.Третьякова. - М.: Физматлит, 2010. 456 с.
4. Гиршефелъдер И. О., Кертис К. Ф., Берд Р. Б. Молекулярная
теория газов и жидкостей. - М., ИЛ, 1961. 931с.
5. Киселев А.В. Межмолекулярные взаимодействия в адсорбции и
хроматографии. - М.: Высш. шк., 1986. 360 с.
6. Макаревич Н.А. Модельные расчеты адсорбционно термодинамических характеристик при исследовании межфазовых
взаимодействий. Дисс. на соиск. докт. хим. наук. - Минск. 1993. 397с.
7. Макаревич Н.А., Афанасьев Н.И., Телышева Г.М., Монаков Ю.Б.
Журнал физической химии. 2000. Т.74. № 12. С 2195-2202.
8. Русанов А.И.. Фазовые равновесия и поверхностные явления, Л.,
Наука, 1967; Фазовые равновесия и поверхностные явления // Современная
теория капиллярности. - Л., Химия, 1980. С. 25.
9. Guggeheim E.A. // Trans. Faraday Soc., 1940, vol. 36, p. 397.
10. Толмачев А.М. Адсорбция газов, паров и растворов. - М.: Изд-во
МГУ, 2012. 239 с.
11. Лопаткин А. А. Теоретические основы физической адсорбции. М.: Изд-во МГУ, 1983. 344 с.
12. Русанов А.И., Куни Ф.М. Адсорбция, адсорбенты и
адсорбционные процессы в нанопористых материалах. М.: Издательская
группа «Граница», 2011. С. 36.
13. Фенелонов В.Б. Введение в физическую химию формирования
супрамолекулярной
структуры
адсорбентов
и
катализаторов.
Новосибирск.: Издательство СО РАН, 2004. 442с; Лекции: «Введение в
основы адсорбции и тектурологии». http://catalysis.ru.
14. Флад Э. Межфазовая граница: газ-твердое тело. - М.: Мир. 1970.
С.18
15. Уэйлес С. Фазовые равновесия в химической технологии. - М.:
Мир. 1989. ч.1.304с.
16. Де Бур Я. Динамический характер адсорбции. - М.: ИЛ.1962.
291с.
17. Ross S., Oliver J.P., On Physical Adsorption. N.Y.: John Wiley &
Sons. 1964.
18. Макаревич Н. А. Докл. АН Беларуси. 1997. Т.41, №2. C.73-78;
Изв. НАН Беларуси. Сер. хим. наук. 2002. №2. С.39-46; Там же. 2006. №.2.
C.34-43; Там же: 2006.№3. С.42-48.
19. Макаревич Н.А. Современное состояние и парспективы развития
теории адсорбции (к 100-летию со дня рождения академика М.М.Дубинина) /
Труды IX Международной конференции по теоретическим вопросам адсорбции
и адсорбционной хроматографии. Москва, 24 - 28 апреля 2001г. С. 229-234, 321¬
326.
20. Эткинс П. Физическая химия. - М. Мир, 1980. Т.1. 293 с.
21. Пригожин
И., Дефэй
Р. Химическая термодинамика.
Новосибирск. Наука, 1966. 502 с.
22. Русанов А. И. Мицеллообразование в растворах поверхностноактивных веществ. Санкт-П: Химия. 1992. 280 с.
23. Беринг Б.П., Серпинский В.В. //ДАН СССР, 1963.Т.148, №6,
с.1331-1334; //Изв.АН СССР.Сер хим., 1971,№4, с.847-849.
2. А Д С О Р Б Ц И Я Н А Т В Е Р Д Ы Х П О В Е Р Х Н О С Т Я Х
2.1. Термодинамика поверхности твердого тела
По
сравнению
с
поверхностью
жидкостей,
описанной
предыдущей главе, поверхность твердых тел во многих
в
случаях
гораздо труднее интерпретировать с теоретической точки зрения.
трудности возникают и при количественном определении некоторых
важных параметров. Изучая физические свойства твердых тел, мы
мысленно
представляем,
что эти тела
находятся
в
состоянии
устойчивого термодинамического равновесия, которое в реальности
не достигается,
что
обусловлено
исключительно
кинетическими
факторами. Равновесие можент быть достигнуто при темературе
абсолютного нуля.
Для
значений
твердой
поверхности,
поверхностной
характерен
свободной
широкий
энергии,
интервал
изменяющейся
от
одного участка поверхности к другому, а также в каждой точке, и в
отличие от жидкости поверхностное натяжение твердых тел не может
быть одинаковым во всех направлениях. Заметим, что поверхностное
натяжение
для
жидкостей,
термодинамическое
придерживаясь
классическим
определенное
в
(в состоянии равновесия)
гиббсовского
уравнением
главе
2
(1.3).
а,
исчерпывается
Гиббса,
поверхностное натяжение с адсорбцией Г
как
мы обозначали
обозначения,
адсорбции
1,
связывающее
Для твердых тел
поверхностное натяжение будем обозначать у, как механическое,
которое
в
литературе
часто
представляют
в
виде
термодинамического, т.е. не различают ( а и у разлачал и Гиббс). На
это в своих теоретических трудах
особо обращает внимание А.И.
Русанов
[1], рассматривая
проблему
деформации
в
неполярных
пористых адсорбентах, при адсорбции газов при высоких давлниях.
Для изотропного твердого тела [2], а позднее и неизотропного
предложено уравнение
da = (а - у)dins
-
r d[i
2
2
где s - п л о щ а д ь поверхности;
//2-химический потенциал сорбата.
Дифференцирование подразумевает растяжение поверхности.
По аналогии с жидкой фазой вместо избытка поверхностного
натяженияа
для
поверхностного
напряжения
сечению
твердой
натяжения
фазы
у,
рассматривают
как
избыток
избыток
поверхностного
по объему поверхностного слоя или по его поперечному
с
толщиной
феменологическая
в
несколько
ангстрем,
тогда
вся
термодинамика (глава 1) может быть перенесена
на твердую поверхность.
Предположим, что поверхностное натяжение у может быть
разложено по двум взаимно перпендикулярным направлениям и что
эти
составляющие
тангенциальное
ds^
можно
записать
как
нормальное
f
и
f*. Если площадь поверхности возрастает на
ds^
то для анизотропного твердого тела общий рост свободной
энергии F задается [3] обратимой работой
s
против напряжений
1
у и
у
(
L
)
d sF T,v,
s
n
= Y ds
x
+ Y~ds
где Fs - свободная энергия единицы поверхности.
При f = f
= у
t
(2.1)
= d(sF ) y
s
T
=
>n
+
p
ds
(dF \
s
s
2
\d s)
3
T>
v
>
)
'
n
dF
Как
правило,
Ф0
dFJd&tO
и
только
dF
кристаллической
поверхности
= 0
dF /ds=0,
s
для
идеальной
тогда F =y.
Это
s
гипотетическое однородное равновесное состояние. В других случаях
между Fs и у сохраняется различие. И тогда говорят, что
нет
оснований у называть удельной поверхностной свободной энергией.
Аналогично
для
энергией Гиббса G
s
y
изотропных
поверхностей
со
(T,p,n=const)
= d(s G ) r , , „ =
s
P
G
s
+
5
/dgs)
ds
\ ds
( 2
числом частиц уравнения
(2.2-2.3) необходимо
_з)
/ т,р,п
При описании состояния твердой поверхности
составляющей
свободной
с переменным
дополнить
химической
энергии Еуп;. При условии идеальности поверхности
F = ys + ^
или F = у + ^
s
s
дГ
£
(2.4)
£
dF
если справедливо
= 0, то справедливо X Mi Г = 0.
Так же
G = YS + ^
5
Mini и л и
G = y + ^
(2.5)
s
но если рост свободной энергии F задается [3] необратимой
s
против напряжений
у и у**, то у меняет знак на противоположный
1
F = -ys
s
+
Если производные ^ ^ ^ 0
^
работой
или
G = -у
s
+ SMiri
(2.6)
и — ^ 0, то а^у. Если — = 0 и
= 0 , то а=у. В этом принципиальное отличие а и у.
Рассмотренные формы записи для потенциалов F и G на
s
твердых
поверхностях
можно
перенести
и
на
s
уравнение
Гиббса-Дюгема, дополнив термом S dT, и представить в развернутом
s
виде
S dT - sdy + ^
s
Свободная
энергия
n d^i
= 0
si
поверхности.
(2.7)
При
рассмотрении
дисперсности (гл.1), мы акцент делали на то, что на дробление
материала затрачивается работа, идущая на увеличение поверхности
s,
следовательно, и
свободной энергии системы G. Удельная
свободная энергия поверхности у связана с энергией когезии твердого
тела АН .
и с числом связей между атомом и его ближайшими
когез
соседями,
которые
поверхности:
у = АЯ
необходимо
N,
к о г е з
s
разорвать
где Z
s
-
ближайших соседей у поверхностного атома;
число
объемного
атома;
^-плотность
для
число
образования
недостающих
Z-координационное
атомов
на
поверхности.
Металлы имеют высокую удельную поверхностную энергию, 1,5-3,0
2
2
Дж/м , ионные кристаллы 0,3-0,5 Дж/м , углеводороды - 0,02-0,03
2
2
Дж/м , для сравнения, вода - 0,072 Дж/м .
Существуют косвенные способы определения поверхностного
натяжения (поверхностного напряжения) твердых тел [4]. Например,
метод
фольги
«нулевой
ползучести»,
в котором образец в виде нити или
нагревают до такой температуры, при которой он начинает
сокращаться по длине под действием поверхностных напряжений.
Одновременно
к
образцу
прикладывается
внешняя
сила
для
поддержания исходной формы образца и по величине внешней силы
определяют
поверхностное
«раскалывания»
напряжение.
Или
в
методе
по величине работы, затрачиваемой на раскалывания
кристалла. В методе растворения
сравниваются удельные теплоты
растворения /АН . массивного кристалла и порошка той же массы с
раств
известной удельной поверхностью з . Тогда а = —-— .
уд
Заметим, что на величину поверхностной энергии твердого тела
сильное
влияние
оказывает
присутствие
адсорбатов
и
веществ
различной природы. Это явление широко используется на практике
для
модифицирования
поверхности,
придавая
ей
необходимые
технологические свойства.
Если твердое тело имеет определенный химический состав в
объеме, то это не значит, что поверхность содержит те же атомы и
тоже расположение, как в объемной фазе. Часто на поверхности могут
быть найдены различные химические группы, образовавшиеся
результате
химического
окружающей
газовой
взаимодействия
фазы.
Наиболее
с
в
компонентами
изученными
примерами
являются оксиды металлов, оксид кремния и угли [3].
Например,
поведения
рутил
TiO
2
представляет
оксидов металлов. Изменения
типичный
пример
в спектре рутила
при
нагревании и откачке объяснены Джексоном и Парфитом [3] с точки
зрения мостиковых и концевых гидроксильных групп, образованных
диссоциацией воды на грани (110).
Частица оксида кремния может быть представлена как полимер
кремневой
кислоты,
силоксановые
который
группировки
имеет
на
=Si—О—81=с
поверхности
кислородом
либо
на
поверхности, либо одну или несколько форм силанольных групп
=Si—ОН, образующихся
как результат взаимодействия
с водой.
Можно определить следующие типы таких групп: изолированная
-поверхностный атом Si одной связью соединен с - ОН-группой,
которая не имеет водородной связи с другой силанольной группой;
вицинальная - две одиночные силанольные группы, соединенные с
разными
атомами,
образуется
сближаются
водородная
связь;
друг
с
другом
геминальная
-
настолько,
две
ОН-
что
группы,
соединенные с одним атомом Si, образуют водородные связи друг с
другом, оставляя атому Si только две связи с объемной структурой.
На поверхности промышленных углей найдено пять основных
типов химических групп [5]: ароматический водород, фенол, хинон,
карбоновые кислоты и лактон. Концентрации поверхностных групп
выражают в мг-экв./г.
Относительно адсорбции на твердых поверхностях заметим, что
адсорбат может окислять и восстанавливать частицы поверхности,
оказывая сильнейшее влияние на величину поверхностной энергии.
Например, при высоких температурах в каталитическом
синтезе
метанола с участием системы Cu/ZnO наблюдали даже растекание и
собирание в капли каталитических частиц на твердой подложке.
Итак,
Гиббс
указывал
на
два
способа
формирования
поверхности твердого тела:
образование новой поверхности идентичной природе исходной;
образование
новой
поверхности
в
результате
растяжения
твердого тела.
При этом Гиббс рассматривал поверхностное натяжение, или,
точнее,
поверхностную
энергию
как
работу,
необходимую
для
образования поверхности, в то время как поверхностное напряжение
как работу, требуемую для растяжения поверхности.
Отличительной особенность твердых тел от жидких является то,
что
поверхностное
натяжение
дает
вклад
в
поверхностное
напряжение твердого тела, а следовательно, в его деформацию, если
поверхность не является плоской. Подробнее этот вопрос рассмотрен
в работах [1, 6].
Концепция
поверхностного
натяжения
применительно
к
твердым телам имеет важное значение так же и для капиллярных
явлений, в связи с уравнением Лапласа. Представим приблизительно
сферический кристалл, для которого, как и для жидкости, можно на¬
писать
2а
Ар = —
г
Перепад давления Ар
(2.8)
приведет к сжатию кристалла.
Если
сжимаемость обозначить через Z, то можно записать приближенное
соотношение
AV
3Аг
-у = — = ~ P
A
Z
( 2 . 9 )
Отсюда из (2.8) и (2.9)
Аг =
—
(2.10)
Явление было изучено [3] для оксида магния (II) с помощью ди¬
фракции
рентгеновских
Значение Аг,
лучей
на
порошкообразных
образцах.
полученное для кристаллита радиусом 60 нм
при
использовании
расчетной
величины
a
=
6,573 Н/м,
близко
к
ожидаемой величине 0,06 нм, что соответствует изменению размера
ячейки на 0,1%. Последующее исследования показали, что адсорбция
некоторых веществ, таких, как пары воды, приводит к расширению
решетки,
а
в
сжатие,
относительная
уменьшением
адсорбтива
отсутствие
размера
для
адсорбированной
величина
которого
кристаллита.
пористых
тел
пленки
это
При
наблюдается
увеличивается
высоких
явление
с
давлениях
детально
изучено,
теоретически и экспериментально подтверждено школой
Беринга
Б.П., Серпинского В.В. Фомкина А.А.[7]
Если провести аналогию между поверхностным напряжением и
напряжением при рассмотрении упругости в объеме тела, при этом
мысленно провести сечение перпендикулярно поверхности кристалла,
то
для
того,
чтобы
поверхность
сохранила
равновесную
конфигурацию и не появились дополнительные напряжения в объеме
кристалла,
необходимо
допустить
наличие
поверхностного
напряжения, которое может быть вызвано локальной релаксацией
кристаллической структуры. Так как составляющие поверхностного
напряжения
соответствуют
по
крайней
мере
симметрии
грани
кристалла, то поверхностное натяжение можно рассматривать как его
частный случай, когда поверхность имеет три (или более)
симметрии вращения. В этом случае нормальные
оси
составляющие
напряжения, пересекающие все линии грани, одинаковы, а сдвиговые
напряжения
равны
нулю,
так
что
нормальные
составляющие
напряжения равны поверхностному натяжению [3].
При упругой или пластической
деформации твердого
тела
результат определяется характером деформации вне зависимости от
природы
деформируемого
деформации
полимеры)
тела.
(жидкости,
не
При
медленной
вязко-текучие
изменяются
ни
пластической
вещества,
расстояния
между
например,
атомами,
ни
химические потенциалы ц, при этом, поверхностное натяжение и
поверхностное напряжения совпадают.
Если бы большинство твердых тел имело
конфигурацию
с
минимальной
энергией,
то
геометрическую
многие
важные
технологические процессы такие, как отжиг металлов и спекание
порошков и т.д., стали бы невозможными. В отличие от жидкости в
твёрдом состоянии вещество сохраняет как форму, так и объём.
Твёрдые
тела
делятся
на
кристаллические
и
аморфные.
С
микроскопической точки зрения твёрдые тела характерны тем, что
молекулы или атомы в них в течение длительного времени сохраняют
своё среднее положение неизменным, только совершая колебании с
небольшой амплитудой вокруг них.
В кристаллах
средние положения атомов или молекул строго
упорядочены, их атомы расположены так, что образуют правильную
трехмерную
решетку
-
периодическую
структуру.
идеальной периодичности могут быть обусловлены
примесями,
атомами
незаполненными
внедрения
(в
(вакантными)
промежутках
между
Нарушения
химическими
атомными
узлами),
узлами,
а
также
дислокациями. Во многих случаях подобными нарушениями
отклонениями
от строгой периодичности
существенным
или
образом
определяются физические свойства кристаллических твердых тел.
Управляя концентрацией подобных дефектов или целенаправленно
создавая их, можно получать «наперед заданные» свойства твердых
тел. Кристаллические твёрдые тела имеют анизотропные свойства, то
есть их отклик на приложенные внешние силы зависит от ориентации
сил относительно кристаллографических осей.
В
аморфных
телах
атомы
колеблются
вокруг
хаотически
расположенных точек, атомы в таких материалах располагаются в
общем так же, как и в жидкостях, т.е. они упорядочены лишь в
пределах нескольких межатомных расстояний от каждого
атома,
принятого за центральный. Иначе говоря, для стекол характерен
ближний порядок в расположении атомов, а не дальний, как в
кристаллической структуре.
Образование новой поверхности в твердых
телах - процесс
значительно более сложный, чем изменение поверхности жидкостей.
Так, при деформации жидкости, сопровождающейся
новой
поверхности,
структура
объемной
фазы
образованием
практически
не
меняется, но изменяется структура поверхностной фазы. В твердых
телах
при образовании новой поверхности может быть затронута
структура объёмной фазы.
Изучение явлений,
включая адсорбцию, с участием твердой
поверхности немыслимо без рассмотрения элементов моделирования
твердого тела.
2.2. Элементы моделирования твердого тела
Моделирование
микроструктуры
супрамолекулярном (надмолекулярном)
на
молекулярном
и
уровнях интересуют такие
материалы, как металлы и сплавы, полупроводники, диэлектрики и
магнитные
материалы.
Многие
из
них
относятся
как
к
кристаллическим, так и аморфным веществам.
В кристаллических
образуют
веществах
правильную
структуру.
трехмерную
Нарушения
обусловлены
их атомы расположены так, что
идеальной
химическими
решетку
-
периодическую
периодичности
примесями,
могут
быть
незаполненными
(вакантными) атомными узлами, атомами внедрения (в промежутках
между узлами), а также дислокациями. Во многих случаях подобными
нарушениями
или
существенным
отклонениями
образом
от
определяются
строгой
периодичности
физические
кристаллических твердых тел. Управляя концентрацией
свойства
подобных
дефектов или целенаправленно создавая их, можно получать «наперед
заданные»
свойства
первостепенную
роль,
твердых
тел.
например,
Такая
технология
в области
играет
полупроводниковой
микроэлектроники.
Другой класс материалов, представляющий интерес для физики
и химии твердого тела, -
это стеклообразные,
или
аморфные,
материалы. Атомы в таких материалах располагаются в общем так же,
как и в жидкостях, т.е. они упорядочены лишь в пределах нескольких
межатомных
расстояний
от
каждого
атома,
принятого
за
центральный. Иначе говоря, для стекол характерен ближний порядок
в расположении
атомов, а не дальний, как в
кристаллической
структуре. Приведем очень краткую характеристику твёрдых тел.
Свойства твердых тел. К физическим свойствам твердых тел
относятся
механические,
тепловые,
электрические,
магнитные
и
оптические свойства. И х изучают, наблюдая, как ведет себя образец
при изменении температуры,
механических
напряжений,
давления или объема,
электрических
и
в условиях
магнитных
температурных градиентов, а также под воздействием
излучений
-
нейтронов
и
света,
т.п.
рентгеновских
Химические
лучей,
свойства
пучков
твердых
полей,
различных
электронов,
тел
особенно
существенны при изучении поверхностных явлений.
Структура. Твердое
тело
состоит
из
атомов.
Само
его
существование указывает на наличие интенсивных сил притяжения,
связывающих атомы воедино, и сил отталкивания, без которых между
атомами
не
было
бы
промежутков.
взаимодействий
атомы
твердого
индивидуальные
свойства,
и
тела
именно
В
результате
частично
этим
таких
теряют
объясняются
свои
новые,
коллективные свойства системы атомов, которая называется твердым
телом.
Какова
природа
этих
сил?
Свободный
атом
состоит
из
положительно заряженного ядра и некоторого числа отрицательно
заряженных электронов (масса которых значительно меньше массы
ядра).
Хорошо
известные
кулоновские
(электрические)
силы,
действующие между заряженными частицами, создают притяжение
между ядром и электронами, а также взаимное отталкивание между
электронами.
Поэтому
твердое
тело
можно
рассматривать
как
состоящее из системы взаимно отталкивающихся ядер и системы
взаимно отталкивающихся
электронов, причем обе эти
системы
притягиваются друг к другу. Физические свойства такого объекта
определяются двумя фундаментальными физическими теориями
квантовой механикой и статистической механикой.
-
2.2.1. Модельные представления твердого тела
В физике твердого тела обычно принимают упрощенные модели
твердого тела и затем проводят вычисления их физических свойств
[8]. Модели должны быть достаточно простыми, для того чтобы было
возможно их теоретическое описание, и в то же время достаточно
сложными, для того чтобы они обладали исследуемыми свойствами.
Например,
для
электрической
объяснения
некоторых
проводимости
вполне
общих
подходит
закономерностей
простая
модель
металла в виде системы положительных ионов, погруженных в газ
подвижных
электронов.
подходящую
Но оказалось
физическую
модель,
крайне трудно
которая
позволила
построить
хотя
бы
качественно объяснить явление сверхпроводимости, открытое в 1911
голландским физиком Камерлинг-Оннесом.
Симметрия и классификация
-
кристаллов.
Кристаллография
наука, описывающая геометрические свойства кристаллов и их
классификацию на основе понятия симметрии [9]. Кристаллография
поверхности представляет собой двумерный аналог кристаллографии
объемных
материалов,
распределения
атомами
атомов
объемного
в
в
котором
рассматривается
различных
кристалла.
плоскостях,
Х.Вейсс
в
1808
характер
формируемых
ввел
систему
кристаллографических осей, определяемую тремя векторами a, b, c,
которые
соответствуют
Бесконечное
множество
определяется
вектором
трем
точек
сторонам
элементарной
ячейки.
положение
которых
(узлов),
г = ща + n b + щс
2
r = ща + n b + n c,
2
3
где П\, п и п - целые числа, называется пространственной решеткой.
2
3
Такая решетка - не кристалл, а чисто математический объект. Однако
с ее помощью можно построить кристалл, если в каждый ее узел
поместить
повторяющийся
элемент,
состоящий
из
одного
или
нескольких атомов (рис.2.1), например NaCl.
И
наоборот,
можно
построить
пространственную
решетку,
соответствующую
выбрать
кристаллу,
произвольную
если
точку
(узел) M , допустим, один из узлов Na,
i
а
Рисунок 2.1. Кристаллическая
структура NaCl.
затем
найти
точки M , M , . . . ,
2
все
остальные
обладающие
3
тем
свойством, что окружение этих точек
выглядит во всех отношениях в точности так же, как оно выглядит из
точки M . Множество точек M , M , M , . . . в таком случае образует
i
i
2
3
пространственную решетку кристалла.
Классификация
симметрии
требует
решеток
и
кристаллов
строгих определений.
на
основе
Операцией
понятия
симметрии
называется такая операция, которая, будучи произведена над твердым
телом, оставляет это тело неизменным, и тогда это тело называется
инвариантным
инвариантна
относительно
по
отношению
этой
к
операции.
вращению
(Например,
вокруг
любой
сфера
оси,
перемещению из одного места в другое, отражению в зеркале и т.п.)
Если двумерную решетку на рис. 2.1 подвергнуть перемещению,
задаваемому вектором а, то мы вновь получим исходную решетку; то
же справедливо, разумеется,
и по отношению
к
перемещению,
задаваемому вектором b. Решетка с элементарной ячейкой, заданной
тремя векторами a, b, c, инвариантна относительно всех операций
трансляции (переноса), определяемых равенством Т = п а + п Ь
1
пс
3
2
=
, где щ, n , n - целые числа. Совокупность всех таких операций
2
3
называется трансляционной
группой
данной решетки.
То есть для
описания различных объемных и поверхностных структур (текстур)
необходимо использовать универсальный язык.
В
случае
например,
двумерной
ось,
решетки,
можно
через
какую-либо
проходящую
представить
точку
себе,
решетки
О
перпендикулярно поверхности. Поворот вокруг этой оси на 180 не
меняет
решетку.
Принято
говорить,
что
такая
ось
обладает
симметрией 2-го порядка. В общем случае тело обладает
осью
О
симметрии n-го порядка, если поворот тела на угол (360 /п) оставляет
тело неизменным. Например, каждая пространственная
куба является
для
него
осью
симметрии
3-го
диагональ
порядка,
а ось,
проведенная через центр куба перпендикулярно какой-либо паре его
граней, является
осью симметрии
4-го
порядка.
Полный
набор
операций симметрии, возможных при условии неподвижности данной
точки
и
оставляющих
тело
неизменным,
называется
точечной
группой этого тела. Для пространственной решетки или кристалла
точечная
симметрия
ограничена требованием
выполнения
также
трансляционной симметрии. Это сокращает число возможных осей
вращения до четырех, обладающих соответственно симметрией 2-, 3-,
4- и 6-го порядков.
Существует
семь
различных
точечных
групп
для
пространственных решеток; ими определяются семь кристаллических
систем, или сингоний. Каждая сингония может быть охарактеризована
видом элементарной ячейки, т.е. углами а, Д, 7 между осями a, b, c и
соотношением длин этих осей. Классификация типов элементарных
ячеек и наименования соответствующих кристаллических сингоний с
обозначением ребер и углов некоторых ячеек приведены ниже в
табл.2.1.
Таблица 2.1.
Соотношения между длинами рёбер a, b, c и углами а, в, у
элементарных ячеек
Кубическая
a =b =c
а = Д= 7= 90°
Тетрагональная
a =bФ c
а = Д= 7= 90°
Орторомбическая
aФbФc
а = Д= 7= 90°
Моноклинная
aФbФc
а= 7= 9 0 V Д
Триклинная
aФbФc
аФ ДФ 7Ф 90°
Гексагональная
a =bФ c
а = Д = 90° 7= 120°
Тригональная
a =b =c
а = Д= 7< 120° Ф 90°
Полная
группа
кристалла,
является
(точечных
операций,
комбинаций),
по
симметрии,
или
совокупностью
трансляций,
отношению
к
пространственная
всех
а
операций
также
которым
их
группа
симметрии
всевозможных
решетка
инвариантна.
Существует 14 различных пространственных групп, которыми может
обладать решетка; им соответствуют 14 различных пространственных
решеток. Впервые эти решетки были описаны Браве в 1848 на основе
тщательного геометрического
анализа и носят его имя.
решетка Браве принадлежит
к одной
из семи
Каждая
кристаллических
сингоний.
Для
характеристики
расположения
атомных
плоскостей
в
кристалле вводят индексы Миллера n,k,l, связанные с отрезками,
отсекаемыми
выбранной
кристаллографической
плоскостью
системы
координат
на
трёх
(не
осях
обязательно
декартовой). Поверхность полностью определяется набором
этих
индексов, которые обычно записывают в скобках рядом с химическим
символом элемента: (111), (101), (110)... Отрицательные значения
индексов n,k,l обозначаются чертой над соответствующим числом.
Возможны три варианта относительного расположения осей и
плоскости: плоскость пересекает все три оси; плоскость пересекает
две оси, а третьей параллельна; плоскость пересекает одну ось и
параллельна двум другим (рис 2.2).
Переходя от формального теоретического описания симметрии
решетки
к
описанию
реального
кристалла,
учитывают
также
симметрию атомов или атомных групп, помещаемых в каждый узел
решетки. В результате
для кристаллов насчитывают
в
общей
сложности 230 различных пространственных групп (по-прежнему при
14 различных типах решеток Браве).
Хотя
кристаллография
сама
по
себе
является
довольно
абстрактной областью науки, симметрия играет важную роль при
описании
физических
свойств
твердых
тел.
Например,
трансляционная симметрия кристаллов позволила развить
весьма
общие теории, описывающие распространение волн в кристаллах, в
том числе упругих волн и волн, связанных с движением электронов.
Точечная симметрия также оказывает определяющее влияние на
физические
свойства
кристаллов.
Коротко
можно
сказать,
что
кристаллография отражает фундаментальный аспект физики и химии
твердого тела.
(001J
(100)
(101)
(HO)
(111)
(111)
(010)
(Oil)
( i l l )
Рисунок 2.2. Базальные плоскости, полученные сечением элементарных ячеек
простейших кристаллических структур
Важным
параметром,
каталитическую способность
определяющим
адсорбционную
и
поверхности твердого тела, является
структура поверхности, плотность и концентрация
связей, находящихся на ней атомов.
ненасыщенных
Для
примера
структуры:
Cu,Ag,
возьмем
три
гранецентрированная
Pt,
Au),
кристаллические
кубическая
объемно-центрированная
металлические
решетка
кубическая
(ГЦК-Ni,
решетка
(ОЦК-Бе)и гексагональная плотная упаковка ( Г П У - С о , Ru). На рис
2.3. показаны элементарные ячейки этих структур, содержащие 2, 4, и
6 атомов в ГЦК, ОЦК и ГПУ-решетках соответственно. Оксиды,
сульфиды, нитриды металлов имеют значительно более сложные
кристаллические решетки.
Рисунок 2.3. Элементарные ячейки гранецентрированной (ГЦК), объемноцентрированной (ОЦК) и гексагональной плотноупакованной (ГПУ) решеток
При моделировании кристаллов плотными упаковками шаров,
то ОЦК- и ГПУ-структуры будут иметь наибольшую плотность. В
этих структурах свободной (пустое)
пространство будет составлять
26%от общего объема, при этом каждый атом внутри кристалла будет
иметь по 12 ближайших соседей, т.е. координационное число для
атома внутри кристалла равно 12. У ГЦК свободное пространство
-32%,
а
координационное число внутреннего атома - 8 . Разницу
между ГЦК-
и ГПУ- структурами
можно понять,
рассматривая
последовательность расположения плотно-упакованных слоем.
Для
ГЦК-структуры плотной упаковке соответствуют плоскости
(111)
- р и с 2.2, а ГПУ-структуры -плоскость (001) [10].
Для
подсчета
числа
ненасыщенных
связей
на
твердой
поверхности необходимо определять число недостающих соседей для
атомов, находящихся на поверхности.
Адсорбционные
центров
при
центры.
моделировании
Для
типичных
поверхности
им
адсорбционных
дают
верхушечный центр, мостиковый (короткий и длинный
названия:
мостик),
полостными центрами, имеющих тройную и четверную координацию.
Число адсорбционных центров на поверхности
определяется
геометрией поверхности. Например, адсорбция на полостном центре с
четвертичной координацией
на поверхности (100) ГЦК кристалла
1/2 2
равна числу элементарных ячеек площадью [(1/2)a2
2
] на одном м .
Здесь a-постоянная ГЦК-решетки. А площадь той же элементарной
2
ячейки на поверхности (100) ОЦК- кристалла составит а .
(100)
О Н )
(110)
Рис. 2.4. Адсорбционные центры на разных поверхностях
Поверхностные
периодические
структуры
описываются
с
помощью двумерных решеток. Узлы решеток представляют в виде
комбинаций двух базисных векторов, с помощью которых задают
наименьшие по размеру ячейки с одинаковым расположением атомов.
В двумерном пространстве можно создать пять различных решеток:
гексагональная
Браве
поверхностей
с
центрированная
служит
элементарной
кубической(111)
и
ГПУ
ячейкой
структурой
для
(001);
прямоугольная
- для поверхностей (110) ОЦК- и
ГЦК-кристаллов, прямоугольная
- для поверхности (100) кубической
решетки. Переносом этих ячеек на расстояние, равное постоянной
решетки получают поверхностные структуры. Подробнее см. [10].
Оксиды и сульфиды металлов, образованные из положительных
п
ионов металла (Ме +) и анионов кислорода или серы имеют более
сложные структуры. Практически во всех оксидах ионы кислорода
О
2 -
п
имеют больший размер, чем ионы Ме +. Катионы на поверхности
являются льюсовскими центрами (кислота) и проявляют себя как
акцепторы
электронов,
ионы
протонов-бренстедовские
адсорбируются
диссоциации.
кислорода
центры
служат
(основание).
на поверхностях оксидов после
Например,
акцепторами
молекула
О
2
на T i O
2
Многие
газы
гетеролитической
диссоциирует
на
дефекте и поставляет атом кислорода, залечивая дефект поверхности,
в то же время молекула CO c одиночной парой электронов «садится»
на льюсовский центрТГ^
Активные центры сульфидов, например, MoS ,
2
слоистой
структурой,
в
которой
металл
занимает
обладающих
«дырки»
в
трехгранных призмах в плоскостях, расположенных между слоями
серы с гексагональной упаковкой, лежат на краях слоев. Базальная
плоскость, образованная атомами серы, как правило, поверхностна
неактивна.
Таким
образом,
прогнозировать
зная
адсорбционную
структуру
и
поверхности
каталитическую
можно
активность.
Однако, для реальных твердых поверхностей,
с ее дефектами и
неоднородностью, делать прогнозы исключительно сложно.
В
заключение
подчеркнем,
что
построение
идеальных
поверхностей для кристаллов носит чисто теоретический характер. И
не только потому, что у реальных кристаллов масса дефектов, даже в
идеальных
структурах
возникают
поверхностные
напряжения,
вызванные тем, чтоповерхностные и объемные атомы находятся в
различных
силовых
полях.
Это
приводит
к
реконструкции
поверхности. О реконструкции поверхности см. [ i 0 , i i ] .
2.2.2. Неидеальность и неоднородность поверхности твердого
тела
Известно,
что
получить
идеальный
объемный
кристалл
практически невозможно, как не достижима и идеальная поверхность.
Дефекты
кристаллических
структур.
Поверхность
кристаллической ионной решетки может иметь те же типы дефектов
структуры, что и объем кристалла. Сохраняются аналоги дефектов
Френкеля и Шоттки. Дефекты
Шоттки
получаются на идеальной
кристаллической поверхности с вакансиями в узлах решетки, тогда
как дефекты
Френкеля
возникают в результате смещения некоторых
ионов (обычно катионов из-за их малого размера) в междоузлия
рядом с вакансиями решетки. Если размеры анионов и катионов
одинаковы, то в объеме кристалла преобладают дефекты Шоттки;
если же катионы намного меньше, чем анионы, то
образуются
дефекты Френкеля, потому что малые ионы могут размещаться в
междоузлиях (рис.2.5).
4-4-- + - + - +
+ - • - + - + - +
4 - 4 - + - + - +
+
+
-
+ - 0 ~ + - + - 4
- + - + - + - + +-+-+-•*•-+
- 4 - 4 - 4 - + -
4-.- + - + - +
+
_ + _ +
-+-+-+-++
+
+
+
_
- + - + - +(~J) + -
-+ -+ - +
+ - 4 - 4 - + -+ -4
+ - + - + -
ttdee/ibwM поверхность
Дчфекиы
Шояти
- +- + - +- + -
Дефект
+ - О "4
- + _ + _
4 - 4 - 4
_ + _+ _
Френкеля
Рисунок 2.5. Модель идеальной поверхности кристалла и с дефектами Ш о т т к и и
Френкеля
На поверхности решетки всегда имеются вакансии, поэтому
дефекты Шоттки легко образуются. При релаксации поверхности так
же легко образуются и дефекты Френкеля
и между этими двумя
типами дефектов сглаживается различие.
Среди
оксидов
металлов
распространенное
явление
-
нестехиометричность. Обычно, она присутствует в большинстве ис¬
пользуемых материалов и даже может
определять их свойства, как
полезные для одних процессов, так и вредные, так и вредные для
других. Например, оксид титана ( I V ) часто находится в формах,
обедненных кислородом, при этом установлено, что формула для
обоих
форм-рутила
и
анатаза-
может
быть
TiO
1j9-2j0
. Этого
достаточно, чтобы дефекты Шоттки находящиеся в объеме кристалла
и, вероятно, на поверхности или достаточно близко от нее, для
локального изменения поверхностной энергии кристалла.
Причиной беспорядка в кристаллах является так ж е примесь
постороннего иона в узлах решетки кристалла, даже если ион имеет
тот ж е заряд, что и ион решетки. Так как, одинаково заряженные но
разные ионы, отличаются друг от друга, как правило, размерами,
поляризуемостью, т.е. имеют разную энергию взаимодействия
3
в
3
решетке. Например, замена А1 + на Бе + в кристалле А12О3 будет
приводить к релаксации кристалла. То же, и при замещения иона на
поверхности. Если валентность постороннего иона отличается от
валентности
иона
решетки,
то
эта
ситуация
напоминает
нестехиометрические кристаллы.
*
0
• • • « • •
Говоря
• • < • • •
о
кристаллов,
в
несовершенствах
следует
отметить
_* * * п 9 * * *
* - •
явление, называемое дислокацией.
-
Дислсжаг/гш-концентрации
' * *
точечных
дефектов
кристаллической
в
решетке.
Они
появляются в результате процессов
зародышеобразования,
кристалла, осаждения из раствора.
Рис.2.6. Схемы краевой дислокации.
Различают
дислокаций
—
графически
изобразил
решетки
инертного
представляет
плоскости
краевая
собой
рисунка.
и
два
винтоваядислокации.
краевую
газа
дислокацию
(рис.
плоскость
Решетку
роста
над
2.6а).
основных
типа
Коттрел
[10]
простой
Штриховая
скольжения,
рисунком
кубической
линия
АВ
перпендикулярную
и под
ним
можно
рассматривать как обычную кубическую, но в верхней части рисунка
пространственная
решетка растянута,
а в нижней
- сжата,
что
вызывает скачок числа атомов в ряду плоскости скольжения. Такие
дислокации (обозначены Т) появляются на поверхности как ступени с
более
высокой
локальной
поверхностной
энергией,
прежде
чем
внешнее давление приведет к восстановлению порядка.
Наличие дислокации указывает на возможность относительного
движения в плоскости дислокации, когда имеется даже небольшое на-
пряжение.
Механизм
такого
этого
процесса,
подобного
пластическому течению, Адамсон [12] сравнил «с движением пледа,
который тянут за нижний край». Количественно природу дислокации
оценивают по
контуру Бюргерса [9]. Он представляет какой-либо
замкнутый
путь от места
кристалла
вокруг
к месту
области,
в бездислокационной
содержащей
дислокации.
части
Если
эта
траектория в совершенном кристалле не образует замкнутой петли, то
говорят, что первый контур должен содержать одну или
более
дислокаций. Вектор, необходимый для того, чтобы замкнуть контур,
называется вектором Бюргерса.
Второй
тип дислокаций-винтовая дислокация, показанная на
рис. 2.6 б. Здесь каждый кубик изображает узел решетки или атом и
характеризуется вектором Бюргерса, параллельным линии дисло¬
кации и перпендикулярным А. Если посмотреть сверху на линию
дислокации, то снижение поверхности на один слой происходит при
повороте на 360° из В вокруг А, до тех пор,
пока линия ВС не
вернется на прежнее место. Поскольку это движение происходит
против часовой стрелки, винтовая дислокация на рисунке называется
левосторонней.
Поверхностная
шероховатость.
Поверхности твердых
тел
можно получить различными способами, например распиливанием,
резанием, скручиванием, полировкой или химической обработкой.
Все эти методы делают поверхность в разной степени шероховатой.
Количественная
оценка
шероховатости
может
быть
дана
с
использованием двух параметров: один из них связан с амплитудой
отклонений
от
среднего
профиля
поверхности,
а
второй-с
увеличением площади из-за шероховатости [3]. На рис. 2.7 изображен
XV-профиль реальной поверхности, а А В представляет идеальную
(молекулярно-гладкую) поверхность твердого тела равного объема.
Поверхность
А В расположена так, чтобы «холмы» на X V (выше
плоскости А В ) были бы равными по объему «долинам» на X V (ниже
плоскости АВ). Отклонения точек поверхности от плоскости А В
могут
быть
выражены
среднеквадратичное
(И
как
среднеарифметическое
),
многократно
с к о
микроскопом, расстояния h
m a x
( Ь ) или
с р
измеренные
под
.
Рис.2.7. Схема, в ы р а ж а ю щ а я шероховатость твердой поверхности. Линия
XY-профиль
поверхности, А В - г и п о т е т и ч е с к а я
(идеальная)
поверхность,
наибольшее расстояние между «холмом» и «долиной» [3].
Для оценки шероховатости вводят так называемый
шероховатости
абсолютной
фактор
-8, выражаемый отношением площадей, взятых
величине,
реальной s i
rea
и идеальной s i
idea
по
поверхностей
[3].
8 =
(2.11)
^ideal
Точность определения 8 зависит от числа и точности измерений.
Пористость.
Пористость
s - характеристика материала как
совокупная мера размеров и количества пор в твёрдом теле [13].
Величина безразмерная, изменяется
от 0 до 1, или выраженная в %
тогда
плотность
от
0
до
100 % ) . Через
твердой
фазы
р
пористость определяется по формуле:
Е
_Ргеш_
=
( .
1
2
1 2
)
Pideal
через число частиц n в единице объема (молярная концентрация)
E
(2.12а)
1_J}reai.
=
П-ideal
Или
£ = 1_Р
- реальная (экспериментально измеренная) плотность;
где p i
rea
Pideal - истинная
материала,
(2.126)
(идеальная, в отсутствие пор и дефектов) плотность
3
кг/м ;
т
П-real
"jT'
где m - масса образца с порами, кг ;
3
V - объем образца с порами, м ;
n
real
n
ideal
- число частиц в образце с порами;
- число частиц в образце в отсутствие пор и дефектов (идеальная упаковка
частиц).
г
Обратим внимание на /3 =
в (2.12а). Это не что иное, как
Pideal
массовая
доля материала с истинной плотностью, содержащегося в
реальном пористом теле. Аналогично, (3 =
U r e a l
- числовая
доля
n
ideal
частиц материала, содержащегося в реальном пористом теле. К
сожалению,
в
литературе
на
это
принципиальное
различие
практически не обращается внимание.
Нетрудно видеть, что в формула (2.12б) е есть частный случай g
- обобщенного фактора неидеальности Макаревича (GNF) [14], см.
гл.1, Приложение к разд.1.6.
При разрушении реальной пористой структуры
истирание) в формулу
(2.12б) будет добавлена доля
(дробление,
пористого
материала,
пошедшая
на его истирание
а, т.е. на
уменьшение
пористости
£ = 1-/3
Следовательно
g=(1-b+a)
е=(1-(3+а)
+ а
станет
(2.12в)
полным
аналогом
GNF
[14].
Таким образом, шероховатость 8 (при условии учета долей
поверхностей, приходящихся на «холмы» - а и «долины» - (3, как
дольная
величина),
связанная
с
отклонением
поверхности, будет частично определять
от
идеальности
величину пористости Е.
Пористость, включающая все виды дефектности твердого тела, это фактор
неидеальности
структуры
g
твердого
твердого тела, включая
тела.
Именно,
неидеальность
топологическую, важна для
адсорбции: чем больше отклонение от идеальности, т.е. больше
пористость, тем выше удельная поверхность твердого тела, о которой
поговорим ниже.
Формальное различие шероховатости твердого тела
пористостью
в
литературе
[10]
изображают
в
виде
с его
схемы,
приведенной на рис. 2.9.
Из схемы видно, что если глубина впадин меньше их ширины,
то такую поверхность называют шероховатой.
Если глубина впадин
больше их ширины, то такую поверхность называют пористой.
Поры
удобно представлять в виде полых цилиндров, хотя на практике, как
увидим позднее, все далеко не так, формы пор могут быть самыми
разнообразными.
Шероховатость:
* глубина впадин меньше ия ширины:
* имеется только
FjHfiijjHHH
поверхности
Пористость:
* глубина впадин бопыие их щирицы;
* имеются внутренняя и внешняя поверхности
Рис.2.9. Схема, иллюстрирующая
пористостью [10].
Твердые
материалы,
типа
различие
между
шероховатостью
кремнезема,
оксида
и
алюминия,
активных углей, и многие другие являются пористыми и обладают
большой внутренней поверхностью. Система пор в таких материалах
считается нерегулярной. Она состоит из крупных пор, связанных с
межкристаллитным пространством и имеющих диаметр около 100nm,
мезопор - с размером 2^50nm и м и к р о п о р - с размером частиц около
и менее 2nm (современную классификацию пор см. ниже).
В продолжение темы о модельных представлениях твердого
тела,
отметим,
ограничиваются
при моделировании
простейшими
реальных
структурными
поверхностей
элементами
не
ПСЭ,
полезными на I—III иерархических уровнях моделирования, однако
локальные
и
усредненные
характеристики
ПСЭ
могут
быть
использованы при моделировании на более высоких уровнях [11].
Возможности
таких
кристаллографическими
структур
ограничиваются
многогранниками
типа
октаэдра, икосаэдра, додекаэдра (рис.2. 9) и др.
правильными
тетраэдра,
куба,
Правильные
кристаллографические
многогранники
(рис.2.9)
описывают лишь строго
упаковки.
Икосаэдр {3,5}
регулярные
Исследованиям
нерегулярных
Додекаэдр (5,3)
упаковок,
Рисунок 2.9. Кристаллографические
преимущественно
многогранники,
используемые
моделировании твердых тел.
посвящено
сфер,
также
в
множество
работ.
В
монографии Б.В. Фенелонова [11] с глубоким пониманием физикохимических основ формирования структуры твердой поверхности, в
частности
таких
выполнен
обзор
используемых
сложных
систем,
современных,
в моделировании
как
пористые
прогрессивных
пористых систем. В
адсорбенты,
подходов,
частности,
подход на основе П С Э в виде полиэдров В о р о н о г о - многогранник,
мозаика Вороного (рис.2.10).
Рисунок 2.10. Двумерная мозаика Вороного для произвольной упаковки
одинаковыхдисков сточками в центре (слева). Комплексное
разбиение
Вороного-Делоне
(справа)
для
двумерного
пространства
(сплошные
л и н и и - м о з а и к а Вороного, п у н к т и р н ы е - м о з а и к а Делоне)
Этот подход применим к регулярным и нерегулярным упаковкам
частиц для проведения различных структурных, термодинамических,
энергетических, механических и других расчетов. Метод приложим к
любой системе точек, произвольно расположенных в пространстве,
где точки обособлены друг от друга и являются, например, центрами
частиц, атомов, молекул и т. д. Построение таких многогранников
осуществляют путем соединения центра данной частицы с центрами
соседних частиц. Далее через середины этих отрезков
перпендикулярные
им
плоскости,
пересечение
проводят
которых
дает
выпуклый многогранник (ПСЭ), который включает частицу и часть
окружающего ее пористого пространства. Ансамбль из таких ПСЭ,
состыкованных без промежутков и наложений, образует решетку или
мозаику.
Аналогичное
расположенных
на
построение
плоскости,
для
приводит
к
системы
двумерной
точек,
мозаике,
образованной многоугольниками. Пример такой двумерной мозаики
Вороного
показан
на
рис.
2.10
(слева).
Геометрия
таких
многогранников и мозаик (решеток) подчиняется правилам, которые
были впервые теоретически доказаны в работах Вороного и Делоне
[9, 15]. Особенности их построения приводят к тому, что такой
многогранник (или многоугольник в двумерном варианте) определяет
объем (поверхность) пространства, которое ближе к центру одной
частицы, чем к центру любой другой. В мозаике, построенной на
системе частиц-шаров равного размера, все многогранники (ПСЭ)
имеют выпуклую форму, в каждой вершине трехмерной мозаики
стыкуется не менее четырех соседних П С Э (обычно четыре), а каждое
ребро образовано стыковкой не менее трех соседних П С Э (обычно
трех).
Рассматриваемая
мозаика
содержит
однозначно
всю
структурную информацию о строении каркаса из сферических частиц
и пористого пространства в промежутках между частицами. В центре
каждого многогранника находится частица, занимающая долю его
объема, число соседних частиц равно числу граней полиэдра. Сферы
заданного радиуса находятся либо в точечном контакте, либо на
некотором расстоянии, создавая зазор, либо пересекаются (взаимное
внедрение).
Создаваемые
относительным
«эффекты»
расстоянием
между
выражаются
сферами
не
(зондами),
размером грани между соседними полиэдрами. В итоге
только
но
и
мозаика
Вороного позволяет анализировать структуру каркаса в виде решетки
узлов-частиц и связей.
Ребра многогранника образуют оси каналов (пор) переменного
сечения между частицами с минимальным размером r
min
части канала и максимальным размером г в
тах
в средней
вершинах полиэдра. Эти
размеры могут быть определены процедурой зондирования - путем
перемещения по оси каналов сферических
зондов
разного размера.
Такой алгоритм может быть использован для выделения границ и
определения
морфологии
пор,
рассматриваемых
как
связанные
области пористого пространства, доступные для перемещения зонда
размера r<r [2]. В этом случае морфология и объем пор определяется
z
размером зонда г .
2
Делоне [15,16] дополнительно
предложил особую
процедуру
построения на тех же центрах мозаики Вороного, но из тетраэдров,
также заполняющих это пространство без наложений и щелей. Такое
разбиение часто называют разбиением
(решеткой, мозаикой, графом)
Делоне (рис. 1.10, справа). Разбиение Делоне упрощает расчеты, т.к. в
многогранниках-тетраэдрах в каждой вершине сходится ровно три
ребра, а числа вершину, ребер е и граней f
связаны
простыми
соотношениями / — 2 = ^ = 3 , т. е. из трех характеристик лишь одна
независимая.
В настоящее время на основе комплексного подхода Вороного—
Делоне разработаны компьютерные программы для полного анализа
структуры
произвольных
перекрывающихся
исследования
шаров
систем
из
перекрывающихся
одинакового
проницаемости
или
и маршрутов
разного
или не
размера,
перемещения
зондов
разного размера [15], включая решение практических задач, - задач
ртутной порометрии [16].
Теория
перколяции.
Перколяция
(от
англ.
percolation)
-
просачивание через лабиринт, что особенно характерно для сложного
лабиринтного
пространства
пористых
адсорбентов
[17]. Теория
описывает не сами связанные системы, а происходящие
процессы.
Однако,
описание
процесса
характеристики системы. Теория перколяции
в них
невозможно
без
- описание закономер¬
ностей процессов, происходящих в системах из большого
числа
случайно связанных друг с другом элементов. Практически любой
процесс связан с преодолением разного рода барьеров,
которые
являются элементами системы. Если это барьеры разной высоты, а
связь их друг с другом случайна, то протекание процесса зависит от
доли преодоленных барьеров. При условии, что эта доля
мала,
процесс затухает, попадая в тупиковые ситуации. В других случаях
количество преодоленных барьеров окажется достаточным, чтобы
процесс охватил всю систему, переводя ее в качественно новое сос¬
тояние.
Теории перколяции предшествовали более простые решеточные
модельные
представления -
решеток: простая квадратная
числом Z=4; решетка
гексагональная
2D-
(шахматная доска) с координационным
Бете
решетка
простейшие типы регулярных
с
с координационным числом Z = 3;
Z=3;
звездчатая
решетка
(Z=4);
треугольная решетка (Z=6). В решеточных моделях пористое тело
представляют в виде решетки узлов и связей. Под узлами, чаще,
подразумевают расширения - полости или частицы разных размеров
и формы, а под связями -
не имеющие объема «окна»
между
полостями или контактные сечения между частицами, тоже разных
размера и формы, или все с точностью наоборот. Удобнее первый
вариант -
весь объем сосредоточен в узлах. Были
предложены
различные варианты представления пор в виде решеток. В частности,
был исследовал трехмерный вариант модели взаимосвязанных пор в
виде простой кубической решетки с координационным числом Z=6 из
пересекающихся цилиндрических капилляров разных радиусов [11].
Эта модель использована для анализа перемещения фронта ртути в
решеточном пространстве при заданном случайном распределении
размеров пор. Были получены правдоподобные результаты и каче¬
ственно новые эффекты, обусловленные взаимосвязью пор. Однако,
наибольшие
достижения
в
описании
пористости
получены
с
использованием перколяционных моделей.
Современное состояние теории перколяции позволяет решать
три основные типы задач, которые могут быть определены как задача
связей, задача узлов и смешанная задача [17].
Задача
связей.
Принимается,
что
проницаемость
решетки
полностью определяется свойствами связей, например, в решетке пор
проницаемость
определяется
исключительно
эффективными
размерами окон rw, т. е. размеры всех узлов (полостей) больше rw и
поэтому не влияют на проницаемость. Если допустить, что весь объем
пористого пространства сосредоточен в полостях (узлах), а окна
(связи) являются лишь двумерными сужениями с эффективными
размерами
rw,i, то
несвязанных
в
простой
капилляров
модели
постоянного
пористого
сечения
при
тела
в
виде
перемещении
менисков флюида, например, ртути, по Лапласу при равновесном
давлении Р флюида будут доступны
размером
r (P)
> r (P)
wi
L
= 2of cosX
все поры с эффективным
,
где
rj (P)—
l
равновесный
радиус кривизны мениска флюида при давлении Р. При повышении
давления
Р
происходит
последовательное
заполнение
пор
убывающего размера.
В капиллярах переменного сечения или решетке из взаимосвя¬
занных узлов и связей разного размера при продавливании флюида
будет складываться другая ситуация. Капилляры с характерным
размером r ( P ) , отвечающие лапласовскому условию, являются лишь
wi
потенциально проницаемыми и не заполняются, если связаны с
флюидом через капилляры меньшего размера. Реальное заполнение
начнется только после образования достаточно большого «связного
кластера» из узлов, связанных окнами размера r ( P ) с массивом
wi
флюида.
Подобная
наблюдается
при
последовательность
десорбции
освобождения
смачивающей
жидкости.
полостей
Основные
отличия сводятся к разным краевым углам смачивания и десорбции из
пленки в уже освободившихся порах полостей.
В достаточно больших для статистической обработки решетках
N
численная доля q = —
связей
N может
связей с размером > r ( P ) от общего числа
wi
рассматриваться
0
как
вероятность
того,
что
произвольно выбранная связь имеет размер > r ( P ) , т. е. является
wi
потенциально проницаемой. Другой важный параметр этой модели —
перколяционная вероятность Q ( q ) - М / М , где М - общее число узлов,
0
а М -
0
число узлов, связанных проницаемыми связями,
величина
Q(q)
численно
равна
вероятности
причем
принадлежности
произвольно выбранного узла такому связному кластеру.
При малых q вероятность образования достаточно протяженного
кластера из связанных узлов исчезающе мала, Q(q)= 0. Поэтому объем
вдавливаемого флюида (ртути) пренебрежимо мал, решетка в целом
не имеет проводимости. Эффектом заполнения отдельных полостей,
непосредственно
примыкающих
к
внешней
поверхности,
в
достаточно больших решетках пренебрегают.
Задача
узлов.
В задаче узлов исследуется
проницаемость
регулярных или нерегулярных 2D и 3D решеток, узлы
различаются.
Это
может
быть,
например,
решетка
из
которых
узлов,
образованных из разных фаз а и (3, а задача сводится к установлению
связности системы по фазе а или (3. В двумерной задаче узлов фаза (3
может быть компонентом, нанесенным на поверхность носителя. В
зависимости от состояния фазы ( связность и размер кластеров из
частиц фазы ( может быть сведена к задаче узлов. В принципе, при
решение задач узлов используется тот же подход, что и в задаче
связей.
В вариантах смешанной
задачи
перколяции
рассматриваются
ситуации,
когда
доступности
вводится
анизотропия
узлов
вероятности
и
связей
перколяции
скоррелированы,
в
некоторых
направлениях и т. д. Детально теоретические основы и практические
возможности теории перколяции рассмотрены, например, в [13, 17].
Фрактальные
объекты:
линии,
поверхности.
поверхности,
Фракталы
-
пространственные
геометрические
тела,
имеющие
сильно изрезанную форму и обладающие свойством самоподобия.
Фрактал от лат. Fractus-дробный,
ломаный, т.е. часть (фракция)
целого, доля. Впервые понятие фрактальной (дробной) размерности
появилось в 1919 г. в работе Феликса Хаусдорфа, но систематическое
изучение фракталов начато именно Бенуа Мандельбротом в 1975 г
[18].
Самоподобие
как основная характеристика
фрактала
означает,
что он более или менее единообразно устроен в широком диапазоне
масштабов. Так, при увеличении маленькие фрагменты
фрактала
получаются очень похожими на большие. В идеальном случае такое
самоподобие приводит к тому, что фрактальный объект оказывается
инвариантным
относительно
реального,
т.е.
предполагает
неизменность основных геометрических особенностей фрактала при
изменении масштаба. Для реального природного фрактала существует
некоторый
минимальный
расстояниях l>>l
min
масштаб длины
l ,
min
такой, что
его основное свойство — самоподобие
на
пропадает.
Поэтому реальные объекты имеют конечный размер, например крона
дерева, снежинка, узоры на окнах в морозную пору, облака и т.д.
Свойство точного самоподобия характерно лишь для
фракталов.
регулярных
Если для построения включить в алгоритм создания
фракталов
некоторый
элемент
случайности
(как
это
бывает,
например, во многих процессах диффузионного роста кластеров), то
возникают
так
называемые
случайные
фракталы.
Основное
их
отличие от регулярных состоит в том, что свойства самоподобия
справедливы только после соответствующего усреднения по всем
статистически независимым реализациям объекта.
Длина
береговой
линии.
Понятие фрактала возникло в связи с
задачей об определении длины береговой линии. При ее измерении по
имеющейся карте местности выяснилась любопытная деталь — чем
более
крупномасштабная
берется
карта,
тем
более
длинной
оказывается эта береговая линия.
Рисунок 2.13. Определение длины береговой линии между точками А и В.
Пусть,
например,
расстояние
по
прямой
между
расположенными на береговой линии точками А и В равно
^(рис.
2.13). Тогда, чтобы измерить длину береговой линии между этими
точками, мы
расставим по берегу жестко связанные друг с другом
вешки так, что расстояние между соседними вешками равнялось бы,
например, l = 10 км. Длину береговой линии в километрах между
точками А и В мы примем тогда равной числу вешек минус одна,
помноженному
на
10.
Следующее
измерение
этой
длины
мы
произведем подобным же образом, но расстояние между соседними
вешками сделаем уже равным l = 1 км. Оказывается, что результат
этих
измерений
будет
различным.
При
уменьшении
единицы
масштаба будем получать все большие и большие значения длины. В
отличие от гладкой кривой, линия морского побережья оказывается
зачастую
настолько
изрезанной
(например,
берег
норвежского
фиорда), что с уменьшением длины звена l величина L — длина
береговой линии — не стремится к конечному пределу, а возрастает
по степенному закону:
D
{R\
L = l(j)
где D >1 — некоторый
фрактальной
D,
тем
,
(2.12)
показатель степени, который называется
размерностью береговой линии. Чем больше величина
более
Происхождение
изрезанной
зависимости
является
(2.12)
эта
береговая
интуитивно
линия.
понятно:
чем
меньший масштаб мы используем, тем меньшие детали побережья
будут
учтены
и дадут
вклад
в
измеряемую
длину.
Наоборот,
увеличивая масштаб, мы "спрямляем" побережье, уменьшая длину L .
При некоторых значениях R периметр начнет включать и устья рек, а
далее - и их береговые линии. Однако детальный анализ показывает,
что в данном случае изображения берегового рельефа в разных
масштабах подобны, степень его изрезанности оказывается
мало
зависящей от масштаба. Эти изображения, как говорят в таких
случаях, в хорошем приближении статистически самоподобны или
масштабно инвариантны, т. е. практически не зависят от масштаба.
Видим, что для определения длины береговой линии L с
помощью жесткого масштаба l
необходимо сделать N = ^ шагов,
причем величина L меняется с l так, что N зависит от l по закону
результате с уменьшением масштаба длина береговой
линии неограниченно возрастает. Это обстоятельство резко отличает
фрактальную кривую от обычной гладкой кривой (типа окружности,
эллипса), для которой предел длины аппроксимирующей ломаной L
при стремлении к нулю длины ее звена l конечен. В результате для
гладкой кривой ее фрактальная
топологической
размерностью
размерность
D = 1, т. е. совпадает с
d.
Наблюдения показали, фрактальная размерность
Британских
островов: D = 1,3; Норвегии - D = 1,5; побережья Австралии - D =
1,1.
Отметим, что d-привычная нам Евклидова размерность ( d = 0 математическая
точка, d = 1 - линия, d = 2 - плоскость, d = 3 -
объемное пространство). Прозондируем фрактальный объект целиком
(d
мерными
"шарами"
радиуса
l).
Предположим,
что
нам
потребовалось для этого не менее, чем N(l) шаров. Тогда, если при
достаточно малых l величина D(l) меняется по степенному закону
D
N ( l ) ~ l , то D — называется хаусдорфной
размерностью
этого
объекта.
[19] или
Очевидно,
что
фрактальной
эта
формула
D
(R\
эквивалентна соотношению N = (-)
, использованному выше для
определения длины береговой линии. Формулу можно переписать в
логарифмическом виде
D = — lim
i^o
InN(l)
,
Inl
(2.13)
Это и есть общее определением фрактальной размерности D.
Величина D является локальной характеристикой данного объекта.
Данное определение дает целочисленные значения размерности
для обычных хорошо известных множеств. Так, для
множества,
состоящего
из
конечного
числа
изолированных
(минимальное число d - мерных "зондов ", с помощью
можем
точек,
D
которых мы
покрыть это множество) при достаточно малом размере
зондов совпадает, очевидно, с количеством точек, т. е. N(l) = N и не
зависит от диаметра этих зондов l (под "зондом" в зависимости от
задачи мы будем понимать также и куб, и квадрат, и просто отрезок
прямой).
Следовательно,
согласно
формуле
(2.13),
фрактальная
размерность этого множества D = 0. Она совпадает с обычной
Евклидовой размерностью изолированной точки d = 0 (точка
-
нульмерный объект).
Для
отрезка
прямой
линии
длиной
L
(состоящего
из
бесконечного числа точек) минимальное число N(l) одномерных
отрезков размера l , с помощью которых можно покрыть данный
отрезок целиком, равно, очевидно, N(l) = L/l. В этом случае, согласно
формуле (2.13) (или (2.12)), фрактальная размерность D = 1, т.е.
совпадает с Евклидовой размерностью отрезка прямой d = 1. Для
области
площадью
S
гладкой
двумерной
поверхности
необходимых для ее покрытия квадратиков N(l)
число
= — N(l) = S/l
достаточно малых l), поэтому фрактальная размерность
(при
гладкой
поверхности D=2. И наконец, для покрытия некоторого конечного
3
объема V необходимо N(l) = V/l кубиков с ребром l. Следовательно,
фрактальная размерность этого множества D = 3.
Итак, основное свойство фрактальных структур - самоподобие
выглядят такие
структуры
идеальных математических
на разных
масштабах
моделях это -
полная
одинаково.
и
В
идентичность
единичных фрагментов, как, например, показано на рис.2.13. В
реальных структурах по виду отдельного фрагмента можно сделать
заключение о строении объекта в целом.
Рисунок 2.13. Идентичность
фрактальной поверхности.
Таким
образом,
установленной
повторяющихся единичных фрагментов а и б на
фрактальная
Мандельбротом
геометрия
[18]
базируется
зависимости
на
доступных
значений периметра, поверхности и объема многих естественных и
синтетических
масштаба
объектов
измерения.
с изъязвленным
Свойством
рельефом
самоподобия
от
единицы
обладают
многие
обычные структуры, поэтому для фракталов принципиальным является
другое свойство: изменение их характеристик (массы, плотности,
площади поверхности, модуля упругости и т. д.) с изменением размера
фрактального объекта или пространственного масштаба, в котором
этот
объект
рассматривают.
Фрактальные
характеристики
степенную зависимость, в которой показатель степени -
имеет
дробное
число. Для таких объектов ряд соотношений, установленных для
привычных
одно-, дву-
или трехмерных
систем,
сохраняется
в
предположении, что их геометрическая размерность является дробным
числом.
Анализ
размерность
фрактальных
систем
любых линейных,
показывает,
поверхностных
что
фрактальная
и объемных
может быть рассчитана по соответствующим уравнениям.
форм
Для периметра
L,в
довольно широком диапазоне изменений
масштаба, результаты измерений определяются уравнением
L(r) = Lor
(2.14)
1-0
где L и D — константы, здесь и далее м ы заменили обозначение радиуса зонда
(щупа) l на более привычное г.
0
Простые уравнения (2.13-2.14) описывают периметр многих
изъязвленных
профилей,
включая
электронно-микроскопические
профили
изображения
галактик,
пористых
облаков,
тел,
или
кластеров, образующихся в перколяционных исследованиях решеток,
причем значения параметра D, изменяются в диапазоне 1<D< 2.
Для
площади
поверхности
с
s(r)
аналогичные
помощью
щупов
измерения
разного
изъязвленной
размерагприводят
к
уравнению
s(r)
согласно
которому
= s r
2 - D
величина
пропорциональна к о н с т а ш ш
0
(2.15)
0
доступной
поверхност^(г)
и радиусу щупаг в степени
(2-D),
причем значения D могут изменяться от 2 (гладкие поверхности) до 3
(предельно изъязвленные поверхности).
По аналогии получено выражение для доступных объемов V(r):
V(r)
3-D
= Vr
(2.16)
0
где значения параметра D изменяются от 3 до 4.
В уравнениях (2.14)—(2.16) целое число в показателе степени
соответствует обычной размерности объекта в рамках эвклидовой
геометрии: единица при измерении длины, 2 — при измерении
поверхности и 3 — при измерении объема. Обозначая это число как
эвклидову размерность d , можно заметить, что в каждом случае
E
пределы изменений фрактального параметра D связаны с обычной
E
размерностью объекта d как
E
d <D <
E
(d
E
(2.17)
+ 1)
E
или в общем виде
d
X (r)
D
=X r E~ E
E
(2.18)
0
где Х - соответствующий геометрический параметр;
Х > d - константа;
D - фрактальная размерность объекта.
Е
0
E
E
В результате периметр, поверхность и объем изъязвленных тел
связаны с размером щупа дробным показателем
Для
тел,
геометрии, D
описываемых
= d,
E
а Х
E
законами
= Х,
Е
-D ).
E
обычной
эвклидовой
и линейные размеры тела, его
0 Е
поверхность и объем не зависят от размера щупа. Н а основе этих
отличий Мандельброт разработал особую геометрию изъязвленных
систем, назвав ее фрактальной
объекты — фрактальными
геометрией,
а соответствующие
объектами.
В ряде случаев фрактальные свойства проявляются и при
измерении
удельной
поверхности
адсорбентов.
выполняются
соотношения,
связывающие
заполненном
монослое
адсорбента
поверхности
с величиной молекулярной
п
т
При
количество
этом
молекул
или величину
в
доступной
площадки адсорбата в
монослое о, м /моль [11]:
2-Ds
П ((0)
т
= П 0)
0
2
2-Ds
(2.19)
ИДИ S((j)) = S 0) 2
0
которые легко проверяются построением соответствующих графиков
в
логарифмических
координатах.
Один
из
них
основан
на
исследовании адсорбции молекул разного размера на фрактальной
поверхности абсорбента.
Рисунок 2.14. Схема зондирования поверхности адсорбента молекулами разного
размера.
Адсорбционные
методы
позволяют
выявить
условия,
при
которых поверхность покрывается монослоем молекул, и измерить
максимальное
число
адсорбированных
молекул
nm.
Тогда
использование экспериментально измеренных значений s («)
1
для
молекул разного размера «позволяет найти D . Для этого строится
s
график зависимости s(co) в координатах lns(m) — lnco, тангенс угла
наклона которого равен
что и позволяет найти фрактальную
размерность поверхности Ds.
Экспериментальные исследования показывают, что значения D
s
для
реально
существующих
поверхностей
могут
изменяться
в
широких пределах, вплоть до d= 3. То есть реально существуют
поверхности
(в основном
у
адсорбентов),
размерность
которых
приближается к эвклидовой размерности трехмерных объектов. Такие
поверхности
практически
полностью
заполняют
пространство.
Поверхности сколов или поверхности травления обладают меньшей
фрактальной размерностью, которая обычно не превышает величину
2,5.
Ширина
фрактальной
поверхности
w(L)
на
некотором
латеральном участке зависит от его размера L. Ширина поверхности
w(L)
при этом определяется как среднеквадратичное
отклонение
профиля на длине
)
L: w(L «= [{l-J^
[hf,
-
2 2
(hfM)] )
(2.Щ
где N — число точек на профиле длиной L ;
hfj — высота в точке j ;
hj(L) — средняя высота профиля длиной L .
L
Для фрактальной поверхности w(L) изменяется
степенному
закону
литературе
[6]
w(L)x
L . 5—показатель
связывают
соотношением:
D =3-5,
с
что
s
с ростом
шероховатости,
L по
в
фрактальной
размерностью
противоречит
определению
шероховатости 5, данному выше (2.11) и размерности dg=3, ( разность
dE=3
и
представляет
собой
разные
по
физическому
смыслу
характеристики).
В
настоящее
исследователями
в
время
фрактальная
приложении
ко
размерность
многим
используется
системам,
включая
адсорбцию. Применение этого метода показало, что многие реальные
объекты
мультифрактальны,
т.
е.
имеют
разную
фрактальную
размерность для разных масштабных диапазонов. Метод фракталов
используют для ограниченных диапазонов размеров. Например, для
описания формы рыхлых кластеров Размер кластера r, определяемый
как радиус наименьшей сферы, в которую вписывается этот кластер,
связан с числом частиц в кластере N и размером этих частиц r
0
соотношением [11]
где s - пористость агрегата.
Фрактальный
подход
используется
также
для
описания
ряда
геометрических свойств кластеров, образующихся при решении задач
методами теории перколяции.
2.2.3. Пористая
структура
Избирательность
определяются
и
адсорбентов
эффективность
структурой
и
адсорбции
природой
во
пористых
многом
веществ,
применяемых в качестве адсорбентов. Известно, что чем больше
величина удельной поверхности пористого тела и ее доступность для
адсорбирующихся или реагирующих молекул, тем выше степень и
селективность
сорбционного
процесса
или,
например,
каталитического превращения веществ в целевые продукты. В идеале
активность
пористых
тел
при
адсорбции
должна
быть
про¬
порциональна величине их удельной поверхности. Такое утверждение
справедливо
при
поверхности
допущении
пористого
тела,
энергетической
равномерном
однородности
распределении
его
активных центров по площади и равной силе их взаимодействия с
молекулами адсорбата. Поскольку химическая природа поверхности
реальных адсорбентов и катализаторов, приготовленных на их основе,
характеризуется
эффективность
неоднородностью,
то
избирательность
и
работы этих адсорбентов и особенно катализаторов
будут зависеть от распределения активных центров по их доступной
поверхности. Зная величину удельной поверхности, ее природу и
геометрическую характеристику, можно с некоторой вероятностью
(не
всегда
с
каталитическую
высокой)
предвидеть
активность
адсорбционную
повепхности.
и
Предвидение
адсорбционной и каталитической активности была и есть — одна из
важнейших задач, стоящих перед исследователи.
Величина поверхности функционально связана с ее пористостью
и является одной из основных, но не единственной характеристикой
сорбционных
и
каталитических
оптимизации
адсорбционного
свойств
или
твердого
тела.
каталитического
Для
процесса
подбирают такую твердую пористую структуру, чтобы в условиях
эксперимента не возникало бы стерических затруднений для подвода
реагентов
внутрь пор и отвода продуктов
реакции в объемную
газовую фазу. Чтобы предсказать размер пор, необходимый
достижения
ожидаемой
активности твердого тела,
для
необходимо
создать модель его пористой структуры. Это уже проблемы синтеза
адсорбентов или удачного выбора природных адсорбентов, заданной
структуры и пористости. Пористость Е, как фактор неидеальности
твердого тела g
неоднородность
[14], характеризует
поверхности
не только
твердого
тела,
но
геометрическую
и
величину адсорбционного потенциала в тонких порах,
определяет
от размеров
которых в свою очередь зависит возможность проникновения внутрь
не любых
молекул
адсорбата,
а только тех, размер,
форма
и
полярность которых допустимы. Решение научных и технологических
проблем межфазовых процессов в значительной степени облегчается
правильным выбором модели пористой структуры, определяемой,
например,
для глобулярных веществ в основном различием
в
упаковке первичных частиц (элементов). Поры в таких системах
представляют зазоры между частицами скелета и зависят от формы,
размера частиц и числа взаимных касаний [20].
Классификация
зависимо от
пористых
систем
по размерам
пор.
Не
строения пористых систем важное значение имеет
размер пор в них. Пористая структура твердого тела фактически
определяет
адсорбцию
газов,
паров
и
жидкостей.
Реальные
адсорбенты, обычно, обладают достаточно широким распределением
пор по размерам.
Классификация по размерам пор (микро- менее 2нм, , мезо- —2 -т
50нм и макропоры—50т 100-200нм) впервые предложена Дубининым
М.И. [21], а затем им же уточнена в отношении микропористых
систем:
микропоры
ультрамикропоры,
были
подразделены
на
более
тонкие
в которых адсорбционный потенциал повышен из-
за близости стенок пор, и супермикропоры,
имеющие промежуточный
размер между ультрамикропорами и мезопорами. По классификации
Дубинина [21] эффективные размеры микропор г ф соизмеримы с
э
эффективными размерами сорбирующихся молекул. Область размеров
(диаметров
или
ультрамикропоры
супермикропоры
ширины)
(собственно
микропор
микропоры)
распределена
на
- до (1,2—1,4) нм и
- от (1,2-1,4) до (3,0-3,2) нм. Поры с эффективными
размерами в интервале (3,0-3,2 < г ф < 100-200 нм) выделены в класс
э
мезопор.
Классификация
Дубинина
была
принята
в
форме
рекомендации Международным Союзом по чистой и прикладной
химии (ИЮПАК) [22].
Нижним пределом радиуса микропор считается
значение -0,13
нм, отвечающее критическому диаметру молекулы Не (0,26 нм),
проникающего
практически
Максимальный
размер
во
микропор
все
по
пустоты
твердого
энергетическим
тела.
расчетам
дисперсионного
диаметра
взаимодействия
молекулы
зависит
адсорбтива
и
также
от
отвечает
критического
эквивалентному
радиусугэкв, равному 2,5 d^[23].
Уточненные Границы линейных размеров мезопор, включающих
переходные области, находятся в интервале от 1,5-1,6 до 100-200 нм
[23], что соответствует пределу применимости уравнения капиллярной
конденсации
Томсона-Кельвина.
Мезопоры
обладают
развитой
удельной поверхностью, на которой последовательно протекают в
начале мономолекулярная, а затем полимолекулярная
завершаемая
заполнением
пор
по
механизму
адсорбция,
капиллярной
конденсации. То же самое и для макропор, но для них вклад от всей
полимолекулярной
адсорбцией
мал
по
сравнению
с
величиной
заполнения в центральной части вне действия поверхностных сил.
Заметим, что макропоры выполняют важную функцию в транспорте
молекул
адсорбтива
при
их
адсорбции
в мезо-
и
микропорах
на
основании
адсорбента.
Предложенная
классификация
построена
адсорбционных измерений и на различии механизмов сорбционных
явлений,
протекающих
в порах,
отличающихся
по размерам,
в
которых реализуется процесс капиллярной конденсации. При малых
размерах преобладает поверхностных потенциал стенок и заполнение
микропор не зависит от величины межмолекулярного взаимодействия.
Для широких пор поверхностным потенциалом практически можно
пренебречь и капиллярная конденсация в них практически ничем не
отличается от конденсации в объемной фазе.
Фомкин
А.А.
[7],
давая
характеристику
микропористым
адсорбентам, делает следующие акценты:
-
потенциальные
значительной
степени
барьеры
на
экранируют
входах
в
микропоры
влияние равновесной
в
фазы
и
молекул в соседних полостях на адсорбированные молекулы в порах.
Адсорбционное
поле
адсорбированному
диспергирует.
микропористого
веществу
свою
адсорбента
структуру
и
навязывает
сильно
его
Например, в каждой полости активного угля
или
цеолита в среднем находится от нескольких молекул до нескольких
десятков
молекул.
адсорбентов
резко
Эти
особенности
меняют
свойства
микропористой
вещества,
системы
находящегося
в
адсорбированном состоянии.
- в процессе адсорбции микропористые адсорбенты являются не
просто инертными носителями адсорбционного
поля, они
также
активно участвуют в адсорбционном взаимодействии [24]. Внешне это
проявляется
в
деформации
адсорбента
и
изменении
его
упругопластических свойств в зависимости от а, р, Т- параметров
состояния адсорбционной системы.
- распространение адсорбционных процессов в область высоких
давлений
привело
к
развитию
термодинамики
адсорбции,
учитывающей не только неидеальность равновесной фазы, но и
неинертность
функций
адсорбента.
адсорбции
Анализ
в зависимости
поведения
термодинамических
от а,р,Т-параметров
системы
позволяет сделать выводы о состоянии и структуре адсорбированного
вещества в микропорах.
- особенности свойств адсорбционных систем «микропористый
адсорбент - адсорбат» особенно ярко проявляются в
поведении
изотерм и изостер адсорбции, адсорбционной деформации адсорбента,
а также в поведении термодинамических функций адсорбционных
систем, их зависимости от а, р, Г-параметров состояния.
Классификация
изучении
пористых
пористых
Морфология,
с
Применительно
тел
тел
вводят
греческого,
по
понятие
это
их
морфологии.
При
«морфология»[11,
— наука
(учение)
о
13].
формах.
к твердым телам нет четкого понятия морфологии.
Однако, исходя из приложения этого понятия к различным сферам
науки (геологии, биологии и т.д.) и языка (в
лингвистическом
смысле), вытекает следующее определение: морфология
о формах
и структуре
значимых
единиц,
это —учение
из которых
система. Если под системой понимать пористое тело, то
пористых
тел изучает
(форму, структуру
как внешнее
строение
морфология
пористой
в целом, или его частей), так и
состоит
системы
внутреннее.
Классификации, основанные на формах, предлагались в работах
многих
авторов.
Широко
применяемая
классификация
по
геометрическому строению классификация —А. В. Киселева (см. в
[13]), предложившегов 1958 г. разделить все пористые тела на два
основных класса: системы с корпускулярной и губчатой структурами.
Пример
простейшей
корпускулярной
системы
силикагеля или в более общем случае —
—
структура
груда хаотично
или
регулярно уложенных частиц. Примеры губчатой структуры — пемза,
губка,
пористые
стекла
и
другие
системы
из
пересекающихся
полостей или капилляров простой или достаточно сложной формы. В
пористое
пространстве
морфологию
каналов
или
проще
характеризовать
полостей,
чем
выделять
размеры
и
отдельные
«частицы». Разделение пористых тел на корпускулярные и губчатые,
по сути, базируется на простоте выделения характерных первичных
элементов — частиц или пор, описания их морфологии и размеров.
Итак, пористые тела по своей форме и структуре делятся на два
типа — корпускулярные и губчатые. Корпускулярные
пористые
тела
это — тела, со слипшимися или сросшимися частицами разной формы
и размера с порами между этими частицами. В
выделить
Губчатые
первичные
пористые
и,
по
возможности,
таких телах можно
вторичные
частицы.
тела—тела, представляющие собой сеть каналов
и полостей различной формы и переменного сечения. В губчатых
телах невозможно выделить первичные структуры.
Большинство пористых систем являются
корпускулярными.
Это адсорбенты и катализаторы, получаемые методами коллоиднохимического осаждения, практически все кристаллические системы.
Губчатые системы образуются, например, при удалении какого-либо
компонента из многофазной системы. Если при таком удалении
остающаяся
фаза
корпускулярная
является
структура
корпускулярно-губчатой
кристаллической,
или
еще
системы.
В
один
таких
то
образуется
тип
смешанной
системах
гранулы
корпускулярного пористого тела пронизывают крупные поры
—
каналы губчатого строения. Исследования морфологии пористых тел
позволяет
понять
морфологическими
природу
пористости.
характеристиками
тела являются форма и размер первичных
Первичными
корпускулярного
пористого
частиц, способ и плотность
их упаковки в разных участках зерна, степень срастания частиц друг с
другом.
В
губчатых
системах
первичными
морфологическими
характеристиками
являются
форма
и размер
полостей
и
их
пространственное распределение, форма, размер и число каналов,
соединяющих
друг с другом
эти
полости.
Эти
характеристики
определяют все вторичные свойства — геометрические и физические.
Морфологическую систематизация типичных пористых мате¬
риалов по форме их первичных текстурных элементов развивал А. П.
Карнаухов
(Карнаухов).
Им
дополнительно
смешанных структур: корпускулярно-губчатые,
частицах
имеются
корпускулярные,
имеются
тонкие
поры
губчатого
выделены
когда в первичных
строения;
когда в крупных полостях
отложения
мелких
частиц.
А
классы
также
губчато-
губчатых
выделено
систем
шесть
наиболее типичных форм частиц в корпускулярных системах: сферы
или овалы, пластины, иглы или волокна, веретена, сплошные трубки
и многогранники. Но форма пор между такими частицами легко
определяется только в регулярных упаковках.
Многочисленные исследования морфологии пористых тел (в
основном,
методом
электронной
микроскопии)
позволили
систематизировать данные о форме первичных, а часто и вторичных
частиц в корпускулярных системах, а также о форме пор в губчатых
системах. Хотя эта форма в некоторых случаях оказалась сложной,
для большинства распространенных пористых тел удалось выделить
элементы сравнительно простой формы. В таблице (2.2) дан пример
систематизации типичных пористых тел по форме их первичных
(ПСЭ) и вторичных (ВСЭ) элементов [13].
Таблица
2.2.
Форма частиц и пор в пористых твердых телах
Тип
структуры
Корпуску­
лярная
Форма
частиц/пор
Сферические
овальные
частицы
Пластинки,
Системы
или Сажи
(ВСЭ).силикагели,
алюмосиликагели,
аэросилы, свежеполученные гели и аэрогели
аморфногостроения, песок
слои Каолинит, ликкит, тальк, слюда, монтмориллонит,
вермикулит, графит, активированные угли (ПСЭ),
сажи (ПСЭ).
гидроксид магния, оксид магния (ВСЭ).оксид
железа, йодистое серебро, оксид молибдена
Иглы, волокна
Гидроксид и оксид железа, оксид вольфрама,
гидроксид меди, гель оксида ванадия, оксид
циркония,бемит и псевдобемит, у - Л 1 0 , (ВСЭ)
волокнистый углерод, бумага, фильтры,пряжа,
волокнистые полимеры
Веретена
Оксид меди (ВСЭ).оксид железа (ПСЭ), сульфат
бария, гидроксил цинка
Трубки
Энделлит.
галлуазит,
хризотил
асбест,
палыгорскит. сепиолит
Мн огогранн ики
Карбонизованные
угли
(ПСЭ),
скелетныекатализаторы (ПСЭ), цеолиты, оксид
магния (ПСЭ), у - А 1 О ( П С Э ) , оксид железа
(ПСЭ),оксид
циркония,
напыленные
пленкиметаллов,
кристаллические
частицы
различного происхождения.
2
2
Губчатая
Эта
(мезопоры)
Каналы,
многогорлые
бутылкообразныепоры
классификация
на
изотермах
3
3
Пористые стекла, активированные угли (ВСЭ),
скелетные катализаторы (ВСЭ), целлюлозные
фильтры, пленки анодного оксида алюминия,
вспененные ипористые материалы из металлов,
керамики, полимеров
основана
на
адсорбции,
выделении
в
области
которых
пор
происходит
капиллярная конденсация адсорбата по гистерезисному механизму
адсорбции(смачивания). Не смотря на достоинства
классификации
Киселева - Карнаухова, она требует расширения из-за невероятно
обширного, разнообразия морфологии пористых материалов.
JI. В. Радушкевич
описания
[25] для более общего
пористых сред предложил
статистического
классифицировать
по
двум
признакам:
механизму
характеру
образования
текстуры.
или
По механизму
происхождения
образования
и
выделены
основные группы: системы сложения и системы роста.
сложения
общему
две
Системы
образуются при случайном соединении (суммировании)
первичных частиц или их агрегатов. Для непористых частиц это
аналог корпускулярных систем А. В. Киселева. Системы роста
—
результат роста системы пор. Например, в процессах выгорания,
растворения и т. д., или ориентированного роста каркаса твердой
фазы,
происходящего,
в частности,
при
образовании
цеолитов,
кораллов. Для систем роста часто характерна индивидуальная, почти
неповторимая
морфология.
Детальное
описание
связывают с механизмами образования, а системы
описываться
общими
статистическими
их
текстуры
сложения
могут
закономерностями.
Комбинации систем роста и сложения приводят к сложным системам.
Классификация
по
системе
сложения—
связана
с
четко
упорядоченной и разупорядоченной структурами и требуют особых
подходов. В.Б. Фенелонов [11] в фундаментальной
монографии,
посвященной
современной
стремительно
развивающейся
области
синергетики - физической химии формирования супрамолекулярной
структуры
адсорбентов
и
катализаторов,
предлагает
дополнить
классификацию Радушкевича классификацией Китайгородского А.И.
[13] по степени упорядоченности
систем, выделением двух классов
моделей разупорядоченных сред: а) модели полного хаоса без какой-
либо корреляции между положениями частиц; б) модели с наличием
таких корреляций (Табл. 2.3) [11].
Таблица. 2.3.
Классификация степени упорядоченности по [Китайгородскому]
Реализация
Регулярная упаковка первичных элементов
Отсутствие ближнего и дальнего порядков
Дефекты в регулярной упаковке
Наличие только ближнего порядка в упаковке
Тип порядка
Порядок
Хаос
Беспорядок в порядке
Порядок в беспорядке
В
моделях
частицы,
так
первого
и
типа
их
допускаются
произвольное
как
изолированные
взаимное
внедрение
(наложение)-класс типа хаотично расположенных сфер.
В моделях второго типа (модели
аморфных тел и жидкостей), в которых
наложение частиц не допускается, они
соприкасаются или разделены зазором.
Взаимное
частиц
определяется
функций
Рисунок
2.15.
Радиальная
функция
распределения
случайной
плотноупакованной
системы
одинаковых
сфер
W(R)
(вверху)
и
схема
ее
построения (внизу) [11]
плотноупакованной
радиуса R
0
расположение
W(R),
атомов
или
корреляционной
которая
определяет
вероятность обнаружения час­
тицы
на
центра
заданном
расстоянии
какой-либо
R
от
произвольно
выбранной частицы. Схема определения
функции
системы
из
W(R)
жестких
для
случайной
монодисперсных
показаны на рис. 2.15. Здесь произвольно
сфер
выбранная
частица выделена черным цветом, ее центр совмещен с началом
координат. Вокруг этого центра описывают сферы возрастающего
радиуса R.
Число
частиц
dN
в
сферическом
слое
толщиной
dR,
находящихся на расстоянии R от произвольно выбранной частицы,
равно
2
dN =
4nR i-jW(R)dR
где N — суммарное число частиц в объеме V ;
N
При
- среднее число частиц в единице объема.
R<R
величина
0
W(R)
=
0,
но
при
R> R
0
растущая
координационная сфера начинает пересекать соседние частицы, в
результате значения W(R) увеличиваются, достигают
некоторого
максимума и начинают снижаться. С увеличением R эта ситуация
повторяется с быстрым размытием максимумов функции W(R). В
пределе
значения
W(R)
пропорциональны
средней
плотности
упаковки. Число достаточно резко выраженных максимумов обычно
не больше трех, положения этих максимумов соответствуют средним
расстояниям от центра выбранной частицы до первых, вторых и т. д.
соседей. Зону первого максимума называют первой координационной
сферой,
площадь
под
этим
максимумом
пропорциональна
координационному числу данной структуры, т. е. среднему числу
ближайших
соседей, зону
второго
максимума
называют
второй
координационной сферой, площадь под ним соответствует числу
соседей второго уровня, и т. д.
Рассмотренные выше модели относятся преимущественно
упаковкам
частиц,
корпускулярной
т.е.
могут
рассматриваться
как
модели А. В. Киселева. Морфология
к
развитие
пористого
пространства в таких системах более сложна, и поры даже для таких
систем обычно моделируются в виде пучков цилиндрических каналов
разных размеров, пор в виде непересекающихся плоских щелей и т. д.
Правило
«обращения».
Твердый
каркас
и
пористое
пространство взаимосвязаны и образуют единую пористую систему.
Поэтому корпускулярные модели могут быть обращены в губчатые и
наоборот. Все зависит от доли корпускул b и доли пор s в пористом
теле, в сумме b +s =1. Это простое правило позволяет моделировать
пористое тело либо как систему пор, либо как систему частиц. Выбор
«точки отсчета» определяется условиями задачи или более простым
способом
описания системы. Часто (рис.2.16) пористое тело можно
представить двумя взаимопроникающими лабиринтами, где лабиринт
пор образует пористое пространство и занимает долю объема, равную
s, а лабиринт частиц образует каркас, который занимает долю объема
£ = (!-£)
(2.22)
причем оба лабиринта имеют общую межфазовую поверхность (для
сравнения см. GNF Макаревича - формула 2.11).
Рис.2.16. Модели гранул из монодисперсных частиц. а — гомогенная,
однородно-пористая упаковка, б — первичные частицы сформированы в агрега­
ты близкого размера (поры в агрегатах и между агрегатами-два разных
лабиринта пор); в — первичные частицы сформированы в агрегаты разного
размера (перераспределения пор в агрегатах и м е ж д у агрегатами) [11].
Эти
лабиринты
неупорядоченную
могут
иметь
упорядоченную
или
структуру, образовывать связные системы или
включать дискретные кластеры в виде изолированных групп пор или
частиц. Многие свойства таких лабиринтов можно
моделировать
решетками узлов и связей, подразумевая под узлами расширения (час­
тицы или полости), а под связями — места контактов узлов (частиц
или полостей). Такие подходы эффективны при анализе свойств и
процессов, определяемых не морфологией индивидуальных пор или
частиц, а их взаимосвязностью.
Пористые
Наиболее
тела
простым
теоретической
глобулярные
классической
способом
интерпретации
структуры
глобулярной
экспериментальной
полученных
пористых
структуры.
проверки
результатов
и
являются
тел, скелет которых построен из
правильно упакованных шаровидных непористых частиц одинакового
размера.
В
корпускулярной
системе
первичными
элементами
являются глобулы. Такая простейшая модель дает относительно ясное
представление о форме пор и структуре твердого остова, а исходя из
адсорбционных измерений, позволяют оценить размеры частиц (d),
числа их касаний (n) и радиусы пор (г). Анализ таких структур
практически сводится к установлению размера частиц (лишенных
пор) и определению капиллярной конденсации для элементарной
сорбционной ячейки, состоящей из двух контактирующих шаров [20].
По типу упаковки, точнее по
максимальному
Рисунок
2.17
(сверху),
заполнению
пространства
порами,
глобулярные
структуры
бесконечное
подобные
множество
имеют
решений,
а
—
которые можно классифицировать по
б
гексагональная;
в
—
координационным
октаэдрическая;
г
—
П
л
о
т
—
т е т
р
н
е
а
я
у
п
а
к
о
йш
кубическая;
а э д
р
в
к
а
ш
а р о в
:
определяемым
и ч е с к а я
ближайших
числам,
соседей,
12-гексагональная
связанных
и кубическая
с
количеством
центральной
гране-центрированная
частицей:
упаковки.
Геометрическая задача построения такой упаковки заключается в том,
что на плоский слой шаров, плотнейшим образом прилегающих друг
к другу (рис. 2.17), накладывается второй слой. Каждый шар второго
слоя помещается в углубление между тремя шарами первого. При
наложении третьего слоя шаров возможны
два варианта: центры
шаров третьего слоя располагаются над центрами шаров первого
(гексагональная
упаковка),
либо
они
займут
промежуточные
положения (кубическая полнейшая упаковка). Доля
пространства,
занятая шарами 0,7405, следовательно, пористость 8=0,2595.
Аналогично,
глобулярные
структуры
с
координационным
числом:
n=8 -кубическая объемацентрированная 8=0,3198;
n=6
(простая
кубическая
упаковка)
выстраиваются
последовательным наложением шаров (рис.2.1 8), упакованных по
квадратной сетке с пористостью 8=0,4764;
n=4 -тетраэдрическая, 8=0,6599;
п=3 и даже п=2 - р ы х л а я упаковка, а 8=0,815 и более.
С учетом допущений в рассматриваемых моделях при их явных
упрощениях
все
же
возникает
возможность
создать
образ
элементарной поры. Такого рода моделирование, основанное
квазиупаковках глобул, в бесконечном ряду которых
на
числа касаний
шлежат в интервале от 2 до 12, позволяет оценивать
значения
пористости 8 от = 1 до 0,26.
Что
бы
пористые
типа
привести
структуры
в
систему
были
реальные
глобулярного
специально
синтезированы образцы силикагелей с
Рис.2.18. Упаковка шаров с
координационным
числом
6:
а-плоская
упаковка
по
квадратной
решетке;
би­
кубическая
упаковка
в
многограннике с элементарными
порами в нем.
широким
диапазоном
текстурных
характеристик с размером глобул от 5
до 9 нм, удельной поверхностью от
800 до 310 м /г и числом
касаний
глобул от 3,1 до 7,4.На их основе был создан эталонный ряд из
восьми образцов от рыхлых до плотноупакованных [13] (Табл. 2.4).
Из
таблицы
наглядно
видно,
что
вариация
экспериментально
полученных первичных параметров - размер глобул и плотность их
упаковки определяют вторично измеряемые параметры: удельная
поверхность s , объем V и размер пор d .
yd
n
n
Таблица 2.4.
Параметры силикагелей эталонного ряда с широким диапазоном
текстурных характеристик.
№
образца
1
2
3
Параметры скелета глобул
4,нм
п
8уд, м / г
310
9,0
3,1
340
8,0
4,0
430
4,0
6,5
2
Параметры пор глобул
У ,см3/г
с1 ,нм
8
1,76
0,795
21,0
0,92
0,67
9,6
0,90
0,665
8,0
п
п
4
5
6
7
8
390
575
625
500
800
Глобулярная
0,80
0,49
0,49
0,39
0,25
4,2
5,5
5,5
6,1
7,4
7,0
5,0
4,5
5,5
5,0
модель
позволяет
0,638
0,52
0,52
0,462
0,35
описать
6,8
3,8
3,0
2,8
2,5
текстуру
многих
реальных пористых материалов, состоящих из аморфных первичных
частиц.
Это в первую очередь
коллоидно-химического
имеют
силикагель,
катализаторы,
системы,
осаждения.
Наибольшее
аэросилы,
аэрогели,
из не силикатных
грубодисперсные
глобулярные
получаемые
методами
распространение
алюмосиликатные
систем-сажи.
Можно
системы-строительные
указать
материалы:
песок, грунты, кирпич и пр.
Как
уже отмечалось
выше,
для характеристики
пористых
структур широко применяется уравнение капиллярной конденсации
Томсона-Кельвина.
2.3. Классическая теория капиллярной конденсации
Теория
пористыми
объемной
постулирует,
телами
что дополнительное
происходит
конденсации
в
порах
на вогнутой
покрытого
адсорбционной
адсорбции
в
адсорбента
поверхности
пленкой.
мезопористых
поглощение
системах
связана
вследствие
твердого
Характерная
с
пара
тела,
особенность
капиллярной
конденсацией, которая может приводить к объемному заполнению
мезопор жидкой фазой адсорбата при относительном давлении паров
Р/Р <1,0
0
[13,
25,
конденсация-наличие
26].
Необходимые
мезопор,
условия
смачиваемость
адсорбированной фазой, температура сорбции ниже
капиллярной
их
стенок
критической.
Причина
капиллярной
конденсации
менисков
адсорбированной
фазы,
-
в
образовании
равновесное
вогнутых
давление
Р
над
которыми определяется уравнением Кельвина
Многочисленными экспериментами доказано, что над выпуклой
поверхностью
равновесное
давление
Р
давление
больше, а
над
вогнутой меньше, чем над плоской поверхностью. Это объясняется
смещением фазового равновесия жидкость — пар для поверхности,
разной по знаку кривизны. Для молекулы пара, попавшей на выпуклую
поверхность, дисперсионное взаимодействие с молекулами жидкости
меньше, а на вогнутую — больше, чем на плоской поверхности из-за
более коротких расстояний между ними. В первом случае молекула
пара удерживается слабее, а во втором — прочнее, чем на плоскости, и,
соответственно, наблюдается сдвиг
равновесие в сторону большего
или меньшего давления насыщенного пара.
Количественно зависимость упругости насыщенного пара от
кривизны сферической поверхности впервые была изучена Кельвиным
(Томсоном) [7]. Уравнение Кельвина следует из закона Лапласа для
искривленных поверхностей (см. ( 1 . 9 1 - 1.95), гл.1)
RTln(j)
= ±
™
г
PJ~-
ж
(2.23)
или в виде
P = P
s
e
X
p { ±
2
^ )
(2.23а)
Оно связывает давление насыщенного пара Р над выпуклым (+)
или вогнутым ( - ) сферическим мениском радиуса r с давлением
насыщенного
поверхностью
пара P
s
при
жидкости,
данной
имеющей
температуре
молярный
T
над
объем
плоской
V
m
и
поверхностное натяжение о.
Т — абсолютная температура, R
—
газовая постоянная.
В реальных
дисперсных
системах, согласно закону Лапласа, для пористых и
систем
важное
значение
имеет
снижение
упругости
насыщенного пара AP. Если поры в твердом теле имеют вогнутую
поверхность
(как
в
губчатых
системах),
то
жидкоподобная
адсорбционная пленка на ней также будет вогнутой. Давление пара над
ней станет насыщенным еще до того, как оно примет значение Р . Чем
0
больше кривизна этой пленки, тем раньше пар будет насыщенным и
тем раньше начнется его конденсация в порах твердого тела. В
системах
с малыми
порами
и высокой
кривизной
поверхности,
капиллярная конденсация начнется раньше, чем в крупнопористых. Это
заключение следует из уравнения Кельвина, связывающего упругость
насыщенного пара с радиусом кривизны сферического мениска. Решая
обратную
задачу
по
упругости
пара
можно
определять
радиус
кривизны сферического мениска г ф. В пористых телах поглощение
с
пара происходит по двум принципиально различным механизмам. Вопервых, это адсорбция пара на поверхности, во-вторых, объемная его
конденсация в порах. Рассматривается и
третий механизм, но он
«работает»
системам
только
в
микропористых
-
объемное
адсорбционное заполнение микропор. Этот механизм будет рассмотрен
в теории объемного заполнения.
Уравнение (2.22) справедливо для капиллярной конденсации
сферических поверхностей. Реальные дисперсные системы имеют
поверхность самой различной формы. Поэтому дают общее описание
этого явления для любых поверхностей через их кривизну (см. раздел
1.7).
Кривизна, как величина обратная радиусу: для сферы
; для
1
цилиндра
; для седловидной (гиперболической) поверхности с
(-+-)
главными радиусами кривизны rj и г
2
равна
Видим, что
кривизна сферы в любой ее точке т.е. радиус кривизны сферы равен
ее геометрическому радиусу. Кривизна цилиндрической поверхности
т.е. радиус кривизны цилиндра равен его удвоенному геометрическому
радиусу, а кривизна цилиндрической поверхности равна половине
кривизны сферы такого же радиуса. Для седловидной поверхности
главные радиусы кривизны имеют противоположные знаки, поскольку
центры для этих радиусов находятся по разные стороны от касательной
плоскости
в
любой
точке
поверхности.
Если
представить
себе
жокейное седло, то плоскости, рассекающие его вдоль, дают кривые с
положительными радиусами кривизны, центры которых находятся над
седлом, а перпендикулярные плоскости (поперек седла) дают кривые с
отрицательными радиусами кривизны, центры которых находятся под
седлом.
Седлообразная поверхность может иметь равную, или наоборот,
различную кривизну в любой точке. Будет ли поверхность седла
вогнутой или выпуклой зависит от соотношения радиусов кривизны r
j
Тогда уравнение
Кельвина
для
соответствующих
радиусов
кривизны поверхностей,
RTln
2aVт
r
±
\P )~
S
(2.24)
в зависимости от представления
пор абсорбента в виде сфер,
цилиндров или гиперболоподобными может быть использовано для
расчетов
радиусов
пор
твердого
материала,
называемого капиллярно-конденсационного
гистерезис
из
так
гистерезиса.
Капиллярно-конденсационный
конденсационный
исходя
гистерезис.
можно
наблюдать
Капиллярнона
изотермах
адсорбции в мезопористых материалах при снятии кривых адсорбциидесорбции. При повышении давления пара на пористом адсорбенте
идут процессы адсорбции и капиллярной конденсации, при уменьшении
давления пара — процессы десорбции и испарения
конденсата,
которые
конденсационным
могут
гистерезисом.
капиллярного
сопровождаться
капиллярно-
Физическая адсорбция обратима и за
гистерезис на изотермах сорбции -десорбции ответственна капиллярная
конденсация.
Модель
гистерезиса,
цилиндрических
рассматривая
пор.
сорбцию
Коэн [27] объяснил
пара
в
простейшей
одиночной цилиндрической поры двух видов — закрытой
конца (пробиркообразная пора) и открытой
цилиндр).
с обоих концов
причину
модели
с одного
(полый
При
постепенном
повышении
давления
пара
толщина адсорбционной пленки
на
стенках
поры
пробиркообразной
увеличивается.
Вогнутая
поверхность пленки имеет
два
радиуса кривизны: на дне поры
радиус
Ti,
равный
геометрическому радиусу
Рисунок 2.19.
Схема капиллярной
конденсации в цилиндрической поре «с
дном» w(а) и «без дна» v(в);
внизу
,- h т. J
показаны изотермы адсорбции. Двойные линии изображают равновесную
адсорбционную пленку на стенках (по
Карнаухову]).
с
ф
е
р
и
ч
е
пленки
стенках
с
к
о
,
v r
л
2.19)
1
и
т
'
т2,
радиус
удвоенному
0
г
ц
поверхности
й
(рис.
г ф=
на
ее
равный
геометрическому
радиусу 2г цилиндрической поверхности пленки: (т =г ф=г ; т = 2 г ф =
ц
1
0
ц
2
0
цУ
2г
На начальной стадии сорбции пар не насыщен по отношению к
сферической, а тем более цилиндрической поверхности адсорбционной
пленки и капиллярная конденсация не имеет места.
Согласно
пара P/P
s
уравнению (2.23) между относительным давлением
и радиусом кривизны сферического мениска r для данного
адсорбтива
и
данной
температуры
существует
функциональная
зависимость. При условии, что относительное давление P/P достигнет
s
значения,
поверхности
соответствующего
адсорбционной
радиусу
пленки
кривизны
на дне поры,
сферической
пар
станет
насыщенным по отношению к этой поверхности и в поре начнется
капиллярная конденсация. Рост толщины пленки h конденсата на дне
поры пленки вызовет уменьшение радиуса кривизны поверхности тЛт сорбированной фазы и по отношению к достигнутому давлению
пара
система
станет
нестабильной,
что
вызовет
спонтанное
заполнение всей поры. В результате у открытого конца поры обра¬
зуется сферический мениск той же кривизны, что и в начале спон¬
танного процесса. При дальнейшем повышении давления пара его
кривизна будет уменьшаться вплоть до образования плоской по¬
верхности конденсата при Р = Р .
s
При десорбции (снижении давления пара) вновь образуется
сферический мениск и в обратном порядке пройдет весь процесс
испарения, включая спонтанное
опорожнение поры и уменьшение
толщины адсорбционной пленки. Обратный процесс будет полностью
соответствовать прямому, поэтому для такой модели цилиндрической
поры гистерезис на изотерме будет отсутствовать.
Процесс сорбции в открытой цилиндрической поре отличается
от
описанного
тем,
что
в
ней
может
образовываться
только
цилиндрический мениск в виде поверхности адсорбционной пленки
на стенках поры. Радиус кривизны этого мениска (уравнение (2.23а))
вдвое больше, чем на дне закрытой поры, поэтому капиллярная
конденсация начнется в соответствии с уравнением Кельвина (2.24)
при большем относительном давлении. Как только будет достигнуто
это давление, пора спонтанно заполняется конденсатом.
испарение
конденсата
Однако
будет происходить точно так же, как
в
закрытой поре, т.е. со сферического мениска в устье поры. Поскольку
заполнение
поры
происходит
при
давлении,
соответствующем
цилиндрическому, а испарение — сферическому мениску, изотерма
адсорбции будет иметь гистерезис.
Рассмотрение
процесса
сорбции
в
двух
моделях
цилиндрических пор показывает, что капиллярная конденсация может
происходить как с гистерезисом на изотермах, так и без гистерезиса, в
зависимости от формы пор.
Модель
пор
бутылкообразных
сыграла
важную
роль
пор.
в
Модель
развитии
«бутылкообразных»
теории
конденсации. Идея этой модели принадлежит
капилляной
Кремеру(1931 г.) а
затем подробно разрвита в работах Мак Бена (1935 г.), Рао (1941 г.) и
Баррер и сотр. [11]
Эти
поры
представляют
собой
комбинацию
сферической
полости и цилиндрического горла. Общее свойство таких моделей в
том, что замкнутая полость с максимальным размером R связана с
n
общим объемом системы через сужение («горло») с минимальным
размером R <R .
z
n
Эти модели являются комбинациями простейших
элементов -сферического и цилиндрического (рис. 2.20, а) или двух
цилиндрических капилляров разного размера (рис. 2.20, б).
Процесс капиллярной конденсации в
происходить
различным
образом в зависимости от
соотношения
них
может
размеров
полости.
учитывается
Рис.2.20.
При
уменьшение
этом
этих
Простейшие
варианты
модели
«бутылкообразных
пор».
Поясн. см. в тексте.
размеров
R
H
адсорбционной
и R
z
за счет
пленки.
толщины
т
Заполнение и освобождение таких пор зависят от соотношения
размеров R
n
и Я
[11]. При R /R <
г
n
2 спонтанная
г
конденсация
начинается в полости и сопровождается полным заполнением всего
капилляра, включая горло. Испарение из такого элемента начинается
с образования полусферического мениска критического размера в
горле и продолжается до полного испарения из полости, в которой
останется только адсорбционная пленка на поверхности. Спонтанное
заполнение «бутылкообразной» поры с размерами R /R <
n
2 должно
z
происходить при т„, уменьшенного наг, а освобождение — при т ..
г
Если поры в твердом теле имеют, например,
седловидную
форму, то при адсорбции, в результате конденсации
заполнение пор будет происходить
адсорбтива,
при кривизне, которую имеет
седлообразный мениск в момент смыкания менисков в горле поры, а
при
десорбционном
происходить
уже
вписанного
в
при
горло
сорбции-десорбции
Поскольку
процессе
-
опорожнение
кривизне
почти
поры.
Это
проявится
на
сферического
различие
ветвях
будет
мениска,
в
характере
графика
изотермы.
кривизна мениска горла поры больше
кривизной седла, то
поры
по сравнению с
адсорбционная ветвь всегда лежит
правее
десорбционной. При этом давление, при котором будет происходить
заполнение широкой части колбообразной поры, учитывая толщину
адсорбционного слоя т, будет иметь место при
Г
Р
2
T
s
где г -Лт
пленки.
2
2
=
Ё Х Р
2aV
m
[ * (г - Аг )Кт\
2
1
(
2
.
2
5
а
)
2
- радиус кривизны седла, у м е н ь ш е н н ы й на толщину адсорбционной
При десорбции испарение из горла поры, перекрытого мениском
большей кривизны, наступает при более низком значении
Г
Pi
=eXP
T
2
a
V
1
m
±
( 2
[ (r -Ar )RT\
s
1
1
"
2 5 б )
т. е. когда давление пара в системе меньше, чем над вогнутым
мениском жидкости в капилляре.
Как видим, при экспериментальном получении изотерм сорбции
-
десорбции
на мезопористых
наблюдается
несовпадение
(гистерезисная
Поскольку
петля),
формы
разнообразными,
гистерезисных
характерных
гистерезиса,
ветвей
капиллярной
адсорбентов
соответственно
На
формы
предложенная
и
приведена
изотерм
десорбции
конденсацией.
могут
разнообразны
рис. 2.21
петель
на кривых
адсорбции
вызванное
пористых
петель.
типов
адсорбентах
быть
и
формы
классификация
капиллярно-конденсационного
комиссией
IUPAC
[22].
Эта
классификация основана на проведенном де Буром анализе ситуаций
в ряде индивидуальных пор простейшей формы.
Н4
Рисунок
2.21. Характерные типы петель
капиллярно-конденсационного
гистерезиса по классификации IUPAC [3]. По ординате величина адсорбции a,
по абсциссе относительное давление пара p/p .
s
Петля гистерезиса типа Н1 обусловлена наличием открытых с
обоих концов капилляров, имеющих трубчатую форму с самой
различной
конфигурацией
поперечного
сечения
(круглая,
трехугольная, квадратная, многогранная и т. д.) и небольшой разброс
радиусов
по
величине.
крупнопористых
и
Тип
Н1
среднепористых
характерен,
например,
силикагелей,
саж
и
для
других
глобулярных адсорбентов.
Петля гистерезиса типа Н2
обусловлена капиллярной
кон¬
денсацией между двумя параллельными пластинами или листами,
сравнительно легко передвигающимися относительно друг друга (рис.
25, а - в). Ярко выражен тип Н2 для некоторых пористых стекол типично
губчатых структур. Для глобулярных,
и для
губчатых
структур наблюдаются оба эти типа, что вероятно, определяющим
форму гистерезиса, является не форма пор, а соотношение размеров
горл и полостей, а также однородность этих размеров.
Петля гистерезиса типа Н3 связана с наличием в веществе
тероидальных, а также сквозных и замкнутых бутылкообразых пор с
одинаковыми радиусами полостей и различными радиусами входных
отверстий. Структуры подобного типа вполне реальны и
образоваться
гелеобразных
в
процессе
адсорбентов.
неравномерной
Тип
НЗ,
как
сушки
могут
некоторых
считают
многие
исследователи, более тесно связан с формой пор. Он наблюдается для
очень
многих
активных
углей
пароводяной
активации
и
модифицированного монтмориллонита с раздвинутыми с л о я м и /
для
В
обоих случаях поры имели щелеввдную форму с почти плоско¬
параллельными стенками.
Кроме того, петлю гистерезиса данного типа дают пористые
тела с конусообразными порами одинаковых размеров и непрерывно
изменяющимся
эффективным
радиусом, если г ф<<г.
Заполнение
э
таких пор, как и в случае открытых цилиндрических, происходит при
относительном
начинается
давлении,
при p/p ,
s
относительном
соответствующем
соответствующем
давлении,
отвечающем
2r,
а
опорожнение
г ф и заканчивается
э
радиусу
г.
при
Аналогичный
гистерезис дают клинообразные капилляры с закрытыми сторонами и
открытыми концами. Адсорбенты с петлей гистерезиса типа
Н3
встречаются редко.
Петля гистерезиса типа Н4 присуща системам с набором не¬
однородных
капилляров,
имеющих
широкую
часть
полости
и
разнообразные по величине короткие узкие горла. Такие капилляры, с
одной стороны, способны сдвинуть адсорбционную ветвь изотермы в
область более высоких относительных давлений, а с другой — в силу
гетерогенности размера горл и равномерности их распределения
обеспечивают постепенный спад десорбционной ветви типа Н3 [20].
Тип Н4 гистерезиса, по-видимому, отражает комбинацию микропор и
мезопор, встречающуюся в некоторых типах активированных углей.
Типы НЗ и Н4 имеют характерную особенность, отличающую их от
других, состоящую в том, что ширина петли, измеренная как разность
ординат десорбции и адсорбции, приблизительно постоянна во всей
области гистерезиса. Кроме того, тип НЗ имеет еще две характерные
особенности. Первая из них заключается в том, что адсорбционная
ветвь гистерезиса имеет типичную для I I типа по классификации
Брунаура
[25],
что
свидетельствует
о
наличии
полимолекулярной адсорбции. Вторая особенность —
только
отсутствие
горизонтального участка на десорбционной ветви, присущего другим
типам. Если гистерезис на изотерме адсорбции
для углей имеет
форму Н4, то это означает, что уже при сравнительно небольшом
давлении произошло заполнение микропор и дальнейшая адсорбция
практически
прекратилась.
адсорбционной
ветви
Если
наблюдается
изотермы
вблизи
Р/Р
0
предположить, основываясь на морфологии
=
крутой
подъем
1,
можно
то
некоторых
активных
углей, что углеродная масса между полостями, имеющими размер
мезо- и макропор, пронизана микропорами близкой к щелевидной
форме [13].
Принцип
капиллярной
использования
капиллярной
конденсации
цилиндрических
просто
капилляров
конденсации.
объяснить,
разного
размера
Принцип
выбрав
набор
(рис.2.23).
C
повышением давления пара на поверхности всех пор капилляров будет
увеличиваться толщина t полимолекулярной пленки.
Внутренняя поверхность этой пленки образует цилиндр, который
принято называть корой. Ее радиус г меньше радиуса цилиндрической
к
поры г . на величину: r
п
K
= т -т. Когда пар достигнет насыщения по
п
отношению к поверхности пленки в наименьшем из
произойдет его спонтанное заполнение капиллярным
цилиндров,
конденсатом
(вертикальный подъем изотермы). Это давление пара p определится
уравнением
Кельвина
(2.24,
с
г ).
ц
Дальнейшее
повышение давления пара приведет к
росту толщина адсорбционной пленки
во всех остальных
насыщении
пара
капиллярах, при
по
отношению
к
поверхности пленки в следующем по
размеру
капилляре,
спонтанное
Рисунок 2.22. Набор открытых
цилиндрических
капилляров
разного размера с толщиной
полимолекулярной
адсорбционной пленки т в н и х
(а), изотерма адсорбции для
данного набора капилляров (б) и
изотерма
адсорбции
при
большом количества капилляров
разного размера с т [13].
произойдет
заполнение.
его
Изотерма
сорбции для всех капилляров
будет
иметь вид, показанный на рис. 2.22, б.
Обратный процесс десорбции начнется
с наиболее широкого капилляра, затем
последовательно
адсорбат
будет
испаряться из более узких капилляров.
Начало
спонтанного
испарения
адсорбата из каждого капилляра определяется уравнением Кельвина
(2.24, с г ф). Ступенчатая десорбционная изотерма отличается от
с
адсорбционной вследствие различий в форме менисков в прямом и
обратном процессах. При значительном
числе капилляров в такой
модельной системе обе ветви изотермы приобретут плавное очертание,
что и наблюдают на практике. Принципиальное значение для расчета
размеров капилляров (радиусов пор твердого тела) из изотермы имеет
ее десорбционная ветвь. В упрощенном виде по десорбционной ветви
определяют распределение пор по размерам dV/dr в исследуемом
адсорбенте,
используя
менисков в виде
уравнению
Кельвина
для
сферических
2oV
RTln
напоминаем, что г ф, м - радиус капилляра (поры), а-10 , Дж/моль
с
поверхностное натяжение адсорбируемого вещества, V, м - о б ъ е м
0
1моля жидкого адсорбтива, Я=8,314Дж/моль-°К, Т, К -абсолютная
температура. Методы расчеты распределения мезопор по изотермам
адсорбции будут рассмотрены далее в разделе 4.
2.4. Динамика адсорбции
2.4.1. Адсорбция на границе газ/твердое тело
Раннее
в
гл.1
дана
качественная
и
количественную
характеристику понятию «адсорбции» а как функции от температуры
Т, давления (для газа) p
или концентрации
Напомним, что при адсорбции
поглощённого
газа
(для растворов)
газа твёрдым телом
пропорционально
массе
с.
количество
образца,
а
точнее
величине его поверхности и зависит от температуры, давления газа,
природы твёрдого тела и газа. Если n - количество адсорбированного
газа, выраженное в молях на грамм вещества, то в общем виде n = f p ,
T, газ, твердое тело). Для данного газа, адсорбированного на твёрдом
теле
при
фиксированной
температуре,
эта
функциональная
зависимость принимает следующий вид: n = А(р,Т) газ, твердое тело.
Если температура ниже критической температуры газа, то более
приемлема другая форма этого уравнения: n = Д(р/р )Т, газ, твердое
8
тело,
где p
s
-
функциональные
давление
насыщенных
зависимости
называют
паров
адсорбтива.
уравнениями
Эти
изотерм
адсорбции. Ход изотермы адсорбции дает информацию о свойствах
поверхности и пористой структуре адсорбентов. Из вида изотермы
адсорбции можно сделать вывод о площади поверхности, пористости
адсорбирующего
адсорбентом
и
тела
и
адсорбатом.
характере
взаимодействия
Измерение
равновесных
между
количеств
адсорбированного на поверхности вещества в выбранном диапазоне
относительных давлений при постоянной температуре
построить
изотерму.
Современные
лабораторные
позволяют
анализаторы
сорбции газов в программированном режиме выстраивают изотермы
по
точкам
измеренных
на
основе
давлениях
измеренных
в
значений
состоянии
объёмов
равновесия.
газа
и
Аналогично
получают изотермы десорбции, измеряя количества выделенного газа
при снижении относительного давления.
Важно получить изотерму адсорбции, но важнее «вытянуть» из
нее
максимум
информации
об
адсорбционном
процессе
и
об
адсорбенте, в частности, из равновесных изотерм адсорбции можно
получить информацию и о термодинамике адсорбционного процесса.
Если экспериментатор ставит перед собой цель узнать что-либо о
механизме адсорбции, тогда необходимо снимать кинетику процесса.
Идеально, если получают и кинетические и равновесные зависимости
в одних и тех же условиях, при которых ведут эксперимент.
Экспериментальный материал составляет основу любой науки,
любой теории, которая пытается объяснить наблюдаемые в явлении
закономерности. Это относится и к адсорбции, как межфазовому
процессу,
протекающему
на
границах
раздела
фаз:
газ/жидкость/твердое тело. Поэтому не случайно, что в течение почти
более двух столетий выдающиеся ученые мира развивали теорию
межфазовых
явлений,
адсорбции -
итальянец Феличе Фонтана (1730—1805),
химик
Карл
называемое
Вильгельм
Шееле,
ТобиасЛовиц
(1757—1804),
(1839—1903),
Михаил
Дмитриевич
адсорбцией:
американец
Семенович
Зелинский
русский
шведский
академик
ДжозайяУиллард
Цвет
(1861—1953),
основоположники
(1872—1919),
Николай
Иоганн
Гиббс
Николай
Александрович
Шилов (1877—1930), А. Фрумкин (1895-1976), Михаил Михайлович
Дубинин (1901-1993) , Леонид Викторович Радушкевич (1900-1972),
Владимир Андреевич Киселев (19
Лопаткин
(1930-2004);
авторы
-1985), Алексей
теории
и
Анфимович
уравнений
изотерм
адсорбции, сыгравших исключительную роль в развитии адсорбции:
И. Ленгмюр, X. Фрейндлих, М. Фольмер, Р. Фаулер, Е. Гугенгейм, Я.
И. Френкель, Т. Хилл, М. Поляни, С. Брунауэр, П. Эммет и Е. Теллер,
Р. Баррер, Д. Эверетт, К. Синг, Д. Никольсон, У. Гаркинс, Н. Адам,
Д.Брек, Р. Эванс, Р. Зигмонди, Дж. де Бур, Дж. Дьюар, Я. Б.
Зельдович, И.З. Рогинский, А. А. Жуховицкий, Б. В. Дерягин, П.А.
Ребиндер, А.И. Русанов, М.И. Темкин, X. Стёкли, и др.
2.4.2. Процессы на поверхности адсорбента
Поверхность твердого тела, находящегося при температуре Т в
контакте
с газом
при давлении p , непрерывно
бомбардируется
молекулами газа. Из кинетической теории газов следует, что число
молекул, ударяющихся о единицу поверхности за единицу времени,
п =
1/2
N p/[2nMRT]
A
где N — число Авогадро;
М — молекулярная масса;
R — универсальная газовая постоянная.
A
При
этом
поверхности,
а
часть
газовых
часть
на
молекул
некоторое
упруго
время
отражается
задерживается,
от
т.е.
адсорбируется. Молекулы, контактируя с поверхностью, образуют
избыточную
концентрацию
по
сравнению
с
концентрацией
на
большом удалении от поверхности. Избыточное содержание молекул
в приповерхностном слое по сравнению с их содержанием вдали от
поверхности по определению и есть
адсорбция.
В гл.1. показано, что при исследовании адсорбции различают
физическую
и
химическую
адсорбцию,
между
которыми
в
пограничных случаях провести четкое различие не всегда удается.
Предполагается,
что
физическая
адсорбция
обусловлена
силами
взаимодействия молекул газа с поверхностью твердых тел и при
адсорбции
не
происходит
заметного
изменения
электронного
строения адсорбирующихся молекул и твердой подложки. Поскольку
силы взаимодействия молекул газа между собой и с атомами твердой
подложки имеют, как правило, одну природу, то теплота, выделяемая
при физической адсорбции, по порядку величины сопоставима с
теплотой конденсации паров. При физической адсорбции на повер¬
хности могут
не только монослои, но и ультратонкие
пленки,
толщина которых составляет несколько молекулярных диаметров.
Физическая адсорбция является обратимой: при понижении давления
газа или повышении температуры адсорбция уменьшается. Однако,
достаточно примеров, что при адсорбции, допустим, кислорода на
графите, нагревание поверхности в вакууме приводит не к удалению
кислорода, а к выделению с поверхности окиси углерода. То есть
возможен
переход
физической
адсорбции
в
химическую
(локализованную) адсорбцию. Хорошо известно, что физическая и
химическая
адсорбция
различаются
не
только
по
теплотам
взаимодействия с поверхностью, но и по характерным
адсорбции/десорбции.
Из
общей
физики
известно,
временам
что
частота
столкновений v молекул газа с поверхностью твердого тела: [28]
c
v =
l/4n v
c
g
T
где % — число молекул газа в единице объема;
v — тепловая скорость молекул.
T
Но из уравнения Аррениуса следует, что не всякие столкновения
молекул с твердой поверхностью приводят к акту адсорбции. Чтобы
произошла физическая адсорбция, молекула должна передать свою
энергию либо твердому телу, либо другим молекулам. Потери энергии,
достаточной для физического захвата молекулы равна, или чуть
больше, энергии активации физической адсорбции. Для физического
захвата
молекулы,
требуется
несколько
столкновений.
А
чтобы
произошла химическая реакция, необходимо дополнительное время,
которое затрачивается на перемещение молекул по поверхности до
реакционного центра и собственно реакцию. Химической адсорбции,
как правило, предшествует физическая адсорбция. По этой причине
химическая адсорбция протекает существенно медленнее физической
адсорбции. Точно рассчитать времена химической
адсорбции
достаточно
сложно,
однако
для
и
физической
обратного
процесса
(десорбции) это время можно оценить по теплоте адсорбции Q .
a
В равновесных условиях величина адсорбции
определяется
равенством скоростей адсорбции и десорбции. При малых покрытиях,
когда вероятность соударения адсорбтива с местом, уже занятым
адсорбатом,
мала,
по
Де
Буру
[29]
среднее
число
молекул,
адсорбированных на единице поверхности, a, может быть оценено как
а = х
ш
(2.27)
где х - коэффициент аккомодации (прилипания) - вероятность прилипания, как
доля прилипших молекул относительно бомбардируемых поверхность
(x=n /n, где n - ч и с л о соударений, п - ч и с л о прилипших молекул);
т - среднее время «жизни» молекулы в адсорбированном состоянии,
величину которого Яков Иванович Френкель (-19) связал с теплотой
десорбции в виде
a
а
т = r exp(Q /RT)
0
(2.28)
a
где то - выражается через статистические суммы для адсорбата и образующегося
активированного комплекса, причем т ~ l / v ~ 10
с, где v - величина порядка
частоты колебаний химических связей.
0
c
c
Следовательно
т=
13
10- exp(Qa/RT)
Это уравнение применимо для оценок, в частности, любопытны
оценки среднего времени т пребывания молекулы в адсорбированном
состоянии
в зависимости
от <2.
а
Для таких
оценок
характерные значения теплоты физадсорбции (рис.2.23).
используем
Q , кДж/моль
a
Рисунок 2.23. Связь теплоты адсорбции Q и расчетного «времени жизни»
адсорбированной молекулы на поверхности т по данным монографии де Бура
[29]. Ж и р н ы м шрифтом выделены теплоты адсорбции.
a
Как видно из рис. 2.23 функцию Q от т можем представить в
a
2 4803
аналитическом
достоверности
виде Q
a
0,97
=0,6777т
в
форме
,
с высоким
степенной
коэффициентом
зависимости.
Эту
аналитическую зависимость можно использовать для оценки времени
«жизни» адсорбированных молекул по их теплотам адсорбции и
наоборот по т оценивать Q . т — период молекулярных колебаний,
a
составляющий порядка 10
0
---10
с. При теплоте адсорбции Q <60
a
кДж/моль время жизни молекул в адсорбированном состоянии составляет
малые доли секунды. При Q >70 кДж/моль
a
время
жизни
резко
возрастает. Так, при Q = 176 кДж/моль (хемосорбция СО на Ni) время
a
жизни молекул в адсорбированном состоянии составляет почти 10
11
лет, что существенно превосходит возраст Земли.
Из приведенных оценок видно, что время «жизни» адсорбата
изменяется в чрезвычайно широких пределах и очень сильно зависит
от температуры и интенсивности межмолекулярного взаимодействия.
В общем случае адсорбат теряет степень свободы поступательного
движения в направлении, перпендикулярном поверхности. Остальные
степени свободы могут сохраняться, в том числе две степени свободы
поступательного
движения,
обеспечивающие
миграцию
по по¬
верхности.
2.4.3. Изотермы адсорбции
Изотерма
и
константа
Генри.
Если
рассматривать
динамическую картину адсорбции, то ее величина будет тем больше,
чем больше число ударов молекул газа о поверхность (т.е. чем больше
давление
газа) и чем больше
время
пребывания
молекулы
на
поверхности от момента удара до момента ее перехода обратно в
газовую фазу. В формуле (2.27) предполагается, что каждый удар
молекулы сопровождается задержкой ее на поверхности, независимо
от
того,
есть
уже
на
ней
другие
молекулы
или
нет.
В
действительности, молекула, ударившаяся в уже занятое место, может
отразиться обратно в газовую фазу или задержаться, но время ее
удержания
будет
иным
и корректироваться
%. С учетом
этих
обстоятельств, приходят к простому уравнению:
а = Кр
н
(2.28)
Оно означает, что в идеальной модели величина адсорбции
прямо пропорциональна давлению газа или пара. Свое название
уравнение Генри получило по аналогии с известным в физической
химии законом Генри, согласно которому объем газа, растворенного в
твердом теле или жидкости, пропорционален его давлению. По
принятым допущениям T=const и p—»0
описывать
экспериментальные
заполнениях
на
однородных
данные,
изотерма Генри должна
полученные
поверхностях.
Однако,
при
малых
адсорбцию
практически всегда измеряют на неоднородных поверхностях. Но
адсорбции при очень малых давлениях отвечают очень малые степени
покрытия
поверхности.
Это означает, что все зависит от того,
насколько неоднородна не вся поверхность, а только малая ее доля,
покрываемая при малых давлениях. В литературе можно
найти
достаточно тех и других примеров.
Уравнение Генри легко получить термодинамическим путем из
условия
равенства
адсорбционном
химических
слое
и
потенциалов
известных
молекул
выражений
для
в
газе
и
химических
потенциалов газа ju и адсорбата ju
g
a
Т\п(
и
V-д = ^дАв РУд)
(
( 2 . 2
V-a = Va,ok T \п С1Уа)
B
9
)
где JUo> UUo — соответствующие стандартные значения химических потенциалов
при pYg = ауа= 1;
y = Ya— соответственно коэффициенты: активности молекул в газе и
адсорбционном слое.
g
При равенстве jjg=ju получим соотношение:
a
/
РУ аУа
д
= exp
(-(
[ [1а,0
-
^д,о))/^вТ]
(
= К
н
)
230
Выражение в правой части (2.30) не зависит от давления и
величины адсорбции и представляет собой константу адсорбционного
равновесия, называемой константа Генри К . При малых давлениях и
Н
соответственно
величинах
адсорбции
коэффициенты
активности
Y =Ya=1, поэтому из соотношения (2.30) вытекает само уравнение —
g
изотерма адсорбции
Генри
а = exp [ - ( | i , o
(
-
a
Изотерма
i
( 2 .
= ^ р]
^g o))/k T
я
B
31
)
адсорбции Генри показывает, что величина адсорбции
пропорциональна давлению газа. Изотерма пригодна в отсутствии
межмолекулярных взаимодействий в адсорбционном слое.
Уравнение Генри можно получить и кинетическим путем, исходя
из кинетической теории газов хорошо известной из общей физики.
По де Буру из (2.27) при х=1 абсорбция a =пт. Следуя всем
упрощениям
в модели Генри и принимая,
что
число
молекул,
ударяющихся о единицу поверхности за единицу времени, п =
—
N a P
± /
(2nMRT)
/
, где N
A
- число Авогадро, М - молекулярная масса, R -
2
универсальная газовая постоянная, подставляем выражения для п и т
по Френкелю из (2.28) немедленно приходим к выражению
1/2
а=
(
/RT)
{N p/[2T nMRT] }e Q
A
(2.32)
0
В этом выражении все члены кроме p величины постоянные,
следовательно, a=K p. А константа Генри имеет вид
H
1/2
К
н
Сравните с K
H
(
/RT)
= [N p/[2nMRT] }e Q
(2.33)
A
(2.30), полученной термодинамическим путем. В
этом ценность выводов уравнений изотерм различными подходами.
Как видно из сравнения уравнений (2.30) и (2.31), константа
Генри может с успехом использоваться при исследовании адсорбции
при любых степенях заполнения поверхности. Константа
выведенная
молекулярной
определяется
с
использованием
статистики
еще
[6]
преимущественно
одного
показывает,
-
метода
что
ее
значением
Генри
метода
значение
взаимодействия газ/поверхность в точке минимума. K
потенциала
H
является
важнейшей характеристикой адсорбционных процессов. Но получить
ее значение в эксперименте требует от исследователей прецизионных
измерений, поскольку измерения при очень малых давлениях могут
давать большую ошибку. Изотерма адсорбции Генри важна и в
практическом и в теоретическом плане: по ней проверяют корректность
ранее и вновь выведенных уравнений изотерм.
Изотерма
Ленгмюра.
Уравнение
изотермы
Генри
верно
описывают адсорбцию при низких заполнения поверхности и не
пригодно при больших покрытиях. Отклонение зависимости a=f(p) от
линейной в 1916 г объяснил
Ленгмюр
(1881-1957),
предложивший
Уравнение
лауреат
уравнение
выведено
американский физико-химик Ирвин
Нобелевской
премии
1932г,
изотермы мономолекулярной алсорбции.
кинетическим
путем
для
однородной
поверхности в отсутствие взаимодействий адсорбат - адсорбат. Важный
момент в выводе -адсорбция
локализованная.
Принимается, что на
поверхности имеется определенное число центров адсорбции Z, часть
которых Z занята адсорбированными молекулами, а часть Z = Z - Z
a
0
a
свободна. Молекулы газовой фазы, сталкиваясь с поверхностью,
захватываются
на эти адсорбционные
центры,
еще не занятые
молекулами. С другой стороны адсорбционные центры, уже занятые
молекулами, могут освобождаться в результате вылета молекул с
достаточной тепловой
энергией.
С течением
времени
наступает
равновесие между числом захватываемых в единицу времени молекул
и числом вылетающих из адсорбционных центров. Согласно формуле
v =1/4n v
c
g
T
частота
идеального газа
столкновений
молекул
с
поверхностью
для
1/4n
v
g
=
T
(1/4v )/k T
TP
(2.32)
B
где p=n k Tдавление, отсюда п р и данной температуре скорость захвата
молекул пропорциональна свободной
поверхности2
давлению газа p и равна
k pZo.
g
B
0
d
Скорость вылетающих молекул пропорциональна концентрации
занятых центров Z и равна k Z , где к и к - константы скоростей
a
прямого
a
(адсорбция)
и
a
а
д
обратного
(десорбция)
процессов
соответственно. При достижении равновесия
kZ
a
Учитывая,
(
= k pZ
a
d
что
= k pZ
0
= 9
z
^
z
)
- Z
d
(2.33)
a
доля
поверхности
занятая
адсорбированными молекулами уравнение (2.33) представим как
9 = b p/(1
+ b p)wm\ в иной форме b p = 9/(1-9)
L
L
(2.34)
L
заметим, что доля свободных центров равна 9
0
- ^ — ) , где
b =^
L
константа адсорбционного равновесия (константа Ленгмюра).
Если ввести обозначение a
для адсорбции, соответствующей
m
заполнению монослоя на поверхности - максимальная адсорбция, то
а
9
а
и уравнение (2.34) можно переписать в терминах адсорбции:
т
/(
а = ambiP 1
+ bLp)
(2.35)
Легко убедиться, что изотерма
(2.34)
имеет
вид,
подобный
представленному на рис. 2.25, то есть
с повышением
давления
адсорбция
выходит на насыщение (на плато).
0
2
4
6
р
Рисунок
2.24.
Теоретически
построенные изотермы адсорбции
Ленгмюра
с уменьшающимися
з
н
а
ч
е
н
1 до 4
и
я
м
и
к
о
н
с
т
а
н
т
b
L
в
р
я
д
у
о
т
При
количество
малых
давлениях
адсорбированного
газа
^ ^
^
пропорционально давлению:
а = abp
m
(2.36)
L
а при высоких стремится к предельному значению, равному a .
m
При малых давлениях изотерма Ленгмюра переходит в изотерму
Генри, так что
К = a bL
н
Уравнение
Ленгмюра
часто
(2.37)
m
используется
на практике. Для
обработки экспериментальных данных его обычно представляют в
линейной форме
р/а
= l/cimh
+ p/cim
(2.38)
Из графика зависимости p/a =f(p) по углу наклона прямой находят
am, а затем по am и точке пересечения прямой с осью абсцисс
-
величину b .
L
Можно просто оценить константы k , k . Постоянная k , равна
a
d
d
обратному времени десорбции в формуле (2.28). Постоянная k.j опреде­
ляется частотой столкновений молекул с поверхностью и площадью с ,
0
приходящейся на адсорбционный центр,
ка = (у а Ра )/4квТ
т
где P —
ad
0
(2.39)
й
вероятность захвата молекулы при ее попадании на адсорбционный
центр.
Комбинируя написанные выше выражения, для ленгмюровской
константы получим
bL = & а Раа)т ехр(()/квТ)/4кв
рассматривали
идеально
т
Здесь
мы
0
монослойную
адсорбцию
исключающую
латеральные
0
для
Т
(2.40)
локализированную
однокомпонентных
взаимодействия
систем,
адсорбированных
молекулах на соседних центрах однородной поверхности.
Достоинством уравнения Ленгмюра является то, что его можно
использовать для конкурентной адсорбции многокомпонентной смеси
газов и жидких растворов фактически в том же виде, в котором оно
выше
представлено,
с
той
лишь
разницей,
суммирование для всех компонентов
что
смеси b pi
Li
проводится
.То
есть
для
компонента i смеси можно записать
0 =
(2.41)
t
г д е 6 j-доля
поверхности не заполненная адсорбатом.
0
Суммирование дает уравнение изотермы адсорбции Ленгмюра для
многокомпонентной смеси веществ по i компоненту
Щ = amihLiVi +
^
/
Выводы
уравнения
Ленгмюра
кинетическим,
термодинамическим,
квазихимическим
и
локализованной
представляет
др.
По
адсорбции,
интерес
своей
LiVi)
даны
многими
способами:
молекулярно-статистическим,
сути
фактически
вывод
( 2 . 4 2 )
b
уравнение
для
этого
выведено
хемосорбции.
знаменитого
для
Поэтому
уравнения
квазихимическим методом.
Вывод уравнения очень прост. Он основан на представлении
адсорбции
в
виде
квазихимической
реакции
между
молекулой
адсорбата М и активным центром Z на поверхности адсорбента М +
[Z] <-> [ M Z ] , где [ M Z ] — локализованный адсорбционный комплекс.
Если пренебречь латеральными взаимодействиями, а так же влиянием
образовавшихся адсорбционных комплексов на соседние активные
центры,
и принять во внимания, что число свободных центров на
поверхности - доля (1-9) от общего числа центров, а число занятых
центров - доля 9, то константа равновесия этой реакции К =
следовательно, снова приходим к (2.34)
К = 9/(1 - 9)
(2.43)
р
Здесь, как и прежде, 9 = —.
а
т
Для смесей вывод тот же, что и для одного компонента. Только
рассматриваются параллельные реакции взаимодействия газов смеси
со свободной поверхностью. Для простоты возьмем два компонента А
и В. Допускаем, что молекулы А и В адсорбируются на одних и тех
же свободных центрах: А (газ) + свободное место [Z] о
+ свободное место [Z] о
[AZ] и В (газ)
[BZ], где [AZ] и [BZ] — соответствующие
поверхностные комплексы. При равновесии для каждого компонента
константы равновесия будут определены как К = — — —
А
г
I-
К
вв
Ту
АРА
KR = — : — - — — , при этом — =
в
F
Рв(1-о -о У
А
о
в
, после преобразований придем к
к
в
и
в
Р
в
>
уравнению Ленгмюра для двухкомпонентной системы
0 = К Р /[1
А
А
+ КР
А
А
+ КР]
А
В
и9=
В
В
К Р /[1
в
+ КР
в
Естественно, что для /компонента
А
+ КР]
А
В
(2.44)
В
смеси нескольких
газов
получим уравнение
9 = K P /[1
t
t
t
+Y , ^ ]
(245)
И, наконец, для суммы всех газов
9 = Y K Pi/[1
I
Все
Ji
характеристики
парциальными,
К—константа
KiPi
+Y
Ji
уравнения
т.е. Р— парциальное
с
]
(246)
индексом
давление
i
являются
компонента
i, a
равновесия этого компонента.
Диссоциативная
адсорбируясь
i
адсорбция.
на активных
Молекулы
поверхности
типа
могут
Н
2
и
О ,
2
диссоциировать
частично или нацело. Процесс можно рассматривать, как химическую
реакцию:
А + 2* <=> 2А*
(2.47)
2
где A 2 - м о л е к у л а
центрах *.
адсорбтива,
распадаясь,
адсорбируется
на двух
активных
При условии, что диссоциация протекает нацело в условиях
равновесия скорости прямой и обратной реакций равны и по закону
действия масс
р 2к (1
2
2
- в)
= кв
О = Рл2к 2(1-
О)
А
а
(2.48)
а
приходим к
2
2
А
(2.49)
адсорбционного равновесия),
(К 2=кс1/ка-константа
А
а от (2.49) и к
равновесным степеням заполнения поверхности
1/2
в = {К ) /(1
р
Это
уравнение
K
1/2
+ Y( P) )
Ленгмюра
(2.50)
для
диссоциативной
однокомпонентной адсорбции [10].
Для многокомпонентной адсорбции по i компоненту
1/2
0t = a /a
t
mi
= (K ) /{1
iVi
K
+Y( ^)
1 / 2
)
(2.51)
Подчеркнем, что уравнения (2.47-2.51) рассмотрены только при
условии полной диссоциации молекулы на атомы. В литературе
рассматривается только этот вариант. Для частично протекающей
диссоциации
Макаревич
Н.А. предложил
[30] заменить
«2» в
показателе степени Уг на g, т.е. в уравнения подобного типа ввести
обобщенный фактор неидеальности g-GNF ^ м . Гл 1., Приложение к
гл. 1), он же ассоциативно-ионизационный множитель i = д = 1 a
/3 + а(у — 1).
Для
рассматриваемого
ассоциации /3=0, v=2 -
выше
случая
число частиц, на которое
степень
распадается
молекула адсорбата, занимая вместо одного активного центра на
поверхности
адсорбента
два, следовательно,
i =2,
a
как это и
представлено в (2.47-2.51).
В реальной ситуации степень диссоциации молекул а равная 1
маловероятна (даже для растворов сильных электролитов она никогда
не
достигает
1), это-идеализированный
случай.
Поэтому
для
реальных систем, где протекают процессы ассоциации и диссоциации
одновременно, но в состоянии равновесия их степени а и /3 могут
сильно различаться и предлагается GNFg либо i .
a
Повторив
процедуру
вывода
уравнений
(2.50-2.51),
рассматривая адсорбцию на активных центрах не только атомов
распавшихся молекул, но и самих молекул, а возможно и их
ассоциатов (димеров, тримеров, . . . ) придем к уравнениям Ленгмюра Макаревича.
1/
в = a /a
t
mi
= (Kp) ^/(l
1
+^ Ш
/
9
)
(252)
Это уравнение для диссоциативной однокомпонентной адсорбции.
Аналогично для многокомпонентной адсорбции по i компоненту
1/9
щ
(KtVi)
А по сумме компонентов
1/9
щ
u
mi
Y,i(Kivd
Х
\.
> /-HK^IVIJ
J
Из вновь предложенных [30] уравнений (2.52-2.54) Л е н г м ю р а -
Макаревича с фактором неидеальности g
компенсации
двух
видно, что при полной
конкурентных
(ассоциативного
и
диссоциативного) процессов g=1, уравнения (2.52-2.54) переходят в
классические
уравнения
Ленгмюра,
а
при малых
заполнениях
адсорбции в классическое уравнение Генри, возможности
которого
резко возрастают, если его модифицировать введением в него фактора
неидеальности д = 1 - (3 + a(v - 1), то получим новое уравнение
изотермы адсорбции
а = (К р) з
= Кр з
1/
(2.55)
1/
н
д
или в логарифмической форме, удобной для определения K и g
g
\na = \г\Кд + (1/д)\пр
(2.55а)
аналогично для смесей веществ в газе
1/9
1/9
Ъ = (K ) i
= KgiV i
mVi
(2.55б)
Изотермы (2.55-2.55б) по формальным признакам похожа на
эмпирическое уравнение
(2.56)
получено
Фрейндлиха,
простой
но уравнение
подгонкой
под
экспериментальные изотермы, и рассматривается
источниках
[3,12
и
математического
др.]
описания
преимущественно
только
как
Фрейндлиха
некоторые
в литературных
уравнение
эксперимента
химиками-технологами
для
и
чисто
используется
при
технико-
экономическом обосновании процессов, связанных с адсорбцией.
1/n
а = Kp
F
Параметры
постоянные,
изотерм,
не
ИДИ \na = \nKg + (1/g) ln р
этого уравнения
получаемые
имеют
K
F
и n, как некие
при аппроксимации
физического
(2.56)
смысла,
публикациях пытаются придать физический
числовые
экспериментальных
хотя
в
некоторых
смысл константе K ,
F
сравнивая ее с константой Генри, на что нет никаких оснований.
В уравнении (2.55) константа Генри F
и G N F - g имеют ясный
H
физический смысл, о чем подробно рассмотрено выше в настоящем
разделе и в Приложении к гл.1. Следует добавить, что g в уравнениях
(2.52-2.55б)
при
соответствующих
допущения
может
быть
постоянной величиной, но в общем случае g=fp,c) -переменная, т.е.
функция от давления газа (от концентрации для растворов). GNF
отслеживает
любые
наблюдаются
в
отклонения
реальных
рассматривалось
ранее
от
системах
идеальности,
и
(гл.1), g легко
процессах.
определяется
которые
Как
уже
сравнением
экспериментальной изотермы адсорбции с теоретической изотермой и
определением
отклонений
от идеальности
при
фиксированных
текущих значениях р . Построение теоретической
параметрами К
р
и а
т
зависимости
производится по предварительно полученным
при обработке экспериментальной изотермы. В результате
получена
зависимость
аналитический
вид,
соответствующей
с
g=fp,c),
которую
путем
ее
математической
можно
аппроксимации
функции
будет
привести
в
подборкой
в редакторах
Excel,
Matcad, Matlab, Origen и др. Затем подставить в выбранное уравнение
(2.52-2.55б),
которое
можно
проверять
на
экспериментальных
результатах, получаемых для данной системы. Во втором варианте,
если
g
принимать
за
постоянную
величину,
то
подгонку
теоретической зависимости g=f(p,c) под экспериментальную просто
проводить численно, например, в редакторе Excel по максимальному
2
значению коэффициента достоверности R .
Возвращаясь
к
уравнениям
(2.34),
становиться
понятным,
почему классическое уравнение Ленгмюра, которое получено для
идеализированных
систем
очень
часто
«работает»
при
анализе
широкого спектра экспериментальных изотерм адсорбции. Ответ: это
-
действие компенсационного
эффекта (наглядно заложенного
в
обобщенном факторе неидеальности Макаревича) и действующего в
реальных системах при g=1, на что в редких случаях обращается
внимание. А
примеров тому
множество, один
из них: если
в
коллоидный раствор электролита (любой ионогенный ПАВ), или
полиэлектролита с их заметной степенью диссоциации
добавить
избыток простого индифферентного электролита (допустим, NaCl), то
в результате сжатия
двойного электрического слоя
коллоидная
частица электролита ведет себя подобно частице неэлектролита. Это
многократно доказывается при измерении многих физико-химических
свойств таких растворов - вязкости, поверхностного натяжения и др.
Все
рассмотренные
до
сих
пор
уравнения
адсорбции
выполняются для мономолекулярной адсорбции, протекающей на
однородном
адсорбенте
с
энергетически
эквивалентными
адсорбционными центрами, т.е. для них теплота адсорбции q = const.
a
В
приближении
к
реальным
условиям
важно
рассмотрение
возможных распределений адсорбционных центров поверхности по
их энергиям. Это не легкая
задача. Одной из попыток такого
рассмотрения можно считать уравнение М.И. Темкина,
который
приняв линейное распределение адсорбционных центров по энергиям
(линейный рост теплоты адсорбции q с заполнением поверхности 6)
на основе уравнения Ленгмюра, получил простое уравнение для
описания средней части изотерм адсорбции
9 = (RT/q a)
\np + const
0
(2.57)
где a - постоянная характеризующая линейное распределение адсорбционных
центров по энергиям;
q - начальная теплота адсорбции.
0
Уравнение Темкина часто записывают в виде
в = (1/1a)\nb p
(2.58)
L
И называют логарифмической
bL
константа
Ленгмюра,
изотермой
отвечающая
адсорбции,
в которой
максимальной
теплоте
адсорбции.
Я.Б.Зельдович
неоднородность
показал,
что
поверхности
если
в
принять
виде
энергетическую
экспоненциального
распределения, то изотерма Темкина в области средних заполнений
поверхности переходит в изотерму типа Фрейндлиха, надо полагать
что и в изотерму (2.55а).
В заключение еще раз сформулируем основные
положения
теории Ленгмюра (мономолекулярной адсорбции), на основе которой
получено множество уравнений.
1. Адсорбция является локализованной и вызывается силами
межмолекулярного
взаимодействия.
Она
представляет
собой
обратимый химический процесс.
2. Адсорбция
молекул
адсорбата
происходит
на
активных
центрах, всегда присутствующих на поверхности адсорбата.
3. Вследствие малого радиуса действия адсорбционных сил и
способности их к насыщению каждый активный центр, адсорбируя
одну молекулу адсорбата, становится неспособным к дальнейшей
адсорбции.
4.
Адсорбированные
молекулы
удерживаются
активными
центрами
в течение
определенного
времени,
затем
происходит
десорбция, после чего активный центр вновь может адсорбировать
молекулы адсорбата.
5. Силы взаимодействия между адсорбированными молекулами
отсутствуют.
2.4.4. Изотермы полимолекулярной адсорбции
Теория Ленгмюра не смогла объяснить ход S-образных кривых
изотерм адсорбции многих веществ на непористых адсорбентах. Вид
таких
изотерм
изображен
на рис.
2.25.
Как
можно
видеть,
в
точке А изотерма Ленгмюра круто поднимается кверху. Очевидно,
связывание
адсорбтива
адсорбентом
не
прекращается
после
образования мономолекулярного слоя, а продолжается дальше, что
предполагало образование второго, третьего и последующих слоев,
вплоть до конденсации пара.
Рис. 2.25. Вид изотермы, характерной для полимолекулярной адсорбции.
Для
объяснения
этого
явления
венгр
Поляни
в
1915
г.
предложил теорию полимолекулярной адсорбции, называемую также
потенциальной
интересуют
или
такие
термодинамической.
подробности,
как
Термодинамику
активные
центры
не
или
неоднородность поверхности твердого тела и пр. Поэтому подход
Поляни принципиально отличался от подхода Ленгмюра.
Рассмотрим
кратко
исходные
положения
этой
теории,
пригодной в случае адсорбции паров на твердом теле:
-
адсорбция
обусловлена
чисто
физическими
силами
(у
Ленгмюра квазихимический подход);
- на поверхности адсорбента нет активных центров (у Ленгмюра
это
-
основа),
а
адсорбционные
силы
действуют
вблизи
от
поверхности адсорбента и образуют около этой поверхности
со
стороны газовой фазы непрерывное силовое поле;
- адсорбционные силы действуют на сравнительно большие
расстояния, (большие, чем размеры отдельных молекул адсорбтива),
создавая
у
поверхности
адсорбента
адсорбционный
объем
V,
удаления
от
заполненный молекулами адсорбтива;
-
действие
адсорбционных
сил
по
мере
поверхности уменьшается и на некотором расстоянии практически
становится равным нулю;
- притяжение данной молекулы поверхностью адсорбента не
зависит от наличия в адсорбционном пространстве других молекул,
вследствие чего возможна полимолекулярная адсорбция;
- адсорбционный потенциал (s) не зависят от температуры, и,
следовательно, с изменением температуры адсорбционный объем V
не изменяется (ds/dT= ds/dT=0). Поэтому адсорбционный потенциал
можно выразить как функцию от объема:
£ = /00
(2.59)
Это не противоречит тому, что с повышением температуры
адсорбция
уменьшается.
В
этом
случае
снижение
адсорбции
обусловлено не уменьшением адсорбционного потенциала, а ростом
интенсивности
теплового
движения
адсорбированных
молекул
в
результате нагрева, что приводит к увеличению десорбции.
Рис. 2.26. Схема адсорбционного объема по представлениям полимолекулярной
теории адсорбции Поляни.
Из рассмотрения положений теории полимолекулярной адсорб¬
ции Поляни
можно
видеть, что силовое
поле, возникающее
у
поверхности адсорбента, во многом сходно с гравитационным полем
(ненасыщаемость
непосредственно
поля
молекулами
адсорбтива,
находящимися
на поверхности адсорбента; независимость
сил,
действующих в поле, от температуры).
На рис. 2.26
схематически
показан разрез
адсорбционного
объема, отвечающий представлению теории полимолекулярной ад¬
сорбции. Как и во всяком силовом поле, в адсорбционном поле можно
представить себе эквипотенциальные поверхности, т е. поверхности с
одним и тем же адсорбционным потенциалом. На рисунке
обозначены
отделяющая
пунктирными
линиями.
адсорбционное
Сплошна
пространство
линия
от
-
газовой
они
граница,
фазы,
адсорбционный потенциал вдоль этой линии равен нулю. Характер
кривой s=f(V), выражающий зависимость адсорбционного потенциала
от
объема
адсорбционного
пространства
между
поверхностью
адсорбента и эквипотенциальными поверхностями, показан на рис.
2.27.
Называется
эта
кривая
характеристической
и,
согласно
потенциальной теории Поляни, не зависит от температуры, но зато
чувствительна к природе адсорбтива. Поэтому отношение
s для
адсорбции двух разных веществ при равных адсорбционных объемах
величина постоянная, и называется эта величина
коэффициентом
аффинности
£2
Р
а
= /si
S3
= /s2
£4
= /s
= -
3
(2.60)
Под
адсорбционным
потенциалом s понимают работу
RTln(p /p), совершаемую против
s
адсорбционных
сил
при
перемещении 1 моля адсорбтива
(пара) из данный точки поля в
У
газовую фазу:
адс
Рис. 2.27. Характеристическая кривая.
£ = RT\n(p /p)
(2.61)
s
где p - давление адсорбтива в газовой фазе;
ps - давление насыщенного пара.
Зная
уравнение
адсорбционного
потенциала
(2.61),
легко
получить необходимые формулы для вычисления изотерм адсорбции
для разных температур и паров по изотерме адсорбции одного пара,
найденной в эксперименте. Очевидно, максимальный адсорбционный
потенциал
должен
существовать
на
границе
адсорбент
—
адсорбционный объем. На границе адсорбционный объем — газовая
фаза, т. е. там, где кончается действие адсорбционных сил, потенциал
s должен быть равным нулю. Уравнение (2.61) в принципе можно
рассматривать как эквивалент уравнения изотермы адсорбции, но с
его помощью нельзя получить основные характеристики структуры
адсорбента, такие как удельная поверхность, распределение пор по их
размерам и т.д. Однако на основе теории Поляни и уравнения Ван дер
Ваальса, т.е. фактически термодинамическим путем, получены ряд
уравнений изотерм, одна из них уравнение Френкеля-Холси-Хилла с
эмпирическим показателем n:
n
(V/Vm)
В
этом
заполнении,
диапазоне
= A/\n(p /p),A
уравнении
^-толщина
n-подбирается
2-3.
распределения
Это
пор
= sJtmRT
s
численно
уравнение
по
пленки
и
(2.62)
при
обычно
используется
размерам
по
монослойном
находится
при
данным
в
анализе
капиллярно-
конденсационных измерений (по гистерезису) [3] и закладывается в
программы современного научного оборудования различных фирм,
например, ASAP-2020.
Уравнение
БЭТ.
Квазихимический
подход,
которого
придерживался Ленгмюр, исключал введения такой характеристики,
как толщина пленки монослойного заполнения, поэтому делались
попытки
получить
уравнение
для
полислойной
адсорбции,
приближенно описывающей реальную адсорбцию, а главное получить
возможность находить правдоподобное значение удельной твердой
поверхности по величине «емкости монослоя» a , как этого требовала
m
практика. Основной недостаток уравнения Ленгмюра в том, что его
можно
использовать
только
при
мономолекулярном
заполнении
адсорбционного слоя. Это условие выполняется достаточно строго
при хемосорбции,
давлениях
и
физической
температурах
адсорбции
выше
газов
критической,
при
небольших
а часто
и
при
адсорбции из растворов. Указанные ограничения для применения
уравнения Ленгмюра связаны не столько с формальным описанием
адсорбции,
значения
сколько
константы
с
невозможностью
адсорбции
b
L
и
получить
емкости
правильные
монослоя
a,
m
соответствующие их физическому смыслу.
В большинстве случаев реальная поверхность твердого тела не
вполне однородна энергетически, адсорбция, как правило, не является
строго локализованной и адсорбированные молекулы практически
всегда взаимодействуют между собой. К тому же, стехиометрия
может нарушаться, вследствие чего адсорбция не будет ограничена
образованием
одного
слоя.
Реальные
изотермы
практически всегда отклоняются от изотермы Ленгмюра.
адсорбции
Сам
Ленгмюр
получить
пытался
уравнение
аналитической
случая
в
форме
для
полимолекулярной
адсорбции, но сделали это три
автора С. Брунауэр, Р.Эммет и
Э.Теллер. Они отказались от
допущений
Ленгмюра,
приводящих
к
мономолекулярной адсорбции.
Для случая, когда температура
Рисунок 2.28. Классификация изотерм
адсорбции по С. Брунауэр, Л.Демингу,
У.Демингу и Э.Теллеру
разработали
получить
теорию
уравнение
многочисленных
Л.Демингом,
адсорбтива ниже критической
,
ч
( т о
е
полимолекулярной
в
изотерм
и
т
ь
э т о
е
щ
адсорбции,
аналитической
реальных
У.Демингом
с
форме.
адсорбции
Э.Теллером
была
е
п а р )
о
н
и
позволившей
После
анализа
С.Брунауэром,
предложена
их
классификация на основе выделения пяти основных типов изотерм I¬
V (рис.2.28).
Кроме пяти классических типов существуют и такие изотермы,
которые трудно отнести к какому-то одному определённому типу.
Ниже даны краткие характеристики изотерм шести типов. Изотермы
типа I отражают мономолекулярную адсорбцию. Изотермы типа I I и
I I I обычно связывают с полимолекулярной адсорбцией. Причем, в
случае
II
взаимодействие
адсорбент
-
адсорбат
сильнее
взаимодействия адсорбат - адсорбат, а в случае I I I - наоборот.
Изотермы типа I V и V отличаются тем, что для них характерна
конечная адсорбция при приближении давления пара к давлению
насыщения p . Изотермы типа I I и I I I характерны для адсорбции на не
s
пористом адсорбенте, а типа I V и V - на пористом твердом теле. Все
пять
типов
изотерм
адсорбции
описываются
теорией
полимолекулярной адсорбции БЭТ, названной так по начальным
буквам фамилий ее авторов. Грег и Синг [26] предложили V I тип
изотерм для непористых адсорбентов с непористой поверхностью.
При
выводе
уравнения
авторы
использовали
Ленгмюра:
рассматривается
локализованная
однородной
поверхности
учета
без
боковых
адсорбция
(нормальных)
взаимодействий
адсорбат.
адсорбат
-
на
(тангенциальных,
латеральных) взаимодействий между молекулами, но
вводится учет «вертикальных»
допущения
дополнительно
межмолекулярных
Предполагается,
что
ударяющиеся молекулы, попадая на уже занятые места, не покидают
их немедленно, а образуют адсорбционные комплексы из групп
молекул. По мере приближения к давлению насыщения P
s
число
свободных мест сокращается, затем сокращается число мест, занятых
комплексами из 1, 2, 3 и т д. молекул (рис.2.30).
Формирование адсорбционных слоев согласно теории БЭТ
Рисунок 2.29. Схематическое распределение молекул в виде комплексов
на поверхности адсорбента.
Применим
квазихимический
полимолекулярную
адсорбцию
квазихимических
реакций
подход
как
и
серию
образования
рассмотрим
последовательных
единичных
и
кратных
комплексов:
адсорбтив + свободная поверхность о [единичные комплексы]
адсорбтив + единичные комплексы о [двойные комплексы]
адсорбтив + двойные комплексы о [тройные комплексы] и т.д.
Пусть 6j, 6 ,6 , в и т.д. - доля поверхности, занятая единичными,
2
4
3
двойными, тройными и т.д. комплексами. Общая величина адсорбции
a с учетом всех типов комплексов и их кратности
а = а (9
т
+ 2 9 + 39 + 49 +
1
2
3
(2.63)
4
где а - емкость одного плотного монослоя.
т
Выражения для констант равновесия соответствующих реакций
имеют вид:
Ki = 9i/P9 ;
0
К2 = 9 /Р9 ;
2
х
К = 9 /Р9
3
Ъ
2
(2.64)
где 6 - д о л я свободной поверхности.
0
Допускается, что величина константы Rj первого адсорбционного
слоя намного больше значений констант равновесия
последущих
слоев.так как взаимодействие. Несмотря на то, что константы R , R ,
2
3
R4 и т.д. не равны друг другу, но из-за быстрого убывания их величин
по мере увеличения расстояния
равными друг другу
и близкими константе равновесия на границе
жидкость - пар R =1/P ,
L
от поверхности, их принимают
s
где P - давление насыщенных паров жидкой
s
фазы адсорбтива при данной температуре. В соответствии с этим
допущением
для
6
запишем
систему
уравнений
(2.65), для
упрощения вывода обозначим относительное давление Р / Д ч е р е з х:
9 —
KIP9Q
в =К Рв
= К Рв
в =К Рв
= (К Р)
2
2
3
1
3
в
ь
2
2
ь
3
= К Рв
4
1
4
= (К Р)
3
Ь
=
в (х)
=
в (х)
=
в (х)
1
г
г
и т.д..
введем их в (2.63) и получим
9 = а/а
2
= К Р9 (1
т
1
+ 2х + 3х + - )
0
(2.66)
Полное заполнение поверхности запишем в виде выражения
2
9 + 9 + 9 + 9 + 9 + - = 9 {1 + К Р(1 + х + х + •••)} = 1,0
0
1
2
3
4
0
1
в котором в квадратных скобках все значения х=Р/Р < 1,
8
представляет убывающую геометрическую прогрессию
2
3
1 + х + х +х
... = 1/(1 - х)
(2.67)
Ряд, заключенный в квадратные скобки в уравнении (2.66),
представляет производную ряда (2.67), поэтому
2
2
1 + 2х + 3х + - = 1/(1 - х)
(2.68)
При подстановке (2.68) в (2.66), получим
а = а К Р9 /(1
т
1
- х)
0
(2.69)
Из уравнений (2.63) и (2.64) запишем
9 =
0
+ К Р/(1
1
- х)] = [1- х]/[1 + К Р - х]
1
(2.70)
Введем уравнение (2.70) в (2.69), заменим Р на х с учетом
К =1/Р ,используем обозначение К /К = С и получим
ь
5
1
а = а С /{[1
т
х
то самое уравнение
-х][1
2
+ (С-
1)х]}
(2.71)
БЭТ, которое уже более 75 лет является
одним из важнейших в адсорбции, где оно используется и сегодня как
основное в методике измерения удельной поверхности адсорбентов и
катализаторов [3,13, 25].
В это уравнение входит две константы
и C, которые легко
определяются из линейной формы уравнения БЭТ
х/а(1
- х) = 1/а С
т
+ (С - 1)х/а С
(2.72)
т
Из наклона графика зависимости x/a(1-x)
от x и отрезка,
отсекаемого на оси ординат графика находят «емкость монослоя» а и
т
константу
С,
называемой
константой
БЭТ.
Эту
константу
представляют произведения двух экснонент,
С
Б Э Т
=
/
(
(2.73)
)/
^S R Q-L RT
e
e
Одна из которых связана с изменениями энтропии адсорбции, а
вторая - с так называемой чистой теплотой
разнице
изостерической
теплоты
адсорбции,
адсорбции
q
st
равной
и
теплоты
конденсации чистого адсорбтива L в жидкость (скрытой теплоты
испарения).
Принципиальным моментом является, то что при С>>1 и малых
относительных давлениях адсорбтива, уравнение БЭТ переходит
в
уравнение Ленгмюра, а последнее в уравнение Генри. На этом
проверяется корректность вывода уравнений изотерм
адсорбции,
подобных уравнениям Ленгмюра и Генри.
Уравнение БЭТ широко используется для расчета «емкости
монослоя»
а ,с
последующим
т
расчетом
площади
удельной
поверхности Б адсорбентов и катализаторов, выражаемой в мкмоль/г
уд
для а , или мкмоль/м с обозначением «емкости монослоя» а
2
т
т
5
у д
= a N a)
m
A
(2.74)
где N - число Авогадро;
со - площадь, приходящаяся на одну молекулу в заполненном монослое на
поверхности адсорбента.
A
Величину молекулярной посадочной площадки со в заполненном
монослое Брунауэр и Эммет предложили определять по расчетной
формуле
а) = 1 . 0 9 1 ( М / N p )
2/3
(2.75)
A
В
эксперименте
для
определения
удельной
поверхности
адсорбентов традиционно используют жидкий азот N
Подставляя
М/р ^ =34,68см
?
/моль,
2
авторы
2
(при 77К).
получили
величину
c =0,162 нм , после долгих дискуссий и сравнения c результатами
N2
независимых измерений
поверхности, ученый
мир согласился с
величиной 0,162 нм , как общепринятым стандартом.
Однако,
при
модифицирующих
адсорбции
наличии
адсорбционные
на поверхностях
(применение
микропор
метода
свойства
твердых
или
примесей,
поверхности,
тел с низкой
БЭТ и значения
при
плотностью
c =0,162 нм становится
N2
некорректным. На помощь приходят другие адсорбаты со своими
посадочными площадками со .
г
Посадочные
площадки
ю
сравниваются
г
с% по
2
правилу
эквивалентов
а со
т
г
=
( 2 . 7 6 )
ci N (i)N
mi
2
2
В таблице 2.3 приведены величины посадочных площадок се>
г
некоторых адсорбатов.
Таблица 2.3.
Расчет величин молекулярных площадок,
приходящих на одну молекулу в заполненном монослое (по [13]).
Адсорбат
N2
Аг
Кг
Xe
CO2
C6H6
со г, нм
0.162
0.176
0.195
0.232
0.170
0.500
Применение
корректным
лишь
уравнения
в
БЭТ
отсутствии
6 14
CH3OH
CCI4
H20
0.562
0.219
0.370
0.125
C
H
может
микропор
быть
и
достаточно
поверхностных
модификаторов. В противном случае применяют другие модельные
подходы.
Логично,
что
авторы
изотермы
БЭТ
не
ограничившись
адсорбцией на гладкой плоской однородной поверхности, сделали
попытку
получить
трехпараметрическое
уравнение
изотермы
адсорбции для пористых адсорбентов [3]. Предположив, что при
достижении насыщения на поверхности пор может
конечное
число
рассматривали
n
адсорбционных
стенки
в
порах
слоев
(для
образоваться
простоты
параллельными),
они
суммирование
энергии адсорбированных молекул по i они провели от 0 до n
получили уравнение
=
в
п
С [1-(п
+ 1)х
х
п
= (1-х)[1
п+1
+
пх ]
1
(
+ (С-1)х-Сх + ]
2
.
7
7
Уравнение не отвечало требованиям непрерывности, и было
получено для пористых адсорбентов улучшенное уравнение Пиккета
Делайеса,
см.
[3, 31]. Пиккет
и Делайес
при
выводе
провели
суммирование не 0 до n, а от 0 до со, в результате (2.77) приобрело
более простой, а главное корректный по физическому смыслу вид
п
С (1-х )
х
в
= (1- )[1
х
Из
рассмотренных
( 2 . 7 8 )
+ ( -1)х]
С
модифицированных
изотерм
БЭТ
заслуживают внимания изотерма Хюттига, см. /3, 31/. Делая вывод
двухпараметрической изотермы БЭТ, авторы молчаливо полагали,
что испарению молекул из i - го слоя мешает i+1 слой. Хюттиг снял
это ограничение и получил более простое по виду, чем уравнение
БЭТ, уравнение изотермы
С (1 + х)
х
в
( 2 7 9 )
= -Г+сГ
Изотермы (2.78 -2.79) как и уравнение БЭТ имеют не меньшее
(а может быть и большее) право на их использование при обработке
экспериментальных адсорбционных данных, но, по договоренности
ученого мира в области адсорбции, уравнение БЭТ при определении
удельной поверхности используется как основное.
Из полученных
в последнее
время «решеточных»
изотерм
полимолекулярной адсорбции можно выделить двух параметрическое
уравнение изотермы Г.И. Арановича [32], которое он вывел в рамках
другого модельного подхода -
Оно -
Кондо
[33] для плоской
однородной полубесконечной поверхности с неограниченным числом
адсорбционных слоев:
Первое,
что
принципиально
отличает
это
уравнение
от
рассмотренных изотерм Ленгмюра и БЭТ, Хюттига др. так это
отсутствие
ограничений
и
на
испарение
молекул
из
любого
адсорбционного слоя и на вакансии по «узлам решетки». Кроме того,
при х=р/р —1 интеграл Гиббса J ad in P не дает (или почти не дает)
s
0
расходимости. Не смотря на качественно корректные признаки о
переходе
уравнения
при
Ленгмюра, а при P/P —0
s
было
подвергнуто,
малых
значениях
P/P
s
в
уравнение
в уравнение Генри, это уравнение так же
как впрочем,
и ее предшественницы.
Но
уравнению БЭТ повезло больше, по стечению ряда обстоятельств,
указанных выше, оно продолжает очень широко использоваться
на
практике
для
определения
удельной
поверхности
твердых
материалов.
Уравнение Арановича формально напоминает уравнение БЭТ,
отличаясь от него по внешним признакам (вместо множителя (С —1)
стоит множитель С, что при высоких значениях С, не существенно),
во-вторых,
вместо
определении
(1-р/р )
констант
линеаризованных
12
1
8
а
т
координатах
1/2
видим
(1-р/р ) .
Поэтому
и
изотермы
Арановича
8
С
необходимо
строить
1
(p/p )/a(1-p/p )
от p/p . Различие ( 1 - р / р ) от ( 1 - р / р )
существенному
расширению
s
s
s
8
интервала
при
в
зависимость
1/2
8
приводит к
применимости
уравнения
Арановича по отношению к экспериментальным данным (см. ниже).
Кроме того, в этом уравнении величина а имеет смысл
избыточной
адсорбции вместо полной адсорбции в уравнении БЭТ. Но заметим,
что разница в этих величинах ничтожна для случая адсорбции пара
на твердых телах. А так же величина С в этом уравнении имеет иной
смысл, а именно, вместо ее значения в уравнении БЭТ (2.73) С
=e
AS/R
e
(Q-L)/RT
Б Э Т
, или, как как его обычно представляют, в виде
С
ВЕТ
= Aexp(q /RT)
(2.78)
0
где q - «чистая» начальная теплота адсорбции;
А
-предэкспоненциальный
множитель,
не и м е ю щ и й
теоретического обоснования, поэтому для расчетов
дифференциальной
адсорбции
предпочтительнее
соотношение /22/
0
С = /p [exp(q /RT)
Pn
K
0
надежного
начальной
применять
- 1]
в котором этот множитель имеет смысл отношения
(2.79)
плотностей
адсорбата в состоянии насыщенного пара (p ) и жидкости (р ) при
n
заданной температуре (Т,К).
ж
Проводя анализ моделей полимолекулярной адсорбции о
достоинствах и
недостатках,
Макаревич [31], выделил
допущения, которые делали авторы
их
основным
при выводе своих изотерм. В
частности, допущений, касающимся изменений свободной энергии
молекул адсорбата и адсорбента в зависимости от номера слоя i.
Согласно этим допущениям двухпараметрическое уравнение Б Э Т
дает
бесконечное
давление
растекания
при
P/P —>1
s
/25/,
а
трехпараметрическое уравнение БЭТ для пористых адсорбентов, не
дает полного заполнения пор даже в состоянии насыщения адсорбата
/3/. Пикгет и Делайес вышли из этого затруднения, изменив в выводе
трехпараметрического уравнения Б Э Т суммирование по элементам
поверхности и объема от
да /17/.
Хюттиг
i =0 до i= n на суммирование от i= 0 до i =
получил,
более
простую
форму
[3, 31], чем
двухпараметрическое уравнение БЭТ, сняв ограничения на испарение
молекул любого адсорбционного слоя. Андерсон [31], приняв, что
теплота адсорбции приблизительно со второго до десятого
слоя
отличается на постоянную величину, равную теплоте конденсации,
ввел
подгоночный
параметр
к. Аранович /32/, учтя
недостатки
полученных ранее уравнений изотерм адсорбции, снял по существу
все запреты на конфигурации расположения молекул и на вакансии
по
"узлам
получил
решетки"
для
в модели
полимолекулярной
полубесконечного
пространства
адсорбции
и
изотерму,
отличающуюся от всех известных аналогов БЭТ, тем, что при Р — P
s
расходимость имеет вид в модели Б Э Т
1/2
a~(1-P/P )~
s
-1
a-a-P/Ps)
(2.80)
Характерной особенностью изотермы Арановича является то, что она
лучше описывает экспериментальные данные адсорбции паров и
газов на непористых адсорбентах, чем ее предшественницы. На рис.
2.2i.
приведены
изотермы
графитированной
саже
Видно,
при
что уже
выполняется,
тогда
адсорбции тетрахлорида углерода
в
координатах
Р/Р > 0,2
уравнение
0
как
его
уравнение
линейной
БЭТ
формы.
(кривая
Арановича
на
1)
не
(кривая
2)
справедливо во всем исследованном интервале давлений. Пределы
его применимости не удается установить из этого графика из-за
отсутствия
экспериментальных
данных
для
Р/Р
> 0,6.
0
Эти
пределы хорошо видны из следующих рисунков. Адсорбция азота
на
хлориде
калия
хорошо
описывается
уравнением
Арановича
вплоть до Р / Р > 0,75, аргона до Р / Р >0,8 (рис. 2.31, справа).
0
О
0.2
0
0,4
0.&
PJP(,
О
0.4
Рис. 2.30. (слева) Изотерма адсорбции паров СС1
саже при
303 К
по данным
4
на
0.-6
P/PQ
графитированной
работы [34] в координатах линейной формы
уравнений БЭТ (1) и Арановича (2).
Рис. 2.31. (справа)
Изотермы адсорбции аргона при 83 К ( 1) и азота
при 78 К (2) на хлориде калия в координатах линейной формы
уравнения
Арановича по данным работы [35].
Диапазон
выполнимости
уравнения
БЭТ
при
описании
макропористых адсорбентов как правило лежит в интервале 0,05-0,35
p/p , в то время как диапазон выполнимости уравнения Арановича на
s
аналогичных сорбентах значительно шире и достигает 0,05-0,8 p/p , и
s
выше.
2.5. Адсорбция в микропористых адсорбентах
Микропористые
твердых
тел,
в
адсорбенты
которых
это -
физическая
особый
класс
адсорбция
пористых
приводит
к
существенному изменению свойств самого адсорбента. Внутри пор
микропористого адсорбента действует адсорбционное поле, которое в
свою
очередь
«навязывает»
адсорбированному
веществу
свою
структуру. Как правило, в каждой полости микропористого активного
угля или цеолита в среднем распределяется от нескольких молекул до
нескольких десятков молекул [36]
То
есть
в
процессе
адсорбции
микропористые
адсорбенты
выступают не в роли инертных носителей адсорбционного поля, они
являются активными участниками адсорбционного процесса.
Эти
меняют
особенности
свойства
микропористой
вещества,
системы
находящегося
адсорбентов
в
резко
адсорбированном
состоянии.
2.5.1. Теория объемного заполнения микропор
Физическая
адсорбция,
макропористой поверхности
протекающая
В
открытой
обусловлена силовым полем твердого
тела и количественно может быть оценена
потенциалом.
на
мезопористых
его адсорбционным
системах
адсорбционная
составляющая так же обусловлена силовым полем, но
добавляется
поглощение пара по механизму капиллярной конденсации.
При адсорбции в микропорах силы адсорбции имеют ту же
природу,
однако из-за близости стенок пор характер
изменяется.
Вместо
практически
толщины адсорбционного
при
достижении
адсорбции
неограниченного
увеличения
слоя вплоть до объемной конденсации
давления
насыщенного
пара, рост
величины
адсорбции геометрически ограничен узким пространством микропор,
к тому же капиллярная
особого состояния
конденсация не может происходить
конденсата под мениском большой
из-за
кривизны.
Адсорбционный потенциал из-за наложения силового поля
близко
расположенных стенок пор заметно возрастает. [13]
По этим причинам закономерности адсорбции в микропорах
резко
отличны от таковых на гладких, мезо- и макропористых
поверхностях.
Вместо
адсорбционных
полимолекулярной
слоев
последовательно
на
адсорбции,
поверхности
Дубинин
потенциальной теории Поляни постулировал
образующихся
адсорбента
[37]
на
в
основе
объемное заполнение
микропористой поверхности и предложил вместе с Радушкевичем,
а затем с Астаховым эмпирические уравнения изотерм адсорбции
в
микропорах,
позднее
наполненные
физическим
содержанием
параметров этих уравнений. Уравнения получили название теории
объемного заполнения микропор (ТОЗМ).
В теории объемного заполнения микропор (ТОЗМ) [37] впервые
были сформулированы основные физико-химические свойства этих
систем.
Адсорбат
в
микропорах
целиком
находится
перекрывающихся адсорбционных полях противоположных
в
стенок
микропор. Поэтому его свойства существенно отличается как от
свойств адсорбата на открытой
поверхности, так и от свойств
вещества в равновесной объемной фазе.
Как уже ранее нами отмечалось по классификации Дубинина [21]
эффективные
размеры
микропор
соизмеримы
с
эффективными
размерами сорбирующихся молекул. Область размеров (диаметров
или
ширины)
микропор
распределена
на
ультрамикропоры
(собственно микропоры) - до (1.2—1.4) нм и супермикропоры - от (1.2¬
1.4) до (3.0-3.2) нм. Поры с эффективными размерами в интервале
(3.0-3.2 < х < 100-200 нм) выделены в класс мезопор. Адсорбция в
мезопорах
происходит
по
механизму
послойного
заполнения,
приводящего к капиллярной конденсации. Размеры мезопор намного
больше
размеров
переходными
адсорбируемых
между
микропорами
молекул.
и
Они
макропорами,
являются
имеющими
размеры более 100-200 нм. Адсорбция в макропорах происходит по
механизму
послойного
незначительную
существенное
роль
влияние
заполнения.
в
величине
на кинетику
Макропоры
адсорбции,
процесса,
играют
но
весьма
оказывают
выполняя,
как и
мезопоры, функцию транспортных пор для адсорбируемых молекул.
Аналогичные принципы положены и в основу классификации пор по
размерам, принятой Международным союзом по чистой и прикладной
химии (ШРАС) [22].
В
отличие
от ленгмюровской
теории
мономолекулярной
и
БЭТовской полимолекулярной и им подобным, ТОЗМ не связана ни с
одной упрощенной моделью адсорбции. По своей сути она является
термодинамической
теорией,
использующей
ряд
эмпирических
соотношений, основанных на выборе и свойствах
системы, таких как:
адсорбента,
химический
потенциал
адсорбционной
ц
микропористого
который изменяется в процессе адсорбции
повышенная адсорбционная активность
сравнению
с
непористыми
флюида;
в микропорах порах по
адсорбентами;
температурная
инвариантность характеристической кривой адсорбции (см. теорию
Поляни).
Что
микропористого
касается
термодинамической
адсорбента,
то
как
показано
неинертности
Берингом
Б.П.,
Серпинским В.В., Якубовым Т.С., Гребенниковым С.Ф. [38, 39],
адсорбции
микропористый
адсорбент,
рассматриваемый
до
как
независимая фаза, после адсорбции перестает быть отдельной фазой и
его
следует
необходимо
вместе
с
одно-
рассматривать
или
уже
как
n-компонентным
единую
двух
флюидом
или
компонентную фазу. В этом принципиальное отличие
(n+1)-
адсорбции
флюида на непористых, макро- и мезопористых адсорбентах от
адсорбции
флюида
в микропорах.
микропористым
Таким
образом,
адсорбентом
спецификой
является
сорбции
образование
однофазной системы.
В ТОЗМ авторами использован
факт
температурной
многократно
инвариантности
так
подтвержденный
называемых
характеристических кривых адсорбции, выражаемых зависимостью
степени заполнения объема микропор в =~~
от дифференциальной
работы
что
адсорбции
Е = RTln(jf).
Заметим,
£ = -AG = - А д .
Величина W соответствует адсорбции при относительном давлении
Р/Ps, выраженной в см нормальной жидкости, отнесённой к 1г адсор¬
бента, W 0 — предельная
величина
адсорбции
при заполнении
микропор, равная удельному объему микропор. Например, если на
активном микропористом угле выстраивать изотермы
бензола в координатах зависимости W от s,
адсорбции
снятые в интервале
температур 293 - 413 К, то получим одну общую
адсорбционную
кривую, которая и называется характеристической кривой адсорбции.
Эту общую зависимость
М.М. Дубинин и В.А. Астахов получили,
используя статистическое распределение Вейбула с параметром n , в
1971 г.
или в логарифмической форме при (3=1
£
£
= о Г (в)\
(2-82)
В уравнении (2.81) параметры W , s -характеристическая энергия
0
0
адсорбции и n характеризуют адсорбент, а параметр ( — адсорбат
(коэффициент аффинности), означающий, что для двух разных паров
при одинаковых заполнениях 6 и n, отношения s /s = s / s = р. Для
2
1
02
01
стандартного (обычно, бензол) адсорбтива (3 = 1, при адсорбции
разных веществ на одном и том же адсорбенте (s0~ const.
Параметр
s
0
возрастает
с уменьшением
среднего
размера
микропор, показатель степени n-подгоночный параметр определяется
энергетической однородностью адсорбента, его значения
обычно
изменяются в пределах 1,5 - 3 , для цеолитов п = 3. Параметр (3
выражает
адсорбционные
свойства
использованного
адсорбтива
относительно стандартного, в качестве которого принят бензол при
293 К или азот при 77 К. Численно (3 принимается равной отношению
парахоров исследуемого и стандартного адсорбтива. Парахор —
1/4
параметр, не зависящий от температуры, равный с / ( р - р ) , где а —
ж
поверхностное натяжение, а р
ж
п
и р - плотность нормальной жидкой
п
фазы и паров адсорбата. Парахор введен Сагденом в 1923 г. для
расчетов а. Для сложных молекул парахор равен сумме парахоров
компонентов данной молекулы. [40].
Согласно (2.82) для заполнения 6 =1/e=0,368, где е-основание
0
натурального
s =s,
логарифма
0
т.е. характеристическая
энергия
адсорбции равна дифференциальной мольной работе адсорбции при
9о=0,368.
При
расчетах
по уравнению
(2.81) экспериментальная
ИА
п
линеаризируется в координатах I n W = 1п(а/р ) от [1п(Р/Р )] . Отрезок,
ж
8
отсекаемый экстраполяцией линейной части графика на оси ординат,
принимается равным
объему микропор W
0
= а /р , где р
0
ж
ж
—
плотность адсорбата, равная плотности нормальной жидкости при
n
температуре опыта. Наклон графиков соответствует [RT/pso)] ,
что
позволяет рассчитывать (3s .
0
Уравнение (2.81) при п = 2 называют уравнением Дубинина—
Радушкевича (ДР) , которое
допущения
потенциала.
о
гауссовском
было получено в 1947 г. на основе
распределении
адсорбционного
W
= -Г Р
(
8 \
(--^-j
0
а
где Vm -p;
=
ех
2
( 2 - 8 3 )
- мольный объем адсорбтива при температуре кипения,
М - его молярная масса.
Термическое уравнение (2.83) при наличия двух микропористых зон
на активных углях ультра- и супермикропор, которым соответствуют
независимые изотермы адсорбции записывают в форме
8i \ l W o ,
2
Wo,i
\
(
со своими значениями
2
x
W i
0 j
иW
0 j 2
\
(
2
е
2
\ 1
(
2
и энергетической константы
8
4
So,i
)
и
£ ,2 для каждой микропористой структуры адсорбента [37].
0
Позднее Дубинин и Стекли предложили обобщенный вариант
уравнения (2.84), согласно которому адсорбционная изотерма
в
микропорах описывается уравнением [41]
2 o,i
W
w
W
\(
= ——ex
V
v
m
в
котором
(
[\
при непрерывном
8
-
VI
i
„(
^ —1
осл
2 - 8 5 )
8
Р 0,1/
распределении
видов
микропор
суммирование заменяется интегрированием и вводится допущение о
нормальном, логнормальном
или другом распределении
объема
микропор по их размерам. Развиваемый Стекли с сотр. подход
позволяет определять не только суммарный объем микропор W , но
0
и
их средний размер и характеристики распределения пор по
размерам.
При допущении о нормальном распределении величины адсорбции
по полуширине микропор
da
а
(x
0
=
dX
e
^ / 2 i
x
p
[
2
—
0
X)
^ С Д ) ^
—
(
2
.
8
6
)
где a - полная адсорбционная емкость микропор,
0
x - полуширина микропор в максимуме кривой распределения и
0
А - дисперсия распределения,
уравнение изотермы Дубинина - Стекли [41] в интегральной форме
имеет вид
a
=
0
Т1 = \
AV2rJ
e
x
p
[ —
Л2
2 А
(
0
здесь m=(1/(3sox). Связь x
] e x p [ —
) 2
2
mx s
2 ] d
x,
(нм) с характеристической
0
( 2 . 8 7 )
энергией
адсорбции s (кДж/моль) стандартного пара (бензола) на углеродных
0
адсорбентах с порами в диапазоне
0,4-2нм
Стекли
предлагает
выражать эмпирическим уравнением
5,4
ТТТ
Хо =
0
(2.88)
£ —11,4
v
7
0
при этом, исходя из модели бесконечной щелевидной поры можно
получить уравнение для расчета удельной поверхности микропор
[Гребенников]
5д = - °
( 2 . 8 9 )
у
x
0
Для однородной микропористой структуры дисперсия А=0 и
вытекает обычное уравнение ТОЗМ
w
2
^0
^
2
exp(—ШХ0^ )
(2.90)
Уравнения достаточно точно описывают изотермы адсорбции на
углеродных
-5
5-10 -0,2.
адсорбентах
в
диапазоне
относительных
давлений
СПИСОК ЛИТЕРАТУРЫ
1. Rusanov A.I. //J.Colloid Interface Sci. 1978.V.63. P.330.
2. Erikson J.C. Surface Sci.1969.V.14.P.221.
3. Джейкок М., Парфит Дж. Химия поверхностей раздела фаз. - М.:
Мир, 1984. - 269 с.
4. Гохштейн А.
Я.
Поверхностное натяжение твердых тел и
адсорбция. - М.: Наука.1976. 400с.
5. Кинле X.,
Бадер
Э., Активные угли и
их промышленное
применение, пер. с нем., Л., 1984. 214 c.
6. Ролдугин В.И. Физикохимия поверхности. Долгопрудный: ИД
"Интеллект", 2011. 564 с.
7. Фомкин А.А. Адсорбция, адсорбенты и адсорбционные процессы
в нанопористых материалах.-М.: Издательская группа «Граница», 2011.
С.133.
8. Киттель Ч.. Введение в физику твердого тела. — М.: Наука,
1978. 789c.
9. Шаскольская М. П. Кристаллография. Учебник для втузов. М.:
Высш. школа.1976. 391 с.
10. Чоркендорф И., Наймантсведрайт Х. Современный катализ и
химическая кинетика. - М.: Интеллект, 2010. 504с.
11. Фенелонов В. Б.. Введение в физическую химию формирования
супрамолекулярной структуры адсорбентов и катализаторов / 2-е изд.
испр. и доп. Новосибирск: Изд-во СО РАН, 2004. 442с.
12. Адамсон А. Физическая химия поверхностей, М.: Мир, 1979.
568с.
13. Карнаухов А.П. Адсорбция. Текстура дисперсных и пористых
материалов. - Новосибирск: Наука. Сиб. предприятие РАН. 1999. 470c.
14. Макаревич Н. А. // Докл. АН Беларуси. 1997. Т.41, №2. C.73-78;
Изв. НАН Беларуси. Сер. хим. наук. 2002. №2. С.39-46; Там же. 2006. №.2.
C.34-43; Там же: 2006.№3. С.42-48.
15. Медведев Н. Н. Метод Вороного—Делоне в исследованиях
структуры некристаллических систем. Новосибирск: Изд-во СО РАН,
2000. 214с.
16. Волошин В. П., Медведев Н. Н., Фенелонов В. Б., Пармон В.
Н.// Докл. РАН. 1999. Т. 364. С. 337.
17. Хейфец Л. И . , Неймарк А. В. Многофазные процессы в
пористом теле. М.: Химия, 1982. 320c.
18. Mandelbrot В. B. The Fractal Geometry of Nature. S.-Francisco:
Frimar, 1982.
19. Федер E. Фракталы. M . : Мир, 1991. 260c.
20. Комаров В.С. Адсорбенты и их свойства. Минск.: Наука и
техника. 1977. 248с.
21. Дубинин М.М. //Изв. АН СССР Сер.хим. 1974 С.996.
22. YUPAC Manual of Symbols and Terminology. Appendix 2. Pt. I //
Colloid and Surface Chemistry. Pure Appl. Chem. 1972. V. 31. P. 578.
23. Товбин
Ю.К.
Молекулярная теория адсорбции в пористых телах. 2013. М.: Физматлит.
624 с.
24. Беринг Б.П., Майерс А., Серпинский B.B.// ДАН СССР. 1970. Т.
193. С. 119.
25. Брунауэр С. Адсорбция газов и паров. М.: ИЛ, 1948. 764с.
26. Грег С., Синг К. Адсорбция, удельная поверхность, пористость,
Мир, М.,1984. 306с.
27. Cohan L.H.//J.Am .Soc.1938.V.60.
28. Сивухин Д.В. Общий курс физики. Т.2. М: Наука 2005. 544с.
29. Де Бур Я. Динамический характер адсорбции, ИЛ, М., 1962. 291с.
30. Макаревич Н.А. Актуальные проблемы теории адсорбции,
пористости и адсорбционной селективности. Мат. Х Всеросийского
симпозиума с участием иностранных ученых. Москва-Клязьма. 2005. С
29.
31. Макаревич Н.А.// ЖФХ. 1991 т.65, №.8, с.1959; ЖФХ.1992, т.66,
№5 с. 1288.
32. Аранович Г.Л. // Журн. физ. химии. 1988 т. 62. С. 3000.
33. Оно С., Кондо С. Молекулярная теория поверхностного
натяжения в жидкостях. М.: ИЛ. 1963.
34. Ларионов О.Г. Дис д-ра хим. наук. М.: Ин-т физ. химии АН
СССР, 1975. С .318.
35. Keenan A.G., Holmes J.M . // J. СО1. Chem. - 1949. - Vol. 53. P. 1309.
36. Брек Д. Цеолитовые молекулярные сита. Пер. с англ. М.: Мир.
1976. 781с.
37. Дубинин М.М. Адсорбция и пористость. М.: ВАХЗ. 1972.126.
38. Беринг Б.П., Майерс А., Серпинский В.В. // Докл АН СССР.
1970.Т.193. №1.С 119.
39. Гребенников С.Ф., Серпинский В.В., Пахомов Ю. И, Якубов Т.С.
// Изв АН СССР. Сер. хим. 1983.№3. С.498
40. Quayle О. R.//Chem. Rev. 1953. V. 53. P. 439
41. Dubinin M.M., Stoecli F.J. Colloid Interface Sci. 1980.V.75. P.34
3. Т Е Р М О Д И Н А М И К А В Т Е О Р И И П О Л И М О Л Е К У Л Я Р Н О И
АДСОРБЦИИ И ТЕОРИИ ОБЪЕМНОГО ЗАПОЛНЕНИЯ
МИКРОПОР
Адсорбция-самопроизвольный
выделением
тепла
dH.
процесс
сопровождающийся
Различают
дифференциальную
изостерическую q , измеренную при постоянной степени заполнения
st
в, и интегральную
характеризует
заполнения
Q теплоту
тепловой
эффект
адсорбционного
адсорбции.
Дифференциальная
в интервале
пространства,
изменения
стремящемся
Измеряется в кДж/моль. Зависимости дифференциальной
-
степени
к нулю.
теплоты
адсорбции от степени заполнения, как правило, носят убывающий ха¬
рактер. При наличии сильного взаимодействия
молекул
друг
с
другом
в
начальной
адсорбированных
области
заполнения
адсорбционной емкости возможно локальное увеличения теплоты
адсорбции. Нижним пределом дифференциальной теплоты сорбции
для степеней заполнения, близких к предельным является теплота
конденсации пара. При интегрировании дифференциальной теплоты
адсорбции q по степени заполнения получают интегральную теплоту
st
адсорбции Q, так же измеряемую в кДж/моль или в эквивалентных
единицах. Интегральную теплоту адсорбции, отнесенную к числу
молей адсорбата, называют средней теплотой адсорбции Q .
cp
измеряют в тех же единицах, что и дифференциальную
адсорбции.
Ее
теплоту
Иногда пользуются понятием чистой изостерической теплоты
адсорбции
q *,
которая
st
представляет
собой
разность
тепловых
эффектов фазового перехода при адсорбции Q и конденсации L.
В термодинамической теории адсорбции одним из обязательных
условий является получение формулы для изотерической теплоты
адсорбции
q
и
st
выражения
для
этой
теплоты
через
термодинамические функции адсорбции. Формально ее получают из
уравнения Клаузиуса - Клапейрона для идеального
равновесного
флюида
dlnP
АН
dT
RT
(1.1)
2
где Р - давление первой фазы;
Т - температура, К ;
R - универсальная газовая постоянная;
ЛИ - теплота фазового перехода флюида.
0
Если
рассматривать термодинамическую систему, состоящую из n
молей однокомпонентного флюида (газа или жидкости) в объеме V и
находящуюся
основным
в адсорбционном
следствием
второго
равенство, связывающее
равновесии
с адсорбентом, то
начала термодинамики
является
термическое и калорическое уравнение
состояния термодинамической системы /4,8/
При переходе к переменным Р и Т получают эквивалентное
уравнение
v
- ^ ^ \ = b l
(
1
3
)
В этих уравнениях U - внутренняя энергия, Н = U + PV
-
энтальпия термодинамической системы.
Эти
оба
классических
уравнения
применимы
термодинамической системе, включая и сложную
к
любой
адсорбционную
систему газ - твердое тело.
3.1. Теплоты адсорбции на основе двух и более
экспериментальных изотерм адсорбции
Данные о теплоте адсорбции могут быть извлечены непосред¬
ственно при анализе экспериментальных изотерм, полученных для
двух и более температур в узком температурном интервале. Для этого
с одним и тем же адсорбентом и адсорбтивом экспериментально
получают несколько изотерм адсорции. Расчет теплот
можно провести графически по следующей схеме.
изотермы
адсорбции
Выстраивают
на одном и том же графике зависимости а или в от
давления p , p/p или от концентрации с. И далее, начиная от меньших,
s
для нескольких
значений
(не менее четырех) параллельно оси
давлений (концентраций) проводят прямые линии, т. е. при a=const
для
каждой
температуры
получают
значения
(коцентрации), по которым в линейных координатах
выстраивают семейства изостер -
давления
lgp -
1/T
давления от темпеатуры при
постоянной адсорбции.
Для примера [1], на рис 3.1 приведены изостеры адсорбции нбутана на промышленных адсорбентах в линейных координатах lgp 1/T. Каждой из этих прямых отвечают разные
Рисунок 3.1. Изостеры адсорбции н-бутана при 0=0,02-5-0,12 на: а
NaX; б —цеолит СаА; в — активный уголь [1 ]
цеолит
степени заполнения поверхности адсорбента. Изостеры адсорбции в
координатах
прямыми
уравнения
линиями.
(3.5)
удовлетворительно
Дифференциальные
рассчитывают по тангенсу угла
описываются
теплоты
наклона изостер.
адсорбции
Метод расчета
теплот адсорбции по изостерам основан на уравнении КлапейронаКлаузиуса, представленного в форме
/ dlnp \
R
•Л*//
Следовательно,
(3.4)
Q = conSt
изостерическая
дифференциальная
теплота
адсорбции
(3.5)
Л;'
Q=const
В табл.3.1 приведены вычисленные средние теплоты адсорбции
предельных и непредельных углеводородов и других веществ по
данным Н.В. Кельцева, А.В. Киселева с сотр. и Астахова В.А. [1].
Таблица 3.1.
Средние теплоты адсорбции Q , кДж/моль и теплоты конденсации L ,
кДж/моль предельных и непредельных углеводородов и других
адсорбтивов на микропористых адсорбентах
cp
СаА
Метан
Этан
Пропан
н-Бутан
н-Пентан
н-Гексан
н-Гептан
н-Октан
9,01
14,71
18,73
22,33
25,85
29,12
32,05
35,03
16,76
26,82
36,03
44,00
55,73
66,20
76,68
87,15
16,76
25,98
36,03
41,90
53,21
62,85
72,91
82,96
39,81
50,28
60,34
69,14
79,1
18,10
25,14
35,74
41,73
51,96
60,55
63,69
71,2
Метилциклогексан
Этилен
31,63
61,59
59,50
-
-
13,53
37,71
36,87
-
-
Из
таблицы
обладающих
Nax
видно,
высокой
Адсорбат
СаА
Активные
угли
СКТ Х С
-
Пропилен
Бутилен
Ацетилен
Метилацетилен
Винилацетилен
Диацетилен
Вода
Диоксид
углерода
Монооксид
углерода
что для предельных
дисперсионной
Цеолиты
Теплота
конденсции
Цеолиты
Теплота
конденсции
Адсорбат
СаА
Nax
18,52
16,89
-
44,83 43,58
58,66 61,59
45,67
54,05
51,12
71,23
75,42 75,42
16,34 32,68
6,03
15,92
-
углеводородов,
составляющей
тепловой
энергии, с ростом длины углеводородной цепи теплоты адсорбции на
микропористых адсорбентах — цеолитах всех типов и активных
углях линейно возрастают на 6— 10 кДж/моль при увеличении длины
цепи на одну метиленовую группу, а по абсолютной величине близки
друг
к другу
и приблизительно
в два раза
выше
их теплот
конденсации [1]. На крупнопористых адсорбентах это соотношение
уменьшается до 1,5 [2].
По данным работ Баррера, Хебгуда, Ширмера, Киселева и
Петерсона с сотр. (табл. 3-2) [1,3], коэффициенты в уравнении,
связывающие
теплоту
адсорбции
с числом
атомов
углерода
в
молекуле нормального парафинового углеводорода, зависят от типа
цеолита.
Вклад
обусловленной
специфической
двойными
составляющей
и тройными
связями
углеводородах, наглядно прослеживается
взаимодействия,
в
непредельных
при сопоставлении теплот
адсорбции разных гомологических рядов.
Таблица 3.2.
Теплоты адсорбции Q (кДж/моль) нормальных парафиновых
углеводородов с п числом углеродных атомов в молекуле
на разных цеолитах
Цеолит
Углеводороды
Н-шабазит
Са-шабазит
С1-С4
С1-С7
HL
KL
Na, Са, M g A
Н-морденит
-
С
4
С
1
-
С
4
1
-
С
1
-
С
4
С
1
-
С
4
С
1
-
С
4
1
-
С
6
С
одной
9-0
1
С
NaX
1 8
9-0
9-0
0,2—0,8
С
С
СаХ
СаА
Замена
Степень
заполнения 9
9-0
9-0
простой
Формула для
определения Q
11,5+8,4 п
27,2+10,5 п
10,5+8,4 п
10,9+9,2 п
22,8+6,5 п
16,8+8,4 п
9-0
9-0
0,8
связи
в
молекуле
18,9+9,2 п
7,1+9,6 п
2,5+13,8 n
углеводорода
(например, пропана) на двойную (пропилен) в случае адсорбции на
цеолитах
вызывает
увеличение
дифференциальной
теплоты
адсорбции в среднем на 8,8 кДж/моль, а при переходе от двойной
связи (пропилен) к тройной (метилацетилен) - на 9,2 кДж/моль. В
случае молекул с двумя тройными связями разница теплот адсорбции,
например, между диацетиленом и бутаном составляет 3 1 кДж/моль, а
диацетиленом и бутиленом 21 кДж/моль. По Барреру [3], вклад
специфической составляющей, обусловленной энергией диполей и
квадруполей молекул, в общую теплоту адсорбции на различных
типах
цеолитов
для
часто
встречающихся
неорганических
адсорбтивов может составлять: для азота — от 28 до 52%; для
диоксида углерода от 40 — до 75%; для аммиака — до 80%.
Экспериментальные данные по теплотам адсорбции получают
из
калориметрических,
наблюдений.
К
хроматографических
экспрессным
хроматографический
метод,
методам
и
термографических
исследования
дающий
относят
достаточную
точность.
Классические калориметрические методы исследования теплот, и в
особенности,
теплоемкостей
трудоемки,
требующие
высокой
квалификации от экспериментатора.
Существенный
вклад
в
получение
расчётных
термодинамических характеристик адсорбции был сделан школой
М.М.
Дубинина.
Берингом
и
Серпинским
[4]
были
термодинамические критерии, определяющие условия
получены
выполнения
основного положения теории объемного заполнения микропор о
температурной инвариантности характеристического уравнения. Эти
критерии были распространены на уравнения для дифференциальных
(мольных)
теплоты
и
энтропии
адсорбции.
Авторы
вывели
уравнения, позволяющие вычислять дифференциальные теплоты и
энтропии адсорбции для различных степеней заполнения по одной
изотерме адсорбции.
3.2.Термодинамика в теории объемного заполнения
микропор
Беринг
и
Серпинский
[4]
исходили
из
общего
термодинамического соотношения, характеризующее адсорбционное
равновесие. То есть при температуре Т и равновесном давлении р
количество адсорбированного вещества составляет а. Если принять в
качестве стандартного состояния для отсчета
термодинамических
функций адсорбата (энтальпии, энтропии, энергии Гиббса) состояние
нормальной жидкой фазы адсорбтива при той же температуре, то
максимальная работа A перехода 1 моль адсорбтива из объемной фазы
на
бесконечно
большое
количество
адсорбента
запишется
по
известному нам выражению
А = -AG = RTln (j)
(3.6)
где p — давление насыщенного пара.
s
На случай неидеальной газовой фазы в уравнение (3.6) и все
дальнейшие уравнения можно вводить летучести вместо давлений.
При
соблюдении
условия
инвариантности
характеристического
уравнения дифференциальная мольная энтропия адсорбции выразится
уравнением
/ dA \
A S
= <аш)
( 3 7 )
<0
т
где а — термический коэффициент предельной сорбции.
Условие
(3.7)
выполняется
для
нижней
границы
области
температурной инвариантности. Как показано в [4], оно соблюдается,
если степень заполнения адсорбционного пространства превышает
0,15—0,20 -
нижняя
граница
применимости
теории
объемного
заполнения микропор.
В условиях инвариантности
общее выражение
ренциальной мольной теплоты адсорбции Q [5]
для
диффе­
Q=A+A aT
(3.8)
- iiL)
T
где X - теплота конденсации.
Величина А определяется по уравнению (3.6), откуда можно
взять производную
/ dA \
(dlnx\
-
\dlna)
T
где x=p/p
s
(
\dlna)
3
9
)
T
- равновесное относительное давление.
С учетом (3.6) и (3.9) из (3.8) получаем:
2
Q=X-
RTlnx + аТ
„ /dlnx\
(—^)
\dlna)
(3.10)
T
Используя уравнение теории объемного заполнения микропор
Дубинина -Астахова [5]
а = а ехр
0
\ — ~^J
(3.11)
преобразовывая его с учетом (3.6) относительно х получают:
1
х
-
.
» = ИЖТ
( 3 . 1 2 )
Дифференцируя (3.12) получают выражение для производной:
О =irA if
lna
\dinа/
nRT V
т
1
(313)
а '
По теории Дубинина - Радушкевича температурную зависимость a
0
выражают уравнением
(
а
0
= а °ехр[-а(Т
— Т )],
0
(3.14)
0
где а — предельная величина адсорбции, найденная при температуре Т для
исходной изотермы, служащей для нахождения характеристической энергии
адсорбции и для оценки показателя степени n.
0
0
После подстановки (3.13) в (3.10)
«--^е^Т^КТ
1
(3.15)
Уравнение (3.15) может быть записано в форме:
1
q-Q-X-A
+ (
) (In —)
п / v а
(3.16)
где q — чистая дифференциальная теплота адсорбции.
Аналогичным образом получено уравнение для дифференциальной
мольной энтропии адсорбции:
1
AS
Используя
—аЕ /. а \п
(ln^f~
п V а
1
п
значение характеристической
.
точки,
(3.17)
соответствующей
степени заполнения объема адсорбционного пространства, равной
обратной величине основания натуральных логарифмов, т. е. 0,368, по
формулам (3.16) и (3.17) получено
-Е 1+
7
*> [ 3 ']
( 3 . 1 8 )
аЕ
AS,,--—
п
(3.19)
аЕТ
Обычно вклад члена
в величину q составляет около 10%.
0
Следовательно, для характеристической точки
характеристическая
энергия адсорбции близка к дифференциальной теплоте адсорбции.
Выражение
(3.19)
показывает,
что
различие
между
q
0
и
Е
определяется энтропийным членом.
Для удобства расчетов уравнения (3.15) и (3.17) представляют в
форме десятичных логарифмов уравнения
a =E 2 3 0 H ^ f +
^
1
0
(3.20)
п
а
AS
а \п
аТ (
2,30^
1-1
аЕ
-1
(3.21)
пп
Ha рис. 3.2 сравниваются вычисленные по уравнению (3.20)
дифференциальные теплоты адсорбции бензола (сплошные кривые) и
экспериментальные изостерические теплоты адсорбции (обозначены
кружочками)
для
двух,
образцов
активных
углей,
изученных
Дубининым и Полстяновым [6].
При
(3.11)
расчетах
n=2.
по
уравнению
Расхождения
в
расчетах
и
теоретических
экспериментальных
значениях,
полученных методом калориметрии,
не превышают 5%.
Зависимость
Рисунок
3.2.
теплоты
дифференциальной
адсорбции
Q
от
количества
адсорбированного бензола а для
двух активных углей
Теория
объемного
заполнения
позволяет,
помимо
микропор
описания адсорбционных равновесий
в
достаточно
широких
интервалах
температур и давлений, с удовлетворительной точностью вычислить
дифференциальные (мольные) теплоты и энтропии адсорбции.
3.3. Термодинамика в теории полимолекулярной адсорбции
Вычисления изостерических теплот адсорбции можно провести
и путем отыскания производной по уравнению
f
dlnP\
°» {цг)
= кт
Изостерическая
а
теплота
2
RT
/dP"
= —{Ит1
адсорбции
( 3 . 2 2 )
численно
равна
энтальпии
адсорбционного процесса, но противоположна по знаку:
dlnPP
RT VdF)
= = ~
+ RT
g s t
=
A
H
A
U
(3.23)
или
3st = 3v + RT
q
v
(3.24)
- дифференциальная теплота адсорбции, выраженная через
внутреннюю энергию (AU). Как указано ранее при адсорбции паров
используется
термин
дифференциальная
«чистая
теплота
изостерическая
адсорбции»,
теплота
минус
т.е.
теплота
конденсации пара:
^ dln
2
9st — L = RT 1 ~
р
\
p P
d T
)
(3.25)
\ Л
М ы видели, что традиционно зависимость q
st
(для газов, паров) или q
st
как функцию от P
= Д(с) - для растворов
рассчитывают,
получив как минимум две или несколько изотермы адсорбции a=f(P
или с). Здесь с - молярная концентрация раствора.
В
отличие
рассматривающего
от
только
возможность
для
Беринга
и
Серпинского
расчет по единственной изотерме
изостерических теплот
fid)
подхода
адсорбции
как функцию от величины адсорбции q =
st
адсорбции
расчета
[4],
в
микропорах,
зависимостей
q
st
единственной, полученной в эксперименте,
= fP
принципиальную
или
с),
т.е.
из
изотермы адсорбции в
любом модельном приближении показал Макаревич Н. А. [7]. Автор
эту
задачу теоретически
решил
достаточно
просто
[7] путем
дифференцирования термического уравнение адсорбции a=f(P или с)
по
температуре
при
6=const
полимолекулярной адсорбции
для
известных
моделей
(БЭТ, Деллайса, Хюттига, Арановича
и др.), включая и уравнения для адсорбции в микропорах,
последующей подстановкой
с
полученного результата в уравнения
Клапейрона - Клаузиуса. (Далее для краткости в q
индекс «st»
st
опустим).
Здесь
x = P /P
s
-
относительное
давление,
Ps
давление
насыщенного пара адсорбата, 0 -степень заполнения адсорбционного
слоя,
^-универсальная
температура.
газовая
постоянная,
Т
-
абсолютная
С-константа адсорбционного равновесия, входящая в
уравнение адсорбции, q - текущая, q - « ч и с т а я » начальная (первая)
0
изостерическая теплота адсорбции. Если при нулевых, заполнениях
константа адсорбционного равновесия С
переходит в константу
Генри К , то справедливость выражения (3.27) не вызывает сомнения.
н
Из уравнения Генри
е = Кр = Кх
н
(3.28)
н
согласно предлагаемому алгоритму дифференцирования
9=f(P)e= omt
C
по температуре для модели Генри (3.28), неотвратимо следует
q = q
0
(3.29)
Для ленгмюровской
монослойной
адсорбции
bp
6 = — —
1 + Ьр
При
степени
заполнения
(3.30)
поверхности
адсорбента
0=const
изостерическая теплота адсорбции, так же как и в (3.28)
(3.31)
q = q0
Здесь и далее 0 = a/a , а - текущая,
a
m
m
- максимальная величины
адсорбции.
Равенство
поверхности
q
= q
0
говорит
адсорбционные
о том, что для
центры
энергетически
однородной
однородны,
поскольку в этих моделях адсорбция рассматривается как процесс
идеальный.
Однако, адсорбция не ограничивается образованием монослоя,
происходит
образование
полимолекулярных
слоев.
Поэтому
предложен ряд уравнений изотерм адсорбции и, соответственно,
получены
[7]
уравнения
изотерм
дифференциальной
теплоты
адсорбции.
С. Брунауэр совместно с Эмметом и Теллером для однородной
непористой
адсорбции
поверхности
построили
теорию
полимолекулярной
(БЭТ) [8], по которой величина адсорбции определяется
уравнением изотермы
Сх
(1-х)[1
+
(С-1)х]
(3.32)
Из этого уравнения так же вытекает уравнение
дифференциальной
изотермы для
теплоты адсорбции как функция относительного
давления [7]:
2
а (1 - х)
q = -^- —j—
1-х
+ Сх
0
2
2
4
2
к
(3.33)
J
Для пористой поверхности сначала Брунауэр, Эммет и Теллер
[8], а затем Пиккет и Делайес
трехпараметрическое
суммирование
[9] получили более
корректное
уравнение при логичном предположении, что
по числу монослоев n в поровом
пространстве
поверхности и объеме следует проводить не от 0 до n, как это делали
Брунауэр с соавторами, а от 0 до оо;
=
9
п
Сх(1 -
" (1-х)[1
х)
( 3 . 3 4 )
+ (С-1)х]
В этой адсорбционной
модели
дифференциальные
теплоты
адсорбции приняли вид [7]:
4
2
2
= \1-х
+ Сх
. (1-х)
Яо
пх (1-х
п
2
(
+ Сх)]
(1-х )(1-х)_
3
.
3
5
п
Из ранее полученных модифицированных изотерм типа БЭТ
заслуживает
внимания
изотерма
Хюттига
[10]. Делая
вывод
двухпараметрической изотермы (12), Хюттиг снял ограничение на
испарение молекул из i - го слоя (мешает i+1 слой) и получил простое
по виду уравнение изотермы;
Сх(1 + х)
Q = —^
1+ х
(3.36)
у
J
И, как следствие, Макаревич [7] получил простое по виду
уравнение изотермы дифференциальной теплоты адсорбции;
4
( 3 . 3 7 )
= 1 + 2х + С 2
Х
Двухпараметрическая изотерма адсорбции Арановича [11] для
плоской однородной полубесконечной
поверхности с неограниченным
числом адсорбционных слоев:
Сое
Э =
(3.38)
г
(1 + Сх)(1 —
х)2
принципиально отличается от приведенных выше уравнений изотерм
(8,10,12), т.к. в нем при выводе нет ограничений на испарение
молекул из любого адсорбционного слоя и на вакансии по «узлам
решетки».
Изотерма
при
низких
давлениях
ленгмюровскую, а затем в модель Генри.
можем выразить через дифференциальные
переходит
в
Изотерма, которую мы
теплоты сорбции, будет,
как и (3.38) качественно корректна в предельных случаях [7]:
а \2(1 — х)]
q =-^°--—-Ц(2 — х + Сх )
0
4
2
(3.39)
к
J
Изотерма (3.38) отвечает множеству экспериментальных
адсорбционных данных, поэтому для расчета
теплот адсорбциии
дифференциальных
по единственной экспериментальной
адсорбционной изотерме также широко может быть использовано
(3.39)
Для
пористых
адсорбентов
изотермы адсорбции Макаревича [7]
трехпараметрическое
уравнение
г
а Сх
т
а =
,
n
±\
+
r
1 - ( 1 - (1 - х)2)
1
(1 + С х ) ( 1 - х ) 2
i
-
(3.40)
приводит к изотерме дифференциальной теплоты адсорбции
Г1 +
<=*>
0 + С ) Г
2
-
(
2(1-*)-,;
2
.
4
1
)
nn
-
(П + 1 ) ( Х + С Х )
3
1 - ( 1 - Х ) 2
-
+-
-
2 (1 - [1 - (1 - х) Г (1 - х) )
В
ленгмюровские
зависимости
с q
=q
0
выражение
(3.41)
переходит при n = I , а (1.50) - при n = 0.
Отметим, что в моделях БЭТ, Хюттига и Пиккета в выражениях
для константы адсорбционного равновесия
0
С^ехр! ; ,
предэкспоненциальный
теоретического
множитель
обоснования,
дифференциальной
теплоты
(3.42)
А
не
поэтому
для
адсорбции
q
0
имеет
надежного
расчетов
начальной
предпочтительнее
применять соотношение [11]
^ ё М И
-
1
( 3 . 4 3 )
]
в котором этот множитель имеет смысл отношения
плотностей
адсорбата в состоянии насыщенного пара (о ) и жидкости (р ) при
п
ж
заданной температуре (Т, К).
На практике для вычисления дифференциальных теплот по
любому
из рассматриваемых
уравнений
изотерм
адсорбции,
за
исключением моделей Генри и Ленгмюра, в которых q=q при всех
0
значениях x, необходимо выразить эту изотерму в линеаризованной
форме, по экспериментальным
уравнения
изотермы
рассчитать
значения
данным в линейных
определить
«чистой»
С и a
m
начальной
координатах
по уравнению
теплоты
q
0
(3.43),
и
по
соответствующему выражению для теплоты адсорбции как функции
от х найти текущие дифференциальные теплоты q. Для сопоставления
калориметрических теплот адсорбции паров адсорбата с расчетными
дифференциальными теплотами к последним добавляют величину
теплоты конденсации L адсорбата (4).
Рисунок 3.3. Зависимости нормированной чистой дифференциальной теплоты
адсорбции (q-q ) от величин р/р и С в моделях адсорбции на непористых
адсорбентах [7]: а - Б Э Т (1.30); б - Х ю т т и г а (1.36); в, г - А р а н о в и ч а
0
8
На рис.3.3. показано, как изменяется теоретически рассчитанная
нормированная на начальную «чистую» теплоту дифференциальная
теплота
адсорбции,
полученная
по
уравнениям
изотерм
дифференциальных
теплот
для
непористых
адсорбентов
в
зависимости от P/P и С в двухпараметрических изотермах.
s
Приведенные зависимости наглядно показывают общность и
различие этих моделей адсорбции. Основное различие в абсолютных
расчетных значениях q/q0 по сравниваемым изотермам наблюдается
при малых значениях С, характерных для адсорбентов с низкой
энергией поверхности, а с константами С порядка нескольких сотен
единиц и выше просматривается общность лишь самой тенденции
изменения
Если
q^).
эксперимент
по
определению
величин
адсорбции
и
дифференциальной теплоты (энтальпии) согласован, то, сопоставляя
теоретическую
говорить
зависимость
об адекватности
q(x)
с
выбранной
экспериментальной,
адсорбционной
можно
модели
и
исследуемой системы адсорбент - адсорбат. К тому же будет получен
ответ о правильности найденных из изотерм адсорбции параметров С
и am, что принципиально
важно для достоверного
определения
удельной поверхности адсорбента.
И,
наконец,
имея
экспериментальную
изотерму
адсорбции
а=1*(х) и расчетную изотерму дифференциальной теплоты адсорбции
q=f(x) в выбранном модельном приближении, исключив х, строим
зависимость q=f(а). Это важно для оценки энергетики поверхности в
зависимости от ее заполнения различными адсорбатами.
3.4. Приложение термодинамической теории
полимолекулярной адсорбции к адсорбции из газовой и
жидкой фаз на твердой гладкой и пористой поверхности
Для иллюстрации
применимости уравнений
(1.39) и (1.40)
рассмотрим классическую изотерму адсорбции аргона и азота на
однородной
поверхности
подчиняющуюся
в
хлорида
соответствии
с
калия
по
данным
классификацией
наиболее общему типу полислойной адсорбции - типу
/11/,
Брунауэра
I I . Как
следует из рис. 1.5,б, изотерма (1.39) охватывает экспериментальные
данные Лг и N в широком диапазоне относительных давлений (от
2
0,1 до 0,8), в то время как в рамках изотерм БЭТ (рис. 1.5,а) этот
диапазон значительно уже (~ 0,05 -т 0,3). Найденные значения С по
изотерме (1.39) для Лг и N составили соответственно - 13.0 и 27,9, а
2
3
емкость монослоя - 0,80 и 0,62 см /г (по БЭТ a равна 0,730 и 0,615
m
см /г), а начальные дифференциальные теплоты для аргона и азота на
поверхности хлорида калия, рассчитанные по соотношению (1.25),
составили при этом 6,2 и 5,5 кДж/моль. По данным /35/, энергия связи
молекул аргона с центром ячейки хлорида калия соответствует 6,0
кДж/моль. Лучшими экспериментальными данными по адсорбции
аргона на хлориде калия признаны данные Хаякавы [12] -
8,71
кДж/моль. Совпадение результатов расчета по изотерме (1.39) и по
данным [12] указывает, с известной оговоркой, на соответствие
уравнения (1.39) экспериментальным данным по адсорбции аргона на
поверхности
теплоты
хлорида
адсорбции
калия.
с
Некоторое
расхождение
калориметрическими
значения
измерениями,
по-
видимому, связано с экспериментальными трудностями, вызванными
малой удельной поверхностью хлорида калия (~2,7 м /г).
Отметим,
что
эти
предосторожностями
уравнения
могут
быть
с
соответствующими
применены
и
для
мезо-
микропористых адсорбентов в негистерезисной области заполнения
поверхности. Примером этому может служить изотерма адсорбции
паров бензола на цеолите Н Ц В М (рис.1.5, в), которая спрямляется в
линейных координатах P/P /a(1s
12
P/P ) T
S
диапазонах относительных давлений: 1 1 0
1
-7,5 10
-1
(при
P/P =7,5 10
s
-1
P/P по уравнению (1.39) в
s
-4
-2
-1
-1
- 410 ; 410 -210 ; 210
начинается
область
¬
капиллярной
конденсации паров бензола).Для каждого из отмеченных диапазонов
характерны и свои значения начальных дифференциальных теплот
адсорбции.
Рисунок 3.4. Изотермы адсорбции аргона (I) и азота (2) на хлориде калия по
данным Кинана и Х о л м с а [11] в координатах уравнения Б Э Т (а) и Арановича (б),
бензола на цеолите Н Ц В М (в) в координатах уравнения Арановича
С
учетом
кДж/моль
теплоты
/37/ q
0
t
конденсации
паров
бензола
(L=30,72
равны соответственно 56,0; 50,9; 48,0 кДж/моль.
Текущее изменение теплоты
q
0
как
t
функции
относительных
давлений представлено на рис. 3.5, кривая 3. Результаты расчета
дифференциальных теплот адсорбции показывают, что адсорбция
бензола
на
цеолите
НЦВМ
предположительно
протекает
по
трехступенчатому механизму, связанному, видимо, с различием в
энергетике внешней и внутренней поверхности
адсорбента. Для
проверки возможности использования уравнений (3.39) и (3.41) при
определении
дифференциальных
теплот
адсорбции
микропористых адсорбентах были рассчитаны
теплоты
адсорбции
клиноптилолита
паров
( L i Кл)
воды
при
25°
адсорбционно-калориметрического
на
дифференциальные
на
монокатионной
по
данным
эксперимента.
форме
совмещенного
В
отличие
от
цеолита Н Ц В М изотерма адсорбции паров воды на цеолите L i К л в
линейных
координатах
уравнения
(3.38)
спрямляется
2
1
диапазонах относительных давлений 1 1 0 - 6 1 0
емкости
монослоя
0,42
ммоль/г
в
1
двух
1
и 6 1 0 - 9 1 0 . При
расчетные
значения
дифференциальных теплот адсорбции в области заполнения до 6 1 0
- 1
отличается от экспериментальных калориметрических не более чем
на 10% (кривые 4, 5 рис. 3.5). Следует отметить, что уравнениями
(3.40)
и
(3.41)
все
же
предпочтительнее
пользоваться
на
макропористых адсорбентах, для которых они и получены.
Таким образом, с помощью изотерм адсорбции (1.39) и теплот
адсорбции
(1.40)
можно
провести
расчеты
дифференциальных
изостерических теплот адсорбции на непористых и с известными
ограничениями на пористых сорбентах в диапазоне относительных
давлений адсорбата, для которых эти уравнения выполняются. Более
детальную
проверку
применимости
изотерм
(1.39) и (1.40) для
исследуемых типов адсорбентов можно осуществить сопоставлением
расчетных и калориметрических теплот адсорбции /7/.
Проследим применимость модели адсорбции (3.38) и (3.39) в
согласованном адсорбционно-калориметрическом
эксперименте по
данным адсорбции паров н-гексана на поверхности промышленного
образца y-Fe O
2
3
/7 /. Априори крупнопористый образец y-Fe O
2
3
относится к адсорбентам с поверхностью, близкой к однородной, об
этом качественно свидетельствует ход кривых дифференциальной
теплоты адсорбции в зависимости от Р/Р
8
(рис. 3.5 кривая 3). Для
найденных из уравнения изотермы адсорбции (1.39) параметров
a =3,64 ммоль/м
m
и С =22,0 «чистая» начальная теплота адсорбции
для интервала Р/Р
5
от 0,01 до 0,2 составит 24,1 кДж/моль, а
соответствующие величины qfaJ+L будут представлены кривой I рис.
3.6.
б,о
Ao
t
з,о
2,0
ip
J о
0
0,2
0,4
0,6
0,8
1,0
Рисунок 3.5. Зависимость дифференциальной теплоты адсорбции от
относительного давления аргона (I), азота (2) на хлориде калия, паров бензола
(3) на цеолите Н Ц Б М и паров воды на LilGi (4-экспериментальные
калориметрические данные [13] ,5 - расчетные).
Если же изотермы (1.39) и (1.40) применить для интервала P/P
s
от 0,001 до 0,004, то при найденном значении С = 409 расчетная
начальная теплота (31,5 + 33,1 кДж/моль) фактически совпадает с
начальной калориметрической. К тому же рассчитанные величины
qfaJ+L
(рис.
3.6,
дифференциальных
исследуемой
совпадения
кривая
2)
не
сильно
калориметрических
(кривая
адсорбционной
теории
недостаточную
с
системы
экспериментом
однородность
мы
не
отличаются
3). То, что для
имеем
указывает,
поверхности
от
полного
видимо,
на
промышленно
приготовленных образцов y-Fe O^ которую следует рассматривать как
2
гомотактическую.
\, кДж/
0
0,1
0,2
P/Ps
Рисунок 3.6. Зависимости расчетных (по модели 3.40) и калориметрических
дифференциальных теплот адсорбции н-гексана на поверхности у -Fe O от Р/Р
в согласованном адсорбционно-калориметрическом эксперименте; I - расчет п р и
С=22;2 -расчет п р и С = 409;3 - эксперимент [7].
2
3
5
Таким образом, сочетание уравнений изотерм адсорбции и
дифференциальных теплот адсорбции позволяет провести не только
проверку
самих
адсорбционных
моделей
и уточнить
величины
удельных поверхностей адсорбентов, но могут быть, применимы
самостоятельно для количественной оценки q(x) по единственной
изотерме полислойной адсорбции практически на любой межфазной
границе: газ - твердое тело, жидкость - газ, жидкость - твердое тело. В
частности,
совместное
использование
изотерм
адсорбции
и
дифференциальных теплот адсорбции позволит объективно оценить
природу вновь синтезируемых адсорбентов, а главное, более точно
определить
величины
их
удельных
поверхностей
эффективного практического использования адсорбентов.
для
более
СПИСОК ЛИТЕРАТУРЫ
1.
Кельцев Н.В. Основы адсорбционной техники. 2-е изд. М.:
Химия. 1984. 592с.
2.
Biachell H.C., Lange K.R.//J. Phys. Chem., 1956.V.60. №3. Р. 307.
3.
Barrer R.M. //J. Colloid Interface Sci. 1966.v.21.№.4.p.415.
4.
Беринг Б.П., Серпинский В.В. //ДАН СССР, 1963.Т.148. №6,
с.1331; //Изв.АН СССР.Сер хим., 1971. №4, с. 847.
5.
Дубинин М.М. Адсорбция и пористость. М.: ВАХЗ. 1972.126с.
6.
Дубинин М.М., Полстянов Е.Ф. //Изв.АН СССР. Сер. хим.1966.
№9. С.1507.
7.
Макаревич Н.А.// ЖФХ.1992, т.66, №5 с. 1288. //ЖФХ. 1991
т.65, №.8, с.1959;
8.
Brunauer S,, Emmett P.H,, Teller E. J. AmChem. Soc, - 1938, 60.P.309;
Брунауэр С., Коупленд I . , Кантро Д. Теории Ленгмюра и Брунауэра,
Эммета и Теллера (БЭТ).//Межфазовая граница: газ-твердое тело. - М.:
Мир. 1970. с 77-97.
9.
Pickett G, //J.Am.Chem. Soc. 1945. V, 67 Р.1958.
10.
Huttig G.P. // Monatsh, Chem, 1948. V. 78. P. 177
11. Аранович Г.Л. //Журн. физ. химии. 1988. т. 62. № II. с. 3000.
12. Джейкок М., Парфит Дж. Химия поверхностей раздела фаз. —
М.: Мир, 1984. — 269 с.
13. Макаревич Н.А., Комаров В.С. //Доклады АН БССР. 1991 т.35
№ 8 с.693.
4. О П Р Е Д Е Л Е Н И Е У Д Е Л Ь Н О Й П О В Е Р Х Н О С Т И
ТВЕРДЫХ ТЕЛ ИЗ ИЗОТЕРМ АДСОРБЦИИ ПАРОВ
Изучение
адсорбционных
свойств
твердых
пористых
тел
требует знания площади их поверхности и внутренней структуры.
Величина удельной поверхности s определяет количество
вещества,
yd
адсорбируемого
результаты
энергии,
единицей
массы
теоретических
работы
и
адсорбента,
расчетов
теплоты
позволяет
адсорбции,
адсорбции
с
сравнить
поверхностной
экспериментальным
результатами. В свою очередь, тип внутренней структуры сорбента,
характер
распределения
пор по размерам
определяют
целый
В настоящее время известно большое количество
методов,
комплекс свойств твердых материалов.
применяемых для определения удельной поверхности твердых тел
[1-12]
.
Некоторые
поверхности,
порошков,
другие
основаны
—
на
проницаемости,
теплопроводности
пористых
на
визуальном
определении
измерении
скорости
растворения
определении
теплот
смачивания,
тел,
интерференции,
дифракции
рентгеновских лучей, адсорбции радиоактивных веществ и красите¬
лей. Нашли применение
фильтрации
разреженного
методы стационарной и нестационарной
воздуха,
адсорбции
паров
из
тока
инертного газа и др. И х можно найти в монографиях Киселева [ 1 ] ,
Грега и Синга [2], Брунауэра [3], Дубинина [7], Джейкока и Парфита
[9], Карнаухова[10], Комарова [11], Адамсона [12], Фенелонова [16] и
др.
Однако не все
из названных
методов определения удельной
поверхности твердых тел находят широкое применение. Причиной
этого является недостаточная точность результатов исследований и
их экспрессность.
Ранее разработан целый ряд газохроматографических методов
определения
удельной
удерживаемых
поверхности
объемов
[10],
по
измерению
удельных
использованию
выходной
хроматограммы для расчета изотермы и методу тепловой десорбиии
[10]. Последний отличается достаточной точностью и возможностью
изучения адсорбентов и катализаторов любой пористой структуры.
Высоко чувствительная современная техника определения
s^,
позволяет создавать глубокий вакуум и определять малые величины
адсорбции, что крайне важно
адсорбентов
и
сложных
при измерении части поверхности
катализаторов
[14,17],
определении
количества и силы активных центров поверхности [10,16] и позволяет
определять внутреннюю структуру пористых тел — характеристику,
не менее важную, чем удельная поверхность.
Адсорбционные
методы определения удельной
поверхности
пористых тел подразделяются на две группы. К первой
группе
относятся методы полимолекулярной адсорбции (БЭТ [3,10], Грегга
[2]),
Хюттига
адсорбированного
поверхности
[5],
основанные
вещества,
мономолекулярным
на
определении
необходимого
слоем,
ко
количества
для
второй
покрытия
—
связанные с определением поверхности адсорбированной
методы,
пленки,
покрывающей адсорбент при полимолекулярной адсорбции паров
(Дубинина [7], Кистлера, Фишера и Фримена [10], Гарвея [10],
Киселева [2]).
Первые количественные оценки величины поверхности были
сделаны
с
помощью хемосорбции.
сопоставил видимую
поверхность
поверхность гладкой)
с
кислорода,
и
водорода
В
1918 г.
платиновой
адсорбированным
монооксида
Ленгмюр
[10]
фольги (считая
на
ней
углерода
ее
количеством
и
нашел,
что
максимальные адсорбированные объемы этих газов соответствуют
монослою
их
атомов (а
поверхности.
В
поверхность
платиновой
каждый
1926
или
одну
экспериментальных
последнем
случае
г. Бентон [10], исходя
поверхностный
водорода
в
черни.
атом
Приняв,
из
что
этого,
при
СО,
он
удельную
на
оценил
насыщении
платины удерживает
молекулу
данных
молекул)
вычислил
один
атом
из
своих
поверхность
образца
2
платиновой черни, получив значение 6 м /г . Методы не получили
широкого
распространения
из-за специфичности
необходимости для каждого
адсорбента
хемосорбции
подбирать
и
подходящий
адсорбтив и определять стехиометрию его хемосорбции, а также
вследствие
чувствительности
загрязнениям
и
хемосорбции
необходимости
к
поэтому
поверхностным
предварительной
тщательной очистки поверхности.
4.1. Метод Гаркинса-Юра
Гаркинс
и
Юра
[см.5,10,11]
разработали
так
называемый
абсолютный метод измерения удельной поверхности по теплотам
смачивания.
По
методу
Гаркинса
поведение
адсорбционных
слоев
и
Юра
предполагается,
на поверхности
твердых
что
тел
аналогично поведению адсорбционных пленок П А В на поверхности
жидкости, описываемого адсорбционным уравнением Гиббса (1.18).
Уравнение
Гиббса
(1.18)
для
случая
адсорбции
паров
с
давлением p и поверхностным натяжением а имееет следующий вид:
V
V
р
/da\
—
(
= YV = TT{^)
4
1
)
PJ
где V — объем адсорбированного газа, приведенный к нормальным условиям;
v — нормальный молярный объем (22,4 л);
S — площадь поверхности адсорбента.
Исходя из уравнения состояния, связывающего изменение а с
v
изменением
поверхностной
концентрации
—
т.е.
с
изменением
объема адсорбированного газа V:
п' = Ъ — Ъ о>о
(4.2)
где л' - давление, в точности соответствующее изменению поверхностного
натяжения а на границе фаз
dn'=d(а -а),
b и b - константы;
а>о - средняя площадь, приходящаяся на одну молекулу (величина, обратная
поверхностной концентрации Г).
1
2
0
j
0
2
После дифференцирования
интегрированием
(4.2), подстановки в (4.1) с п о с л е д у ю щ и м
полученного
выражения,
придем
к уравнению
Гаркинса - Юра
2
2
BSv
2
Inp =
—
2
R
T
y
2
+
c
o
n
s
t
(
4
.
3
)
или в относительных давлениях x=p/p
s
А
Ых = В——
(4.4)
у
где V - величина адсорбции, см /г, п р и нормальных давлениях и температуре;
р и p - равновесное давление пара и давление насыщенного пара, мм рт. ст.;
В - константа интегрирования;
А - константа, пропорциональная S :
2
s
Из уравнения изотермы адсорбции (4.4) следует, что логарифм
2
относительного
давления изменяется линейно с 1/V
и тангенс угла
наклона этой прямой (отрицательный) A пропорционален квадрату
площади поверхности адсорбента (4.4а).
При взятой V в расчете на 1 г адсорбента величина А будет
пропорционалена
удельной
квадрату удельной
поверхности
находят,
поверхности
s-уд. Величину
известному
коэффициенту
по
пропорциональности k между тангенсом угла наклона А и квадратом
величины
удельной
измерением
поверхности.
изотерм
адсорбции
Коэффициент
на
k
адсорбенте
определяют
с
известной
поверхностью (относительный метод) или путем определения теплот
смачивания образца (абсолютный метод).
Метод
определить
Гаркинса
поверхность
поверхность—
для
-
Юра
позволяет
непористых
пористых.
совершенно
адсорбентов
Эксперимент
или
ведут
строго
внешнюю
следующем
образом: адсорбент, предварительно насыщенный парами адсорбата
(например, Н2О), погружают затем в жидкий адсорбат в калориметре.
То
есть
на
поверхности
частиц
исследуемого
порошка
предварительно адсорбируется пленка жидкости при выдержке его
в
насыщенном
адсорбента
паре
покрывается,
этой
по
жидкости.
крайней
При этом
мере,
несколькими слоями
адсорбированного пара. Подготовленный таким
погружают
в жидкость
измеряют
теплоту
той
же
смачивания
самой
Q^,
поверхность
образом адсорбент
химической
которая
природы
выделяется
и
в
результате замены поверхности раздела адсорбционная пленка —
пар на поверхность раздела адсорбционная пленка — жидкость.
По изменению теплоты смачивания AQ ,
(на 1 г
0M
адсорбента),
находят удельную поверхность
Бу
Д
=
(4.5)
—
Чж/г
где ц /
ж г
— удельная поверхностная энергия.
Для Н 0 (при 20
2
2
°С) q
=11,85 мкДж/см .
ж/г
прецизионных
измерений
дифференциальные
Метод
AQ .
Современные
с м
калориметры
требует
позволяют
без
особых
трудностей выполнять такой эксперимент.
Преимущество метода состоит в том, что он не связан ни
с какими допущениями о размерах адсорбируемых молекул и не
требует сравнения со свойствами эталонного образца (поэтому он
и был назван
абсолютным
адсорбционной пленки
считали,
что
в
пленка толщиной
выполнение
выводе уравнения.
свойства
атмосфере
5—7
насыщенного
молекулярных
пара
слоев
основного допущения, сделанного при
Однако исследования показало, что достаточно
двух адсорбционных слоев.
теплоты смачивания
предварительно
Поверхностные
зависят от ее толщины. Гаркинс и Ю р а
образующаяся
адсорбционная
гарантирует
методом).
оксида
На рис. 4.1
титана
адсорбированного
Роукеролом и сотр. [см. 10].
в
показана
воде
водяного
от
пара.
зависимость
количества
изученная
Q,
МКИПЛ1./1
Рис. 7.1. Зависимость теплоты смачивания оксида титана от толщины
предварительно адсорбированной пленки воды [7]. Кривая I — теплота
смачивания; кривая I I — изотерма адсорбции паров воды.
Точка А
соответствует
линия).
Следовательно,
адсорбента
в
двум
насыщенном
адсорбционным
слоям
неконтролируемому
паре
смачивания
следует
предпочесть
поверхности
адсорбатом. Всего в
перед
(штриховая
выдерживанию
измерением
дозируемое
теплоты
покрытие
работе [7] было
его
изучено
11
разных адсорбентов и показано, что силовое поле их поверхности
экранируется при покрытии 1,5 - 2 монослоями воды.
Метод Гаркинса Юра, так же как и метод БЭТ, основан на
адсорбционных явлениях, но в основе его лежит совершенно новый
подход к измерениям величины поверхности методом
адсорбции
газов.
Основным ограничением этого метода является то, что образование и
существование конденсированной пленки на поверхности твердого
тела имеет место лишь в узкой области значенийр, т. е. 0,2<р/ро<0,4,
являющихся
пределами
применимости теории Гаркинса и
Юра.
Несмотря на это, удельные поверхности, рассчитанные по данному
методу
и
методу
оказываются
БЭТ, особенно
весьма
близкими
в
между
случае
собой.
адсорбции
азота,
Объяснить
данное
совпадение результатов, полученных столь различными способами
интерпретации изотерм низкотемпературной адсорбции, до сих
удалось. Видимо, метод Гаркинса и Ю р а дает наиболее
не
полное
соответствие данных только тогда, когда константа с уравнения БЭТ
имеет величину около 100.
4.2. Метод Грегга
Грегг [2] предложил метод теоритически схожий с методом
Гаркинса и Юра, основанный на изучении свойств адсорбционных
пленок в зависимости произведения их поверхностного давления (л')
на
величину
конденсированном
поверхность.
(се>о),
площадки
занимаемой
7c'S^, где
слое, от значения
Оба эти произведения
молекулой
в
- удельная
могут быть определены из
изотерм адсорбции с помощью уравнения адсорбции Гиббса
1
fdn'\
после интегрирования
f
n =RT\
Tlnp
(4.7)
где Г = п/Ылёуд - количество адсорбированного вещества,
р - равновесное давление газа,
n - число адсорбированных молекул вещества.
Отсюда
П
' =
к
Г
{ ^
/
п
р
8
(4. )
моль/см
;
Величина посадочной площадки, приходящейся на одну молекулу,
co =Syg/n, т.е.
0
л'ш =л'§уд/п.
0
Делая допущение, что при низких р
величина
адсорбции
пропорциональна давлению (идеальный газ), интегрирование
(4.8)
сводится к п =кр, при этом
7
^
п
1 д
= к Т,
в
или
п'щ
= кТ
(4.9)
в
То есть принимается, что в области давлений, соответствующей
области идеального двумерного газа, величина л'ш
0
не зависит от
n'sуд и с ростом степени заполнения линейно возрастает, отсекающий
на оси ординат отрезок, по величине очень близкий к значению
0
в
Syg определяется по тангенсу угла наклона зависимости
Поэтому
л'ш
к Т.
-n'sу .
Д
Зная величину посадочной площадки молекулы co , легко
0
рассчитать удельную поверхность.
Метод Грегга применяется
в основном
для активированного
угля и схожих с ним адсорбентов с тонкой структурой пор, однако,
учитывая допущения, сделанные при выводе уравнения,
предположить, что достоверность результатов, метода,
можно
невысока.
Хотя при применении его к изучению изотерм низкотемпературной
адсорбции азота результаты могут быть весьма близки к данным,
полученным по методу Гаркинса-Юра.
4.3. Метод Киселева
Метод определения удельной поверхности пористых тел по
Киселеву
[1] основан
на
строгой
термодинамической
теории
капиллярной конденсации пара на поверхности любой формы . Автор
получил общее уравнение для конденсации пара на искривленной
поверхности адсорбционной пленки и вывел формулу расчета ее
величины.
В основу вывода положено условие равновесия гетерогенной
системы, состоящей из двух объемных а- и (3-фаз и поверхностного
слоя, при постоянстве температуры и объема системы.
Общее
термодинамическое
уравнение,
характеризующее
условие
равновесия изохорно-изотермической системы
a
a
13
p dV
а
- pPdV
+ ads = 0
(4.10)
р
a
b
г д е р и р - гидростатическое давление в фазах, и м е ю щ и х объемы V и V ;
о - поверхностное натяжение на границе пленка—пар;
s - поверхность раздела м е ж д у объемными фазами а и (3.
a
Для неизменного объема системы dV
b
= — dV из (4.10)
ods = -sda
где s=RTln(p /p)
s
(4.11)
- дифференциальная молярная работа адсорбции пара,
а — количество адсорбированного вещества.
Для пористых адсорбентов размер поверхности s , на которой
yd
происходит
капиллярная
конденсация,
находят
путем
интегрирования уравнение (4.11). При этом в качестве
предела
интегрирования
берется
величина
сорбции,
началу капиллярной конденсации—гистерезиса
верхнего —
предельное
значение
сорбции
отвечающая
(аь), а в
a,
s
нижнего
качестве
соответствующее
полному заполнению пор. При этом допускается, что
величина
внешней поверхности ничтожно мала с внутренней поверхностью
адсорбента
J^J*
5уд = — I
о
г as
Jah
\n(Ps/P)
(4.12)
Интеграл находят графическим путем по всей области капиллярной
конденсации,
используя
данные
десорбционной
ветви
изотермы.
Величина удельной поверхности, рассчитанная таким образом, равна
площади (заштрихованной на рис. 4.2) под кривой в координатах
ln(p /p) - а (легко вычисляемой из экспериментальных значений р и
s
а).
Определение
величины
8
уд
исключает ошибки, вносимые при
оценке
емкости
мономолекулярного
площадки,
занимаемой
молекулой
интегрирования
и
с
(а )
т
в
и
нем
адсорбированного
(се>о).
вещества
Рис.4.2. Зависимость ln(ps/p) от
количества
адсорбированного
вещества
x=a
в
области
капиллярной конденсации.
слоя
Погрешность
может быть связана с точностью
определения
допущением
нижнего
равенства
предела
поверхностного
натяжения на границе пленка - пар и обычной жидкости.
Уравнение
(4.12)
дает
достаточно
высокую
точность
определения удельной поверхности крупнопористых адсорбентов, но
дает заниженные результаты поверхностей в случае тонкопористых
адсорбентов,
поры
которых
объемно
заполняются
капиллярной конденсации. Однако, если использовать
образец
сравнения
с
известной
удельной
до
эталонный
поверхностью
сравнения), то для сходных по форме изотерм
сделать соответствующую поправку на величину Б
начала
(метод
адсорбции легко
уд
4.4. Измерение удельной поверхности по методу БЭТ
Величина поверхности твердых тел необходима для анализа
процессов,
происходящих
на
этой
поверхности
с участием
молекул или атомов (адсорбция, катализ, гидратация, горение
и
т.д .). Речь идет не о геометрической поверхности твердого тела, а
о его доступной для тех или иных молекул поверхности.
Если
измерять величину поверхности с помощью молекул или атомов,
нужно,
казалось
бы, уложить
их на этой
поверхности
в один
слой и подсчитать потом затраченное количество. Сама природа
предоставила
явление
в
наше
распоряжение
такого
" укладчика"
адсорбции [11]. А методом исследования
основанный
на
физической
пропорционально зависит
Брунауэр
адсорбции (физическая
от
[3], анализируя
явился
величины
в
метод,
адсорбция
поверхности).
1937 г. форму
—
изотерм
Эммет
и
физической
адсорбции, обратили внимание на то, что после первоначального
крутого подъема большинство изотерм замедляет рост адсорбции
с
ростом
давления
практически
и
в
прямолинеен
средней
(IUPAC).
части
изотермы
После
этот подъем
анализа
нескольких
характерных точек изотермы авторы остановились на точке начала
прямолинейного
подъема,
предположив,
что
она
завершению образования первого слоя, а сам подъем —
отвечает
началу
заполнения второго слоя*. Она была названа точкой B. Обозначив
соответствующую
ей емкость
предложили вычислять удельную
s
где N
ю
0
yA
= a Naj
m
m
монослоя
а
т
поверхность Б
(в
уд
молях/г),
они
по уравнению
(4.13)
- число Авогадро,
- площадь, приходящаяся на одну молекулу в монослое.
Опробовав несколько адсорбтивов для определения Б ЭТИМ
УД
эмпирическим методом, авторы остановились на адсорбции азота
при температуре его кипения 77 К. Выбор оказался
удачным, и в
настоящее время, спустя почти 80 лет, азот успешно применяется
для определения удельной поверхности. В дальнейшем
Брунауэр
вместе
с
Теллером
полимолекулярной
физической
константы a
просто
m
и С,
[3, 10,11]
вывели уравнение
адсорбции,
определяются
Эммет и
согласно
из
которому
линейной
формы
уравнения (4.14)
х / а ( 1 - х) = 1/а С
т
+ (С - 1)х/а С
(4.14)
т
X
при
построении
определения а
зависимости
строить изотерму адсорбции в
давлений x=p/p ,
Достаточно
— — - от x .
по этому уравнению нет никакой
т
s
величины
Для
необходимости
широком интервале относительных
в который бы обязательно входила величина а .
т
иметь
лишь
несколько
экспериментальных
точек
(минимально две) в интервале применимости этого уравнения, в
том числе в области покрытий, далеких от завершения монослоя.
Вычисленная
таким
образом
емкость
монослоя весьма близка
к
определенной по точке В; расхождения обычно не превышают 10
%.
В этом случае не
требуется построения
всей
изотермы
адсорбции и, следовательно, измерения многих экспериментальных
точек (по крайней мере 6—8), а достаточно минимально двух и
даже одной.
Точность
измерения
удельной
поверхности
надежности определения двух величин — а
т
[2]
проанализировали
правильность
зависит
от
и се>. Грег и Синг
0
определения а
т
на
основе
изучения
литературных
данных
о форме
кривых
зависимости
теплоты и энтропии адсорбции от ее величины и сделали заключение,
что резкое изменение формы этих кривых наблюдается как раз при
такой величине адсорбции,
которая
наблюдения являются достаточным
оценки а
из уравнения
БЭТ
характеристикой
8
т
важной
отвечает
величине а
т
подтверждением правильности
с точностью до 10—15
уд
. Эти
является
%. Очень
величина
площади,
приходящейся на одну молекулу при монослойном покрытии <э .
0
Многочисленными независимыми измерениями было установлено,
что
для молекулы азота:
одноатомных
молекул
<э = 0,162
аргона
0
нм ,
и криптона
для
сферических
<э равны
0,138 нм и
0
0,152 нм , соответственно.
Метод точки «В». Величина емкости монослоя, как
показано
Эмметтом
и Брунауэром
[3], для
изотерм
с
было
хорошо
выраженной точкой перегиба может быть оценена по точке
В,
указывающей на окончание заполнения монослоя (ат). Достоверность
определения а
т
этим методом в свою очередь зависит от точности
определения положения самой точки В. Чем круче изгиб изотермы,
что соответствует большему значению с и чистой теплоте адсорбции,
тем легче и четче определяется точка В, а следовательно, и емкость
монослоя (рис. 4.3). В случае пологого подъема изотермы точность
определения точки В резко падает, а иногда она и вообще не
определяется или определяется с достоверностью от 20 до 100% [11].
V,CM (0°750MM)
3
о
zoo 400 боа f>m
Рис 4.3. Изотермы адсорбции с Рис.4.4.
Примеры
изотерм
выраженным (1) и пологим (2) низкотемпературной
адсорбции
перегибом.
газов (кислород, аргон,
оксид
углерода I I , азот, оксид серы IV, нбутан) на силикагеле.
Метод точки «В» применим и дает удовлетворительные
результаты для изотерм пористых материалов, структура которых
обогащена
мелкими
адсорбционным
порами,
потенциалом
обладающими
в области
низких
повышенным
относительных
давлений. Для крупнопористых адсорбентов при соответствующем
подборе адсорбата можно получить изотермы двух типов: изотермы с
наличием крутого изгиба, переходящего в прямолинейный участок, и
изотермы,
медленно
поднимающейся
с ростом
относительного
давления. Это говорит о том, что, помимо структуры, существенно
влияющей
на
поверхностью
энергию
адсорбента,
взаимодействия
тип изотермы
молекул
зависит
адсорбата
от
с
природы
адсорбата и его сродства к поверхности твердого тела (рис. 4.3, 4.4).
Если энергия взаимодействия молекул адсорбата незначительно
отличается от энергии межмолекулярного взаимодействия, то метод
точки «В» для определения емкости монослоя крайне ненадежен.
Например, изотерма адсорбции бутана ( р и с . 4.4) на всем своем
протяжении
весьма
близка
к
прямой
линии,
вследствие
чего
определить точку В на ней почти невозможно.
Метод «единственной точки». При сильном взаимодействии
адсорбированных
молекул с поверхностью
адсорбента
(значение
константы С в уравнении БЭТ велико)
х/а(1
— х) = 1/а С
+ (С — 1)х/а С
т
т
, т.е. величина 1/а С
мала, а
т
[(С — 1)/С] ~ 1 , тогда a =a(1—x).
m
Следовательно,
график БЭТ, проходящий через начало координат,
имеет наклон, равный обратной величине am. Поэтому если соединить
экспериментально
найденную
точку
в
области
относительных
давлений 0,2—0,3 с началом координат, то по наклону линии для Sобразных
изотерм
(теплота
адсорбции
велика)
можно
оценить
величину емкости монослоя, а, следовательно, и величину удельной
поверхности.
Величина емкости монослоя а , определенная данным методом, как
т
показал Брунауэр и др., отличалась на 1—5% от а ,
т
найденного
построением полного графика БЭТ.
Хелаш
и
Шай
[см.11]
предложили
более
точный
метод
«единственной точки», придав уравнению БЭТ следующий вид:
а
т
Это
форма
поправочным
= а(1 — х)(1
уравнение
к
(4.14)
БЭТ
—
+ — —)
отличается
множителем
(4.15)
от уравнения
{1+(1-x)/Cx},
(4.14)
уточняющим
значение а , полученное методом «единственной точки», к значению
т
а , найденному по методу БЭТ.
т
Газохроматографический
метод.
Одним
из
способов
определения удельной поверхности является газовая хроматография
широко используется для определения удельной поверхности твердых
тел. Преимущество этого метода перед статическими заключается в
том, что он не связан с вакуумной аппаратурой, обладает высокой
чувствительностью, позволяет определять поверхность от 0,01 д о
1000 м /г. Газохроматографические установки просты в монтаже и
эксплуатации,
величины
высокопроизводительны
удельных
поверхностей
и позволяют
определять
в
протекания
условиях
адсорбционных и каталитических процессов.
Определения
удельной
поверхности
твердых
тел
можно
провести, используя: метод удерживания объемов; расчет изотермы
по размытой стороне хроматограммы с последующим вычислением
поверхности по методу БЭТ; фронтальный метод измерения изотерм
адсорбции; метод тепловой десорбции [см.11].
Первые три метода являются недостаточно точными и могут
служить лишь для ориентировочной оценки поверхности твердых тел.
Признание из за простоты, высокой чувствительности, быстроты
расчета удельной поверхности и возможности применения его для
исследования адсорбентов любой пористой структуры получил метод
тепловой десорбции. Впервые этот метод был предложен Нельсоном
и Эггертсеном
и независимо Грубнером
и нашел
дальнейшее
развитие в других работах [см.10,11].
Метод основан на адсорбции азота твердым телом из потока
смеси азот — гелий при температуре жидкого азота. Затем, повышая
температуру, десорбируют
поглощенный
адсорбат
в поток
этой
смеси. Изменение концентрации адсорбата в процессе его адсорбции
и десорбции
регистрируется
катарометром
и регистрируется
на
мониторе в виде отрицательных пиков по отношению к нулевой
линии.
Количество
сорбированного
вещества
определяется
по
площади десорбционного пика как более симметричного (рис. 4.5):
V
a = k S
3KC
d
(4.16)
где к - постоянная детектора;
S - площадь десорбционного пика;
V KC
и v - объемные скорости потоков газовой смеси в эксперименте и при
калибровке прибора.
д
3
K
Количества
необходимого
адсорбата,
для
образования
мономолекулярного слоя, определяют
по нескольким измерениям адсорбции
для разных парциальных давлений ад¬
Рис.4.5.Типичная
хроматограмма
адсорбционного
десорбционного
методе тепловой
сорбируемого
(1)
и
(2) пиков
в
десорбции
вещества
и
строят
изотерму адсорбции. Расчет удельной
поверхности
производят
методом
БЭТ.
В ряде работ показано, что наиболее подходящим адсорбатом
является аргон, адсорбция которого мало чувствительна к химической
природе поверхности твердого тела. Применение аргона вместо азота
по ряду причин дает возможность увеличить точность измерений, а
соответственно и точность определяемых удельных поверхностей,
пропорциональных площадям десорбционных пиков:
S
(4.17)
где S и S., - площади десорбционных пиков рабочего и эталонного образцов, см ;
и s
- удельная поверхность рабочего и эталонного образцов, м /г (или
см \г);
g — вес образцов, г.
w
2
4.5. Метод Хюттига
Как рассмотрено в гл.2 Хюттиг вывел уравнение изотермы адсорбции
С (1 + х)
в =
„
х
х
путем существенного
(4.18)
видоизменения кинетического вывода
БЭТ
[3,5]. Он предположил, что скорость адсорбции в (i+1)-M слое
пропорциональна числу свободных молекул в i-м слое (в согласии с
Б Э Т ) , а скорость испарения молекул из i-го слоя пропорциональна
количеству
молекул в этом слое и совершенно
не зависит
от
присутствия молекул в i+1 -м слое (в отличие от теории БЭТ, где в
этом случае учитывается количество «непокрытых» молекул
i-го
слоя). В остальном предпосылки обеих теорий одинаковы.
Уравнение
Хюттига,
подобно
уравнению
БЭТ,
удачно
описывает форму изотермы полимолекулярной адсорбции. С его
помощью
были
успешно
определены
величины
поверхностей
твердых тел для области относительных давлений р/р
вплоть до
я
0,35. Уравнение Хюттига, как впрочем и уравнение
рассматривать
как
полимолекулярной
одну
из
возможных
адсорбции
и,
БЭТ, можно
теоретических
одновременно,
как
моделей
удачное
эмпирическое уравнение, позволяющее с неплохой во многих случаях
точностью определять величину а . Значения а ,
т
т
определенные по
данному уравнению, отличаются от емкости монослоя, рассчитанной
по БЭТ, не более чем, на 20% при
условии, что константа С достаточно велика (С~100).
4.6. Сравнительные адсорбционные методы
Кроме метода
называемые
БЭТ в настоящее время
сравнительные
методы
используются
так
определения
удельной
сравнения
изотерм
поверхности.
Методы
абсолютных
величин
четкого
разделения
текстурных
и
адсорбции. Для
влияние
физико-химических
факторов на адсорбционные
Киселев
[1]
абсолютных
мкмоль/м
в
относилась
Рис.
4.5.
Изотермы
абсолютных
адсорбции
метанола
на
тонкопористом
(1)
и
крупнопористом
(2)
алюмосиликагелях
и
на
непористом кварце (3) [11].
в
е
л
и
ч
и
н
не
мкмоль/г
а к
а,мкмоль/
м
сравнивать
самых
предложил
величин
2
свойства,
адсорбции
котором
к
метод
адсорбция
единице
единице
.
различных
по
массы, a,
поверхности,
Это
изотермы
а,
позволило
адсорбции
на
текстуре
и
химии поверхности адсорбентах.
На рис. 4.5.
построены изотермы абсолютных величин
метанола на адсорбентах близкой полярности
-
адсорбции
тонкопористом,
крупнопористом алюмосиликагелях и непористом кварце, удельная
поверхность
полностью
расходились
которых различалась
совпадали
в
более чем на порядок.
начальной
из-за дополнительного
Кривые
области адсорбции и резко
поглощения
пара
за
счет
капиллярной конденсации в крупных порах
геометрических
тонких
ограничений
порах (кривая
(кривая
адсорбционного
1). Это
сравнение
2)
и
из-за
пространства
наглядно
в
доказывает
влияние геометрии пор на адсорбционные свойства адсорбентов.
U . икмоль/ М '
В случае (рис 4.6.) взяты адсорбенты
разной
полярности
полипропилен,
силикагель
и
корунд).
На
слабополярный
достаточно
0.2
0.8
P/P
-
полярный
корунде
высоким
0,1
(неполярный
с более
адсорбционным
потенциалом изотерма круче, чем на
T
Рис.
4.6.
Изотермы
абсолютных
величин
адсорбции аргона на силикагеле
(1),
корунде
(2)
и
полипропилене (3) [11].
силикагеле
и
значительно
более
крутая, чем на пропилене с низким
адсорбционным потенциалом. Однако,
в области относительных давлений 0,1
и выше изотермы практически параллельны.
Следовательно,
из приведенных сравнений следует, что метод
абсолютных величин
определять
адсорбции позволяет
удельную
поверхность
достаточно
адсорента
на
просто
основе
сопоставления его адсорбционных свойств со свойствами другого
адсорбента,
названного
стандартным,
с
известной
удельной
адсорбция
зависит,
поверхностью.
Исходя из допущения, что
главным
образом,
от
физическая
величины
поверхности,
то
отношение
величин адсорбции при давлении, при котором выполняется условие
афинности
можно
с
известной
точностью
считать равным
отношению удельных поверхностей
_
^уд.и
где индексы «и» и «ст» относятся, соответственно к измеряемым и стандартным
характеристикам.
Используя, разные способы нормировки, аналогично тому, как это
проделал
А.В. Киселев
(1949
г.) в виде
отношения
адсорбции, а, мкмоль/г к удельной поверхности Б
г.) в качестве нормировки выбрал отношение
адсорбции а к адсорбции в монослое a
m
уд
величины
м /г. Пирс (1959
текущей величины
по БЭТ a/a
m
и назвал ее
числом статистических монослоев п.
Де
Бур
с
сотр.
среднестатистическую
применяли
толщину
так
адсорбционной
называемую
пленки
t=aV/s
yd
[см.5], где V - мольный объем сорбированной фазы или толщина
монослоя (на оси
образце,
абсцисс
на оси ординат
откладываются
t
на
стандартном
- V). В методе t-кривой математическое
выражение для азота
Уа
t = 1,541——,нм
5
где
У
- адсорбированный объем, м л НТД/г (объем жидкого адсорбата со
свойствами нормальной жидкости) п р и данном давлении,
sroi- - удельная поверхность по БЭТ, м /г
а
Коэффициент
газа
(4.21)
БЭТ
в
1,547
объем
получен переводом объема
в указанных
адсорбированного
единицах физических
величин (в
ангстремах коэффициент равен 15,47 ). Авторы
использовали
оксидов металлов
для них
зависимости
и
величин
построили
t
от
р/р
единую
8
ряд
кривую
[36 ] , а затем сгруппировали
экспериментальные данные по адсорбции азота на оксидах титана,
циркония
и
магния,
сернокислого
бария
и
кремнезема
в
три
универсальные t-кривые (рис 4.7).
О
0,2
ф
0
0,8 p/p
>S
s
Рис.4.7.(слева) Зависимость вычисленных величин t от относительного давления
для BaSO (1), TiO (2), Л 1 0 з ( 3 ) , ZrO (4), MgO(5); (справа) три типа графиков для
зависимости объема адсорбированного вещества от толщины адсорбционного
слоя [11]
4
2
2
2
Синг (1969 г.) использовал нормировку в виде отношения ag=
ос/осод,
где (Ход—абсолютная величина адсорбции при p/p =0,4
s
и т. д.
Как видим, все эти нормировки взаимосвязаны, а методы: метод
абсолютных величин адсорбции Киселева, t-метод де Бура, os-метод
Синга и др. являются вариантами единого сравнительного метода [2].
Отметим, что из перечисленных
нормировка по А.В. Киселеву не
требует спорных допущений.
Наиболее
адсорбции N
2
часто
сравнительный
метод
при 77 К, и как показывает практика
авторов расходятся в области р/р<, > 0,50.
результат
используется
необоснованного
при
изотермы ряда
Эти расхождения
выбора образцов для
стандартных изотерм адсорбции. В результате возникают
—
получения
эффекты,
связанные
с
кривизной
поверхности
и
возможностью
дополнительного вклада капиллярной конденсации.
изотермы адсорбции рекомендуют
минимально
искривленной
Стандартные
измерять как на образцах с
поверхностью,
т.е.
с
невысокой
величиной поверхности, так и на образцах с высокой поверхностью с
применением высокопрецизионного оборудования.
4.7. Сравнительный адсорбционный метод Комарова
На фоне часто используемым
методов
на практике сравнительных
определения удельной поверхности твердых материалов
отметим метод, предложенный В.С. Комаровым [11].
состоит
в
графическом
изображении
изотерм
Суть метода
адсорбции
в
относительных координатах адсорбции 6=a/a и давления р/р , т.е. 6=
m
Такое
выражение
изотерм,
по
8
мнению
автора,
позволяет
выяснить, какими структурными особенностями должен обладать
адсорбент,
чтобы
сорбционный
процесс
на
нем
проявлял
селективность, и, наоборот, при каких условиях будет наблюдаться
пропорциональная сорбция пара в зависимости от величины его
относительного
потенциалов
давления.
паровой
и
Исходя
из
равенства
адсорбционных
коэффициент распределения К=[9/(р/р,)] ^
р
фаз
автор
константа
характеристика,
распределения
которая
может
вводит
. Добавим, по мнению
0
авторов данного пособия, K в таком выражении, для
есть
химических
-
[6/(р/р )] ^ ,
s
p
0
термодинамическая
быть
использована,
например,
для определения
системы:
AG=RTlnK.
свободной
энергии
адсорбционной
Выражение изотерм адсорбции в координатах 6 — р/р^
имеет
ряд преимуществ, позволяющих более полно оценить сорбционные
особенности адсорбентов, область их практического использования и
структурную характеристику,
а главное исключает
разночтение
изотерм и четко определяет принадлежность их к тому или иному
структурному типу. При таком изображении
изотермы нечетко вы¬
раженного вида, которые, иногда трудно отнести к определенному
типу пористой структуры, приобретают точную приписку (рис. 4.8).
Из
рис.
4.8
видно,
адсорбции,
что
представляющие
различные
структурные
адсорбентов,
АВ,
Рис 4.8. Основные типы изотерм
адсорбции газов и паров
в
относительных координатах:
1- непористые адсорбенты,
2- мелкопористые,
3 - идеальный тип структуры,
4 - пестропористые,
5 - крупнопористые адсорбенты.
относительно
выходящей
координат
под
мелкопористой
лежащие
ниже
из
углом
начала
45°
пропорциональную
адсорбции
и
прямо
от
зависимость
величины
отно¬
сительного давления адсорбата.
Адсорбенты, изотермы которых
структурой
выше
или,
в
данной
прямой,
прямой
крайнем
обогащены мелкими порами. Наоборот, изотермы
адсорбции,
прямой
характеризующей
расположены
обладают
типы
по-разному
располагаются
линии
изотермы
АВ,
случае,
относительной
свидетельствуют
о
наличии
крупнопористой
структуры,
и,
наконец,
изотермы
S-
образной формы с положительным отклонением от прямой АВ
области низких значений p/p
s
относительном
давлении
в
и отрицательным при более высоком
характеризуют
пористые
тела
с
пестропористой структурой. Безусловно, в зоне действия каждой из
рассмотренных изотерм возможны случаи, когда структура адсорбен­
та в той или иной степени обогащена более крупными или более
мелкими порами, вследствие чего изотерма относительной сорбции
может приближаться к прямой АВ или удаляться от нее. В пределе
каждая
из
этих
кривых
может
перейти
в
свою
крайнюю
противоположность — изотерму непористых адсорбентов (рис. 4.8,
кривая
1).
При
этом
не
исключен новый структурный тип
адсорбента,
относительная
изотерма
адсорбции
совпадает
с
прямой
которого
АВ
или
проходит параллельно ей. Форма
изотерм
такого
встречается
Рис.4.9.Изотерма адсорбции паров
СС1
на
алюмосиликате
(15%
Л 1 0 , 8 5 % SiO ), полученном из 3%
-ных растворов A 1 ( N 0 ) и N a S i 0
при р Н 8,5
типа
на
представляет
часто
практике
собой
и
границу
4
2
3
2
3
3
2
перехода
от
мелкопористых
к
3
крупнопористым адсорбентам или,
наоборот, от крупнопористых к мелкопористым (рис. 4.9).
Характерной
особенностью
таких
пористых
тел
является
пропорциональная зависимость величины адсорбции от давления
пара
адсорбата,
которая
обусловлена
строгим
и
равномерным
прогрессивно
размерам.
увеличивающимся
Поэтому
адсорбционными
распределением
пористые
материалы,
особенностями,
автор
объема
пор
обладающие
предлагает
по
такими
выделять
в
отдельный структурный тип, назвав его «идеальным», отличающимся
от известных структур характером распределения пор по размерам и
сорбционными закономерностями.
Адсорбенты данного структурного типа в ярко выраженном
виде встречаются редко, поэтому вполне естественно, что они могли
остаться
незамеченными,
классификации
тем более что существующая
пористых
тел
не
позволяет
строго
система
определить
границы каждого структурного типа.
Выражение изотерм адсорбции в координатах 6 — р/р
5
личие от традиционного
в от­
выигрышно, т.к. в явной форме дает
сорбционную характеристику адсорбента. Так, например, изотермы
или их отдельные участки, лежащие выше прямой АВ,
обладают
положительной
изотермы
адсорбции,
адсорбцией
расположенные
К=9/р/р >1,
и,
8
ниже
прямой
наоборот,
АВ,
характеризуют
отрицательную адсорбцию К< 1). Изотермы, лежащие на линии АВ,
имеют нулевую избирательность адсорбции (К=1), т. е. величина
поглощения
прямо
пропорциональна
давлению
пара
Выражение изотерм адсорбции в координатах 6—р/р
величине коэффициента распределения К ,
ст
стандартного
образца
(Б
у д
по
БЭТ
известна)
8
адсорбата.
позволяет по
определенного
и
величине
для
К
1у
найденного для исследуемого образца, определить его удельную
поверхность Б ,1 по формуле:
уд
KV
1
S
yA.1 =
1
у
к
S
(
cxB3T
4
.
2
2
)
Точность удельных поверхностей, определенных по формуле
(4.22) эквивалентна точности метода БЭТ и зависит
допущенных при определении значений К. Автор
метод надежен,
в уравнении
как впрочем,
от ошибок,
отмечает,
что
и метод БЭТ, когда константа
С
БЭТ близка к 100.
4.8. Сравнительный метод определения объема микропор и
поверхности мезопор
В
методе
абсолютных
сравнивались изотермы,
величин
изображаемые
адсорбции
в
обычных
Киселева
координатах:
адсорбция в виде функции от давления. Первыми, кто предложил
иной выбор координат, были Дубинин и Заверина [7, см.10]. На
оси
абсцисс
они
стандартного
образца,
соответствующие
ординат —
этих
на
Таким
адсорбции
параллельной,
относительного
образом,
адсорбционных
для
второй оси —
давления;
на оси
их
свойств. Если эти свойства были подобны
(т.е.
был
одного
изображал
от
получался
свойств
график
при
образца
аффинны), график
различались,
величины
величины адсорбции для исследуемого образца
адсорбционных
изотермы
и
им значения
давлениях.
зависимость
откладывали
прямолинеен,
криволинейный
аффинности тангенс угла наклона
график.
если
В
они
случае
прямой линии равен отношению
удельных поверхностей, что позволяет при известной поверхности
стандартного
образца
вычислить
удельную
поверхность
исследуемого.
Интерес
к
этому
методу
возник
только
после
публикаций де Бура, Липпенса и Линсена [см.10], основанных на
аддитивности адсорбции, протекающей одновременно на различных
участках поверхности, а также
допущении, что удельные величины
адсорбции на поверхности мезо- и макропор до начала капиллярной
конденсации идентичны стандартной изотерме адсорбции. В этом
случае
вклад адсорбции на поверхности мезо- и макропор можно
представить в виде
^ме
где
(
^-^ме
.
4 23
)
— суммарная удельная поверхность мезо- и макропор,
а — абсолютная величины адсорбции на единице поверхности.
Кроме
адсорбента
этого,
изотерму адсорбции
для микро-мезопористого
в области до начала капиллярной конденсации может
быть также представлена в виде суммы изотерм адсорбции в микро а
ц
и в мезопорах, а :
м е
а =
Надежность
расчетов
по
+
(4.24)
«ме^ме
уравнению
(4.24)
подтверждена
анализом изотерм по адсорбции а, измеренной в экспериментах на
механических
смесях микропористого
(цеолит)
и
мезопористого
(силикагель) адсорбентов [16]:
а = ^ + ^ме«
(4.25)
На рис. 4.8 приведен типичная для микропористых систем изотерма
адсорбции, на которой показаны адсорбционная и десорбционная
ветви.
Адсорбционная
ветвь
в
таких
координатах представлена двумя
линейными участками с разным
наклоном.
участок
Первый
(в
области
давлений)
микропорах
Рис.4.8. Изотерма адсорбции азота на
монтморрилоните
малых
соответствует
одновременной
линейность
линейный
и
и
адсорбции
в
мезопорах.
Его
экстраполяция
начало
координат
тем,
что
в
обусловлены
микропоры
в
рассматриваемом случае относятся к супермикропорам, а наклон
пропорционален суммарной поверхности всех пор. В области излома
происходит
определяется
полное
заполнение
наклоном
второго
микропор
линейного
и
далее
участка.
адсорбция
Если
затем
исследуемый график перестроить путем сравнения со стандартным, и
горизонтальную
адсорбционную
ветвь
сравнительного
экстраполировать до оси ординат, то отсекаемый
адсорбции
будет
соответствовать
объему
графика
отрезок на оси
супермикропор
[16].
Подобные графики с двумя явно разделяемыми зонами адсорбции
характерны не только для микропористых, но и просто однороднотонкопористых систем, где тонкие поры, например, мезопоры малого
размера с суммарным объемом предельно заполняются в некоторой
узкой области, а последующая адсорбция происходит на оставшейся
поверхности 8 .
ме
Преимущество сравнительного метода (СМ) перед методом БЭТ
в том, что он по своей сути является дифференциальным, так как
основан на прямом сопоставлении приращений величин адсорбции в
некоторой области изотермы. Метод БЭТ, в свою очередь, является
интегральным,
адсорбции,
стадиях.
поскольку
включающих
Поэтому
базируется
на
суммарных
адсорбцию
на
всех
наличие
аномалий
в
величинах
предшествующих
области
адсорбции
до
заполнения монослоя может радикально искажать результаты расчета
по уравнению БЭТ, но не влияет на расчеты СМ. Кроме того, СМ
имеет более обоснованную метрологическую
базу,
единственное
используемое в этом методе модельное допущение сводится к тому,
что
приращения
адсорбции
в
полимолекулярной
области
пропорциональны поверхности вне зависимости от ее природы.
4.9.
Современная
практика
определения
удельной
поверхности методом БЭТ
Метод
БЭТ
определения
проверку временем.
Более
удельной
чем
поверхности выдержал
шестидесягилетняя
практика
применения превратила его в международный стандартный метод.
Если в первые годы наряду с ним применялись и другие методы,
то
теперь
множестве
этот
метод
практически
стал
публикуемых работ приводятся
монопольным.
данные
об
Во
удельной
поверхности твердых тел, определенные именно им. Хотя основы
метода
остались
теми
значительно изменилась.
же,
но практика
его
применения
В первые годы после того, как был предложен метод БЭТ,
во
многих
работах
пытались
применять
адсорбтивы:
аргон, криптон,
кислород,
метанол
многие
Перечень
и
величины
другие.
приведены
в обзоре
другие,
СО ,
азота,
СО, бензол,
2
этих
кроме
вода,
адсорбтивов
Мак-Клеллана
и
и
их
Харнсбергера
[31]. В настоящее время используются почти исключительно азот,
аргон и криптон.
Расширен диапазон дисперсности
материалов, для
которых
возможно применение метода БЭТ. Брунауэр в своей книге [3]
указывал,
что
самая
малая,
достаточно
точно
измеренная
величина поверхности составляет 0,15 м /г. Этот предел зависит от
экспериментальной
точности
измерений
и
определяется
соотношением количества адсорбтива на поверхности и
"мертвого пространства"
применяется
кПа
установки (см. гл. 3). В случае, когда
азот, адсорбция
измеряется
(250 торр) и при малых
адсорбтива по отношению к
очень мала и
Биби
с
сотр.
до
давлений
поверхностях доля
около
этот
недостаток
объеме
Брауном, а затем
преодолен
тем,
используется адсорбтив с малой упругостью насыщенного пара
Для криптона, в частности, Р =
0
33
поглощенного
его количеству в мертвом
измеряется неточно. Вутеном и
[см. 16]
в объеме
что
Р.
0
0,35 кПа (2,6 торра ), а измерения
удельной поверхности ведутся при еще меньшем давлении — до
0,13 кПа
количество
(1 торр).
Эго значит,
в "мертвом"
объеме
что для
меньше
этого адсорбтива
его
примерно в 250
раз,
хотя количество на поверхности почти такое же, как для азота.
Этим приемом удалось снизить потолок измерений з
уд
с 0,15
до
2
0,01
2
м /г
т.е.
до
100 см /г.
Изменив же
конструкцию
адсорбционной установки, а именно, сильно уменьшив объем
мертвого "
датчиков
пространства
давления
ртутью),
за
(вместо
получили
счет
"
применения
компактных
приборов,
заполненных
громоздких
возможность
измерять
поверхность
загруженного образца площадью всего 10 см .
Значительное
много раз
развитие
возросшей
получили экспресс-методы
потребности
в
измерениях
из-за
во
удельной
поверхности. За рубежом выпускаются фирменные автоматические
приборы, работающие без участия оператора круглые сутки и с
помощью ЭВМ выдающие готовый результат.
Не
утратил
своего
адсорбционно-десорбционный
помощью которого
применения
метод
хроматографический
измерения
поверхности,
с
в современном исполнении удается измерить
2
величину поверхности в несколько см .
Упрощена
удельной
методика
расчетов.
поверхности
экспериментальных
Если
обычно
точек
для
для
вычисления
использовалось
того,
чтобы
5—6
построить
соответствующий график и определить обе константы уравнения
БЭТ, то теперь часто
[см. 10]. Измерив
используют одноточечный
всего
одну
точку
величину а при каком-либо р/р ,
0
Б . Как
уд
изотермы,
т.е.
получив
можно вычислить а , а затем и
т
показал анализ, отклонение принятой константы С от
действительной
определение
намного
метод Темкина
вносит
Б ,
уд
очень
небольшую
экспериментальная
упрощается.
Кроме
того,
же
и
отпадает
погрешность
в
расчетная работа
необходимость
в
построении
графиков
принята
большинстве
в
БЭТ. Именно
такая
работающих
методика
установок
расчетов
по
методу
термической десорбции. Точность одноточечного метода несколько
ниже,
чем
многоточечного.
неизбежном
для
любых
учитывается только
для
многих
точек
одно
Это
объясняется
измерений
что
при
в
нем
разбросе точек
экспериментальное
изотерма
тем,
проводится
значение, тогда
с
как
усреднением этих
значений.
Оценка
двух
независимых
адсорбционных
методов
-визуальный, по скорости растворения и по теплотам смачивания
имеют ограниченное
применение
из-за того,
что
они наиболее
приемлемы лишь для порошкообразных материалов, поэтому эти
методы каждый в отдельности, а еще лучше, совместно, наиболее
пригодны
для
изучения
стандартных
образцов,
которые
для
многих целей должны быть непорисгыми. По сути, имеется лишь
два альтернативных универсальных
(т.е. пригодных
для
любых
образцов) метода: метод БЭТ и сравнительный метод. Метод БЭТ,
как - международный стандартный метод, для него разработаны
и производятся фирмами специальные приборы, действующие по
специальным программам. Разработаны также хроматографические
приборы,
отлажена
соответствующая
методика
расчетов. Недостатком метода БЭТ является его
в некоторых
случаях к химической
проявляется
в том,
заметно отклоняются
этих
значений
с
что
от
природе
величины
стандартных
помощью
метода
измерений
и
чувствительность
поверхности.
молекулярных
значений.
теплот
Она
площадей
Корректировка
смачивания
и
сравнительного
метода
позволяет
повысить
надежность
стандартного метода БЭТ.
СПИСОК ЛИТЕРАТУРЫ
1. Киселев А.В. Методы исследования структуры высокодисперсных и
пористых тел. - М.: Изд-во АН СССР, 1953. - С. 86.
2. Грег С., Синг К. Адсорбция, удельная поверхность, пористость. М.:
Мир. 1984. 306с.
3. Брунауер С. Адсорбция газов и паров. — М.: ИЛ, 1948. С. 41.
4. Экспериментальные
метода в адсорбции и
молекулярной
хроматографии. — М.: Изд-во МГУ, 1973. - 447 с.; 1990. - 316
с.
5. Парфит Г., Рочестер К. Адсорбция из растворов на поверхностях
твердых тел. М.: Мир. - 1986. - 488 с.
6. Кельцев Н.В. Основы адсорбционной техники. 2-е изд. М.: Химия.
1984. 592с.
7. Дубинин М.М. Адсорбция и пористость. М.: ВАХЗ. 1972.126с.
8. Буянова Н.Е., Карнаухов А.П., Алабужев Ю.А. Определение
удельной поверхности дисперсных и пористых материалов.
—
Новосибирск: Институт катализа, 1978. 74 с.
9. Джейкок М., Парфит Дж. Химия поверхностей раздела фаз. — М.:
Мир, 1984. — 269 с.
10. Карнаухов А.П. Адсорбция. Текстура дисперсных и пористых
материалов. - Новосибирск: Наука. Сиб. предприятие РАН. 1999.
470c.
11. Комаров В.С. Адсорбенты и их свойства. Минск.: Наука и техника.
1977. 248с.
12. Адамсон А. Физическая химия поверхностей. М.: Мир. 1979. 568с.
13. Хейфец Л. И., Неймарк А. В. Многофазные процессы в пористом
теле. М.: Химия, 1982. 320c.
14. Kruger A., Kataoka F., Ozawa M . , Fujino T., Suzuki Y., Aleksenskii
A.E., Vul A.Y., Osawa E. // Unusually Tight Aggregation in Detonation
Nanodiamond: Identification and Disintegration: Carbon 2005, 43,
с.1722.
15. Фенелонов В.Б. // Лекции, институт Катализа им.Г.К. Борескова СО
РАН: http://www.catalysis.ru/.
16. Фенелонов В.Б. Введение в физическую химию формирования
супрамолекулярной структуры адсорбентов и катализаторов.
Новосибирск: Издательство СО РАН, 2004. 442с
17. Вячеславов А.С., М. Ефремова. Определение площади поверхности
и пористости материалов методом сорбции газов. 2011. Москва.
МГУ. http://www. nanometer.ru/.
5. Р А С П Р Е Д Е Л Е Н И Е П О Р П О Р А З М Е Р А М
Известно,
что
при
адсорбции
на непористых
и
пористых
адсорбентах на разных участках адсорбционной изотермы величина
адсорбции газа или пара изменяется по разному. Например,
для
непористых или микропористых адсорбентов влияние природы и
текстура адсорбента, а также условий проведения эксперимента более
заметно проявляется в области низких относительных давлений, в то
время как для крупнопористых его действие ощутимо только при
более
высоких
давлениях,
близких
к
давлению
насыщения.
Характерно, что в области заполнения монослоя рост адсорбции
замедляется с повышением давления, образуя на изотерме адсорбции
пологий
участок,
величина
которого
зависит
от
внутренней
структуры пористого тела. При дальнейшем повышении давления
количество
адсорбированного
вещества
увеличивается
за
счет
полимолекулярной адсорбции, завершающейся в случае пористых тел
капиллярной
конденсацией.
При
этом
характер
адсорбционной
изотермы, отражающей внутреннюю структуру твердых тел, дает
возможность определить степень развития пор того или другого вида,
установить структурный тип адсорбента, величину и природу его
удельной поверхности.
Изотермы адсорбции и десорбции паров позволят получить
важные
сведения
о
внутренней
структуре
адсорбентов
и
катализаторов.
Различают
много типов пористых систем. Как в
разных
образцах, так и в одном и том же образце поры могут значительно
отличаться как по форме, так и по размеру. Особый интерес во
многих случаях представляет поперечный размер пор, например,
диаметр
цилиндрических
пор
или
расстояние
щелевидных пор. Классификация пор, принятая
между
стенками
Международным
союзом по теоретической и прикладной химии (IUPAC) основана на
следующем принципе: каждому интервалу размеров пор (микропоры
< ~3нм, мезопоры ~3-И00нм, макропоры > ~100нм) соответствует
характерные адсорбционные свойства, находящие свое выражение в
изотермах адсорбции.
В
микропорах
взаимодействия
из-за
с
близости
адсорбированными
стенок
пор
молекулами
потенциал
значительно
больше, чем в более широких порах, и величина адсорбции при
данном относительном давлении соответственно также больше.
В
мезопорах
изотермах
происходит
адсорбции
паров
капиллярная
наблюдается
конденсация
и
на
характерная
петля
адсорбционно-десорбционного гистерезиса смачивания поверхности
адсорбента.
Диаметр
макропор
соответствует
давлению
p/p =1,
вблизи
0
поэтому возможность определения диаметра макропор зависит от
точности измерения давлений в этом диапазоне.
Граница
между
различными
классами
не является
жестко
определенной, поскольку она зависит и от формы пор,
природы, в частности от
от их
поляризуемости молекул адсорбата. Так,
наибольший размер пор (и соответственно наибольшее p/p0),
при
котором еще наблюдается увеличение адсорбции, т.е. верхний предел
размеров
микропор
для
различных
адсорбтивов
может
быть
различным. Часто характерное для микропор возрастание потенциала
взаимодействия
прекращаются
и,
как
при
следствие,
таком
возрастание
относительном
адсорбции
давлении
соответствующем размере пор), которое еще не достигает p/p
0
петли гистерезиса.
Поэтому
в последние
(и
начала
годы, по уточненным
данным [1], микропоры принято подразделять на очень узкие - так
называемыеультрамикропоры с диаметром (1.2--1.4нм), для которых
характерен эффект возрастания адсорбции и супермикропоры
1.2-1.4нм до 3.0-3.2нм), которые находятся в интервале
ультрамикропорами
и мезопорами.
Границы
линейных
(от
между
размеров
мезопор находятся в интервале от 3.0- 3.2нм до 100- 200нм, что
соответствует
пределу
применимости
уравнения
капиллярной
конденсации Томсона-Кельвина.
Нижним пределом радиуса r микропор считают ~0,13нм, что
отвечает
критическому
проникающей
диаметру
практически
во
молекулы
He
все пустоты.
(~0,26нм),
Верхний
предел
пористых тел -макропоры «размазан» (~200нм), для которых вклад от
всей полимолекулярной адсорбции, мал по сравнению с заполнением
поверхности центральной области мезопор.
развитой
удельной
поверхностью,
на
Мезопоры
которой
обладают
последовательно
протекают в начале мономолекулярная, а затем полимолекулярная
адсорбция, завершаемая заполнением пор по механизму капиллярной
конденсации.
Граница между микропорами и мезопорами (второй областью
размеров пор) экспериментально
фиксируется по исчезновению-
появлению петли гистерезиса при строго равновесных измерениях
изотерм адсорбции-десорбции с уменьшением-увеличением размера
пор.
Диапазон
размеров
мезопористых
систем,
традиционно
исследуемых методами адсорбционной порометрии с характерным
размером до 100 нм, предлагается [1] разбивать на участки:
- I - й участок размеров r находится до ~4 нм - в нем отсутствует
петля гистерезиса и капиллярная конденсация из-за малых размеров
цилиндрических
фазовый
каналов.
переход,
Здесь
должен
проявляющийся
наблюдаться
на
концентрационных
температурных зависимостях теплоемкости
исключительной
прецизионности
размытый
подобных
фазовые переходы не обнаружены. Поэтому
адсорбата.
Но,
измерений,
и
из-за
такие
пока единственным
доказательством этого являются прямые адсорбционные измерения.
Предполагается, что для глобулярных и других систем со сложной
формой полостей, в том числе и щелевидных пор, ограниченного
объема, величина ~4 нм должна относиться к «сквозной» части
каналов;
I I - й участок размеров г лежит в диапазоне от ~4нм до 15нм область,
так
называемых
«узких»
пор
в
которой
реализуются
непрямые взаимодействия между стенками за счет кооперативного
поведения
адсорбата.
Наблюдается
зависимость
критической
температуры расслаивания от размера поры, которая подтверждена
теоретическими методами и прямыми адсорбционными измерениями;
I I I - й участок размеров г - от 15нм до 100нм включает в себя
относительно
широкие поры, в которых отсутствует
перекрытие
поверхностных потенциалов. В этой области происходит
полное
ослабление
непрямых
взаимодействий
стенок
за
счет
фазового
состояние адсорбата.
Рассматриваемая
кооперативного
пористых
поведения
систем.
потенциал
классификация
При
адсорбата
наличии
взаимодействия
[1 ]
в
отражает
характер
ограниченных
дальнодействующего
адсорбат-стенка
объемах
вклада
эти
в
области
соответственно увеличиваются пропорционально радиусу потенциала
взаимодействия между молекулами адсорбата.
Сама
измерений
классификация
и
протекающих
на
построена на основе
различии
в порах,
механизмов
отличающихся
адсорбционных
сорбционных
по размерам,
явлений,
в
которых
реализуется процесс капиллярной конденсации. При малых размерах
пор
под действием поверхностных потенциалов стенок заполнение
микропор протекает в не зависимости от величины межмолекулярного
взаимодействия.
Для
широких
пор
поверхностным
практически можно пренебречь и в результате
потенциалом
межмолекулярного
взаимодействия капиллярная конденсация в них практически ничем не
отличается от конденсации в объемной фазе.
5.1. Методы определения пористости
Выше нами были рассмотрены методы определения удельной
поверхности адсорбентов, основанные на использовании той части
изотермы, которая отвечает низким давлениям (р/р <0,4)
&
Часть
изотермы,
отвечающая
более
высоким
давлениям,
[8-10].
дает
сведения о структуре пор твердого тела, поскольку, в области
давлений
проявляется
явление
капиллярной
конденсации,
обусловленное
смачивания
адсорбционно-десорбционным
[11-14].
гистерезисом
Это явление, рассмотренное
в гл. 1 и 2
описывается уравнением Томсона-Кельвина
P = V*p(
Я7У
)
(5.1)
где Р = Р о , - равновесное давление пара над плоской поверхностью жидкости
при температуре Т. Здесь, знак ( - ) относится к фазам с вогнутой
поверхностью (вогнутый мениск).
0
п
Его часто записывают в виде
Т^г-
^77" =
где
!
— — относительное
а и V
m
давление
пара,
( 5 . 2 )
находящегося
в
равновесии
с
мениском, и м е ю щ и м радиус кривизны г;
- поверхностное натяжение и молярный объем жидкого адсорбтива
соответственно; (с индексами «п» и «ж» относятся соответственно к
пару и жидкости, с индексом «г» - к искривленной и индексом «0» - к
плоской границе раздела).
Из формулы (5.1) следует, что давление пара уменьшается с
уменьшением радиуса пор. В результате этого более мелкие поры
заполняются раньше, чем крупные, а величина сорбции при каждом
равновесном давлении будет функционально зависеть от объема пор
определенного радиуса, содержащегося в единице массы адсорбента.
Характерной
особенностью
процесса
заполнения
пор,
или
капиллярной конденсации, является наличие петли гистерезиса на
изотермах
гистерезиса
адсорбции.
При
обусловлена
этом
адсорбционная
полимолекулярной
ветвь
петли
адсорбцией
и
капиллярной конденсацией, в то время как десорбционная ветвь
выражает лишь капиллярную
конденсацию. В результате
этого
десорбционная ветвь изотермы и ширина петли гистерезиса служат
выражением структуры пористого тела, отражением размера и в
некоторой степени формы пор. Так, для твердых тел с малыми
порами
гистерезисные
петли
чрезвычайно
узки,
и,
наоборот,
расширение гистерезисных петель свидетельствует о наличии более
крупных пор.
Наиболее правдоподобное объяснение такой связи состоит в том,
что в первом случае адсорбционные слои заполняют поры без
участия капиллярных сил, в результате чего процесс адсорбции и
десорбции
обусловлен
конденсация
имеющих
и
одними
испарение
различные
и теми же
происходят
значения
с
силами,
частей
адсорбционного
во
втором
поверхности,
потенциала,
и,
следовательно, обусловлены разными силами.
В системах с очень большими порами, в которых практически
отсутствует
капиллярная
конденсация,
наблюдается
обратная
картина, сопровождающаяся не только сужением петли гистерезиса,
но и исчезновением ее. Другими словами, пределом больших пор
является полное отсутствие пор вообще и приближение системы по
всем характеристикам к свойствам непористых веществ.
Таким
образом,
путем
простого
рассмотрения
адсорбционно-
десорбционных изотерм можно получить правильное представление
о распределении пор по размерам. Более точную характеристику о
структуре высокодисперсных тел и распределении пор по размерам
дает теория капиллярной конденсации, основываясь на выводах
которой
можно
кривую
адсорбента.
уравнению
каждому
по
Томсона
изотермам
Для
этого,
вычисляют
значению р/р ,
0
сорбции
как
получить
будет
радиусы
и графически
структурную
показано
пор,
ниже,
по
соответствующие
выражают
зависимость
объема адсорбционного вещества в жидком состоянии как функцию
радиусов
капилляров.
Наиболее
наглядно
характер
структуры
обнаруживается на дифференциально-структурных кривых.
В связи с этим интересно отметить, что до настоящего времени,
несмотря
на
большое
число
работ,
посвященных
изучению
структуры адсорбентов, в литературе нет единого мнения по вопросу
о выборе ветвей гистерезисной петли для расчета радиусов пор и
кривых распределения.
Одни
исследователи
сорбционной
ветви
оценку
изотермы,
размера
пор производят
другие
—по
по
адсорбционной
деи,
наконец, известны случаи, когда некоторые авторы для определения
наиболее вероятных радиусов пор пользовались обеими ветвями
гистерезисной петли, не отдавая предпочтения ни той, ни другой.
Отсутствие
адсорбентов
данных,
единого
подхода
значительно
полученных
в
затрудняет
различными
методе
расчета
сравнение
авторами,
структуры
литературных
дезориентирует
исследователя и иногда дает ложную картину распределения пор по
радиусам.
Так,
В.П.
Ждановым
[2]
при
изучении
структуры
пористых стекол показано, что для одного и того же образца в
зависимости от метода расчета может быть получен бидисперсный
характер структуры, отчетливо обнаруживающий себя на кривых
распределения объема пор по эффективным радиусам, рассчитанным
по десорбционной ветви изотермы, или монодисперсный — при
расчете по адсорбционной ветви. В связи с этим возникает вопрос, в
каком случае функция распределения пор по эффективным радиусам,
т. е. рассчитанная по адсорбционной или десорбционной ветви петли
гистерезиса, правильно отражает характер структуры адсорбента.
Ответ на данный вопрос может быть двояким: в одних случаях,
особенно при изучении кинетики адсорбционных, десорбционных и
каталитических процессов, важно знать самую узкую часть поры,
лимитирующую скорость протекания этих процессов, в то время как
в случаях, связанных с изучением закономерностей
паров
в порах,
возникает
необходимость
конденсации
определения
радиуса
полости поры, т. е. в зависимости от цели поставленной задачи
структурная характеристика адсорбентов и катализаторов
производиться как по десорбционной, так и по
ветвям
изотермы.
Расчет
по
данным
может
адсорбционной
десорбции
дает
радиус
горлышка поры, а по адсорбционным данным — радиус ее полости, в
результате чего максимум на кривой распределения в первом случае
сдвинут в область более мелких пор, а во втором — в область более
крупных.
Адсорбционно-структурные
состоящих,
например,
из
исследования
смеси
мелко-
и
образцов
[5],
крупнопористого
силикагелей, показывают, что на кривой распределения
пор
по
размерам,
по
ад¬
рассчитанной
как
по
десорбционной,
так
и
сорбционной ветвям изотермы, имеются два максимума, каждый из
которых отвечает структуре взятых силикагелей. Это говорит о том,
что внутренняя структура пористого тела, представленная двумя или
тремя размерами однородных пор, независимо от методов расчета,
должна, согласно уравнению (5.1), проявляться на обеих ветвях
изотермы. Отличие заключается лишь в четкости максимумов и
положении их на оси абсцисс. Одним из примеров
механизм
может быть
высыхания дисперсных и пористых систем. Из практики
известно, что сушка подобных систем вследствие действия
сил
капиллярной контракции сопровождается уменьшением их объема,
изменением
формы,
возникновением
напряжений
и
внутренних
разрывов, растрескиванием и пр. При этом наибольшее развитие сил
капиллярной
контракции
в
процессе
высыхания
максимально
увлажненных систем начинается в самом поверхностном слое. В
результате этого частицы дисперсной фазы сближаются,
образуя
уплотненный слой, который, преодолевая нарастающее в нем сопро¬
тивление
структуры,
капиллярному
стремится
подсасыванию
сократиться,
жидкости
из
способствуя
этим
глубинных
слоев
высыхающего тела. Вместе с жидкостью в порах мигрируют
макроповерхности
и накопляются там частицы
к
тонкодисперсных
фракций, уплотняя тем самым поверхностный слой и сужая устья его
пор. Иначе говоря, формирование пор рассматриваемых систем идет в
направлении сужения их верхней части с образованием горлышка,
радиус которого определяется режимом сушки и местонахождением
поры в зерне образца (на поверхности или в объеме).
Данный механизм сужения устья пор и отклонения последних от
их геометрической
формы, образованной элементами
структуры,
может в зависимости от степени действия указанных
факторов
сопровождаться образованием пор как с равновеликими устьями, так
и
с устьями
двух
или трех
размеров.
Объем
таких
сужений,
составляет 0,1—2,0% от предельной сорбционной емкости образца.
Несмотря
на
это,
формальный
подход
при
расчете
кривой
распределения объема пор по радиусам приводит иногда, особенно
при
наличии
прерывистости
десорбционной
ветви
изотермы,
к
ошибочным выводам о характере структуры пористого тела.
Поэтому единственно правильным и общим принципом от¬
несения структуры изучаемых пористых материалов к бидисперсной
или
тридисперсной
структуре
является
наличие
на
кривых
распределения, независимо от того, рассчитаны они по данным
адсорбционной или десорбционной ветви изотермы соответствующих
максимумов
[5]. В противном
случае, т. е. если
дисперсность
структуры обнаружена только по данным десорбционной
изотермы
и
не
подтверждена
данными
адсорбционной
ветви
ветви,
структуру пористого тела следует рассматривать как моно - или
пестропористую с наличием пор, устья которых обладают двумя или
тремя размерами.
5.2. Типы гистерезисных петель
Де Бур отметил, что форма гистерезисных петель значительно
различается для разных пористых адсорбентов
[3]. Им
сделана
попытка классифицировать форму гистерезиса и связать ее с формой
m
7
ш
У
На
рис.
2.20
продублированы)
пор. Классификация
де Бура
слегка
рекомендациях
изменена
в
была
И Ю П А К и в таком виде дается ниже.
(гл.2)
типы
приведены
(здесь
гистерезисных
для
петель
наглядности
по
этой
классификации. Тип Н1 характерен, например, для крупнопористых
и
среднепористых
силикагелей,
саж
и
других
глобулярных
адсорбентов. Гистерезисные петли тип Н2 для некоторых пористых
стекол-типично
губчатых
структур.
петель типа Н1 и Н2 могут
Но
примеры
гистерезисных
наблюдаться и для глобулярных, и для
губчатых структур, поэтому делаются предположения, что в этих
случаях
главным
фактором,
определяющим
форму
гистерезиса,
является не форма пор, а соотношение размеров горл и полостей, а
также
однородность
этих
размеров.,
имеющих
своеобразную
морфологию. Петли типа Н2 получают так же для некоторых углей,
например, ZnCl2 активации.
Многие исследователи при анализе гистерезисных петель тип НЗ
склоняются к тому, что этот тип связан с формой пор материала. Он
наблюдается для очень многих активных углей пароводяной активации
и для модифицированного монтмориллонита с раздвинутыми слоями.
В этих случаях поры имеют
щелевидную форму с почти плоско¬
параллельными стенками.
Тип
Н4
гистерезиса,
как
правило,
отражает
комбинацию
микропор и мезопор, встречающуюся в некоторых типах активирован¬
ных углей.
Типы НЗ и Н4 гистерезиса имеют характерную особенность,
отличающую их от других, заключающуюся
в том, что ширина
петли, измеренная как разность ординат десорбции и адсорбции,
приблизительно постоянна во всей области гистерезиса. Тип НЗ имеет
характерные особенности: 1) адсорбционная ветвь гистерезиса имеет
типичную для I I типа по классификации Брунауэра форму изотермы и
свидетельствует
о наличии
полимолекулярной
адсорбции;
2)
на
десорбционной
ветви
отсутствует
горизонтальный
участок,
присущий другим типам петель.
Если гистерезис на изотерме адсорбции имеет форму Н4, то это
как правило означает, что уже при сравнительно небольшом давлении
произошло
заполнение
практически
прекратилась.
изотермы
вблизи
Р/Р
0
микропор
=
и
дальнейшая
Крутой подъем
1, вероятно,
адсорбция
адсорбционной
обусловлен
ветви
капиллярной
конденсацией в мезо- и макропорах при доступе пара в них по
механизму многократных процессов конденсации — испарения. При
этом
ширина
гистерезиса,
связана
с
количеством
адсорбата,
заблокированного в мезо- и макропорах, из которого и рассчитывают
объем пор.
Использование
пористости
численными
моделирования последних лет [1] п о к а з ы в а ю т , ч т о
методами
рекомендации
IUPAC весьма неоднозначны, так как полностью
игнорируют
в з а и м о с в я з ь пор. Р а н е е к п о д о б н о м у в ы в о д у п р и ш е л Э в е р е т т [ 4 ] ,
который
пытался
гистерезиса
пористого
на
создать
основе
тела,
общую
моделей
действующих
теорию
из
как
адсорбционного
простейших
отдельные
элементов
независимые
д о м е н ы . Г л а в н ы й в ы в о д из его и с с л е д о в а н и й — н е о б х о д и м о с т ь
у ч е т а в з а и м о с в я з и п о р , в л и я ю щ е й на п р о ц е с с ы к а к а д с о р б ц и и ,
т а к и д е с о р б ц и и . Т а к и е п о д х о д ы сейчас и н т е н с и в н о р а з в и в а ю т с я .
Изучение пористой структуры мезопористых твердых
всего связывают
с
интерпретацией
изотерм
чаще
адсорбции I V типа.
Этот тип изотерм характерен именно для адсорбции в мезопорах.
В области низких давлений начальный участок изотерм I V и I I типа
идентичны друг другу. Однако,
изотерма I V типа
отклоняется
начиная
с
некоторой
вверх, а затем при более высоких
давлениях ее наклон уменьшается. При приближении
насыщенных
паров
точки
(p/p =1) величина
к
давлению
адсорбции может
s
заметно
возрастать
Форма
петли типа I V может
быть
различной
для
разных
адсорбционных систем; однако, как видно из рис. 5.1, величина
адсорбции
при
любом
данном относительном давлении для
десорбционной ветви (2) всегда больше, чем для адсорбционной (1).
IV
тип
изотерм
адсорбции
часто
наблюдается
для
неорганических оксидов, для углей и других пористых тел.
Интерпретируя эти изотермы,
особенно изотермы
адсорбции
азота
можно
при 77 К,
приемлемой
с
точностью
оценить удельную поверхность
и
получить
приблизительную
характеристику
Р
и
с
5
.
1
.
Х
а
р
а
к
т
е
р
н
а
я
и
з
о
т
е
р
м
а
с
п
е
т
л
е
й
пор
по
распределения
размерам.
Для
гистерезиса типа I V .
интерпретации
капиллярной
таких
изотерм, Зигмонди
конденсации,
служила
основой
изотерм
I V типа.
которая
практически
всех
в
той
предложил
или иной
теоретических
Согласно термодинамическим
теорию
форме
анализов
соотношениям,
равновесное давление пара Р над вогнутым мениском жидкости
должно быть меньше, чем давление насыщенного пара Р при той же
s
температуре. Это означает, что в порах твердого тела пар способен
конденсироваться
в жидкость,
давление
единицы.
меньше
даже
Для
если
его
относительное
применения
к адсорбционным
данным используют уравнение Кельвина (5.1). Модель
Зигмонди,
которой наиболее широко пользуются и сегодня, подразумевает,
что в начальной части изотермы адсорбция ограничена
лишь
образованием тонкого слоя на стенках пор. Точка у основания
петли гистерезиса соответствует началу капиллярной конденсации
в
наиболее
заполняются
тонких
все
порах.
По
более
широкие
вся
система
насыщенного
пара
конденсатом.
Следуя
мере
возрастания
поры,
не
Зигмонди,
все
пока
при
окажется
первые
давления
давлении
заполненной
исследователи
допускали, что поры имеют цилиндрическую форму и что краевой
угол
смачивания
равен
нулю,
так
что
мениск
является
полусферическим. В этом случае средний радиус кривизны г
m
равен
радиусу поры за вычетом толщины адсорбционной пленки на ее
стенках.
Применяя
уравнение
Кельвина,
можно
вычислить
по
точке у основания петли гистерезиса минимальный радиус пор,
в
которых
мнимальный
имеет место
радиус
капиллярная
зависит
конденсация.
Этот
от природы изучаемого образца,
однако он редко бывает меньше, чем ~ 1 нм. Верхний предел
применимости
уравнений
Кельвина
г
m
~
100
нм
практически; он определяется экспериментальными
установлен
трудностями
измерения очень малого снижения давления паров. Корректность
определения размеров мезопор
в
пределах
определяется, таким образом, применимостью
классических
уравнений,
от ~ 3 до ~ 100 нм
в этом
интервале
описывающих капиллярные явления, в
частности, уравнения Кельвина.
5.3.
Традиционные
методы
расчета
PSD
(роге
size
distribution)
Большинство современных методов расчета PSD базируется на
модификациях численного решения уравнения Уилера для баланса
объема при адсорбции или десорбции в системе непересекающихся
капилляров постоянного сечения [6]:
V(r) = V S
3
/ °° 7i(r-t) L(r)dr
(5.3)
д
где V(r) - объем пор с размерами r>R,
R = R(P/P )
- функция, задаваемая уравнением Кельвина.
V - суммарный объем пор, определяемый по предельно достигнутой величине
адсорбции (предполагается, что к этому моменту все поры заполнены),
L(r) - суммарная длина капилляров с радиусами г + dr,
t - толщина адсорбционной пленки на поверхности (задаваемая как функция
s
s
t(P/Ps)).
В большинстве модификаций этого метода функция L(r) под знаком
интеграла заменяется
V(r)/r
на эквивалентные
выражения
Б(Г)/2ЛГ
или
, где s(r) - геометрическая поверхность пор с размерами r>R.
В практических расчетах интегралы заменяются суммами.
Это уравнение
было предложено для системы из параллельно
расположенных прямых цилиндрических капилляров, открытых с
двух концов, но при введении соответствующих
коэффициентов
формы используется и для других простейших форм пор. Такие
модификации метода расчета PSD были предложены Шаллом (1948
г.), Барретом, Джойнером и Халендой (1951 г.), Кренстоном и Инкли
(1960 г.), Доллимором и Хилом (1970 г.) и др.
[6]. Эти методики
отличаются выбором геометрической модели пор (цилиндрические
капилляры
«с дном»,
полости
между
регулярно
упакованными
монодисперсными
глобулами
или
плоскощелевидные
поры),
адсорбционной или десорбционной ветви для проведения расчетов
(чаще используется десорбционная ветвь), способами разбиения экс¬
периментальной изотермы на интервалы и расчета средних значений
г
для
каждого
интервала,
расчетом
вклада
полимолекулярной
адсорбции на стенках освобожденных пор (т.е. видом используемой
функции t(P/Ps)).
Наиболее употребительны методы Баррета, Джойнера и Халенды
(метод БДХ) и метод Доллимора и Хила (метод ДХ), базирующиеся
на модели «цилиндры с дном» и десорбционной ветви изотермы.
Иногда используется метод ДББ, основанный на работах Дерягина, де
Бура и Брукхоффа и предусматривающий более сложный расчет
функции t(P/P ).
0
Традиционные методы расчета PSD, как правило,
базируются
на моделях индивидуальных пор простейшей формы в виде: прямых
цилиндров
постоянного сечения «с дном» или «без дна»,
щелей
пор
и
между
монодисперсных
элементами
сферических
из
глобул.
регулярно
Такие
плоских
упакованных
расчеты
обычно
проводят для области кельвиновских радиусов от 3 до 50-100 нм.
Нижний
предел ограничен диапазоном применимости
Кельвина,
давления
равновесия
а
верхний
вблизи
в
приравнивается
р/р
этой
0
определяется
~
1,0
области.
плотности
погрешностями
и низкой
При
скоростью
этом
нормальной
измерения
установления
плотность
жидкости,
уравнения
а
адсорбата
равновесное
давление пара определяется уравнением Кельвина. Расчеты ведут
начиная от предельных величин адсорбции при максимально дос¬
тигнутых в эксперименте значениях р/р .
8
Уравнение
Кельвина
для адсорбции
азота
при 77
К
и
сферических менисков записывается в преобразованном виде
г
к
0,4078
=
v '
<4
н
м
(
5
.
4
)
Так, например, при подстановке максимальных значений р/р =
s
0,95, 0,98 и 0,99 получим значения кельвиновских радиусов 18,3, 46,5
и 93,4 нм, при P/P = 0,9995 получим г = 1877 нм и т. д., т. е. в этой
s
области
к
относительных
давлений
близких
к
1,0
погрешность
определения размера пор очень чувствительна к точности измерения
р/р^ На практике предельный размер измеряемых этим методом пор
— около 50 нм для обычных исследовательских установок и около
100 нм — для наиболее прецизионных.
Для проведения расчетов
изотерма адсорбации разбивается на
интервалы по оси давлений. Каждому интервалу давлений
ставят в
соответствие среднее значение кельвиновского радиуса гк. Н а первом
шаге
расчета
допускают,
что
десорбция
происходит
из пор
наибольшего размера R, который связан с г соотношением
к
Р
V
R = r - + t^-
(5.5)
K
которое
учитывает
оставшуюся
на
стенках
освобожденного
капилляра адсорбционную пленку равновесной толщины t(p/p ) (Рис
s
5.2.).
Рис. 5.2. Схема расчета размеров пор: а — исходное состояние, цилиндрический
капилляр радиуса R полностью заполнен конденсатом; б — состояние после
освобождения сердцевины пор с кельвиновским радиусом г ( Р Л ^ ) , на стенках
остается адсорбционная пленка т о л щ и н о й t(P/Ps) [6].
к
При заданной модельной форме капилляров и известному из
адсорбционной
изотермы
по
определенному
десорбированному
объему рассчитывается геометрическая поверхность s и объем V
капилляров,
а
адсорбционной
также
величина
пленкой.
На
поверхности
каждом
s(t),
следующем
покрытая
шаге
расчета
учитывается десорбция как из утончающейся адсорбционной пленки
t(P/Ps) со всей поверхности уже освободившихся капилляров, так и из
объема
сердцевин
освобождающихся
r ( Р / Р ) . В процессе подобных
к
s
капилляров
с
радиусом
расчетов проводят суммирование
поверхности освободившихся пор, покрытой адсорбционной пленкой,
по которой и рассчитывают геометрическую поверхность соответст¬
вующих
цилиндрических
геометрический
суммируют и
объем
получают
капилляров.
освободившихся
Затем
рассчитывают
капилляров,
результаты
графики кумулятивного (интегрального) и
дифференциального распределения объема и поверхности пор по
радиусам соответствующих цилиндрических капилляров. Аналогично
проводят расчеты в рамках модели плоскощелевидных пор и других
пор простейшей геометрии.
Для
примера,
на
рис.
5.3
показана
изотерма
с
петлей
гистерезиса и полученные из нее графики PSD, рассчитанные по
адсорбционной
изотерма
и десорбционной
ветвям петли гистерезиса.
Эта
измерена на механической смеси двух пористых тел с
узким распределением пор по размерам, максимумы PSD (на Рис.5.3,
справа), рассчитанные по десорбционной ветви изотермы. Расчет по
адсорбционной ветви изотермы дает размытый график с одним
максимумом,
который
не
выражает
особенности
текстуры
компонентов смеси. Поэтому расчет распределения пор по размерам
предпочтительнее вести по десорбционной ветви петли капиллярноконденсационного гистерезиса смачивания пористого материала.
А
]
J
1
•
\
4
J\
я
Рис 5.3. Изотерма адсорбции с капиллярно-конденсационным гистерезисом
механической
смеси двух адсорбентов разной пористости (слева)
и
распределение объема пор по размерам - dV/dr (справа), вычисленного по
адсорбционной (пунктир) и десорбционой (сплошная линия) ветви [6].
Этот
и другие примеры расчетов пористых систем
не являются
убедительными до тех пор, пока не будет выбрана некая реальная
адсорбционная модель, близкая к идеалу. Такой моделью
стала
реальная пористая структура мезопористых мезофазных материалов
типа М С М - 4 1 , описанных впервые в 1992 г. Эта реальная модельная
пористая
структура
используется
при
«обкатке»
некоторых
теоретических моделей, в частности, теории функционала плотности
ТЛФ. В приложении к анализу структуры нанопористых адсорбентов
ТЛФ, в ее различных вариантах, глубоко проработана и встроена в
программное обеспечение адсорбционного современного фирменного
оборудования Е.А. Устиновым с сотр. [7].
Мезопористая
структура
типа
образована
гексагональными
мезопорами - с «окнами» одинакового размера, которые можно при
синтезе направленно регулировать в диапазоне 3 -т 5 нм и более. Эти
мезопоры
ориентированы
параллельно
друг
другу,
и
образуют
гексагонально упорядоченную структуру, т.е. идеальную модельную
систему из непересекающихся пор одинаковой формы.
Стандартные методы расчета структур типа МСМ-41 (методы
БДХ,
ДХ,
ДББ),
а
также
современные
численные
методы
молекулярного моделирования дают значения, на 20—30 % ниже
результатов
более
надежных
независимых
измерений.
Обычно
расхождения с расчетами классическими методами вызваны разными
численными значениями коэффициентов уравнения Френкеля-Хелси
- Хилла, по которому рассчитываются значения t(P/P ).
s
5.4.
Методы
расчета
пористых
систем
на
современном
оборудовании
В
настоящее
время
для
анализа
пористой
структуры
адсорбентов (вычисление доли пор различного диаметра в общей
пористой
структуре)
по изотермам
адсорбции
на
современном
оборудовании используют дополнительные расчетные модели, одним
из вариантов которых является метод Баррета, Д ж о й н е р а и Х а л е н д ы
(БДХ). Метод Barrett-Joyner-Halenda (BJH), предложенный в 1951 г.,
изначально
был разработан
для относительно
широкопористых
адсорбентов, обладающих широким распределением пор по размерам.
Однако было многократно показано, что он может быть успешно
применим практически ко всем типам пористых материалов. В основу
модели положено допущение о цилиндрической форме пор и то, что
радиус
поры
равен
сумме
радиуса
Кельвина
и
толщины
адсорбированной на стенке поры пленки.
Распределение пор по объему с учетом их размера оценивают,
отдавая предпочтение десорбционной ветви гистерезисной изотермы
адсорбции. Десорбционная ветвь изотермы для того же объема газа
представляет
меньшее
относительное
давление,
т.е.
изотерма
десорбции ближе к истинному термодинамическому равновесию. И
все же, в некоторых случаях рекомендуется использование так же и
изотермы
адсорбции.
В
качестве
адсорбата
при
анализе
распределения пор по размерам почти всегда используется азот как
наиболее подходящий и хорошо изученный. Например, современный
прибор ASAP 2020 допускает использование в процессе анализа как
одной, так и другой ветви изотермы.
Вячеславов А.С. и
оценке
распределения
Ефремова М. в практическом пособии по
пор по
размерам
достаточно
подробно
приводят алгоритм расчетов пористости (по методу BJH), получаемой
с помощью современной техники
относительном давлении (P/P )
s
жидкостью;
в самых
крупных
[8], согласно которому:
при
близко к 1, все поры заполнены
порах
радиуса
r
p1
присутствует
физически адсорбированный слой молекул азота толщиной tf, внутри
этого слоя имеются капиллярные каналы радиуса r , через которые,
m
при
снижении
P/P
происходит
s
испарение,
соотношение
между
объемом пор V и объемом внутренних капилляров V (по Кельвину):
pl
m
•г
2
V
_
v
г
m1
р1
г
с
„
( 5 . 6 )
V
P1
'ml
И далее при снижении относительного давления с (P/P )\
s
(P/P )
s 2
до
с поверхности десорбируется объем V . Этот объем жидкости
f
определяется
объемом жидкости в крупных порох за исключением
толщины физически адсорбированного слоя на величину A t . За счет
f
уменьшения
относительного
давления
изменение
толщины
слоя
составляет, в среднем A t / 2 . Объем самых крупных пор:
-
V1
)
(5.7
Vi ^ (^^щ)
P
При последующем снижении относительного давления до
(P/P )
s
объем десорбированной жидкости составит:
V
AtJ
-
Vp2 l
+ 2/
\т 2
т
<V2~V, )
t2
(
)
5.8
где
V
At2
si
c
— площадь
опорожненных
- М2 • А
с±
пор,
из
которых
адсорбированный
газ
десорбировался.
Уравнение (5.8) можно обобщить для любой последующей стадии
десорбции
n-1
V
— At • ^
Atn
A.
n
(5.9)
c
7=1
Сумма
в уравнении
опорожнившихся
значения V
Atn
за
-
счет
это суммарная
десорбции
средняя
площадь
пор. Подстановка
общего
в уравнение (5.8) позволяет произвести расчет объема
пор при различных относительных давлениях.
Уп
Р
= (
^ д ^ )
• (дЦг -
Поскольку площадь s
At^Ac^J
(5.10)
для любого размера пор не является
c
постоянной величиной, а изменяется с каждым уменьшением Р/Р , ее
0
следует оценить.
Площадь каждой поры s - величина постоянная и ее можно
p
рассчитать из объема поры, если принять за основу цилиндрическую
геометрию пор:
А
Zip
—
Тр
Теперь,
поскольку
для каждого
шага
процесса
десорбции
известно значение sp, площадь пор можно накопительно суммировать.
Метод BJH рассчитывает ^scj для каждого шага изменения давления
следующим
образом:
вычисления
проводятся
процесса десорбции с известными значениями
накопительно
каждого
суммируется.
шага
для каждого
s p,
yd
площадь пор
Метод BJH рассчитывает
изменения
давления
шага
следующим
^ дС
у
для
образом:
предполагается, что все поры, освободившиеся от конденсата при
снижении
относительного
давления
имеют
средний
радиус
r,
рассчитанный из полученных по уравнению Кельвина наибольшего и
наименьшего значений радиусов на шаг снижения P/P .
s
Средний
радиус капилляров рассчитывается как:
Т
tf
Тр
с
где t - толщина адсорбированного слоя для пор среднего радиуса для
f
данного шага снижения относительного давления и рассчитывается из
уравнения. Значение "с" вычисляется из:
Т
с
Тр
Для
пор
цилиндрического
tf
Тр
Тр
вида
расчет
размеров
мезопор
производится с помощью уточненного по поверхностному натяжению
а уравнению Кельвина (5.1).
Напомним, что в (5.1) а- поверхностное натяжение азота в точке
кипения (8.85-10 Дж/см
при 77К), V — молярный объем жидкого
L
3
азота (34.7 см /моль), Т —температура кипения азота (77К), P/P —
s
относительное давление азота, r — радиус пор по Кельвину.
m
Вводя соответствующие постоянные для азота, размер пор в А
4,15
1оЖ/Р)
Напоминаем, что радиус пор по Кельвину (r ) — это радиус при
m
котором
в
порах
происходит
конденсация
при
относительном
давлении P/P . Поскольку перед началом конденсации имеет место
s
адсорбция на стенках пор, rm не является истинным радиусом пор, тем
более, что при десорбции адсорбированный слой остается на стенках
при испарении. Истинный радиус пор вычисляется по уравнению:
где t - толщина адсорбированного слоя.
Эту
статистическую
3,54-(V /V ),
ads
ads
t
можно
отношение объема адсорбированного
m
считать
равной
где 3,54 А - толщина молекулярного слоя азота, а
m
V /V -
величину
относительном
азота при
давлении к объему, необходимому
для
данном
создания
сплошного монослоя на непористом образце такого же состава. Более
удобный метод определения t предложен Хэлси в виде уравнения
(5.12) и его также используют в программе ASAP для расчета
распределения размеров пор, А:
t
=
3
,
5
4
/3
(
• [2,303 •lo (P /P)}
9
5
Л
2
)
s
Система обработки данных ASAP рассчитывает распределение
пор
по
размерам,
используя
метод,
предложенный
Барретом,
Джойнером и Халендой - BJH (Barrett, Joyner и Halenda).
Другой
доступный
ASAP
для
расчета
метод
основан
на
уравнении Бэра (Boer):
= [
1
13,99
1 /
] 2
[
( 5 . 1 3 )
= 0,034 + 1од(Р /Р)\
0
и уравнении для сорбции на углероде:
2
t
CB
= 0,88 • ( P / P 0 ) + 6,45 • ( Р / Р о ) + 2,98 А
Методы
определения
удельной
поверхности.
(5.14)
Удельная
поверхность является одной из мер силы взаимодействия твердого
тела с окружающей средой, будь то газ, жидкость или другое твердое
тело.
Такие
характеристики
материалов,
как
каталитическая
активность, электростатические свойства порошков, светорассеяние,
способность
к
агломерации,
свойства
обжига
и
глазурования,
способность удерживать влагу, срок хранения и множество других
свойств сильно связаны со значением удельной поверхности. Поэтому
определение
удельной
поверхности
является
одним
из
самых
распространенных методов исследования показателей дисперсности
наноматериалов Определение удельной поверхности является одним
из
самых
распространенных
методов
исследования
показателей
дисперсности наноматериалов [8-11].
Для
практической
широко используются
реализации
данной
твердым
азота.
телом
Суть метода состоит
при
наиболее
сорбционные волюметрические
объёма) анализаторы, основанные на методе
адсорбции
методики
постоянной
(измерение
низкотемпературной
в анализе сорбции
криогенной
газа
температуре
и
постепенном повышении давления. Образец исследуемого вещества
предварительно очищается путем нагрева в условиях вакуума либо
путем продувки в динамической газовой атмосфере. После очистки в
ячейку с образцом подается небольшое количество газа-адсорбата,
молекулы
которого
конденсируются
на
поверхности
образца,
постепенно образуя монослой. По количеству газа, ушедшего на
образование монослоя, зная поперечное сечение его молекул и массу
образца, можно судить о величине удельной поверхности
этого
материала.
Общий
вид
анализатора удельной
поверхности
по
методу
низкотемпературной адсорбции азота ASAP 2020, представлен на
рисунке:
Рисунок 6.7. - В н е ш н и й вид установки анализатора площади поверхности
и пористости ASAP 2020
Анализатор ASAP 2020 включает в себя две независимые
вакуумные системы: одна для подготовки образцов, а вторая — для их
анализа. Наличие двух отдельных систем, а также отдельных портов
для
подготовки
образцов
позволяет
параллельно
осуществлять
подготовку и анализ образцов, т. е. реализовать непрерывную работу
прибора. Между вакуумным насосом и коллектором в системах
анализа и дегазации встроены охлаждаемые ловушки. Рядом с портом
анализа
образцов
находится
пробирка
для измерения
давления
насыщения образца (Psat). На боковой панели анализатора удобно
расположены патрубки напуска газа и электрические разъемы.
Анализатор ASAP 2020 оснащен подъемным механизмом для
автоматического подъема и опускания сосуда Дьюара с рабочей
жидкостью
закрывается
для
анализа.
съемным
предусмотрены
изотермические
В
целях
щитком.
В
запатентованные
кожухи
для
безопасности
сосуд
Дьюара
анализаторе
ASAP
компанией
Micromeritics
пробирок
с
образцами.
2020
Эти
изотермические кожухи обеспечивают равномерное распределение
температуры по всей длине образца и пробирок для
измерения
давления.
СПИСОК ЛИТЕРАТУРЫ
14. Товбин Ю.К. Молекулярная теория адсорбции в пористых
телах. М.: Физматлит.2013. 624с.
15. Жданов В.П. Элементарные физико-химические процессы на
поверхности. Новосибирск: Наука, Сиб. Отделение. 1988. 320 с.
16. Де Бур Я. Динамический характер адсорбции, ИЛ, М., 1962.
291с.
17. Everett D.N. // Trans/ Faraday Soc/ 1954.V.50. P. 1077.
18. Комаров В.С. Адсорбенты и их свойства. Минск.: Наука и
техника. 1977. 248с
19. Фенелонов В. Б.. Введение в физическую химию формирования
супрамолекулярной структуры адсорбентов и катализаторов / 2-е изд.
испр. и доп. Новосибирск: Изд-во СО РАН, 2004. 442с.
20. Устинов Е.А. Адсорбция, адсорбенты и адсорбционные
процессы в нанопористых материалах.-М.: Издательская группа
«Граница», 2011. С.208.
21. Вячеславов А.С., М. Ефремова. Определение площади
поверхности и пористости материалов методом сорбции газов. 2011.
Москва. МГУ. http://www.nanometer.ru/.
22. Грег С., Синг К. Адсорбция, удельная поверхность, пористость.
М.: Мир. 1984. 306с.
23. Брунауэр С. Адсорбция газов и паров. М.: ИЛ, 1948. — С. 41.
24. Экспериментальные метода в адсорбции и молекулярной
хроматографии. — М.: Изд-во МГУ, 1973. 447 с.; 1990. - 316 с.
25. Kruger A., Kataoka F., Ozawa M . , Fujino T., Suzuki Y.,
Aleksenskii A.E., Vul A.Y., Osawa E. // Unusually Tight Aggregation in
Detonation Nanodiamond: Identification and Disintegration: Carbon 2005, 43,
с.1722.
26. Фенелонов В.Б. // Лекции, институт Катализа им. Г.К.
Борескова СО РАН: http: //www.catalysis. ru/
27. Understanding Adsorption in Micropores. A study of carbons, soils
and zeolites: http: //dare.uva.nl/document/37483.
28. Marczewski A.W.// A Practical Guide to Isotherms of Adsorption
on Heterogeneous Surfaces: http://adsorption.org/awm/ads/Ads.htm
6. М Е Т О Д Ы И З М Е Р Е Н И Я В Е Л И Ч И Н А Д С О Р Б Ц И И
И ТЕПЛОТ АДСОРБЦИИ
Измерение
динамическими
методов
величины
адсорбции
методами [1,4,5]. При
сорбент помещают
проводят
статическими и
использовании
в замкнутую
статических
систему
и
измеряют
либо убыль адсорбтива An из газовой (или жидкой ) фазы, либо
его прибыль Am на адсорбенте (рис. 4.1). Величина адсорбции
а = An = Am
В
динамических
включенной
в
методах
проточную
адсорбирующийся
адсорбтив.
на
(6.1)
адсорбент
систему.
адсорбенте
находится
Через
нее
в
проходит,
газ-носитель,
Измерение ведут, фиксируя
колонке,
не
содержащий
изменение
концентрации
адсорбтива в газе-носителе, происходящее в результате адсорбции
или десорбции (рис. 6.1 б ).
В настоящее время западными
(Карло
Эрба
в
фирмами
Италии,
Майкромеритикс Инструмент в США,
и
ряд других) разработаны автоматические
адсорбционные установки, действующие
в
Рис. 6.1. Принципиальная
схема
измерения
адсорбции: статический (а) и
динамический (б) методы.
1 - колонка с адсорбентом;
2 - приборы для измерения
текущей концентрации
на
входе и выходе.
установках,
программированном
вычислением
величин
режиме
с
адсорбции
и
параметров текстуры адсорбентов.
Статические
адсорбции
осуществляется
изготовленных
из
в
методы.
этих
обычно
стекла, тефлона
Измерение
методах
в вакуумных
или
металла.
Адсорбент
при
предварительно
нагреве
для
адсорбированных
откачивается (вакуумная
удаления
с
тренировка)
поверхности загрязнений
на воздухе веществ. Различают
или
объемные
и
весовые методы.
Объемный
метод.
(волюмометрический)
Принципиальная
схема
объемной установки, изготавливаемой
обычно из стекла, показана на рис.
6.2. Адсорбент, помещают в ампулу
1,
отделенную
системы
от
измерительной
4.
Измерительная
краном
система включает в себя прибор для
измерения давления 3 и прибор для
точного
Рис. 6.2. Принципиальная схема
измерения адсорбции объемным
методом:
г
адсорбентом;
„ ампула
J
2
-
газовая
о
б
ъ
е
м
а
краны
измерения
г
а
з
а
-
б
ю
р
и
е
т
к
дозирования
а
2 .
Ч
е
р
е
з
6 и / система соединяется с
^
U
вакуумным
насосом
либо
через
манометр; 4-8 - краны; 9 - к
вакуумному насосу;
10 к краны 6 и 8 с колбой, наполненной
колбе с запасом газа.
б
ю
р
е
т
к
а
;
3
-
р
т
у
т
н
ы
й
-
газом-адсорбтивом. После тренировки
образца,
которая
обычно
проводится
при
повышенных
температурах, вакуумный насос отключают от системы краном
/
и
в
из
колбы,
открывают кран
8,
набирают
газ-адсорбтив
измерительную систему. Количество газа дозируют в зависимости
от массы загруженного адсорбента, развитости его поверхности и
желаемого
положения
экспериментальной точки
на
изотерме
адсорбции, варьируют его объемом изменяя давление в манометре.
При
измерении
физической
адсорбции
обычно
0
температура 300 С , при измерении хемосорбции
0
450—500 С . Термостат
открывают кран
4.
или
После
в
сосуд
достаточна
ее повышают до
Дьюара
с
того, ка к установится
охладителем,
равновесие
в
бюретке измеряют равновесное давление.
Количество
молей
адсорбтива
n в
измерительной
системе
определяется алгебраической суммой количеств молей до n и после
n установления
равновесия и
2
заполняющего объем
п -количеством
молей адсорбтива,
3
ампулы
без
адсорбента («мертвый»
объем)
составит
п = п - п - п
1
Расчет nj, n ,
п
2
n=pV/RT,
3
(6.2)
3
ведут по уравнению Меделеева -
определяя
содержащей
2
Vi
«заготовку»
-
объем
газа, в
Клапейрона:
измерительной
том
числе
системы,
объем
всех
ее
коммуникаций, найденный специальной калибровкой установки, V
2
- объем измерительной системы после установления
равновесия
при
объем.
Т и
1
Т
2
, соответственно, и
V
3
-
«мертвый»
V
3
определяют калибровкой ампулы с адсорбентом - инертным газом
(обычно гелием) до или после проведения опыта, набирая его в
измерительную
систему,
указанные
операции
и
изотермы.
Следующие
а
затем
впуская
вычисления,
точки
в ампулу.
получают
находят,
Проведя
первую точку
добавляя
газ
в
измерительную систему (при закрытом кране 4) и учитывая при
вычислениях уже имеющееся на адсорбенте и в мертвом объеме
количество адсорбтива. Как видим, процесс измерений трудоемкий и
длительный.
Рис.б.З.Современный волюмометрический автоматизированный прибор.
В современном автоматизированном оборудовании
(рис.6.3),
если адсорбтивом служит азот, то снятие изотермы составляет около
14 часов, если углекислый газ, то - около 6 часов, т.е. длительность
выхода системы на равновесие зависит и от температуры и от
природы адсорбтива.
Весовой
объемным
(гравиметрический)
метод.
относительно прост. В
Метод по сравнению с
этом
методе
взвешивают
адсорбент до и после установления адсорбционного
равновесия.
Прибыль массы количественно выражает адсорбцию. Существуют
два
вида
Последние
весовых
весьма
установок
сложны
в
—
пружинные
изготовлении,
точных механических работ и монтажа внешней
и
рычажные.
так как
требуют
электромагнитной
системы для уравновешивания изменения массы адсорбента, которое
должно
оболочку,
быть
осуществлено
где находятся
весы.
через
стеклянную
Изготовление
вакуумную
пружинных весов
значительно проще. В них заложен известный принцип
работы
динамометра. На рис. 6.4 изображена схема пружинных весов МакБэна — Бакра.
В
стеклянной трубке
спиральной
1
пружине
на
2,
изготавливаемой из кварцевой нити,
подвешена
чашечка
3
адсорбентом.
Спираль
предварительно
Рис. 6.4. Принципиальная схема
измерения адсорбции весовым
методом Мак-Бэна - Бакра. 1 стеклянная гильза; 2 - кварцевая
спираль;
3 - чашечка
с
сорбентом; 4 - ампула с жидким
адсорбтивом
(или
колба
с
запасом газа); 5 - ртутный U манометр; 6-8 - краны.
адсорбента
открытием
калибруется
загрузкой в чашечку
разновесов
аналитических
и
происходящего
измерением
при этом
удлинения
спирали. Обычно кварцевые спирали
хорошо
т.е.
увеличению
пропорционально
с
крана
подчиняются
их
растяжение
массы.
6
закону
в
После
Гука,
строго
тренировки
трубку впускают
пары
адсорбтива и по изменению давления в манометре 5 наблюдают
за установлением
равновесия.
При
необходимости
может быть добавлен из ампулы 4 с жидким
колбы
с
определяется
катетометра
запасом
газа.
по удлинению
(оптический
длины на расстоянии).
Масса
Как
ясно
измеряемому
точно
из
измеряющий
принципа
газ
адсорбтивом или
поглощенного
спирали,
прибор
пар или
адсорбтива
с
помощью
изменение
работы
этого
прибора, не требуется вводить ни каких поправок на количество
пара в его объеме. Для увеличения производительности установки
обычно
монтируют 4-8 трубок
со спиралями
и, следовательно,
ведут одновременное измерение адсорбции на 4-8 образцах.
Рис. 6.5. Современный гравиметрический прибор.
Важным преимуществом весового метода является прямое измерение
величин
адсорбции
(привеса)
в
каждой
точке
изотермы,
вне
зависимости от численных величин, полученных при предыдущих
измерениях.
В
объемном
методе
измеряются приращения адсорбции
и
на
каждом
шаге
проводится суммирование
приращений на всех предыдущих шагах. Это приводит к накоплению
погрешности измерения.
Современные
чувствительность
величиной
микровесы
(порядка
навески
(обычно
-7
1 0 г),
(рис.6.5)
но
- доли
имеют
ограничены
грамма),
высокую
допустимой
что приводит
к
появлению погрешностей, связанных с неоднородностью адсорбента
или случайным выбором непредставительной его пробы. В свою
очередь,
объемный
метод
позволяет
использовать
достаточно
большие навески образца, что уменьшает вероятность погрешностей
этого типа, а также позволяет проводить измерения очень малых
удельных величин адсорбции, которые недоступны для обычных
микровесов. Наконец, образец в весовом методе подвешен в чашке и
отделен
от
термостата
пространством,
вакуумированным
или
заполненным парами адсорбтива, что осложняет термостатирование
собственно образца. Эта проблема в объемном методе решается за
счет контакта образца с стенкой ампулы, а при необходимости введением дополнительных теплопроводящих элементов.
Не смотря на простоту измерений адсорбции весовым методом,
в
современном
предпочтение
автоматизированном
объемному
методу,
оборудовании
как
более
отдают
простому
для
его
реализации в чисто техническом и экономическом плане.
Динамические
методы
изучения
адсорбции.
Динамика
адсорбции рассматривает пространственно-временное распределение
компонентов между фазами системы возникающих при перемещении
фаз друг относительно друга. Процессы адсорбции экзотермичны,
десорбции
-эндотермичны.
динамики
адсорбции
температуры
в
Поэтому
необходимо
контактирующих
при
анализе
учитывать
фазах,
ряда
задач
распределение
например,
по
фронту
адсорбции, допустим, лабораторного или промышленного адсорбера.
Если динамику адсорбции рассматривать с позиции динамического
метода для получения величин адсорбции, то в этом плане идеальным
решением является метод газовой
хроматографии:
импульсный и термической десорбции.
фронтальный,
Наиболее
распростанеными
термодесорбции
и
импульсный.
измерительным
прибором
являются
В
обоих
служит детектор,
—
методы
методах основным
регистрирующий
концентрацию адсорбтива в газе-носителе. В детекторах разного
вида
используется
свойства,
состава
часто,
смеси.
зависимость
ка кого-либо
теплопроводности,
ионизации
Простейший - детектор
по
физического
газа
и
т.д.
от
теплопроводности,
называемые катарометром, выступающий в мостовой электрической
цепи в роли термосопротивления.
Метод
термической
десорбции
[4,5]. Через
колонку
с
адсорбентом пропускают с постоянной скоростью поток смеси газаносителя (чаще всего гелия) с адсорбтивом, обычно
газом, например
низкокипящим
азотом, аргоном, кислородом. Если
температура
колонки достаточно высока, чтобы адсорбтив не адсорбировался
колонке,
мониторе
состав смеси до и после колонки будет одинаков,
будет
выписываться
в
на
нулевая линия. Если поместить
колонку в сосуд Дьюара с жидким азотом), состав смеси на выходе
изменится
за
отклонение от
достигнуто
счет
адсорбции
нулевой
равновесие,
газа
на
линии. Через
т.е.
соответствовать парциальному
величина
адсорбенте
и получим
некоторое время
будет
адсорбции
будет
давлению адсорбтива в смеси,
и
поглощение его прекратится, на диаграмме выпишется пик. Состав
смеси на входе и выходе вновь станет одинаковым и на диаграмме снова нулевой линия (рис. 6.6).
Простое
убирание
вызовет
десорбцию
сосуда
адсорбтива,
дополнительное его
смесь
(и
обогащение).
Дьюара
т.е.
поступление
в
соответствующее
ее
Выписанный пик будет
Рис. 6.6. Адсорбционный (а)
и десорбционный (б) пики.
обращен в другую
сторону. Вторая из
Штриховая — нулевая линия.
описанных
операций
название
методу
Нельсоном
и Эггертсеном.
находят
из
термической
здесь
десорбции,
Величину
площади
дала
предложенному
адсорбции
соответствующего
и
или десорбции
пика,
используя
калибровочные данные. При калибровке в поток газа-носителя за
колонкой
шприцем
вводят
через
специального
полученного
известную
порцию
иглу, вкалываемую
крана-дозатора)
и
пика. Каждому
адсорбтива
(например,
в мембрану, или поворотом
сопоставляют
парциальному
ее
с площадью
давлению
адсорбтива с газом носителем соответствует одна точка
Для
получения
следующих
вводя
дополнительные
смеси,
точек, требуется
количества
в
смеси
изотермы.
изменять
состав
адсорбтива. Обычно
такие смеси готовят заранее в специальных баллонах.
Импульсный
вводится
доза
метод. В этом
(импульс)
методе
в поток
адсорбтива [4]. В колонке
газа-носителя
происходит
вначале полное его поглощение и на выходе он не детектируется.
Затем,
колонку
если
адсорбция
газ-носитель
концентрация
обратима, непрерывно
вымывает
его в носителе
мере расходования,
падает.
идущий
адсорбированное
вначале
Получается
возрастает,
пик
через
вещество,
а затем,
по
на хроматограмме,
площадь которого пропорциональна всему количеству адсорбтива в
импульсе,
если
произошла
полная десорбция.
Поэтому
в
этом
методе площадь пика не дает точку изотермы, как в предыдущем
методе.
Из
теории
неидеальной
форма пика (его нисходящая
равновесной
часть для
хроматографии
выпуклой
[4],
изотермы
и
восходящая часть для вогнутой) связана определенным образом с
формой
изотермы
адсорбции.
Поэтому,
математически
обрабатывая полученные хроматограммы с помощью
разработанных
для
этого
методов,
удается
по
специально
одному
пику
рассчитать всю изотерму адсорбции. Если условия опыта исключали
диффузионное и кинетическое размывание фронта адсорбтива
в
колонке,
в
то
полученные
удовлетворительном
методами.
согласии
Импульсный
аналитических
изотермы
с
метод
целей. Если
находятся
измеряемыми
широко
вводимая
доза
статическими
применяется
представляет
для
собой
смесь различных веществ, то их вымывание после адсорбции в
колонке
происходит
адсорбируемоемости.
в
порядке
Первым выходит
возрастания
наименее
их
удерживаемый
компонент и выписывается соответствующий пик, затем следующий
по прочности его связи с адсорбентом и так далее. В результате
вся
смесь
положение
природой
оказывается
представленной
которых на хроматограмме
компонентов,
а
пропорционально площади пиков.
их
совокупностью
пиков,
определяется
химической
количество
в
смеси
Методы
могут
измерения
быть
определены
вычислением
называемые
теплот
из
адсорбции.
в
основном
Теплоты адсорбции
двумя
способами:
температурной зависимости адсорбции
изостеричесике
теплоты)
и прямым
(так
измерением
в
калориметрах (калориметрические теплоты) [1,4].
Изостерические
зависимость
теплоты. Изостерой
равновесного
давления
адсорбции
газа
называется
или
пара
от
температуры, при которой количество адсорбированного вещества
сохраняется
постоянным.
зависимость давления
Из
термодинамики
от температуры
известно,
при равновесных
что
фазовых
переходах выражается уравнением Клаузиуса — Клапейрона
d/nP
АЯ
dT
РГ
(6.3)
2
Расчеты изостерических теплот адсорбции см. раздел 3.
Калориметрические
теплоты.
Экспериментальное
измерение
теплот адсорбции может быть осуществлено в калориметрах разного
типа. Экспериментальное определение теплоты адсорбции
может
быть осуществлено в калориметрах различного типа: изотермических,
адиабатических,
компенсационных,
калориметрах
с
постоянным
обменом. Каждый из этих калориметров имеет свои особенности, но
позволяет
количество
по изменению
теплоты
АН,
температуры
системы
выделившейся
или
АТ
определить
поглощенной
результате протекания в калориметре определенного
в
физического
или химического процесса: АН=с'АТ, где с' - постоянная калориметра
Теплота Q = АТС,
где АТ — подъем температуры в адсорбционном опыте,
(6 .4)
С — теплоемкость всей калориметрической системы.
Адиабатические
средой
сведен
калориметры.
к
минимуму,
В них теплообмен с внешней
что
достигается
хорошей
теплоизоляцией. [4].
При измерении теплоты адсорбции необходимо помнить, что
измеренные теплоты адсорбции не должны включать в себя теплоты
побочных процессов. Теплоты адсорбции могут быть связаны с
процессами диффузии на поверхности твердого тела, в том числе, с
диффузией
примесей,
адсорбированных
веществ
и
продуктов
взаимодействия примесей с адсорбированными веществами.
СПИСОК ЛИТЕРАТУРЫ
1. S.Brunauer, L.S.Deming, W.S.Deming, and E.Teller, J.Amer.Chem.
Soc. 1940.62 С.1723.
2. R. Defay, I.Prigogine, Tension Superficielle at Adsorption, Desoer,
Liege, 1951, R. Defay, I.Prigogine and A.Bellamans. Surface Tension and
Adsorption., Longmans.London. 1966.
3. Брунауер С. Адсорбция газов и паров. М.: ИЛ, 1948. С. 41.
4. Экспериментальные метода в адсорбции и молекулярной
хроматографии. Под ред. А.В. Киселева и В.П. Древинга. М.: Изд-во МГУ,
1973. - 447 с.; то же, под ред Ю.С. Никитина и Р.С. Петровой. М.: Издво МГУ, 1990, 316 с.
5. Карнаухов А.П. Адсорбция. Текстура дисперсных и пористых
материалов. - Новосибирск: Наука. Сиб. предприятие РАН. 1999. 470c.
6. Richard Wigmans. Calorimetry. Scientifica Acta 2. 2008. No. 1. Р.
18-55.
7. О Б Щ А Я Х А Р А К Т Е Р И С Т И К А Н Е К О Т О Р Ы Х П О Р И С Т Ы Х
АДСОРБЕНТОВ
Активные угли. Основная доля промышленных адсорбентов
приходится на активные угли [1]. Активные угли — высокопористые
адсорбенты на основе углерода. Их удельная поверхность может
достигать 2000 м /г. Сырьем для их получения служат: дерево всех
пород (чаще береза) и продукты древесной переработки (опилки,
отходы целлюлозно - бумажного производства - лигнины), твердое
топливо различной степени метаморфизма (торф, бурый и каменный
угль,
кокс, антрацит),
сапропели,
отходы
кожевенной
промыш¬
ленности, кости животных. Активные угли с высокой механической
прочностью, получают из скорлупы кокосовых и других орехов, а
также из косточек различных плодовых растений. Развивающиеся
страны для получения активных углей используют преимущественно
местное сырье. Например, в
Индии угли получают из стеблей,
скорлупы, коры и других частей тропических растений.
В наиболее развитых в промышленном отношении
странах
активные угли выпускают в большом количестве и в широком
ассортименте. Общий годовой объем потребления активных углей в
мире — до 1,5 млн т., в России — менее 20 тыс. т в год. Потребность
этого вида продукции в стране растет высокими темпами за счет
увеличения закупок импортного активированного угля. К сожалению,
производство
активированного
угля
в
России
незначительно и в настоящее время составляет
увеличивается
около 5 тыс. т/г при
потреблении — около 15 тыс. т. Общий годовой объем мирового
производства активных углей по другим странам следующий: С Ш А
— 34 %, страны Европы — 24 %, Азия — 9 %, Китай — 14 %, Япония
— 18 %. В С Ш А главными производителем углеродных сорбентов
является компания Calgon Carbon Corporation (37 % от общего
производства). Крупнейшим производителем активированного угля в
России является О А О «Сорбент» (г. Пермь). На этом предприятии
выпускается 8 1 % общероссийской выработки.
Около
23
%
всего
количества
углеродных
сорбентов
используется для получения питьевой воды, 21 % — для очистки
сточных вод; 13 % — в пищевой промышленности, 10 % — в
химической и фармацевтической, 13 % — для очистки воздуха, 10 %
— для потребительских нужд, 9 % — в других областях.
Активные
угли
как
сорбенты
имеют
ряд
особенностей,
определяемых природой их поверхности и пористой структуры [1-3].
Поверхность активного угля представлена кристаллитами графита
(рис 7.1) и аморфного угля и, как правило, электронейтральна, а
адсорбция
на углях
в основном
определяется
дисперсионными
силами взаимодействия.
Рис.7.1. Структура графитовых слоев: а) упорядоченная с т р у к т у р а в г р а ф и т е ,
б) с т р у к т у р а а л л о т р о п н о й ф о р м ы у г л е р о д а - г р а ф е н а .
Графен образованная
двумерная
слоем
аллотропная
атомов
углерода
модификация
толщиной
в
углерода,
один
атом,
2
находящихся в Бр -гибридизации и соединённых посредством о- и п связей в гексагональную двумерную кристаллическую решётку. Его
можно представить как одну плоскость графита, отделённую от
объёмного кристалла.
Структура угля представлена широким спектром
пор всех
размеров, причем адсорбционная емкость и скорость адсорбции газов
преимущественно определяются содержанием микропор в единице
массы
или
объема
гранул.
В
процессе
адсорбции
микропоры
заполняются адсорбатом объемно и в согласно ТОЗМ количество
адсорбированного вещества в микропорах определяется
константой
предельного адсорбционного объема W .
0
В активных углях распределены
щелевидные
микропоры
межкристаллитные
имеют
микропоры,
цилиндрическую
угля — полуширина
в
форму
щели,
две разновидности
кристаллитах
которые
энергией (Е ), входящей в уравнение Дубинина
0
Для углей характерно
с
—
классификация
и
приближении
размер
микропор
характеристической
Астахова.
наличие всех разновидностей
, мезо-, супер- и ультрапоры,
разделах
углерода
в первом
[2]. Характерный
в нм — связана
микропор:
которых
пор: макро¬
приведена
в
2,3.
Отрицательной особенностью активного угля как промышлен¬
ного адсорбента является его окисляемость и горючесть. На воздухе
окисление углей начинается при температуре выше 250 °С.
Практически все промышленные активные угли в том или ином
количестве
содержат зольные
(минеральные
примеси)
нежелательных
реакций,
примеси. Зола и ее
являются
которые
ингредиенты
катализаторами
могут
протекать
многих
в
адсорбере.
Например, если вести очистку спиртово-водных растворов активным
углем с зольными примесями при повышенных температурах, то
некоторая часть этилового
спирта
превращается в ацетальдегид и
диоксид углерода, что, естественно, не желательно для готовой
продукции.
Многообразие типов активных углей требует их классификации.
Классифицируют
угли:
гранулированные,
по
дробленые,
форме
гранул
сферические,
(зерненые
порошковые);
по типу
углеродсодержащего сырья (торфяные, каменноугольные,
косточковые,
полимерные, углеродсодержащие
опилки
др.);
и
брикитированные,
по
способу
отходы
формования
жидкоформованные);
по
-
древесные,
-
лигнины,
(экструзионные,
способу
активации
(парогазовая активация водяным паром или смесью водяного пара и
диоксида углерода, газовая-СО ,
2
предварительная
перед
С1 , N H , SO и др., химическая
2
3
-
2
прокаливанием
пропитка
углеродсодержащего сырья: ^ P O ^ K C O , K O H , ZnCl , M g C l , N H C l
2
3
2
2
4
и др.); по областям применения (газовые при адсорбции примесей
газов с низкой концентрацией, рекуперационные
пары
с концентрацией
растворов,
пористой
масел,
осветляющие
полупродуктов
структуры
макропористые,
«5г/л,
(мико-,
от
адсорбируемые
для очистки
примесей);
супермикро-,
смешанного типа)
-
по
характеру
субмикро-,
[3]. В настоящее
воды,
мезо-,
время при
классификации активных углей больше склоняются к их применению
в конкретных адсорбционных технологиях: очистка питьевой воды,
очистка природного газа, очистка почв, химические поглотители,
противогазовая
техника,
включая
средства
индивидуальной
и
коллективной защиты населения, и как более общее применение защита окружающей среды.
Для
любых
марок
активных
углей,
кроме
порошковых,
предъявляют жесткие требования по прочности: механической (по
истиранию,
раздавливанию
и удару,
стойкости
к
деформации,
вибрации), термическому воздействию и т.д.
Наиболее
широко
применяемые
марки
углей:
древесные
активные угли типа Б А У и ОУ, торфяные активные угли типа СКТ,
активные угли на полимерной
(сополимер фурфурола) основе типа
ФАС и ПАУ, активные каменноугольные угли типа АГ, косточковые
типа С 0 8 и многие другие. В последние годы повышенный интерес
проявился к углеродным нанопористым материалам не только как
адсорбентам с высокой удельной поверхностью, но как материалам
со строго упорядоченной структурой, что позволяет использовать их
в
качестве
модельных
систем
[2,6]
для
обоснования
как
классической, так и современных
теорий адсорбции, в частности,
локальной и нелокальной теории
функционала плотности Л Т Ф П и
Н Л Т Ф П [6].
Рис.7.2
Фуллерены-аллотропная
форма
молекулярного
углерода
наноразмерной структурой, преимущественно
в виде шести - С
пятигранников - С .
5 4 0
с
и
60
Фуллереновые
материалы
материалов
уникального
структурой
(типа
-
новый
строения
футбольного
с
тип
шестью
мяча),
углеродистых
и
пятигранной
служащие
в
форме
фуллереновых саж компонентом в композиционных сорбирующих
материалах [7].
В последние годы вызывают повышенный интерес порошковые
активные
угли
2
поверхностью,
получения
наноразмерного
выше 2000м /г.
типа
с
высокой
Такие угли служат
суперконденсаторов,
на
созданная
основой
использование
настоящее время наблюдается повышенный спрос.
удельной
которых
для
в
Научная школа,
профессором Н.И. Богдановичем, наладила синтез таких
уникальных видов активных углей на основе
лигноцеллюлозных
материалов [4].
Силикагели.
промышленной
Одним
практике
из
наиболее
минеральных
распространенных
адсорбентов
силикагель, обладающий достаточно развитой
внешнему
прозрачные
виду
или
силикагель
матовые,
представляет
бесцветные
является
пористостью [5]. По
собой
или
в
твердые
зерна:
светло-коричневые.
Выпускается силикагель в виде шариков, таблеток или кусочков
неправильной формы с зернами размером в пределах 0,1—7,0 мм. В
зависимости от аппаратурного оформления рекомендуют следующий
гранулометрический
процессов
с
жидкофазных
адсорбента;
состав
кипящим
силикагеля:
слоем
процессов
и
0,1—0,25
адсорбента;
процессов
с
мм
—
-0,5—2,0
мм—для
движущимся
2,0—7,0 мм — для процессов
для
в газовой
слоем
фазе со
стационарным слоем адсорбента.
Основой силикагелей служит диоксида кремния, который, как
известно,
существует
в
кристаллической
(кварц,
тридимит,
кристобалит) и аморфной формах. Силикагель по своей химической
природе
является
Si0 nH 0.
2
2
Его
гидратированным
превращения
аморфным
протекают
по
кремнеземом
механизму
по¬
ликонденсации [73]
wSi(OH)4
Si 02„n
m
с образованием
+ (2n — m) H2O
коллоидных
частиц
по форме,
близкой
к
сферической и размером « 2-^20 нм.
При высушивании гидрогеля кремневой кислоты глобулярная
структура кремне-кислородного каркаса, образованная из связанных
между собой сферических частиц, сохраняется. Поры этого каркаса зазоры
между
частицами.
Основные
характеристики
пористой
структуры определяются размером частиц и плотностью их упаковки.
На
рис.
7.3
представлены
модели
глобулярных
систем,
составленных мелкими и крупными частицами с разной плотностью
упаковки (координационным числом) [9].
Рис. 7.3. а - м е л к о п о р и с т о й с и л и к а г е л ь с к о о р д и н а ц и о н н ы м ч и с л о м - 6;
б - крупнопористой с координационным числом - 3
Химические
и
адсорбционные
чительной мере определяются
свойства
силикагеля
в
зна­
наличием группы =Si—ОН.
ОН-
группы занимают в основном вершины тетраэдров, выходящие на
поверхность скелета силикагеля. Изменяют адсорбционные свойств
силикагелей путем химического модифицирования его поверхности введения в состав силикагеля амино-, сульфо- и нитрильных групп,
атомов
фтора,
алкильных
Модифицирование
и
алкенильных
радикалов.
позволяет получить силикагели с качественно
новыми свойствами.
Силикагель - один из самых первых минеральных синтетиче¬
ских адсорбентов, нашедших широкое применение в промышленной
практике. Несмотря на то, что в последние годы бурно развиваются
адсорбционные
процессы
с
использованием
уникальных
кристаллических сорбентов - цеолитов, силикагель не потерял своего
промышленного
крупнотоннажном
значения.
Низкая
промышленном
себестоимость
производстве,
высокая
при
меха-
ническая прочность по отношению к истиранию и раздавливанию
обеспечили силикагелям долгую «жизнь».
Активный оксид алюминия. Иным типом
неорганических
адсорбентов, широко применяемых в технике для осушки различных
сред и для других целей, являются активный оксид алюминия и
алюмогели [5,8]. Рост потребности в активном оксиде алюминия
обусловлен развитием процессов нефтепереработки
(риформинг,
гидроочистка, гидрокрекинг (в которых используются катализаторы,
содержащие
80
-
99%
оксида
алюминия),
а
также
широким
применением его в процессах адсорбции. Благодаря таким свойствам
оксида алюминия как термическая стабильность, относительная лег¬
кость получения, а также доступность
сырья обеспечили
ему
широкое применение наряду с силикагелями и цеолиты.
Оксид
алюминия
алюминия
с
получают
образованием
прокаливанием
различных
форм
гидрооксидов
оксида
алюминия:
Структура оксида алюминия зависит от типа исходного гидрооксида,
остаточного содержания воды, присутствия оксидов щелочных и
щелочноземельных
обработки.
металлов,
Различают
низкотемпературные
(получают
при
высокотемпературные
а также
следующие
оксиды
от условий
типы
(А1 O •nН O),
температурах
2
3
2
не
оксидов
в
термической
алюминия:
которых
выше
600
0<n<0,6
°С);
оксиды (почти безводные), получаемые при
900—1000 °С; при температурах 1000 °С и выше получают инертный
а-оксид алюминия (корунд).
На практике оксид алюминия используется как эффективный
осушитель от паров воды (олефинсодержащие потоки при крекинге
углеводородов)
при
этом
сохраняется
высокая
водостойкость
адсорбента. А так же для адсорбционной очистки масел (прежде всего
трансформаторных), как эффективный осушитель при консервации
приборов и оборудования, в виде «дыхательных клапанов» цистерн,
трансформаторов
и
для
адсорбционной
очистки
газовых
и
жидкостных потоков от соединений, содержащих фтор-ионы.
Цеолиты. Цеолиты — алюмосиликаты, содержащие в своем
составе
оксиды
отличаются
щелочных
и
щелочноземельных
строго регулярной структурой пор
обычных температурных условиях заполнены
размеры которых - 0,2 нм.
нагреве
выделяется
-
металлов,
—
[5], которые
в
молекулами
воды,
Эта вода, названная «цеолитной» при
цеолиты
«кипят»,
отсюда
и
произошло
сочетание двух греческих корней «цео» и «лит», т. е. «кипящие
камни».
Общая химическая формула цеолитов
Ме
2 / п
А1 0 ;йЮ уН О
2
3
2
2
(где Me — катион щелочного металла, а п — его валентность).
Кристаллическая структура природных и искусственных
образована тетраэдрическими группами
объединёнными
общими
пронизанный
полостями
вершинами
и
SiO
в
2/4
и
трёхмерный
каналами
(окнами)
цеолитов
AlO ,
2/4
каркас,
размером
2-15 ангстрем.
Различают:
волокнистые
цеолиты
-
натролит,
мезолит,
томсонит, сколецитломонтит, гоннардит, эдингтонит, морденит,
нит,
листоватые
жисмондин (абразит), феррьерит и
(или
эрио
другие;
пластинчатые)
цеолиты
-
стильбит,
изометрические
гейландит,
брюстерит
и
другие;
цеолиты - шабазит, филлипсит, гармотом, фоязи,
гмелинит, дакиардит и другие.
Кристаллы цеолитов пронизаны системой каналов или полостей,
обладают
хорошо
развитой
внутренней
поверхностью.
строение цеолитов позволяет цеолитам избирательно
Такое
сорбировать
молекулы, компоненты сточных и питьевых вод, т.е. играть роль
«молекулярных сит». В дегидратированном состоянии эти минералы
сорбируют аммоний, спирт, нитраты и другие вещества. Размеры
каналов достаточны для проникновения в них органических молекул
и катионов, а суммарный объем их вместе с порами достигает 50%.
Свойства цеолитов — распространенность, доступность, дешевизна,
возможность неоднократного применения.
Ионообменная
емкость
цеолитов
—
одно
из
основных
параметров, характеризующих их сорбционные и технологические
свойства.
Максимальная
ионообменная
емкость
соответствует
полному замещению одного иона другим во всех кристаллических
позициях, что соответствует максимальной сорбционной способности
цеолита.
Если из цеолита удалить воду, поры могут быть заполнены
снова водой
или другим
веществом,
что и предопределяет
их
использование в процессах осушки, очистки и разделения веществ.
Поглощение вещества происходит в основном, в адсорбционных
полостях цеолитов. Однако не все вещества могут проникать в эти
адсорбционные полости и поглощаться в них. Это объясняется тем,
что адсорбционные полости соединяются друг с другом входами —
окнами и строго определенного размера. Проникнуть через окно
могут только те молекулы, критический диаметр которых меньше
диаметра входного окна.
Как минеральный вид цеолиты известны уже более 200 лет.
Длительное время они рассматривались в качестве редких минералов,
не
образующих
промышленных
скоплений
и
не
имеющие
практического применения.
Цеолиты
являются
ценнейшими
в
промышленности
минералами, обладающие открытой каркасно-полостной структурой
типа
[(Si,Al)O ],
имеющей
4
компенсируется
отрицательный
нейтрализующими,
заряд.
положительно
Последний
заряженными
катионами (Na, K, M g , Ca, Sr, Ba, Са), содержащихся в цеолите.
Природный цеолит является достаточно эффективным более дешевым
заменителем искусственного и некоторых естественных минеральных
соединений типа мела, каолина, диатомита.
В
многотоннажных
технологических процессах, где применение синтетических цеолитов
не выгодно, большое значение приобретает
использование
этих
природных материалов в связи с охраной окружающей среды и их
дешевизны.
В природе цеолиты распространены достаточно широко. Они
образовались в результате изменения вулканических туфов в морских
и
континентальных
туфогенно-осадочный
бассейнах
и
таким
образом
представляют
тип месторождений. Катионы, входящие
в
состав цеолитов, под воздействием среды могут замещаться на ионы
других металлов. Варьирование условий гидротермального синтеза и
протекание
реакций
катионного
обмела
в
природных
условиях
предопределило большое разнообразие типов природных цеолитов.
Рис 7.4. Минералы (слева направо) фожазит - (Na ,Ca)Al Si O -8H O, морденит
- (Na2,Ca,K2MAl8Si40)O96 * 28H2O, шобазит - C a K N a ^ S r X A b S L A ^ I ^ O
2
2
4
12
2
Широкое распространение получили синтетические
X,Y,A
цеолиты
и др. (структурные аналоги природных минералов), которые
активно
внедряются
в
процессы
химической
технологии
(гидрокрекинг - каталитический крекинг, протекающий в присутствии
водорода и при повышенном давлении, удаление примесей серо- и
азотсодержащих примесей из нефтяных фракций, нефтехимический
синтез и др.). На их основе создаются катализаторы нейтрализации
вредных
соединений
в
отходящих
газах
производств
и
автомобильных двигателей, способность цеолитов к ионному обмену
используется, например, в синтетических моющих средств, в составе
которых содержится около 30% цеолита.
Рис 7.5. Структура синтетических цеолитов типов А (а) и Х (б)
Синтез цеолитов впервые провел
проф. Баррер. В 1948 г. он
шабазита,
анальцима,
английский физико- химик
синтезировал цеолиты типа морденита,
филлипсита,
фожазита,
стронциевых
бариевых цеолитов. Работами Баррера и его сотрудников
и
были
намечены пути синтеза в условиях пониженных температур (100°С)
при нормальном давлении [92],
Самую простую структуру имеет каркасный силикат - содалит.
В земной коре обнаружено
хлорсодалит
лазурит
пять модификаций
(6Ка81Л1О -КаС1),гидросодалит
4
(4NaSiЛ10 •2Na2S), гаюин
4
этого
вещества:
(6NaSiA10 -2NaOH),
4
(6NaSiЛ1О •2CaS0 )
4
4
и
нозеан
(6NaSiA10 -Na S0 ) [82]. Содалит является строительным блоком для
4
2
4
разнообразных форм природных и синтетических цеолитов. Плотная
упаковка кубооктаэдров (содалитовых единиц) в структуре этого
минерала приводит к образованию полостей, которые по форме
являются также кубооктаэдрами.
Разные
цеолиты
отличаются
разными
структурами
и
свойствами. Вот несколько структур, обычно использующихся в
области катализа.
Цеолит Y (FAU) является трехмерным цеолитом с крупными
порами, структура которого имеет большие полости, объединенные в
систему каналами, образованными из циклов с 12 элементами (в
цикле имеется 12 катионов (Si
-
и A l ) и 12 анионов O ) .
Цеолит бета (BEA) представляет собой трехмерный цеолит с
крупными порами, содержащий поры, образованные из циклов с 12
элементами во всех направлениях.
Широко применяемый на практике цеолит
ZMS-5 (MFI) -пентасил (рис.7.6)
представляет
собой квазитрехмерный цеолит с Рис 7.6. Цеолит
ZMS-5. порами средних размеров, содержащий
поры, образованные из циклов с 10 элементами в
Р и с
Z
M
7 . 6 .
S
-
5
Ц
е
о
л
и
т
одном
направлении,
которые
соединены
зигзагообразными каналами, образованными из
.
циклов
с
10 элементами
(вот почему
такая
структура считается квазитрехмерной).
Морденит
(MOR) является
цеолитом
с крупными
порами,
образованными из циклов с 12 элементами, с каналами, идущими в
единственном
маленькие
направлении,
карманы,
и имеющий
образованные
между этими
из циклов
с
8
каналами
элементами.
Морденит имеет тетраэдрическую структуру, в которой атом кремния
или алюминия окружен четырьмя атомами кислорода.
Тетраэдры
группируются в цепи. Внутри цепей расположены адсорбционные
полости.
Ферьерит
порами
(FER)
средних
представляет
размеров,
собой
двумерный
содержащий
цеолит
основные
с
каналы,
образованные из циклов с 10 элементами, которые связаны через
боковые каналы, образованные из циклов с 8 элементами.
Цеолиты являются важными каталитическими материалами и
широко применяются в кислотных каталитических реакциях, таких
как крекинг, в частности гидрокрекинг, FCC (каталитический крекинг
в
псевдоожиженном
изомеризации,
технологиях
слое)
и
в частности
превращения
крекинг
парафинов
метанола,
олефинов,
в
реакциях
и олефинов,
а также
в
(соответственно
метанол
в
олефины, пропилен и бензин).
В последнее время темплантным методом
(Бек, 1992 г.) стали
получать мезопористые мезоструктурированные материалы (МММ)
[6,
9].
Эти
материалы,
подобно
цеолитам,
можно
называть
молекулярными ситами, так как они способны разделять молекулы по
размерам. Размер пор в цеолитах изменяется в диапазоне 0.3-1.2 нм,
М М М расширяют диапазон молекулярных сит до 10 нм и более.
Кроме того, например, МСМ-41 превосходит все известные типы
цеолитов по величине удельной поверхности и объему пор, по
крайней мере, в два раза, что важно при их использовании в катализе
и адсорбции. Материал типа МСМ-41 является наиболее ярким и
хорошо
изученным
представителем
семейства
мезопористых
материалов на основе диоксида кремния. Структура материала М С М 41 представляет собой каркас в форме пчелиных сот,
диаметр
которых
составляет
около
3,5
нм.
Стенки
пор МСМ-41
на
молекулярном уровне аморфны и имеют толщину порядка 0,8 нм.
Удельная поверхность материала варьируется в пределе от 1000-1200
м 2 /г, объем пор достигает 1 см3 /г. Сформировать такую структуру
оказалось возможным с помощью темплатного метода, используя
мицеллы
различных
поверхностно-активных
веществ
(ПАВ) в
качестве шаблона, например СТАВг цетилтриметиламмония бромид.
ПАВ, обычно используемые для получения М С М - 4 1 , описываются
формулой C H + i N ( C H ) B r c n = 12-П8. В воде такие молекулы
n
диссоциируют
2n
3
с
3
образованием
гидрофильной «головой» [N(CH3)3]
«хвостом»
^ ^ ^ ^ ^ 1 ] .
алкиламмониевого
+
образована
с
и гидрофобным нейтральным
Уже при очень малых концентрациях в воде
эти ионы П А В образуют цилиндрические мицеллы,
которых
катиона
положительно
заряженными
поверхность
головами. При
введении в такой мицеллярный раствор противоположно заряженных
неорганических комплексов, например, анионов [SiO(OH) ] - , эти
3
анионы
сорбируются
на
поверхности
мицеллы,
вытесняя
"собственные" противоионы П А В . Одновременно такие
мицеллы
самопроизвольно образуют регулярную гексагональную
упаковку.
Далее неорганические комплексы, сорбированные на поверхности
мицеллы и в межмицеллярном объеме, полимеризуются (обычно —
при нагревании), взаимодействуя друг с другом за счет реакции
дегидратации. В результате между мицеллами образуется каркас из
аморфной фазы SiO2. Органическая часть мицеллы после сушки
выжигается
прокалкой
на
воздухе
при
400-700
°С
(или
экстрагируется) и остается твердый М М М . На рисунке 7.7 показано
схематическое строение материала типа М С М - 4 1 .
Silica Source
Рис. 7.7. Основные характеристики материала М С М - 4 1
По
изотермам
эксперименте
на
адсорбции,
полученным
адсорбентах
типа
в
прецизионном
МСМ-41
проверяются
возможности и достоверность вновь предлагаемых теорий адсорбции,
в
частности,
модная
ныне
нелокальная
теория
функционала
плотности [10].
Пористые
стекла.
Это
пористые
силикатные
адсорбенты
различной структуры. Их получают в результате воздействия кислот
на натриево-боросиликатное стекло, в результате которого борат
натрия удаляется и остается кремнеземный скелет [5]. Пористую
структуру
таких
адсорбентов
определяют
состав
и
структура
исходного стекла, а также условия его варки. Изменение
этих
параметров позволяет варьировать преимущественный размер пор в
очень широком интервале.
Поручить
структуры
микропористые
оказалось
возможным
и
бипористые
путем
стекла
изменения
разной
структуры
исходного стекла сплошной борокислородной сетки и отдельных
включений боратной фазы (рис.7.8).
При наличии в стекле только борокислородной сетки после ее
растворения
образуется чисто микропористая
структура.
Если
в
стекле имеются отдельные включения боратной фазы, образуются
бутылкообразные поры с широкими полостями и очень узкими
порами. Наконец, при слиянии этих включений конечный продукт
представляет бипористую систему, состоящую из крупных пор и
отходящих от них узких микропор.
Изменяя степень растворения стенок пор, регулируют размер и
объем
макропор.
Радиусы
пор
макропористых
стекол
обычно
изменяются от 50 до 200 нм, а их объемы от 0,5 до 2,0 см /г.
Пористые стекла нашли применение для решения некоторых
задач разделения веществ, например, в медицине [5].
Природные
породы.
Среди
значительное
глинистые
глинистые
адсорбентов
место
породы,
занимают
в
состав
которых обычно входят минералы с
регулярной структурой. Глинистые
минералы
по
Ю.И.Тарасевича
классификации
[134]
можно
разбить на три основные группы:
-
монтмориллонит
и
вермикулит - слоистые минералы с
расширяющейся
относятся
к
решеткой.
Они
мелкопористым
сорбентам. И х структура имеет, по
аналогии с гранулированными цеолитами, первичную и вторичную
пористость. Первичная
пористость
обусловлена
кристаллическим
строением минералов, вторичные поры образованы зазорами между
контактирующими-частицами.
При адсорбции
полярных
веществ
решетка первичных пор расширяется, и в межпакетное пространство
внедряется
один
поверхность
или
несколько
первичных
пор
слоев
адсорбата.
достигает
Удельная
420—470
м /г.
Преимущественный радиус вторичных пор составляет 5—10 нм, их
удельная поверхность не превышает 60 м /г;
- палыгорскит
Первичные
поры
и сепиолит
-
слоисто-ленточные
слоисто-ленточной
группы
минералы.
представлены
цеолитнымн каналами 0,37X0,64 и 0,56X1,1 нм соответственно. В эти
каналы проникают молекулы воды, метанола, аммиака, но не угле¬
водородов. Поверхность вторичных пор этих минералов достаточно
хорошо развита, в связи с чем адсорбенты активно
поглощают
высокомолекулярные вещества, в частности, углеводороды;
-
тальк,
минералы
с
обусловлена
пирофиллит,
гидрослюда,
жесткой
решеткой.
зазорами
между
каолинит
Пористость
-
этих
контактирующими
слоистые
минералов
частицами,
микропоры отсутствуют, удельная поверхность не превышает 150
2
м /г. Плоские частицы слоистых минералов с жесткой
укладываются
преимущественно
базисными
плоскостями
решеткой
друг к
другу» т. е. в основном ориентировано (рис. 7.9.).
Рис 7.9. Пористая структура слоистых материалов: а) одинаковой и б) различной
толщины.
Удельная поверхность белорусских активированных глин, по
данным В.С. Комарова [8], колеблется от 20 до 100 м /г, но может
достигать 200 м /г, средний эффективный радиус пор изменяется от 3
до 9,5 нм.
Модифицируют поверхности структуры глин путем
их кислотами
обработки
и другими реагентами. Замена катионов, входящих в
состав монтмориллонита, на катионы больших размеров приводит к
«раскрытию»
межслоевого
пространства,
которое
становится
доступным для молекул углеводородов. Так, внедрение катионов К+,
NH + Rb+ в решетку монтмориллонита увеличивает адсорбционную
4
емкость этого минерала по гексану в 1,5 раза, а внедрение катионов
Cs+ - в 4,5 раза.
Природные
адсорбенты
нефтеперерабатывающей
применяют
главным
промышленности
для
образом
очистки
в
и
регенерации смазочных, трансформаторных и других специальных
масел, для тонкой очистки и повышения качества жидких топлив.
Кроме того, их используют для осветления фруктовых соков, вин и
пива, рафинирования растительных масел, воды.
СПИСОК ЛИТЕРАТУРЫ
29. Кинле X.,
Бадер
Э. Активные угли и
их промышленное
применение, пер. с нем., Л.: 1984. 214 с.
30. Фенелонов В.Б.
Пористый
углерод.
Новосибирск,
изд-во
Института катализа СО РАН, 1995, 518с.
31. Мухин В.М., Тарасов А.В., Клушин В.Н. Активные угли России. М.: Металлургия, 2000 г. - 352.
32. Богданович Н.И. Ресурсосбережение и повышение экологической
безопасности предприятий химико-лесного комплекса с применением
методов пиролиза. Дисс. в виде научн. доклада на соиск. уч. степ. докт.
техн. наук, Архангельск, АГТУ, 1998, 56 с.
33. Кельцев Н.В. Основы адсорбционной техники. 2-е изд. М.:
Химия. 1984. 592с.
34. Устинов Е.А. Адсорбция, адсорбенты и адсорбционные процессы
в нанопористых материалах.-М.: Издательская группа «Граница», 2011.
С.208.
35. Самонин В.В., Подвязников М.Л. Адсорбция, адсорбенты и
адсорбционные процессы в нанопористых материалах. -М.: Издательская
группа «Граница», 2011. С.447.
36. Комаров В.С. Адсорбенты и их свойства. Минск: Наука и
техника. 1977. 248с.
37. Kresge C.T., Leonovich M.E., Roht w.J., Vartuli J.C., Beck J.S.
//Narure. 1992.. V.359. P.68.
38. Ustinov E.A.//Langmuir. 2008. V.13. P.6668.
39. Тарасевич
процессы
в
Ю.И. Адсорбция,
нанопористых
«Граница», 2011. С.190.
адсорбенты
материалах. -М.:
и
адсорбционные
Издательская
группа
ЗАКЛЮЧЕНИЕ
В
многообразном
мире
пористых
материалов
и в
теории
адсорбции за последние 30-40 лет произошло много изменений:
расширился класс адсорбентов - открыты углеродные нанопористые
структуры
развитие
семейства
фулеренов
темплантный
синтез
и
графена,
адсорбентов
и
получил
широкое
синтез
пористых
материалов, базирующийся на принципах самоорганизации материи
(супрамолекулярная
ожидаемыми и
Качественно
химия), с целью получения
уникальными,
материалов
не предсказуемыми
с
свойствами.
изменилась экспериментальная адсорбционная база на
основе колоссальных достижений современной вычислительной и
измерительной техники (сорбтометры типа ASAP 2020, электронные,
атомно-силовые и полевые сканирующие микроскопы,
спектроскопия,
Я М Р , хромато-масс-спектроскопия,
дифференциальные микрокалориметры и многие
расширилось
Монте
применение
Карло,
в адсорбции
молекулярной
прецизионные
др.). Значительно
вычислительных
динамики,
ИК-Фурье
теории
методов
функционала
плотности, квантовой химии и др. Однако, никогда не уменьшиться
значение
классических
уравнений
адсорбции,
по
которым
исследователи сверяли и будут сверять новые достижения в теории и
практике адсорбции.