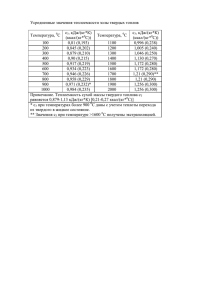
Определение отношения теплоемкостей

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ухтинский государственный технический университет»
(УГТУ)
13
Определение отношения
теплоемкостей СР /CV для воздуха
методом адиабатного расширения
Методические указания к лабораторной работе
для студентов всех направлений
дневной и заочной формы обучения
Ухта 2012
УДК 53 (075)
С 25
ББК 22.3. Я7
Северова, Н. А.
Определение отношения теплоёмкостей Сp/Cv для воздуха методом
адиабатического расширения [Текст] : метод. указания к лабораторной работе
для студентов всех направлений дневной и заочной формы обучения /
Н. А. Северова. – Ухта : УГТУ, 2012. – 10 с.; ил.
Методические указания предназначены для выполнения лабораторных работ по
теме «Теплоёмкость газов» для студентов всех направлений и видов обучения.
Методические указания рассмотрены и одобрены кафедрой физики от
30.01.12 г., пр. № 1 и предложены для издания.
Содержание методических указаний соответствует рабочей учебной программе.
Рецензент: И. К. Серов, доцент кафедры физики Ухтинского государственного
технического университета.
Редактор: В. Н. Шамбулина, доцент кафедры физики Ухтинского государственного технического университета.
В методических указаниях учтены предложения рецензента и редактора.
План 2012 г., позиция 76.
Подписано в печать 31.01.2012 г. Компьютерный набор: Нелюбин С. С.
Объем 10 с. Тираж 100 экз. Заказ № 261.
© Ухтинский государственный технический университет, 2012
169300, Республика Коми, г. Ухта, ул. Первомайская, 13.
Типография УГТУ.
169300, Республика Коми, г. Ухта, ул. Октябрьская, 13.
10. Водород массой m = 20 г был нагрет на ∆T = 100 К при постоянном
переданное газу; 2)
давлении. Определить: 1) количество теплоты Q,
приращение ∆U внутренней энергии газа; 3) работу А расширения.
Ответ: 1) 29,3 кДж ; 2) 20,9 кДж ; 3) 8,4 кДж.
11. Кислород объемом 2 л находится под давлением 1 МПа. Определить,
какое количество теплоты необходимо сообщить газу, чтобы увеличить его
давление вдвое в результате изохорного процесса.
Ответ: 5 кДж.
12. Некоторый газ массой 2 кг находится при температуре 300 К и под
давлением 0,5 МПа. В результате изотермического сжатия давление газа
увеличилось в три раза. Работа, затраченная на сжатие, А = -1,37 кДж.
Определить: 1) какой это газ; 2) первоначальный удельный объем газа.
Ответ: 1) гелий; 2) 1,25 м3/кг.
находится под
13. Двухатомный идеальный газ занимает объем V1 = 1 л и
давлением p1 = 0,1 МПа. После адиабатического сжатия газ
характеризуется объемом V2 и давлением p2. В результате последующего
изохорного процесса газ охлаждается до первоначальной температуры, а
его давление будет составлять p3 = 0,2 МПа. Определить: 1) объем V2; 2)
давление p2. Представить эти процессы графически.
Ответ: 1) 0,5 л ; 2) 0,26 МПа.
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ
СР /CV ДЛЯ ВОЗДУХА
МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ
Краткая теория
Величина, определяемая количеством теплоты, которое необходимо
сообщить телу (системе), чтобы повысить его температуру на 1 К, называется
теплоемкостью тела:
С =
dQ
.
m ⋅ dT
с =
dQ
.
ν ⋅ dT
между
удельной
С = сµ .
(3)
и
молярной
теплоемкостью
(4)
Для газов величина теплоемкости зависит от условий их нагревания. Если
нагревание газа производить при постоянном объеме, то получаем
соответственно теплоемкости (удельную сv и молярную Cv) газа при
постоянном объеме.
Если нагревание газа производить при постоянном давлении, то будем
иметь теплоемкости (удельную ср и молярную Ср) газа при постоянном
давлении, Сv всегда меньше, чем Ср. Это объясняется тем, что при нагревании
газа при постоянном объеме все количество теплоты, подводимое ему, идет на
изменение его внутренней энергии, а при нагревании газа при постоянном
давлении - на изменение внутренней энергии и совершение работы при
расширении.
Уравнением Майера называется выражение, показывающее разность
теплоемкостей:
СР – СV = R ,
10
(2)
Молярной теплоемкостью С вещества называется величина, численно
равная количеству теплоты, необходимой для нагревания одного моля вещества
на 1 К:
Следовательно, связь
определяется формулой:
1) Трофимова Т.И. Основы термодинамики./Т. И. Трофимова // Курс физики:
Учеб.пособие для вузов. – М.: Высш.шк., 2000. – Гл. 9., § 50, 51,53,55. - С.
100-110.
2) Трофимова Т.И. Основы термодинамики./Т. И. Трофимова // Физика в
таблицах и формулах: Учеб.пособие. – М.: Издательский Центр
«Академия», 2008. – Гл. 2.2., § 2.2.1-2.2.6. - С. 90-100.
(1)
Удельной теплоемкостью С вещества называется величина, численно
равная количеству теплоты, которую необходимо сообщить 1 кг этого вещества
для нагревания ее на 1 К:
С =
Библиографический список:
dQ
.
dT
3
(5)
где R - универсальная газовая постоянная.
Из молекулярно-кинетической теории газов известно, что молярные
теплоемкости выражаются следующим образом:
CV =
i
R,
2
C
p
=
i+ 2
R ,
2
Cp
Cν
=
i+2
.
i
(7)
В соответствии с (6) для одноатомных молекул газа (i = 3) имеем:
5
γ =
= 1 . 67 ,
3
для жестких двухатомных молекул (i = 5):
γ =
Непосредственное определение Сv и Ср газов затруднительно в силу того,
что теплоемкости газа малы по сравнению с теплоемкостью сосуда, в котором
заключен газ. Проще определять отношение теплоемкостей γ = Ср/Сv, пользуясь
уравнением Пуассона для адиабатического процесса в газах:
(8)
Адиабатическим называется такой процесс, при котором изменение
состояния газа происходит без теплообмена с окружающей средой.
Вывод расчетной формулы
Выведем рабочую формулу, позволяющую рассчитывать γ для воздуха
рассматриваемым методом.
Пусть в закрытом сосуде находится воздух при комнатной температуре и
под атмосферным давлением. Выделим мысленно внутри сосуда некоторую
массу газа dm. Пусть ее параметры в начальном состоянии будут Po, Vo, To.
Закачаем в сосуд некоторое количество воздуха и подождем некоторое
время, пока температура газа в сосуде не понизится до комнатной. Тогда
4
б) изменение внутренней энергии газа;
2
в) количество тепла, полученного газом.
V1
V2
V
Рис. 3
5. Некоторое количество газа (кислорода) (рис.4) занимает объем V1=3 л при
температуре t =270С и давлении P1 =8,2·105 Н/м2. Во втором состоянии газ
имеет давление P2 = 6 ·105 Н/м2.
Найти: а) количество тепла,
полученного газом;
P1
1
P2
2
б) работу, совершенную газом при
изменении состояния;
в) изменение внутренней энергии газа;
V
Рис. 4
8
= 1 . 33 .
γ =
6
= const .
1
P1
V1
для жестких трехатомных и многоатомных молекул (i = 6):
γ
а) работу, совершенную газом при расширении;
P
7
= 1 . 40 ,
5
pV
Найти:
P
(6)
где i – число степеней свободы молекул газа.
Отношение теплоемкости при постоянном давлении СР к теплоемкости при
постоянном объеме СV для газов играет большую роль при адиабатических или
близких к ним процессах. Так, например, это отношение используется для
определения скорости распространения звука в газах, при изучении течения
газа по трубам со звуковыми и сверхзвуковыми скоростями.
Из уравнений (6) для отношения теплоемкостей газа получаем:
γ =
4. Некоторое количество кислорода (рис. 3) занимает объем V1 =3 л при
температуре t=270С и давлении р=8,2·105 Н/м2. Во втором состоянии объем
газа принял значение V=4,5 л.
6. Считая азот идеальным газом, определить его удельную теплоемкость:
1) для изобарного процесса; 2) для изохорного процесса.
Ответ: 1) Cv=742 Дж/кг·К; 2)Cp=1,04 кДж/кг·К
7. Применяя первое начало термодинамики и уравнение состояния идеального
газа, показать, что разность удельных теплоемкостей будет связана
R
C p − Cν =
.
уравнением Майера:
M
8. Каковы удельные теплоемкости Cv и Cp смеси газов, содержащей кислород
массой m1=10 г и азот массой m2=20 г?
Ответ: 715 кДж/кг·К; 1,01 кДж/кг·К
9. Азот массой 1 кг находится при температуре 280 К. Определить:
1) внутреннюю энергию молекул азота; 2) среднюю кинетическую энергию
вращательного движения молекул азота. Газ считать идеальным.
Ответ: 1) 208 кДж ; 2) 83,1 кДж.
9
Контрольные вопросы
1. Что называется удельной и молярной теплоемкостью, как они связаны
между собой?
2. Какова связь между Ср и Сv для идеального газа?
3. Какой процесс называется адиабатическим?
4. Что происходит с внутренней энергией газа при адиабатическом процессе?
выделенная масса газа (рис.1) будет иметь параметры Р1, V1, Т1 = Т0 (первое
состояние).
Откроем кран, соединяющий сосуд с атмосферой. В результате давление
газа понизится до атмосферного давления ,и у выделенной массы газа будут
новые параметры Р2 = Ро, V2, Т2 (второе состояние).
Если расширение газа происходило достаточно быстро, то процесс
расширения можно считать адиабатическим и к переходу газа из первого
состояния во второе применить уравнение Пуассона, т.е. записать:
5. Как изменяется температура газа при адиабатическом процессе?
p 1V
6. Что называется числом степеней свободы « i »?
 V1

 V2



γ
=
1
γ
=
p 2V
откуда
8. Может ли γ быть меньше 1?
или, логарифмируя последнее выражение:
γAn
,
(9)
p1
,
p2
7. Вычислите теоретическое значение γ на основе молекулярно-кинетической
теории; для воздуха число степеней свободы i = 5.
9. Какие процессы изменения состояний газа имеют место в данной работе?
γ
2
V2
p1
= An
.
V1
p2
(10)
Индивидуальные задания
1.
P
2
3
Какой график (см. рис. 2) соответствует
изотермическому процессу? Поясните!
1
Рис. 2
Рис. 1
V
2. Какие параметры соответствуют состоянию газа в баллоне сейчас же после
расширения в нашей лабораторной установке?
1) Р=Ратм.+ρgh1, Т=Ткомн.;
2) Р=Ратм ;
Т < Ткомн.;
3) Р=Ратм.+ρgh2, Т=Ткомн...
3. Определить удельные теплоемкости Сv и Сp некоторого
двухатомного газа, если плотность этого газа при нормальных условиях 1,43
кг/м3.
Ответ: Сv=650 Дж/(кг⋅К), Сp=910 Дж/(кг⋅К).
Т.к. определение объемов газа V1 и V2 , занимаемого массой dm до и после
расширения в данном случае затруднительно, то измерение объемов надо
заменить измерением каких-либо других параметров газа, а именно давления.
Если закрыть кран на сосуде сразу после адиабатического расширения газа,
то газ, охладившийся в результате расширения, будет нагреваться до комнатной
температуры, а его давление повысится. Спустя некоторое время параметры
выделенной массы газа dm будут P3, V3 = V2, T3 = T0 (третъе состояние).
Легко заметить, что температура выделенной массы газа в первом и третьем
состояниях одна и та же (комнатная), т.е. к переходу газа из первого состояния
в третье можно применить закон Бойля-Мариотта:
p 3V 3 = p 1V 1 ,
(11)
откуда
8
V3
p
= 1 ,
V1
p3
5
а т.к. V3 = V2, то
6.
V2
p
= 1 .
V1
p3
Заменяя отношение объема в уравнении (6) отношением давлений, получим:
A np1 − Anp 2
γ =
.
A np1 − Anp 3
(12)
8.
В полученной формуле присутствует только один параметр - давление, которое
может быть легко измерено с помощью манометра. Т.к. давления Р1, Р2, P3 в
условиях опыта мало отличается друг от друга, то отношение разностей
логарифмов этих величин можно заменить отношением разностей самих этих
величин, что следует из теории бесконечно малых. Тогда:
p1 − p 2
.
p1 − p 3
γ =
(13)
Выразим давления Р1, Р2, P3 через атмосферное давление Р0 и давление
водяного столба в манометре:
p 1 = p 0 + ρ gh 1 ,
p2 = p0 ,
(14)
p 3 = p 0 + ρ gh 2 ,
где ρ - плотность жидкости в манометре. Подставляем в (13) равенства (14),
получим:
γ =
h1
.
h1 − h 2
(15)
Полученная формула является расчетной для данной работы.
Выполнение работы
1.
2.
3.
4.
5.
Закрывают кран и осторожно закачивают в сосуд воздух до тех пор, пока
давление в сосуде не станет больше атмосферного на 200-300 мм водяного
столба. Закручивают зажим на шланге насоса для устранения утечки и
выжидают 1-2 минуты, пока температура воздуха в сосуде не понизится до
комнатной.
Убедившись, что давление больше не снижается, записывают в таблицу
избыточное давление h1 в мм водяного столба.
Осуществляют адиабатический процесс, для чего открывают на 1-2 сек.
кран для выхода воздуха.
Закрывают кран в тот момент, когда прекратится выход газа, что очень
хорошо фиксируется на слух.
Выжидают 1-2 минуты, пока охладившийся газ не нагреется до комнатной
температуры. Убедившись, что давление газа в сосуде больше не
повышается, записывают в таблицу избыточное давление газа h2.
6
7.
Освобождают шланг насоса от зажима и вновь накачивают воздух в сосуд.
Таким образом, проводят еще 9 опытов, изменяя величину избыточного
начального давления h1 в пределах 200-300 мм.
По формуле (15) вычисляют отношение теплоемкостей γ для каждого
опыта, находят среднее арифметическое значение γср .
Абсолютную погрешность измерения ∆γ вычисляют по правилам
нахождения случайных погрешностей, рассматривая каждое значение γi
как результат прямого измерения.
Таблица измерений и вычислений
№
h1
h2
h1- h2
γi
(γ − γ )
2
γ − γi
i
γ ± ∆γ
1
2
3
4
5
6
7
8
9
10
γ
∑
9. Границы доверительного интервала вычисляются по методу Стьюдента:
∆ γ = tα N
(
)
2
Σ γ −γi
N (N − 1 )
7
.
(16)