Длинные линии
реклама
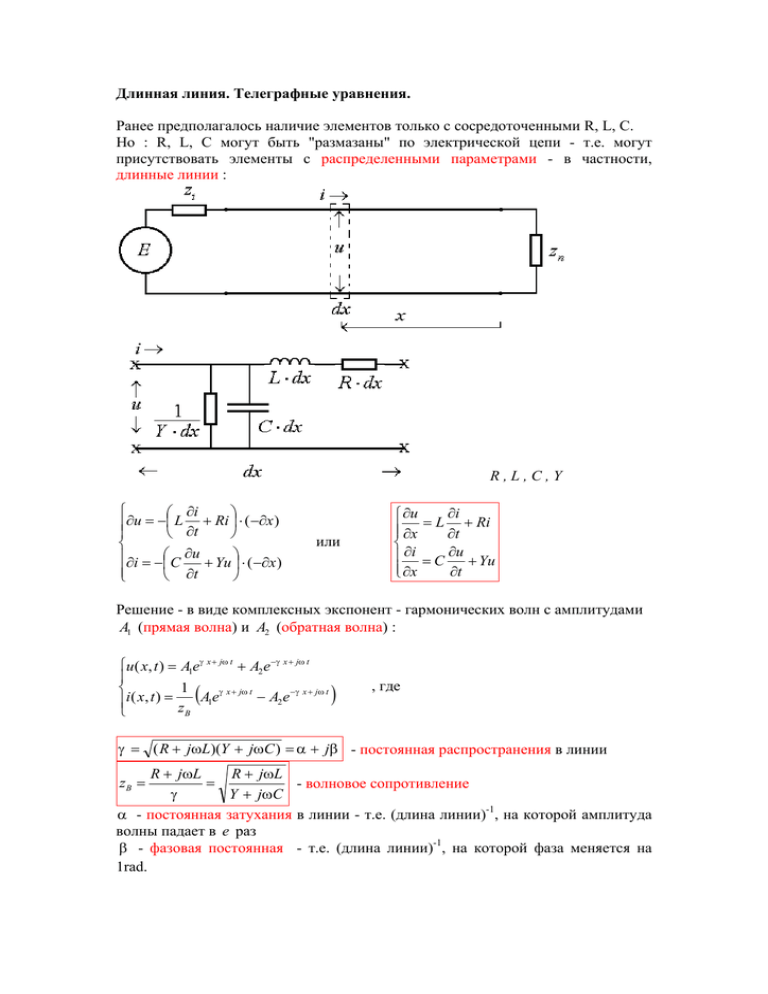
Длинная линия. Телеграфные уравнения. Ранее предполагалось наличие элементов только с сосредоточенными R, L, C. Но : R, L, C могут быть "размазаны" по электрической цепи - т.е. могут присутствовать элементы с распределенными параметрами - в частности, длинные линии : R,L,C,Y ∂i ∂u = − L ∂t + Ri ⋅ ( −∂x ) ∂i = − C ∂u + Yu ⋅ ( −∂x ) ∂t или ∂i ∂u ∂x = L ∂t + Ri ∂i = C ∂u + Yu ∂x ∂t Решение - в виде комплексных экспонент - гармонических волн с амплитудами A1 (прямая волна) и A2 (обратная волна) : u( x, t ) = A1eγ x + jω t + A2e −γ x + jω t 1 γ x + jω t − A2 e −γ x + jω t ) i ( x, t ) = z (A1e В , где γ = ( R + jωL)(Y + jωC ) = α + jβ - постоянная распространения в линии R + jωL R + jωL = - волновое сопротивление γ Y + jωC α - постоянная затухания в линии - т.е. (длина линии)-1, на которой амплитуда волны падает в e раз β - фазовая постоянная - т.е. (длина линии)-1, на которой фаза меняется на 1rad. zВ = Переходя от u (t ) и i (t ) к U& и I& U& = A&1eα x e jβ x + A& 2 e −α x e − jβ x & A&1 α x jβ x A& 2 −α x − jβ x I = z e e − z e e В В - где A&1 и A& 2 - комплексные амплитуды прямой и обратной волн -----------------------------------------------------------------------------------------------------Условия прохождения сигналов по линии без искажений : 1) одинаковая задержка для всех гармонических волн - т.е. независимость фазовой скорости от частоты : ω − jβ ⋅ VФt + jωt = 0 (т.е. при x = −VФt ) ⇒ VФ = = const (ω ) - отсутствие β дисперсии 2) одинаковое затухание всех частот (сигнал как целое уменьшается в e −α x раз) т.е. α = const (ω ) Простейший случай - линия без потерь - R = 0 и Y = 0 ⇒ γ = − ω 2 LC = jω LC - когда α = 0 , β = ω LC , L zВ = C L zВ = ρ = - чисто вещественное C Т.о. фазовые скорости прямой и обратной волн VФ = ω = β 1 не зависят от LC частоты, а амплитуды не зависят от x . -----------------------------------------------------------------------------------------------------Отражение волны от нагрузки. Соотношение амплитуд прямой и обратной волн. На конце линии x = 0 ⇒ & & & & U = A1 + A2 = U н 1 I& = ( A&1 − A& 2 ) = I&н ρ U& & н = zн I н zн = ρ A&1 + A&2 A&1 − A& 2 A& 1 + &2 1 + pU A1 =ρ &A = ρ 1 − p U 1 − &2 A ⇒ 1 z −ρ A& pU = 2 = н &A zн + ρ 1 A& ρ − zн pI = − 2 = A& ρ+z 1 - коэффициент отражения волны напряжения - коэффициент отражения волны тока н Три важных крайних случая : 1) zн = ρ ⇒ pU = 0 , pI = 0 и A& 2 = 0 - есть только прямая волна, полностью поглощаемая нагрузкой - нет отражения - т.н. согласованная нагрузка 2) zн = ∞ ⇒ pU = 1 , pI = −1 и х.х.) амплитуда отраженной напряжения при отражении (инвертируется) ⇒ напряжение ток равен 0. A& 2 = A&1 - при разомкнутом конце линии (режим волны равна амплитуде падающей; фаза сохраняется, а тока обращается на 180° на конце линии имеет удвоенную амплитуду, а В самой линии - т.н. стоячая волна : - ток и напряжение в любой точке (по x) сдвинуты на 90° - нет передачи энергии (есть зоны с I& = 0 или с U& = 0 ) 3) zн = 0 ⇒ pU = −1 , p I = 1 и A& 2 = − A&1 - напряжение на конце линии 0, а ток удвоенный (режим к.з.) : -----------------------------------------------------------------------------------------------------Более общие случаи : 4) zн = Rн > ρ ⇒ pU > 0 , pI < 0 U min , 0 ≤ k ≤1 ; U max ρ КБВ = Rн Вводят КБВ = k = для Rн > ρ КСВ = 1 U = max , 1 ≤ КСВ < ∞ КБВ U min 5) zн = Rн < ρ ⇒ pU < 0 , pI > 0 для Rн < ρ КБВ = Rн ρ 6) В общем виде для произвольной нагрузки zн имеем комплексный z −ρ коэффициент отражения n2 = н и A& 2 = n2 A&1 zн + ρ 1 − n2 КБВ = 1 + n2 -----------------------------------------------------------------------------------------------------Входное сопротивление линии для синусоидального (стационарного) сигнала : U& ВХ U& l = - на расстоянии x=l от конца для линии длиной l ⇒ I&ВХ I&l A&1eγ l + A& 2 e −γ l = zВ A& eγ l − A& e −γ l z ВХ = zВХ 1 2 Три основных случая : 1) zН = zВ = ρ ⇒ A& 2 = 0 и zВХ = zВ = ρ = L C 2π l 2) z Н = ∞ ⇒ A& 2 = A&1 и zВХ = − jρ ctg λ 2π l = ω l LC λ 2π l 3) zН = 0 ⇒ A& 2 = − A&1 и z ВХ = jρ tg λ λ= 2π ; ω LC Линия фиксированной длины - аналог контура без потерь, но с множеством резонансов : ⇒ длинная линия, аналогично колебательному контуру, трансформатором ток-напряжение или напряжение-ток. может быть При подключении чисто реактивной нагрузки происходит смещение нулей и максимумов zВХ и y ВХ ; при чисто активной (но ≠ ρ ) появляется "конечная добротность" - в линии есть и бегущая, и стоячая волны, z ВХ и y ВХ нигде не обращаются в 0 или в ∞ , а сами zВХ и y ВХ становятся комплексными. В частности zВХ = Rн при l = ρ2 zВХ = при Rн трансформатор m λ - не зависимо от ρ - т.н. полуволновая передающая линия 2 l= m− 2 1 2 λ - трансформатор R - т.н. четвертьволновой н Применение длинных линий : частотно-избирательные цепи, согласующие трансформаторы, четвертьволновые изоляторы, линии задержки, передача сигналов и ВЧ-энергии. -----------------------------------------------------------------------------------------------------Переходные процессы в линии. Пусть в t = 0 включаем источник - мгновенный скачек напряжения и в линии возникает волна напряжения и тока; скорость волны v . За время ∆t в линию втекает заряд ∆q = Cu0 ⋅ v ∆t ∆q откуда i0 = = Cu0v ∆t Мощность, отдаваемая источником p = i0u0 = u02Cv Эта мощность равна энергии, запасаемой за единицу времени в C и L линии за счет продвижения волны : Cu02 Li02 Cu02 Li02 u u v = p = u02Cv ⇒ = ⇒ i0 = 0 = 0 + 2 2 2 ρ L 2 C т.е. в начале процесса входное сопротивление линии равно ее волновому сопротивлению (и не зависит от Rн ) Если Ri ≠ 0 то в начальный момент uВХ = u0 ρ - делитель Ri + ρ Если источник согласован с линией и Ri = ρ - то uВХ = амплитудой 1 u0 - возникает волна с 2 1 u0 : 2 Далее все зависит от нагрузки линии : 1) Rн = ρ - нет отражения, и на линии устанавливается u = 1 u0 - то же, что и 2 на постоянном токе 2) Rн = ∞ - волна напряжения отражается без инверсии, тока - с инверсией - т.е. после отражения линия заряжается до u = u0 , а ток в ней исчезает : По достижению отраженной волной источника она поглотится сопротивлением Ri = ρ , ток исчезнет во всей линии, а напряжение везде будет u0 3) Rн = 0 - к.з. линии - волна напряжения отражается с инверсией, тока - без : По достижению отраженной волной источника она поглотится Ri = ρ , ток во u u всей линии станет i = 0 = 0 , а напряжение везде будет 0. Ri ρ 4) Если нагрузка Rн конечная и ≠ ρ - то после поглощения отраженной волны в u0 u0 uR uR линии установится ток i = = и напряжение u = 0 н = 0 н Rн + Ri Rн + ρ Rн + Ri Rн + ρ -----------------------------------------------------------------------------------------------------Если нагрузка и источник не согласованы с линией, то возникают многократные затухающие отражения - и только постепенно (в пределе) устанавливаются u0 uR i= и u = 0 н ⇒ при передаче сигналов для предотвращения Rн + Ri Rн + Ri искажения их формы из-за отражений применяют согласованные линии - хотя бы с одной стороны (в идеале - с двух сторон) -----------------------------------------------------------------------------------------------------Пример применения - формирование прямоугольных импульсов : -----------------------------------------------------------------------------------------------------Конструкции линий : 1) Двухпроводная обычно ρ ≈ 100 ÷ 300Ω v≈c Варианты - "витая пара", симметричная полосковая линия, т.д. 2) Коаксиальная ρ ≈ 50 ÷ 150Ω v ≈ (0.5 ÷ 0.7)c ≈ c - для полиэтилена ε ≈ 2.5 ε ------------------------------------------------------------------------------------------------------