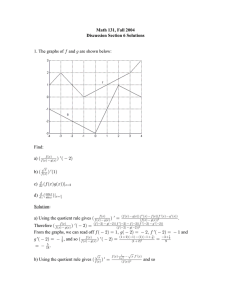
н ж ь ср п е ь с × ² гть я п срьжсп
реклама

Hamilton’s principle
Variational Methods &
Optimal Control
lecture 25
Matthew Roughan
<matthew.roughan@adelaide.edu.au>
Discipline of Applied Mathematics
School of Mathematical Sciences
University of Adelaide
We now have a group of equivalent methods
◮ Euler-Lagrange equations
◮ Hamilton’s equations
◮ Hamilton-Jacobi equation
We saw earlier that these can give us other methods
◮ Hamilton’s principle ⇒ Newton’s laws of motion
◮ When L is not explicitly dependent on t, then the Hamiltonian H is
constant in time.
⊲ conservation of energy
⊲ this is an illustration of a symmetry in the problem appearing in
the Hamiltonian
April 14, 2016
Variational Methods & Optimal Control: lecture 25 – p.1/29
Variational Methods & Optimal Control: lecture 25 – p.3/29
Conservation laws
Given the functional
Conservation Laws
One of the more exciting things we can derive relates to fundamental
physics laws: conservation of energy, momentum, and angular
momentum. We can now derive all of these from an underlying principle:
Noether’s theorem.
F{y} =
Z
x1
f (x, y, y′ , . . . , y(n) ) dx
x0
if there is a function φ(x, y, y′, . . . , y(k) ) such that
d
φ(x, y, y′ , . . . , y(k) ) = 0
dx
for all extremals of F, then this is called a kth order conservation law
◮ use obvious extension for functionals of several dependent variables.
Variational Methods & Optimal Control: lecture 25 – p.2/29
Variational Methods & Optimal Control: lecture 25 – p.4/29
Conservation law example
Given the functional
F{y} =
Z
x1
f (y, y′ ) dx
x0
◮ physically interesting
⊲ tell you about system of interest
◮ can simplify solution
where f is not explicitly dependent on t, we know that the Hamiltonian
H = y′
Conservation laws
∂f
−f
∂y′
is constant, and so
dH
=0
dx
is a first order conservation law for the system.
⊲ φ(x, y, y′ , . . . , y(k) ) = const is an order k DE, rather than E-L
equations which are order 2n
◮ φ(x, y, y′ , . . . , y(k) ) = const is often called the first integral of the
E-L equations
⊲ RHS is a constant of integration (determined by boundary
conditions)
◮ how do we find conservation laws?
⊲ Noether’s theorem
Variational Methods & Optimal Control: lecture 25 – p.5/29
Variational Methods & Optimal Control: lecture 25 – p.7/29
Several independent variables
Variational symmetries
For functionals of several independent variables, e.g.
The key to finding conservation laws lies in finding symmetries in the
problem.
◮ “symmetries” are the result of transformations under which the
functional is invariant
F{z} =
ZZ
Ω
z(x, y) dx dy
◮ E.G. time invariance symmetry results in constant H
the equivalent conservation law is
∇·φ = 0
For some function φ(x, y, z, z , . . . , z ).
′
(k)
◮ Results here can be extended to these cases, but we won’t look at
them here.
Variational Methods & Optimal Control: lecture 25 – p.6/29
◮ more generally, take a parameterized family of smooth transforms
where
X = θ(x, y; ε),
Y = φ(x, y; ε)
x = θ(x, y; 0),
y = φ(x, y; 0)
e.g. we get the identity transform for ε = 0
◮ examples translations and rotations
Variational Methods & Optimal Control: lecture 25 – p.8/29
Example transformations
Jacobian
The Jacobian is
◮ translations (ε is the translation distance)
θ θ x y J=
= θx φy − θy φx
φx φy X = x+ε
Y
= y
◮ smooth: if functions x and y have continuous partial derivatives.
y
◮ non-singular: if Jacobian is non-zero (and hence an inverse
transform exists)
Now for ε = 0, we require the identity transform, so J = 1. Also, we
require a smooth transform, so J is a smooth function of ε, and so for
sufficiently small |ε|, the transform is non-singular.
(X,Y)=(x+ ε,y)
(x,y)
ε
x
Variational Methods & Optimal Control: lecture 25 – p.11/29
Variational Methods & Optimal Control: lecture 25 – p.9/29
Example transformations
Example transformations
◮ translations (ε is the translation distance)
or
X = x+ε
X = x
Y
Y
◮ translations (ε is the translation distance)
X = x+ε
= y
= y+ε
both have Jacobian
Y
Y
= y
y
J=1
and inverse transformations
or
x = X −ε
x = X
y = Y
y = Y −ε
ε
(x,y)
(X,Y)=(x+ ε,y)
X
Variational Methods & Optimal Control: lecture 25 – p.10/29
x
Variational Methods & Optimal Control: lecture 25 – p.12/29
Example transformations
Example transformations
◮ rotations (ε is the rotation angle)
X = x cos ε + y sin ε
◮ rotations (ε is the rotation angle)
Y = −x sin ε + y cos ε
has Jacobian
X = x cos ε + y sin ε
Y = −x sin ε + y cos ε
To derive this, change coordinates to polar coordinates
J = cos ε + sin ε = 1
2
2
and inverse
x = r cos(θ) and y = r sin(θ)
Under a rotation by ε, the new coordinates (X,Y ) are
x = X cos ε −Y sin ε
X = r cos (θ − ε)
y = X sin ε +Y cos ε
and Y = r sin (θ − ε)
Use trig. identities cos(u − v) = cos u cos v + sin u sin v and
sin(u − v) = sin u cos v − cos u sin v, to get
X
Y
= r cos(θ) cos(ε) + r sin(θ) sin(ε) = x cos(ε) + y sin(ε)
= r sin(θ) cos(ε) − r cos(θ) sin(ε) = y cos(ε) − x sin(ε)
Variational Methods & Optimal Control: lecture 25 – p.15/29
Variational Methods & Optimal Control: lecture 25 – p.13/29
Example transformations
Transformation of a function
◮ rotations (ε is the rotation angle)
X = x cos ε + y sin ε
Y = −x sin ε + y cos ε
Given a function y(x), we can rewrite Y (X) using the inverse
transformation, e.g.
φ−1 (X,Y (X); ε) = y(x) = y(θ−1 (X,Y ; ε))
y
For example, taking the curve y = x under rotations
Y
X sin ε +Y cos ε = X cos ε −Y sin ε
(x,y)
which we rearrange to get
x
ε
Y (X) =
cos ε − sin ε
X
cos ε + sin ε
Similarly we can derive Y ′ (X)
X
Variational Methods & Optimal Control: lecture 25 – p.14/29
Variational Methods & Optimal Control: lecture 25 – p.16/29
Examples
Transform invariance
If
Z
x1
f (x, y, y′ (x)) dx =
x0
Z
◮ translations:
X1
f (X,Y,Y ′ (X)) dX
X0
for all smooth functions y(x) on [x0 , x1 ] then we say that the functional in
invariant under the transformation.
◮ also called variational invariance
◮ The transform is called a variational symmetry
◮ Related to conservation laws
or
(X,Y ) = (x + ε, y)
(X,Y ) = (x, y + ε)
◮ rotations:
X = θ(x, y; ε) = x cos ε + y sin ε
ξ =
η =
∂θ =
∂ε ε=0
∂φ =
∂ε Variational Methods & Optimal Control: lecture 25 – p.17/29
Infinitesimal generators
Y = φ(x, y; ε) = −x sin ε + y cos ε
ε=0
−x sin ε + y cos ε|ε=0 = y
−x cos ε − y sin ε|ε=0 = −x
Variational Methods & Optimal Control: lecture 25 – p.19/29
Emmy Noether
For small ε we can use Taylor’s theorem to write
∂θ + O(ε2 )
X = θ(x, y; 0) + ε ∂ε (x,y;0)
∂φ Y = φ(x, y; 0) + ε + O(ε2 )
∂ε (x,y;0)
and then for small ε
(ξ, η) = (1, 0)
(ξ, η) = (0, 1)
So
Also note that the E-L equations are invariant under such a transform, e.g.
they produce the same extremal curves.
Define the infinitesimal generators
∂θ ξ(x, y) =
∂ε (x,y;0)
⇒
⇒
∂φ η(x, y) =
∂ε (x,y;0)
X ≃ x + εξ
Y ≃ y + εη
Variational Methods & Optimal Control: lecture 25 – p.18/29
◮ Amalie Emmy Noether, 23 March 1882 – 14 April
1935
◮ Described by Einstein and many others as the most
important woman in the history of mathematics.
◮ Most of her work was in algebra
◮ Worked at the Mathematical Institute of Erlangen
without pay for seven years
◮ Invited by David Hilbert and Felix Klein to join the
mathematics department at the University of
Göttingen, a world-renowned center of
mathematical research. The philosophicqal faculty
objected, however, and she spent four years
lecturing under Hilbert’s name.
Variational Methods & Optimal Control: lecture 25 – p.20/29
Noether’s theorem
Example (ii)
Suppose the f (x, y, y′ ) is variationally invariant on [x0 , x1 ] under a
transform with infinitesimal generators ξ and η, then
Invariance in translations in y, i.e.
ηp − ξH = const
(X,Y ) = (x, y + ε)
(ξ, η) = (0, 1)
along any extremal of
F{y} =
Z
x1
′
So, a system with such invariance has
f (x, y, y ) dx
x0
p = const
which is what we showed earlier regarding functionals with no explicit
dependence on y.
Variational Methods & Optimal Control: lecture 25 – p.21/29
Variational Methods & Optimal Control: lecture 25 – p.23/29
Example (i)
More than one dependent variable
Invariance in translations in x, i.e.
Transforms with more than one dependent variable
(X,Y ) = (x + ε, y)
(ξ, η) = (1, 0)
T = θ(t, q; ε)
Qk = φk (t, q; ε)
and the infinitesimal generators are
So, a system with such invariance has
H = const
which is what we showed earlier regarding functionals with no explicit
dependence on x.
Variational Methods & Optimal Control: lecture 25 – p.22/29
ξ =
ηk =
∂θ ∂ε ε=0
∂φk ∂ε ε=0
Variational Methods & Optimal Control: lecture 25 – p.24/29
More than one dependent variable
.
Noether’s theorem: Suppose L(t, q, q) is variationally invariant on [t ,t ]
under a transform with infinitesimal generators ξ and ηk . Given
n
∂L
p=
,
H = ∑ pk qk − L
∂qk
k=1
.
.
Then
0 1
n
∑ pk ηk − Hξ = const
k=1
along any extremal of
F{q} =
Z
Common symmetries
.
. . .
2
2
2
Given a system in 3D with Kinetic Energy T (q) = 21 m q1 + q2 + q3 , and
Potential Energy V (t, q).
◮ invariance of L under time translations corresponds to conservation
of Energy
◮ invariance of L under spatial translations corresponds to
conservation of momentum
◮ invariance of L under rotations corresponds to conservation of
angular momentum
t1
.
L(t, q, q) dt
t0
Variational Methods & Optimal Control: lecture 25 – p.25/29
Variational Methods & Optimal Control: lecture 25 – p.27/29
Example: rotations
Finding symmetries
Invariance in rotations, i.e.
Testing for non-trivial symmetries can be tricky.
Useful result is the Rund-Trautman identity:
It leads also to a simple proof of Noether’s theorem
(T, Q1 , Q2 ) = (t, q1 cos ε + q2 sin ε, −q1 sin ε + q2 cos ε)
(t, q1 , q2 ) = (T, Q1 cos ε − Q2 sin ε, Q1 sin ε + Q2 cos ε)
The infinitesimal generators are
ξ = 0
η1 = −q1 sin ε + q2 cos ε|ε=0 = q2
η2 = −q1 cos ε − q2 sin ε|ε=0 = −q1
So, a system with such invariance has
2
∑ pi ηi − Hξ = p1 q2 − p2 q1 = const
i=1
So angular momentum in conserved.
Variational Methods & Optimal Control: lecture 25 – p.26/29
Variational Methods & Optimal Control: lecture 25 – p.28/29
More advanced cases
◮ Laplace-Runge-Lenz vector in planetary motion corresponds to
rotations of 3D sphere in 4D
◮ symmetries in general relativity
◮ symmetries in quantum mechanics
◮ symmetries in fields
Variational Methods & Optimal Control: lecture 25 – p.29/29