R4-2
реклама
4.3 Геометрические приложения определенного интеграла.
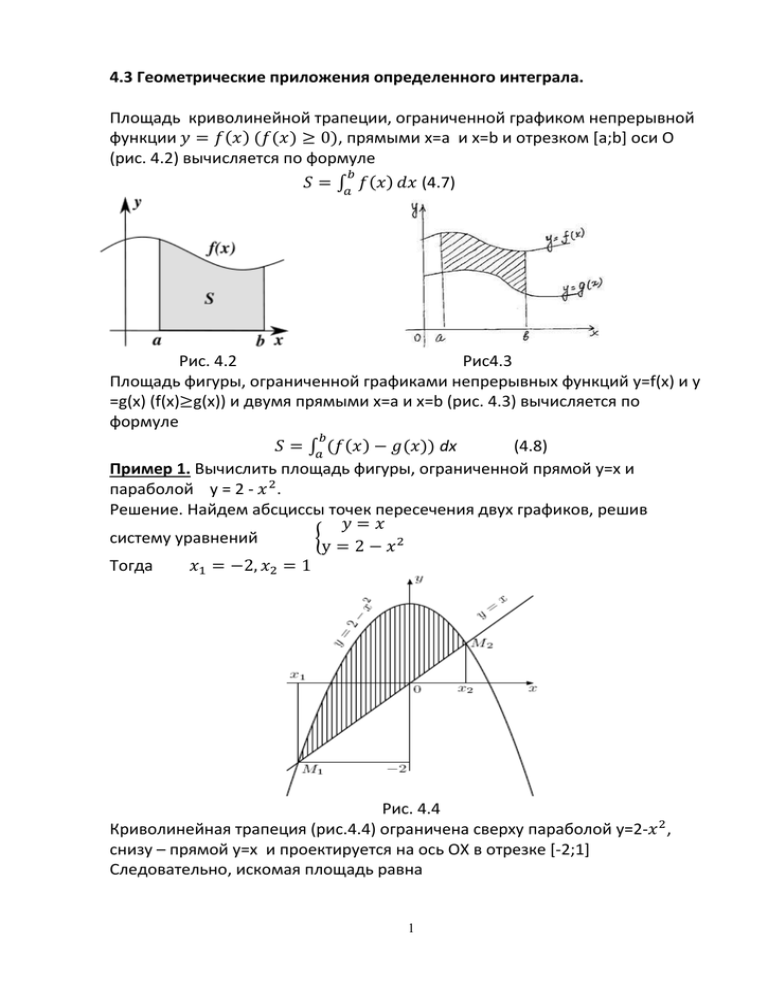
Площадь криволинейной трапеции, ограниченной графиком непрерывной
функции 𝑦 = 𝑓(𝑥) (𝑓(𝑥) ≥ 0), прямыми х=а и х=b и отрезком [a;b] оси O
(рис. 4.2) вычисляется по формуле
𝑏
𝑆 = ∫𝑎 𝑓(𝑥) 𝑑𝑥 (4.7)
Рис. 4.2
Рис4.3
Площадь фигуры, ограниченной графиками непрерывных функций y=f(x) и у
=g(x) (f(x)≥g(x)) и двумя прямыми x=a и x=b (рис. 4.3) вычисляется по
формуле
𝑏
𝑆 = ∫𝑎 (𝑓(𝑥) − 𝑔(𝑥)) dx
(4.8)
Пример 1. Вычислить площадь фигуры, ограниченной прямой у=х и
параболой у = 2 - 𝑥 2 .
Решение. Найдем абсциссы точек пересечения двух графиков, решив
𝑦=𝑥
систему уравнений
{
у = 2 − 𝑥2
Тогда
𝑥1 = −2, 𝑥2 = 1
Рис. 4.4
Криволинейная трапеция (рис.4.4) ограничена сверху параболой у=2-𝑥 2 ,
снизу – прямой y=x и проектируется на ось OX в отрезке [-2;1]
Следовательно, искомая площадь равна
1
1
𝑆 = ∫[(2 − 𝑥
−2
2)
𝑥3 𝑥2 1
− 𝑥]𝑑𝑥 = (2𝑥 − − ) |
= 9/2
3
2 −2
Пример 2. Найти площадь фигуры, ограниченной параболами 𝑦 2 = 𝑥 и
𝑦2 = 2 − 𝑥
Решение. Если криволинейная трапеция ограничена графиками
непрерывных функций 𝑥 = 𝑓1 (𝑦), и 𝑥 = 𝑥2 (𝑦), (𝑓2 (𝑦) ≥ 𝑓1 (𝑦)), и прямыми
у=с и у=d (c<d), (рис. 4.5), то площадь криволинейной трапеции вычисляется
по формуле
𝑑
𝑆 = ∫𝑐 [𝑓2 (𝑦) − 𝑓1 (𝑦)]𝑑𝑦 (4.9)
Здесь 𝑥 = 𝑓1 (𝑦) - левая граница, 𝑥 = 𝑓2 (𝑦) – правая граница криволинейной
трапеции. В нашем случае криволинейная трапеция имеет вид (рис. 4.6)
Рис 4.5
Рис. 4.6
2
Здесь 𝑥 = 𝑦 – левая граница, 𝑥 = 2 − 𝑦 – правая граница и площадь S
вычисляется по формуле (4.9)
Для того, чтобы найти пределы интегрирования, решим систему уравнений
2
𝑦2 = 𝑥
𝑥=1; 𝑦=1
{ 2
↔ [𝑥=1;𝑦=−1
𝑦 =2−𝑥
Ординаты точек пересечения парабол определяют пределы интегрирования
в формуле (4.9).
Таким образом, площадь криволинейной трапеции равна
1
𝑆 = ∫(2 − 𝑦 2 − 𝑦 2 )𝑑𝑦 = (2𝑦 − 2𝑦 3 /3)|
−1
1
= 8/3
−1
Если фигура ограничена кривой, заданной параметрическими уравнениями
x=x(t), y=y(t), прямыми х=а, x=b и отрезком [a,b] оси ОХ, то площадь этой
фигуры вычисляется по формуле
𝑡
𝑆 = ∫𝑡 1 𝑦(𝑡) ∙ 𝑥 ′ (𝑡)𝑑𝑡,
(4.10)
2
где 𝑡1 и 𝑡2 определяются из уравнений 𝑥(𝑡1 ) = 𝑎 и 𝑥(𝑡2 ) = 𝑏, причем y(t)≥0
на отрезке [𝑡1 , 𝑡2 ].
2
Формула (4.10) применяется также для вычисления площади фигуры,
ограниченно замкнутой кривой, при этом изменение параметра t от 𝑡1 до 𝑡2
должно соответствовать обходу граници фигуры по часовой стрелке.
Пример 3. Найти площадь фигуры, ограниченной одной аркой циклоиды
x=a(1-cost) и осью ОХ.
Решение. Циклоидой называется траектория точки, лежащей на окружности
круга, который без скольжения катится по прямой. Принимая прямую за ось
ОХ и полагая, что в исходном положении точка находится в начале
координат, получаем параметрические уравнения циклоиды x=a(t-sin t),
y=a(1-сos t), где t – переменный параметр, а – радиус круга. Первая арка
циклоиды вычерчивается точкой при изменении t в пределах от 0 до 2𝜋, так
как y(0)= о и у (2𝜋)=0, а в остальных точках интервала (0, 2𝜋)у>0 (рис. 4.7)
Рис. 4.7
Площадь фигуры, ограниченной одной аркой циклоиды и осью ОХ
определяется по формуле (4.10)
𝑡2
𝑆 = ∫ 𝑦(𝑡)𝑥′(𝑡) 𝑑𝑥 =
𝑡1
2𝜋
2𝜋
2
= ∫ 𝑎(1 − 𝑐𝑜𝑠𝑡)𝑎(1 − 𝑐𝑜𝑠𝑡)𝑑𝑡 = 𝑎 ∫ (1 − 2𝑐𝑜𝑠𝑡 + 𝑐𝑜𝑠 2 𝑡)𝑑𝑡
0
0
𝑡 𝑠𝑖𝑛2𝑡 2𝜋
= 𝑎2 (𝑡 − 2𝑠𝑖𝑛𝑡 + +
) | = 3𝜋𝑎2
0
2
4
Если фигура ограничена графиком непрерывной функции 𝜌 = 𝜌(𝜑), 𝜌 ≥ 0,
двумя лучами 𝜑 = 𝛼, 𝜑 = 𝛽, где 𝜑 и 𝜌 - полярные координаты (рис. 4.8), то
ее называют криволинейным сектором, площадь которого вычисляют по
формуле
1
𝛽
𝑆 = ∫𝛼 𝜌2 (𝜑)𝑑𝜑 (4.11)
2
3
Рис. 4.8
Пример 4. Вычислить площадь фигуры, ограниченной линией 𝜌 = 4 cos 𝜑.
Решение. Так как значения радиуса-вектора 𝜌 неотрицательны, то
возможные значения полярного угла 𝜑 определяются из решения
неравенства cos 𝜑 ≥ 0. Откуда следует, что – 𝜋/2 + 2𝜋𝑘 ≤ 𝜑 ≤ 𝜋/2 + 2𝜋𝑘.
Но, так как полярный угол принимает возможные значения на интервале
длинной не больше 2𝜋, то – 𝜋/2 ≤ 𝜑 ≤ 𝜋/2. При изменении 𝜑 от
– 𝜋/2 до 𝜋/2 конец радиуса 𝜌 = 𝑐𝑜𝑠𝜑 описывают замкнутую фигуру.
Площадь этой фигуры вычисляют по формуле (4.11)
𝜋
𝜋/2
1 2
1 + 𝑐𝑜𝑠2𝜑
𝑠𝑖𝑛2𝜑 𝜋/2
2
𝑆 = ∫ 16𝑐𝑜𝑠 𝜑𝑑𝜑 = 8 ∫
𝑑𝜑 = 4 (𝜑 +
= 4𝜋
)|
−𝜋/2
2 −𝜋
2
2
−𝜋/2
2
Пример 5. Найти площадь фигуры, ограниченной дугами окружностей 𝑥 2 +
𝑦 2 − 2𝑥 = 0 и 𝑥 2 + 𝑦 2 − 2𝑦 = 0.
Решение. Уравнение 𝑥 2 − 2𝑥 + 𝑦 2 =0 задает окружность радиуса 1 с
центром в точке (1;0). Действительно, это уравнение можно преобразовать к
виду (𝑥 − 1)2 + 𝑦 2 = 1. Аналогично, уравнение 𝑥 2 + 𝑦 2 − 2𝑦 = 0 задает
окружность радиуса 1 с центром (0;1).
Так как уравнения границ заданной области содержат выражение 𝑥 2 + 𝑦 2 , то
необходимо перейти к полярным координатам: 𝑥 = 𝜌 cos 𝜑, 𝑦 = 𝜌 sin 𝜑.
Тогда 𝑥 2 + 𝑦 2 = 𝜌2 и уравнения окружностей в полярных координатах
приобретают вид: 𝜌 = 2 cos 𝜑 и 𝜌 = 2 sin 𝜑.
Окружности пересекаются при 𝜑 = 𝜋/4 и рассматриваемая фигура
симметрична относительно луча 𝜑 = 𝜋/4 (рис. 4.9)
4
Рис. 4.9
Площаль этой фигуры надо вычислять по формуле (4.11). В силу симметрии
площадь всей фигуры равна удвоенной площади заштрихованной части,
которая представляет собой сектор, ограниченной линией 𝜌 = 2 sin 𝜑 и
лучами 𝜑 = 0 и 𝜑 = 𝜋/4. Тогда
𝜋
𝜋
𝜋
4
1 4
𝑠𝑖𝑛2𝜑
𝜋
2
𝑆 = 2 ∙ ∫ 4𝑠𝑖𝑛 𝜑𝑑𝜑 = 2 ∫ (1 − 𝑐𝑜𝑠2𝜑) 𝑑𝜑 = 2 (𝜑 −
) |4 = ( − 1)
2 0
2
2
0
0
С помощью определенного интеграла можно вычислить длину дуги кривой.
Если кривая задана уравнением y=f(x) на отрезке [a,b], где f(x) – непрерывно
дифференцируемая функция, то длина соответствующей дуги этой кривой
находится по формуле
𝑏
𝐿 = ∫𝑎 √1 + (𝑦′)2 𝑑𝑥 (4.12)
Если кривая задана параметрическими уравнениями x=x(t), y=y(t), где x(t) и
y(t) – непрерывно дифференцируемые функции, то длина дуги,
соответствующей монотонному изменению параметра t от 𝑡1 до 𝑡2 , находится
по формуле
𝑡
𝐿 = ∫𝑡 2 √(𝑥𝑡′ )2 + (𝑦𝑡′ )2 𝑑𝑡 (4.13)
1
Аналогично выражается длина дуги пространственной кривой, заданной
параметрическими уравнениями x=x(t), y=y(t), z=z(t), 𝑡1 ≤ 𝑡 ≤ 𝑡2 :
𝑡
𝐿 = ∫𝑡 2 √(𝑥𝑡′ )2 + (𝑦𝑡′ )2 + (𝑧𝑡′ )2 𝑑𝑡 (4.14)
1
Если дуга кривой задана уравнением в полярных координатах
𝜌 = 𝜌(𝜑), 𝜑1 ≤ 𝜑 ≤ 𝜑2 , то длина дуги равна
𝜑
𝐿 = ∫𝜑 1 √𝜌2 + (𝜌′ )2 𝑑𝜑 (4.15)
2
Пример 6. Найти длину дуги полукубической параболы 𝑦 2 = 𝑥 3 от начала
5
координат до точки (4;8).
Решение. Так как точка (4;8) находится в верхней полуплоскости, то на
3
отрезке изменения х от 0 до 4 𝑦 = 𝑥 3/2 и 𝑦′ = 𝑥 1/2 . В этом случае длина
2
дуги вычисляется по формуле (4.12)
4
9
4 2
9
8
4
𝐿 = ∫ √1 + 𝑥𝑑𝑥 = ∙ (1 + 𝑥)3/2 | =
(10√10 − 1).
0 27
4
9 3
4
0
Пример 7. Вычислить длину дуги кривой
𝑥 = 𝑒 𝑡 sin 𝑡
𝑦 = 𝑒 𝑡 cos 𝑡 , 0 ≤ 𝑡 ≤ 𝜋/2
Решение. Длину дуги найдем по формуле (4.13). Для этого
продифференцируем по t параметрические уравнения
𝑥′𝑡 = 𝑒 𝑡 sin 𝑡 + 𝑒 𝑡 cos 𝑡
{
𝑦′𝑡 = 𝑒 𝑡 cos 𝑡 − 𝑒 𝑡 sin 𝑡
Тогда
𝜋/2
𝐿=∫
0
√𝑒 2𝑡 (sin 𝑡 + cos 𝑡) 2 + 𝑒 2𝑡 (cos 𝑡 − sin 𝑡) 2 𝑑𝑡 =
𝜋
2
=∫
0
√2𝑒 2𝑡 𝑑𝑡
𝜋
2
𝜋
= ∫ √2𝑒 𝑑𝑡 = √2𝑒 |2 = √2(𝑒 𝜋/2 − 1).
0
0
𝑡
𝑡
Пример 8. Найти длину дуги кардиоиды 𝜌 = 2(1 − 𝑐𝑜𝑠𝜑), расположенной в
верхней полуплоскости.
Решение. При изменении 𝜑 от 0 до 𝜋 длина радиуса-вектора 𝜌 возрастает от 0
до 4, а конец радиуса вектора 𝜌 описывает дугу ОМВ, расположенную в
верхней полуплоскости (рис 4.10)
Рис. 4.10
Вычислим длину этой дуги, используя формулу (4.15). Найдем
𝜌′ = 2 sin 𝜑 , √𝜌2 + (𝜌′ 𝜑 )2 = √4(1 − cos 𝜑)2 + 4𝑠𝑖𝑛2 𝜑 = 2√2(1 − cos 𝜑).
6
𝜋
𝜋
𝐿 = 2 ∫ √2(1 − cos 𝜑)𝑑𝜑 = 4 ∫ sin
0
0
𝜑
𝑑𝜑 = 8.
2
Определенный интеграл используется для вычисления площадей
поверхностей вращения.
Если поверхность образована вращением вокруг оси ОХ дуги кривой,
заданной непрерывно дифференцируемой функцией y=f(x), 𝑎 ≤ 𝑥 ≤ 𝑏, то
площадь этой поверхности вычисляется по формуле
𝑏
𝑆 = 2𝜋 ∫𝑎 𝑓(𝑥)√1 + (𝑓 ′ (𝑥))2 𝑑𝑥 (4.16)
Если дуга задана параметрическими уравнениями x=x(t), y=y(t), 𝑡1 ≤ 𝑡 ≤ 𝑡2 ,
где x(t) и y(t) – непрерывно дифференцируемые функции на [𝑡1 , 𝑡2 ], то
𝑡
𝑆 = 2𝜋 ∫𝑡 1 𝑦(𝑡) √(𝑥 ′ (𝑡))2 + (𝑦 ′ (𝑡))2 𝑑𝑡 (4.17)
2
Если дуга задана в полярных координатах 𝜌 = 𝜌(𝜑), 𝛼 ≤ 𝜑 ≤ 𝛽, то
𝛽
𝑆 = 2𝜋 ∫𝛼 𝜌 sin 𝜑 √𝜌2 + (𝜌′ 𝜑 )2 𝑑𝜑 (4.18)
Пример 9. Вычислить площадь поверхности шара радиуса R.
Решение. Будем считать, что шар получен вращением вокруг оси ОХ верхней
чести полукруга, ограниченного окружностью 𝑥 2 + 𝑦 2 = 𝑅 2 , (𝑦 ≥ 0).
Перейдем к полярным координатам : 𝑥 = 𝜌𝑐𝑜𝑠𝜑, 𝑦 = 𝜌 sin 𝜑. Тогда
уравнение окружности принимает вид 𝜌2 = 𝑅2 → 𝜌 = 𝑅. При изменении 𝜑
0 до 𝜋 радиус-вектор 𝜌 = 𝑅 описывает верхнюю дугу окружности. Для
вычисления площади поверхности шара воспользуемся формулой (4.18), в
которой 𝜌 = 𝑅, √𝜌2 + (𝜌′𝜑 )2 = 𝑅 и
𝜋
π
𝑆 = 2𝜋 ∫ 𝑅2 sin 𝜑𝑑𝜑 = 2𝜋𝑅2 (− cos φ)| = 4πR2 .
0
0
Вычисление объемов тел вращения также производится с помощью
определенного интеграла.
Если криволинейная трапеция, ограниченная кривой y=f(x) и прямыми y=0,
x=a и x=b вращается вокруг оси ОХ, то объем тела, образованного при
вращении, вычисляется по формуле
𝑏
𝑉 = 𝜋 ∫𝑎 𝑦 2 𝑑𝑥 (4.19).
Если фигура, ограниченная кривыми
𝑦1 = 𝑓1 (𝑥) и 𝑦2 = 𝑓2 (𝑥), 0 ≤ 𝑓1 (𝑥) ≤ 𝑓2 (𝑥), и прямыми x=a и x=b,
7
вращается вокруг оси ОХ, то объем тела, образованного при вращении,
вычисляется по формуле
𝑏
𝑉 = 𝜋 ∫𝑎 (𝑦22 − 𝑦12 ) 𝑑𝑥 (4.20)
Пример 10. Найти объем тела, образованного при вращении одной арки
циклоиды x=a(t-sint), y=a(1-cost) вокруг оси ОХ.
Решение. Рассмотрим арку циклоиды, соответствующую изменению
параметра t от 0 до 2𝜋. Тогда абсциссы точек на этой дуге изменяются от
x(0)=0 до 𝑥(2𝜋) = 2𝜋𝑎 и объем тела вращения вычисляют по формуле (4.19)
Перейдем к переменной t, полагая x=a(t-sint), и при изменении x от 0 до 2𝜋𝑎
переменная t меняется от 0 до 2𝜋, dx=a(1-cost)dt и y=a(1-cost).
2𝜋
2𝜋
𝑉 = 𝜋𝑎3 ∫ (1 − cos 𝑡)3 𝑑𝑡 = 𝜋𝑎3 ∫ (1 − 3 cos 𝑡 + 3𝑐𝑜𝑠 2 𝑡 − 𝑐𝑜𝑠 3 𝑡)𝑑𝑡 =
0
0
3
3
𝑠𝑖𝑛3 𝑡 2𝜋
3
= 𝜋𝑎 (𝑡 − 3𝑠𝑖𝑛𝑡 + 𝑡 + 𝑠𝑖𝑛2𝑡 − 𝑠𝑖𝑛𝑡 +
) | = 5𝜋 2 𝑎3 .
0
2
4
3
Задачи для самостоятельного решения
1. Вычислить площадь фигуры, ограниченной параболой 𝑦 = 𝑥 2 + 1 и
прямой x+y=3.
2. Вычислить площадь эллипса, границы которого заданы уравнениями
x=2cost, y=3sint.
3. Вычислить площадь фигуры, ограниченной линией 𝜌 = 9 sin 𝜑.
𝜋
𝜋
4. Вычислить длину дуги кривой 𝑦 = 𝑙𝑛𝑠𝑖𝑛 𝑥 от 𝑥 = до 𝑥 = .
3
2
5. Вычислить длину дуги кривой, заданной параметрически уравнением
𝑡3
𝑥 = − 𝑡, 𝑦 = 𝑡 2 + 2 от 𝑡 = 0 до 𝑡 = 3.
3
6. Вычислить длину дуги кривой, заданной уравнениями в полярных
координатах 𝜌 = 16 sin 𝜑 .
7. Вычислить объем тела, образованного вращением фигуры,
ограниченной линиями xy=4, x=1, x=4, y=0 вокруг оси ОХ.
Ответы:
1. 4,5; 2. 6𝜋; 3. 9𝜋; 4. 0.5ln3; 5. 12; 6. 16𝜋; 7. 12𝜋;
===
8