9.8. Задания на выполнение расчетно-графических работ 4 Содержание задания

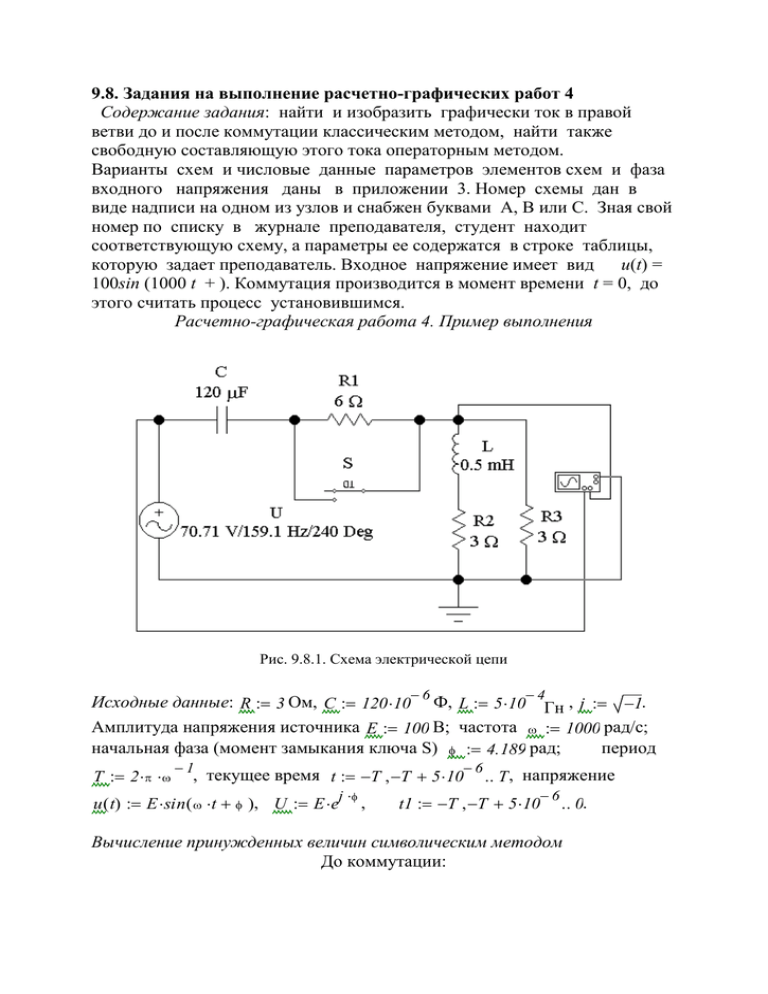
9.8. Задания на выполнение расчетно-графических работ 4
Содержание задания: найти и изобразить графически ток в правой
ветви до и после коммутации классическим методом, найти также
свободную составляющую этого тока операторным методом.
Варианты схем и числовые данные параметров элементов схем и фаза
входного напряжения даны в приложении 3. Номер схемы дан в
виде надписи на одном из узлов и снабжен буквами A, B или C. Зная свой
номер по списку в журнале преподавателя, студент находит
соответствующую схему, а параметры ее содержатся в строке таблицы,
которую задает преподаватель. Входное напряжение имеет вид
u(t) =
100sin (1000 t + ). Коммутация производится в момент времени t = 0, до
этого считать процесс установившимся.
Расчетно-графическая работа 4. Пример выполнения
Рис. 9.8.1. Схема электрической цепи
Исходные данные: R  3 Ом, C  120 10 6 Ф, L  5 10 4Гн , j  1.
Амплитуда напряжения источника E  100 В; частота   1000 рад/с;
начальная фаза (момент замыкания ключа S)   4.189 рад;
период
T  2  
1
, текущее время t  T T  5 10 6  T , напряжение
j 
u ( t)  E sin (  t   ), U  E e ,
6
t1  T T  5 10
 0.
Вычисление принужденных величин символическим методом
До коммутации:
j
z2 z3
, z2  R  j  L, z3  R, z23 
, z  z1  z23,
 C
z2  z3
U
U23
I1
,
.
I1  , U23  I1 z23,
I2 
Uc 
z
z2
j  C
Мгновенное значение принужденного тока до коммутации
i3n ( t)  I3 sin (  t  arg ( I3) ).
z1  2 R 
Начальные условия: ток в катушке индуктивности i l0 и напряжение
на конденсаторе uc0:
i l0  Im ( I2) ;
uc0  Im ( Uc) .
После коммутации:

z1k  z1  R 2, I1k  U  z1k  z23
 1, U23k  I1k z23, I2k  U23k z2 1,
1
1
I3k  U23k z3 , Uck  I1k ( j  C ) .
Мгновенное значение принужденного тока равно
i3nk ( t)  I3k sin  t  arg I3k .

 
Принужденные величины в нуле тока в катушке i l0k и
на конденсаторе uc0k : i l0k  Im  I2k  uc0k  Im  Uck 
напряжения
Вычисление свободной составляющей операторным методом
uc0  uc0k 
uc0
Операторные ЭДС: il0 L  i l0  i l0k  L ,
.

p
p
Рис 9.8.2. Операторная схема замещения
Уравнения для контурных токов i1 в правом и i3 в левом контуре:
i1 ( R  p L)  i3 ( 2 R  p L) L il0 ,
 1  R  p L   i3 ( R  p L) L il0  uc0 .
i1 

p
 p C

Операторное выражение для свободной составляющей тока и обратное
преобразование Лапласа для него:
 uc0  uc0  il0 
 p 

L
R C 
 R
i3c1 ( p ) 
invlaplace p  .
R
1 
2
2

p  p  

 L R C  L C
Свободная составляющая тока равна
i3c1 ( t)  17.8 exp ( 4389 t) cos ( 3751 t)  7.55exp ( 4389 t) sin ( 3751 t).
Полный ток равен: i3 ( t)  i3nk ( t)  i3c1 ( t), t2  0 0  5 10 6  T .
5
0
i3n ( t1)
i3nk ( t2)  5
i3c1 ( t2)  10
i3 ( t2)
 15
 20
 25
3
3
3
3
 410  310  210  110
0
110
3
210
3
t1 t2
Рис. 9.8.3. Выходной ток по результатам расчета
Расчет свободной составляющей классическим методом.
 t
i3c2 ( t)  e ( A cos (  t)  B sin (  t) )
Корни характеристического уравнения равны
1 
2
2
R
p  p  
solve p  равно

 L R C  L C
 39500  500 i  4559 
 9
  4.389  103  3.751i  103 
9
,


3
3

39500
500


i  4559   4.389  10  3.751i  10 
9
 9

коэффициент затухания   4389; собственная частота   3751.
Принужденный ток в нуле i3nk ( 0)  3.533 . Полный ток в нуле равен


1
i30c2  u ( 0)  uc0 R
A  i30c2  i3nk ( 0).
. Свободный ток в нуле равен А:
Отсюда находим
A  1A .
a 
Производная от принужденного тока в нуле
Производная от напряжения источника в нуле
Производная от напряжения на конденсаторе в нуле


c  i l0  i30c2 C
 
Re I3k .
b   Re ( U ).

1
.
1
Производная от полного тока в нуле
h  R ( b  c).
Производная от свободной составляющей при t = 0 имеет вид
( h  a  A  )
,
h  a  A   B  . Отсюда получим: B 

3
4
a  4.914  10 , b  4.998  10 ,
5
4
c  2.142  10 , h  5.475  10 , B  7.55 .
Результаты расчетов операторным и классическим методами совпали.
В общем случае операторное выражение для свободного тока имеет вид
p d  q
. Корни знаменателя
i ( p ) 
2
p  g p  w
равны: p 1  0.5 g  ( 0.5 g ) 2  w ,
2
p 2  0.5 g  ( 0.5 g )  w .
1. Корни действительные и
2. Корни действительные и равные:
различные. Ответ имеет вид
p 1   , p 2   ,   0.5 g.
p t d p 1  q
p t d p 2  q
. Ответ имеет вид e t [ t (  d  q)  d].
e 1 
e 2 
2 p 1  g
2 p 2  g
3. Корни комплексные сопряженные. Ответ имеет вид
 t  d    q

2
e 
sin   c t  d cos   c t ,  c  w  ( 0.5 g ) .



c
A
B
Рис. 9.8.4. Результат моделирования: форма входного (А) и выходного (В) напряжения
Таблица
Числовые данные параметров схем для
расчетно-графической работы 4
Расчет переходных процессов в линейных цепях
с сосредоточенными параметрами
Номер
группы
R,
Ом
L,
Гн
C,
Ф
1A
5
5 . 10-3
1
 10 3
36
1B
5
1C
5
5 . 10-3
5 . 10-3
5 . 10-5
10-4
2A
5
10-2
1
 10 3
18
2B
5
2C
5
10-2
10-2
10-4
2 . 10-4
3A
10
2 . 10-2
1
 10 3
36
3B
10
2 . 10-2
5 . 10-5
3C
10
5 . 10-3
2.5 . 10-5
4A
5
2 . 10-2
4B
10
10-2
4C
10
10-2
5A
10
2 . 10-2
1
 10 3
9
1
 10  4
4
1
 10  4
2
1
 10 3
36
5B
10
5C
10
4 . 10-2
4 . 10-2
10-4
2 . 10-4
6A
10
4 . 10-2
6B
20
4 . 10-2
1
10 3
18
5
 10 5
2
6C
20
4 . 10-2
5 . 10-5
7A
20
4 . 10-2
5
 10  4
36
7B
20
7C
20
8 . 10-2
8 . 10-2
5 . 10-5
10-4
Значения 
 , град
Номера схем
60
45
30
30
45
60
120
135
150
210
225
240
16
11
3, 18
1, 2, 19, 22, 25
8, 9
17, 24, 27
5, 13, 15
10, 28
14, 21
4, 20, 23
12
6, 7, 26