Свойства и график функции у=arctgx

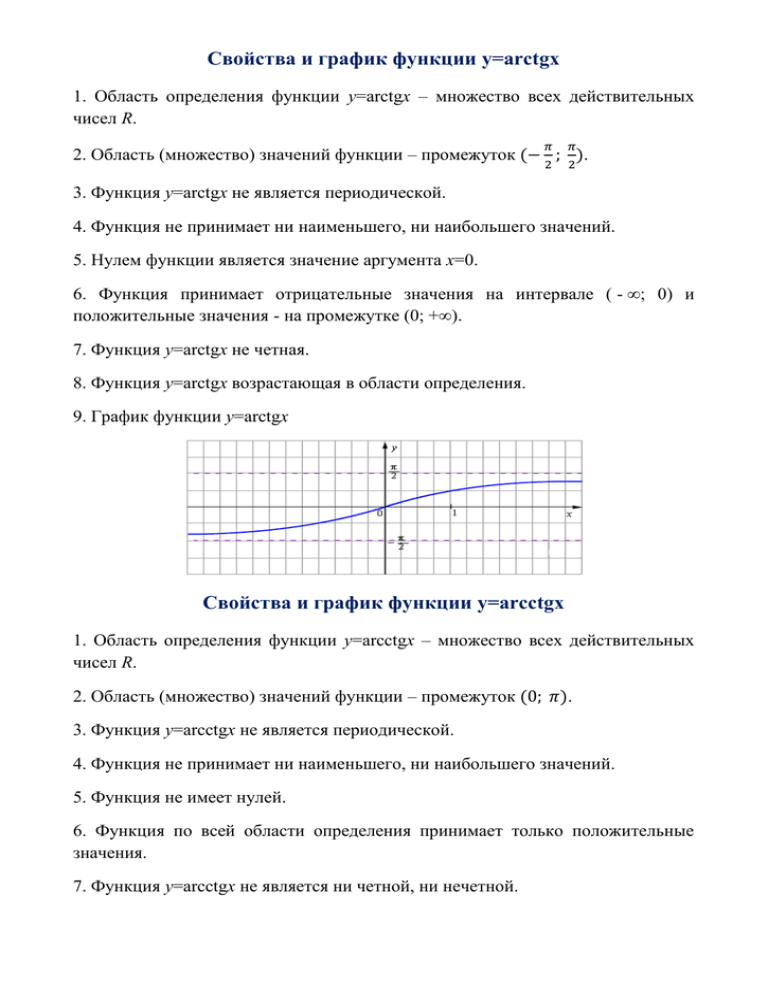
Свойства и график функции у=arctgx
1. Область определения функции у=arctgx – множество всех действительных
чисел R.
𝜋
𝜋
2
2
2. Область (множество) значений функции – промежуток (− ; ).
3. Функция у=arctgx не является периодической.
4. Функция не принимает ни наименьшего, ни наибольшего значений.
5. Нулем функции является значение аргумента х=0.
6. Функция принимает отрицательные значения на интервале ( - ∞; 0) и
положительные значения - на промежутке (0; +∞).
7. Функция у=arctgx не четная.
8. Функция у=arctgx возрастающая в области определения.
9. График функции у=arctgx
Свойства и график функции у=arcсtgx
1. Область определения функции у=arcсtgx – множество всех действительных
чисел R.
2. Область (множество) значений функции – промежуток (0; 𝜋).
3. Функция у=arcсtgx не является периодической.
4. Функция не принимает ни наименьшего, ни наибольшего значений.
5. Функция не имеет нулей.
6. Функция по всей области определения принимает только положительные
значения.
7. Функция у=arcсtgx не является ни четной, ни нечетной.
8. Функция у=arcсtgx убывающая в области определения.
9. График функции у=arcсtgx
Примеры решения задач
Пример 1. Решите уравнение arctg (5𝑥 − 8) =
𝜋
4
Решение: arctg (5𝑥 − 8) = arctg 1, значит, 5х – 8=1, откуда х=
9
5
Ответ:
3𝑥
Пример 2. Решите уравнение arcctg (
3𝑥
Решение: arcctg (
2
2
9
5
− 𝜋) = 0.
𝜋
3𝑥
2
2
− 𝜋) = arcctg , значит,
𝜋
− 𝜋 = , откуда х=.
2
Ответ: 
𝑥
𝜋
2
4
Пример 3. Решите неравенство arctg ( − 5) ≤ .
𝑥
Решение: по условию arctg ( − 5) ≤ arctg 1. Поскольку функция
2
𝑥
тангенс возрастающая, то данное неравенство равносильно неравенству − 5 ≤
2
1, откуда х12.
Ответ: ( - ∞; 12]
Пример 4. Найти sin(arctg( - 2).
Решение. sin(arctg( - 2)=
tg (arctg (−2))
√1+tg2
(arctg(−2))
=−
2
√5
Ответ: −
2
Пример 5. Найти tg(arccos ).
3
2
√5
2
Решение. tg(arccos )=
3
2
3
2
cos(arccos )
3
sin(arccos )
2
3
√1−cos2(arccos )
=
2
3
√5
2
=
Ответ:
Упражнения
1. Укажите область определения и область значения функции:
1) 𝑓(𝑥) = arctg
3) 𝑓(𝑥) = arctg
2
2) 𝑓(𝑥) = arcctg (4 −
2+𝑥
𝑥
1
9) 𝑓(𝑥) = arcctg
6)
5−𝑥
7) 𝑓(𝑥) = arctg(−
1
2𝑥
)
4) 𝑓(𝑥) = arcctg √𝑥 4 − 16
𝑥 2 −3
5) 𝑓(𝑥) = arcctg
1
4𝑥 2
+ 1)
8)
1
𝑥 2 −1
10) 𝑓(𝑥) = arctg √
2
𝑥 2+9
2. Укажите координаты точек пересечения с осями Ох и Оу графика функции:
1) 𝑦 = arcctg(3𝑥 − √3)
2) 𝑦 =
3) 𝑦 =
4) 𝑦 = arctg(4𝑥 − √3)
5) 𝑦 =
6) 𝑦 =
7) 𝑦 = arctg(𝑥 2 − 2𝑥 − 3)
8) 𝑦 =
9) 𝑦 =
10) 𝑦 = arcctg(𝑥 2 + 3𝑥 + 2)
3. Определите, четной или нечетной является функция:
1) 𝑓(𝑥) = arctg 𝑥 − 7 arctg (−𝑥)
2) 𝑓(𝑥) = arctg 2 𝑥 + (−4 sin 𝑥)4
3) 𝑓(𝑥) = 2arctg 𝑥 − 2arctg 𝑥 9
4) 𝑓(𝑥) = arctg 𝑥 − 5𝑥 5 acctg|𝑥|
5) 𝑓(𝑥) = arctg 2 𝑥 + 8 cos 𝑥
6) 𝑓(𝑥) = √arctg 2 𝑥 − 6arcctg |𝑥|
7)
8)
9)
10)
4. Функция задана на множестве D. Укажите для нее:
√5
2
а) наименьшее и наибольшее значение;
б) промежутки возрастания и убывания;
в) промежутки, где функция принимает отрицательные и положительные
значения;
г) нули функции
1) 𝑓(𝑥) = arctg 𝑥, 𝐷 ∈ [−
1
√3
; 0)
3) 𝑓(𝑥) = arcctg 𝑥, 𝐷 ∈ [− √3; √3]
5) 𝑓(𝑥) = arcctg 𝑥, 𝐷 ∈ [−1;
√3
]
3
2) 𝑓(𝑥) = arcctg 𝑥, 𝐷 ∈ [0; √3)
4) 𝑓(𝑥) = arctg 𝑥, 𝐷 ∈ [−
√ 3 √3
; ]
3
3
6) 𝑓(𝑥) = arctg 𝑥, 𝐷 ∈ [−
√3
;
3
7)
8)
9)
10)
1]
5. Решите уравнения:
1) arctg(𝑥 2 − 11𝑥 + 10) = 0
3) arcctg(16 − 2𝑥 − 𝑥 2 ) =
5) arcctg(√3𝑥 + 6) =
2) arcctg(𝑥 2 + 14𝑥 + 12) =
𝜋
4) arctg(𝑥 2 + 10𝑥 − 23) =
4
5𝜋
𝜋
2
𝜋
4
6)
6
7) arctg(𝑥 2 + 8𝑥 + 11) = −
𝜋
8) arctg(√3𝑥 − 6) = −
4
9)
𝜋
6
10) arcctg(13 − 9𝑥 + 𝑥 2 ) =
3𝜋
4
6. Решите неравенство:
𝜋
1) arctg(1 − 2𝑥) > −
4) arcctg(6 − 2𝑥) ≤
2
𝜋
2
7) arcctg(𝑥 + 5) < 𝜋
2) arctg𝑥 <
𝜋
3) arctg(4 + 4𝑥) >
6
5) arctg(18 − 12𝑥) ≤
8) arcctg(7𝑥 + 2) <
𝜋
3
𝜋
2
6) arcctg𝑥 ≤
7. При каких значениях р верно равенство:
𝑝
𝑝+5𝜋
2) arcctg 2 𝑥 = −𝑝 − 𝜋
2
𝜋
4
9) arctg(7𝑥 + 8) ≥ −
10) arctg(𝑥 + 2) ≤ 0
1) arcctg𝑥 =
𝜋
3) arcctg𝑥 =
𝑝−3𝜋
𝑝
𝜋
3
4) arctg 2 𝑥 = 𝑝 +
𝜋
2
7)
5)
6) arctg𝑥 =
8)
9) arctg𝑥 =
𝑝
𝑝+4𝜋
𝑝−0,1𝜋
𝑝
10)
8. Постройте график функции:
1) 𝑦 = − arctg 𝑥
2) 𝑦 = − arcctg 𝑥
5) 𝑦 = 2 arctg 𝑥
6) 𝑦 = arcctg 𝑥
9) 𝑦 = | arctg 𝑥|
10) 𝑦 = arcctg |𝑥|
1
2
3) 𝑦 = arcctg(−𝑥) 4) 𝑦 = arctg(−𝑥)
7) 𝑦 = arcctg
𝑥
2
8) 𝑦 = arctg 3𝑥
9. Постройте график функции:
𝑥
1
1) 𝑦 = 2 arctg ( + ) − 1,5
2
2
𝑥
2) 𝑦 = |0,5 arctg 𝑥 − 1|
3) 𝑦 = −2 arcctg ( + 1) + 3
4) 𝑦 = |0,5 arcctg 𝑥 − 1|
5) 𝑦 = 3 arcctg(2𝑥 − 6) + 3
6) 𝑦 = | arcctg(2𝑥 + 6) − 2|
7) 𝑦 = −4 arctg(3𝑥 − 1) + 1
8) 𝑦 = | arctg(2𝑥 + 4) − 1|
9) 𝑦 = 1 − arctg(2𝑥 − 1)
10) 𝑦 = −2 arcctg(2𝑥 − 3)
2
3
2
3
2