ЕГЭ 2013x

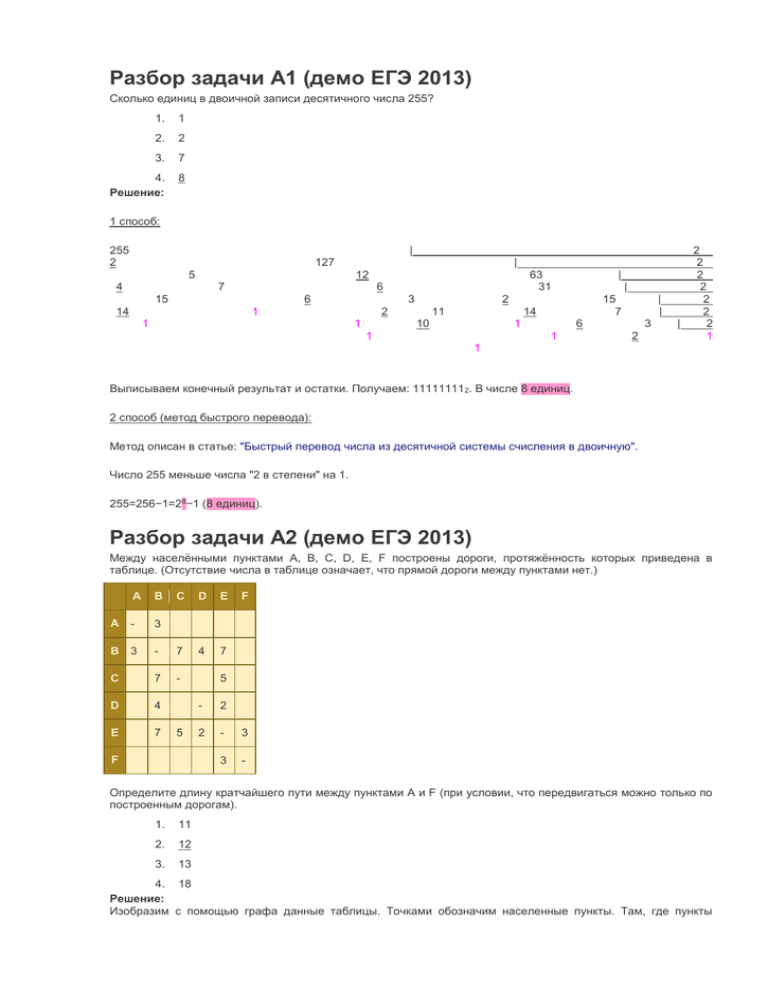
Разбор задачи A1 (демо ЕГЭ 2013)
Сколько единиц в двоичной записи десятичного числа 255?
1.
1
2.
2
3.
7
4.
Решение:
8
1 способ:
255
2
|
127
5
|
12
4
7
63
31
6
15
6
14
3
1
1
|
2
2
1
|
11
15
7
14
10
1
1
|
|
6
1
3
2
|
2
2
2
2
2
2
2
1
1
Выписываем конечный результат и остатки. Получаем: 11111111 2. В числе 8 единиц.
2 способ (метод быстрого перевода):
Метод описан в статье: "Быстрый перевод числа из десятичной системы счисления в двоичную".
Число 255 меньше числа "2 в степени" на 1.
255=256−1=28−1 (8 единиц).
Разбор задачи A2 (демо ЕГЭ 2013)
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в
таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
A
B
C
D
E
4
7
A -
3
B 3
-
7
C
7
-
D
4
E
7
5
F
F
5
-
2
2
-
3
3
-
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по
построенным дорогам).
1.
11
2.
12
3.
13
4. 18
Решение:
Изобразим с помощью графа данные таблицы. Точками обозначим населенные пункты. Там, где пункты
соединены
дорогой,
там
соединяем
Нарисуем путь из пункта А в F. Начнем с конца, с пункта F. В него идет дорога из Е:
В пункт Е ведут дороги из B, C и D:
В пункт B ведет дорога из A, в пункт С ведет дорога из В, в пункт D ведет дорога из B:
В пункт В ведет дорога из А:
точки.
Видим, что из А в F ведет 3-и пути. Надо найти кратчайший путь из трех. Добавим в граф значение
расстояний между пунктами:
1-й путь: A−B−E−F=3+7+3=13
2-й путь: A−B−C−E−F=3+7+5+3=18
3-й путь: A−B−D−E−F=3+4+2+3=12
Получили кратчайший путь: A−B−D−E−F. Его длина равна 12.
Разбор задачи A3 (демо ЕГЭ 2013)
Дан фрагмент таблицы истинности выражения F.
№
области
x1
x2
x3
x4
x5
x6
x7
F
1
1
1
0
1
1
1
1
0
2
1
0
1
0
1
1
0
0
3
0
1
0
1
1
0
0
1
Каким из приведённых ниже выражений может быть F?
1.
¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\ ¬x7
2.
¬x1 \/ x2 \/ ¬x3 \/ x4 \/ ¬x5 \/ ¬x6 \/ x7
3.
x1 /\ ¬x2 /\ x3 /\ ¬x4 /\ x5 /\ x6 /\ ¬x7
4.
Решение:
x1 \/ ¬x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ x6 \/ ¬x7
Сначала определим, как связаны переменные в F: с помощью конъюнкции (Λ) или дизъюнкции (V).
Если выражение содержит только конъюнкции, то оно может быть истинно только на одной области.
В данном случае F истинна (равна 1) на одной области (область №3 в таблице выше), поэтому начнем с
проверки выражений, содержащих конъюнкции. Это вариант 1 и вариант 3.
F=¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\
¬x7
(вариант 1)
F=x1 /\ ¬x2 /\ x3 /\ ¬x4 /\ x5 /\ x6 /\
¬x7
(вариант 3)
x1
x2
x3
x4
x5
x6
x7
F
1
1
0
1
1
1
1
0
0Λ1Λ1Λ1Λ1Λ0Λ0=0
1Λ0Λ0Λ0Λ1Λ1Λ0=0
1
0
1
0
1
1
0
0
0Λ0Λ0Λ0Λ1Λ0Λ1=0
1Λ1Λ1Λ1Λ1Λ1Λ1=1
0
1
0
1
1
0
0
1
1Λ1Λ1Λ1Λ1Λ1Λ1=1
Получили вариант 1: ¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\ ¬x7
Разбор задачи A4 (демо ЕГЭ 2013)
Для групповых операций с файлами используются маски имён файлов. Маска представляет собой
последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут
встречаться
следующие
символы.
Символ
«?»
(вопросительный
знак)
означает
ровно
один
произвольный
символ.
Символ «*» (звездочка) означает любую последовательность символов произвольной длины, в том числе «*»
может
задавать
и
пустую
последовательность.
В каталоге находится 6 файлов:

asc.wma

casting.wmv

last.wma

pasta.wmvx

pasta.wri
 vast.wma
Определите, по какой из перечисленных масок из этих 6 файлов будет отобрана указанная группа файлов:

casting.wmv

last.wma

pasta.wmvx

vast.wma
1.
?as*.wm?
2.
*as?.wm*
3.
?as*.wm*
4.
?as*.w*
Решение:
1 способ
Найдем, что общего у отобранных 4-х файлов:

casting.wmv

last.wma

pasta.wmvx
 vast.wma
Розовым
выделено
общее.
У всех файлов в названии:

Исходя
из
этого
маска
может
быть
такой:
?ast*.wm*
перед ast стоит 1 символ, поэтому поставлен символ "?";
 после ast стоит от 0 до 3 символов, поэтому поставлен символ "*".
У всех файлов в расширении после wm стоит от 1 до 2 символов, поэтому поставлен символ "*".
В вариантах ответа символ "t" не фигурирует, поэтому его опустим, он будет в составе символа "*".
Нашу маска ?ast*.wm* станет такой: ?as*.wm*. Это вариант 3.
2 способ (метод подстановки)
Рассмотрим предлагаемые маски.
Вариант
ответа
Маска
Ошибки
Комментарий
1
?as*.wm? не будет выбран файл
pasta.wmvx;
Символ "?" заменяет ровно 1
символ, а у нас 2 символа
2
*as?.wm* не будут выбраны файлы:
casting.wmv, pasta.wmvx и
будет ошибочно выбран
файл: asc.wma;
Символ "?" заменяет ровно 1
символ, а у нас 4 и 2
символа.
Символ "*" может заменить
0 символов, это приведет к
неверному выбору asc.wma
3
?as*.wm*
-
4
?as*.w *
будет ошибочно выбран
файл: pasta.wri;
w* не достаточно, это
приведет к неверному
выбору pasta.wri
Получили маску: ?as*.wm*
Перейти к другим задачам.
Разбор задачи A5 (демо ЕГЭ 2013)
Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не
превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам
строится новое шестнадцатеричное число по следующим правилам.

Вычисляются два шестнадцатеричных числа – сумма старших разрядов полученных чисел и
сумма младших разрядов этих чисел.

Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания
(без разделителей).
Пример.
Исходные
числа:
66,
43.
Поразрядные
суммы:
A,
9.
Определите, какое из предложенных чисел может быть результатом работы автомата.
1.
9F
Результат:
9A.
2.
911
3.
42
4.
Решение:
7A
Введем обозначения:

первое число - x1x2
 второе число - y1y2
Ограничения исходя из условия задачи:

x1≤6, x2≤6, y1≤6, y2≤6 => x1+y1≤C, x2+y2≤C. Получили С, т.к. 6+6=1210=С16. Сумма разрядов не может
быть больше С.
Рассмотрим предлагаемые варианты чисел.
9F-не подходит, т.к. сумма разрядов =F, a F>C.
911-не подходит, т.к. сумма разрядов =11, a 11>C.
42-не подходит, т.к. числа не записаны в порядке убывания.
7A-подходит.
Получили число: 7A.
Перейти к другим задачам.
Разбор задачи A6 (демо ЕГЭ 2013)
Ниже представлены две таблицы из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке
и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке
таблицы 1. Определите на основании приведённых данных фамилию и инициалы внучки Петровой С.М.
Таблица1
Фамилия_И.О.
Пол
25
Жвания К.Г.
Ж
49
Черняк А.П.
М
62
Петрова М.Н.
Ж
76
Ильченко Т.В.
Ж
82
Петрова С.М.
Ж
96
Басис В.В.
Ж
ID
102 Ильченко В.И.
М
123 Павлыш Н.П.
Ж
134 Черняк П.Р.
М
...
...
...
Таблица2
ID_Родителя
ID_Ребёнка
25
134
76
49
76
123
82
76
82
96
102
76
102
96
134
49
134
123
...
...
1.
Басис В.В.
2.
Ильченко Т.В.
3.
Павлыш Н.П.
4.
Решение:
Петрова М.Н.
Сначала нам нужно найти детей Петровой С.М., а затем найти дочек у этих детей.
Определим ID Петровой С.М. по таблице 1:
Таблица1
Фамилия_И.О.
ID
Пол
25
Жвания К.Г.
Ж
49
Черняк А.П.
М
62
Петрова М.Н.
Ж
76
Ильченко Т.В.
Ж
82
Петрова С.М.
Ж
96
Басис В.В.
Ж
102
Ильченко В.И.
М
123
Павлыш Н.П.
Ж
134
Черняк П.Р.
М
...
...
...
ID Петровой С.М.=82.
Находим в таблице 2 строки, где ID_Родителя=82 (найдем детей Петровой С.М.):
Таблица2
ID_Родителя
ID_Ребёнка
25
134
76
49
76
123
82
76
82
96
102
76
102
96
134
49
134
123
...
...
ID детей: 76, 96:
В таблице 1 найдем записи, где ID=76 и 96. Определим пол:
Таблица1
Фамилия_И.О.
ID
Пол
25
Жвания К.Г.
Ж
49
Черняк А.П.
М
62
Петрова М.Н.
Ж
76
Ильченко Т.В.
Ж
82
Петрова С.М.
Ж
96
Басис В.В.
Ж
102
Ильченко В.И.
М
123
Павлыш Н.П.
Ж
134
Черняк П.Р.
М
...
...
Получили, что у Петровой С.М. две дочки: Ильченко Т.В. (ID=76) и Басис В.В. (ID=96) Теперь ищем их детей.
Находим в таблице2 строки, где ID_Родителя=76 и 96:
Таблица2
ID_Родителя
ID_Ребёнка
25
134
76
49
76
123
82
76
82
96
102
76
102
96
134
49
134
123
...
...
В
поле
"ID_Родителя"
нет
значения
96,
следовательно,
У
Определим
детей
Ильченко
Т.В.
Их
ID
В таблице 1 найдем записи, где ID=49 и 123. Определим пол:
Басис
В.В.
детей
равно:
49,
нет.
123:
Таблица1
Фамилия_И.О.
ID
Пол
25
Жвания К.Г.
Ж
49
Черняк А.П.
М
62
Петрова М.Н.
Ж
76
Ильченко Т.В.
Ж
82
Петрова С.М.
Ж
96
Басис В.В.
Ж
102
Ильченко В.И.
М
123
Павлыш Н.П.
Ж
134
Черняк П.Р.
М
...
...
ID=49-м.п.,
это
сын
Ильченко
Т.В.,
внук
Петровой
С.М.
ID=123-ж.п., это дочь Ильченко Т.В., внучка Петровой С.М. Ее ФИО - Павлыш Н.П. ФИО выделено в таблице
выше.
Схематично решение обозначено на рисунке ниже:
Перейти к другим задачам.
Разбор задачи A8 (демо ЕГЭ 2013)
Производится одноканальная (моно) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в
секунду, для записи каждого значения используется 32 бит. Запись длится 4 минуты, её результаты
записываются в файл, сжатия данных не производится. Какая из приведённых ниже величин наиболее близка
к размеру полученного файла?
1.
44 Мбайт
2.
87 Мбайт
3.
125 Мбайт
4.
Решение:
175 Мбайт
Объем звукозаписи (размер аудиофайла) определяют по формуле:
V=υ*r*t*a,
где υ-частота дискретизации, r-разрешение, t-время, a-коэффициент.
υ=48 000 Гц=48*103 Гц
r=32 бита=32\8=4 байта
t=4 мин=4*60=240 сек
a=1-для монозвука
V=48*103*4*240*1=3*16*(5*2)3*4*3*8*5*2=3*24*53*23*22*3*23*5*2=32*54*213=9*625*213=5625*213 байт
Выбазим в мегабайтах:
1 мегабайт=220
213*5625\220=5625\27=5625\128=43,95≈44 мегабайта.
Перейти к материалу: "Как происходит кодировании звука"
Перейти к другим задачам.
Разбор задачи A9 (демо ЕГЭ 2013)
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется
неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную
последовательность.
Вот
этот
код:
А
–
00,
Б
–
01,
В
–
100,
Г
–
101,
Д
–
110.
Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было
декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1.
для буквы Д – 11
2.
это невозможно
3.
для буквы Г – 10
4.
Решение:
для буквы Д – 10
Построим графы, образующие используемые коды:
На графе видно, что для букв А, Б, В и Г сократить длину кода нельзя.
Возьмем, к примеру, букву А. Ее код - 00. Сократим на 1 разряд и получим 0 (идем вверх от кода 00 по ветке
графа). Тогда буква Б не сможет использоваться. Код буквы Б, 01, будет раскодирован как буква А, и
останется нераскодированный код 1.
Поэтому сократить длину кода можно только для буквы Д. Идем вверх от кода 110 по ветке графа и получаем
код 11.
Получили, буква Д с кодом 11.
Разбор задачи A10 (демо ЕГЭ 2013)
На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Выберите такой отрезок A, что формула
(
(x
∈
А)
→
(x
∈
P)
)
\/
(x
∈
Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
1.
[0, 3]
2.
[3, 11]
3.
[11, 15]
4.
Решение:
[15, 17]
Нужно решить уравнение: ( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)=1.
1 способ
Будем решать методом от противного. Пусть ( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)=0.
Преобразуем данное уравнение в систему уравнений:
Отрезки P и Q нам заданы, изобразим их:
Mы можем решить уравнения (2) и (3) в системе. x∈P=0 => x∉P. Аналогично, x∉Q.
Получили интервал: (−∞;2)υ[14;+∞).
Мы решали методом от противного, поэтому инвертируем полученный интервал: [2;14].
Рассмотрим предложенные варианты:
[0, 3] - не подходит;
[3, 11] - подходит, т.к. [3, 11] включен в [2;14];
[11, 15] - не подходит;
[15, 17] - не подходит;
Получили, А∈[3; 11]
2 способ
Решим уравнение: ( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)=1 методом подстановки.
В уравнение вместо P, Q впишем сами отрезки: [2, 10] и [6, 14].
(x ∈ А)=1 для всех вариантов.
Значения x
для проверки
(границы интервала)
((x ∈ А) → (x ∈ [2, 10]) ) \/ (x ∈ [6, 14])
[0, 3]
0,
3
(1→0)V0=0
(1→1)V0=1
2
[3, 11]
3,
11
1
(1→0)V1=1
3
[11, 15]
11,
15
1
(1→0)V0=0
4
[15, 17]
15,
17
0
(1→0)V0=0
Вариант
ответа
Интервал A
1
В таблице розовым выделен искомый интервал.
Перейти к другим задачам.
Разбор задачи A11 (демо ЕГЭ 2013)
В некоторой стране автомобильный номер длиной 5 символов составляют из заглавных букв (задействовано
30
различных
букв)
и
любых
десятичных
цифр
в
любом
порядке.
Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым
количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и
минимально
возможным
количеством
Определите объём памяти, отводимый этой программой для записи 50 номеров.
1.
100 байт
2.
150 байт
3.
200 байт
4.
Решение:
250 байт
бит).
Необходимо закодивовать: 30 букв + 10 цифр (от 0 до 9) = 40 символов.
Для кодирования необходимо 6 бит, т.к. 32<40<64 или 25<40<26.
Для кодирования 1 автомобильного номера нужно: 6*5=30 бит.
30 нацело не делится на 8. А нам по условию дано, что 1 номер должен кодироваться целым количеством
байтов. Поэтому округляем 30 до 32.
32\8=4 байта-отводится на 1 автомобильный номер.
Для кодирования 50 номеров нужно: 4*50=200 байт.
Перейти к другим задачам.
Разбор задачи A12 (демо ЕГЭ 2013)
В программе описан одномерный целочисленный массив A с индексами от 0 до 10. Ниже представлен
фрагмент этой программы, записанный на разных языках программирования, в котором значения элементов
массива сначала задаются, а затем меняются.
Бейсик
Паскаль
FOR i=0 TO 10
A(i)=i-1
NEXT i
FOR i=1 TO 10
A(i-1)=A(i)
NEXT i
A(10)=10
Си
for i:=0 to 10 do
A[i]:=i-1;
for i:=1 to 10 do
A[i-1]:=A[i];
A[10]:=10;
Алгоритмический язык
for (i=0;i<=10;i++) нц для i от 0 до 10
A[i]=i-1;
A[i]:=i-1
for (i=1;i<=10;i++) кц
A[i-1]=A[i];
нц для i от 1 до 10
A[10]=10;
A[i-1]:=A[i]
кц
A[10]:=10
Как изменятся элементы этого массива после выполнения фрагмента программы?
1.
все элементы, кроме последнего, окажутся равны между собой
2.
все элементы окажутся равны своим индексам
3.
все элементы, кроме последнего, будут сдвинуты на один элемент вправо
4.
Решение:
все элементы, кроме последнего, уменьшатся на единицу
В программе выполняется два цикла. В 1-м цикле элементам массива присваивается значение, равное №-у
индекса, уменьшенному на 1:
№ индекса
0
1
2
3
4
5
6
7
8
9
10
Значение элемента
массива
-1
0
1
2
3
4
5
6
7
8
9
Во 2-м цикле элементы с 1-го по 10-й будут сдвинуты на один элемент влево, а в освободившейся 10-й
позиции запишется значение 10.
Значения элементов массива до выполнения 2-го цикла. Розовым выделены элементы, которые будут
сдвинуты:
№ индекса
0
1
2
3
4
5
6
7
8
9
10
Значение
элемента
массива
1
0
1
2
3
4
5
6
7
8
9
Значения элементов массива после выполнения 2-го цикла.
№ индекса
0
1
2
3
4
5
6
7
8
9
10
Значение
элемента
массива
0
1
2
3
4
5
6
7
8
9
10
Получили, что все элементы окажутся равны своим индексам.
Перейти к другим задачам.
Разбор задачи A13 (демо ЕГЭ 2013)
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости,
включает в себя 4 команды-приказа и 4 команды проверки условия. Команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓,
влево
←,
вправо
→.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится, и программа
прервётся.
Другие 4 команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где
находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА
последовательность
КОНЕЦ
выполняется,
В
пока
условие
ЕСЛИ
ТО
ИНАЧЕ
выполняется
НАЧАЛО
ПОКА
команда1
(если
слева
условие
свободно
ЕСЛИ
КОНЕЦ
истинно)
или
команда2
ИЛИ
слева
(если
сверху
условие
команд
ПОКА
истинно.
конструкции
условие
команда1
команда2
ЕСЛИ
условие
ложно).
свободно
свободно
ТО
ИНАЧЕ
КОНЕЦ
КОНЕЦ
КОНЕЦ
влево
вверх
ЕСЛИ
ПОКА
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную
программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка А1)?
1.
8
2.
12
3.
17
4.
Решение:
21
Сначала построим траекторию движения робота. Она изображена на рисунке:
Синим цветом показана стена.
Робот может ходить только влево или вверх. Ходит вверх он только тогда, когда слева стена, в остальных
случаях - только влево. Робот может обойти стену слева при условии, что сверху стены нет. Поэтому "Г"
образный барьер робот не сможет преодолеть. На рисунке ниже показана данная тупикаовая ситуация:
Найдем тупиковые пути. На рисунке ниже они обозначены синим цветом. Розовым обозначены успешные
пути, приводящие к клетке А1.
По ходу синих путей все клетки тупиковые: непозволяющие роботу добратья до клетки А1. Они показаны на
рисунке ниже:
Посчитаем их количество. Получили 15 клеток.
Всего клеток: 6*6=36.
Количество успешных клеток: 36−15 = 21 клетка.
Перейти к другим задачам.
Разбор задачи B1 (демо ЕГЭ 2013)
У
исполнителя
Арифметик
две
команды,
которым
присвоены
номера:
1.
прибавь
2,
2.
умножь
на
3.
Первая
из
них
увеличивает
число
на
экране
на
2,
вторая
утраивает
его.
Например,
21211
–
это
программа
умножь
на
3
прибавь
2
умножь
на
3
прибавь
2
прибавь
2,
которая
преобразует
число
1
в
число
19.
Запишите порядок команд в программе преобразования числа 3 в число 69, содержащей не более 5 команд,
указывая лишь номера команд. Если таких программ более одной, то запишите любую из них.
Ответ: 11212
Решение:
Решим обратную задачу: из 69-и получим 3. Будем использовать команды:убавь на 2, раздели на 3. Первая
команда убавляет от числа 2, а вторая-делит число на 3. Выполним 5 команд. Изобразим ход выполнения
команд:
Изобразим ход выполнения команд в виде графа:
На рисунке видно,что в ходе выполнения команды получили число 3, оно выделено темно-розовым цветом. К
3-м приведет ветка графа: 69→23→21→7→5→3
Изобразим прямой ход выполнения, т.е. из 3-х получим 69:
3→5→7→21→23→69
Распишем подробно:
1 команда: 3+2=5 (1.прибавь 2).
2 команда: 5+2=7 (1.прибавь 2).
3 команда: 7*3=21 (2.умножь на 3).
4 команда: 21+2=23 (1.прибавь 2).
5 команда: 23*3=69 (2.умножь на 3).
Получили порядок команд: 11212.
Перейти к другим задачам.
Разбор задачи B2 (демо ЕГЭ 2013)
Определите значение переменной c после выполнения следующего фрагмента программы (записанного ниже
на разных языках программирования). Ответ запишите в виде целого числа.
Бейсик
a = 30
b = 14
a=a–2*b
IF a > b THEN
Паскаль
a := 30;
b := 14;
a := a – 2 * b;
if a > b then
c=b+2*a
ELSE
c=b-2*a
ENDIF
c := b + 2 * a
else
c := b - 2 * a;
Си
Алгоритмический
a = 30;
b = 14;
a = a – 2 * b;
if (a > b)
c = b + 2 * a;
else
c = b - 2 * a;
a := 30
b := 14
a := a – 2 * b
если a > b
то c := b + 2 * a
иначе c := b - 2 * a
все
Ответ: 10
Решение:
На франменте программы описана работа оператора ветвления "если-иначе" (if-else). На его входе
проверяется, удовлетворяют ли входящие a и b условию: a > b.
a=30.
b=14.
a=a – 2 * b=30−2*14=30−28=2.
a < b. Поэтому условие не выполняется. c = b - 2 * a=14−2*2=10.
Перейти к другим задачам.
Разбор задачи B3 (демо ЕГЭ 2013)
Дан фрагмент электронной таблицы.
A
B
1
2
2
= (B1 – A1)/2 = 2 – A1/2
C
4
= (C1 – A1)*2 – 4
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений
диаграмма по значениям диапазона ячеек A2 : С2 соответствовала рисунку? Известно, что все значения
диапазона,
по
которым
построена
диаграмма,
имеют
один
и
тот
же
знак.
Ответ: 5
Решение:
Определим значения в ячейках: А2,B2,C2.
A2=(B1 – A1)\2=(4−2)\2=1.
B2=2 – A1\2=2\2=1.
C2=(C1 – A1)*2 – 4. Значение ячейки C1 неизвестно. Его и нужно найти. Обозначим C1 за х.
C2=(x−2)*2−4.
По диаграмме видно, что соотношение значений в ячейках : А2,B2,C2 равно 1:1:2
А2=1,В2=1. Поэтому C2=2. Отсюда (x−2)*2−4=2 => 2x−4−4=2 => 2x=10 => x=5.
Получим, C1=5.
Перейти к другим задачам.
Разбор задачи B4 (демо ЕГЭ 2013)
Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и
тире. Сколько различных символов (цифр, букв, знаков пунктуации и т. д.) можно закодировать, используя код
азбуки Морзе длиной не менее четырёх и не более пяти сигналов (точек и тире)?
Ответ: 48
Решение:
Количество различных комбинаций из "точек" и "тире" определяется по формуле:
N=Xy,
где X - количество вариантов символов,
y - длина последовательности сигналов.
2 варианта символов: «точка» и «тире» (Х=2).
Длина последовательности 1 - 4 сигнала (y1=4).
Длина последовательности 2 - 5 сигналов (y2=5).
N1=Xy1=24=16 комбинаций.
N2=Xy2=25=32 комбинации.
N=N1+N2=16+32=48 комбинаций из "точек" и "тире", т.е. могут быть закодированы 48 различных символов.
Перейти к другим задачам.
Разбор задачи B5 (демо ЕГЭ 2013)
Определите, что будет напечатано в результате выполнения программы (записанной ниже на разных языках
программирования).
Бейсик
Паскаль
DIM N, S AS INTEGER var n, s: integer;
N=0
begin
S=0
n := 0;
WHILE S <= 35
s := 0;
N=N+1
while s <= 35 do
S=S+4
begin
WEND
n := n + 1;
PRINT N
s := s + 4
end;
write(n)
end.
Си
Алгоритмический
#include<stdio.h>
void main()
{
int n, s;
n = 0;
s = 0;
while (s <= 35)
{
n = n + 1;
s = s + 4;
}
printf("%d", n);
}
алг
нач
цел n, s
n := 0
s := 0
нц пока s <= 35
n := n + 1
s := s + 4
кц
вывод n
кон
Ответ: 9
Решение:
В данном фрагменте программы описана работа оператора цикла "пока" (while). Выполняется очередной
проход цикла, пока s≤35. На входе цикла n=0, s=0. При первом проходе к s прибавляем 4. n показывает
сколько проходов было в цикле (это счетчик). Цикл перестанет выполняться, когда s станет равной 36.
Значит,последний цикл, когда на входе s=32 (32 кратно 4-м и <36). При последнем проходе на выходе s=36.
36\4=9 - количество проходов в цикле, а это и есть n.
Ход выполнения программы отображен ниже:
Значение при № цикла:
Переменная
0
(вход цикла)
1
2
3
4
5
6
7
8
9
n
0
1
2
3
4
5
6
7
8
9
s
0
4
8
12 16 20 24 28 32 36
Перейти к другим задачам.
Разбор задачи B6 (демо ЕГЭ 2013)
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(1)
=
1
F(n)
=
F(n–1)
*
n,
при
n
>1
Чему
равно
значение
функции
F(5)?
В ответе запишите только натуральное число.
Ответ: 120
Решение:
Это задача на знание рекурсии.
1 способ
F(1) = 1
F(2) = F(1)*2
F(3) = F(2)*3
F(4) = F(3)*4
F(5) = F(4)*5=F(3)*4*5=F(2)*3*4*5=F(1)*2*3*4*5=1*2*3*4*5=24*5=120
2 способ (быстрый, если разобраться)
Функция F(n) - это факториал числа n, т.е. F(n)=n!
Рассмотрим, почему данный алгоритм описывает поиск факториала.
Рекурентная формула факториала имеет вид:
Подставляя вместо n! F(n) и учитывая, что мы начали с n=1, получим формулу:
А это и есть алгоритм, приведенный в задании. Поэтому данная задача сводится к поиску факториала числа
5:
5!
Факториал вычисляется следующим образом (упрощенный вид):
n!=1*2*...*n.
Подставляя значение 5 вместо n, получим:
5!=1*2*3*4*5=120.
Получили, F(n)=120.
Перейти к другим задачам.
Разбор задачи B7 (демо ЕГЭ 2013)
Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней
цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Ответ: 15
Решение:
При переводе числа из десятичной системы в другую, мы делим десятичное число на основание другой
системы счисления.
Первый остаток от деления - это последняя цифра числа в этой системе счисления. Чтобы в остатке был 0,
мы должны подобрать десятичное число, которое будет кратно основанию системы счисления, в которую
переводим. Для системы с основанием 3, такими числами могут быть: 3, 6, 9 и т.д. Для системы с основанием
5 - 5, 10, 15 и т.д.
По заданию, число должно быть минимально, поэтому для системы с основанием 3 - это число 3, а с
основанием 5 - это число 5.
3|3
3
0
1
5
5|5
1
0
310=103 и 510=103
Чтобы остаток числа был равен 0-ю в обеих системах счисления (с остатком 3 и 5), десятичное число должно
быть кратно числам: 3 и 5.
3*5=15 - это и есть искомое десятичное число.
15|3
15
0
5
15
15|5
3
0
1510=503 и 1510=305
Перейти к другим задачам.
Разбор задачи B8 (демо ЕГЭ 2013)
Ниже на четырёх языках записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: a и b.
Укажите наименьшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 21.
Бейсик
DIM X, A, B AS INTEGER
INPUT X
A=0: B=1
WHILE X > 0
A = A+1
B = B*(X MOD 10)
X = X \ 10
WEND
PRINT A
PRINT B
Си
#include<stdio.h>
void main()
{
int x, a, b;
scanf("%d", &x);
a=0; b=1;
while (x>0){
a=a+1;
b=b*(x%10);
x= x/10;
}
printf("%d\n%d", a, b);
Паскаль
var x, a, b: integer;
begin
readln(x);
a:=0; b:=1;
while x>0 do
begin
a:=a+1;
b:=b*(x mod 10);
x:= x div 10
end;
writeln(a); write(b);
end.
Алгоритмический
алг
нач
цел x, a, b
ввод x
a:=0; b:=1
нц пока x>0
a:=a+1
b:=b*mod(x,10)
x:=div(x,10)
кц
вывод a, нс, b
кон
}
Ответ: 37
Решение:
В программе отражена работа цикла while ("пока"). Суть программы следующая:
Вводится какое-то число x, затем мы анализируем цифры, входящие в это число. В каждом проходе цикла мы
делим нацело x на 10. Соответственно, двигаемся от единиц к более старшим разрядам: десяткам, сотням и
т.д. Затем мы выводим количество цифр, входящих в введенное число, и произведение этих цифр.
a - счетчик: хранит число, которое показывает сколько проходов было выполнено в цикле (сколько цифр в
числе). На выходе печатается значение a=2, поэтому цикл выполнялся 2 раза. Следовательно, в числе
содержится 2-е цифры.
b - хранит произведение цифр, входящих в число. Т.к. в числе 2-е цифры, то в b будет записано произведение
цифр, находящихся в позиции "единица" и "десяток", соответственно.
На выходе b=21, поэтому произведение равно 21. 21=3*7, поэтому входящее число может быть равно 37 или
73. По условию, число должно быть наименьшим.
Получили, x=37.
Перейти к другим задачам.
Разбор задачи B9 (демо ЕГЭ 2013)
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться
только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город
Л?
Ответ: 13
Решение:
Нарисуем путь из пункта А в Л. Начнем с конца, с пункта Л. К нему ведут дороги из И, Ж, К:
В пункт И ведет дорога из Д. В пункт Ж ведут дороги из Д, В, Е. В пункт К ведет дорога из Е.
В пункт Д ведут дороги из Б и В. В пункт В ведут дороги из Б, А, Г. В пункт Е ведет дорога из Г.
В пункт Б ведет дорога из А. В пункт В ведут дороги из Б, А, Г. В пункт Г ведет дорога из А.
В пункт Б ведет дорога из А. В пункт Г ведет дорога из А.
В итоге путь из пункта А в Л выглядит так:
Посчитаем, сколько "А" получилось. Из каждой "А" идет свой маршрут. На рисунке 13 различных путей.
Перейти к другим задачам.
Разбор задачи B10 (демо ЕГЭ 2013)
Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами.
А.
Сжать
архиватором,
передать
архив
по
каналу
связи,
распаковать.
Б.
Передать
по
каналу
связи
без
использования
архиватора.
Какой способ быстрее и насколько, если:

средняя скорость передачи данных по каналу связи составляет 220 бит в секунду;

объём сжатого архиватором документа равен 20% исходного;

время, требуемое на сжатие документа, – 5 секунд, на распаковку – 1 секунда?
В ответе напишите букву А, если быстрее способ А, или Б, если быстрее способ Б. Сразу после буквы
напишите
число,
обозначающее,
на
сколько
секунд
один
способ
быстрее
другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
Единиц измерения «секунд», «сек.», «с.» к ответу добавлять не нужно.
Ответ: A122
Решение:
Преобразуем некоторые данные, заданные в условии задачи
Объем документа переведем из мегабайт в байты:
V=20 Мб=20*220 =5*4*220=5*222байт.
Скорость передачи данных переведем из бит\сек в байт\сек:
ϑ=220бит\сек=220\23=217 байт\сек.
Теперь рассчитаем время передачи документа при ипользовании способов А и Б.
Способ А (с архивированием)
Объем сжатого документа равен:
Vсж=V\5 - это 20%.
Vсж=5*222\5=222 байт.
Время передачи сжатого файла:
t=Vсж\ϑ=222\217=25=32 сек.
Время, затраченное на сжатие файла, его передачу и распаковку:
tобщ=tсж+t+tрасп=5+32+1=38 сек.
Время передачи по способу А:
tА=38 сек.
Способ Б (без использования архиватора)
Время передачи файла:
t=V\ϑ=5*222\217=5*25=5*32=160 сек.
Время передачи по способу Б:
tБ=160 сек.
Получили, что способ А быстрее, чем Б. Найдем насколько секунд способ А быстрее способа Б:
tБ-tА=160-38=122 сек.
Получили А122.
Перейти к другим задачам.
Разбор задачи B11 (демо ЕГЭ 2013)
В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса
узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по
тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к
заданному
IP-адресу
узла
и
маске.
По
заданным
IP-адресу
узла
и
маске
определите
адрес
сети.
IP-адрес
узла:
217.19.128.131
Маска:
255.255.192.0
При записи ответа выберите из приведённых в таблице чисел четыре элемента IP-адреса сети и запишите в
нужном порядке соответствующие им буквы, без использования точек.
A
B
C
D
E
F
G
H
0
16 19 64 128 131 192 217
Пример.Пусть искомый IP-адрес: 192.168.128.0, и дана таблица
A
B
C
D
128 168 255 8
E
F
G
127 0
H
17 192
В этом случае правильный ответ будет записан в виде: HBAF
Ответ: HCEA
Решение:
IP-адрес состоит из 4-х байт.
255=111111112 (8 единиц, т.к. 28=256).
Поразрядная конъюнкция с IP-адресом узла, где байт маски равен 255 в итоге даст байт IP-адреса узла, т.к.
конъюнкция 111111112 и любого числа даст в итоге это последнее число.
Поразрядная конъюнкция с IP-адресом узла, где байт маски равен 0 в итоге даст 0, т.к. конъюнкция 0 и любого
числа даст в итоге 0.
IP-адрес сети: 217.19.х.0, где х-поразрядная конъюнкция 128 и 192.
Переведем числа 128 и 192 в двоичную систему счисления:
1способ:
128
12
|
64
8
8
6
4
0
2__
2__
2__
2__
2_
2_
2
1
|
32
16
2
12
4
0
|
|
16
12
0
0
0
8
8
4
|
4
2
|
|
0
2
0
Выписываем конечный результат и остатки.Получаем: 128=100000002
192
18
12
12
|
96
|
8
48
16
0
|
4
16
24
8
0
8
0
0
4
4
|
2
12
12
0
|
6
6
|
3
0
|
2
2__
2__
2__
2__
2_
2_
2
1
1
Выписываем конечный результат и остатки.Получаем: 192=110000002
2 способ (метод быстрого перевода):
Метод описан в статье: "Быстрый перевод числа из десятичной системы счисления в двоичную".
128=100000002 (7 нулей, т.к. 128=27)
192=128+64=27+26
27=100000002
26=10000002
192Λ128=
Видно, что поразрядная конъюнкция равна второму слагаемому, т.е. 128.
IP-адрес сети: 217.19.128.0.
Получаем: HCEA.
Перейти к другим задачам.
Разбор задачи B12 (демо ЕГЭ 2013)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|»,
а
для
логической
операции
«И»
–
символ
«&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Запрос
Фрегат | Эсминец
Найдено страниц
(в тысячах)
3400
Фрегат & Эсминец 900
Фрегат
2100
Какое
количество
страниц
(в
тысячах)
будет
найдено
по
запросу
Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все
искомые слова, не изменялся за время выполнения запросов.
Ответ: 2200
Решение:
Изобразим запросы в виде диаграмм Эйлера-Венна.
Запрос "Фрегат" обозначим символом "Ф", "Эсминец" - символом "Э".
Э=(Ф|Э)-Ф+(Ф&Э)=3400-2100+900=2200.
Перейти к другим задачам.
Разбор задачи B13 (демо ЕГЭ 2013)
У
исполнителя
Удвоитель
две
команды,
1.
прибавь
2.
умножь
Первая
из
них
увеличивает
на
1
число
на
Программа
для
Удвоителя
–
это
Сколько есть программ, которые число 3 преобразуют в число 23?
Ответ: 22
Решение:
которым
присвоены
номера:
1,
на
2.
экране,
вторая
удваивает
его.
последовательность
команд.
Нам нужно построить граф, описывающий выполнение команд Удвоителя. Строим его до тех пор, пока не
получим число 11. 23/2=11 с остатком. Числа больше 11 дают только одну программу, т.к. нельзя применить
команду "умножить на 2". Если при построении графа получаем числа больше 11, то дальше от таких чисел
ветки не строим. Также поступаем и с числами, которые уже есть в графе.
Построим этот граф:
После выполнения 4-х команд получаем число 11.
Обозначим количество программ-решений для получения из числа n числа 23 как Р(n).
Определим P(11):
12*2>23, поэтому к 23 ведет только 1 решение.
22*2>23, поэтому к 23 ведет только 1 решение.
Получили, P(11)=1+1=2.
Зная P(11), можно определить P(10):
P(11)=2 решения.
20*2>23, поэтому к 23 ведет только 1 решение.
Получили, P(10)=2+1=3.
Зная P(10) можно определить P(8):
P(10)=3 решения.
18*2>23, поэтому к 23 ведет только 1 решение.
16*2>23, поэтому к 23 ведет только 1 решение.
Получили, P(8)=3+1+1=5.
Зная P(8) можно определить P(6):
P(8)=5 решений.
14*2>23, поэтому к 23 ведет только 1 решение.
12*2>23, поэтому к 23 ведет только 1 решение.
Получили, P(6)=5+1+1=7.
Зная P(6) можно определить P(5):
P(6)=7 решений.
P(10)=3 решения.
Получили, P(5)=7+3=10.
Теперь можно определить P(3):
P(5)=10 решений.
P(8)=5 решений.
P(6)=7 решений.
P(3)=10+5+7=22.
Получили 22 программы.
Краткое решение:
P(n)=1 при n>11.
P(11)=P(12)+P(22)=2 программы.
P(10)=P(11)+P(20)=2+1=3 программы.
P(8)=P(9)+P(16)=P(10)+P(18)+P(16)=3+1+1=5 программ.
P(6)=P(7)+P(12)=P(8)+P(14)+P(12)=5+1+1=7 программ.
P(5)=P(6)+P(10)=7+3=10
программ.
P(3)=P(4)+P(6)=P(5)+P(8)+P(6)=10+5+7=22 программы.
Перейти к другим задачам.
Разбор задачи B14 (демо ЕГЭ 2013)
Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для Вашего
удобства алгоритм представлен на четырёх языках).
Бейсик
Паскаль
DIM A, B, T, M, R AS INTEGER
A = -20: B = 20
M = A: R = F(A)
FOR T = A TO B
IF F(T) < R THEN
M=T
R = F(T)
ENDIF
NEXT T
PRINT M
FUNCTION F(x)
F = 3*(x-8)*(x-8)
END FUNCTION
var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F := 3*(x-8)*(x-8)
end;
begin
a := -20; b := 20;
M := a; R := F(a);
for t := a to b do begin
if (F(t)<R) then begin
M := t;
R := F(t)
end
end;
write(M);
end.
Си
Алгоритмический
#include<stdio.h>
int F(int x)
{
return 3*(x-8)*(x-8);
}
void main()
{
int a, b, t, M, R;
a = -20; b = 20;
M = a; R = F(a);
for (t=a; t<=b; t++){
if (F(t)<R) {
M = t; R = F(t);
}
}
printf("%d", M);
}
алг
нач
цел a, b, t, R, M
a := -20; b := 20
M := a; R := F(a)
нц для t от a до b
если F(t)< R
то
M := t; R := F(t)
все
кц
вывод M
кон
алг цел F(цел x)
нач
знач := 3*(x-8)*(x-8)
кон
Ответ: 8
Решение:
Данная программа анализирует функцию F=3*(x-8)*(x-8) на интервале, где х ∈ [-20, 20] (цикл проходит с шагом
1 все значения х на этом интервале: -20,-19 и т.д).
М хранит значение х, а R-значение F(x), где F(x)-минимальное. Т.е. программа осуществляет поиск минимума
функции: min F(x) и соответствующее минимуму значение х. Выводится х. Поэтому х мы должны определить.
1 способ.
Нарисуем, как выглядит функция 3*(x-8)*(x-8):
На рисунке видно ,что функция минимальна при х=8.
2 способ.
Преобразуем функцию F=3*(x-8)*(x-8):
3*(x-8)*(x-8)=3(х2-16х+64)=3х2-48х+192.
Найдем F´(x):
F´(x)=6х-48.
В точках экстремума F´(x)=0. Тогда 6х-48=0. Отсюда х=48\6=8.
Экстремум у нас один, поэтому x=8 - минимум.
Перейти к другим задачам.
Разбор задачи B15 (демо ЕГЭ 2013)
Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, y1, y2 y3, y4, которые
удовлетворяют
всем
перечисленным
ниже
условиям?
(x1
→
x2)
/\
(x2
→
x3)
/\
(x3
→
x4)
=
1
(¬y1
\/
y2)
/\
(¬y2
\/
y3)
/\
(¬y3
\/
y4)
=
1
(y1
→
x1)
/\
(y2
→
x2)
/\
(y3
→
x3)
/\
(y4
→
x4)
=
1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, y1, y2 y3, y4, при
которых
выполнена
данная
система
равенств.
В качестве ответа Вам нужно указать количество таких наборов.
Ответ: 15
Решение:
Преобразуем систему уравнений к виду:
(x1 → x2) /\ (x2 → x3) /\ (x3 → x4) = 1 (1)
(y1 → y2) /\ (y2 → y3) /\ (y3 → y4) = 1 (2)
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) = 1 (3)
Розовым выделено уравнение, которое было преобразовано. ¬y1 \/ y2=y1 → y2. Аналогично и для остальных
частей данного уравнения.
Решим уравнение (1).
1 способ
Уравнение (1) содержит импликации (→), связанные конъюнкцией (/\). Соответственно, чтобы уравнение было
истинно, все входящие импликации должны быть истинны:
x1 → x2=1,
x2 → x3=1,
x3 → x4=1.
Таблица истинности для импликации на примере x1 → x2:
x1
x2
x1→x2
0
0
1
0
1
1
1
0
0
1
1
1
Розовым выделена комбинация, когда импликация ложна. Видно, что в ней идут подряд "1" и "0". Выпишем
комбинации для x1x2x3x4, в которых не встречается подряд "1" и "0", чтобы импликации x1 → x2, x2 → x3, x3
→ x4 не были равны 0-ю.
x1
x2
x3
x4
0
0
0
0
0
0
0
1
0
0
1
1
0
1
1
1
1
1
1
1
Получили 5 комбинаций.
2 способ
Решим методом от противного. Рассмотрим случаи, когда уравнение (x1 → x2) /\ (x2 → x3) /\ (x3 → x4)=0.
Импликация ложна, когда посылка истинна, а следствие ложно. Таблица истинности приведена выше:
Исходя из этого определим случаи, когда импликация ложна.
Если x1 → x2=0:
x1
x2
x3
x4
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
x1=1, x2=0,
x3 и x4 - 0 или 1, поэтому они дают 22=4 комбинации.
Если x2 → x3=0:
x1
x2
x3
x4
0
1
0
0
0
1
0
1
1
1
0
0
1
1
0
1
x2=1, x3=0,
x1 и x4 - 0 или 1, поэтому они дают 4 комбинации.
Если x3 → x4=0:
x1
x2
x3
x4
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
0
x3=1, x4=0,
x1 и x2 - 0 или 1, поэтому они дают 4 комбинации.
Получили 4*3=12 комбинаций.
Также нужно учеть повторные комбинации. В данном случае повторная комбинация одна: 1010. В таблицах
выше такая комбинация выделена синей рамкой. Она встретилась 2 раза, поэтому общее число комбинаций с
учетом повторов:
12−1=11.
Мы решали уравнение методом от противного. Теперь перейдем к исходному уравнению.
Общее число комбинаций при 4-х переменных: 24=16. 16-11=5 комбинаций.
Перейдем к уравнению (2):
(y1 → y2) /\ (y2 → y3) /\ (y3 → y4) = 1.
Это уравнение содержит переменные y1, y2, y3, y4, которые не связаны с уравнением (1). Уравнения (1) и (2)
независимы друг от друга. Но вид уравнения (2) аналогичен виду уравнения (1), которое мы решили выше.
Поэтому получаем 5 комбинаций.
y1
y2
y3
y4
0
0
0
0
0
0
0
1
0
0
1
1
0
1
1
1
1
1
1
1
Добавим к системе уравнение (3):
(y1 → x1) /\ (y2 → x2) /\ (y3 → x3) /\ (y4 → x4) = 1
Выпишем рядом решения уравнений (1) и (2)
y1
y2
y3
y4
x1
x2
x3
x4
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
1
0
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
Будем решать систему уравнений методом от противного. Уравнение (3) равно 0-ю.
y1 → x1=0:
y1=1, x1=0
y1
y2
y3
y4
x1
x2
x3
x4
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
1
0
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
Получили 4 комбинации.
y2 → x2=0:
y2=1, x2=0. Строку 1111 (y1y2y3y4) не берем во избежания повторов.
y1
y2
y3
y4
x1
x2
x3
x4
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
1
0
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
Получили 3 комбинации.
y3 → x3=0
y3=1, x3=0. Строки 1111, 0111 (y1y2y3y4) не берем во избежания повторов.
y1
y2
y3
y4
x1
x2
x3
x4
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
1
0
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
Получили 2-е комбинации.
y4 → x4=0
y4=1, x4=0. Строки 1111, 0111, 0011 (y1y2y3y4) не берем во избежания повторов.
y1
y2
y3
y4
x1
x2
x3
x4
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
1
0
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
Получили 1-у комбинацию.
Всего комбинаций: 4+3+2+1=10.
Мы решали систему уравнений методом от противного. Теперь перейдем к исходной системе.
Общее число комбинаций: 5*5=25. Уравнения (1) и (2) дают по 5 независимых комбинаций.
25-10=15 комбинаций.
Перейти к другим задачам.
Разбор задачи C1 (демо ЕГЭ 2013)
Требовалось написать программу, при выполнении которой с клавиатуры считывается координата точки на
прямой (x – действительное число) и определяется принадлежность этой точки одному из выделенных
отрезков
В
и
D
(включая
границы).
Программист торопился и написал программу неправильно.
Бейсик
INPUT x
IF x>=-3 THEN
IF x<=9 THEN
IF x>1 THEN
PRINT "не принадлежит"
ELSE
Паскаль
var x: real;
begin
readln(x);
if x>=-3 then
if x<=9 then
if x>1 then
PRINT "принадлежит"
ENDIF
ENDIF
ENDIF
END
write('не принадлежит')
else
write('принадлежит')
end.
Си
Алгоритмический язык
void main(void)
алг
{
нач
float x;
вещ x
scanf("%f",&x);
ввод x
if(x>=-3)
если x>=-3 то
if(x<=9)
если x<=9 то
if(x>1)
если x>1 то
printf("не принадлежит");
вывод 'не принадлежит'
else
иначе
printf("принадлежит");
вывод 'принадлежит'
}
все
все
все
кон
Последовательно
выполните
следующее.
1. Перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах,
принадлежащих различным областям (A, B, C, D и E). Границы (точки –3, 1, 5 и 9) принадлежат
заштрихованным областям (B и D соответственно).
Область
Условие 1
(x >= –3)
Условие 2
(x <= 9)
Условие 3
(x > 1)
Программа
выведет
Область
обрабатывается
верно
A
B
C
D
E
В столбцах условий укажите «Да», если условие выполнится; «Нет», если условие не выполнится; «—»
(прочерк), если условие не будет проверяться; «не изв.», если программа ведет себя по-разному для разных
значений, принадлежащих данной области. В столбце «Программа выведет» укажите, что программа выведет
на экран. Если программа ничего не выводит, напишите «—» (прочерк). Если для разных значений,
принадлежащих области, будут выведены разные тексты, напишите «не изв.». В последнем столбце укажите
«Да»
или
«Нет».
2. Укажите, как нужно доработать программу, чтобы не было случаев её неправильной работы. (Это можно
сделать несколькими способами, достаточно указать любой способ доработки исходной программы.)
Решение:
1 часть:
Рассмотрим подробно каждую область. Выразим их через условия: x≥−3, x≤9, x>1.
Обозначим условия 1, 2 и 3 через Y1, Y2, Y3:
Y1=(x≥−3)
Y2=(x≤9)
Y3=(x>1)
Рассмотрим подробно каждую область.
Область А∈(−∞;−3). A: (x<−3)Λ(x≤9)Λ(x≤1):
(x<−3)Λ(x≤9)Λ(x≤1)=¬Y1ΛY2Λ¬Y3. Поэтому условие1 и условие 3 не выполняются.
Область B∈[−3;1]. B: (x≥−3)Λ(x≤9)Λ(x≤1):
(x≥−3)Λ(x≤9)Λ(x≤1)=Y1ΛY2Λ¬Y3. Поэтому условие 3 не выполняется.
Область С∈(1;5). С: (x≥−3)Λ(x≤9)Λ(x>1):
(x≥−3)Λ(x≤9)Λ(x>1)=Y1ΛY2ΛY3. Поэтому все условия выполняется.
Область D∈[5;9]. D: (x≥−3)Λ(x≤9)Λ(x>1):
(x≥−3)Λ(x≤9)Λ(x>1)=Y1ΛY2ΛY3. Поэтому все условия выполняется.
Область E∈(9;+∞). E: (x≥−3)Λ(x>9)Λ(x>1):
(x≥−3)Λ(x>9)Λ(x>1)=Y1Λ¬Y2ΛY3. Поэтому условие 2 не выполняется.
Заполним левую часть таблицы, которая касается условий.
Если первое условие: x≥-3 не выполняется, то программа не будет проверять остальные условия: x≤9, x>1.
Если x≥-3 выполняется, но не выполняется второе условие: x≤9, то не будет проверяться третье условие: x>1.
В таких случаях в таблице ставим "−".
Область
Условие 1
(x >= –3)
Условие 2
(x <= 9)
Условие 3
(x > 1)
A
Нет
−
−
B
Да
Да
Нет
C
Да
Да
Да
D
Да
Да
Да
E
Да
Нет
−
Теперь посмотрим, как работает программа:
Получили области

[-3;1] (область B)- программа выведет: "принадлежит" (∈)

(1;9] (область CVD) - программа выведет "не принадлежит"(∉)
Другие области: A, E программа вообще не будет обрабатывать и ничего не выведет, поэтому в таблице ниже
ставим "−". Эти области обрабатываются неверно, т.к. программа, должна была вывести для них "не
принадлежит".
Определим корректность работы программы для областей B, C, D. Программа должна искать
принадлежность
x
к
областям
B
и
D:
Область
B
обрабатывается
верно,
т.к.
программа
выводит
Область
С
обрабатывается
верно,
т.к.
программа
выводит
"не
Область D обрабатывается неверно, т.к. программа выводит "не принадлежит".
Заполним правую часть таблицы, которая касается вывода текста и корректности работы:
"принадлежит".
принадлежит".
Область
обрабатывается
верно
Программа
выведет
Область
A
−
Нет
B
принадлежит
Да
C
не принадлежит
Да
D
не принадлежит
Нет
E
−
Нет
2 часть (доработка программы):
На языке алгебры логики искомая область определяется так:
BVD
(x≥−3)Λ(x≤1)V(x≥5)Λ(x≤9).
Доработка для корректной работы программы на языках программирования:
Бейсик
Паскаль
IF x>=−3 AND x<=1 OR
if (x>=−3) and (x<=1) or
x>=5 AND x<=9 THEN
(x>=5) and (x<=9) then
PRINT "принадлежит"
write('принадлежит')
ELSE
else
PRINT "не принадлежит"
write('не принадлежит')
Си
Алгоритмический язык
if ((x>=−3)&&(x<=1)||
если x>=−3 и x<=1 или
(x>=5)&&(x<=9))
x>=5 и x<=9 то
printf("принадлежит");
вывод 'принадлежит'
else
иначе
printf("не принадлежит");
вывод 'не принадлежит'
Разбор задачи C2 (демо ЕГЭ 2013)
Дан целочисленный массив из 30 элементов. Элементы массива могут принимать целые значения от 0 до
100. Опишите на русском языке или на одном из языков программирования алгоритм, позволяющий найти и
вывести произведение элементов массива, которые имеют нечётное значение и делятся на 3. Гарантируется,
что в исходном массиве есть хотя бы один элемент, значение которого нечётно и кратно 3.
Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные
ниже, но разрешается не использовать часть из них. Исходные данные всегда подобраны так, что результат
произведения не выходит за пределы объявленных типов данных.
Паскаль
const
N=30;
var
a: array [1..N] of longint;
i, j, p: longint;
begin
for i := 1 to N do
readln(a[i]);
…
end.
Бейсик
N=30
Алгоритмический язык
алг
нач
цел N=30
целтаб a[1:N]
цел i, j, p
нц для i от 1 до N
ввод a[i]
кц
...
кон
Си
#include <stdio.h>
DIM A(N) AS LONG
DIM I, J, P AS LONG
FOR I = 1 TO N
INPUT A(I)
NEXT I
…
END
#define N 30
void main(void){
long a[N];
long i, j, p;
for (i=0; i<N; i++)
scanf("%ld", &a[i]);
…
}
Русский (естественный) язык
Объявляем массив A из 30 элементов.
Объявляем целочисленные переменные I, J, P.
В цикле от 1 до 30 вводим элементы массива A с 1-го по 30-й.
В качестве ответа Вам необходимо привести фрагмент программы (или описание алгоритма на естественном
языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом
языке программирования (укажите название и используемую версию языка программирования, например
Free Pascal 2.4) или в виде блок-схемы. В этом случае Вы должны использовать те же самые исходные
данные и переменные, какие были предложены в условии (например, в образце, записанном на
естественном языке).
Решение:
Фрагмент решения в программе выделен розовым:
Паскаль
Алгоритмический язык
алг
нач
цел N=30
целтаб a[1:N]
цел i, j, p
нц для i от 1 до N
ввод a[i]
кц
const
N=30;
var
a: array [1..N] of longint;
i, j, p: longint;
begin
for i := 1 to N do
readln(a[i]);
p := 1;
for i := 1 to N do
if (a[i] mod 2<>0) and (a[i] mod 3=0) then
p := p * a[i];
writeln(p);
p := 1
нц для i от 1 до N
если mod(a[i],2)<>0 и mod(a[i],3)=0
то
p := p * a[i]
все
кц
вывод p
end.
кон
Бейсик
Си
N=30
DIM A(N) AS LONG
DIM I, J, P AS LONG
FOR I = 1 TO N
INPUT A(I)
NEXT I
#include <stdio.h>
#define N 30
void main(void){
long a[N];
long i, j, p;
for (i=0; i<N; i++)
scanf("%ld", &a[i]);
P=1
FOR I = 1 TO N
IF A(I) MOD 2<>0 AND A(I) MOD 3=0 THEN
P = P * A(I)
ENDIF
NEXT I
PRINT P
p=1;
for (i=0; i<N; i++)
if (a[i]%2!=0 && a[i]%3==0)
p=p*a[i];
printf("%ld", p);
}
END
Русский (естественный) язык
Объявляем массив A из 30 элементов.
Объявляем целочисленные переменные I, J, P.
В цикле от 1 до 30 вводим элементы массива A с 1-го по 30-й.
Записываем в P (произведение элементов массива) значение, равное 1. В цикле от 1-го до 30-го элемента
ищем числа, которые являются нечетными (остаток от деления элемента массива на 2 не равен 0) и кратны 3м (остаток от деления на 3 равен 0). Если в очередном проходе цикла находим такое число, то тогда считаем
произведение данного элемента массива и значения переменной P. Результат сохраняем в переменную P.
Переходим к следующему элементу массива.
Когда цикл завершается, выводится значение переменной P
Разбор задачи C3 (демо ЕГЭ 2013)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по
очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить
количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из
16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра
завершается в тот момент, когда количество камней в куче становится не менее 22. Победителем считается
игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 22 или больше камней. В
начальный
момент
в
куче
было
S
камней,
1
≤
S
≤
21.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах
противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации,
которая
ему
может
встретиться
при
различной
игре
противника.
Выполните
следующие
задания.
Во
всех
случаях
обосновывайте
свой
ответ.
1.
а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что
найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня
может
выиграть
своим
первым
ходом.
Опишите
выигрышную
стратегию
Вани.
2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём

Петя не может выиграть за один ход, и

Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня. Для
каждого указанного значения S опишите выигрышную стратегию Пети.
3. Укажите значение S, при котором:

у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при
любой игре Пети, и
 у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных
при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто
делает ход, в узлах – количество камней в куче.
Решение:
часть 1
а) Петя может выиграть за один ход.
При S≥22 игра завершается. Пети может:

добавить в кучу один камень (+1),

увеличить количество камней в куче в два раза (*2).
Рассмотрим каждый вариант:

(+1):S= 22−1=21
 (*2): S=22\2=11 =>S∈[11;21]
11*2=22
12*2=24
...
21*2=42
Получим следующие стратегии:

при S∈[11;20] надо удвоить количество камней
(>22)
(>22)
 при S=21 надо добавить один камень или удвоить количество камней
б)
Ваня
может
выиграть
за
один
ход
при
любом
ходе
Пети.
Используем решение предыдущей задачи. Ваня может выиграть при S≥11. Но Ваня ходит 2-м, а Петя 1-м.
Нам
нужно
подобрать
S.
11
можно
получить
следующим
образом:
10+1
Построим дерево решений для S=10:
Получили,
Стратегия будет такой:
часть
Петя не может выиграть 1-м ходом,
Используем
решение
Дерево решений имеет вид:
S=10.
он
может выграть
задачи
Нам
нужно
10 можно получить следующим образом:

9+1
 5*2
Получаем следующие деревья решений при S=5 и S=9:
за
2 хода
части
подобрать
при
любом
1
ходе
2
Вани:
(б).
S.
Красным крестом обозначена проигрышная ветка для Пети. При S=5 такая ветка приведет к тому, что никто
не выиграет. При s=9 такая ветка приведет к тому, что Выиграет Ваня первым ходом, получая 36. В решении
проигрышные
стратегии
указывать
не
нужно.
Здесь
они
приведены
для
наглядности.
Получим следующие выигрышные стратегии:
Получили,
S=5
и
S=9.
часть
3
Ваня может выиграть за 1 или 2 хода при любых ходах Пети. Ваня не может гарантированно выйграть 1-м
ходом.
Используем решение части 2. Стратегии, приведенные выше гарантируют выйгрыш 2-м ходом.
Нам
нужно
подобрать
S.
5 можно получить следующим образом:
 4+1
9 можно получить следующим образом:
 8+1
Построим
Дерево для S=4:
деревья
решений.
Из дерева видно, что Ваня не сможет выиграть 1-м ходом, т.к. 9<22 и 16<22 (правая ветка дерева, ветки
4→8→9
и
4→8→16),
поэтому
s=4
не
подходит.
Дерево для S=8:
Из
дерева
видно,
Получили,
Стратегия будет такой:
что
Ваня
сможет
выиграть
1-м
ходом,
32>22
(ветка
8→16→32).
S=8.
Разбор задачи C4 (демо ЕГЭ 2013)
На вход программе подаются сведения о пассажирах, желающих сдать свой багаж в камеру хранения на
заранее известное время до полуночи. В первой строке сообщается число пассажиров N, которое не меньше
3, но не превосходит 1000; во второй строке – количество ячеек в камере хранения K, которое не меньше 10,
но
не
превосходит
1000.
Каждая из следующих N строк имеет следующий формат:
<Фамилия> <время сдачи багажа> <время освобождения ячейки>,
где
<Фамилия>
–
строка,
состоящая
не
более
чем
из
20
непробельных
символов;
<время сдачи багажа> – через двоеточие два целых числа, соответствующие часам (от 00 до 23 – ровно 2
символа)
и
минутам
(от
00
до
59
–
ровно
2
символа);
<время
освобождения
ячейки>
имеет
тот
же
формат.
<Фамилия>, <время сдачи багажа> и <время освобождения ячейки> разделены одним пробелом.
Время
освобождения
больше
времени
сдачи.
Сведения отсортированы в порядке времени сдачи багажа. Каждому из пассажиров в камере хранения
выделяется свободная ячейка с минимальным номером. Если в момент сдачи багажа свободных ячеек нет,
то
пассажир
уходит,
не
дожидаясь
освобождения
одной
из
них.
Требуется написать программу (укажите используемую версию языка программирования, например Borland
Pascal 7.0), которая будет выводить на экран для каждого пассажира номер ему предоставленной ячейки
(можно сразу после ввода данных очередного пассажира). Если ячейка пассажиру не предоставлена, то его
фамилия
не
печатается.
Пример
входных
данных:
3
10
Иванов
09:45
12:00
Петров
10:00
11:00
Сидоров
12:00
13:12
Результат
работы
программы
на
этих
входных
данных:
Иванов
1
Петров
2
Сидоров 1
Решение:
Программа написана на языках:

Паскаль (среда разработки Turbo Pascal 7.0),

Бейсик (среда разработки Quick Basic 4.5),

Си (среда разработки Borland C++ 3.1),

Алгоритмический язык (среда разработки Кумир 1.9.0).
Чтобы прочесть комментарии к программе, наведите мышью на соответствующую строку. Строки,
снабженные комментарием, выделены фиолетовым цветом.
Напротив названия языка программирования в скобках содержатся ссылки на скачку исходников и ехе
(исполняемых файлов).
Паскаль (исходник, exe-файл)
Алгоритмический язык (исходник)
var
алг
i,j,N,K,time1,time2: integer;
нач
p:array[1..1000] of integer;
цел i, j, N, K, time1,time2
c,c1:char;
целтаб p[1:1000]
name:string;
лит str,name
begin
ввод N
readln(N,K);
ввод K
for i:=1 to K do
нц для i от 1 до K
p[i]:=0;
p[i]:=0
for i:=1 to N do
кц
begin
нц для i от 1 до N
name:='';
ввод str
repeat
j:=1
read(c);
name:=""
name:=name+c;
нц
until c=' ';
name:=name+str[j]
read(c,c1);
j:=j+1
time1:=60*((ord(c)-ord('0'))*10+ ord(c1)-ord('0'));
кц при str[j]=" "
read(c,c,c1);
time1:=(код(str[j+1])-код('0'))*60*10
time1:=time1+(ord(c)-ord('0'))*10+ord(c1)-ord('0');
time1:=time1+(код(str[j+2])-код('0'))*60
read(c,c,c1);
time1:=time1+(код(str[j+4])-код('0'))*10
time2:=60*((ord(c)-ord('0'))*10+ ord(c1)-ord('0'));
time1:=time1+(код(str[j+5])-код('0'))
readln(c,c,c1);
time2:=(код(str[j+7])-код('0'))*60*10
time2:=time2+(ord(c)-ord('0'))*10+ord(c1)-ord('0');
time2:=time2+(код(str[j+8])-код('0'))*60
for j:=1 to K do
time2:=time2+(код(str[j+10])-код('0'))*10
if p[j]<=time1 then
begin
p[j]:=time2;
writeln(name,j);
break;
end;
end;
readln
end.
time2:=time2+(код(str[j+11])-код('0'))
нц для j от 1 до K
если time1>=p[j] то
p[j]:=time2
вывод name,' ',j,нс
выход
все
кц
кц
кон
Бейсик (исходник)
СИ (исходник, exe-файл)
DIM i, j, N, K, time1, time2 AS INTEGER
DIM p(1000) AS INTEGER
DIM nm AS STRING
DIM s AS STRING
INPUT N
INPUT K
FOR i = 1 TO K
p(i) = 0
NEXT i
FOR i = 1 TO N
LINE INPUT s
c$ = MID$(s, 1, 1)
j=1
WHILE NOT (c$ = " ")
j=j+1
c$ = MID$(s, j, 1)
WEND
nm = MID$(s, 1, j - 1)
time1 = (ASC(MID$(s, j + 1, 1))-ASC("0"))*60*10
time1 = time1+(ASC(MID$(s, j+2,1))-ASC("0"))*60
time1 = time1 +(ASC(MID$(s, j+4,1))-ASC("0"))*10
time1 = time1 + (ASC(MID$(s, j + 5, 1))-ASC("0"))
time2 = (ASC(MID$(s, j + 7,1))-ASC("0"))*60*10
time2 = time2 +(ASC(MID$(s, j+8,1))-ASC("0"))*60
time2 =time2+(ASC(MID$(s, j+10,1))-ASC("0"))*10
time2 = time2 + (ASC(MID$(s, j+11,1))-ASC("0"))
FOR j = 1 TO K
IF time1 >= p(j) THEN
p(j) = time2
PRINT nm; j
GOTO 10
END IF
NEXT j
10 NEXT i
END
#include <stdio.h>
#include <string.h>
#include <conio.h>
void main()
{
int i,j,N,K,time1,time2,chas1,min1,chas2,min2;
int p[1000];
char name[20];
scanf("%d",&N);
scanf("%d",&K);
for(i=0;i<K;i++){
p[i]=0;
}
for(i=0;i<N;i++){
scanf("%s %d%*c%d%d %*c%d",
name,&chas1,&min1,&chas2,&min2);
time1=chas1*60+min1;
time2=chas2*60+min2;
for(j=0;j<K;j++){
if(p[j]<=time1){
p[j]=time2;
printf("%s %d\n",name,j+1);
break;
}
}
}
Работа программы на этих языках:
getch();
}