Планы семинарских занятий по дисциплине «Линейная алгебра» специальность «Бизнес-информатика» (2009-2010 уч.г.)

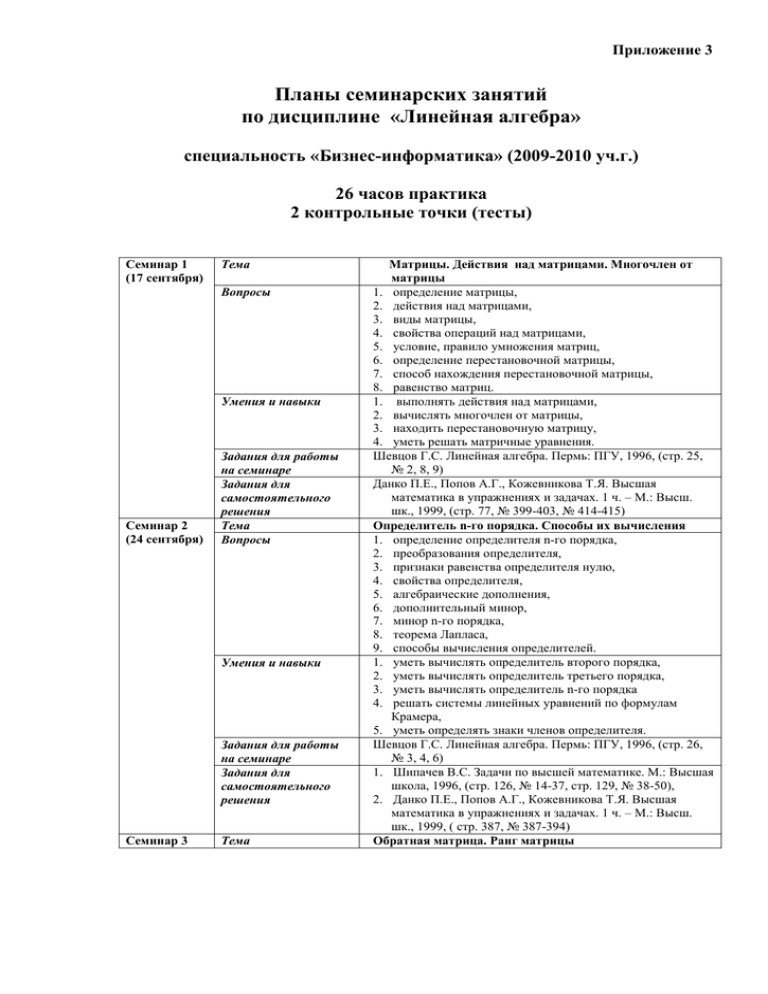
Приложение 3
Планы семинарских занятий
по дисциплине «Линейная алгебра»
специальность «Бизнес-информатика» (2009-2010 уч.г.)
26 часов практика
2 контрольные точки (тесты)
Семинар 1
(17 сентября)
Тема
Вопросы
Умения и навыки
Семинар 2
(24 сентября)
Задания для работы
на семинаре
Задания для
самостоятельного
решения
Тема
Вопросы
Умения и навыки
Задания для работы
на семинаре
Задания для
самостоятельного
решения
Семинар 3
Тема
Матрицы. Действия над матрицами. Многочлен от
матрицы
1. определение матрицы,
2. действия над матрицами,
3. виды матрицы,
4. свойства операций над матрицами,
5. условие, правило умножения матриц,
6. определение перестановочной матрицы,
7. способ нахождения перестановочной матрицы,
8. равенство матриц.
1. выполнять действия над матрицами,
2. вычислять многочлен от матрицы,
3. находить перестановочную матрицу,
4. уметь решать матричные уравнения.
Шевцов Г.С. Линейная алгебра. Пермь: ПГУ, 1996, (стр. 25,
№ 2, 8, 9)
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. 1 ч. – М.: Высш.
шк., 1999, (стр. 77, № 399-403, № 414-415)
Определитель n-го порядка. Способы их вычисления
1. определение определителя n-го порядка,
2. преобразования определителя,
3. признаки равенства определителя нулю,
4. свойства определителя,
5. алгебраические дополнения,
6. дополнительный минор,
7. минор n-го порядка,
8. теорема Лапласа,
9. способы вычисления определителей.
1. уметь вычислять определитель второго порядка,
2. уметь вычислять определитель третьего порядка,
3. уметь вычислять определитель n-го порядка
4. решать системы линейных уравнений по формулам
Крамера,
5. уметь определять знаки членов определителя.
Шевцов Г.С. Линейная алгебра. Пермь: ПГУ, 1996, (стр. 26,
№ 3, 4, 6)
1. Шипачев В.С. Задачи по высшей математике. М.: Высшая
школа, 1996, (стр. 126, № 14-37, стр. 129, № 38-50),
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. 1 ч. – М.: Высш.
шк., 1999, ( стр. 387, № 387-394)
Обратная матрица. Ранг матрицы
Приложение 3
(1 октября)
Вопросы
Умения и навыки
Семинар 4,5
(8 октября
?? ноября)
Задания для работы
на семинаре
Задания для
самостоятельного
решения
Тема
Вопросы
Умения и навыки
Семинар 5
(?? ноября)
Семинар 6
Задания для работы
на семинаре
Задания для
самостоятельного
решения
Тема
Вопросы
Умения и навыки
Тема
Вопросы
Умения и навыки
Семинар 6
Тема
Вопросы
Определение обратной матрицы,
способ нахождения обратной матрицы,
определение матричных уравнений,
способ решения матричных уравнений,
ранг матрицы,
способы нахождения ранга матрицы,
элементарные преобразования матриц.
уметь находить обратную матрицу,
решать матричные уравнения с помощью обратной
матрицы,
3. уметь решать системы уравнений в матричном виде,
4. уметь находить ранг матрицы.
Шевцов Г.С. Линейная алгебра. Пермь: ПГУ, 1996, (стр. 27,
№ 7, 8, 9, стр. 52, № 4)
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. 1 ч. – М.: Высш.
шк., 1999, (стр. 86, № 428-437)
Системы линейных уравнений
1. определение решения системы уравнений,
2. определенная и неопределенная система уравнений,
3. совместная и несовместная система уравнений,
4. эквивалентные системы уравнений,
5. эквивалентные преобразования,
6. метод Гаусса,
7. общее и частное решение системы,
8. основные и свободные неизвестные,
9. способы решения систем линейных уравнений,
10. способ решения системы уравнений с помощью ранга,
11. определение окаймляющий минор.
1. уметь решать системы линейных уравнений различными
способами,
2. уметь определять основные и свободные неизвестные,
3. уметь определять совместна ли система или нет,
4. уметь определять базисный минор.
Шевцов Г.С. Линейная алгебра. Пермь: ПГУ, 1996, (стр. 25,
№ 1, 6, 8, стр. 53, № 9)
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. 1 ч. – М.: Высш.
шк., 1999, ( стр. 89, № 439-451)
Межотраслевой баланс. Модель Леонтьева
1.
2.
3.
4.
5.
6.
7.
1.
2.
Собственные значения и собственные векторы
1. собственные значения матрицы,
2. характеристический многочлен матрицы,
3. характеристическое уравнение матрицы,
4. собственный вектор матрицы.
1. составлять характеристическое уравнение матрицы,
2. находить собственные значения матрицы,
3. находить собственные вектора матрицы.
Квадратичные формы
1. определение квадратичной формы,
2. матрица квадратичной формы,
3. положительно определенная квадратичная форма,
4. отрицательно определенная квадратичная форма,
5. главные миноры матрицы квадратичной формы,
6. критерий Сильвестра.
Приложение 3
Умения и навыки
Семинар 7
Семинар 8,9
Тема
Вопросы
Умения и навыки
Тема
Вопросы
Умения и навыки
Задания для работы
на семинаре
Задания для
самостоятельного
решения
Семинар 10
Тема
Вопросы
Умения и навыки
1. определять квадратичную форму,
2. составлять матрицу квадратичной формы,
3. определять знаки главных миноров матрицы
квадратичной формы,
7. определять положительно определенную квадратичную
форму,
4. определять отрицательно определенную квадратичную
форму.
Контрольная работа по теме «Матрицы.
Определители. Системы линейных уравнений»
Представлены в семинарах 1-6.
Представлены в семинарах 1-6.
Векторная алгебра
1. определение вектора,
2. длина вектора,
3. определение нулевого вектора,
4. определение противоположного вектора,
5. равенство двух векторов,
6. определение ортогональных векторов
7. определение коллинеарных векторов,
8. определение компланарных векторов,
9. операции над векторами,
10. смешанное произведение (определение, свойства, способ
вычисления),
11. скалярное произведение (определение, свойства, способ
вычисления),
12. векторное произведение (определение, свойства, способ
вычисления),
13. угол между векторами,
14. определение правой (левой) тройки векторов,
15. определение линейно зависимых или линейно
независимых систем векторов.
1. уметь определять линейно зависимые или линейно
независимые системы векторов,
2. находить скалярное произведение,
3. находить векторное произведение,
4. находить смешанное произведение,
5. вычислять площадь треугольника, параллелограмма,
6. вычислять объем пирамиды, параллелепипеда,
7. определять ортогональные, коллинеарные, компланарные
вектора.
Шевцов Г.С. Линейная алгебра. Пермь: ПГУ, 1996, (стр. 51,
№ 1, 2, 3)
1. Шипачев В.С. Задачи по высшей математике. М.: Высшая
школа, 1996, (стр. 152, Глава 10, пар. 1-6),
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. 1 ч. – М.: Высш.
шк., 1999, (стр. 48, № 246-249, стр. 51, № 268-284)
Уравнение прямой на плоскости и в пространстве
1. общее уравнение прямой на плоскости,
2. условие параллельности и перпендикулярности прямых,
3. параметрическое и каноническое уравнение прямой,
4. расстояние от точки до прямой,
5. угол между двумя прямыми,
6. уравнения прямой с угловым коэффициентом и в
отрезках,
7. уравнение прямой в пространстве.
1. записывать различные виды уравнений прямой на
плоскости и в пространстве,
2. определять взаимное расположение прямых на плоскости
и в пространстве,
3. находить угол между прямыми.
Приложение 3
Семинар 11
Задания для работы
на семинаре
Задания для
самостоятельного
решения
Тема
Вопросы
Умения и навыки
Семинар 12
Семинар 13
Задания для работы
на семинаре
Задания для
самостоятельного
решения
Тема
Задания для работы
на семинаре
Тема
Вопросы
Умения и навыки
Шипачев В.С. Задачи по высшей математике. М.: Высшая
школа, 1996, (стр. 172, № 130-150)
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. 1 ч. – М.: Высш.
шк., 1999, (стр. 17, № 67-77, стр. 23, № 99-120)
Уравнение плоскости в пространстве
1. общее уравнение плоскости,
2. взаимное расположение двух и трёх плоскостей,
3. условие
параллельности
и
перпендикулярности
плоскостей,
4. уравнение прямой в пространстве,
5. углы между прямыми; между прямой и плоскостью.
1. записывать различные виды уравнений плоскости в
пространстве,
2. определять взаимное расположение плоскостей в
пространстве,
3. находить угол между прямой и плоскостью.
Шипачев В.С. Задачи по высшей математике. М.: Высшая
школа, 1996, (стр. 168, № 101-129, стр. 174, № 151-164)
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. 1 ч. – М.: Высш.
шк., 1999, (стр. 56, № 296-315)
Кривые 2-го порядка
Представлены отдельно
Контрольная работа по теме «Векторная алгебра.
Аналитическая геометрия»
Представлены в семинарах 8-12.
Представлены в семинарах 8-12.