Конкина-И.А.

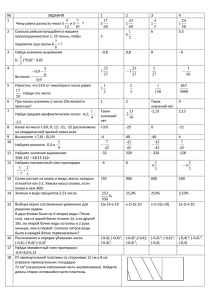
Картотека заданий по математике
Тема «Пропорции"(6 класс).
Конкина И. А.,
учитель математики ГБОУ ЦО №936
Блок №1. Развитие и диагностика
предметных образовательных результатов базового уровня.
1. Расставь слова в правильном порядке: отношений, равенство, двух, пропорцией, называют.
2. Составь верную пропорцию из чисел: 7, 2, 14, 4
3. Подчеркни пропорции:
4. Даны пропорции:
𝟐
𝟏𝟒
= , 21:3=70:10;
𝟏𝟏
𝟕𝟕
3
4
а
𝟏𝟏
15
= 20, 7 + 11 = 36 : 2;
=
𝟏𝟒
в
;
𝟎,𝟏
𝟓
72 : 9 = 16 : 2;
1
5
= 20 : 4; 5 • 40 = 100 • 2
х
= ; m:3=0,5:n; а:b=c:d
𝟗
Заполни таблицу:
Пропорция
Средние
члены
пропорции
Крайние
члены
пропорции
5. Даны пропорции:
𝟐
𝟏𝟒
=
, 21:3=70:10;
𝟏𝟏
𝟕𝟕
а
=
𝟏𝟏
𝟏𝟒
;
в
𝟎,𝟏
𝟓
х
= 𝟗; m:3=0,5:n; а:b=c:d
Заполни таблицу:
Произведение
крайних членов
пропорции
Произведение
средних членов
пропорции
6. Заполни пропуски:
В ______ пропорции произведение ___________ членов равно _________ средних.
7. Запиши обратное утверждение.
𝟐𝟔
8. Проверь, верны ли пропорции: 𝟒 =
Какое свойство ты использовал?
𝟓𝟐
𝟖
,
14:3=9:42
9. Составь кроссворд с данными словами: определение, процент, отрезок, площадь, частное,
уравнение, центнер, числитель, девять.
Дай полное определение получившемуся слову по вертикали.
Блок №2 Развитие и диагностика метапредметных образовательных результатов
(познавательные УУД/мыслительные умения)
В искусстве — соотношение величин элементов художественного произведения.
А в математике?
1. Придумай слово, чтобы пропорция была верна:
стол
мебель
2. Придумай число, чтобы пропорция была верной:
𝟑
𝟒
=
осел
существительное
∗
что?
;
𝟓
= ∗,
=
прилагательное
∗
5:15=*:*
3. Из чисел 6,5,18,15 составь всевозможные верные пропорции.
4. Верно ли высказывание: Из любых четырех натуральных чисел можно составить пропорцию?
5. Из фразы “Из любых четырех натуральных чисел можно составить пропорцию” исключите
одно слово, чтобы это высказывание стало неверным.
6. В данную фразу “Из любых четырех натуральных чисел можно составить пропорцию”
вставьте одно слово, чтобы высказывание стало неверным.
7. 5 и 12 средние члены пропорции. Какими могут быть крайние члены пропорции?
8. 7 и 11 крайние члены пропорции. Какими могут быть средние члены пропорции?
9. 50 раз выпустил Иванушка стрелу из лука и только 7 из них попали в болото. Каков процент
попадания в болото?
Блок №3. Развитие и диагностика метапредметных образовательных результатов
(коммуникативные УУД)
1. Расскажи, как найти неизвестный средний член пропорции.
2. Расскажи, как найти неизвестный крайний член пропорции.
3. Объясните, что означают высказывания: а) 7%-ый раствор столового уксуса; б) молоко 3,2%
жирности; в) 96%-ый спирт.
4. Сопоставь числа в верхней и нижней таблице, заполни таблицу и угадай слово.
Р
𝟏
𝟐
𝟏
𝟒
𝟕
𝟏𝟎
0,75
0,5
И
Ц
0,6
75%
О
𝟑
𝟓
𝟑
𝟖
𝟑
𝟒
60%
50%
0,7
Я
П
25%
0,375
5. Винтик уложил в ящик 9 кг гвоздей за 14 мин., а Шпунтик - 14 кг гвоздей за 21 мин. Кто из них
работает быстрее? А почему?
6. В 90 г воды растворили 10 г сахара. Какова концентрация этого раствора? Объясни.
7. В стакан, где было налито 150 г воды, добавили 25 г сахарного песку. Какова концентрация
этого раствора? Поясни это.
8. В стакан, где было налито 140 г воды, добавили 20 г лимонного сока. Какова концентрация
раствора? Предложи несколько способов решения этой задачи.
9. Линия длиной 5 см изображает на карте участок дороги длиной 15 км. Определи масштаб
карты.
10. Придумай задачу к следующему краткому условию:
а:b=3:5
MN=36 см
Блок №4. Развитие и диагностика метапредметных результатов
(регулятивные УУД) и задания творческого уровня
1. Длина
вытянутых в стороны рук будет равна росту человека! Нарисуй рисунок,
иллюстрирующий это утверждение.
Расстояние от кончика подбородка до носа и от корней волос до бровей одинаково. Нарисуй.
2. Идеальная, с точки зрения современного художника человеческая фигура имеет величину,
равную семи длинам головы. Если хотите выполнить карикатуру на человека или показать, что
он выше или ниже среднего роста, вы легко сможете это сделать: сохраните неизменными
показатели ширины, использованные для фигуры величиной в восемь единиц (голов) и
сократите рост до пяти или шести единиц или увеличьте его до девяти или десяти единиц.
Будут ли при этом сохранены пропорции?
3. Реши задачу: Луна легче Земли в 6 раз. Поэтому сила притяжения ее меньше земной во столько
же раз. Все, что окажется на Луне, предметы и люди, станет легче. Узнай свой вес на Луне.
4. При каждом вылете 5 пчел посещает примерно 750 цветков в день, а пчелиное семейство 30
млн. цветков. Составь пропорцию и узнай величину пчелиной семьи?
5. Лев, чтобы насытиться, должен съесть 20 кг. мяса. Но такое количество еды лев потребляет не
каждый день. Насытившись, царь зверей отправляется на отдых в укромное местечко, где в
течение 3 дней переваривает пищу. Составьте пропорцию, чтобы узнать, сколько мяса
понадобится льву на месяц? А на год? (Считаем, что в месяце 30 дней)
6. Перед тобой решение уравнения:
4
3 4
Х: 25 = 4: 5;
3
4 4
3
4
3
1
Х∙ 4 = 25: 5;
5
Х∙ 4 = 25 ∙ 4;
Х∙ 4 = 5;
Х=
3
1
5
3
∙ ;
4
Х=20
Найди ошибки и исправь их
7. Для приготовления гречневой каши требуется взять гречневую крупу и воду. Проанализируйте
данные и составьте таблицу соотношений исходных продуктов и получаемой каши:
Крупа (чашка)
1
Вода (чашка)
2
Каша ( тарелки)
12
24
5
8. Как получить 100 г 8% -ного раствора сахарного сиропа?
9. Сколько кусочков сахара надо положить в стакан, чтобы получить 200 г раствора указанной
концентрации, если масса кусочка сахара 8 г.
10. В классе 30 учеников. В течение учебного года число успевающих по математике на «4» и «5»
возросло с 15 учеников в начале года до 18 учеников в конце года. Какую часть класса в конце
года составляли успевающих по математике на «4» и «5»?
Картотека заданий по математике
Тема «Противоположные числа. Модуль. Сравнение чисел», 6 класс.
Конкина И. А.,
учитель математики ГБОУ ЦО №936
Блок №1. Развитие и диагностика
предметных результатов базового уровня.
1. Какие числа называются противоположными? Найди пары взаимно противоположных чисел:
13
13
–3; +22; + 2,15; + 3; –7 12; –22; +7 12; +2,15
2
2. Назови число, противоположное данному: +14; –5,5; + 3; –0,001; –3003; 0
2
3. Даны числа: + 9; 0; – 7,7; – 0,001; + 11,3; –2,15, 6 3
Заполни таблицу:
Положительные числа
Отрицательные числа
Не
положительные
и
неотрицательные числа
1
4. Отметь на координатной прямой точки: A(–2); B(1,5); C(2); D(–1 2);
этих точек находятся на одинаковом расстоянии от 0?
E(–3); K(3,5). Какие из
1
5. Прочитай записи: |2|; –(–3); |1, 5|; |−2|; +(–5,2); |−3|; |3,5|; |−1 2|. Подчеркни те, которые
обозначают модуль числа.
6. Прочитай равенство, используя слова «модуль» и «расстояние». Являются ли эти высказывания
истинными? |2|=2; |−3|=3; |−2,5|=2; |−5|= –5; |0|=0
7. Какое значение температуры больше, а какое– меньше? Запиши ответ, используя знаки > или <:
3°С и 0°С; –3°С и 0°С; 3°С и –3°С;
2°С и –3°С; –13°С и –6°С
8. Отметь точки на координатной прямой и сравни координаты точек с нулем: а)А(–3); B(–5); C(–
8); б) А(3); B(5); C(8).
Заполни таблицу:
Справа от нуля
Координаты точек-………..
Слева от нуля
Координаты точек ………
9. Расположи координаты точек на схеме
а)А(–3); B(5); C(–8); D(3); E(–5); K(8); M(–1).
10. Заполни пропуски:
положительное
отрицательное
=
небо
= выход
Блок №2. Развитие и диагностика метапредметных результатов
(познавательные УУД/мыслительные умения)
2
1. Даны числа: 9; – 7,7; – 0,001; 0; + 11,3; – (– 2,15), – (– (– 6 3).
Заполни таблицу:
Положительные числа
Отрицательные числа
Не
положительные
и
неотрицательные числа
2. Закончи предложение:
а) Если число положительно, то противоположное к нему число …..
б) Если число отрицательно, то противоположное к нему число …..
3. Допиши равенства так, чтобы они были верными:
3
– (…) = 5; (…) = –3; – (…) = –2,3; – (…) = − 11; – (…) = 0
4. Продолжи ряд:
-9; 9; 81; 162
-5; __; __; __
4; __; __; __
5. Отметь на координатной прямой точки, модуль которых равен 4; 2,5; 0.
Сколько точек отмечено?
6. Реши уравнение: |х|=2; |а|=5; |у|=–4; |с|=0. Объясни свое решение, пользуясь термином
«расстояние».
7. Высказывание: «Модуль числа равен: 6; 5,6; –11; 0». Найди лишнее. Ответ объясни.
8. Известно, что |х|=9. Чему равен −|х|? Объясни свой ответ.
9. Отметь схематически числа на координатной прямой и сравни их.
–3 и 5
–8 и –2
5 и –9,6
–30 и –44
3
7
5
7
– 13 и 13
– 21 и – 21
–2,23 и 1,15
–6,12 и –9,54
Что общего и что различного в примерах каждого столбца?
10. Поставь вместо звездочек знак < или > :
5
13
5
7
0 *–2,3; –5,3 * 2,1; –2,23 * –2, 24; – 21 * 21; – 11 * – 12
Какие правила применялись для сравнения?
Блок №3. Развитие и диагностика метапредметных результатов
(коммуникативные УУД)
1.
а) Если число положительно, то противоположное к нему число отрицательно.
б) Если число отрицательно, то противоположное к нему число неотрицательно.
Найди ошибки в высказываниях и прокомментируй их.
2. + (+а) = + а; + (–а)= – а; – (+а) = – а; – (–а)= + а
Сформулируй правила и заполни таблицу определения знака:
+(+)=…
+(–)=…
–(+)=…
–(–)=…
3. Отметь на координатной прямой точки, модуль которых равен 4; 2,5; 0.
Сколько точек отмечено?
4. Заполни пропуски:
положительное
отрицательное
=
внимательный
= добрый
5. Проанализируй данные чертежа и заполни пропуски знаками
<, > или =
a
b
1) a …0; 2) b….0; 3) a….b; 4) |𝑎| … . |𝑏|
0
x
6. Известно, что |х|= –9, тогда |−х| = 9. Найди ошибку и исправь ее. Докажи правильность твоего
ответа.
7. Расположи числа в порядке возрастания их модуля:
2
–3,1; 2,5; 9. Сформулируй правила, которые при этом использовались.
8. Расположи числа в порядке убывания. Сопоставь ответы буквам и расшифруй название
геометрической фигуры:
1
3,2
–38
п
и
–9
0
34
р
е
я
1
–203
т
–3,2
0,2
а
ц
9. Выполни задание и выясни, какому рисунку какой ответ соответствует:
1) |𝑥| =5; 2) |𝑥| + 3=5, где х<0; 3) – ( – х)= 5
А)
0
В)
0
С)
0
10. Найди сумму модулей наибольшего отрицательного и наименьшего положительного из данных
чисел: –4,3; –8,1; 9; 11,33
Запиши последовательность рассуждений.
Блок №4. Развитие и диагностика метапредметных результатов
(регулятивные УУД) и задания творческого уровня
1. Прочитай равенство и объясни, почему оно верно:
а) – (+ 5) = −5; б) – (– 10) = 10; в) – 0 = 0
2. Имеют ли смысл следующие выражения: |х|= 0,001; |−х|= 59; |х|= –9
Объясни свой ответ.
3. Заполни пропуски:
положительное
отрицательное
=
гипербола
= кто?
5
1
4. Вычисли: а) |−3,6| – |−2,9|; б) |−1 9| – | − 6 |
5. Известно, что |х|= –9, тогда −|х| = 9, а −|−х| = −9. Найди ошибку в рассуждениях и исправь
ее.
6. Найди координаты точек координатной прямой, удаленных :а) на 2 единицы от точки А(5); б)
на 3 единицы от точки В(–4). Сколько решений имеет задача?
7. Прочитай неравенство и найди множество его целых решений:
а) |х| ≤ 9; б) 1< |х| ≤3. Сделай пояснительный рисунок.
8. Определи координаты точек А, В и С:
А
В
С
0
n
9. Реши уравнение: |𝑥 + 5|=11
Запиши последовательность рассуждений.
10. Запиши в виде схемы алгоритм рассуждений, необходимых для сравнения положительных и
отрицательных чисел.