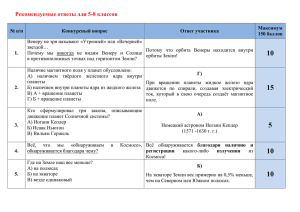
Особенности решения расчетных задач по астрономии

Особенности решения расчетных задач по астрономии
Осуществляя решения задач по астрономии учащиеся должны знать не только
общий алгоритм решения задач, но и уметь работать с частными структурами процесса
решения задач. Приведем примеры таких структур, описанных в работах А.В. Усовой и
адаптированных нами к задачам с астрономическим содержанием [1].
Правила решения астрономических задач
Этап 1. Понять суть задачи.
1. Внимательно прочитать текст задачи.
2. Разбить текст задачи на такие фрагменты, в каждом из которых речь идет только
об одной теме, об одном явлении, об одном астрономическом объекте, об одной
астрофизической или астрономической величине.
3. Выяснить смысл всех непонятных слов и выражений.
4. Записать, что дано (известно из условия задачи) и что требуется найти.
5. Сделать схематический рисунок или серию рисунков, если позволяет характер
задачи. Указать на чертеже все векторные величины, выбрать систему отсчета.
6. Кратко, одним-двумя предложениями, сделать запись, выражающую суть задачи.
Этап 2. Составить план решения задачи.
1. Рассмотреть астрономическую (астрофизическую) картину задачи, уяснив для
себя, о каких темах и взаимодействиях тел идет речь в задаче, какие явления и процессы
имеют место, какие принимаются упрощения (идеализация), какие величины описывают
свойства астрономических объектов и явлений, какие связи (отношения) существуют
между этими величинами.
2. Провести анализ задачи. Пояснить все буквенные обозначения величин.
3. Составить план решения задачи. Приведя систему уравнений – следует пояснить
каждое из них.
Этап 3. Реализовать план решения задачи.
1. Найти решение задачи в общем виде, проверить, правильная ли размерность
получается у искомой величины.
2. Выполнить операции с наименованиями единиц измерения астрономических
(астрофизических) величин, произвести необходимые расчеты, соблюдая правила
приближенных вычислений и.
Этап 4. Проанализировать полученный результат.
1. Оценить правдоподобность полученного численного результата.
2. Установить и оценить все частные (предельные) случаи.
3. Записать полученный ответ в требуемой форме.
Общий алгоритм решения астрономических (астрофизических) задач
1. Внимательно прочитайте условие задачи и уясните основной вопрос;
представьте процессы и явления, описанные в условии задачи.
2. Повторно прочитайте содержание задачи для того, чтобы четко представить
основной вопрос задачи, цель ее решения, известные величины, опираясь на которые
можно вести поиски решения.
3. Произведите краткую запись условия задачи с помощью общепринятых
буквенных обозначений.
4. Выполните рисунок или чертеж к задаче.
5. Определите, каким методом будет решаться задача; составьте план ее решения.
6. Запишите основные уравнения, описывающие процессы, предложенные
задачной системой.
7. Запишите решение в общем виде, выразив искомые величины через заданные.
8. Проверьте правильность решения задачи в общем виде, произведя действия с
наименованиями величин.
9. Произведите вычисления с заданной точностью.
10. Произведите оценку реальности полученного решения.
11. Запишите ответ в требуемой форме.
Алгоритм преобразования единиц физических величин
1. Запишите в левой части равенства численное значение рассматриваемой
величины с указанием наименования единицы ее измерения, а в правой части
равенства выделите наименование величины с коэффициентом «единица»:
1 кпк = 3,25 · 103 · 1 св. лет.
2. Запишите соотношение заданной единицы величины с новыми единицами
измерения:
1 св. год = 3 · 108(м/с) · 3600 · 24 · 365 (с)= 9,5 · 1015 (м).
3. В левой части равенства запишите численное значение заданной величины,
а в правой – соотношения через новые единицы:
1 кпк = 3,25 · 103 · 9,5 · 1015 м.
4. В правой части равенства осуществите все действия с ко эффициентами и
наименованиями:
1 кпк = 3,0875 · 1018 м.
Алгоритм выполнения действий с единицами
физических величин
1.
Напишите формулу, выражающую связь величины, единицу которой
нужно определить, с другими величинами (их единицы уже известны и являются
исходными).
Например, необходимо определить единицу силы в СИ. Для этого запишите
определяющую формулу для величины силы:
(1)
F  ma
2.
Вместо букв, обозначающих значения величин, запишите наименования их
единиц измерения в системе СИ:
[F] = l к г · 1 м/с2.
(2).
Произведите действия с единицами:
[F] = 1 кг · м/с2 = Н.
4. Если есть необходимость, то введите название единицы, т. е.
3.
1 кг · м/с2 = 1 Н.
Рассмотрим примеры решения задач с астрономическим содержанием с
использованием выше описанных частных структур процесса решения задач.
1. Искусственный спутник обращается по круговой орбите вокруг планеты
радиусом 3400 км, совершая один оборот за 2 часа. Ускорение свободного падения на
поверхности планеты равно 4 м/с2. Определить радиус орбиты спутника.
Комментарий к решению. Воспользуемся правилом решения астрономических
задач. Свяжем центростремительное ускорение спутника на орбите с радиусом траектории
и периодом обращения спутника вокруг планеты, а так же воспользуемся вторым законом
Ньютона и законом гравитации для определения центростремительного ускорения:
à
42R c
F GM
GM T2
3
.
,
a


,
R

c
T2
m
R c2
42
Для определения массы планеты воспользуемся формулой ускорения свободного
GM
падения: g  2 , GM  gR02 . Подставив полученное выражение для произведения
R0
гравитационной постоянной и массы планеты в формулу для вычисления куба радиуса
gR 02T 2
.
42
Подставим числовые значения, предварительно переведя единицы измерения в систему
СИ и получим значение радиуса орбиты спутника 400 км.
орбиты спутника и, преобразовав ее, получим радиус орбиты спутника R c 
3
2. На поверхности Марса тело свободно падает с высоты 100 м в течение примерно
7 с. С какой скоростью тело коснется поверхности Марса, падая с такой высоты?
Комментарий к решению. Воспользуемся правилом решения астрономических
задач и представлением о свойствах явления свободное падение. Используя формулу
расчета высоты свободно падающего тела, найдем ускорение свободного падения на
gt2
2h
, g  2 .В уравнение скорости подставим полученное выражение
Марсе: h 
2
t
2h
v  gt, v 
и вычислим скорость 28,6м/с.
t
3. Звезда и массивная планета обращаются вокруг неподвижного центра масс по
круговым орбитам. Найдите массу планеты m, если известно, что скорость движения
планеты равна v1 , а скорость движения и период обращения звезды равны v2 и Т
соответственно.
Комментарий к решению. Свяжем центростремительное ускорение звезды с силой
v2
M m
её притяжения планетой: M  2  G
, где M и m - массы звезды и планеты,
2
R
 r R 
соответственно, R и r – радиусы их планет. Поскольку центр масс, остающийся
неподвижным, всегда находится на прямой, соединяющей центры звезды и планеты, то
r
R
период обращения планеты и звезды: T  2 ; T  2 . Решая систему трех уравнений
v1
v2
относительно массу планеты, получаем: m 
v22(r R )2 (v1  v2 )2  v2T

GR
2G
4. Масса планеты составляет 0,2 от массы Земли, диаметр планеты втрое меньше
диаметра Земли. Чему равно отношение периодов обращения искусственных спутников
Ò
планеты и Земли п , двигающихся по круговым орбитам на небольшой высоте?
ÒЗ
Комментарий к решению. Ускорение спутника, движущегося со скоростью v по
G M
v2 G  M
окружности радиусом R, равно g 
, следовательно v 
. Период

2
R
R
R
2R
R3
 2
обращения спутника T 
. Отношения периодов обращения ИСЗ планеты
v
G M
и Земли
Òп

ÒЗ
Rп
RЗ
Ì
Ì
п
,
Òп
 0,185  0,43
ÒЗ
З
5. Когда Земля (4 января) находится в перигелии, Солнце движется по небу с
угловой скоростью 61' в сутки, а 4 июля, когда Земля в афелии, – 57' в сутки. Определите
эксцентриситет земной орбиты.
Комментарий к решению. Используя третий закон Кеплера, формулы для расчёта
перигельного q = а(1 - е) и афельного Q = а(1+ е) расстояний, формул для расчета
G  M 1 e
G  M 1 e


угловой скорости планет в перигелии vп2 
и в афелии va2 
a 1 e
a 1 e
v 1 e
v  va
находим эксцентриситет земной орбиты a 
, å п
.
vп 1 e
vп  va
61  57
е
 0,0338
61  57
6. Для разгона космических аппаратов в отрытом космосе и коррекции их орбит
предложено использовать солнечный парус – скреплённый с аппаратом лёгкий экран
большой площади из тонкой проволоки, которая зеркально отражает солнечный свет.
Найдите ускорение, сообщаемое аппарату массой 500 кг (включая массу паруса), если
парус имеет форму квадрата 100 м  100 м. Мощность W солнечного излучения,
падающего на 1 м2 поверхности, перпендикулярной солнечному свету, составляет 1370
Вт.
Комментарий к решению. Воспользуемся правилом решения астрономических
задач и зависимостью давления солнечного излучения от мощности, коэффициента
W
 1 k  cos2  . Из формулы, определяющей значения
отражения и угла падения: p 
S0  c
давления, производимого силой на твёрдую поверхность, находим, что сила давления:
F
S W
F  S p
 1 k  cos2  . Из второго закона Ньютона a  . Следовательно:
m
S0  c
a
S W
 1 k  cos2  ,
m  S0  c
a
104 1370
 1 1  cos2 0  1,8104 м/с2.
8 
500  3 10
7. Для разгона космических аппаратов в открытом космосе и коррекции их орбит
предложено использовать солнечный парус, скрепленный с аппаратом легкий экран
большой площади из тонкой пленки, которая зеркально отражает солнечный свет. Какой
должна быть минимальная площадь паруса S, чтобы давление лучей солнечною света
могло сообщить аппарату массой 500 кг (включая массу паруса), находящемуся у орбиты
Марса, ускорение 104g? Мощность W солнечного излучения, падающего на 1 м2
поверхности, перпендикулярной солнечным лучам, составляет вблизи Земли 1370 Вт.
Считать, что Марс находится в 1,5 раза дальше от Солнца, чем Земля.
Комментарий к решению. Воспользуемся правилом решения астрономических
задач и зависимостью давления солнечного излучения от мощности, коэффициента
W
отражения и угла падения: p 
 1 k  cos2  . Из формулы давления находим, что
S0  c


S W
сила давления: Fд  S  p 
 1 k  cos2  . Второй закон Ньютона: 0  F д  Fгр ,
S0  c
a m
.
à m  p S , S 
p
Учитывая, что Марс дальше от Солнца, чем Земля, считаем, что его солнечная
L W
постоянная в 1,5 раза меньше: W  W 0 0  0 .
L 1,5
м
м
1,5 500 кг 105 2  3 108 2
1,5 m  a  c
с
с  8,2 1012 м2
Следовательно: S 
, S
Вт
W 0  (1 k) cos2 
2 0
1370 2  (1 1) cos 0
м
8. Тёмная пылинка сферической формы под действием силы притяжения к Солнцу
и силы светового давления движется через Солнечную систему равномерно и
прямолинейно. Плотность пылинки составляет 5 · 102 кг/м3. Найдите радиус r пылинки.
Учесть, что на расстоянии D0 Земли от Солнца ускорение А, сообщаемое всем телам силой
притяжения Солнца, равно 6 · 10-3 м/с2, а мощность W солнечного излучения, падающего
на 1 м2 поверхности, перпендикулярной солнечным лучам, составляет 1370 Вт.
Комментарий к решению. Воспользуемся правилом решения астрономических
задач и зависимостью давления солнечного излучения от мощности, коэффициента
W
 1 k  cos2  . Из формулы, определяющей значения
отражения и угла падения: p 
S0  c
давления, производимого силой на твердую поверхность находим, что сила давления:
S W
Fд  S  p 
 1 k  cos2  . Второй закон Ньютона для описанного в задаче явления:
S0  c


0  F д  Fгр , учтем как в рамках данной задачной ситуации рассчитывается сила
гравитации и сила давления: A  m  p  S .
1 4
Из формулы плотности находим, что масса: m   V        r3 .
2 3
1 4
S

W
 1 k  cos2 
Следовательно: A       r3 
2 3
S0  c
3 W
r

4  S0  c A 
3  1370
r
 cos2 0  1,142106
3
4  6 10  3 108  5102
Литература
1. Усова, А.В. Практикум по решению физических задач: для студентов физ.-мат. фак.
/ А.В.Усова, Н.Н. Тулькибаева. – М.: Просвещение, 2001.
2. Шефер, О.Р. Сборник задач и заданий к разделу «Строение Вселенной» курса
физики средней (полной) школы: сборник задач / О.Р. Шефер, В.В. Шахматова. –
Челябинск: Изд-во «Центр научного сотрудничества», 2011.