Отрицание (часть 1)

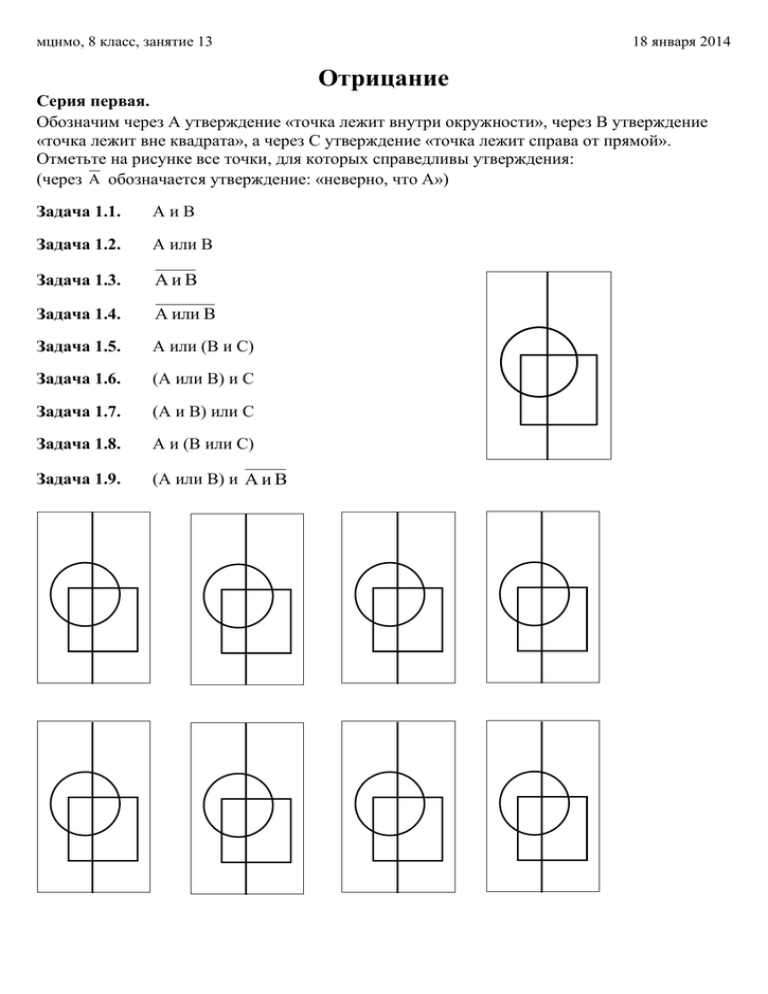
мцнмо, 8 класс, занятие 13
18 января 2014
Отрицание
Серия первая.
Обозначим через А утверждение «точка лежит внутри окружности», через В утверждение
«точка лежит вне квадрата», а через C утверждение «точка лежит справа от прямой».
Отметьте на рисунке все точки, для которых справедливы утверждения:
(через A обозначается утверждение: «неверно, что А»)
Задача 1.1.
АиВ
Задача 1.2.
А или В
Задача 1.3.
AиB
Задача 1.4.
A или B
Задача 1.5.
А или (В и С)
Задача 1.6.
(А или В) и С
Задача 1.7.
(А и В) или С
Задача 1.8.
А и (В или С)
Задача 1.9.
(А или В) и A и B
мцнмо, 8 класс, занятие 13
18 января 2014
Серия вторая.
Сформулируйте отрицания следующих утверждений (упростите их как можно сильнее,
избавляйтесь от сочетаний «не существует» и «не для всех»):
Задача 2.1. Паша умный и красивый
__________________________________________________________________________
__________________________________________________________________________
Задача 2.2. Леша веселый или сытый
__________________________________________________________________________
__________________________________________________________________________
Задача 2.3. Если в этом доме водятся мыши, то они белые
__________________________________________________________________________
__________________________________________________________________________
Задача 2.4. Если окно открыто, то дома кто-то есть
__________________________________________________________________________
__________________________________________________________________________
Задача 2.5. Если открыто окно, то дома кто-то есть и он приготовил ужин.
__________________________________________________________________________
__________________________________________________________________________
Задача 2.6. Если дверь заперта, а окно открыто, то дома никого нет, или там Карлсон.
__________________________________________________________________________
__________________________________________________________________________
Задача 2.7. Все здесь присутствующие хотя бы раз
получали двойку.
__________________________________________________
__________________________________________________
Задача 2.8. Каждый воробей летал в Африку
__________________________________________________
__________________________________________________
Задача 2.9. Все преподаватели умные и красивые
__________________________________________________
__________________________________________________
Задача 2.10. Существует восьмиклассник, который не может правильно сложить никакие
две дроби.
__________________________________________________________________________
__________________________________________________________________________
Задача 2.11. Для любого восьмиклассника можно подобрать такую задачу, что никакую
более сложную задачу он не сможет решить.
__________________________________________________________________________
__________________________________________________________________________
Задача 2.12. Если ученик весёлый, то либо у него день рождения, либо он сытый и сдал
все задачи.
__________________________________________________________________________