Задания по математике для 11А класса
реклама
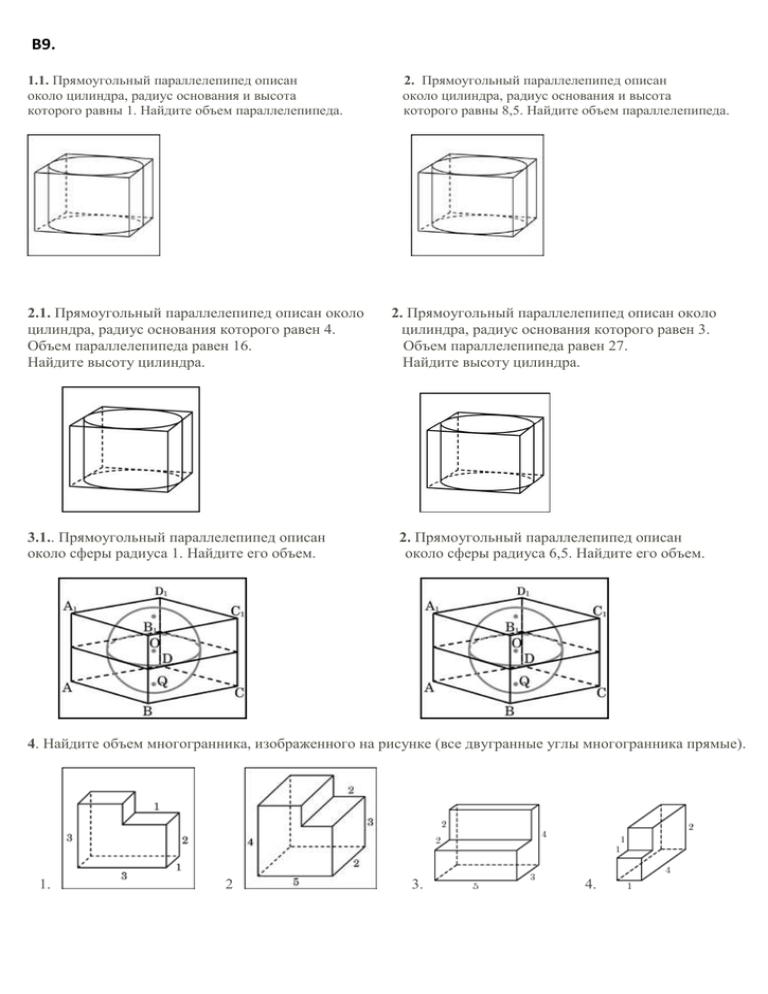
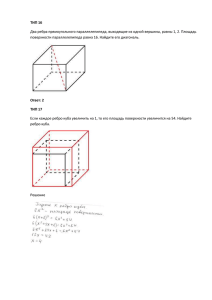
В9. 1.1. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда. 2.1. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра. 3.1.. Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем. 2. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 8,5. Найдите объем параллелепипеда. 2. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объем параллелепипеда равен 27. Найдите высоту цилиндра. 2. Прямоугольный параллелепипед описан около сферы радиуса 6,5. Найдите его объем. 4. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые). 1. 2 3. 4. В9. 5. 1.В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? 2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? 6. 1.В основании прямой призмы лежит прямоугольный 2. В основании прямой призмы лежит прямоугольный треугольник с катетами 1 и 10. Боковые ребра равны . треугольник с катетами 3 и 3. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. Найдите объем цилиндра, описанного около этой призмы. 7. 1. В основании прямой призмы лежит квадрат со 2. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. стороной 7. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. 8. 1. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25. 2. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 63. В9. 9. 1. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. 10. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. 2. Объем конуса равен 168. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. 11. Площадь поверхности куба равна 18. Найдите его диагональ. 12.Найдите площадь боковой поверхности правильной 13. Объем куба равен 8. Найдите площадь его поверхности. шестиугольной призмы, сторона основания которой равна 5, а высота — 10. 14. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на . 15. Площадь большого круга шара равна 3. Найдите площадь поверхности шара. В9. 16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. 18. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. 17. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба. 19. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760. 20. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, которого равны 1. Найдите площадь боковой поверхности призмы. радиус основания которого равен 22. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 2. , , а высота равна 2. 23. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. В9. 24. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы. 26. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды. 25. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды. 27. Объем параллелепипеда Найдите объем треугольной пирамиды равен 9. . 28. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. 29. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза? 30. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара. В9. 31. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба. 33. Объем параллелепипеда Найдите объем треугольной пирамиды 33. Объем параллелепипеда Найдите объем треугольной пирамиды 35. Объем параллелепипеда Найдите объем треугольной пирамиды равен . равен 3,6. . равен . 32. Объем параллелепипеда Найдите объем треугольной пирамиды . 34. Объем параллелепипеда Найдите объем треугольной пирамиды 34. Объем параллелепипеда Найдите объем треугольной пирамиды . 36. Объем параллелепипеда Найдите объем треугольной пирамиды равен 6. . равен . . равен . . равен . . В9. 37. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 38. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). 1. 2. 5. 6. 9. 12. 17. 3. 4. 7. 8. 10. 13. 18. 11. 14. 19. 15. 20. 16. 21. В9. 39. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). 1. 2. 5. 3. 6. 9. 4. 7. 10. 8. 11. 40. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 1. 4. 9. 2. 5. 6. 10. 3. 7. 11. 8. 12. В9. 41. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите 1. 2. 6. 17. 4. 7. 9. 12. 3. 11. 14. 18. 5. 8. 10. 13. . 15. 19. 16. В9. 42. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите 1. 6. 2. 7. 3. . 4. 8. 9. 5. 10. 43. 1. Вершина куба со стороной является центром шара. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите . 2. Вершина куба со стороной является центром шара. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите . 44. 1. Середина ребра куба со стороной является центром шара радиуса поверхности шара, лежащей внутри куба. В ответе запишите . . Найдите площадь S части 2. Середина ребра куба со стороной является центром шара радиуса поверхности шара, лежащей внутри куба. В ответе запишите . . Найдите площадь S части 45. 1. Объем тетраэдра равен . Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра. 2. Объем тетраэдра равен . Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра. В9. 46. 1. Объем тетраэдра равен . Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра. 47.1. Площадь поверхности тетраэдра равна 2. Объем тетраэдра равен . Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра. 2. Площадь поверхности тетраэдра равна . Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра. 3. Площадь поверхности тетраэдра равна . Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра. 4. Площадь поверхности тетраэдра равна 1. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра. 5. Площадь поверхности тетраэдра равна . Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра. 6. Площадь поверхности тетраэдра равна . Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра. .