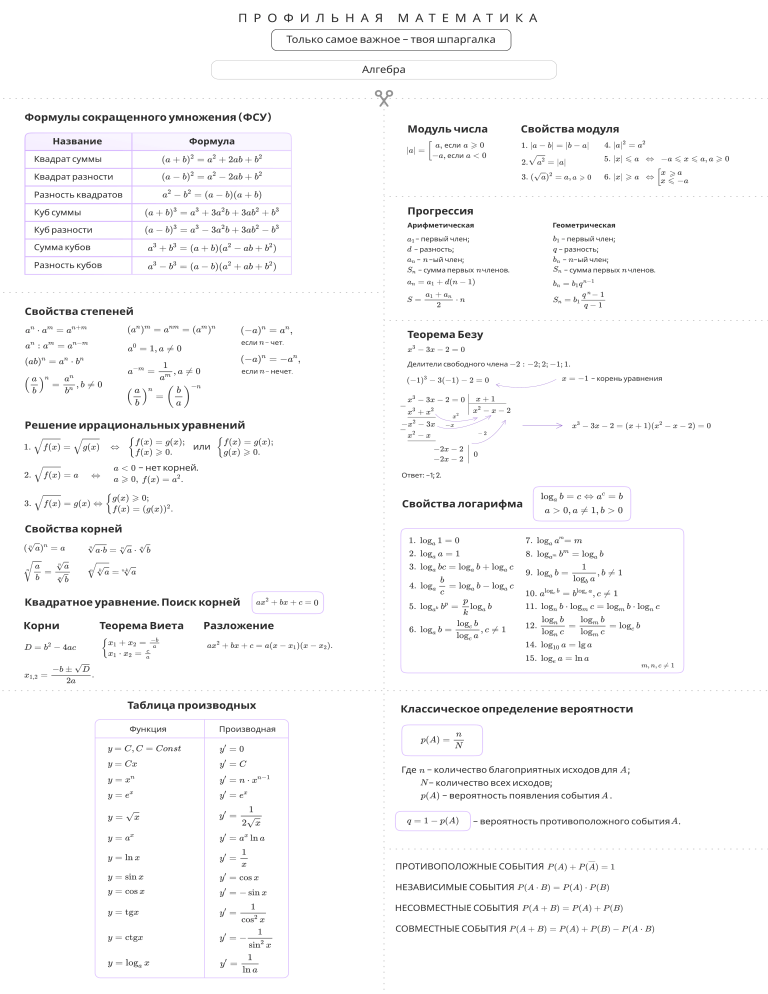
Профильная математика Только самое важное – твоя шпаргалка Алгебра Формулы сокращенного умножения (ФСУ) Название Формула 2022 Модуль числа если если Квадрат суммы Квадрат разности Разность квадратов Куб суммы Куб разности Сумма кубов Разность кубов Свойства модуля Прогрессия Арифметическая – первый член; – разность; – –ый член; – сумма первых членов. Геометрическая – первый член; – разность; – –ый член; – сумма первых членов. Свойства степеней если – чет. если – нечет. Теорема Безу Делители свободного члена – корень уравнения Решение иррациональных уравнений или – нет корней. Ответ: –1; 2. Свойства логарифма Свойства корней Квадратное уравнение. Поиск корней Корни Теорема Виета Разложение Таблица производных Функция Классическое определение вероятности Производная Где – количество благоприятных исходов для ; – количество всех исходов; – вероятность появления события . – вероятность противоположного события . ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ НЕЗАВИСИМЫЕ СОБЫТИЯ НЕСОВМЕСТНЫЕ СОБЫТИЯ СОВМЕСТНЫЕ СОБЫТИЯ Правила дифференцирования ПОМНИМ ПРО ОДЗ! Метод рационализации Часто используемые производные “Правило матрешки” Показательные неравенства где Логарифмические неравенства и Неравенства с модулем , где Иррациональные неравенства Тригонометрия Тригонометрическая окружность Двойной угол Тройной угол Общий вид решения Половинный угол Тригонометрические тождества Формулы понижения степени Табличные значения триг. функций угол Знаки тригонометрических функций по четвертям Частные случаи решения тригонометрических уравнений Формулы сложения Таблица формул приведения Аргумент Функция Тригонометрические формулы произведений Формулы суммы синусов и косинусов Формулы, которые редко встречаются на экзамене Задание 10 Функция синуса Функция косинуса Роль коэффициентов (преобразования графиков) (среднее арифметическое и значений функции). (половина амплитуды) Функция «модуль» Уравнение прямой Квадратичная функция Простейшая функция: при при – координата вершины по – координата вершины по Квадратичная функция где и – точки пересечения параболы с осью Простейшая функция квадратного корня Показательная функция Смещение функции корня 1) для случая 1) Коэффициент отвечает за смещение по оси Если то вверх. Если то вниз. 2) Коэффициент отвечает за смещение по оси Если то влево. Если то вправо. Обратная пропорциональность . 2) для случая – гипербола Смещение гиперболы Смещение показательной функции 1) Коэффициент отвечает за смещение по оси Если то вверх. Если то вниз. 2) Коэффициент отвечает за смещение по оси Если то влево. Если то вправо. . Асимптоты: Алгоритм определения функции по графику 1) Определим асимптоты по и . Это и будут коэффициенты и . 2) Находим удобную точку, через которую проходит гипербола: 3) Подставим точку , коэффициенты и в функцию: 4) Находим коэффициент 5) Записываем явный вид функции. 1) Коэффициент отвечает за смещение по оси Если то вверх. (считая от точки Если то вниз. 2) Коэффициент отвечает за смещение по оси Если то влево. Если то вправо. . ). Смещение функции логарифма Логарифмическая функция 1) для случая 2) для случая где 1) Коэффициент отвечает за смещение по оси Если то вверх. Если то вниз. . 2) Коэффициент отвечает за смещение по оси Если то влево. Если то вправо. Относительно точки Планиметрия Равносторонний треугольник Формулы площади треугольника – высота; где – высота к стороне ; – площадь; где – угол между и ; – периметр; где – полупериметр, – радиус впис. окружности; где – радиус описанной окружности; – формула Герона. – радиус вписанной окружности; Все стороны равны . Все углы равны – радиус описанной окружности. Теорема Пифагора Радиус описанной окружности около прямоугольного треугольника Прямоугольный треугольник Свойство №1. Катет прямоугольного треугольника меньше гипотенузы. Свойство №2. Сумма острых углов прямоугольного треугольника равна Радиус вписанной окружности в прямоугольный треугольник Свойство №3. Катет прямоугольного треугольника, лежащий против угла , равен половине гипотенузы. Свойство №4. Прямоугольный треугольник с углом – равнобедренный. Равносторонний шестиугольник B A O F C а E H D Коэффициент подобия треугольников Отношение площадей с общим углом – большая диагональ; – меньшая диагональ; – радиус описанной окружности; – радиус вписанной окружности; – площадь; Все стороны равны . Все углы равны – периметр. Свойство медиан Длина медианы Средняя линия отсекает по площади в четыре раза меньший, чем исходный Биссектрисы треугольника Точка пересечения медиана, проведенная к стороне , равна: Свойство медианы Медиана, проведенная биссектрис углов треугольника – это центр вписанной в треугольник окружности. – биссектриса из прямого угла, равна половине гипотенузы или . Формулы высоты из прямого угла bc b c h ac a Формула площади любого выпуклого четырехугольника Площади четырехугольников a b a a a где – полупериметр четырехугольника. h a A a a b b Свойства высот треугольника Серединный перпендикуляр B Серединный перпендикуляр к отрезку – прямая, проходящая через середину отрезка перпендикулярно к нему. a α a Трапеция Прямоугольник Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон b на косинус угла между ними a где – высота ромба; Площадь описанного четырехугольника Теорема косинусов a a α h α Площадь вписанного четырехугольника Квадрат Ромб Параллелограмм c Свойства серединного перпендикуляра C Теорема Вариньона (параллелограмм Вариньона) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка (верно и обратное). Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники: Теорема Менелая старт Отношение площадей треугольников Теорема Чевы старт Лемма о “ласточкином хвосте” Пусть треугольники имеет общую сторону. Продолжим ее до пересечения с отрезком, соединяющим вершины треугольников, не принадлежащие общей стороне. Тогда отношение, в котором делится этот отрезок, равно отношению площадей треугольников. Свойство биссектрисы Отношение отрезков, на которые биссектриса делит сторону, равно отношению двух сторон того угла, из которого ее провели. Свойства ортоцентра Свойства ортоцентра Радиусы описанной окружности, проведенные к вершинам треугольника, перпендикулярны соответствующим сторонам ортотреугольника. Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной около него окружности. A1 Точка, симметричная ортоцентру относительно середины стороны треугольника, лежит на описанной около него окружности и диаметрально противоположна вершине треугольника, противолежащей данной стороне. B1 Расстояние от вершины треугольника до ортоцентра в 2 раза больше расстояния от центра описанной окружности до противолежащей стороны. а) Стороны ортотреугольника образуют равные углы с соответствующими сторонами данного треугольника. б) Ортоцентр остроугольного треугольника является точкой пересечения биссектрис ортотреугольника (центром его вписанной окружности). 2х х C A1 B1 H B A C1 С Угол между радиусом и стороной равен углу между высотой и стороной (все они выходят из одной вершины). С умма квадратов расстояния от вершины треугольника до его ортоцентра и длины стороны, противолежащей этой вершине, равна квадрату диаметра описанной окружности. С α О M О Н Н α А В А C1 Вписанный и центральный углы Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. Вписанные углы, опирающиеся на одну дугу, равны. В Окружность, описанная около четырехугольника ля того чтобы вокруг четырехугольника можно было описать окружность, необходимо и достаточно выполнение любого из условий: 1) Суммы противоположных углов четырехугольника равны 2) Угол равен углу (эти углы опираются на одну хорду и являются вписанными). Д Окружность, вписанная в четырехугольник Угол между двумя секущими Угол между двумя хордами Теорема синусов и ее следствие Теорема о дугах, стягиваемых равными хордами Окружность внутри трапеции Равные хорды стягивают равные дуги, меньшие полуокружности. И наоборот: равные дуги стягиваются равными хордами. Угол между касательной и хордой . – биссектрисы углов и , так как окружность вписана в эти углы. 1 3 2. 4 . . Окружность, описанная вокруг прямоугольного треугольника Построение вневписанной окружности В любом треугольнике бисскетрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке. Окружность, описанная вокруг квадрата D B О A C I Окружность, описанная Окружность, описанная вокруг вокруг прямоугольника правильного треугольника тереометрия С Призма. Основные формулы Ц илиндр Объем цилиндра: Объем призмы: , где – высота призмы. Площадь боковой поверхности: осн. бок. пов. осн. бок. пов. осн. осн. Прямоугольный параллелепипед. Основные формулы Объем параллелепипеда: бок. пов. осн. пол. пов. бок. пов. осн. Конус Объем конуса: , где осн. Площадь боковой поверхности: . осн. Площадь полной поверхности: пол. пов. осн. Площадь полной поверхности: осн. бок. пов. бок. пов. – высота цилиндра. Площадь боковой поверхности: Площадь полной поверхности: пол. пов. , где осн. осн. Диагональ параллелепипеда: – высота конуса. Площадь боковой поверхности: , где осн. бок. пов. – образующая конуса. Площадь полной поверхности: пол. пов. Ш бок. пов. . осн. ар и сфера Объем шара: Куб. Основные формулы Объем куба: Площадь поверхности шара (сферы): пов. шара Площадь боковой поверхности: бок. пов. Пирамида. Основные формулы Объем пирамиды: Площадь полной поверхности: пол. пов. осн. , где – высота пирамиды. Площадь боковой поверхности: Диагональ куба: бок. пов. осн. , где – апофема. Площадь полной поверхности: пол. пов. бок. пов. осн. осн. осн. та формула работает в правильной пирамиде! Э Перпендикулярность прямой и плоскости Угол между скрещивающимися прямыми Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Углом между двумя пересекающимися прямыми в пространстве является наименьший из углов, образованный лучами этих прямых с вершиной в точке их пересечения. Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна и самой плоскости. Формула для косинуса: cos (α) = Теорема (признак перпендикулярности прямой и плоскости). а b2 + c2 – a2 , 2bc где b и c – это стороны треугольника (соответственно параллельные а скрещивающимся прямым), между которыми заключен искомый угол α. m b α l α α c a α – угол между прямыми m и l Угол между прямой и плоскостью Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, есть угол между прямой и ее проекцией на эту плоскость. М АМ – проекция АМ Свойства перпендикулярных прямой и плоскости 1. Если плоскость перпендикулярна одной b а из двух параллельных прямых, то она перпендикулярна и другой прямой. 2. Две прямые, перпендикулярные одной и той же плоскости, параллельны. α γ А α Если а α и b || a, то b α. М (AM; γ) = (AM; AM ) = α Теорема о трех перпендикулярах нак лон на я Прямая теорема: Прямая, проведенная на плоскости перпендикулярно проекции некоторой наклонной, перпендикулярна и самой наклонной. Обратная теорема: Прямая, проведенная в плоскости перпендикулярно наклонной, перпендикулярна и ортогональной проекции этой наклонной. пря м ая ия й ц к ое но пр клон на Признак скрещивающихся прямых Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые – скрещивающиеся (не лежат в одной плоскости). Расстояние между скрещивающимися прямыми a 1 способ нахождения: Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра: d ρ(а, b) = d d a, d b b a 2 способ нахождения: Расстояние между скрещиващимися прямыми – это расстояние между одной из этих прямых и плоскостью, проходящей через вторую прямую параллельно первой. Угол между скрещивающимися прямыми Угол между двумя скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся. Признак скрещивающихся прямых Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающимися. d b c α Двугранный угол Двугранный угол – фигура, образованная двумя полуплоскостями, исходящими из одной прямой. АВ – ребро двугранного угла, α и β – стороны (грани) двугранного угла. Линейный угол двугранного угла β ꝩ А Двугранный угол между плоскостями равен углу, образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей. В грани α ребро ꝩ – линейный угол двугранного угла АВ. Расстояние между точками ьность прямой и плоскости Параллел a Определение. Если требуется найти расстояние от точки А до В, то необходимо соединить эти точки и заключить их в отрезок. Прямая называется параллельной некоторой плоскости, если она не имеет с ней общих точек. α А С А А a Признак. Если прямая параллельна некоторой прямой, В В лежащей в плоскости, тогда она параллельна α b В Находим АВ: всей плоскости. – или через теорему косинусов; a || b b a || α – или через теорему Пифагора, если треугольник АВС – прямоугольный. α Расстояние от точки до плоскости М Метод объемов М Для нахождения расстояния от точки С до плоскости АВС. ρ (М, ) = ММ1 α двумя способами: М1 α Считаем объем одной и той же треугольной пирамиды α Расстояние от точки до плоскости – это перпендикуляр. Признак перпендикулярности прямой и плоскости: Если прямая перпендикулярна двум пересекающимся прямым, лежащим Ищем площади и находим d – это и будет расстояние в данной плоскости, то она перпендикулярна всей плоскости. от точки С до плоскости АВС. Пере ход от точки к точке через плоскость Теорема о пропорциональных расстояниях Если плоскость проходит через середину Пусть прямая пересекает плоскость B α в точке О. A Возьмем две любые точки А и В на этой прямой (отличные от О), и пусть х и у выражают расстояния от данных точек до плоскости α. Тогда: отрезка, то концы отрезка равноудалены от данной плоскости. O α х ОА = у О у х N M В щадь ортогональной проекции многоугольника ьный перенос перпендикуляра Пло B Площадь ортогональной проекции многоугольника на плоскость равна площади проецируемого многоугольника, плоскостью многоугольника и плоскостью α где α– угол между плоскостями b параллельна прямой, перпендикулярной к плоскости, то и она перпендикулярна C1 A1 проекции. a Теорема. Если некоторая прямая C A умноженной на косинус угла между SA1B1C1 = SABC ∙ cos , Параллел α этой плоскости. B1 АВ Си А1В1 1 С Алгоритм получения уравнения плоскости К ы середины отрезка К ы точки, делящей отрезок на части оординат – не лежат на одной прямой 1 . 2 3 Определитель матрицы оординат . Ре ш ить систему, получить . Уравнение плоскости 1 . 2В . ычисляем определитель и получаем уравнение плоскости Угол между плоскостями 2 Уравнение плоскости A, B, C – координаты вектора нормали к плоскости x, y, z – координаты точек , принадлежащих плоскости D– , свободный член который показывает смещение плоскости относительно начала координат Расстояние от точки до плоскости Угол между прямой и плоскостью n Алгебра и теория чисел Таблица простых чисел 5 2 3 23 59 97 137 179 227 29 31 37 41 43 47 53 61 67 71 73 79 83 89 101 103 107 109 113 127 131 139 149 151 157 163 167 173 181 191 193 197 199 211 223 229 233 239 241 251 257 263 7 11 13 Таблица квадратов 17 19 269 271 277 281 283 293 307 311 Признак делимости на 2. Число делится на 2 тогда и только тогда, когда его последняя цифра чётна. Признак делимости на 3. Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Признак делимости на 4. Число делится на 4 тогда и только тогда, когда двузначное число, образованное двумя его последними цифрами (в том же порядке), делится на 4. Признак делимости на 5. Число делится на 5 тогда и только тогда, когда его последняя цифра равна 0 или 5. Признак делимости на 8. Число делится на 8 тогда и только тогда, когда трёхзначное число, образованное тремя его последними цифрами (в том же порядке), делится на 8. Признак делимости на 9. Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9. Признак делимости на 10. Число делится на 10 тогда и только тогда, когда последняя цифра равна 0. Признак делимости на 11. У данного числа найдём сумму цифр, стоящих на чётных местах, и сумму цифр, стоящих на нечётных местах. Число делится на 11 тогда и только тогда, когда разность этих сумм делится на 11 (в частности, равна нулю). Признак делимости на 12. Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4. Признак делимости на 13. Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 949 делится на 13, так как 94 + 4 ⋅ 9 = 130 делится на 13) Признак делимости на 14. Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7. Признак делимости на 15. Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5. Признак делимости на 17. Число делится на 17 тогда и только тогда, когда разность между числом его десятков и упятеренным числом единиц, кратно 17. Признак делимости на 19. Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19. Десятичная запись числа Взаимно простые числа Десятичная запись числа – это повседневная запись натуральных чисел, её можно представить в виде суммы разрядных слагаемых. Натуральные числа a и b называют взаимно простыми, если их наибольший общий делитель равен 1. Приведем пример для числа 1974: Обозначение: НОД (a; b) = 1. число тысячи сотни десятки единицы В общем же виде формула для четырехзначного числа имеет вид: Сравнение по модулю Если два целых числа и при делении на дают одинаковые остатки, то они называются сравнимыми (или равноостаточными) по модулю числа Записывается это следующим образом: «число сравнимо с по модулю » Операции со сравнениями Если , то: Другими словами, если числа a и b не имеют никаких общих делителей, кроме 1, то они – взаимно простые. Примеры пар взаимно простых чисел: 2 и 5, 13 и 16, 35 и 88 и т. д.








