НЕПРЕРЫВНОСТЬ И РАЗРЫВЫ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
1. Определение непрерывной функции. 2. Основные свойства
непрерывной функции: непрерывность алгебраических операций,
непрерывность сложной функции. 3. Односторонняя непрерывность. 4. Классификация точек разрыва
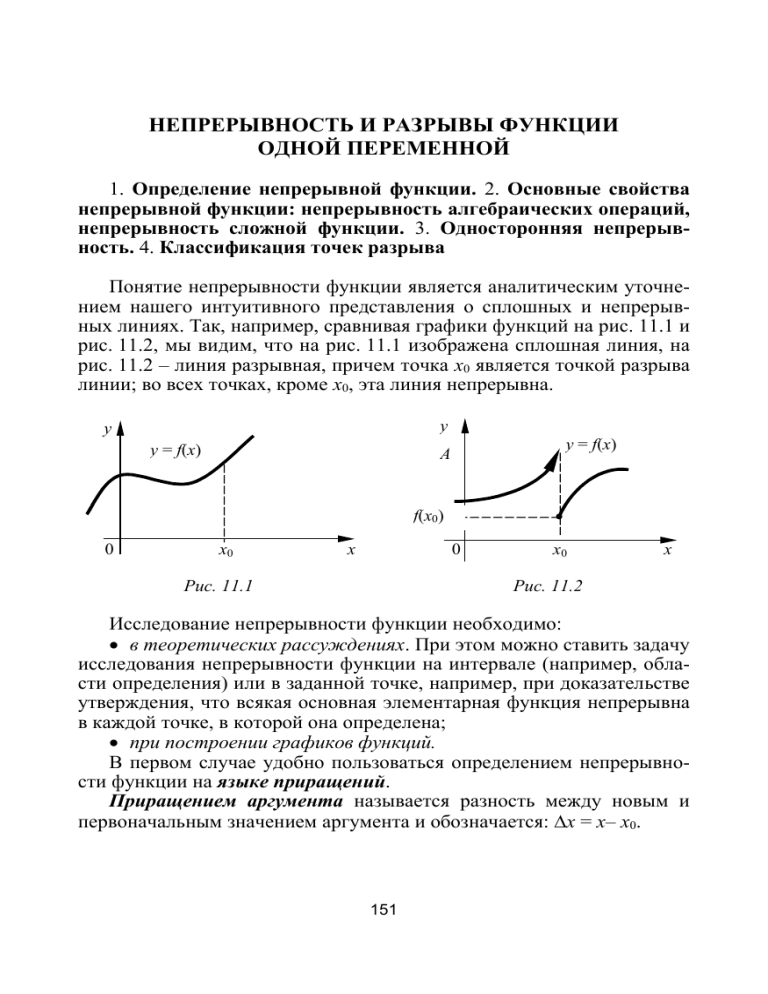
Понятие непрерывности функции является аналитическим уточнением нашего интуитивного представления о сплошных и непрерывных линиях. Так, например, сравнивая графики функций на рис. 11.1 и
рис. 11.2, мы видим, что на рис. 11.1 изображена сплошная линия, на
рис. 11.2 – линия разрывная, причем точка х0 является точкой разрыва
линии; во всех точках, кроме х0, эта линия непрерывна.
у
y
у = f(x)
у = f(x)
А
f(x0)
0
x0
х
0
Рис. 11.1
x0
х
Рис. 11.2
Исследование непрерывности функции необходимо:
в теоретических рассуждениях. При этом можно ставить задачу
исследования непрерывности функции на интервале (например, области определения) или в заданной точке, например, при доказательстве
утверждения, что всякая основная элементарная функция непрерывна
в каждой точке, в которой она определена;
при построении графиков функций.
В первом случае удобно пользоваться определением непрерывности функции на языке приращений.
Приращением аргумента называется разность между новым и
первоначальным значением аргумента и обозначается: х = х– х0.
151
Приращением функции называется разность между значением функции
в новой точке и ее значением в первоf(x)
начальной точке и обозначается:
y
y = f(x) – f(x0).
f(x0)
Функция y = f(x) называется непреx
рывной в точке х0, если в этой точке
бесконечно малому приращению ар0 x0
x
x
гумента соответствует бесконечно маРис. 11.3
лое приращение функции (рис. 11.3)
x 0 y 0.
Во втором случае, при построении графиков функции, лучше использовать определение на языке предела. Функция y = f(x) называется непрерывной в точке х0, если выполняется условие:
у
lim f ( x) f ( x0 ).
(11.1)
x x0
Анализируя определение непрерывности (11.1), мы видим, что оно
содержит в себе три условия:
1. В точке непрерывности х0 функция определена, т. е. f(x0) существует;
2. Существует конечный предел функции f(x) при х х0 : lim f ( x) ;
x x0
3. Предел функции при х х0 равен значению функции в точке х0:
lim f ( x) f ( x0 ).
x x0
Отметим, что условие 2 (существует предел функции f(x) при х х0)
означает существование пределов функции f(x) слева при х х0 – 0
и справа при х х0 + 0. Если нарушается условие непрерывности,
сформулированное на языке приращений или хотя бы одно из трех
условий, сформулированное на языке предела, тогда точка х0 называется точкой разрыва функции. Такова точка х0 на рис.11.2. Условие 1
в ней выполнено, но, как видно по графику
lim f ( x) A, lim f ( x) f ( x0 ) , но А f(x0).
x x0 0
x x0 0
152
Таким образом, при х х0 функция f(x) имеет правый и левый
пределы, но они не равны между собой. Следовательно, lim f ( x) не
x x0
существует, так как нарушено условие 2, поэтому точка х0 – точка
разрыва функции.
Классификация точек разрыва:
1. Точка х0 – точка разрыва I рода, если:
а) lim f ( x) существует
lim f ( x) lim f ( x) , но либо
x x0
xx0 0
x x0 0
функция не определена в точке х0, либо нарушено условие
lim f ( x) f ( x0 ), тогда точка х0 – точка устранимого разрыва
x x0
функции.
б) lim f ( x) не существует
x x0
lim f ( x) lim f (x) , тогда точx x0 0
x x0 0
ка х0 – точка скачка. Разность lim f ( x) – lim f ( x) определяет
x x0 0
x x0 0
величину скачка.
2. Точка х0 – точка разрыва II рода (разрыв бесконечный), если
хотя бы один из односторонних пределов не существует или равен
бесконечности.
Примеры разрывных функций и их графиков приведены в таблице.
Функция f(x) называется
непрерывной в точке х0 слева, если lim f ( x) = f(x0) (рис. 11.4);
x x0 0
непрерывной в точке х0 справа, если
lim f ( x) = f(x0) (рис. 11.5).
x x0 0
Например, функции у = [x] и у = {x}, графики которых представлены на рис. 11.6 и 11.7 соответственно, непрерывны справа в каждой
точке х = n и непрерывны во всех точках, исключая целые значения
х n.
Очевидно, условие lim f ( x) = lim f ( x) = f(x0) (т. е. непрерывx x0 0
x x0 0
ность и слева, и справа) является необходимым и достаточным для
непрерывности функции в точке х0.
Если функция непрерывна в каждой точке некоторой области (интервала, отрезка и т. п.), то она называется непрерывной в этой области.
153
Разрыв I рода
Разрыв II рода
устранимый
f ( x) =
sin x
x
скачок
бесконечный
f(x)= sign x
f(x) = e1/x
у
у
у
1
-
0
ххх.эжхз-0
Х =0DF
f ( x) =
1
0
х
x
–1
мx , x <1
f ( x) = н
о 0, x і 1
x2 - 1
x- 1
х
0
f(x) = ctg x
y
y
y
–1
0
1
–1
x
0
1
х
- /2
0
/2
1
2
Х =1DF
у
у
у
у
2
0
х0
Рис. 11.4
х
0
х0
х
1
–1
0
Рис. 11.5
1
1
2
Рис. 11.6
154
3 х
–1 0
Рис.11.7
х
Пример 11.1. Используя определение непрерывности на языке приращений, докажем, что основные элементарные функции а) y = ln x, б)
y = sin x непрерывны в области определения.
а) y = ln x, Df = {x| x > 0}. Пусть х – приращение аргумента,
найдем соответствующее приращение функции y:
x x
x
y = ln(x + х) – lnx = ln
ln 1
.
x
x
x x
Если х 0, то ln 1
0 , поэтому функция y = lnx
~
x
x
непрерывна в области определения.
б) y = sin x, Df = {x|x R}. Найдем y, если х – приращение аргумента:
y = sin (x + х) – sin x = [используем формулу sin – sin =
= 2cos
2 x x
x
= 2cos
.
sin
sin
2
2
2
2
2 x x
cos x и является функцией огра2
x
x
ниченной: |cosx| 1, a sin
~
, поэтому y 0, что дока2
2
зывает непрерывность функции y = sinx в области определения.
Если х 0, то cos
Рассматривая все основные элементарные функции, можно доказать теорему о непрерывности основных элементарных функций и
сформулировать свойства непрерывных функций.
Всякая основная элементарная функция непрерывна в каждой точке, в которой она определена.
Если функции f(x) и g(x) непрерывны в точке х0, тогда:
1) функции f(x) g(x) и f(x) g(x) непрерывны в точке х0;
2) если g(x0) 0, то функция f(x)/g(x) непрерывна в точке х0;
3) если функция u = (x) непрерывна в точке х0, f(u) непрерывна в
точке и0 = (х0), то сложная функция f((x)) непрерывна в точке х0.
155
Из рассмотренных выше теоремы и свойств следует, что всякая
элементарная функция непрерывна в каждой точке, в которой она
определена.
Последнее позволяет, например, утверждать, что функции y =
tg x
= ctg 2x + x2, y = 3–x sinx, y = ln cosx, y =
непрерывны во всех точx2
ках, где эти функции определены.
1
Пример 11.2. Для функции y 3 x 3 и двух значений аргумента
х1 = 2 и х2 = 3 (используя второе определение непрерывности):
1) установить, является ли данная функция непрерывной или разрывной для указанных значений аргумента;
2) в случае разрыва функции определить тип разрыва, найдя односторонние пределы.
3) построить схематический график функции в окрестности точки
х2 = 3.
1
x
y 3 3
1. Функция
является элементарной, определенной при
х 3: Df = {x | x (–, 3) (3, + )}. Так как x1 = 2 Df, данная
функция непрерывна при х1 = 2:
1
1
x
3
2
lim 3
3 3 31 f (2). Точка
x 2
х2 = 3 Df, поэтому функция терпит разрыв в точке х2 = 3.
2. Найдем односторонние пределы функции в точке х2 = 3.
lim
1
x
3 3
lim
1
x
3 3
x 3 0
x 3 0
1
1
1
x 3 (3 0) 3 0 , 3 0 0 .
1
1
1
x 3 (3 0) 3 0 , 3 .
y
0
3
х
Сравнив значения односторонних
пределов, мы делаем вывод: в точке х2 = 3
функция имеет разрыв II рода (рис. 11.8),
поскольку пределы не равны и один из
них равен + .
Рис. 11.8
156
З а м е ч а н и е. Если функция задана несколькими формулами,
то непрерывность каждой части исследуется отдельно и, кроме того,
исследуются точки «склейки».
Пример 11.3. Найти точки разрыва функции, исследовать их характер. В случае устранимого разрыва доопределить функцию «по
непрерывности», построить схематический график функции:
1/( x 1), x 1
х 2 1, х 2
2,
x 1
а) у 5 ,
б) y
;
x2;
x
/
2,
1
x
2
x 1, x 2
0,
x2
cos x, x 0
в) у 1 x, 0 x 1 ;
1,
x 1
1
2
г) y 2 x .
а) Функция задана на всей числовой оси. Точка «склейки» –
точка х = 2. В этой точке функция определена: f (2) = 5. Каждая из
функций: х2 – 1 (если х 2), х + 1 (х 2) является непрерывной в тех
интервалах, в которых заданы. Поэтому односторонние пределы
находим при х 2:
lim f ( x) lim ( x 2 1) 3,
x 20
x 2 0
lim f ( x) lim ( x 1) 3.
x 2 0
x 2 0
Следовательно, предел при х 2
lim f ( x) 3 ,
существует:
но
x 2
lim f ( x) f (2) , поэтому разрыв в точке
у
х = 2 является устранимым: изменив
значение функции в одной точке, а
именно положив f (2) = 3, мы получим
непрерывную функцию (рис. 11.9).
б) Точки «склейки»: х1 = 1, х2 = 2.
Причем для х 1, функция 1/(х + 1)
определена для всех х – 1, причем
1
1
lim
,
lim
, поx10 x 1
x10 x 1
5
3
x 2
157
0
2
4
–1
Рис. 11.9
х
этому точка х = – 1 является точкой разрыва II рода. В точке х = 1
1
1
lim f ( x) lim
функция определена: f (1) = 2 и
,
x 1 0
x10 x 1 2
x 1
lim f ( x) lim . Так как lim f ( x) lim f ( x) , поэтому
x 1 0
x 1 0
x10
x10 2
2
точка х = 1 – точка устранимого разрыва, можно положить f (1) = 1/2.
Рассмотрим поведение функции в
точке х = 2:
у
2
x20
1
–1
x
1 ,
x20 2
lim f ( x) lim
0
1
2
lim f ( x) lim 0 0 .
х
Рис. 11.10
x 2 0
x 2 0
Точка х = 2 является точкой скачка функции, причем величина скачка равна: lim f ( x) – lim f ( x) 1
x 2 0
x 2 0
(рис. 11.10)
Ответы: в) в х = 0 функция непрерывна; х = 1 – разрыв первого
рода, скачок; г) функция четная, х = 0 – точка разрыва второго рода:
у + при х 0.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
11.1. Докажите, что функции а) y = x2 , б) y = ex непрерывны в области определения.
11.2. При каком выборе параметров, входящих в определение f(x),
эта функция f(x) будет непрерывной?
x 1
x 1,
а) f ( x) 2
;
ax 2, x 1
x / 2
ax 1,
б) f ( x)
.
b sin x, x / 2
158
11.3. Найдите точки разрыва функции, исследуйте их характер
(в случае устранимого разрыва доопределите функцию) и постройте
схематический график функции в окрестности точки разрыва:
1
а) f(x) = 1 – x sin ;
x
x
e ,
г) f ( x) x 1,
x 5,
б) f ( x)
x2
x2
x0
0 x 3.
x3
159
;
в)
1
1
f ( x) 2 x ;








